
- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.


2.5: The Riemann Hypothesis
- Last updated
- Save as PDF
- Page ID 60304

- J. J. P. Veerman
- Portland State University via PDXOpen: Open Educational Resources
Definition 2.19
The Riemann zeta function \(\zeta(z)\) is a complex function defined as follows on \(\{z \in \mathbb{C} | \mbox{Re}z > 1\}\)
\[\zeta (z) = \sum_{n=1}^{\infty} n^{-z} \nonumber\]
On other values of \(z \in \mathbb{C}\) it is defined by the analytic continuation of this function (except at \(z = 1\) where it has a simple pole).
Analytic continuation is akin to replacing \(e^x\) where \(x\) is real by \(e^z\) where \(z\) is complex. Another example is the series \(\sum_{j=0}^{\infty} z^j\). This series diverges for \(|z| > 1\). But as an analytic function, it can be replaced by \((1-z)^{-1}\) on all of \(\mathbb{C}\) except at the pole \(z = 1\) where it diverges.
Recall that an analytic function is a function that is differentiable. Equivalently, it is a function that is locally given by a convergent power series. If \(f\) and \(g\) are two analytic continuations to a region \(U\) of a function \(h\) given on a region \(V \subset U\), then the difference \(f-g\) is zero on some \(U\) and therefore all its power expansions are zero and so it must be zero on the the entire region. Hence, analytic conjugations are unique. That is the reason they are meaningful. For more details, see for example [ 4 , 14 ].
It is customary to denote the argument of the zeta function by \(s\). We will do so from here on out. Note that \(|n-s| = n-\mbox{Re} s\), and so for \(\mbox{Re} s > 1\) the series is absolutely convergent. At this point, the student should remember – or look up in [ 23 ] – the fact that absolutely convergent series can be rearranged arbitrarily without changing the sum. This leads to the following proposition.
Proposition 2.20
For \(\mbox{Re} s > 1\) we have
\[\sum_{n=1}^{\infty} n-s = \prod_{p prime} (1-p^{-s})^{-1} \nonumber\]
There are two common proofs of this formula. It is worth presenting both.
The first proof uses the Fundamental Theorem of Arithmetic. First, we recall that use geometric series
\[(1-p^{-s})^{-1} = \sum_{k=0}^{\infty} p^{-ks} \nonumber\]
to rewrite the right hand of the Euler product. This gives
\[\prod_{p prime} (1-p^{-s})^{-1} = (\sum_{k_1 = 0}^{\infty} p_{1}^{-k_{1}s}) (\sum_{k_2 = 0}^{\infty} p_{2}^{-k_{2}s}) (\sum_{k_3 = 0}^{\infty} p_{3}^{-k_{3}s}) \nonumber\]
Re-arranging terms yields
\[\dots = (p_{1}^{k_{1}}p_{2}^{k_{2}}p_{3}^{k_{3}} \dots)^{-s} \nonumber\]
By the Fundamental Theorem of Arithmetic, the expression \((p_{1}^{k_{1}}p_{2}^{k_{2}}p_{3}^{k_{3}} \dots)\) runs through all positive integers exactly once. Thus upon re-arranging again we obtain the left hand of Euler’s formula.
The second proof, the one that Euler used, employs a sieve method. This time, we start with the left hand of the Euler product. If we multiply \(\zeta\) by \(2^{-s}\), we get back precisely the terms with \(n\) even. So
\[(1-2^{-s}) \zeta(s) = 1+3^{-s}+5^{-s}+\cdots = \sum_{2 \nmid n} n^{-s} \nonumber\]
Subsequently we multiply this expression by \((1-3^{-s})\). This has the effect of removing the terms that remain where \(n\) is a multiple of \(3\). It follows that eventually
\[(1-p_{l}^{-s}) \dots (1-p_{1}^{-s}) \zeta (s) = \sum_{p_{1} \nmid n, \cdots p_{l} \nmid n} n^{-s} \nonumber\]
The argument used in Eratosthenes sieve (Section 1.1) now serves to show that in the right hand side of the last equation all terms other than \(1\) disappear as l tends to infinity. Therefore, the left hand tends to 1, which implies the proposition.
The most important theorem concerning primes is probably the following (without proof).
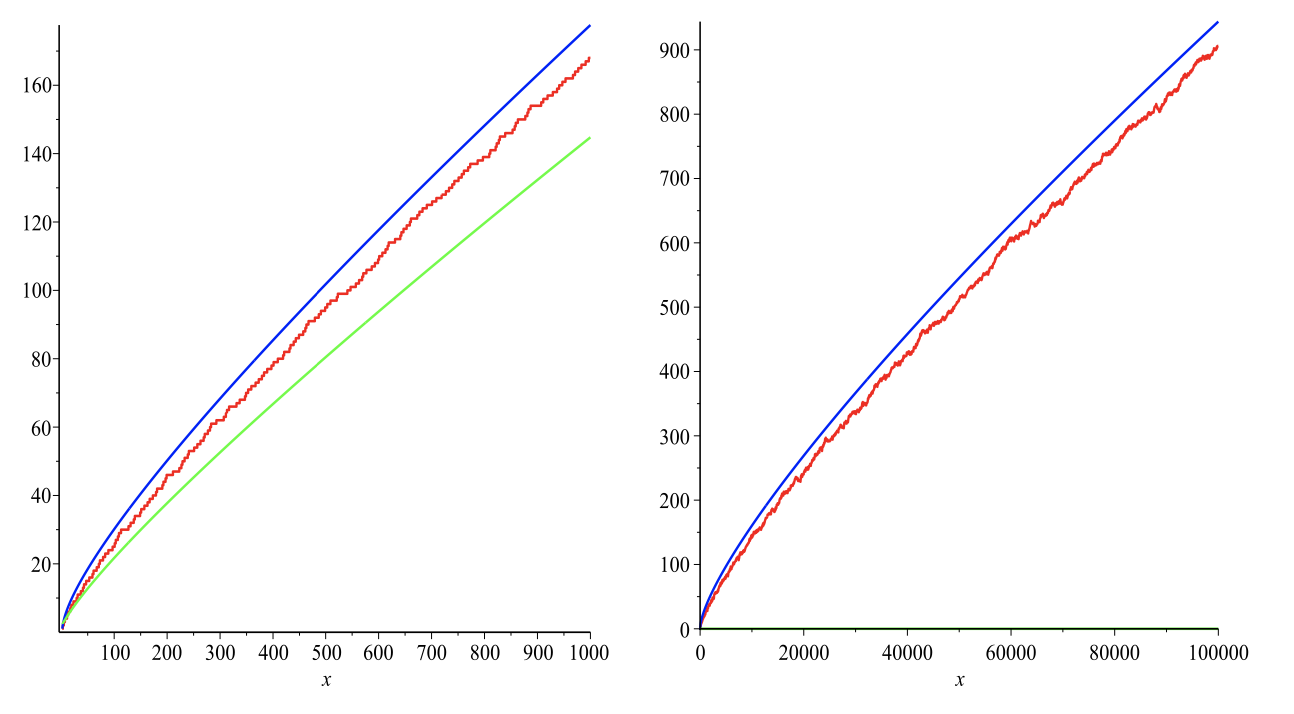
Figure 3. On the left, the function \(\int_{2}^{x} \mbox{ln} t dt\) in blue, \(\pi (x)\) in red, and \(x/ \mbox{ln}x\) in green. On the right, we have \(\int_{2}^{x} \mbox{ln} t dt - x/\mbox{ln} x\) in blue, \(\pi (x)- x/\mbox{ln} x\) in red.
Theorem 2.21 (Prime Number Theorem)
Let \(\pi (x)\) denote the prime counting function, that is: the number of primes less than or equal to \(x > 2\).
- \(\lim_{x \rightarrow \infty} \frac{\pi (x)}{(x/\mbox{ln} x)} = 1\) and
- \(\lim_{x \rightarrow \infty} \frac{\pi (x)}{\int_{2}^{x} \mbox{ln} t dt} = 1\)
where \(\mbox{ln}\) is the natural logarithm.
The first estimate is the easier one to prove, the second is the more accurate one. In Figure 3 on the left, we plotted, for \(x \in [2,1000]\), from top to bottom the functions \(\int_{2}^{x} \mbox{ln} t dt\) in blue, \(\pi (x)\) in red, and \(x/\mbox{ln} x\). In the right hand figure, we augment the domain to \(x \in [2, 100000]\). and plot the difference of these functions with \(x/\mbox{ln} x\). It now becomes clear that \(\int_{2}^{x} \mbox{ln} t dt\) is indeed a much better approximation of \(\pi (x)\). From this figure one may be tempted to conclude that \(\int_{2}^{x} \mbox{ln} t dt - \pi (x)\) is always greater than or equal to zero. This, however, is false. It is known that there are infinitely many n for which \(\int_{2}^{x} \mbox{ln} t dt - \pi (x) < 0\). The first such \(n\) is called the Skewes number. Not much is known about this number, except that it is less than 10317.
Perhaps the most important open problem in all of mathematics is the following. It concerns the analytic continuation of \(\zeta (s)\) given above.
Conjecture 2.22 (Riemann Hypothesis)
All non-real zeros of \(\zeta (s)\) lie on the line \(\mbox{Re} s = \frac{1}{2}\)
In his only paper on number theory [ 20 ], Riemann realized that the hypothesis enabled him to describe detailed properties of the distribution of primes in terms of of the location of the non-real zero of \(\zeta ( s )\). This completely unexpected connection between so disparate fields – analytic functions and primes in \(\mathbb{N}-\)spoke to the imagination and led to an enormous interest in the subject. In further research, it has been shown that the hypothesis is also related to other areas of mathematics, such as, for example, the spacings between eigenvalues of random Hermitian matrices [ 2 ], and even physics [ 5 , 6 ].
Riemann Hypothesis
A more general statement known as the generalized Riemann hypothesis conjectures that neither the Riemann zeta function nor any Dirichlet L-series has a zero with real part larger than 1/2.
Legend holds that the copy of Riemann's collected works found in Hurwitz's library after his death would automatically fall open to the page on which the Riemann hypothesis was stated (Edwards 2001, p. ix).
Proof of the Riemann hypothesis is number 8 of Hilbert's problems and number 1 of Smale's problems .
In 2000, the Clay Mathematics Institute ( http://www.claymath.org/ ) offered a $1 million prize ( http://www.claymath.org/millennium/Rules_etc/ ) for proof of the Riemann hypothesis. Interestingly, disproof of the Riemann hypothesis (e.g., by using a computer to actually find a zero off the critical line ), does not earn the $1 million award.
The Riemann hypothesis is equivalent to the statement that all the zeros of the Dirichlet eta function (a.k.a. the alternating zeta function)
By modifying a criterion of Robin (1984), Lagarias (2000) showed that the Riemann hypothesis is equivalent to the statement that
There is also a finite analog of the Riemann hypothesis concerning the location of zeros for function fields defined by equations such as
According to Fields medalist Enrico Bombieri, "The failure of the Riemann hypothesis would create havoc in the distribution of prime numbers" (Havil 2003, p. 205).
In Ron Howard's 2001 film A Beautiful Mind , John Nash (played by Russell Crowe) is hindered in his attempts to solve the Riemann hypothesis by the medication he is taking to treat his schizophrenia.
In the Season 1 episode " Prime Suspect " (2005) of the television crime drama NUMB3RS , math genius Charlie Eppes realizes that character Ethan's daughter has been kidnapped because he is close to solving the Riemann hypothesis, which allegedly would allow the perpetrators to break essentially all internet security.
In the novel Life After Genius (Jacoby 2008), the main character Theodore "Mead" Fegley (who is only 18 and a college senior) tries to prove the Riemann Hypothesis for his senior year research project. He also uses a Cray Supercomputer to calculate several billion zeroes of the Riemann zeta function. In several dream sequences within the book, Mead has conversations with Bernhard Riemann about the problem and mathematics in general.
Portions of this entry contributed by Len Goodman
Explore with Wolfram|Alpha
More things to try:
- riemann hypothesis
- Champernowne constant
Cite this as:
Goodman, Len and Weisstein, Eric W. "Riemann Hypothesis." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/RiemannHypothesis.html
Subject classifications
Search Clay Mathematics Institute
Home — Millennium Problems — Riemann Hypothesis
Riemann Hypothesis
The prime number theorem determines the average distribution of the primes. The Riemann hypothesis tells us about the deviation from the average. Formulated in Riemann’s 1859 paper, it asserts that all the ‘non-obvious’ zeros of the zeta function are complex numbers with real part 1/2.
Some numbers have the special property that they cannot be expressed as the product of two smaller numbers, e.g., 2, 3, 5, 7, etc. Such numbers are called prime numbers, and they play an important role, both in pure mathematics and its applications. The distribution of such prime numbers among all natural numbers does not follow any regular pattern. However, the German mathematician G.F.B. Riemann (1826 – 1866) observed that the frequency of prime numbers is very closely related to the behavior of an elaborate function ζ(s) = 1 + 1/2 s + 1/3 s + 1/4 s + … called the Riemann Zeta function . The Riemann hypothesis asserts that all interesting solutions of the equation ζ(s) = 0 lie on a certain vertical straight line.
This has been checked for the first 10,000,000,000,000 solutions. A proof that it is true for every interesting solution would shed light on many of the mysteries surrounding the distribution of prime numbers.
Related videos

John Tate (Austin)
The millennium prize problems I
24 May 2000
Timothy Gowers (Cambridge)
The importance of mathematics
25 May 2000
Further resources

Jeffery Vaaler (Austin)
Riemann hypothesis
02 May 2001
Official Problem Description by E. Bombieri
Riemann's 1859 Manuscript
Rules for the Millennium Prize

Sketches of Physics pp 191–263 Cite as
A Primer on the Riemann Hypothesis
- Michael E. N. Tschaffon 21 ,
- Iva Tkáčová 22 ,
- Helmut Maier 23 &
- Wolfgang P. Schleich 24 , 25
- First Online: 15 September 2023
385 Accesses
Part of the book series: Lecture Notes in Physics ((LNP,volume 1000))
We provide an introduction for physicists into the Riemann Hypothesis. For this purpose, we first introduce, and then compare and contrast the Riemann function and the Dirichlet L-functions, with the Titchmarsh counterexample. Whereas the first two classes of functions are expected to satisfy the Riemann Hypothesis, the Titchmarsh counterexample is known to violate it. Throughout our article we employ elementary mathematical techniques known to every physicist. Needless to say, we do not verify the Riemann Hypothesis but suggest heuristic arguments in favor of it. We also build a bridge to quantum mechanics by interpreting the Dirichlet series central to this field as a superposition of probability amplitudes leading us to an unusual potential with a logarithmic energy spectrum opening the possibility of factoring numbers.
This is a preview of subscription content, log in via an institution .
Buying options
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
M. Abramowitz, I.A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables , vol. 55 (US Government Printing Office, Washington, 1948)
MATH Google Scholar
C.M. Bender, D.C. Brody, M.P. Müller, Hamiltonian for the zeros of the Riemann zeta function. Phys. Rev. Lett. 118 (13), 130201 (2017)
Google Scholar
M.V. Berry, J.P. Keating, A new asymptotic representation for \(\zeta \) ( \(1/2\) + it) and quantum spectral determinants. Proc. R. Soc. Lond. A Math. Phys. Sci. 437 (1899), 151–173 (1992)
M.V. Berry, J.P. Keating, The Riemann zeros and eigenvalue asymptotics. SIAM Rev. 41 (2), 236–266 (1999)
Article ADS MathSciNet MATH Google Scholar
P. Borwein, S. Choi, B. Rooney, A. Weirathmueller, The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike . CMS Books in Mathematics Series (Springer, New York, 2008)
D. Cassettari, G. Mussardo, A. Trombettoni, Holographic realization of the prime number quantum potential. PNAS Nexus 2 (1), 1–9 (2022)
M. Du Sautoy, The Music of the Primes (Harper Collins, New York, 2003)
H.M. Edwards, Riemann’s Zeta Function (Academic, New York, 1974)
W.J. Ellison, F. Ellison, Prime Numbers (Wiley, New York, 1985)
C. Feiler, W.P. Schleich, Entanglement and analytical continuation: an intimate relation told by the Riemann zeta function. New J. Phys. 15 (6), 063009 (2013)
C. Feiler, W.P. Schleich, Dirichlet series as interfering probability amplitudes for quantum measurements. New J. Phys. 17 (6), 063040 (2015)
G. Freiling, V.A. Yurko, Inverse Sturm-Liouville Problems and Their Applications (NOVA Science Publishers, Huntington, 2001)
F. Gleisberg, W.P. Schleich, Factorization with a logarithmic energy spectrum of a central potential. Acta Phys. Pol. A 143 , S112 (2023)
Article ADS Google Scholar
F. Gleisberg, R. Mack, K. Vogel, W.P. Schleich, Factorization with a logarithmic energy spectrum. New J. Phys. 15 (2), 023037 (2013)
F. Gleisberg, M. Volpp, W.P. Schleich, Factorization with a logarithmic energy spectrum of a two-dimensional potential. Phys. Lett. A 379 (40–41), 2556–2560 (2015)
Article ADS MATH Google Scholar
F. Gleisberg, F. Di Pumpo, G. Wolff, W.P. Schleich, Prime factorization of arbitrary integers with a logarithmic energy spectrum. J. Phys. B 51 (3), 035009 (2018)
I.S. Gradstein, I.M. Ryzhik, Tables of Integrals, Sums, Series and Products (Academic Press, New York, 1994)
R. Grimm, M. Weidemüller, Y.B. Ovchinnikov, Optical dipole traps for neutral atoms. Adv. Atom. Mol. Opt. Phys. 42 , 95–170 (2000)
D. Hilbert, Mathematische Probleme. Arch. Math. Phys. 1 , 44–63 and 213–237 (1901). English translation by Mary Newson. Bull. Am. Math. Soc. 8 , 437–479 (1901)
H. Iwaniec, E. Kowalski, Analytic Number Theory (American Mathematical Society, Providence, 2003)
B.M. Levitan, Inverse Sturm-Liouville Problems (VNK Science Press, Utrecht, 1987)
Book MATH Google Scholar
R. Mack, J.P. Dahl, H. Moya-Cessa, W.T. Strunz, R. Walser, W.P. Schleich, Riemann \(\zeta \) function from wave packet dynamics. Phys. Rev. A 82 (3), 032119 (2010)
G.E. Mitchell, A. Richter, H.A. Weidenmüller, Random matrices and chaos in nuclear physics: nuclear reactions. Rev. Mod. Phys. 82 (4), 2845 (2010)
J.W. Neuberger, C. Feiler, H. Maier, W.P. Schleich, Newton flow of the Riemann zeta function: separatrices control the appearance of zeros. New J. Phys. 16 , 103023 (2014)
J.W. Neuberger, C. Feiler, H. Maier, W.P. Schleich, The Riemann hypothesis illuminated by the Newton flow of \(\zeta \) . Phys. Scr. 90 , 108015 (2015)
B Riemann, Monatsberichte der Berliner Akademie (1859). Transcribed German version and English translation by D. R. Wilkins see http://www.claymath.org/publications/riemanns-1859-manuscript
D. Rockmore, Stalking the Riemann Hypothesis: The Quest to Find the Hidden Law of Prime Numbers (Pantheon Books, New York, 2005)
K. Sabbagh, The Riemann Hypothesis: The Greatest Unsolved Problem in Mathematics (Farar, Straus and Giroux, New York, 2003)
W.P. Schleich, Quantum Optics in Phase Space (VCH-Wiley, Weinheim, 2001)
W.P. Schleich, I. Bezdĕková, M.B. Kim, P.C. Abbott, H. Maier, H.L. Montgomery, J.W. Neuberger, Equivalent formulations of the Riemann Hypothesis based on lines of constant phase. Phys. Scr. 93 , 065201 (2018)
D. Schumayer, D.A.W. Hutchinson, Physics of the Riemann hypothesis. Rev. Mod. Phys. 83 (2), 307 (2011)
C.L. Siegel, Über Riemanns Nachlaß zur analytischen Zahlentheorie. Quellen Stud. Geschichte Math. Astron. Phys. Abt. B: Stad 2 (1932), p. 45
R. Spira, Some zeros of the Titchmarsh counterexample. Math. Comput. 63 , 747–748 (1994)
E.C. Titchmarsh, The Theory of the Riemann Zeta-Function (Clarendon Press, Oxford, 1967)
J. Twamley, G.J. Milburn, The quantum Mellin transform. New J. Phys. 8 (12), 328 (2006)
F. Ullinger, M. Zimmermann, W.P. Schleich, The logarithmic phase singularity in the inverted harmonic oscillator. AVS Quantum Sci. 4 (2), 024402 (2022)
J.A. Wheeler, in Studies in Mathematical Physics: Essays in Honor of Valentine Bargmann . ed. by E.H. Lieb, B. Simon, A.S. Wightman (Princeton University Press, Princeton, 1976)
E.T. Whittaker, G.N. Watson, A Course of Modern Analysis (Cambridge University Press, Cambridge, 1996)
M. Wolf, Will a physicist prove the Riemann Hypothesis? Rep. Prog. Phys. 83 (3), 036001 (2020)
Download references
Acknowledgements
We thank P. C. Abbott, M. B. Kim, H. L. Montgomery, J. W. Neuberger, M. Zimmermann for many fruitful discussions, E. P. Glasbrenner for technical assistance and J. Pohl for her help with the scans of Riemann’s article. Moreover, we are most grateful to the Niedersächsische Staats- und Universitätsbibliothek and, in particular, R. B. Röper for allowing us to present excerpts of Riemann’s original manuscript. W. P. S. is also grateful to Texas A & M University for a Faculty Fellowship at the Hagler Institute for Advanced Study at Texas A& M University and to Texas A& M AgriLife for the support of this work. The research of the IQST is financially supported by the Ministry of Science, Research and Arts Baden-Württemberg. I. B. is grateful for the financial support from the Technical University of Ostrava, Grant No. SP2018/44.
Author information
Authors and affiliations.
Institut für Quantenphysik and Center for Integrated Quantum Science and Technology (IQST), Universität Ulm, Ulm, Germany
Michael E. N. Tschaffon
Department of Physics, Faculty of Electrical Engineering and Computer Science, VSB-Technical University of Ostrava, Ostrava, Poruba, Czech Republic
Iva Tkáčová
Institut für Reine Mathematik, Universität Ulm, Ulm, Germany
Helmut Maier
Wolfgang P. Schleich
Hagler Institute for Advanced Study, Institute for Quantum Science and Engineering (IQSE), and Texas A&M AgriLife Research, Texas A&M University, College Station, TX, USA
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Michael E. N. Tschaffon .
Editor information
Editors and affiliations.
Department of Physics “E.R.Caianiello”, University of Salerno, Fisciano, Italy
Roberta Citro
Quantum Optics Theory, Institute of Photonic Sciences, Castelldefels (Barcelona), Spain
Maciej Lewenstein
Theory Department, Max Planck Institute for the Structure and Dynamics of Matter, Hamburg, Germany
Angel Rubio
Institute of Quantum Physics, University of Ulm, Ulm, Germany
Physics Department, University of Michigan–Ann Arbor, Ann Arbor, MI, USA
James D. Wells
CSPAR & SPA, University of Alabama in Huntsville, Huntsville, AL, USA
Gary P. Zank
Appendix 1: Functional Equation of Jacobi Theta Function
In this Appendix we briefly rederive the functional equation, Eq. ( 26 ), of the Jacobi theta function
defined by Eq. ( 21 ), in order to bring out most clearly the origin of the difference to the corresponding relation, Eq. ( 155 ), for the generalized Jacobi theta function given by Eq. ( 154 ).
Since the summation index n appears in \(\omega \) as a square, we can immediately include negative values of n together with a factor of \(1/2\) . However, the term corresponding to \(n=0\) is unity. Thus, we have to subtract this contribution, and arrive at the representation
of \(\omega \) .
Next we employ the Poisson summation formula
where \(b=b(\nu )\) is a continuous extension of the discrete coefficients \(b_n\) . We emphasize that the specific form of the extension is of no consequence as long as \(b(n)\equiv b_n\) .
Indeed, this fact is a result of the identity
which is at the very heart of the Poisson summation formula.
For the choice
and with the help of the integral relation
we arrive at the identity
which leads us with the representation, Eq. ( 195 ), of \(\omega \) to
that is, the familiar functional equation
We emphasize that the second term in Eq. ( 202 ), which is independent of \(\omega \) , is a consequence of the absence of the term \(n=0\) in the definition, Eq. ( 194 ), of the Jacobi theta function \(\omega \) leading to the subtraction of unity in Eq. ( 195 ).
Appendix 2: Equivalent Condition for Non-trivial Zeros
In Sect. 2.4 we have derived the condition, Eq. ( 39 ) , for a zero on the critical line given by the identity of an integral
containing an oscillatory integrand with a Lorentzian. We devote this appendix to the derivation of an alternative but equivalent formulation by casting the integral into a different form.
In particular, we analyze the asymptotic behavior of J . For this purpose, we first derive an exact alternative expression for J , and then consider the limit \(\tau \rightarrow \infty \) .
We start by introducing in J the new integration variable \(y\equiv (1/2)\ln x\) , or \(x=\exp (2y)\) , which with the identity \(\mathrm {d}y=\mathrm {d}x/(2x)\) leads us to the form
Next, we obtain by integration by parts the equivalent representation
where we have used the fact that the boundary terms vanish, and find performing the differentiation
Finally, we introduce the new integration variable \(\theta \equiv \tau y\) , and arrive at the expression
When we recall from Eq. ( 21 ) the definition
of \(\omega \) , the differentiation yields the explicit formula
which decays for increasing \(\tau \) as \(1/ \tau ^2\) which is identical to the decrease of the Lorentzian on the right-hand side of Eq. ( 39 ).
When we now compare this representation of J to the initial one, Eq. ( 203 ), we find, apart from the decay with \(1/\tau ^2\) , three distinct features: (i) The oscillatory function in the integral is independent of \(\tau \) . (ii) We have a double-exponential decay, but (iii) this rapid decay only sets in for integration variables \(\theta > \tau /2\) .
Hence, the expression, Eq. ( 209 ), for J shows that the main contribution to this integral results from the decays characterized by the summation index n that are fast compared to the oscillation period, in complete agreement with the discussion of Sect. 2.4 .
Appendix 3: Exponential Product
In this appendix we cast the product
where q is an integer and \(\kappa =0,1\) , into an exponential form, which allows us to derive in a straight-forward way an asymptotic limit of \(\lambda \) . This term is not only a factor in the definition, Eq. ( 151 ), of the Dirichlet L-function \(\Lambda \) but also appears in the Riemann function \(\xi \) , defined by Eq. ( 40 ) for the special case \(q=1\) and \(\kappa =0\) .
We first derive a general expression for \(\lambda \) and then perform the asymptotic limit. Finally, we address the special case of the Riemann function.
1.1 General Expression
We start from the definition, Eq. ( 210 ), of \(\lambda \) in the exponential form
and recall the representation [ 17 ]
of the logarithm of the Gamma function with the remainder
which leads us for the argument \((s+\kappa )/2\) to the expression
Here we have introduced the abbreviation
and \(\bar {R}\) is defined by Eq. ( 213 ).
1.2 Asymptotic Limit
Next we consider the limit \(s \rightarrow \infty \) . In this case we find with the help of the expansion
the relation
Moreover, the generating function [ 1 ]
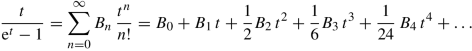
of the Bernoulli numbers \(B_n\) with
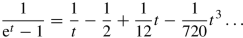
allows us to expand the remainder \(\bar {R}\) given by Eq. ( 213 ) into inverse powers of s with the leading contribution
Hence, we arrive in the lowest order of \(1/s\) at the asymptotic expression
for \(\mathcal {R}\) , which apart from the constant term decays as \(1/s\) .
1.3 Special Case: Riemann Function
Finally, we discuss the example \(q=1\) and \(\kappa =0\) corresponding to the Riemann function \(\xi \) . In this case, Eq. ( 214 ) reduces to
where \(\mathcal {R}\) given by Eq. ( 215 ) simplifies to
With the help of the asymptotic limit Eq. ( 221 ), we find the expression
for the remainder, which together with Eq. ( 224 ) is consistent with Eq. ( 222 ) for \(\kappa =0\) .
Appendix 4: Lines of Constant Height and Constant Phase
In Sect. 3.6.3 we have derived an asymptotic expression for \(\xi \) which arises solely from the product \((\wp /2)\pi ^{-s/2}\Gamma \left (s/2\right )\) since we have made the approximation \(\zeta =1\) . This formula is in terms of the complex variable s .
In this appendix, we first cast this expression in terms of amplitude and phase, and then consider two special cases. We conclude by verifying these approximations using the Cauchy-Riemann differential equations in amplitude and phase discussed in the Chapter “Insights into Complex Functions” of this volume.
1.1 Decomposition in Amplitude and Phase
We start by decomposing the approximation
of \(\alpha _{\xi }\) into its real and imaginary parts \(\Sigma \) and \(\Phi \) , that is,
determining the absolute value
and the phase \(\Phi \) of \(\xi \) . Here, we first derive general expressions for \(\Sigma \) and \(\Phi \) , and then consider the two extreme limits \(1<\sigma \ll \tau \) and \(0\leq \tau \ll \sigma \) .
With the identity
leading us to
we find the explicit expressions
We emphasize that the decomposition, Eq. ( 227 ), of the approximation, Eq. ( 226 ), of \(\alpha _{\xi }\) into \(\Sigma \) and \(\Phi \) given by Eqs. ( 231 ) and ( 232 ) is exact.
1.2 Special Limits
In order to gain insight into the dependence of \(\Sigma \) and \(\Phi \) on \(\sigma \) and \(\tau \) , we now consider two extreme limits, and derive approximate but analytic expressions for \(\Sigma \) and \(\Phi \) .
1.2.1 At the Center of the Complex Plane
We start with the case of \(1<\sigma \ll \tau \) , and arrive with the help of the approximations
at the expressions
In this limit, the lines \(\tau _{\Phi } = \tau _{\Phi }(\sigma )\) of constant phase \(\Phi \) satisfy an interesting symmetry relation. Indeed, for a given value \(\tau \) the lines of constant phase corresponding to \(\Phi \) and \(\Phi +\pi \) are separated in their values of \(\sigma \) and \(\sigma ^{\prime }\) by 4. This property follows from Eq. ( 237 ) which for \(\Phi +\pi \) reads
and a comparison with Eq. ( 237 ) immediately yields the connection
and thus the identity
Next, we derive an explicit expression for \(\tau _{\Phi }\) . Unfortunately, Eq. ( 237 ) is a transcendental equation, that is, the Lambert equation, and cannot be solved directly. However, in the limit of large \(\tau \) we obtain an approximate expression for \(\tau _{\Phi }\) by iteration.
For this purpose, we first cast Eq. ( 237 ) into the form
and replace \(\tau _{\Phi }\) in the slowly varying logarithm by the right-hand side leading us to the formula
We conclude by noting that this expression obviously also satisfies the periodicity property, Eq. ( 240 ).

1.2.2 At the Right Edge of the Complex Plane
Next we consider the case \(0\leq \tau \ll \sigma \) and arrive with
In this limit \(\Sigma \) , and thus \(|\xi |\) grows exponentially with \(\sigma \ln (\sigma /2\pi )\) for increasing \(\sigma \) , but decays like a Gaussian due to the term \(-\tau ^2/(4\sigma )\) for \(\tau \) increasing from zero. Moreover, \(\Phi \) increases linearly with \(\tau \) with a rate mainly given by \(\ln (\sigma /2\pi )\) .
According to Eq. ( 247 ), in this asymptotic limit the lines \(\tau _{\Phi } = \tau _{\Phi }(\sigma )\) of constant phase \(\Phi \) read
and decay with a rate, that is, inversely proportional to \(\ln (\sigma /(2\pi ))\) . In particular, \(\tau = 0\) , that is, the real axis, corresponds to the phase \(\Phi = 0\) , and all phase lines approach it as \(\sigma \rightarrow \infty \) .
In the last step of Eq. ( 248 ), we have neglected the correction term \(3/\sigma \) since in obtaining the general expression, Eq. ( 226 ), of \(\alpha _{\xi }\) we have already neglected terms of the order \(1/s\) .
1.3 Cauchy-Riemann Differential Equations
Next we probe the consistency of our approximations, Eqs. ( 236 ) and ( 246 ), as well as Eqs. ( 237 ) and ( 247 ) for the amplitude \(\Sigma \) as well as the phase \(\Phi \) of the exponential representation
of \(\xi \) by applying the Cauchy-Riemann differential equations
discussed in the Chapter “Insights into Complex Functions” of this volume.
We start with the asymptotic expressions
obtained in the previous section for \(1<\sigma \ll \tau \) .
Indeed, by direct differentiation we find
in complete agreement with the Cauchy-Riemann differential equation, Eq. ( 250 ).
Moreover, we also obtain the result
which is consistent with the expression
that is, with Eq. ( 256 ) when we neglect the terms proportional to \(1/\tau \) . Indeed, in the derivation of the expression, Eq. ( 253 ) for \(\Phi \) we have already neglected contributions of this order.
Next, we address the approximations
valid for \(0\leq \tau \ll \sigma \) , and find immediately
where in the last step we have neglected the term \((\tau /\sigma )^2\ll 1\) . Hence, we have verified the Cauchy-Riemann differential equation, Eq. ( 250 ).
Moreover, we obtain from Eq. ( 258 ) the relation
and Eq. ( 259 ) yields
Hence, we satisfy the Cauchy-Riemann differential equation, Eq. ( 251 ), in the approximation \(\sigma \ll 1\) .
Appendix 5: Special Examples of Normalized Gauss Sums
In Sect. 5 we have shown that the normalized Gauss sum
is given by a phase factor whose phase \(\beta \) is determined by the Dirichlet character \(\chi \) . We now illustrate this result by evaluating the normalized Gauss sum of three different characters.
For this purpose, we first consider the normalized Gauss sums associated with the Dirichlet characters forming the Titchmarsh counterexample. In these examples, the phase is non-vanishing. We then calculate the normalized Gauss sum of a character where the phase does vanish.
1.1 Non-vanishing Phase
We start by evaluating the Gauss sums \(G_1\) and \(G_2\) corresponding to the characters \(\chi _1\) and \(\chi _2\) defined \(\mathrm {mod}\;5\) with the values
and demonstrate that they are phase factors, in complete accordance with Eq. ( 143 ). Since \(\chi _1\) and \(\chi _2\) are the complex conjugate of each other, the corresponding phases must satisfy the symmetry relation, Eq. ( 144 ).
We start by noting that in both characters \(q=5\) . Thus, we find with \(\chi _j(-1) = \chi _j(4-5) = \chi _j(4)\) for \(j=1,2\) , and the definitions Eqs. ( 264 ) and ( 265 ) of \(\chi _1\) and \(\chi _2\) , the result \(\chi _1(-1)=\chi _2(-1)=-1\) which yields with Eq. ( 127 ) the parameter
Hence, the Gauss sum \(G_1\) , corresponding to the character \(\chi _1\) reads
and takes with the help of the definition, Eq. ( 264 ), of \(\chi _1\) , the form
where in the last step we have taken advantage of the \(2\pi \) -periodicity of the Fourier factors.
In terms of trigonometric functions, we find
and the values
finally yield the expression
for the Gauss sum \(G_1\) as a phase factor where
We conclude by briefly addressing the Gauss sum
associated with
Indeed, this symmetry enforces that in \(G_2\) the second and the third term in Eq. ( 267 ) change their signs, but everything else remains the same.
As a result, we arrive at a negative rather than a positive phase, that is,
We emphasize that the sign change in the phase due to the transition from \(G_1\) to \(G_2,\) Eqs. ( 269 ) and ( 272 ), can also be viewed as a consequence of the connection, Eq. ( 271 ), between \(\chi _1\) and \(\chi _2\) , and the symmetry relation, Eq. ( 144 ).
1.2 Vanishing Phase
We conclude by discussing an example of a character \(\chi \) where the phase of the corresponding normalized Gauss sum vanishes. For this purpose, we consider the real-valued character
with an integer k .
Since \(\chi \) is \(\mathrm {mod} \; 4\) we find \(q=4\) and with \(\chi (-1) = \chi (3-4)=\chi (3) = -1\) following from the definition, Eq. ( 273 ), of \(\chi \) , we obtain with the help of Eq. ( 127 ) the value \(\kappa =1.\)
Hence, the normalized Gauss sum, Eq. ( 263 ), takes the form
which with the definition, Eq. ( 273 ), of the character \(\chi \) reads
For the character \(\chi \) , given by Eq. ( 273 ), we obtain indeed a vanishing phase \(\beta \) for G .
Appendix 6: Functional Equation of Generalized Jacobi Theta Function
Since the functional equation
of the generalized Jacobi theta function plays a crucial role in the analytic continuation of the Dirichlet L-functions, as discussed in Sect. 6 , we devote the present Appendix to a brief summary of the derivation. This analysis also brings out most clearly the origins of the Gauss sum G and the character in its complex conjugate form.
Here we proceed in two steps: (i) We first show that due to the appearance of the character \(\chi \) and the term \(n^\kappa \) in the definition of \(\omega \) we can express the summation in \(\omega \) from unity to infinity, into one from minus infinity to plus infinity by merely introducing a factor \(1/2\) . This additional symmetry is the deeper reason for the simplicity of the functional equation, Eq. ( 275 ), of the Jacobi theta function for \(\Lambda ,\) compared to the one for \(\xi \) . (ii) Next we take advantage of the periodicity of the character together with the Poisson summation formula, and arrive at the functional equation, Eq. ( 275 ), of \(\omega \) corresponding to \(\Lambda .\)
We conclude by briefly comparing the derivation of the functional equation of the Jacobi theta function \(\omega \) corresponding to \(\Lambda \) to that for \(\xi \) . In particular, we show that the origin of the quadratic polynomial \(s(s-1)\) and the off-set \(1/2\) in the analytic continuation, Eq. ( 43 ), of \(\xi \) is the fact that the term \(n=0\) in \(\omega \) corresponding to \(\xi \) is nonzero.
1.1 Extension of Summation
We start by verifying the representation
For this purpose we consider the sum
and decompose S into a sum over all positive, and one over all negative integers including zero, that is,
where in the sum over negative n we have replaced \(-n\) by \(n.\)
When we recall the connection, Eq. ( 128 ), between \(\chi (-n)\) and \(\chi (n)\) together with \(\chi (0) = 0\) , Eq. ( 119 ), we find the expression
The values, Eq.( 127 ), of \(\kappa \) together with the relation \(\chi (-1) = \pm 1\) yield the identity
and the definition, Eq. ( 277 ), of \(\omega \) the desired representation, Eq. ( 276 ).
1.2 Emergence of Gauss Sum
Since the character \(\chi \) satisfies the periodicity condition, Eq. ( 116 ), it is useful to apply the summation formula
valid for any appropriately converging sum of coefficients \(d(n)\) , to S in the form
where we have introduced the abbreviation
Indeed, with the help of Eq. ( 116 ) we immediately find the representation
of S which with the Poisson summation formula
takes the form
Finally, the new integration variable
yields the expression
where we have interchanged the two summations, and have recalled the definition, Eq. ( 130 ), of the Gauss sum \(\tilde {G}(\chi ,m).\)
Next we use the reduction formula, Eq. ( 129 ), which allows us to factor \(\tilde {G}(\chi ,1)\) out of the sum over m and to find
With the definition of h , Eq. ( 282 ), and the integral formula
we finally arrive at
that is, the functional equation, Eq. ( 275 ), of \(\omega \) when we use the relation, Eq. ( 276 ). Moreover, we have recalled the definition, Eq. ( 142 ), of the Gauss sum.
1.3 Comparison to Jacobi Theta Function of \(\xi \)
We conclude by briefly comparing and contrasting this derivation of the functional equation of the Jacobi theta function of \(\Lambda \) to the corresponding one for the Jacobi theta function of \(\xi \) , defined by Eq. ( 21 ) and discussed in Appendix 1.
In contrast to the generalized Jacobi theta function, Eq. ( 154 ), where the term \(n=0\) vanishes due to \(\chi (0)=0\) , Eq. ( 119 ), the contribution in the one for \(\xi \) is unity. This difference is important since the term in Eq. ( 202 ) independent of \(\omega \) is a consequence of the subtraction of the term \(n=0\) in Eq. ( 195 ). As a result, in the corresponding functional equation, Eq. ( 275 ), for the generalized Jacobi theta function only the contribution proportional to \(\omega (1/x)\) enters.
Rights and permissions
Reprints and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter.
Tschaffon, M.E.N., Tkáčová, I., Maier, H., Schleich, W.P. (2023). A Primer on the Riemann Hypothesis. In: Citro, R., Lewenstein, M., Rubio, A., Schleich, W.P., Wells, J.D., Zank, G.P. (eds) Sketches of Physics. Lecture Notes in Physics, vol 1000. Springer, Cham. https://doi.org/10.1007/978-3-031-32469-7_7
Download citation
DOI : https://doi.org/10.1007/978-3-031-32469-7_7
Published : 15 September 2023
Publisher Name : Springer, Cham
Print ISBN : 978-3-031-32468-0
Online ISBN : 978-3-031-32469-7
eBook Packages : Physics and Astronomy Physics and Astronomy (R0)
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
Wolfram Demonstrations Project
Riemann hypothesis.
- Open in Cloud
- Download to Desktop
- Copy Resource Object
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products .
Do not show again

Contributed by: Baris Altunkaynak (March 2011) Open content licensed under CC BY-NC-SA

Related Links
- Riemann Hypothesis ( Wolfram MathWorld )
- Riemann Zeta Function ( Wolfram MathWorld )
- Riemann Zeta Function Zeros ( Wolfram MathWorld )
Permanent Citation
Baris Altunkaynak "Riemann Hypothesis" http://demonstrations.wolfram.com/RiemannHypothesis/ Wolfram Demonstrations Project Published: March 7 2011
Share Demonstration
Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.
Related Topics
- Complex Analysis
- Special Functions
Subscribe or renew today
Every print subscription comes with full digital access
Science News
Mathematicians report possible progress on proving the riemann hypothesis.
A new study of Jensen polynomials revives an old approach

STILL ELUSIVE Researchers may have edged closer to a proof of the Riemann hypothesis — a statement about the Riemann zeta function, plotted here — which could help mathematicians understand the quirks of prime numbers.
Jan Homann/Wikimedia Commons
Share this:
By Emily Conover
May 24, 2019 at 12:03 pm
Researchers have made what might be new headway toward a proof of the Riemann hypothesis, one of the most impenetrable problems in mathematics. The hypothesis, proposed 160 years ago, could help unravel the mysteries of prime numbers.
Mathematicians made the advance by tackling a related question about a group of expressions known as Jensen polynomials, they report May 21 in Proceedings of the National Academy of Sciences . But the conjecture is so difficult to verify that even this progress is not necessarily a sign that a solution is near ( SN Online: 9/25/18 ).
At the heart of the Riemann hypothesis is an enigmatic mathematical entity known as the Riemann zeta function. It’s intimately connected to prime numbers — whole numbers that can’t be formed by multiplying two smaller numbers — and how they are distributed along the number line. The Riemann hypothesis suggests that the function’s value equals zero only at points that fall on a single line when the function is graphed, with the exception of certain obvious points. But, as the function has infinitely many of these “zeros,” this is not easy to confirm. The puzzle is considered so important and so difficult that there is a $1 million prize for a solution , offered up by the Clay Mathematics Institute.
But Jensen polynomials might be a key to unlocking the Riemann hypothesis. Mathematicians have previously shown that the Riemann hypothesis is true if all the Jensen polynomials associated with the Riemann zeta function have only zeros that are real, meaning the values for which the polynomial equals zero are not imaginary numbers — they don’t involve the square root of negative 1. But there are infinitely many of these Jensen polynomials.
Studying Jensen polynomials is one of a variety of strategies for attacking the Riemann hypothesis. The idea is more than 90 years old, and previous studies have proved that a small subset of the Jensen polynomials have real roots. But progress was slow, and efforts had stalled.
Now, mathematician Ken Ono and colleagues have shown that many of these polynomials indeed have real roots, satisfying a large chunk of what’s needed to prove the Riemann hypothesis.
“Any progress in any direction related to the Riemann hypothesis is fascinating,” says mathematician Dimitar Dimitrov of the State University of São Paulo. Dimitrov thought “it would be impossible that anyone will make any progress in this direction,” he says, “but they did.”
It’s hard to say whether this progress could eventually lead to a proof. “I am very reluctant to predict anything,” says mathematician George Andrews of Penn State, who was not involved with the study. Many strides have been made on the Riemann hypothesis in the past, but each advance has fallen short. However, with other major mathematical problems that were solved in recent decades, such as Fermat’s last theorem ( SN: 11/5/94, p. 295 ), it wasn’t clear that the solution was imminent until it was in hand. “You never know when something is going to break.”
The result supports the prevailing viewpoint among mathematicians that the Riemann hypothesis is correct. “We’ve made a lot of progress that offers new evidence that the Riemann hypothesis should be true,” says Ono, of Emory University in Atlanta.
If the Riemann hypothesis is ultimately proved correct, it would not only illuminate the prime numbers, but would also immediately confirm many mathematical ideas that have been shown to be correct assuming the Riemann hypothesis is true.
In addition to its Riemann hypothesis implications, the new result also unveils some details of what’s known as the partition function , which counts the number of possible ways to create a number from the sum of positive whole numbers ( SN: 6/17/00, p. 396 ). For example, the number 4 can be made in five different ways: 3+1, 2+2, 2+1+1, 1+1+1+1, or just the number 4 itself.
The result confirms an earlier proposition about the details of how that partition function grows with larger numbers. “That was an open question … for a long time,” Andrews says. The real prize would be proving the Riemann hypothesis, he notes. That will have to wait.
More Stories from Science News on Math

How two outsiders tackled the mystery of arithmetic progressions
A predicted quasicrystal is based on the ‘einstein’ tile known as the hat.

Here’s how much fruit you can take from a display before it collapses

Here are some astounding scientific firsts of 2023

‘Is Math Real?’ asks simple questions to explore math’s deepest truths

An enduring Möbius strip mystery has finally been solved

Non-Western art and design can reveal alternate ways of thinking about math

Seen Bigfoot or the Loch Ness Monster? Data suggest the odds are low
From the nature index.
Subscribers, enter your e-mail address for full access to the Science News archives and digital editions.
Not a subscriber? Become one now .
Things Of Interest
The riemann hypothesis for dummies.
The Riemann Hypothesis is a problem in mathematics which is currently unsolved.
To explain it to you I will have to lay some groundwork.
First: complex numbers , explained. You may have heard the question asked, "what is the square root of minus one?" Well, maths has an answer and we call it i . i multiplied by i equals -1. If the real number line ...-4, -3, -2, -1, 0, 1, 2, 3, 4... is represented as a horizontal line, then the numbers ...-4i, -3i, -2i, -i, 0, i, 2i, 3i, 4i... can be thought of as the vertical axis on this diagram. The whole plane taken together is then called the complex plane . This is a two-dimensional set of numbers.
Every complex number can be represented in the form a + b i. For real numbers, we simply take b =0.
Next: functions. In mathematics, a function is a black box which, when you put a number into it, spits a different number out. A function is represented by a letter - usually " f ". If you put a number x into the function you call f , then what f then spits out is written " f ( x )".
In most cases there is a convenient way to express f ( x ) in terms of x . For example, f ( x )= x 2 is a very simple function. Whatever x you put in, you'll get x 2 out. f (1)=1. f (2)=4. f (3)=9. And so on.
You're probably most familiar with real functions , or functions where you put a real number in and always get a real number out. HOWEVER. There's nothing stopping you from putting these weird new complex numbers into a function. For example, if f ( x )= x 2 and we let x =i, which is the square root of minus one I mentioned above, then you'll get f (i)=-1. That's just the beginning of what's more generally known as complex functions - where you can put any complex number a + b i in and get (potentially) any complex number out.
The Riemann Zeta Function is just such a complex function. "Zeta" is a Greek letter which is written "ζ". For any complex number a + b i, ζ ( a + b i) will be another complex number, c + d i.
The actual description of the Zeta Function is too boringly complicated to explain here.
Now, a zero of a function is (pretty obviously) a point a + b i where f ( a + b i)=0. If f ( x )= x 2 then the only zero is obviously at 0, where f (0)=0. For the Riemann Zeta Function this is more complicated. It basically has two types of zeros: the "trivial" zeroes, that occur at all negative even integers, that is, -2, -4, -6, -8... and the "nontrivial" zeroes, which are all the OTHER ones.
As far as we know, all the nontrivial zeroes occur at 1/2 + b i for some b . No others have been found in a lot of looking... but are they ALL like that? The Riemann Hypothesis suggests that they are... but nobody has yet been able to prove it.


IMAGES
VIDEO
COMMENTS
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1 / 2.Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers.
Conjecture 2.22 (Riemann Hypothesis) All non-real zeros of ζ(s) ζ ( s) lie on the line Res = 12 Re s = 1 2. In his only paper on number theory [ 20 ], Riemann realized that the hypothesis enabled him to describe detailed properties of the distribution of primes in terms of of the location of the non-real zero of \ (\zeta ( s )\).
First published in Riemann's groundbreaking 1859 paper (Riemann 1859), the Riemann hypothesis is a deep mathematical conjecture which states that the nontrivial Riemann zeta function zeros, i.e., the values of s other than -2, -4, -6, ... such that zeta(s)=0 (where zeta(s) is the Riemann zeta function) all lie on the "critical line" sigma=R[s]=1/2 (where R[s] denotes the real part of s). A ...
Riemann extended the study of the zeta function to include the complex numbers x + iy, where i = Square root of√−1, except for the line x = 1 in the complex plane. Riemann knew that the zeta function equals zero for all negative even integers −2, −4, −6,… (so-called trivial zeros) and that it has an infinite number of zeros in the ...
The Riemann hypothesis tells us about the deviation from the average. Formulated in Riemann's 1859 paper, it asserts that all the 'non-obvious' zeros of the zeta function are complex numbers with real part 1/2. Some numbers have the special property that they cannot be expressed as the product of two smaller numbers, e.g., 2, 3, 5, 7, etc ...
The Riemann Hypothesis is a famous conjecture in analytic number theory that states that all nontrivial zeros of the Riemann zeta function have real part.From the functional equation for the zeta function, it is easy to see that when .These are called the trivial zeros. This hypothesis is one of the seven millenium questions.. The Riemann Hypothesis is an important problem in the study of ...
The Riemann hypothesis for the Euler zeta function is a corollary. 1. Generalization of the Gamma Function. The Riemann hypothesis is the conjecture made by Riemann that the Euler zeta func-tion has no zeros in a half-plane larger than the half-plane which has no zeros by the convergence of the Euler product.
The Riemann hypothesis is a mathimatical question . Finding a ... As a tangible example, in order to use quadratic formula to solve some equations, the answer sometimes has to be an imaginary number, and historically this was the reason why imaginary numbers were invented in the first place.
Abstract. We provide an introduction for physicists into the Riemann Hypothesis. For this purpose, we first introduce, and then compare and contrast the Riemann function and the Dirichlet L-functions, with the Titchmarsh counterexample. Whereas the first two classes of functions are expected to satisfy the Riemann Hypothesis, the Titchmarsh ...
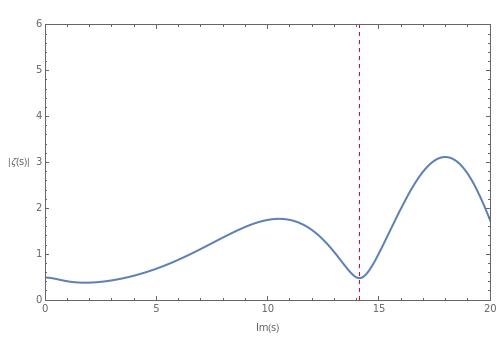
The hypothesis was first formulated by Riemann in 1859 and has remained unsolved since then. It is known that the nontrivial zeros are located in the crtical strip , moreover if we define , then , which shows that the zeros must be symmetric with respect to the critical line.. This Demonstration plots the absolute value of the zeta function with respect to the imaginary part of its argument.
NOTES ON THE RIEMANN HYPOTHESIS RICARDO PEREZ-MARCO Abstract. Our aim is to give an introduction to the Riemann Hypothesis and a panoramic view of the world of zeta and L-functions. We rst review Riemann's foundational article and discuss the mathematical background of the time and his possible motivations for making his famous conjecture. We
The Riemann hypothesis, posited in 1859 by German mathematician Bernhard Riemann, is one of the biggest unsolved puzzles in mathematics. The hypothesis, which could unlock the mysteries of prime ...
Statement of Riemann hypothesis and the Hasse-Weil Inequality 7 6. Example 7 7. Proof of the Hasse-Weil Inequality 8 8. The Weil conjectures 9 9. Further Reading 10 ... One of the most important open questions about the Riemann zeta function is the Rie-mann hypothesis. It is one of the oldest and most central open problems in number theory.
Examples include 3 + 4i and 2 − 6i. In these cases, the 3 and the 2 are the real parts, while the 4 and −6 are the imaginary parts. ... It's a far cry from proving the Lindelöf hypothesis, let alone Riemann's question, but it's something. "We haven't made any progress on the Riemann hypothesis in 150 years, whereas this is a ...
The Riemann hypothesis is, and will hopefully remain for a long time, a great moti-vation to uncover and explore new parts of the mathematical world. After reviewing its ... formulas (of which (1) is the prime example) and possible strategies to attack the problem, stressing the value of the elaboration of new concepts rather than "problem ...
The Riemann hypothesis suggests that the function's value equals zero only at points that fall on a single line when the function is graphed, with the exception of certain obvious points ...
The Riemann hypothesis is a conjecture about the Riemann zeta function. ζ(s) =∑n=1∞ 1 ns ζ ( s) = ∑ n = 1 ∞ 1 n s. This is a function C → C C → C. With the definition I have provided the zeta function is only defined for R(s) > 1 ℜ ( s) > 1.
The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field of number theory. It's named after the German mathematician Bernhard Riemann, who introduced the hypothesis in 1859. RH: All non-trivial zeros of the Riemannian zeta-function lie on the critical line.
HILBERT AND THE RIEMANN HYPOTHESIS "If I were to awaken after having slept for a thousand years, my first question would be: Has the Riemann ... TAKEAWAY FROM THESE EXAMPLES • Red roots are good approximations to geniune roots. • Blue spurious roots are annoying and become more
The Riemann Zeta Function is just such a complex function. "Zeta" is a Greek letter which is written "ζ". For any complex number a + b i, ζ ( a + b i) will be another complex number, c + d i. The actual description of the Zeta Function is too boringly complicated to explain here. Now, a zero of a function is (pretty obviously) a point a + b i ...
The Riemann Hypothesis states that all non trivial zeros of the Riemann zeta function have a real part equal to 0.5. But what does this mean? A zero of a function is a value that you can put into the function and get zero to come out. For example if you have a function f (x) = x - 1, then x = 1 is a zero of this function because using it as x ...
$\begingroup$ (Apparently pregunton removed their comment with the link to the other question. I have now put the link below.) What I wanted to say: once we are at that point we might ask a simpler (but still very hard) question: is there an intuitive explanation why the Riemann zeta FUNCTION (rather than hypothesis) contains interesting information about the distribution of primes in language ...
The answer is either yes or no, depending on how stringently you interpret your various requirements. You should look at the discussion of the Selberg class of functions, which is Selberg's conjectural characterization of functions satisfying the Riemann Hypothesis. In particular, if you read the comments on the definition in the wikipedia ...