Rejecting the Null Hypothesis Using Confidence Intervals
- Tech Trends

In an introductory statistics class, there are three main topics that are taught: descriptive statistics and data visualizations, probability and sampling distributions, and statistical inference. Within statistical inference, there are two key methods of statistical inference that are taught, viz. confidence intervals and hypothesis testing . While these two methods are always taught when learning data science and related fields, it is rare that the relationship between these two methods is properly elucidated.
In this article, we’ll begin by defining and describing each method of statistical inference in turn and along the way, state what statistical inference is, and perhaps more importantly, what it isn’t. Then we’ll describe the relationship between the two. While it is typically the case that confidence intervals are taught before hypothesis testing when learning statistics, we’ll begin with the latter since it will allow us to define statistical significance.

Hypothesis Tests
The purpose of a hypothesis test is to answer whether random chance might be responsible for an observed effect. Hypothesis tests use sample statistics to test a hypothesis about population parameters. The null hypothesis, H 0 , is a statement that represents the assumed status quo regarding a variable or variables and it is always about a population characteristic. Some of the ways the null hypothesis is typically glossed are: the population variable is equal to a particular value or there is no difference between the population variables . For example:
- H 0 : μ = 61 in (The mean height of the population of American men is 69 inches)
- H 0 : p 1 -p 2 = 0 (The difference in the population proportions of women who prefer football over baseball and the population proportion of men who prefer football over baseball is 0.)
Note that the null hypothesis always has the equal sign.
The alternative hypothesis, denoted either H 1 or H a , is the statement that is opposed to the null hypothesis (e.g., the population variable is not equal to a particular value or there is a difference between the population variables ):
- H 1 : μ > 61 im (The mean height of the population of American men is greater than 69 inches.)
- H 1 : p 1 -p 2 ≠ 0 (The difference in the population proportions of women who prefer football over baseball and the population proportion of men who prefer football over baseball is not 0.)
The alternative hypothesis is typically the claim that the researcher hopes to show and it always contains the strict inequality symbols (‘<’ left-sided or left-tailed, ‘≠’ two-sided or two-tailed, and ‘>’ right-sided or right-tailed).
When carrying out a test of H 0 vs. H 1 , the null hypothesis H 0 will be rejected in favor of the alternative hypothesis only if the sample provides convincing evidence that H 0 is false. As such, a statistical hypothesis test is only capable of demonstrating strong support for the alternative hypothesis by rejecting the null hypothesis.
When the null hypothesis is not rejected, it does not mean that there is strong support for the null hypothesis (since it was assumed to be true); rather, only that there is not convincing evidence against the null hypothesis. As such, we never use the phrase “accept the null hypothesis.”
In the classical method of performing hypothesis testing, one would have to find what is called the test statistic and use a table to find the corresponding probability. Happily, due to the advancement of technology, one can use Python (as is done in the Flatiron’s Data Science Bootcamp ) and get the required value directly using a Python library like stats models . This is the p-value , which is short for the probability value.
The p-value is a measure of inconsistency between the hypothesized value for a population characteristic and the observed sample. The p -value is the probability, under the assumption the null hypothesis is true, of obtaining a test statistic value that is a measure of inconsistency between the null hypothesis and the data. If the p -value is less than or equal to the probability of the Type I error, then we can reject the null hypothesis and we have sufficient evidence to support the alternative hypothesis.
Typically the probability of a Type I error ɑ, more commonly known as the level of significance , is set to be 0.05, but it is often prudent to have it set to values less than that such as 0.01 or 0.001. Thus, if p -value ≤ ɑ, then we reject the null hypothesis and we interpret this as saying there is a statistically significant difference between the sample and the population. So if the p -value=0.03 ≤ 0.05 = ɑ, then we would reject the null hypothesis and so have statistical significance, whereas if p -value=0.08 ≥ 0.05 = ɑ, then we would fail to reject the null hypothesis and there would not be statistical significance.
Confidence Intervals
The other primary form of statistical inference are confidence intervals. While hypothesis tests are concerned with testing a claim, the purpose of a confidence interval is to estimate an unknown population characteristic. A confidence interval is an interval of plausible values for a population characteristic. They are constructed so that we have a chosen level of confidence that the actual value of the population characteristic will be between the upper and lower endpoints of the open interval.
The structure of an individual confidence interval is the sample estimate of the variable of interest margin of error. The margin of error is the product of a multiplier value and the standard error, s.e., which is based on the standard deviation and the sample size. The multiplier is where the probability, of level of confidence, is introduced into the formula.
The confidence level is the success rate of the method used to construct a confidence interval. A confidence interval estimating the proportion of American men who state they are an avid fan of the NFL could be (0.40, 0.60) with a 95% level of confidence. The level of confidence is not the probability that that population characteristic is in the confidence interval, but rather refers to the method that is used to construct the confidence interval.
For example, a 95% confidence interval would be interpreted as if one constructed 100 confidence intervals, then 95 of them would contain the true population characteristic.
Errors and Power
A Type I error, or a false positive, is the error of finding a difference that is not there, so it is the probability of incorrectly rejecting a true null hypothesis is ɑ, where ɑ is the level of significance. It follows that the probability of correctly failing to reject a true null hypothesis is the complement of it, viz. 1 – ɑ. For a particular hypothesis test, if ɑ = 0.05, then its complement would be 0.95 or 95%.
While we are not going to expand on these ideas, we note the following two related probabilities. A Type II error, or false negative, is the probability of failing to reject a false null hypothesis where the probability of a type II error is β and the power is the probability of correctly rejecting a false null hypothesis where power = 1 – β. In common statistical practice, one typically only speaks of the level of significance and the power.
The following table summarizes these ideas , where the column headers refer to what is actually the case, but is unknown. (If the truth or falsity of the null value was truly known, we wouldn’t have to do statistics.)

Hypothesis Tests and Confidence Intervals
Since hypothesis tests and confidence intervals are both methods of statistical inference, then it is reasonable to wonder if they are equivalent in some way. The answer is yes, which means that we can perform hypothesis testing using confidence intervals.
Returning to the example where we have an estimate of the proportion of American men that are avid fans of the NFL, we had (0.40, 0.60) at a 95% confidence level. As a hypothesis test, we could have the alternative hypothesis as H 1 ≠ 0.51. Since the null value of 0.51 lies within the confidence interval, then we would fail to reject the null hypothesis at ɑ = 0.05.
On the other hand, if H 1 ≠ 0.61, then since 0.61 is not in the confidence interval we can reject the null hypothesis at ɑ = 0.05. Note that the confidence level of 95% and the level of significance at ɑ = 0.05 = 5% are complements, which is the “H o is True” column in the above table.
In general, one can reject the null hypothesis given a null value and a confidence interval for a two-sided test if the null value is not in the confidence interval where the confidence level and level of significance are complements. For one-sided tests, one can still perform a hypothesis test with the confidence level and null value. Not only is there an added layer of complexity for this equivalence, it is the best practice to perform two-sided hypothesis tests since one is not prejudicing the direction of the alternative.
In this discussion of hypothesis testing and confidence intervals, we not only understand when these two methods of statistical inference can be equivalent, but now have a deeper understanding of statistical significance itself and therefore, statistical inference.
Learn More About Data Science at Flatiron
The curriculum in our Data Science Bootcamp incorporates the latest technologies, including artificial intelligence (AI) tools. Download the syllabus to see what you can learn, or book a 10-minute call with Admissions to learn about full-time and part-time attendance opportunities.

About Brendan Patrick Purdy
Brendan is the senior curriculum developer for data science at the Flatiron School. He holds degrees in mathematics, data science, and philosophy, and enjoys modeling neural networks with the Python library TensorFlow.
Related Resources

NYC Campus Tour

Quantifying Rafael Nadal’s Dominance with French Open Data

The Art of Data Exploration
Privacy overview.
| Cookie | Duration | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Understanding Confidence Intervals | Easy Examples & Formulas
Understanding Confidence Intervals | Easy Examples & Formulas
Published on August 7, 2020 by Rebecca Bevans . Revised on June 22, 2023.
When you make an estimate in statistics, whether it is a summary statistic or a test statistic , there is always uncertainty around that estimate because the number is based on a sample of the population you are studying.
The confidence interval is the range of values that you expect your estimate to fall between a certain percentage of the time if you run your experiment again or re-sample the population in the same way.
The confidence level is the percentage of times you expect to reproduce an estimate between the upper and lower bounds of the confidence interval, and is set by the alpha value .
Table of contents
What exactly is a confidence interval, calculating a confidence interval: what you need to know, confidence interval for the mean of normally-distributed data, confidence interval for proportions, confidence interval for non-normally distributed data, reporting confidence intervals, caution when using confidence intervals, other interesting articles, frequently asked questions about confidence intervals.
A confidence interval is the mean of your estimate plus and minus the variation in that estimate. This is the range of values you expect your estimate to fall between if you redo your test, within a certain level of confidence.
Confidence , in statistics, is another way to describe probability. For example, if you construct a confidence interval with a 95% confidence level, you are confident that 95 out of 100 times the estimate will fall between the upper and lower values specified by the confidence interval.
Your desired confidence level is usually one minus the alpha (α) value you used in your statistical test :
Confidence level = 1 − a
So if you use an alpha value of p < 0.05 for statistical significance , then your confidence level would be 1 − 0.05 = 0.95, or 95%.
When do you use confidence intervals?
You can calculate confidence intervals for many kinds of statistical estimates, including:
- Proportions
- Population means
- Differences between population means or proportions
- Estimates of variation among groups
These are all point estimates, and don’t give any information about the variation around the number. Confidence intervals are useful for communicating the variation around a point estimate.
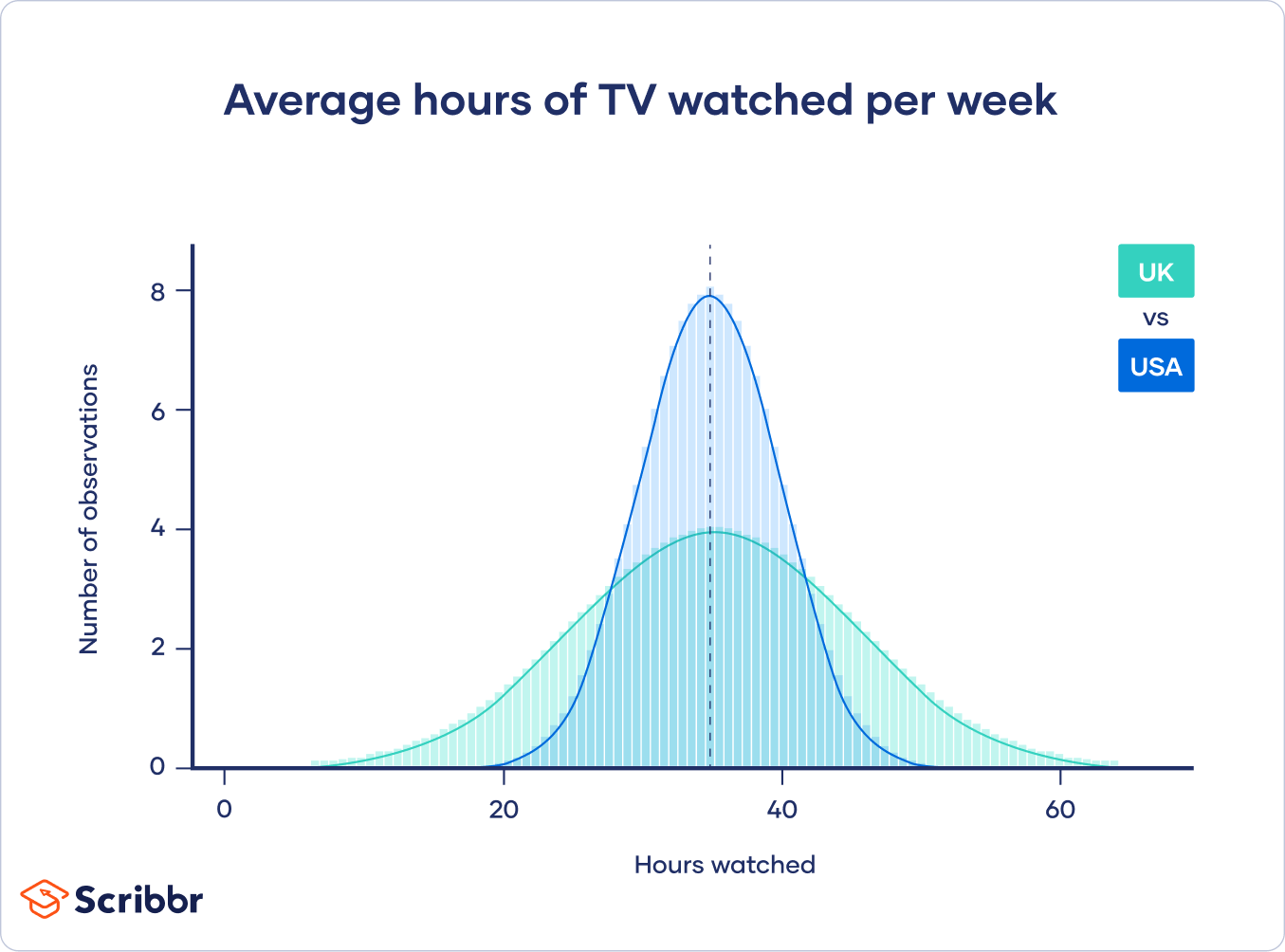
However, the British people surveyed had a wide variation in the number of hours watched, while the Americans all watched similar amounts.
Even though both groups have the same point estimate (average number of hours watched), the British estimate will have a wider confidence interval than the American estimate because there is more variation in the data.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
Most statistical programs will include the confidence interval of the estimate when you run a statistical test.
If you want to calculate a confidence interval on your own, you need to know:
- The point estimate you are constructing the confidence interval for
- The critical values for the test statistic
- The standard deviation of the sample
- The sample size
Once you know each of these components, you can calculate the confidence interval for your estimate by plugging them into the confidence interval formula that corresponds to your data.
Point estimate
The point estimate of your confidence interval will be whatever statistical estimate you are making (e.g., population mean , the difference between population means, proportions, variation among groups).
Finding the critical value
Critical values tell you how many standard deviations away from the mean you need to go in order to reach the desired confidence level for your confidence interval.
There are three steps to find the critical value.
- Choose your alpha (α) value.
The alpha value is the probability threshold for statistical significance . The most common alpha value is p = 0.05, but 0.1, 0.01, and even 0.001 are sometimes used. It’s best to look at the research papers published in your field to decide which alpha value to use.
- Decide if you need a one-tailed interval or a two-tailed interval.
You will most likely use a two-tailed interval unless you are doing a one-tailed t test .
For a two-tailed interval, divide your alpha by two to get the alpha value for the upper and lower tails.
- Look up the critical value that corresponds with the alpha value.
If your data follows a normal distribution , or if you have a large sample size ( n > 30) that is approximately normally distributed, you can use the z distribution to find your critical values.
For a z statistic, some of the most common values are shown in this table:
| Confidence level | 90% | 95% | 99% |
|---|---|---|---|
| alpha for one-tailed CI | 0.1 | 0.05 | 0.01 |
| alpha for two-tailed CI | 0.05 | 0.025 | 0.005 |
| statistic | 1.64 | 1.96 | 2.57 |
If you are using a small dataset (n ≤ 30) that is approximately normally distributed, use the t distribution instead.
The t distribution follows the same shape as the z distribution, but corrects for small sample sizes. For the t distribution, you need to know your degrees of freedom (sample size minus 1).
Check out this set of t tables to find your t statistic. We have included the confidence level and p values for both one-tailed and two-tailed tests to help you find the t value you need.
For normal distributions, like the t distribution and z distribution, the critical value is the same on either side of the mean.
For a two-tailed 95% confidence interval, the alpha value is 0.025, and the corresponding critical value is 1.96.
Finding the standard deviation
Most statistical software will have a built-in function to calculate your standard deviation, but to find it by hand you can first find your sample variance, then take the square root to get the standard deviation.
- Find the sample variance
Sample variance is defined as the sum of squared differences from the mean, also known as the mean-squared-error (MSE):
To find the MSE, subtract your sample mean from each value in the dataset, square the resulting number, and divide that number by n − 1 (sample size minus 1).
Then add up all of these numbers to get your total sample variance ( s 2 ). For larger sample sets, it’s easiest to do this in Excel.
- Find the standard deviation.
The standard deviation of your estimate ( s ) is equal to the square root of the sample variance/sample error ( s 2 ):
- 10 for the GB estimate.
- 5 for the USA estimate.
Sample size
The sample size is the number of observations in your data set.
Normally-distributed data forms a bell shape when plotted on a graph, with the sample mean in the middle and the rest of the data distributed fairly evenly on either side of the mean.
The confidence interval for data which follows a standard normal distribution is:
- CI = the confidence interval
- X̄ = the population mean
- Z* = the critical value of the z distribution
- σ = the population standard deviation
- √n = the square root of the population size
The confidence interval for the t distribution follows the same formula, but replaces the Z * with the t *.
In real life, you never know the true values for the population (unless you can do a complete census). Instead, we replace the population values with the values from our sample data, so the formula becomes:
- ˆx = the sample mean
- s = the sample standard deviation
To calculate the 95% confidence interval, we can simply plug the values into the formula.
For the USA:
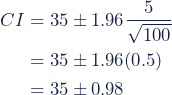
So for the USA, the lower and upper bounds of the 95% confidence interval are 34.02 and 35.98.
The confidence interval for a proportion follows the same pattern as the confidence interval for means, but place of the standard deviation you use the sample proportion times one minus the proportion:
- ˆp = the proportion in your sample (e.g. the proportion of respondents who said they watched any television at all)
- Z*= the critical value of the z distribution
- n = the sample size
Prevent plagiarism. Run a free check.
To calculate a confidence interval around the mean of data that is not normally distributed, you have two choices:
- You can find a distribution that matches the shape of your data and use that distribution to calculate the confidence interval.
- You can perform a transformation on your data to make it fit a normal distribution, and then find the confidence interval for the transformed data.
Performing data transformations is very common in statistics, for example, when data follows a logarithmic curve but we want to use it alongside linear data. You just have to remember to do the reverse transformation on your data when you calculate the upper and lower bounds of the confidence interval.
Confidence intervals are sometimes reported in papers, though researchers more often report the standard deviation of their estimate.
If you are asked to report the confidence interval, you should include the upper and lower bounds of the confidence interval.
One place that confidence intervals are frequently used is in graphs. When showing the differences between groups, or plotting a linear regression, researchers will often include the confidence interval to give a visual representation of the variation around the estimate.
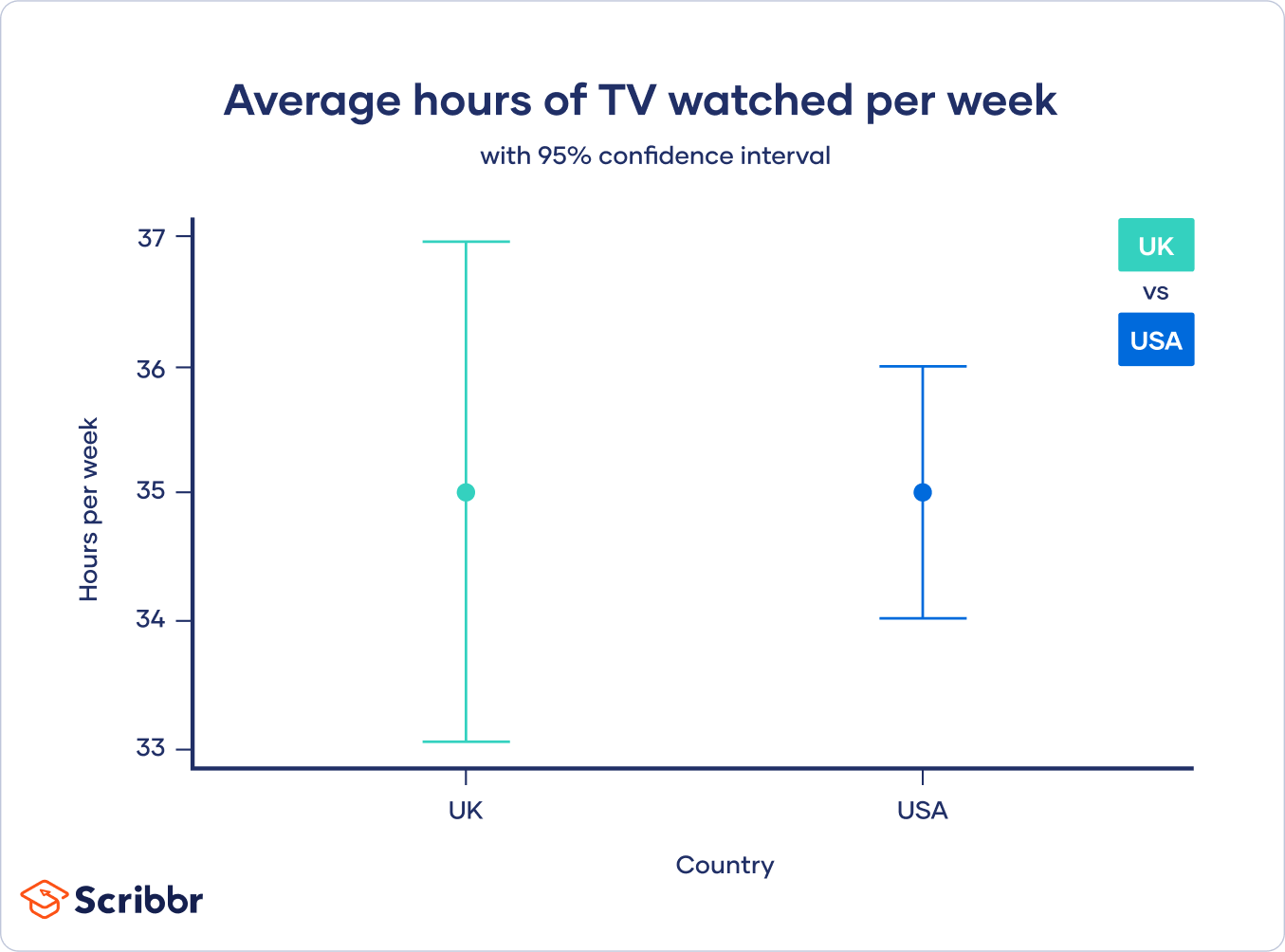
Confidence intervals are sometimes interpreted as saying that the ‘true value’ of your estimate lies within the bounds of the confidence interval.
This is not the case. The confidence interval cannot tell you how likely it is that you found the true value of your statistical estimate because it is based on a sample, not on the whole population .
The confidence interval only tells you what range of values you can expect to find if you re-do your sampling or run your experiment again in the exact same way.
The more accurate your sampling plan, or the more realistic your experiment, the greater the chance that your confidence interval includes the true value of your estimate. But this accuracy is determined by your research methods, not by the statistics you do after you have collected the data!
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
The confidence level is the percentage of times you expect to get close to the same estimate if you run your experiment again or resample the population in the same way.
The confidence interval consists of the upper and lower bounds of the estimate you expect to find at a given level of confidence.
For example, if you are estimating a 95% confidence interval around the mean proportion of female babies born every year based on a random sample of babies, you might find an upper bound of 0.56 and a lower bound of 0.48. These are the upper and lower bounds of the confidence interval. The confidence level is 95%.
To calculate the confidence interval , you need to know:
Then you can plug these components into the confidence interval formula that corresponds to your data. The formula depends on the type of estimate (e.g. a mean or a proportion) and on the distribution of your data.
The standard normal distribution , also called the z -distribution, is a special normal distribution where the mean is 0 and the standard deviation is 1.
Any normal distribution can be converted into the standard normal distribution by turning the individual values into z -scores. In a z -distribution, z -scores tell you how many standard deviations away from the mean each value lies.
The z -score and t -score (aka z -value and t -value) show how many standard deviations away from the mean of the distribution you are, assuming your data follow a z -distribution or a t -distribution .
These scores are used in statistical tests to show how far from the mean of the predicted distribution your statistical estimate is. If your test produces a z -score of 2.5, this means that your estimate is 2.5 standard deviations from the predicted mean.
The predicted mean and distribution of your estimate are generated by the null hypothesis of the statistical test you are using. The more standard deviations away from the predicted mean your estimate is, the less likely it is that the estimate could have occurred under the null hypothesis .
A critical value is the value of the test statistic which defines the upper and lower bounds of a confidence interval , or which defines the threshold of statistical significance in a statistical test. It describes how far from the mean of the distribution you have to go to cover a certain amount of the total variation in the data (i.e. 90%, 95%, 99%).
If you are constructing a 95% confidence interval and are using a threshold of statistical significance of p = 0.05, then your critical value will be identical in both cases.
If your confidence interval for a difference between groups includes zero, that means that if you run your experiment again you have a good chance of finding no difference between groups.
If your confidence interval for a correlation or regression includes zero, that means that if you run your experiment again there is a good chance of finding no correlation in your data.
In both of these cases, you will also find a high p -value when you run your statistical test, meaning that your results could have occurred under the null hypothesis of no relationship between variables or no difference between groups.
If you want to calculate a confidence interval around the mean of data that is not normally distributed , you have two choices:
- Find a distribution that matches the shape of your data and use that distribution to calculate the confidence interval.
- Perform a transformation on your data to make it fit a normal distribution, and then find the confidence interval for the transformed data.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Understanding Confidence Intervals | Easy Examples & Formulas. Scribbr. Retrieved September 9, 2024, from https://www.scribbr.com/statistics/confidence-interval/
Is this article helpful?
Rebecca Bevans
Other students also liked, understanding p values | definition and examples, test statistics | definition, interpretation, and examples, how to calculate standard deviation (guide) | calculator & examples, what is your plagiarism score.
Warning: The NCBI web site requires JavaScript to function. more...
An official website of the United States government
The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
- Browse Titles
NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.
StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].
Hypothesis testing, p values, confidence intervals, and significance.
Jacob Shreffler ; Martin R. Huecker .
Affiliations
Last Update: March 13, 2023 .
- Definition/Introduction
Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.
- Issues of Concern
Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.
Hypothesis Testing
Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:
Research Question: Is Drug 23 an effective treatment for Disease A?
Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.
Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.
The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.
Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.
Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).
To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1] When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]
Significance
Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3] Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4] When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5] One criterion often used to determine statistical significance is the utilization of p values.
P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6] Hypothesis testing allows us to determine the size of the effect.
An example of findings reported with p values are below:
Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.
Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.
For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7] The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.
While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3] In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]
When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]
Confidence Intervals
A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12] Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13] A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14] Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15] confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]
In consideration of the similar research example provided above, one could make the following statement with 95% CI:
Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).
It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14] A larger width indicates a smaller sample size or a larger variability. [16] A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]
Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15] Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.
Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14] In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13] An example is below:
Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).
- Clinical Significance
Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14] Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.
Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4] Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]
The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.
- Nursing, Allied Health, and Interprofessional Team Interventions
All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care.
- Review Questions
- Access free multiple choice questions on this topic.
- Comment on this article.
Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.
Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.
This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.
- Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.
In this Page
Bulk download.
- Bulk download StatPearls data from FTP
Related information
- PMC PubMed Central citations
- PubMed Links to PubMed
Similar articles in PubMed
- The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). [PeerJ. 2021] The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). Messam LLM, Weng HY, Rosenberger NWY, Tan ZH, Payet SDM, Santbakshsing M. PeerJ. 2021; 9:e12453. Epub 2021 Nov 24.
- Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. [J Pharm Pract. 2010] Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. Ferrill MJ, Brown DA, Kyle JA. J Pharm Pract. 2010 Aug; 23(4):344-51. Epub 2010 Apr 13.
- Interpreting "statistical hypothesis testing" results in clinical research. [J Ayurveda Integr Med. 2012] Interpreting "statistical hypothesis testing" results in clinical research. Sarmukaddam SB. J Ayurveda Integr Med. 2012 Apr; 3(2):65-9.
- Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. [Dermatol Surg. 2005] Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. Alam M, Barzilai DA, Wrone DA. Dermatol Surg. 2005 Apr; 31(4):462-6.
- Review Is statistical significance testing useful in interpreting data? [Reprod Toxicol. 1993] Review Is statistical significance testing useful in interpreting data? Savitz DA. Reprod Toxicol. 1993; 7(2):95-100.
Recent Activity
- Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls
Your browsing activity is empty.
Activity recording is turned off.
Turn recording back on
Connect with NLM
National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894
Web Policies FOIA HHS Vulnerability Disclosure
Help Accessibility Careers

8.6 Relationship Between Confidence Intervals and Hypothesis Tests
Confidence intervals (CI) and hypothesis tests should give consistent results: we should not reject [latex]H_0[/latex] at the significance level [latex]\alpha[/latex] if the corresponding [latex](1 - \alpha) \times 100\%[/latex] confidence interval contains the hypothesized value [latex]\mu_0[/latex]. Two-sided confidence intervals correspond to two-tailed tests, upper-tailed confidence intervals correspond to right-tailed tests, and lower-tailed confidence intervals correspond to left-tailed tests.
A [latex](1 - \alpha) \times 100\%[/latex] two-sided [latex]t[/latex] confidence interval is given in the form [latex](\bar{x} - t_{\alpha / 2} \frac{s}{\sqrt{n}}, \bar{x} + t_{\alpha / 2} \frac{s}{\sqrt{n}})[/latex]. A [latex](1 - \alpha) \times 100\%[/latex] upper-tailed t confidence interval is given by [latex](\bar{x} - t_{\alpha} \frac{s}{\sqrt{n}}, \infty)[/latex] and the number [latex]\bar{x} - t_{\alpha} \frac{s}{\sqrt{n}}[/latex] is called the lower bound of the interval. A [latex](1 - \alpha) \times 100\%[/latex] lower-tailed t confidence interval is given by [latex](- \infty, \bar{x} + t_{\alpha} \frac{s}{\sqrt{n}})[/latex] and the number [latex]\bar{x} + t_{\alpha} \frac{s}{\sqrt{n}}[/latex] is called the upper bound of the interval. We can also use confidence intervals to make conclusions about hypothesis tests: reject the null hypothesis [latex]H_0[/latex] at the significance level [latex]\alpha[/latex] if the corresponding [latex](1 - \alpha) \times 100\%[/latex] confidence interval does not contain the hypothesized value [latex]\mu_0[/latex]. The relationship is summarized in the following table.
Table 8.3 : Relationship Between Confidence Interval and Hypothesis Test
| Null hypothesis | [latex]H_0: \mu = \mu_0[/latex] | [latex]H_0: \mu \leq \mu_0[/latex] | [latex]H_0: \mu \geq \mu_0[/latex] |
|---|---|---|---|
| Alternative | [latex]H_a: \mu \neq \mu_0[/latex] | [latex]H_a: \mu \: \gt \: \mu_0[/latex] | [latex]H_a: \mu |
| [latex](1 - \alpha) \times 100\%[/latex] CI | [latex](\bar{x} - t_{\alpha / 2} \frac{s}{\sqrt{n}}, \bar{x} + t_{\alpha / 2} \frac{s}{\sqrt{n}})[/latex] | [latex](\bar{x} - t_{\alpha} \frac{s}{\sqrt{n}}, \infty)[/latex] | [latex](- \infty, \bar{x} + t_{\alpha} \frac{s}{\sqrt{n}})[/latex] |
| Decision | |||

Here is the reason we should reject [latex]H_0[/latex] if [latex]\mu_0[/latex] is outside the corresponding confidence interval.
Take the right-tailed test for example, we should reject [latex]H_0[/latex] if the observed test statistic [latex]t_o[/latex] falls in the rejection region, that is if [latex]t_o \geq t_{\alpha}[/latex]. This implies [latex]t_o = \frac{\bar{x} - \mu_0}{s / \sqrt{n}} \geq t_{\alpha} \Longrightarrow \mu_0 \leq \bar{x} - t_{\alpha} \frac{s}{\sqrt{n}}.[/latex] Given that the upper-tailed confidence interval for a right-tailed test is [latex](\bar{x} - t_{\alpha / 2} \frac{s}{\sqrt{n}}, \infty)[/latex], [latex]\mu_0 \leq \bar{x} - t_{\alpha} \frac{s}{\sqrt{n}}[/latex] means the value of [latex]\mu_0[/latex] is outside the confidence interval. The same rationale applies to two-tailed and left-tailed tests. Therefore, we can reject [latex]H_0[/latex] at the significance level [latex]\alpha[/latex] if [latex]\mu_0[/latex] is outside the corresponding (1– [latex]\alpha[/latex] )×100% confidence interval.
Example: Relationship Between Confidence Intervals and Hypothesis Tests
The ankle-brachial index (ABI) compares the blood pressure of a patient’s arm to the blood pressure of the patient’s leg. The ABI can be an indicator of different diseases, including arterial diseases. A healthy (or normal) ABI is 0.9 or greater. Researchers obtained the ABI of 100 women with peripheral arterial disease and obtained a mean ABI of 0.64 with a standard deviation of 0.15.
- Set up the hypotheses: [latex]H_0: \mu \geq 0.9[/latex] versus [latex]H_a: \mu < 0.9[/latex].
- The significance level is [latex]\alpha = 0.05[/latex].
- Compute the value of the test statistic: [latex]t_o = \frac{\bar{x} - \mu_0}{s / \sqrt{n}} = \frac{0.64 - 0.9}{0.15 / \sqrt{100}} = \frac{-0.26}{0.015} = -17.333[/latex] with [latex]df = n-1 = 100 -1 = 99[/latex] (not given in Table IV, use 95, the closest one smaller than 99).
- Find the P-value. For a left-tailed test, the P-value is the area to the left of the observed test statistic [latex]t_o[/latex]. [latex]\mbox{P-value} = P(t \leq t_o) = P(t \leq -17.333) = P(t \geq 17.333) 2.629(t_{0.005})[/latex].
- Decision: Since the P- value [latex]< 0.005 < 0.05(\alpha)[/latex], we should reject the null hypothesis [latex]H_0[/latex].
- Conclusion: At the 5% significance level, the data provide sufficient evidence that, on average, women with peripheral arterial disease have an unhealthy ABI.
[latex]\left( - \infty, \bar{x} + t_{\alpha} \frac{s}{\sqrt{n}} \right)= \left( - \infty, 0.64 + 1.661 \times \frac{0.15}{\sqrt{100}} \right) = (- \infty , 0.665)[/latex].
- Does the interval in part b) support the conclusion in part a)? In part a), we reject [latex]H_0[/latex] and claim that the mean ABI is below 0.9 for women with peripheral arterial disease. In part b), we are 95% confident that the mean ABI is less than 0.9 since the entire confidence interval is below 0.9. In other words, the hypothesized value 0.9 is outside the corresponding confidence interval, we should reject the null. Therefore, the results obtained in parts a) and b) are consistent.
Introduction to Applied Statistics Copyright © 2024 by Wanhua Su is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Confidence Intervals
Hypothesis testing is the approach to statistical inference that we use when we have two competing theories that we are trying to choose between. A second approach to statistical inference is confidence intervals, which allow us to present a range of reasonable values for our unknown population parameter. The range of reasonable values allows us to understand the corresponding population better without requiring any ideas to be fully specified.
General Motivation and Framework
We have access to our sample, but we would really like to make a statement about the corresponding population. For example, we can calculate that the median price per night for a Chicago Airbnb was \$126 for a sample. What we really want to know, though, is what the median price per night for a Chicago Airbnb is for the entire population of Airbnbs, so that we can make an appropriate statement for the population.
How can we extend our knowledge from the sample to the population? We can use confidence intervals to help us generate a range of reasonable values for our unknown parameter. This will help us to make reasonable conclusions that should extend to the population appropriately.
To do so, we will combine our knowledge of sampling distributions with our specific sample value. This has many similar flavors to hypothesis testing but is approaching the problem through a different framework. Below, we'll walk through an example followed by the process to generate a confidence interval.
Confidence Interval Example
Like mentioned above, the median price per night for a Chicago Airbnb was $126 in our sample. Can we generate a sampling distribution for the possible values that the median price per night could take from repeated random samples?
We will use the resampling approach to generating a sampling distribution as described previously.
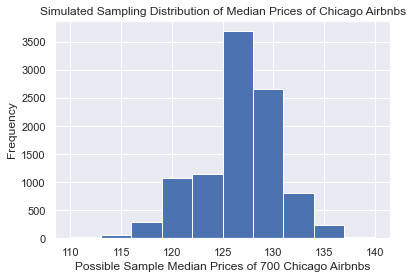
Histogram of the sampling distribution for the median price of a Chicago Airbnb.
We've now generated our sampling distribution for sample median prices of Airbnbs in Chicago. Now, suppose that I want to create a range of reasonable values for the population median prices with 90% confidence (we'll define what 90% confidence means soon). To do so, I'll find the middle 90% of this distribution by calculating the 5th percentile and the 95th percentile.
For our simulated sampling distribution, the middle 90% are between \$120 and \$132 per night for a Chicago Airbnb.
At last, we'll make a jump from making statements about samples to making statements about populations. We could say that a range of reasonable values for the population median price per night of a Chicago Airbnb is between \$120 and \$132 per night.
Confidence Interval Steps
To generate a confidence interval, we follow the same set of steps. We do apply some steps differently depending on our specific parameter of interest.
To generate a confidence interval, we should:
- Identify and define the parameter of interest
- Determine the confidence level
- Generate or use theory to specify the sampling distribution and check conditions
- Calculate the middle region of your sampling distribution, according to your confidence level
- Write a conclusion in the context of the problem.
Identify Parameter of Interest
We discussed identifying and defining the parameter of interest when we first described hypothesis testing. This is repeated for confidence intervals.
In this example, our population of interest is all Chicago Airbnbs. We likely would want to specify a time frame as well, and since we are using March 2023 data, we may specify that this is for all Chicago Airbnbs in March 2023.
Our parameter of interest (the summary measure) is the median. We may define the parameter of interest as $M$, the population median price per night for a Chicago Airbnb.
Determine the Confidence Level
The confidence level is analogous to the significance level. We'll provide a more exact definition and interpretation of the confidence level shortly. Confidence levels should be greater than 0% and less than 100%.
Confidence levels do not depend on the data and should be selected before observing the data. The confidence level is generally chosen based on the stakeholders and their requirements for the confidence in results. More confidence in the results are associated with higher confidence levels.
Common confidence levels include 90%, 95%, 98%, and 99%.
Determine the Sampling Distribution for the Sample Statistic
We again will use the sampling distribution of the sample statistic as the basis for our confidence interval calculation. To do so, we can follow the same process outlined for hypothesis testing. Recall, that we chose between a simulation-based resampling approach or a theory-based approach using the Central Limit Theorem to define the sampling distribution.
The biggest distinction between generating sampling distributions for confidence intervals compared to hypothesis testing is that we don't need to make any adjustments to our sampling distribution so that it is consistent with the null hypothesis. That is, recall that we wanted to adopt the skeptic's claim in hypothesis testing. When we were generating a sampling distribution, we would make any modifications necessary so that the sampling distribution fulfilled the condition of the null hypothesis. This distinction should be considered in two ways:
- when generating the sampling distribution
- when checking any necessary conditions
For example, if we were performing hypothesis testing with a simulation-based approach, we would need to first adjust the data so that the sample median was equal to the null value. However, without that condition for confidence intervals, we would use the data exactly as it is in the sample.
Similarly, some conditions for sampling distributions use information about the parameter of interest. For example, the theory-based approach with proportions requires that $n \times p$ and $n \times (1-p)$ are both at least 10. When we have a hypothesis, we should plug in the null value from the null hypothesis into these checks. With confidence intervals, if we don't have any requirements for the parameter, we can use our best estimate for $p$, which is often $\hat{p}$ when checking the conditions.
Again, the simulation-based approach requires the least number of assumptions. For our example, it is the only option for estimating the sampling distribution, since we haven't introduced theory that relates to the sampling distribution for a sample median.
Calculate the Confidence Interval
After we have determined the sampling distribution, we want to actually calculate the confidence interval, which is the range of reasonable values for our parameter of interest.
We want to find the central part of the sampling distribution that corresponds to our confidence level to generate the confidence interval, regardless of the approach for generating the sampling distribution. That is, if we want a 95% confidence interval, we will want to find the 2.5th percentile and the 97.5th percentile of the sampling distribution, so that the middle 95% is contained within those two values. In general, if we say that our confidence level is represented as CL%, then we want the (100-CL)/2 and (100+CL)/2 percentiles. We can find these percentiles both for a simulated sampling distribution or for a well-defined distribution, as long as we provide Python with the appropriate information.
This might seem counterintuitive, as we are using information about our sample to generate a guess about our population. To understand this, let's start by saying that this range would be a range of typical values for a sample statistic as calculated from our available data. Then, we're going to switch the order of the statement. This indicates that a sample statistic like the one we found would be reasonable if our parameter were anywhere in that range instead. Therefore, we'll say that the confidence interval that we calculated represents a range of reasonable values for the parameter.
Write a Conclusion in the Context of the Problem
Finally, we've generated our confidence interval and want to communicate our results to other stakeholders. What exactly does the confidence interval mean?
Informally, we might say something like: it is reasonable to claim that the population median price for a Chicago Airbnb is between \$120 and \$136 per night, with 90% confidence.
The formal interpretation is that we are 90% confident that the true population median price for a Chicago Airbnb falls in the range of \$120 and \$136 per night.
Confidence Interval Widths
Say that a stakeholder is not satisfied with a confidence interval. A common concern is that a confidence interval is too wide; that is, your stakeholder would like a narrower range of reasonable values. What can be changed to satisfy your stakeholder?
The two adjustable factors that affect the width of the confidence interval are the:
- sample size
- confidence level
Larger sample sizes result in narrower sampling distributions (recall this feature of the standard error from our sampling distribution module). This will also result in our confidence interval being narrower.
Larger confidence levels require a larger component of the sampling distribution to be included in the confidence interval. This will result in a wider confidence interval.
Therefore, if your stakeholder wants a narrower confidence interval, you could add more observations to your sample size or you could reduce your confidence level. It is also possible to estimate a desired sample size before gathering data that results in a confidence interval with limitations on the width of the confidence interval. We will skip over this calculation for our course, although you may encounter it in a future course.
Confidence Interval Misconceptions and Misinterpretations
We've discussed briefly what a confidence interval means. Equally important is what a confidence interval does not imply.
A confidence interval does not correspond to:
- the probability that the parameter is in the confidence interval
- a range of reasonable values for the sample data
- a range of reasonable values for a sample statistic
- a range of reasonable values for any future results from another sample
These last three misconceptions stem from misunderstanding that the confidence interval is about the parameter of interest and not about the sample or any of its corresponding characteristics.
For the first statement, consider that the population is already defined, and the corresponding parameter value for the population could then be calculated. It is a specific number, and it doesn't change. For example, it might be 120 or it could be 145. However, since the population is fixed, it is that exact number.
Once the confidence interval is calculated, then the confidence interval is also set and determined. It won't change. In this case, the parameter will either be contained in our confidence interval or it won't be, so the probability associated with the parameter being in the confidence interval is either 0 (the confidence interval isn't correct) or 1 (the confidence interval is correct).
Confidence Level Interpretation
We now understand how to calculate a confidence interval, what the confidence interval indicates, and what it doesn't indicate. However, we need to return to the second step where we set the confidence level for the interval. We know that this will have ramifications for the following steps of generating a confidence interval. But, what does it mean?
The confidence level means:
"If we gathered repeated random samples of the same size and calculated a CL% confidence interval for each, we would expect CL% of the resulting confidence intervals to contain the true parameter of interest."
Generally, this means that we expect CL% of our intervals to be correct. However, as we discussed above, we can't apply this reasoning to one specific interval after it's been calculated. This still does allow for variability and for different confidence intervals being generated from different samples.
Hypothesis Testing Decisions through Confidence Intervals
You may have noticed that many of the steps used for confidence intervals are shared with hypothesis testing. While there are distinctions between the two, we can also use confidence intervals to help us determine the result of a hypothesis test.
Suppose that a friend found it reported that the median price for all Chicago hotels is $160 per night. They suspect that Airbnbs are less expensive per night, and the population median price for Chicago Airbnbs is less expensive.
That is, the parameter of interest would be $M$ the population median price per night for all Chicago Airbnbs in March 2023. We can (and have) found the corresponding sample statistic, $m$ or the median price per night for the Chicago Airbnbs from our sample.
Because we don't have any data to analyze for Chicago hotels, we'll use this number as if it were true and treat this as a test for only one population. Our hypotheses would be:
$H_0: M = 160$
$H_a: M < 160$
What does the data say? If we've already generated a confidence interval, we don't need to repeat many of the steps for hypothesis testing. Instead, we can consider our calculated confidence interval as a range of reasonable values for our parameter. That is, it is reasonable that the population median price per night for all Chicago Airbnbs is between \$120 and \$136. In this case, the null value of 160 is not included in the range of reasonable values. Everything reasonable falls under the alternative hypothesis. We would want to reject the null hypothesis and adopt the alternative hypothesis as a more reasonable claim.
In this case, our confidence interval clearly supports our alternative hypothesis rather than our null hypothesis. However, in order to use confidence intervals to anticipate the decision for a hypothesis test, we need to ensure that we are using comparable confidence and significance levels:
- for a two-sided alternative hypothesis, use a confidence level of $1-\alpha$
- for a one-sided alternative hypothesis, use a confidence level of $1-2\times\alpha$
Save 10% on All AnalystPrep 2024 Study Packages with Coupon Code BLOG10 .
- Payment Plans
- Product List
- Partnerships

- Try Free Trial
- Study Packages
- Levels I, II & III Lifetime Package
- Video Lessons
- Study Notes
- Practice Questions
- Levels II & III Lifetime Package
- About the Exam
- About your Instructor
- Part I Study Packages
- Parts I & II Packages
- Part I & Part II Lifetime Package
- Part II Study Packages
- Exams P & FM Lifetime Package
- Quantitative Questions
- Verbal Questions
- Data Insight Questions
- Live Tutoring
- About your Instructors
- EA Practice Questions
- Data Sufficiency Questions
- Integrated Reasoning Questions

Hypothesis Testing
After completing this reading, you should be able to:
- Construct an appropriate null hypothesis and alternative hypothesis and distinguish between the two.
- Construct and apply confidence intervals for one-sided and two-sided hypothesis tests, and interpret the results of hypothesis tests with a specific level of confidence.
- Differentiate between a one-sided and a two-sided test and identify when to use each test.
- Explain the difference between Type I and Type II errors and how these relate to the size and power of a test.
- Understand how a hypothesis test and a confidence interval are related.
- Explain what the p-value of a hypothesis test measures.
- Interpret the results of hypothesis tests with a specific level of confidence.
- Identify the steps to test a hypothesis about the difference between two population means.
- Explain the problem of multiple testing and how it can bias results.
Hypothesis testing is defined as a process of determining whether a hypothesis is in line with the sample data. Hypothesis testing tries to test whether the observed data of the hypothesis is true. Hypothesis testing starts by stating the null hypothesis and the alternative hypothesis. The null hypothesis is an assumption of the population parameter. On the other hand, the alternative hypothesis states the parameter values (critical values) at which the null hypothesis is rejected. The critical values are determined by the distribution of the test statistic (when the null hypothesis is true) and the size of the test (which gives the size at which we reject the null hypothesis).
Components of the Hypothesis Testing
The elements of the test hypothesis include:
- The null hypothesis.
- The alternative hypothesis.
- The test statistic.
- The size of the hypothesis test and errors
- The critical value.
- The decision rule.
The Null hypothesis
As stated earlier, the first stage of the hypothesis test is the statement of the null hypothesis. The null hypothesis is the statement concerning the population parameter values. It brings out the notion that “there is nothing about the data.”
The null hypothesis , denoted as H 0 , represents the current state of knowledge about the population parameter that’s the subject of the test. In other words, it represents the “status quo.” For example, the U.S Food and Drug Administration may walk into a cooking oil manufacturing plant intending to confirm that each 1 kg oil package has, say, 0.15% cholesterol and not more. The inspectors will formulate a hypothesis like:
H 0 : Each 1 kg package has 0.15% cholesterol.
A test would then be carried out to confirm or reject the null hypothesis.
Other typical statements of H 0 include:
$$H_0:\mu={\mu}_0$$
$$H_0:\mu≤{\mu}_0$$
\(μ\) = true population mean and,
\(μ_0\)= the hypothesized population mean.
The Alternative Hypothesis
The alternative hypothesis , denoted H 1 , is a contradiction of the null hypothesis. The null hypothesis determines the values of the population parameter at which the null hypothesis is rejected. Thus, rejecting the H 0 makes H 1 valid. We accept the alternative hypothesis when the “status quo” is discredited and found to be untrue.
Using our FDA example above, the alternative hypothesis would be:
H 1 : Each 1 kg package does not have 0.15% cholesterol.
The typical statements of H1 include:
$$H_1:\mu \neq {\mu}_0$$
$$H_1:\mu > {\mu}_0$$
Note that we have stated the alternative hypothesis, which contradicted the above statement of the null hypothesis.
The Test Statistic
A test statistic is a standardized value computed from sample information when testing hypotheses. It compares the given data with what we would expect under the null hypothesis. Thus, it is a major determinant when deciding whether to reject H 0 , the null hypothesis.
We use the test statistic to gauge the degree of agreement between sample data and the null hypothesis. Analysts use the following formula when calculating the test statistic.
$$ \text{Test Statistic}= \frac{(\text{Sample Statistic–Hypothesized Value})}{(\text{Standard Error of the Sample Statistic})}$$
The test statistic is a random variable that changes from one sample to another. Test statistics assume a variety of distributions. We shall focus on normally distributed test statistics because it is used hypotheses concerning the means, regression coefficients, and other econometric models.
We shall consider the hypothesis test on the mean. Consider a null hypothesis \(H_0:μ=μ_0\). Assume that the data used is iid, and asymptotic normally distributed as:
$$\sqrt{n} (\hat{\mu}-\mu) \sim N(0, {\sigma}^2)$$
Where \({\sigma}^2\) is the variance of the sequence of the iid random variable used. The asymptotic distribution leads to the test statistic:
$$T=\frac{\hat{\mu}-{\mu}_0}{\sqrt{\frac{\hat{\sigma}^2}{n}}}\sim N(0,1)$$
Note this is consistent with our initial definition of the test statistic.
The following table gives a brief outline of the various test statistics used regularly, based on the distribution that the data is assumed to follow:
$$\begin{array}{ll} \textbf{Hypothesis Test} & \textbf{Test Statistic}\\ \text{Z-test} & \text{z-statistic} \\ \text{Chi-Square Test} & \text{Chi-Square statistic}\\ \text{t-test} & \text{t-statistic} \\ \text{ANOVA} & \text{F-statistic}\\ \end{array}$$ We can subdivide the set of values that can be taken by the test statistic into two regions: One is called the non-rejection region, which is consistent with H 0 and the rejection region (critical region), which is inconsistent with H 0 . If the test statistic has a value found within the critical region, we reject H 0 .
Just like with any other statistic, the distribution of the test statistic must be specified entirely under H 0 when H 0 is true.
The Size of the Hypothesis Test and the Type I and Type II Errors
While using sample statistics to draw conclusions about the parameters of the population as a whole, there is always the possibility that the sample collected does not accurately represent the population. Consequently, statistical tests carried out using such sample data may yield incorrect results that may lead to erroneous rejection (or lack thereof) of the null hypothesis. We have two types of errors:
Type I Error
Type I error occurs when we reject a true null hypothesis. For example, a type I error would manifest in the form of rejecting H 0 = 0 when it is actually zero.
Type II Error
Type II error occurs when we fail to reject a false null hypothesis. In such a scenario, the test provides insufficient evidence to reject the null hypothesis when it’s false.
The level of significance denoted by α represents the probability of making a type I error, i.e., rejecting the null hypothesis when, in fact, it’s true. α is the direct opposite of β, which is taken to be the probability of making a type II error within the bounds of statistical testing. The ideal but practically impossible statistical test would be one that simultaneously minimizes α and β. We use α to determine critical values that subdivide the distribution into the rejection and the non-rejection regions.
The Critical Value and the Decision Rule
The decision to reject or not to reject the null hypothesis is based on the distribution assumed by the test statistic. This means if the variable involved follows a normal distribution, we use the level of significance (α) of the test to come up with critical values that lie along with the standard normal distribution.
The decision rule is a result of combining the critical value (denoted by \(C_α\)), the alternative hypothesis, and the test statistic (T). The decision rule is to whether to reject the null hypothesis in favor of the alternative hypothesis or fail to reject the null hypothesis.
For the t-test, the decision rule is dependent on the alternative hypothesis. When testing the two-side alternative, the decision is to reject the null hypothesis if \(|T|>C_α\). That is, reject the null hypothesis if the absolute value of the test statistic is greater than the critical value. When testing on the one-sided, decision rule, reject the null hypothesis if \(T<C_α\) when using a one-sided lower alternative and if \(T>C_α\) when using a one-sided upper alternative. When a null hypothesis is rejected at an α significance level, we say that the result is significant at α significance level.
Note that prior to decision-making, one must decide whether the test should be one-tailed or two-tailed. The following is a brief summary of the decision rules under different scenarios:
Left One-tailed Test
H 1 : parameter < X
Decision rule: Reject H 0 if the test statistic is less than the critical value. Otherwise, do not reject H 0.
Right One-tailed Test
H 1 : parameter > X
Decision rule: Reject H 0 if the test statistic is greater than the critical value. Otherwise, do not reject H 0.
Two-tailed Test
H 1 : parameter ≠ X (not equal to X)
Decision rule: Reject H 0 if the test statistic is greater than the upper critical value or less than the lower critical value.
H 0 : μ < μ 0 vs. H 1 : μ > μ 0.
The second graph represents the rejection region when the alternative is a one-sided upper. The null hypothesis, in this case, is stated as:
H 0 : μ > μ 0 vs. H 1 : μ < μ 0.

Example: Hypothesis Test on the Mean
Consider the returns from a portfolio \(X=(x_1,x_2,\dots, x_n)\) from 1980 through 2020. The approximated mean of the returns is 7.50%, with a standard deviation of 17%. We wish to determine whether the expected value of the return is different from 0 at a 5% significance level.
We start by stating the two-sided hypothesis test:
H 0 : μ =0 vs. H 1 : μ ≠ 0
The test statistic is:
$$T=\frac{\hat{\mu}-{\mu}_0}{\sqrt{\frac{\hat{\sigma}^2}{n}}} \sim N(0,1)$$
In this case, we have,
\(\hat{μ}\)=0.075
\(\hat{\sigma}^2\)=0.17 2
$$T=\frac{0.075-0}{\sqrt{\frac{0.17^2}{40}}} \approx 2.79$$
At the significance level, \(α=5\%\),the critical value is \(±1.96\). Since this is a two-sided test, the rejection regions are ( \(-\infty,-1.96\) ) and (\(1.96, \infty \) ) as shown in the diagram below:
The example above is an example of a Z-test (which is mostly emphasized in this chapter and immediately follows from the central limit theorem (CLT)). However, we can use the Student’s t-distribution if the random variables are iid and normally distributed and that the sample size is small (n<30).
In Student’s t-distribution, we used the unbiased estimator of variance. That is:
$$s^2=\frac{\hat{\mu}-{\mu}_0}{\sqrt{\frac{s^2}{n}}}$$
Therefore the test statistic for \(H_0=μ_0\) is given by:
$$T=\frac{\hat{\mu}-{\mu}_0}{\sqrt{\frac{s^2}{n}}} \sim t_{n-1}$$
The Type II Error and the Test Power
The power of a test is the direct opposite of the level of significance. While the level of relevance gives us the probability of rejecting the null hypothesis when it’s, in fact, true, the power of a test gives the probability of correctly discrediting and rejecting the null hypothesis when it is false. In other words, it gives the likelihood of rejecting H 0 when, indeed, it’s false. Denoting the probability of type II error by \(\beta\), the power test is given by:
$$ \text{Power of a Test}=1–\beta $$
The power test measures the likelihood that the false null hypothesis is rejected. It is influenced by the sample size, the length between the hypothesized parameter and the true value, and the size of the test.
Confidence Intervals
A confidence interval can be defined as the range of parameters at which the true parameter can be found at a confidence level. For instance, a 95% confidence interval constitutes the set of parameter values where the null hypothesis cannot be rejected when using a 5% test size. Therefore, a 1-α confidence interval contains values that cannot be disregarded at a test size of α.
It is important to note that the confidence interval depends on the alternative hypothesis statement in the test. Let us start with the two-sided test alternatives.
$$ H_0:μ=0$$
$$H_1:μ≠0$$
Then the \(1-α\) confidence interval is given by:
$$\left[\hat{\mu} -C_{\alpha} \times \frac{\hat {\sigma}}{\sqrt{n}} ,\hat{\mu} + C_{\alpha} \times \frac{\hat {\sigma}}{\sqrt{n}} \right]$$
\(C_α\) is the critical value at \(α\) test size.
Example: Calculating Two-Sided Alternative Confidence Intervals
Consider the returns from a portfolio \(X=(x_1,x_2,…, x_n)\) from 1980 through 2020. The approximated mean of the returns is 7.50%, with a standard deviation of 17%. Calculate the 95% confidence interval for the portfolio return.
The \(1-\alpha\) confidence interval is given by:
$$\begin{align*}&\left[\hat{\mu}-C_{\alpha} \times \frac{\hat {\sigma}}{\sqrt{n}} ,\hat{\mu} + C_{\alpha} \times \frac{\hat {\sigma}}{\sqrt{n}} \right]\\& =\left[0.0750-1.96 \times \frac{0.17}{\sqrt{40}}, 0.0750+1.96 \times \frac{0.17}{\sqrt{40}} \right]\\&=[0.02232,0.1277]\end{align*}$$
Thus, the confidence intervals imply any value of the null between 2.23% and 12.77% cannot be rejected against the alternative.
One-Sided Alternative
For the one-sided alternative, the confidence interval is given by either:
$$\left(-\infty ,\hat{\mu} +C_{\alpha} \times \frac{\hat{\sigma}}{\sqrt{n}} \right )$$
for the lower alternative
$$\left ( \hat{\mu} +C_{\alpha} \times \frac{\hat{\sigma}}{\sqrt{n}},\infty \right )$$
for the upper alternative.
Example: Calculating the One-Sided Alternative Confidence Interval
Assume that we were conducting the following one-sided test:
\(H_0:μ≤0\)
\(H_1:μ>0\)
The 95% confidence interval for the portfolio return is:
$$\begin{align*}&=\left(-\infty ,\hat{\mu} +C_{\alpha} \times \frac{\hat{\sigma}}{\sqrt{n}} \right )\\&=\left(-\infty ,0.0750+1.645\times \frac{0.17}{\sqrt{40}}\right)\\&=(-\infty, 0.1192)\end{align*}$$
On the other hand, if the hypothesis test was:
\(H_0:μ>0\)
\(H_1:μ≤0\)
The 95% confidence interval would be:
$$=\left(-\infty ,\hat{\mu} +C_{\alpha} \times \frac{\hat{\sigma}}{\sqrt{n}} \right )$$
$$=\left(-\infty ,0.0750+1.645\times \frac{0.17}{\sqrt{40}}\right)=(0.1192, \infty)$$
Note that the critical value decreased from 1.96 to 1.645 due to a change in the direction of the change.
The p-Value
When carrying out a statistical test with a fixed value of the significance level (α), we merely compare the observed test statistic with some critical value. For example, we might “reject H 0 using a 5% test” or “reject H 0 at 1% significance level”. The problem with this ‘classical’ approach is that it does not give us details about the strength of the evidence against the null hypothesis.
Determination of the p-value gives statisticians a more informative approach to hypothesis testing. The p-value is the lowest level at which we can reject H 0 . This means that the strength of the evidence against H 0 increases as the p-value becomes smaller. The test statistic depends on the alternative.
The p-Value for One-Tailed Test Alternative
For one-tailed tests, the p-value is given by the probability that lies below the calculated test statistic for left-tailed tests. Similarly, the likelihood that lies above the test statistic in right-tailed tests gives the p-value.
Denoting the test statistic by T, the p-value for \(H_1:μ>0\) is given by:
$$P(Z>|T|)=1-P(Z≤|T|)=1- \Phi (|T|) $$
Conversely , for \(H_1:μ≤0 \) the p-value is given by:
$$ P(Z≤|T|)= \Phi (|T|)$$
Where z is a standard normal random variable, the absolute value of T (|T|) ensures that the right tail is measured whether T is negative or positive.
The p-Value for Two-Tailed Test Alternative
If the test is two-tailed, this value is given by the sum of the probabilities in the two tails. We start by determining the probability lying below the negative value of the test statistic. Then, we add this to the probability lying above the positive value of the test statistic. That is the p-value for the two-tailed hypothesis test is given by:
$$2\left[1-\Phi [|T|\right]$$
Example 1: p-Value for One-Sided Alternative
Let θ represent the probability of obtaining a head when a coin is tossed. Suppose we toss the coin 200 times, and heads come up in 85 of the trials. Test the following hypothesis at 5% level of significance.
H 0 : θ = 0.5
H 1 : θ < 0.5
First, not that repeatedly tossing a coin follows a binomial distribution.
Our p-value will be given by P(X < 85) where X `binomial(200,0.5) with mean 100(np=200*0.5), assuming H 0 is true.
$$\begin{align*}P\left [ z< \frac{85.5-100}{\sqrt{50}} \right]&=P(Z<-2.05)\\&=1–0.97982=0.02018 \end{align*}$$
Recall that for a binomial distribution, the variance is given by:
$$np(1-p)=200(0.5)(1-0.5)=50$$
(We have applied the Central Limit Theorem by taking the binomial distribution as approx. normal)
Since the probability is less than 0.05, H 0 is extremely unlikely, and we actually have strong evidence against H 0 that favors H 1 . Thus, clearly expressing this result, we could say:
“There is very strong evidence against the hypothesis that the coin is fair. We, therefore, conclude that the coin is biased against heads.”
Remember, failure to reject H 0 does not mean it’s true. It means there’s insufficient evidence to justify rejecting H 0, given a certain level of significance.
Example 2: p-Value for Two-Sided Alternative
A CFA candidate conducts a statistical test about the mean value of a random variable X.
H 0 : μ = μ 0 vs. H 1 : μ ≠ μ 0
She obtains a test statistic of 2.2. Given a 5% significance level, determine and interpret the p-value
$$ \text{P-value}=2P(Z>2.2)=2[1–P(Z≤2.2)] =1.39\%×2=2.78\%$$
(We have multiplied by two since this is a two-tailed test)
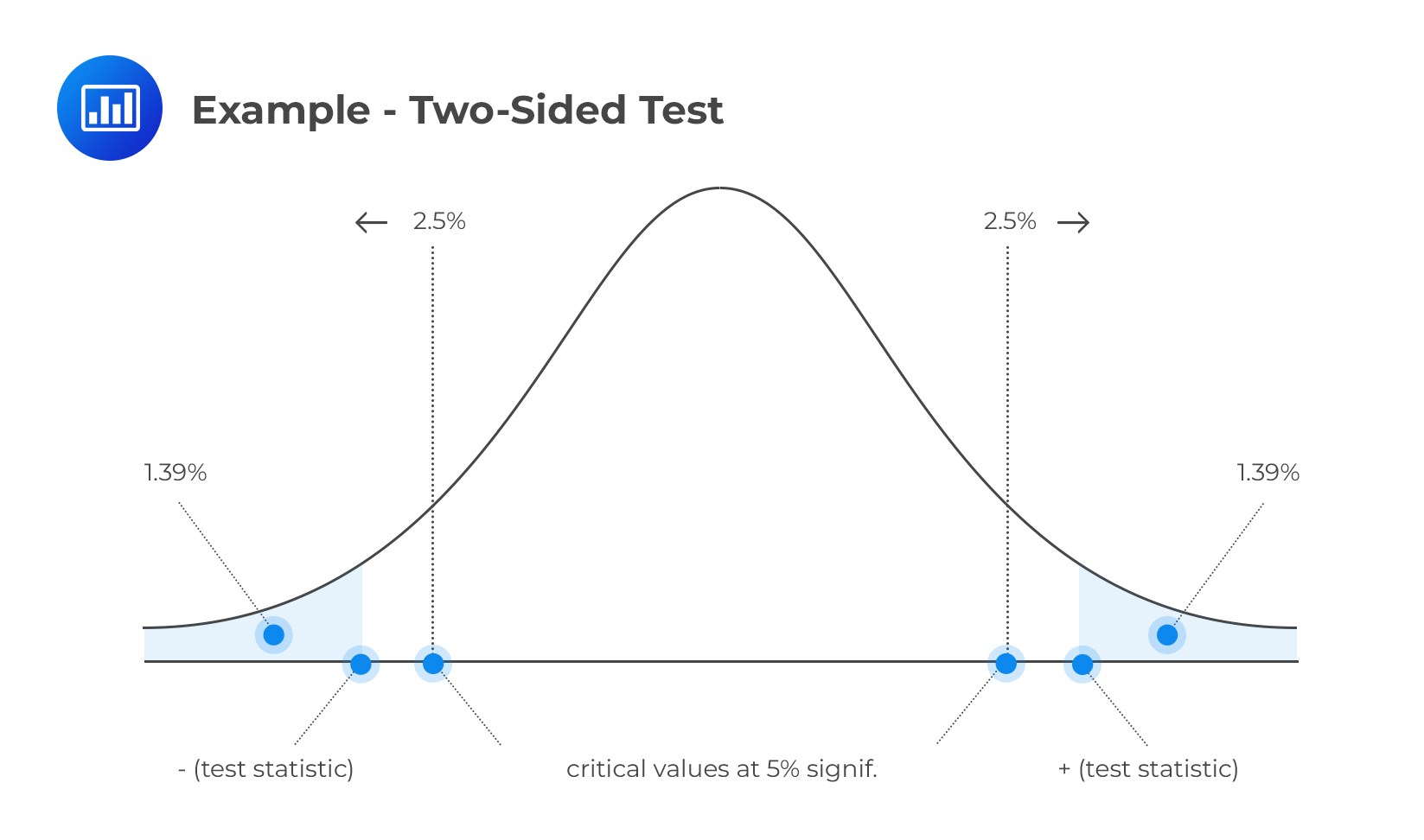
The p-value (2.78%) is less than the level of significance (5%). Therefore, we have sufficient evidence to reject H 0 . In fact, the evidence is so strong that we would also reject H 0 at significance levels of 4% and 3%. However, at significance levels of 2% or 1%, we would not reject H 0 since the p-value surpasses these values.
Hypothesis about the Difference between Two Population Means.
It’s common for analysts to be interested in establishing whether there exists a significant difference between the means of two different populations. For instance, they might want to know whether the average returns for two subsidiaries of a given company exhibit significant differences.
Now, consider a bivariate random variable:
$$W_i=[X_i,Y_i]$$
Assume that the components \(X_i\) and \(Y_i\)are both iid and are correlated. That is: \(\text{Corr} (X_i,Y_i )≠0\)
Now, suppose that we want to test the hypothesis that:
$$H_0:μ_X=μ_Y$$
$$H_1:μ_X≠μ_Y$$
In other words, we want to test whether the constituent random variables have equal means. Note that the hypothesis statement above can be written as:
$$H_0:μ_X-μ_Y=0$$
$$H_1:μ_X-μ_Y≠0$$
To execute this test, consider the variable:
$$Z_i=X_i-Y_i$$
Therefore, considering the above random variable, if the null hypothesis is correct then,
$$E(Z_i)=E(X_i)-E(Y_i)=μ_X-μ_Y=0$$
Intuitively, this can be considered as a standard hypothesis test of
H 0 : μ Z =0 vs. H 1 : μ Z ≠ 0.
The tests statistic is given by:
$$T=\frac{\hat{\mu}_z}{\sqrt{\frac{\hat{\sigma}^2_z}{n}}} \sim N(0,1)$$
Note that the test statistic formula accounts for the correction between \(X_i \) and \(Y_i\). It is easy to see that:
$$V(Z_i)=V(X_i )+V(Y_i)-2COV(X_i, Y_i)$$
Which can be denoted as:
$$\hat{\sigma}^2_z =\hat{\sigma}^2_X +\hat{\sigma}^2_Y – 2{\sigma}_{XY}$$
$$ \hat{\mu}_z ={\mu}_X-{\mu}_Y $$
And thus the test statistic formula can be written as:
$$T=\frac{{\mu}_X -{\mu}_Y}{\sqrt{\frac{\hat{\sigma}^2_X +\hat{\sigma}^2_Y – 2{\sigma}_{XY}}{n}}}$$
This formula indicates that correlation plays a crucial role in determining the magnitude of the test statistic.
Another special case of the test statistic is when \(X_i\), and \(Y_i\) are iid and independent. The test statistic is given by:
$$T=\frac{{\mu}_X -{\mu}_Y}{\sqrt{\frac{\hat{\sigma}^2_X}{n_X}+\frac{\hat{\sigma}^2_Y}{n_Y}}}$$
Where \(n_X\) and \(n_Y\) are the sample sizes of \(X_i\), and \(Y_i\) respectively.
Example: Hypothesis Test on Two Means
An investment analyst wants to test whether there is a significant difference between the means of the two portfolios at a 95% level. The first portfolio X consists of 30 government-issued bonds and has a mean of 10% and a standard deviation of 2%. The second portfolio Y consists of 30 private bonds with a mean of 14% and a standard deviation of 3%. The correlation between the two portfolios is 0.7. Calculate the null hypothesis and state whether the null hypothesis is rejected or otherwise.
The hypothesis statement is given by:
H 0 : μ X – μ Y =0 vs. H 1 : μ X – μ Y ≠ 0.
Note that this is a two-tailed test. At 95% level, the test size is α=5% and thus the critical value \(C_α=±1.96\).
Recall that:
$$Cov(X, Y)=σ_{XY}=ρ_{XY} σ_X σ_Y$$
Where ρ_XY is the correlation coefficient between X and Y.
Now the test statistic is given by:
$$T=\frac{{\mu}_X -{\mu}_Y}{\sqrt{\frac{\hat{\sigma}^2_X +\hat{\sigma}^2_Y – 2{\sigma}_{XY}}{n}}}=\frac{{\mu}_X -{\mu}_Y}{\sqrt{\frac{\hat{\sigma}^2_X +\hat{\sigma}^2_Y – 2{\rho}_{XY} {\sigma}_X {\sigma}_Y}{n}}}$$
$$=\frac{0.10-0.14}{\sqrt{\frac{0.02^2 +0.03^2-2\times 0.7 \times 0.02 \times 0.03}{30}}}=-10.215$$
The test statistic is far much less than -1.96. Therefore the null hypothesis is rejected at a 95% level.
The Problem of Multiple Testing
Multiple testing occurs when multiple multiple hypothesis tests are conducted on the same data set. The reuse of data results in spurious results and unreliable conclusions that do not hold up to scrutiny. The fundamental problem with multiple testing is that the test size (i.e., the probability that a true null is rejected) is only applicable for a single test. However, repeated testing creates test sizes that are much larger than the assumed size of alpha and therefore increases the probability of a Type I error.
Some control methods have been developed to combat multiple testing. These include Bonferroni correction, the False Discovery Rate (FDR), and Familywise Error Rate (FWER).
Practice Question An experiment was done to find out the number of hours that candidates spend preparing for the FRM part 1 exam. For a sample of 10 students , the average study time was found to be 312.7 hours, with a standard deviation of 7.2 hours. What is the 95% confidence interval for the mean study time of all candidates? A. [307.5, 317.9] B. [310, 317] C. [300, 317] D. [307.5, 312.2] The correct answer is A. To calculate the 95% confidence interval for the mean study time of all candidates, we can use the formula for the confidence interval when the population variance is unknown: \[\text{Confidence Interval} = \bar{X} \pm t_{1-\frac{\alpha}{2}} \times \frac{s}{\sqrt{n}}\] Where: \(\bar{X}\) is the sample mean \(t_{1-\frac{\alpha}{2}}\) is the t-score corresponding to the desired confidence level and degrees of freedom \(s\) is the sample standard deviation \(n\) is the sample size In this case: \(\bar{X} = 312.7\) hours (the average study time) \(s = 7.2\) hours (the standard deviation of study time) \(n = 10\) students (the sample size) To find the t-score (\(t_{1-\frac{\alpha}{2}}\)), we look at the t-table for the 95% confidence level (which corresponds to \(\alpha = 0.05\)) and 9 degrees of freedom (\(n – 1 = 10 – 1 = 9\)). The t-score is 2.262. Now, we can plug these values into the confidence interval formula: \[\text{Confidence Interval} = 312.7 \pm 2.262 \times \frac{7.2}{\sqrt{10}}\] Calculating the margin of error: \[\text{Margin of Error} = 2.262 \times \frac{7.2}{\sqrt{10}} \approx 5.2\] So the confidence interval is: \[\text{Confidence Interval} = 312.7 \pm 5.2 = [307.5, 317.9]\] Therefore, the 95% confidence interval for the mean study time of all candidates is [307.5, 317.9] hours.
Offered by AnalystPrep

Approaches to Asset Allocation
Random variables.
After completing this reading, you should be able to: Describe and distinguish a... Read More
Bayesian Analysis
After completing this reading you should be able to: Describe Bayes’ theorem and... Read More
After completing this reading, you should be able to: Identify the major risks... Read More
Deciphering the Liquidity and Credit C ...
After completing this reading, you should be able to: Describe the key factors... Read More
Leave a Comment Cancel reply
You must be logged in to post a comment.
Using a confidence interval to decide whether to reject the null hypothesis
Suppose that you do a hypothesis test. Remember that the decision to reject the null hypothesis (H 0 ) or fail to reject it can be based on the p-value and your chosen significance level (also called α). If the p-value is less than or equal to α, you reject H 0 ; if it is greater than α, you fail to reject H 0 .
- If the reference value specified in H 0 lies outside the interval (that is, is less than the lower bound or greater than the upper bound), you can reject H 0 .
- If the reference value specified in H 0 lies within the interval (that is, is not less than the lower bound or greater than the upper bound), you fail to reject H 0 .
- Minitab.com
- License Portal
- Cookie Settings
You are now leaving support.minitab.com.
Click Continue to proceed to:
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Null Hypothesis: Definition, Rejecting & Examples
By Jim Frost 6 Comments
What is a Null Hypothesis?
The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test.

- Null Hypothesis H 0 : No effect exists in the population.
- Alternative Hypothesis H A : The effect exists in the population.
In every study or experiment, researchers assess an effect or relationship. This effect can be the effectiveness of a new drug, building material, or other intervention that has benefits. There is a benefit or connection that the researchers hope to identify. Unfortunately, no effect may exist. In statistics, we call this lack of an effect the null hypothesis. Researchers assume that this notion of no effect is correct until they have enough evidence to suggest otherwise, similar to how a trial presumes innocence.
In this context, the analysts don’t necessarily believe the null hypothesis is correct. In fact, they typically want to reject it because that leads to more exciting finds about an effect or relationship. The new vaccine works!
You can think of it as the default theory that requires sufficiently strong evidence to reject. Like a prosecutor, researchers must collect sufficient evidence to overturn the presumption of no effect. Investigators must work hard to set up a study and a data collection system to obtain evidence that can reject the null hypothesis.
Related post : What is an Effect in Statistics?
Null Hypothesis Examples
Null hypotheses start as research questions that the investigator rephrases as a statement indicating there is no effect or relationship.
| Does the vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does the new additive increase product strength? | The additive does not affect mean product strength. |
| Does the exercise intervention increase bone mineral density? | The intervention does not affect bone mineral density. |
| As screen time increases, does test performance decrease? | There is no relationship between screen time and test performance. |
After reading these examples, you might think they’re a bit boring and pointless. However, the key is to remember that the null hypothesis defines the condition that the researchers need to discredit before suggesting an effect exists.
Let’s see how you reject the null hypothesis and get to those more exciting findings!
When to Reject the Null Hypothesis
So, you want to reject the null hypothesis, but how and when can you do that? To start, you’ll need to perform a statistical test on your data. The following is an overview of performing a study that uses a hypothesis test.
The first step is to devise a research question and the appropriate null hypothesis. After that, the investigators need to formulate an experimental design and data collection procedures that will allow them to gather data that can answer the research question. Then they collect the data. For more information about designing a scientific study that uses statistics, read my post 5 Steps for Conducting Studies with Statistics .
After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.
When the sample data provide sufficient evidence, you can reject the null hypothesis. In a hypothesis test, this process involves comparing the p-value to your significance level .
Rejecting the Null Hypothesis
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!
When you can reject the null hypothesis, your results are statistically significant. Learn more about Statistical Significance: Definition & Meaning .
Failing to Reject the Null Hypothesis
Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. The sample data provides insufficient data to conclude that the effect exists in the population. When the p-value is high, the null must fly!
Note that failing to reject the null is not the same as proving it. For more information about the difference, read my post about Failing to Reject the Null .
That’s a very general look at the process. But I hope you can see how the path to more exciting findings depends on being able to rule out the less exciting null hypothesis that states there’s nothing to see here!
Let’s move on to learning how to write the null hypothesis for different types of effects, relationships, and tests.
Related posts : How Hypothesis Tests Work and Interpreting P-values
How to Write a Null Hypothesis
The null hypothesis varies by the type of statistic and hypothesis test. Remember that inferential statistics use samples to draw conclusions about populations. Consequently, when you write a null hypothesis, it must make a claim about the relevant population parameter . Further, that claim usually indicates that the effect does not exist in the population. Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests.
Related posts : Descriptive vs. Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics
Group Means
T-tests and ANOVA assess the differences between group means. For these tests, the null hypothesis states that there is no difference between group means in the population. In other words, the experimental conditions that define the groups do not affect the mean outcome. Mu (µ) is the population parameter for the mean, and you’ll need to include it in the statement for this type of study.
For example, an experiment compares the mean bone density changes for a new osteoporosis medication. The control group does not receive the medicine, while the treatment group does. The null states that the mean bone density changes for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group means are equal in the population: µ 1 = µ 2 , or µ 1 – µ 2 = 0
- Alternative Hypothesis H A : Group means are not equal in the population: µ 1 ≠ µ 2 , or µ 1 – µ 2 ≠ 0.
Group Proportions
Proportions tests assess the differences between group proportions. For these tests, the null hypothesis states that there is no difference between group proportions. Again, the experimental conditions did not affect the proportion of events in the groups. P is the population proportion parameter that you’ll need to include.
For example, a vaccine experiment compares the infection rate in the treatment group to the control group. The treatment group receives the vaccine, while the control group does not. The null states that the infection rates for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group proportions are equal in the population: p 1 = p 2 .
- Alternative Hypothesis H A : Group proportions are not equal in the population: p 1 ≠ p 2 .
Correlation and Regression Coefficients
Some studies assess the relationship between two continuous variables rather than differences between groups.
In these studies, analysts often use either correlation or regression analysis . For these tests, the null states that there is no relationship between the variables. Specifically, it says that the correlation or regression coefficient is zero. As one variable increases, there is no tendency for the other variable to increase or decrease. Rho (ρ) is the population correlation parameter and beta (β) is the regression coefficient parameter.
For example, a study assesses the relationship between screen time and test performance. The null states that there is no correlation between this pair of variables. As screen time increases, test performance does not tend to increase or decrease.
- Null Hypothesis H 0 : The correlation in the population is zero: ρ = 0.
- Alternative Hypothesis H A : The correlation in the population is not zero: ρ ≠ 0.
For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
The preceding examples are all for two-tailed hypothesis tests. To learn about one-tailed tests and how to write a null hypothesis for them, read my post One-Tailed vs. Two-Tailed Tests .
Related post : Understanding Correlation
Neyman, J; Pearson, E. S. (January 1, 1933). On the Problem of the most Efficient Tests of Statistical Hypotheses . Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337.
Share this:

Reader Interactions
January 11, 2024 at 2:57 pm
Thanks for the reply.
January 10, 2024 at 1:23 pm
Hi Jim, In your comment you state that equivalence test null and alternate hypotheses are reversed. For hypothesis tests of data fits to a probability distribution, the null hypothesis is that the probability distribution fits the data. Is this correct?
January 10, 2024 at 2:15 pm
Those two separate things, equivalence testing and normality tests. But, yes, you’re correct for both.
Hypotheses are switched for equivalence testing. You need to “work” (i.e., collect a large sample of good quality data) to be able to reject the null that the groups are different to be able to conclude they’re the same.
With typical hypothesis tests, if you have low quality data and a low sample size, you’ll fail to reject the null that they’re the same, concluding they’re equivalent. But that’s more a statement about the low quality and small sample size than anything to do with the groups being equal.
So, equivalence testing make you work to obtain a finding that the groups are the same (at least within some amount you define as a trivial difference).
For normality testing, and other distribution tests, the null states that the data follow the distribution (normal or whatever). If you reject the null, you have sufficient evidence to conclude that your sample data don’t follow the probability distribution. That’s a rare case where you hope to fail to reject the null. And it suffers from the problem I describe above where you might fail to reject the null simply because you have a small sample size. In that case, you’d conclude the data follow the probability distribution but it’s more that you don’t have enough data for the test to register the deviation. In this scenario, if you had a larger sample size, you’d reject the null and conclude it doesn’t follow that distribution.
I don’t know of any equivalence testing type approach for distribution fit tests where you’d need to work to show the data follow a distribution, although I haven’t looked for one either!
February 20, 2022 at 9:26 pm
Is a null hypothesis regularly (always) stated in the negative? “there is no” or “does not”
February 23, 2022 at 9:21 pm
Typically, the null hypothesis includes an equal sign. The null hypothesis states that the population parameter equals a particular value. That value is usually one that represents no effect. In the case of a one-sided hypothesis test, the null still contains an equal sign but it’s “greater than or equal to” or “less than or equal to.” If you wanted to translate the null hypothesis from its native mathematical expression, you could use the expression “there is no effect.” But the mathematical form more specifically states what it’s testing.
It’s the alternative hypothesis that typically contains does not equal.
There are some exceptions. For example, in an equivalence test where the researchers want to show that two things are equal, the null hypothesis states that they’re not equal.
In short, the null hypothesis states the condition that the researchers hope to reject. They need to work hard to set up an experiment and data collection that’ll gather enough evidence to be able to reject the null condition.
February 15, 2022 at 9:32 am
Dear sir I always read your notes on Research methods.. Kindly tell is there any available Book on all these..wonderfull Urgent
Comments and Questions Cancel reply

- Quality Improvement
- Talk To Minitab
Understanding Hypothesis Tests: Confidence Intervals and Confidence Levels
Topics: Hypothesis Testing , Data Analysis , Statistics
In this series of posts, I show how hypothesis tests and confidence intervals work by focusing on concepts and graphs rather than equations and numbers.
Previously, I used graphs to show what statistical significance really means . In this post, I’ll explain both confidence intervals and confidence levels, and how they’re closely related to P values and significance levels.
How to Correctly Interpret Confidence Intervals and Confidence Levels
A confidence interval is a range of values that is likely to contain an unknown population parameter. If you draw a random sample many times, a certain percentage of the confidence intervals will contain the population mean. This percentage is the confidence level.
Most frequently, you’ll use confidence intervals to bound the mean or standard deviation, but you can also obtain them for regression coefficients, proportions, rates of occurrence (Poisson), and for the differences between populations.
Just as there is a common misconception of how to interpret P values , there’s a common misconception of how to interpret confidence intervals. In this case, the confidence level is not the probability that a specific confidence interval contains the population parameter.
The confidence level represents the theoretical ability of the analysis to produce accurate intervals if you are able to assess many intervals and you know the value of the population parameter. For a specific confidence interval from one study, the interval either contains the population value or it does not—there’s no room for probabilities other than 0 or 1. And you can't choose between these two possibilities because you don’t know the value of the population parameter.
"The parameter is an unknown constant and no probability statement concerning its value may be made." —Jerzy Neyman, original developer of confidence intervals.
This will be easier to understand after we discuss the graph below . . .
With this in mind, how do you interpret confidence intervals?
Confidence intervals serve as good estimates of the population parameter because the procedure tends to produce intervals that contain the parameter. Confidence intervals are comprised of the point estimate (the most likely value) and a margin of error around that point estimate. The margin of error indicates the amount of uncertainty that surrounds the sample estimate of the population parameter.
In this vein, you can use confidence intervals to assess the precision of the sample estimate. For a specific variable, a narrower confidence interval [90 110] suggests a more precise estimate of the population parameter than a wider confidence interval [50 150].
Confidence Intervals and the Margin of Error
Let’s move on to see how confidence intervals account for that margin of error. To do this, we’ll use the same tools that we’ve been using to understand hypothesis tests. I’ll create a sampling distribution using probability distribution plots , the t-distribution , and the variability in our data. We'll base our confidence interval on the energy cost data set that we've been using.
When we looked at significance levels , the graphs displayed a sampling distribution centered on the null hypothesis value, and the outer 5% of the distribution was shaded. For confidence intervals, we need to shift the sampling distribution so that it is centered on the sample mean and shade the middle 95%.
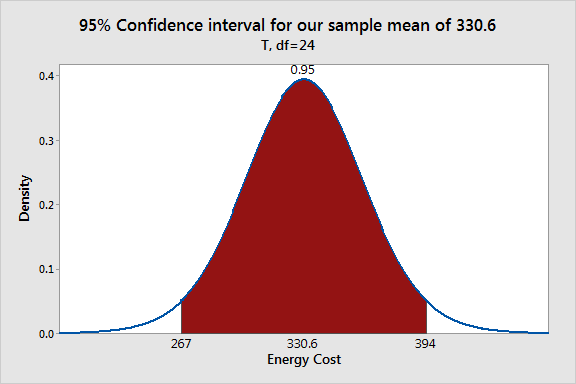
The shaded area shows the range of sample means that you’d obtain 95% of the time using our sample mean as the point estimate of the population mean. This range [267 394] is our 95% confidence interval.
Using the graph, it’s easier to understand how a specific confidence interval represents the margin of error, or the amount of uncertainty, around the point estimate. The sample mean is the most likely value for the population mean given the information that we have. However, the graph shows it would not be unusual at all for other random samples drawn from the same population to obtain different sample means within the shaded area. These other likely sample means all suggest different values for the population mean. Hence, the interval represents the inherent uncertainty that comes with using sample data.
You can use these graphs to calculate probabilities for specific values. However, notice that you can’t place the population mean on the graph because that value is unknown. Consequently, you can’t calculate probabilities for the population mean, just as Neyman said!
Why P Values and Confidence Intervals Always Agree About Statistical Significance
You can use either P values or confidence intervals to determine whether your results are statistically significant. If a hypothesis test produces both, these results will agree.
The confidence level is equivalent to 1 – the alpha level. So, if your significance level is 0.05, the corresponding confidence level is 95%.
- If the P value is less than your significance (alpha) level, the hypothesis test is statistically significant.
- If the confidence interval does not contain the null hypothesis value, the results are statistically significant.
- If the P value is less than alpha, the confidence interval will not contain the null hypothesis value.
For our example, the P value (0.031) is less than the significance level (0.05), which indicates that our results are statistically significant. Similarly, our 95% confidence interval [267 394] does not include the null hypothesis mean of 260 and we draw the same conclusion.
To understand why the results always agree, let’s recall how both the significance level and confidence level work.
- The significance level defines the distance the sample mean must be from the null hypothesis to be considered statistically significant.
- The confidence level defines the distance for how close the confidence limits are to sample mean.
Both the significance level and the confidence level define a distance from a limit to a mean. Guess what? The distances in both cases are exactly the same!
The distance equals the critical t-value * standard error of the mean . For our energy cost example data, the distance works out to be $63.57.
Imagine this discussion between the null hypothesis mean and the sample mean:
Null hypothesis mean, hypothesis test representative : Hey buddy! I’ve found that you’re statistically significant because you’re more than $63.57 away from me!
Sample mean, confidence interval representative : Actually, I’m significant because you’re more than $63.57 away from me !
Very agreeable aren’t they? And, they always will agree as long as you compare the correct pairs of P values and confidence intervals. If you compare the incorrect pair, you can get conflicting results, as shown by common mistake #1 in this post .
Closing Thoughts
In statistical analyses, there tends to be a greater focus on P values and simply detecting a significant effect or difference. However, a statistically significant effect is not necessarily meaningful in the real world. For instance, the effect might be too small to be of any practical value.
It’s important to pay attention to the both the magnitude and the precision of the estimated effect. That’s why I'm rather fond of confidence intervals. They allow you to assess these important characteristics along with the statistical significance. You'd like to see a narrow confidence interval where the entire range represents an effect that is meaningful in the real world.
If you like this post, you might want to read the previous posts in this series that use the same graphical framework:
- Part One: Why We Need to Use Hypothesis Tests
- Part Two: Significance Levels (alpha) and P values
For more about confidence intervals, read my post where I compare them to tolerance intervals and prediction intervals .
If you'd like to see how I made the probability distribution plot, please read: How to Create a Graphical Version of the 1-sample t-Test .

You Might Also Like
- Trust Center
© 2023 Minitab, LLC. All Rights Reserved.
- Terms of Use
- Privacy Policy
- Cookies Settings
Confidence intervals and hypothesis testing
- Understand the t value and Pr(>|t|) fields in the output of lm
- Be able to think critically about the meaning and limitations of strict hypothesis tests
Confidence intervals and hypothesis tests
T-statistics.
Suppose we’re interested in the value \(\beta_k\) , the \(k\) –th entry of \(\betav\) in for some regression \(\y_n \sim \betav^\trans \xv_n\) . Recall that we have been finding \(\v\) such that
\[ \sqrt{N} (\beta_k - \beta) \rightarrow \gauss{0, \v}. \]
For example, under homoskedastic assumptions with \(\y_n = \xv_n^\trans \beta + \res_n\) , we have
\[ \begin{aligned} \v =& \sigma^2 (\Xcov^{-1})_{kk} \textrm{ where } \\ \Xcov =& \lim_{N \rightarrow \infty} \frac{1}{N} \X^\trans \X \textrm{ and } \\ \sigma^2 =& \var{\res_n}. \end{aligned} \]
Typically we don’t know \(\v\) , but have \(\hat\v\) such that \(\hat\v \rightarrow \v\) as \(N \rightarrow \infty\) . Again, under homoeskedastic assumptions,
\[ \begin{aligned} \hat\v =& \hat\sigma^2 \left(\frac{1}{N} \X^\trans \X \right)_{kk} \textrm{ where } \\ \hat\sigma^2 =& \frac{1}{N-P} \sumn \reshat_n^2. \end{aligned} \]
Putting all this together, the quantity
\[ \t = \frac{\sqrt{N} (\betahat_k - \beta_k)}{\sqrt{\hat\v}} = \frac{\betahat_k - \beta_k}{\sqrt{\hat\v / N}} \]
has an approximately standard normal distribution for large \(N\) .
Quantities of this form are called “T–statistics,” since, under our normal assumptions, we have shown that
\[ \t \sim \studentt{N-P}, \]
exactly for all \(N\) . Despite it’s name, it’s worth remembering that a T–statistic is actually not Student T distributed in general; it is asymptotically normal. Recall that for large \(N\) , the Student T and standard normal distributions coincide.
Plugging in values for \(\beta_k\)
However, there’s something funny about a “T-statistic” — as written, you cannot compute it, because you don’t know \(\beta_k\) . In fact, finding what values \(\beta_k\) might plausibly take is the whole point of statistical inference.
So what good is a T–statistic? Informally, one way to reason about it is as follows. Let’s take some concrete values for an example. Suppose guess that \(\beta_k^0\) is the value, and compute
\[ \betahat_k = 2 \quad\textrm{and}\quad \sqrt{\hat\v / N} = 3 \quad\textrm{so}\quad \t = \frac{2 - \beta_k^0}{3}. \]
We use the superscript \(0\) to indicate that \(\beta_k^0\) is our guess, not necessarily the true value.
Suppose we plug in some particular value, such as \(\beta_k^0 = 32\) . Using this value, we compute our T–statistic, and find that it’s very large — in our example, we would have \(\t = (2 - 32) / 3 = -30\) . It’s very unlikely to get a standard normal (or Student T) draw this large. Therefore, either:
- We got a very (very very very very) unusual draw of our standard normal or
- We guessed wrong, i.e. \(\beta_k \ne \beta_k^0 = 32\) .
In this way, we might consider it plausible to “reject” the hypothesis that \(\beta_k = 32\) .
There’s a subtle problem with the preceding reasoning, however. Suppose we do the same calculation with \(\beta_k^0 = 1\) . Then \(\t = (2 - 1) / 3 = 1/3\) . This is a much more typical value for a standard normal distribution. However, the probability of getting exactly \(1/3\) — or, indeed, any particular value — is zero, since the normal distribution is continuous valued. (This problem is easiest to see with continuous random variables, but the same basic problem will occur when the distribution is discrete but spread over a large number of possible values.)
Rejection regions
To resolve this problem, we can specify regions that we consider implausible. That is, suppose we take a region \(R\) such that, if \(\t\) is standard normal (or Student-T), then
\[ \prob{\t \in R} \le \alpha \quad\textrm{form some small }\alpha. \]
For example, we might take \(\Phi^{-1}(\cdot)\) to be the inverse CDF of \(\t\) if \(\beta_k = \beta_k^0\) . Then we can take
\[ R_{ts} = \{\t: \abs{t} \ge q \} \quad\textrm{where } q = \Phi^{-1}(\alpha / 2)\\ \]
where \(q\) is an \(\alpha / 2\) quantile of the distribution of \(\t\) . But there are other choices, such as
\[ \begin{aligned} R_{u} ={}& \{\t: \t \ge q \} \quad\textrm{where } q = \Phi^{-1}(1 - \alpha) \\ R_{l} ={}& \{\t: \t \le q \} \quad\textrm{where } q = \Phi^{-1}(\alpha) \\ R_{m} ={}& \{\t: \abs{\t} \le q \} \quad\textrm{where } q = \Phi^{-1}(0.5 + \alpha / 2) \quad\textrm{(!!!)}\\ R_{\infty} ={}& \begin{cases} \emptyset & \textrm{ with independent probability } \alpha \\ (-\infty,\infty) & \textrm{ with independent probability } 1 - \alpha \\ \end{cases} \quad\textrm{(!!!)} \end{aligned} \]
The last two may seem silly, but they are still rejection regions into which \(\t\) is unlikely to fall if it has a standard normal distribution.
How can we think about \(\alpha\) , and about the choice of the region? Recall that
- If \(\t \in R\) , we “reject” the proposed value of \(\beta_k^0\)
- If \(\t \notin R\) , we “fail to reject” the given value of \(\beta_k^0\) .
Of course, we don’t “accept” the value of \(\beta_k^0\) in the sense of believing that \(\beta_k^0 = \beta_k\) — if nothing else, there will always be multiple values of \(\beta_k^0\) that we do not reject, and \(\beta_k\) cannot be equal to all of them.
So there are two ways to make an error:
- Type I error: We are correct and \(\beta_k = \beta_k^0\) , but \(\t \in R\) and we reject
- Type II error: We are incorrect and \(\beta_k \ne \beta_k^0\) , but \(\t \notin R\) and we fail to reject
By definition of the region \(R\) , we have that
\[ \prob{\textrm{Type I error}} \le \alpha. \]
This is true for all the regions above, including the silly ones!
What about the Type II error? It must depend on the “true” value of \(\beta_k\) , and on the shape of the rejection region we choose. Note that
\[ \t = \frac{\betahat_k - \beta_k^0}{\sqrt{\hat\v / N}} = \frac{\betahat_k - \beta_k}{\sqrt{\hat\v / N}} + \frac{\beta_k - \beta_k^0}{\sqrt{\hat\v / N}} \]
So if the true value \(\beta_k \gg \beta_k^0\) , then our \(\t\) statistic is too large, and so on.
For example:
- Then \(\t\) is too large and positive.
- \(R_u\) and \(R_{ts}\) will reject, but \(R_l\) will not.
- The Type II error of \(R_u\) will be lowest, then \(R_{ts}\) , then \(R_l\) .
- \(R_l\) actually has greater Type II error than the silly regions, \(R_\infty\) and \(R_m\) .
- Then \(\t\) is too large and negative.
- \(R_l\) and \(R_{ts}\) will reject, but \(R_u\) will not.
- The Type II error of \(R_l\) will be lowest, then \(R_{ts}\) , then \(R_u\) .
- \(R_u\) actually has greater Type II error than the silly regions, \(R_\infty\) and \(R_m\) .
- Then \(\t\) has about the same distribution as when \(\beta_k^0 = \beta_k\) .
- All the regions reject just about as often as we commit a Type I error, that is, a proportion \(\alpha\) of the time.
Thus the shape of the region determines which alternatives you are able to reject. The probability of “rejecting” under a particular alternative is called the “power” of a test; the power is one minus the Type II error rate.
The null and alternative
Statistics has some formal language to distinguish between the “guess” \(\beta_k^0\) and other values.
- Falsely rejecting the null hypothesis is called a Type I error
- By construction, Type I errors occurs with probability at most \(\alpha\)
- Falsely failling to reject the null hypothesis is called a Type II error
- Type II errors’ probability depends on the alternative(s) and the rejection region shape.
The choice of a test statistic (here, \(\t\) ), together with a rejection region (here, \(R\) ) constitute a “test” of the null hypothesis. In general, one can imagine constructing many different tests, with different theoretical guarantees and power.
Confidence intervals
Often in applied statistics, a big deal is made about a single hypothesis test, particularly the null that \(\beta_k^0 = 0\) . Often this is not a good idea. Typically, we do not care whether \(\beta_k\) is precisely zero; rather, we care about the set of plausible values \(\beta_k\) might take. The distinction can be expressed as the difference between statistical and practical significance:
- Statistical significance is the size of an effect relative to sampling variability
- Practical significance is the size of the effect in terms of its effect on reality.
For example, suppose that \(\beta_k\) is nonzero but very small, but \(\sqrt{\hat\v / N}\) is very small, too. We might reject the null hypothesis \(\beta_k^0 = 0\) with a high degree of certainty, and call our result statistically significant . However, a small value of \(\beta_k\) may still not be a meaningful effect size for the problem at hand, i.e., it may not be practically significant .
A remendy is confidence intervals, which are actually closely related to our hypothesis tests. Recall that we have been constructing intervals of the form
\[ \prob{\beta_k \in I} \ge 1-\alpha \]
\[ I = \left(\betahat_k \pm q \hat\v / \sqrt{N}\right), \]
where \(q = \Phi^{-1}(\alpha / 2)\) , and \(\Phi\) is the CDF of either the standard normal or Student T distribution. It turns out that \(I\) is precisely the set of values that we would not reject with region \(R_{ts}\) . And, indeed, given a confidence interval, a valid test of the hypothesis \(\beta_k^0\) is given by rejecting if an only if \(\beta_k^0 \in I\) .
This duality is entirely general:
- The set of values that a valid test does not reject is a valid confidence interval
- Checking whether a value falls in a valid confidence interval is a valid test
Source Code
- Search Search Please fill out this field.
- How It Works
- Calculation
The Bottom Line
- Fundamental Analysis
What Is a Confidence Interval and How Do You Calculate It?
Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.
:max_bytes(150000):strip_icc():format(webp)/adam_hayes-5bfc262a46e0fb005118b414.jpg)
Charlene Rhinehart is a CPA , CFE, chair of an Illinois CPA Society committee, and has a degree in accounting and finance from DePaul University.
:max_bytes(150000):strip_icc():format(webp)/CharleneRhinehartHeadshot-CharleneRhinehart-ca4b769506e94a92bc29e4acc6f0f9a5.jpg)
Investopedia / Julie Bang
A confidence interval refers to the probability that a population parameter will fall between a set of values for a certain proportion of times.
A confidence interval, in statistics, refers to the probability that a population parameter will fall between a set of values for a certain proportion of times. Analysts often use confidence intervals that contain either 95% or 99% of expected observations. Thus, if a point estimate is generated from a statistical model of 10.00 with a 95% confidence interval of 9.50 to 10.50, it means one is 95% confident that the true value falls within that range.
Statisticians and other analysts use confidence intervals to understand the statistical significance of their estimations, inferences, or predictions. If a confidence interval contains the value of zero (or some other null hypothesis) , then one cannot satisfactorily claim that a result from data generated by testing or experimentation is to be attributable to a specific cause rather than chance.
Key Takeaways
- A confidence interval displays the probability that a parameter will fall between a pair of values around the mean.
- Confidence intervals measure the degree of uncertainty or certainty in a sampling method.
- They are also used in hypothesis testing and regression analysis.
- Statisticians often use p-values in conjunction with confidence intervals to gauge statistical significance.
- They are most often constructed using confidence levels of 95% or 99%.
Understanding Confidence Intervals
Confidence intervals measure the degree of uncertainty or certainty in a sampling method. They can take any number of probability limits, with the most common being a 95% or 99% confidence level. Confidence intervals are conducted using statistical methods, such as a t-test .
Statisticians use confidence intervals to measure uncertainty in an estimate of a population parameter based on a sample. For example, a researcher selects different samples randomly from the same population and computes a confidence interval for each sample to see how it may represent the true value of the population variable. The resulting datasets are all different; some intervals include the true population parameter and others do not.
A confidence interval is a range of values, bounded above and below the statistic's mean , that likely would contain an unknown population parameter. Confidence level refers to the percentage of probability, or certainty, that the confidence interval would contain the true population parameter when you draw a random sample many times.
Or, in the vernacular, "we are 99% certain (confidence level) that most of these samples (confidence intervals) contain the true population parameter."
The biggest misconception regarding confidence intervals is that they represent the percentage of data from a given sample that falls between the upper and lower bounds. For example, one might erroneously interpret the aforementioned 99% confidence interval of 70-to-78 inches as indicating that 99% of the data in a random sample falls between these numbers.
This is incorrect, though a separate method of statistical analysis exists to make such a determination. Doing so involves identifying the sample's mean and standard deviation and plotting these figures on a bell curve .
Confidence interval and confidence level are interrelated but are not exactly the same.
Calculating Confidence Intervals
Suppose a group of researchers is studying the heights of high school basketball players. The researchers take a random sample from the population and establish a mean height of 74 inches.
The mean of 74 inches is a point estimate of the population mean. A point estimate by itself is of limited usefulness because it does not reveal the uncertainty associated with the estimate; you do not have a good sense of how far away this 74-inch sample mean might be from the population mean. What's missing is the degree of uncertainty in this single sample.
Confidence intervals provide more information than point estimates. By establishing a 95% confidence interval using the sample's mean and standard deviation , and assuming a normal distribution as represented by the bell curve, the researchers arrive at an upper and lower bound that contains the true mean 95% of the time.
Assume the interval is between 72 inches and 76 inches. If the researchers take 100 random samples from the population of high school basketball players as a whole, the mean should fall between 72 and 76 inches in 95 of those samples.
If the researchers want even greater confidence, they can expand the interval to 99% confidence. Doing so invariably creates a broader range, as it makes room for a greater number of sample means. If they establish the 99% confidence interval as being between 70 inches and 78 inches, they can expect 99 of 100 samples evaluated to contain a mean value between these numbers.
A 90% confidence level, on the other hand, implies that you would expect 90% of the interval estimates to include the population parameter, and so forth.
What Does a Confidence Interval Reveal?
A confidence interval is a range of values, bounded above and below the statistic's mean, that likely would contain an unknown population parameter. Confidence level refers to the percentage of probability, or certainty, that the confidence interval would contain the true population parameter when you draw a random sample many times.
Why Are Confidence Intervals Used?
Statisticians use confidence intervals to measure uncertainty in a sample variable. For example, a researcher selects different samples randomly from the same population and computes a confidence interval for each sample to see how it may represent the true value of the population variable. The resulting datasets are all different where some intervals include the true population parameter and others do not.
What Is a Common Misconception About Confidence Intervals?
The biggest misconception regarding confidence intervals is that they represent the percentage of data from a given sample that falls between the upper and lower bounds. In other words, it would be incorrect to assume that a 99% confidence interval means that 99% of the data in a random sample falls between these bounds. What it actually means is that one can be 99% certain that the range will contain the population mean.
What Is a T-Test?
Confidence intervals are conducted using statistical methods, such as a t-test. A t-test is a type of inferential statistic used to determine if there is a significant difference between the means of two groups, which may be related to certain features. Calculating a t-test requires three key data values. They include the difference between the mean values from each data set (called the mean difference), the standard deviation of each group, and the number of data values of each group.
How Do You Interpret P-Values and Confidence Intervals?
A p-value is a statistical measurement used to validate a hypothesis against observed data that measures the probability of obtaining the observed results, assuming that the null hypothesis is true. In general, a p-value less than 0.05 is considered to be statistically significant, in which case the null hypothesis should be rejected. This can somewhat correspond to the probability that the null hypothesis value (which is often zero) is contained within a 95% confidence interval.
Confidence intervals allow analysts to understand the likelihood that the results from statistical analyses are real or due to chance. When trying to make inferences or predictions based on a sample of data, there will be some uncertainty as to whether the results of such an analysis actually correspond with the real-world population being studied. The confidence interval depicts the likely range within which the true value should fall.
:max_bytes(150000):strip_icc():format(webp)/Autocorrelation-FINAL-3b2d9f40e52d4d85aa399528e7133083.jpg)
- Terms of Service
- Editorial Policy
- Privacy Policy
Pardon Our Interruption
As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:
- You've disabled JavaScript in your web browser.
- You're a power user moving through this website with super-human speed.
- You've disabled cookies in your web browser.
- A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .
To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.

IMAGES
VIDEO
COMMENTS
In other words, if the the 95% confidence interval contains the hypothesized parameter, then a hypothesis test at the 0.05 \(\alpha\) level will almost always fail to reject the null hypothesis. If the 95% confidence interval does not contain the hypothesize parameter, then a hypothesis test at the 0.05 \(\alpha\) level will almost always ...
The relationship between the confidence level and the significance level for a hypothesis test is as follows: Confidence level = 1 - Significance level (alpha) For example, if your significance level is 0.05, the equivalent confidence level is 95%. Both of the following conditions represent statistically significant results: The P-value in a ...
As a hypothesis test, we could have the alternative hypothesis as H 1 ≠ 0.51. Since the null value of 0.51 lies within the confidence interval, then we would fail to reject the null hypothesis at ɑ = 0.05. On the other hand, if H 1 ≠ 0.61, then since 0.61 is not in the confidence interval we can reject the null hypothesis at ɑ = 0.05.
To calculate the 95% confidence interval, we can simply plug the values into the formula. For the USA: So for the USA, the lower and upper bounds of the 95% confidence interval are 34.02 and 35.98. For GB: So for the GB, the lower and upper bounds of the 95% confidence interval are 33.04 and 36.96.
Definition/Introduction. Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators.
We can also use confidence intervals to make conclusions about hypothesis tests: reject the null hypothesis [latex]H_0[/latex] at the significance level [latex]\alpha[/latex] if the corresponding [latex](1 - \alpha) \times 100\%[/latex] confidence interval does not contain the hypothesized value [latex]\mu_0[/latex]. The relationship is ...
Below, we'll walk through an example followed by the process to generate a confidence interval. Confidence Interval Example. Like mentioned above, the median price per night for a Chicago Airbnb was $126 in our sample. ... We would want to reject the null hypothesis and adopt the alternative hypothesis as a more reasonable claim. In this case ...
An example of a typical hypothesis test (two-tailed) where "p" is some parameter. First, we state our two kinds of hypothesis:. Null hypothesis (H0): The "status quo" or "known/accepted fact".States that there is no statistical significance between two variables and is usually what we are looking to disprove.
Recap: Hypothesis testing for a population mean. Set the hypotheses. H0 : = null value HA : < or > or 6= null value. Check assumptions and conditions. Independence: random sample/assignment, 10% condition when sampling without replacement Normality: nearly normal population or n 30, no extreme skew.
A confidence interval can be defined as the range of parameters at which the true parameter can be found at a confidence level. For instance, a 95% confidence interval constitutes the set of parameter values where the null hypothesis cannot be rejected when using a 5% test size.
A confidence interval (CI) is a range of values that is likely to contain the value of an unknown population parameter. These intervals represent a plausible domain for the parameter given the characteristics of your sample data. Confidence intervals are derived from sample statistics and are calculated using a specified confidence level.
H 0 (Null Hypothesis): Population parameter =, ≤, ≥ some value. H A (Alternative Hypothesis): Population parameter <, >, ≠ some value. Note that the null hypothesis always contains the equal sign. We interpret the hypotheses as follows: Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.
Remember that the decision to reject the null hypothesis (H 0) or fail to reject it can be based on the p-value and your chosen significance level (also called α). If the p-value is less than or equal to α, you reject H 0; if it is greater than α, you fail to reject H 0. Your decision can also be based on the confidence interval (or bound ...
When your sample contains sufficient evidence, you can reject the null and conclude that the effect is statistically significant. Statisticians often denote the null hypothesis as H 0 or H A.. Null Hypothesis H 0: No effect exists in the population.; Alternative Hypothesis H A: The effect exists in the population.; In every study or experiment, researchers assess an effect or relationship.
If the \(95\%\) confidence interval contains zero (more precisely, the parameter value specified in the null hypothesis), then the effect will not be significant at the \(0.05\) level. Looking at non-significant effects in terms of confidence intervals makes clear why the null hypothesis should not be accepted when it is not rejected: Every ...
If the P value is less than alpha, the confidence interval will not contain the null hypothesis value. For our example, the P value (0.031) is less than the significance level (0.05), which indicates that our results are statistically significant. Similarly, our 95% confidence interval [267 394] does not include the null hypothesis mean of 260 ...
Step 1: Set up the null hypothesis: Two tails: H0: Ᾱ = μ ... one sample mean confidence interval. where Ᾱ is the sample's mean, and t can be found in the t table above based on the confidence level and degree of freedom. For example, for a sample with 10 observations, the t value for the 95% confidence interval is 2.262. ...
A remendy is confidence intervals, which are actually closely related to our hypothesis tests. Recall that we have been constructing intervals of the form. P (β k ∈ I) ≥ 1 − α. where. I = (β ^ k ± q v ^ / N), where q = Φ − 1 (α / 2), and Φ is the CDF of either the standard normal or Student T distribution.
A hypothesis test involves collecting data from a sample and evaluating the data. Then, the statistician makes a decision as to whether or not there is sufficient evidence, based upon analysis of the data, to reject the null hypothesis. 12.3.1: Null and Alternative Hypotheses; 12.3.2: Outcomes and the Type I and Type II Errors
To perform a hypothesis test in the real world, researchers will obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis: Null Hypothesis (H 0): The sample data occurs purely from chance. Alternative Hypothesis (H A): The sample data is influenced by some non-random cause.
Organized by textbook: https://learncheme.com/ Made by faculty at the University of Colorado Boulder, Department of Chemical & Biological Engineering.
It is the probability of seeing what we see or something more extreme given the null hypothesis is true. In the IRS example, let's find \(S^+\), or in other words, let's find the number of observations that fall above 160. ... The interpretation of the confidence interval for the median has the same template interpretation as the confidence ...
Investopedia / Julie Bang. A confidence interval, in statistics, refers to the probability that a population parameter will fall between a set of values for a certain proportion of times. Analysts ...
1. 2. If you construct confidence intervals for each sample, you can find out if the population mean is within that interval. This tells you if you can reject or fail to reject your null hypothesis. If you find that the number of samples with the population mean is 100, you can see how close the data matches a 95% confidence interval. 3.
A sample of 15 bearings shows a sample standard deviation of .014 inches. a) Use α = .10 to determine whether the sample indicates that the maximum acceptable variance is being exceeded. b) Compute the 90% confidence interval estimate of the variance of the ball bearings in the population.