null hypothesis power calculation

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

25.2 - power functions, example 25-2 section  .

Let's take a look at another example that involves calculating the power of a hypothesis test.

Let \(X\) denote the IQ of a randomly selected adult American. Assume, a bit unrealistically, that \(X\) is normally distributed with unknown mean \(\mu\) and standard deviation 16. Take a random sample of \(n=16\) students, so that, after setting the probability of committing a Type I error at \(\alpha=0.05\), we can test the null hypothesis \(H_0:\mu=100\) against the alternative hypothesis that \(H_A:\mu>100\).

What is the power of the hypothesis test if the true population mean were \(\mu=108\)?

Setting \(\alpha\), the probability of committing a Type I error, to 0.05, implies that we should reject the null hypothesis when the test statistic \(Z\ge 1.645\), or equivalently, when the observed sample mean is 106.58 or greater:

because we transform the test statistic \(Z\) to the sample mean by way of:

\(Z=\dfrac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\qquad \Rightarrow \bar{X}=\mu+Z\dfrac{\sigma}{\sqrt{n}} \qquad \bar{X}=100+1.645\left(\dfrac{16}{\sqrt{16}}\right)=106.58\)

Now, that implies that the power, that is, the probability of rejecting the null hypothesis, when \(\mu=108\) is 0.6406 as calculated here (recalling that \(Phi(z)\) is standard notation for the cumulative distribution function of the standard normal random variable):

\( \text{Power}=P(\bar{X}\ge 106.58\text{ when } \mu=108) = P\left(Z\ge \dfrac{106.58-108}{\frac{16}{\sqrt{16}}}\right) \\ = P(Z\ge -0.36)=1-P(Z<-0.36)=1-\Phi(-0.36)=1-0.3594=0.6406 \)

and illustrated here:

In summary, we have determined that we have (only) a 64.06% chance of rejecting the null hypothesis \(H_0:\mu=100\) in favor of the alternative hypothesis \(H_A:\mu>100\) if the true unknown population mean is in reality \(\mu=108\).

What is the power of the hypothesis test if the true population mean were \(\mu=112\)?

Because we are setting \(\alpha\), the probability of committing a Type I error, to 0.05, we again reject the null hypothesis when the test statistic \(Z\ge 1.645\), or equivalently, when the observed sample mean is 106.58 or greater. That means that the probability of rejecting the null hypothesis, when \(\mu=112\) is 0.9131 as calculated here:

\( \text{Power}=P(\bar{X}\ge 106.58\text{ when }\mu=112)=P\left(Z\ge \frac{106.58-112}{\frac{16}{\sqrt{16}}}\right) \\ = P(Z\ge -1.36)=1-P(Z<-1.36)=1-\Phi(-1.36)=1-0.0869=0.9131 \)

In summary, we have determined that we now have a 91.31% chance of rejecting the null hypothesis \(H_0:\mu=100\) in favor of the alternative hypothesis \(H_A:\mu>100\) if the true unknown population mean is in reality \(\mu=112\). Hmm.... it should make sense that the probability of rejecting the null hypothesis is larger for values of the mean, such as 112, that are far away from the assumed mean under the null hypothesis.

What is the power of the hypothesis test if the true population mean were \(\mu=116\)?

Again, because we are setting \(\alpha\), the probability of committing a Type I error, to 0.05, we reject the null hypothesis when the test statistic \(Z\ge 1.645\), or equivalently, when the observed sample mean is 106.58 or greater. That means that the probability of rejecting the null hypothesis, when \(\mu=116\) is 0.9909 as calculated here:

\(\text{Power}=P(\bar{X}\ge 106.58\text{ when }\mu=116) =P\left(Z\ge \dfrac{106.58-116}{\frac{16}{\sqrt{16}}}\right) = P(Z\ge -2.36)=1-P(Z<-2.36)= 1-\Phi(-2.36)=1-0.0091=0.9909 \)

In summary, we have determined that, in this case, we have a 99.09% chance of rejecting the null hypothesis \(H_0:\mu=100\) in favor of the alternative hypothesis \(H_A:\mu>100\) if the true unknown population mean is in reality \(\mu=116\). The probability of rejecting the null hypothesis is the largest yet of those we calculated, because the mean, 116, is the farthest away from the assumed mean under the null hypothesis.

Are you growing weary of this? Let's summarize a few things we've learned from engaging in this exercise:

• First and foremost, my instructor can be tedious at times..... errrr, I mean, first and foremost, the power of a hypothesis test depends on the value of the parameter being investigated. In the above, example, the power of the hypothesis test depends on the value of the mean \(\mu\).
• As the actual mean \(\mu\) moves further away from the value of the mean \(\mu=100\) under the null hypothesis, the power of the hypothesis test increases.

It's that first point that leads us to what is called the power function of the hypothesis test . If you go back and take a look, you'll see that in each case our calculation of the power involved a step that looks like this:

\(\text{Power } =1 - \Phi (z) \) where \(z = \frac{106.58 - \mu}{16 / \sqrt{16}} \)

That is, if we use the standard notation \(K(\mu)\) to denote the power function, as it depends on \(\mu\), we have:

\(K(\mu) = 1- \Phi \left( \frac{106.58 - \mu}{16 / \sqrt{16}} \right) \)

So, the reality is your instructor could have been a whole lot more tedious by calculating the power for every possible value of \(\mu\) under the alternative hypothesis! What we can do instead is create a plot of the power function, with the mean \(\mu\) on the horizontal axis and the power \(K(\mu)\) on the vertical axis. Doing so, we get a plot in this case that looks like this:

Now, what can we learn from this plot? Well:

We can see that \(\alpha\) (the probability of a Type I error), \(\beta\) (the probability of a Type II error), and \(K(\mu)\) are all represented on a power function plot, as illustrated here:

We can see that the probability of a Type I error is \(\alpha=K(100)=0.05\), that is, the probability of rejecting the null hypothesis when the null hypothesis is true is 0.05.

We can see the power of a test \(K(\mu)\), as well as the probability of a Type II error \(\beta(\mu)\), for each possible value of \(\mu\).

We can see that \(\beta(\mu)=1-K(\mu)\) and vice versa, that is, \(K(\mu)=1-\beta(\mu)\).

And we can see graphically that, indeed, as the actual mean \(\mu\) moves further away from the null mean \(\mu=100\), the power of the hypothesis test increases.

Now, what would do you suppose would happen to the power of our hypothesis test if we were to change our willingness to commit a Type I error? Would the power for a given value of \(\mu\) increase, decrease, or remain unchanged? Suppose, for example, that we wanted to set \(\alpha=0.01\) instead of \(\alpha=0.05\)? Let's return to our example to explore this question.

Example 25-2 (continued) Section  

Let \(X\) denote the IQ of a randomly selected adult American. Assume, a bit unrealistically, that \(X\) is normally distributed with unknown mean \(\mu\) and standard deviation 16. Take a random sample of \(n=16\) students, so that, after setting the probability of committing a Type I error at \(\alpha=0.01\), we can test the null hypothesis \(H_0:\mu=100\) against the alternative hypothesis that \(H_A:\mu>100\).

Setting \(\alpha\), the probability of committing a Type I error, to 0.01, implies that we should reject the null hypothesis when the test statistic \(Z\ge 2.326\), or equivalently, when the observed sample mean is 109.304 or greater:

\(\bar{x} = \mu + z \left( \frac{\sigma}{\sqrt{n}} \right) =100 + 2.326\left( \frac{16}{\sqrt{16}} \right)=109.304 \)

That means that the probability of rejecting the null hypothesis, when \(\mu=108\) is 0.3722 as calculated here:

So, the power when \(\mu=108\) and \(\alpha=0.01\) is smaller (0.3722) than the power when \(\mu=108\) and \(\alpha=0.05\) (0.6406)! Perhaps we can see this graphically:

By the way, we could again alternatively look at the glass as being half-empty. In that case, the probability of a Type II error when \(\mu=108\) and \(\alpha=0.01\) is \(1-0.3722=0.6278\). In this case, the probability of a Type II error is greater than the probability of a Type II error when \(\mu=108\) and \(\alpha=0.05\).

All of this can be seen graphically by plotting the two power functions, one where \(\alpha=0.01\) and the other where \(\alpha=0.05\), simultaneously. Doing so, we get a plot that looks like this:

This last example illustrates that, providing the sample size \(n\) remains unchanged, a decrease in \(\alpha\) causes an increase in \(\beta\) , and at least theoretically, if not practically, a decrease in \(\beta\) causes an increase in \(\alpha\). It turns out that the only way that \(\alpha\) and \(\beta\) can be decreased simultaneously is by increasing the sample size \(n\).

Hypothesis Testing Calculator

Related: confidence interval calculator, type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

Power – A Quick Introduction

In statistics, power is the probability of rejecting a false null hypothesis.

Power Calculation Example

Power & alpha level, power & effect size, power & sample size, 3 main reasons for power calculations, software for power calculations - g*power, power - minimal example.

• In some country, IQ and salary have a population correlation ρ = 0.10.
• A scientist examines a sample of N = 10 people and finds a sample correlation r = 0.15.
• He tests the (false) null hypothesis H 0 that ρ = 0. The significance level for this test, p = 0.68.
• Since p > 0.05, his chosen alpha level, he does not reject his (false) null hypothesis that ρ = 0.

Now, given a sample size of N = 10 and a population correlation ρ = 0.10, what's the probability of correctly rejecting the null hypothesis? ρ = 0.0? -->This probability is known as power and denoted as (1 - β) in statistics. For the aforementioned example, (1 - β) is only 0.058 (roughly 6%) as shown below.

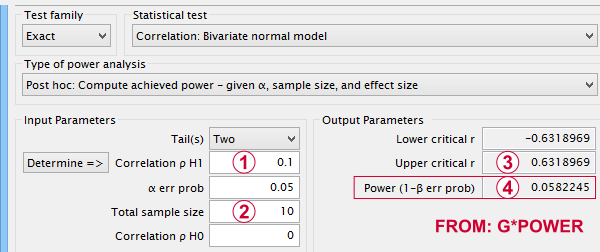
So even though H 0 is false, we've little power to actually reject it. Not rejecting a false H 0 is known as a committing a type II error.

Type I and Type II Errors

Any null hypothesis may be true or false and we may or may not reject it. This results in the 4 scenarios outlined below.

As you probably guess, we usually want the power for our tests to be as high as possible. But before taking a look at factors affecting power, let's first try and understand how a power calculation actually works.

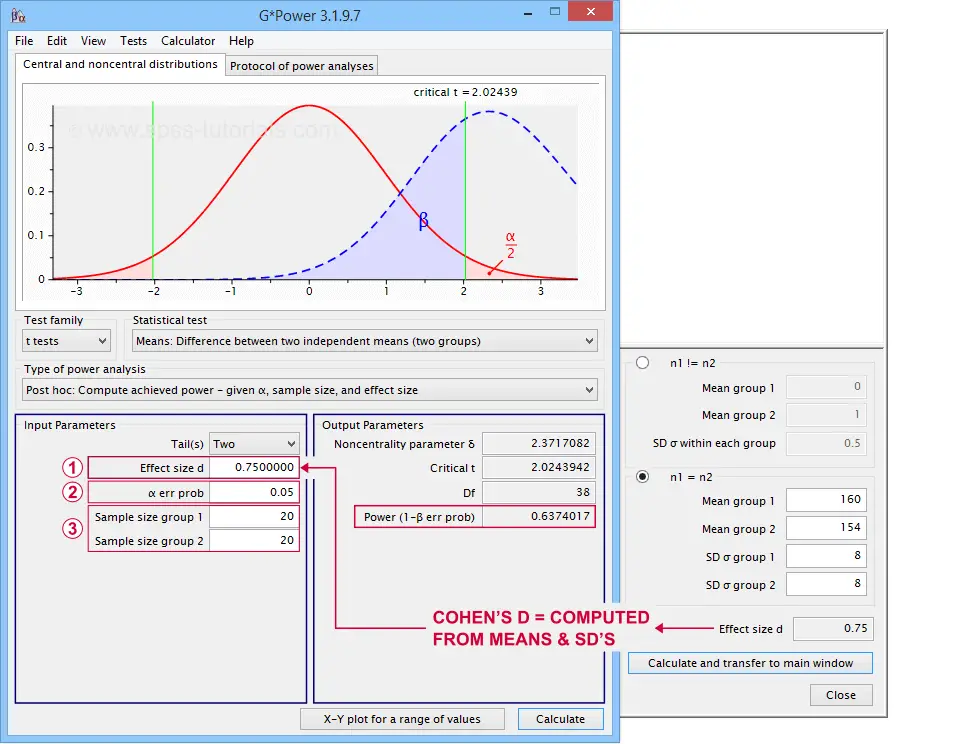
A pharmaceutical company wants to demonstrate that their medicine against high blood pressure actually works. They expect the following:

• the average blood pressure in some untreated population is 160 mmHg;
• they expect their medicine to lower this to roughly 154 mmHg;
• the standard deviation should be around 8 mmHg (both populations);
• they plan to use an independent samples t-test at α = 0.05 with N = 20 for either subsample.

Given these considerations, what's the power for this study? Or -alternatively- what's the probability of rejecting H 0 that the mean blood pressure is equal between treated and untreated populations?

Obviously, nobody knows the outcomes for this study until it's finished. However, we do know the most likely outcomes : they're our population estimates. So let's for a moment pretend that we'll find exactly these and enter them into a t-test calculator.

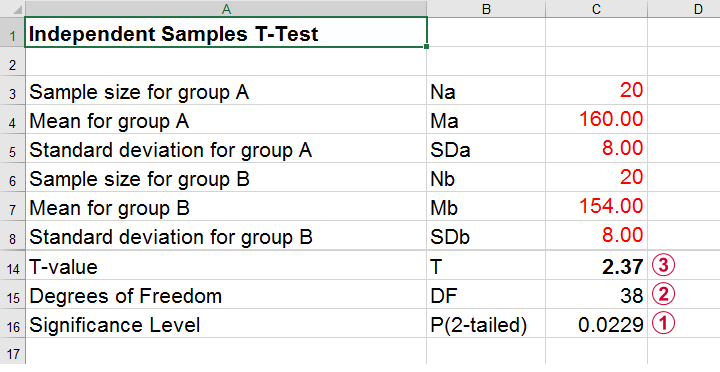
Now, this expected (or average) t = 2.37 under the alternative hypothesis H a is known as a noncentrality parameter or NCP. The NCP tells us how t is distributed under some exact alternative hypothesis and thus allows us to estimate the power for some test. The figure below illustrates how this works.

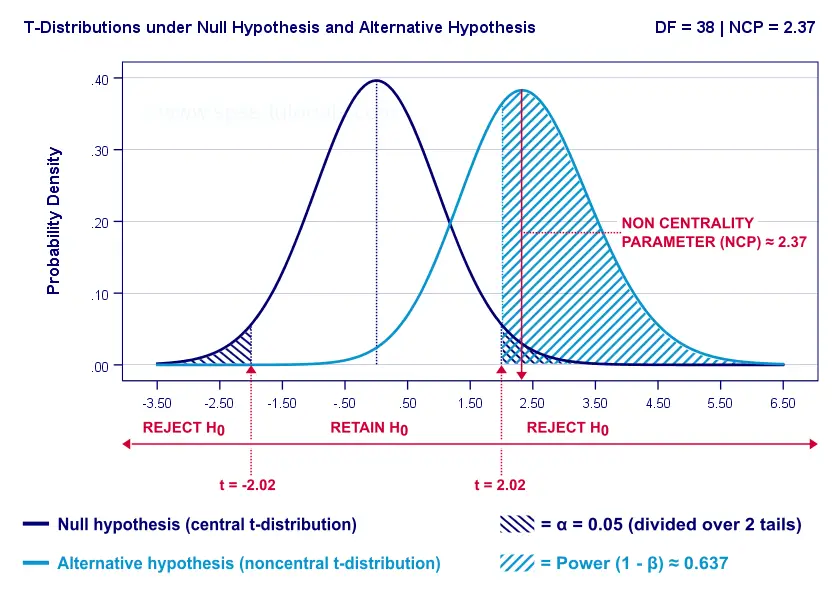
• First off, our H 0 is tested using a central t-distribution with df = 38;
• If we test at α = 0.05 (2-tailed), we'll reject H 0 if t < -2.02 (left critical value) or if t > 2.02 (right critical value);
• If our alternative hypothesis H A is exactly true, t follows a noncentral t-distribution with df = 38 and NCP = 2.37;
• Under this noncentral t-distribution, the probability of finding t > 2.02 ≈ 0.637. So this is roughly the probability of rejecting H 0 -or the power (1 - β) - for our first scenario.

A minor note here is that we'd also reject H 0 if t < -2.02 but this probability is almost zero for our first scenario. The exact calculation can be replicated from the SPSS syntax below.

Power and Effect Size

Like we just saw, estimating power requires specifying

• an exact null hypothesis and
• an exact alternative hypothesis.

In the previous example, our scientists had an exact alternative hypothesis because they had very specific ideas regarding population means and standard deviations. In most applied studies, however, we're pretty clueless about such population parameters. This raises the question how do we get an exact alternative hypothesis?

For most tests, the alternative hypothesis can be specified as an effect size measure : a single number combining several means, variances and/or frequencies. Like so, we proceed from requiring a bunch of unknown parameters to a single unknown parameter.

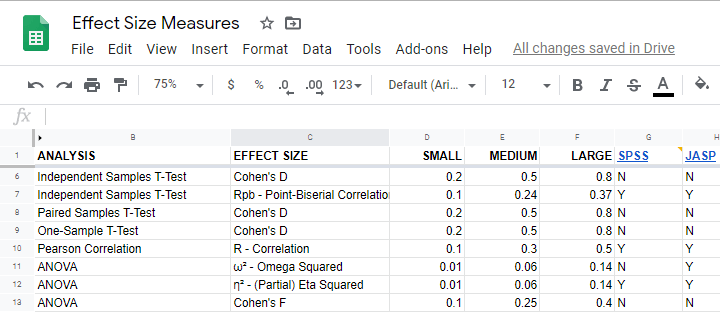
What's even better: widely agreed upon rules of thumb are available for effect size measures. An overview is presented in this Googlesheet , partly shown below.

In applied studies, we often use G*Power for estimating power. The screenshot below replicates our power calculation example for the blood pressure medicine study.

Factors Affecting Power

The figure below gives a quick overview how 3 factors relate to power.

Let's now take a closer look at each of them.

Before taking a closer look at each, we need to point out that increasing your sample size(s) is the only sound way to increase power. This is because

• increasing alpha increases power but also increases the risk of committing a type I error. Testing at α > 0.05 is unacceptable under common statistical conventions.
• you can't choose

Everything else equal, increasing alpha increases power. For our example calculation, power increases from 0.637 to 0.753 if we test at α = 0.10 instead of 0.05.

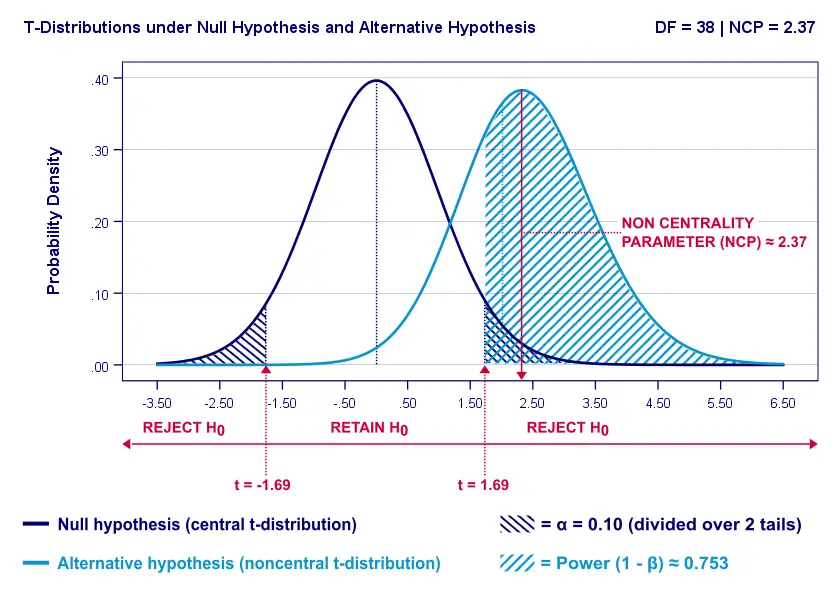
A higher alpha level results in smaller (absolute) critical values: we already reject H 0 if t > 1.69 instead of t > 2.02. 1.69 has a higher probability under H A than finding t > 2.02. -->So the light blue area, indicating (1 - β) , increases. We basically require a smaller deviation from H 0 for statistical significance.

However, increasing alpha comes at a cost: it increases the probability of committing a type I error (rejecting H 0 when it's actually true). Therefore, testing at α > 0.05 is generally frowned upon. In short, increasing alpha basically just decreases one problem by increasing another one.

Everything else equal, a larger effect size results in higher power. For our example, power increases from 0.637 to 0.869 if we believe that Cohen’s D = 1.0 rather than 0.8.

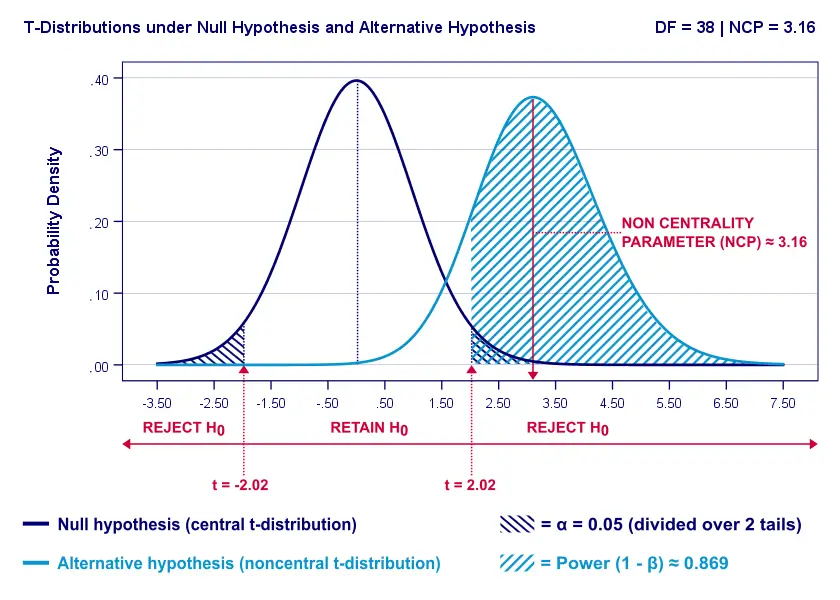
A larger effect size results in a larger noncentrality parameter (NCP). Therefore, the distributions under H 0 and H A lie further apart. This increases the light blue area, indicating the power for this test.

Keep in mind, though, that we can estimate but not choose some population effect size. If we overestimate this effect size, we'll overestimate the power for our test accordingly. Therefore, we can't usually increase power by increasing an effect size.

An arguable exception is increasing an effect size by modifying a research design or analysis. For example, (partial) eta squared for a treatment effect in ANOVA may increase by adding a covariate to the analysis.

Everything else equal, larger sample size(s) result in higher power. For our example, increasing the total sample size from N = 40 to N = 80 increases power from 0.637 to 0.912.

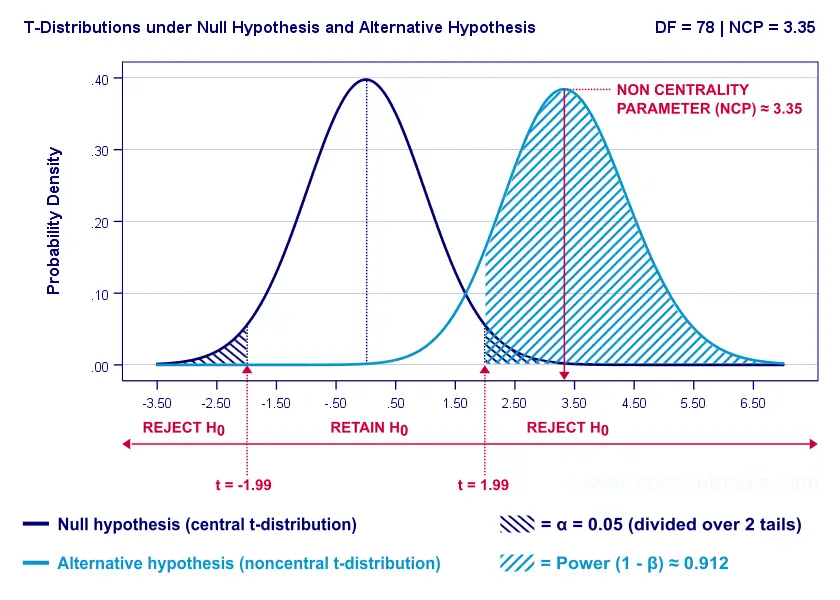
The increase in power stems from our distributions lying further apart. This reflects an increased noncentrality parameter (NCP). But why does the NCP increase with larger sample sizes?

Well, recall that for a t-distribution, the NCP is the expected t-value under H A . Now, t is computed as

$$t = \frac{\overline{X_1} - \overline{X_2}}{SE}$$

where \(SE\) denotes the standard error of the mean difference. In turn, \(SE\) is computed as

$$SE = Sw\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}$$

where \(S_w\) denotes the estimated population SD of the outcome variable. This formula shows that as sample sizes increase, \(SE\) de creases and therefore t (and hence the NCP) in creases.

On top of this, degrees of freedom increase (from df = 38 to df = 78 for our example). This results in slightly smaller (absolute) critical t-values but this effect is very modest.

In short, increasing sample size(s) is a sound way to increase the power for some test.

Power & Research Design

Apart from sample size, effect size & α, research design may also affect power. Although there's no exact formulas, some general guidelines are that

• everything else equal, within-subjects designs tend to have more power than between-subjects designs;
• for ANCOVA , including one or two covariates tends to increase power for demonstrating a treatment effect;
• for multiple regression , power for each separate predictor tends to decrease as more predictors are added to the model;

Power calculations in applied research serve 3 main purposes:

• compute the required sample size prior to data collection. This involves estimating an effect size and choosing α (usually 0.05) and the desired power (1 - B), often 0.80;
• estimate power before collecting data for some planned analyses. This requires specifying the intended sample size, choosing an α and estimating which effect sizes are expected. If the estimated power is low, the planned study may be cancelled or proceed with a larger sample size;
• estimate power after data have been collected and analyzed. This calculation is based on the actual sample size, α used for testing and observed effect size.

G*Power is freely downloadable software for running the aforementioned and many other power calculations. Among its features are

• computing effect sizes from descriptive statistics (mostly sample means and standard deviations);
• computing power, required sample sizes, required effect sizes and more;
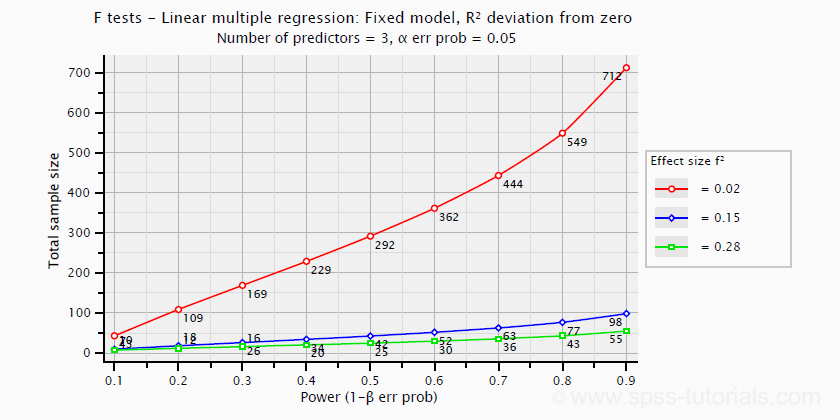
• creating plots that visualize how power, effect size and sample size relate for many different statistical procedures. The figure below shows an example for multiple linear regression.

Altogether, we think G*Power is amazing software and we highly recommend using it. The only disadvantage we can think of is that it requires rather unusual effect size measures. Some examples are

• Cohen’s f for ANOVA and
• Cohen’s W for a chi-square test .

This is awkward because the APA and (perhaps therefore) most journal articles typically recommend reporting

• (partial) eta-squared for ANOVA and
• the contingency coefficient or (better) Cramér’s V for a chi-square test.

These are also the measures we typically obtain from statistical packages such as SPSS or JASP. Fortunately, G*Power converts some measures and/or computes them from descriptive statistics like we saw in this screenshot .

Software for Power Calculations - SPSS

In SPSS , observed power can be obtained from the GLM, UNIANOVA and (deprecated) MANOVA procedures. Keep in mind that GLM - short for General Linear Model- is very general indeed: it can be used for a wide variety of analyses including

• (multiple) linear regression;
• ANCOVA (analysis of covariance);
• repeated measures ANOVA .

Other power calculations (required sample sizes or estimating power prior to data collection) were added to SPSS version 27, released in 2020.

In my opinion, SPSS power analysis is a pathetic attempt to compete with G*Power. If you don't believe me, just try running a couple of power analyses in both programs simultaneously. If you do believe me, ignore SPSS power analysis and just go for G*Power.

Thanks for reading.

Tell us what you think!

This tutorial has 5 comments:.

By Bogdan on November 17th, 2022

Thanks for the very clear and detailed explanations, they really helped a lot!

By john on November 18th, 2022

At last I've found a very clear description of statistical power. Great explanation. Thanks for this.

By Sabby Grg on May 6th, 2023

Thank you for the clear explanation. I had a few questions about the a priori gpower analysis for the sample size and sensitivity analysis after the data collection. For my project, I initially wanted to run a correlation matrix and then run a multiple linear regression analysis. But the correlation matrix showed that none of the predictors correlated with the outcome variable, so I had to conduct a Spearman’s ranked correlation (data was non-normally distributed). Firstly, should I mention in my report that initially a sample size was determined through f-test power analysis with multiple regression as the statistical test (N=85). But also mention that as there was a change in statistical test, another power analysis was done with t test family and correlation: point biserial model as the statistical test (N=82). As a priori analysis is done before the study, it seemed silly to mention another analysis was done after the study but also doesn’t make sense to just mention the power analysis for multiple regression when I used a correlation test instead.

Secondly, it was recommended to conduct a sensitivity analysis to see what effect size I was powered to detect with my sample size of 81, as I was very close to the required sample size. I did it on G*power with t tests, correlation and sensitivity and the effect size calculation showed a medium effect size, which was what I was aiming for. Even though I didn’t add meet the required sample size, my sample achieved a medium effect size. How should I explain this in my results?

Would the best method be to mention that a power analysis was done with multiple regression as the statistical test, resulting in a sample size of 85. But during data analysis, the correlation matrix showed non-significant relationship between outcome and predictor variables so the appropriate test was Spearman’s rho correlation. A sensitivity analysis showed that even with the sample size of 81, a medium effect size for a correlation test was still achieved (+ justification).

Apologies for the lengthy query. Thank you in advance for your help.

By Ruben Geert van den Berg on May 7th, 2023

Honestly, I'm not buying any of this.

My basic conclusion is that you're just not willing to accept that the effects you're looking for probably aren't there.

For sample sizes of, say, N > 25, Pearson correlations don't require normality. Failing to detect them at N = 81 is pretty clear evidence that some variables just aren't linearly related.

They could still be non linearly related but you should model that via CURVEFIT or non linear transformations rather than going for Spearman correlations.

I'd simply report that the relations you're looking for are probably weak at best. And perhaps use a larger sample size next time.

But blaming lack of power for "non significant" results doesn't strike me as very convincing.

By Sabby Grg on May 7th, 2023

Thank you for your reply. Oh dear, in hindsight, I have worded my query utterly horribly. I think there may have been a misunderstanding, mainly from my lack of knowledge. Firstly, I completely understand your point on the Pearson’s r. I already let my supervisor know that for pre-analysis, I did the Pearson’s correlation before the regression based on the central limit theorem. As there were no significant results from the pre-analysis correlation matrix, it was recommended to do a Spearman’s correlation and justify why (non-normality), instead of regression. Upon reflection, it might be better to use Pearson’s r for the main test since it was already justified through central limit theorem.

Regardless, it was already established that my results are non significant and I had already accepted it. But one of the feedback was to do a sensitivity analysis to check the effect size of my sample of 81. Now, I can see where my initial query seems very misleading because I used the term, justify, when it should have been explain. I thought the recommendation of sensitivity analysis was to explain that my sample size was still powered enough to detect a result but that said result was non-significant. Initially, I wanted to understand how my sample was less than the a priori sample size calculation yet, still was powered to show a medium effect size (indicated by sensitivity analysis). Then after, I was going to explain how the study/sample was powered enough to show a medium effect size but the correlation test showed non-significant results so, it means that there just isn't any relationship between the variables <— This is the part I should’ve added in the initial query and this was my intention. In all honesty, I believe it might be best to leave my sensitivity analysis out if there is such misunderstanding when trying to explain it.

I do apologise for the misunderstanding as trying to justify the non-significant result with power, was not my intention. I was simply trying to understand what explanation there could be for my sample size (81) showing the same effect size as the a priori calculation (85). I know this may all sound amateur from an expert’s point of view but unfortunately, I am at that phase. Even this whole explanation might be flawed but I ask for your consideration.

I will just report inferential statistics using Pearsons’s and leave out the sensitivity analysis. But I do want to thank you for your reply as it has helped me review and reflect.

Privacy Overview

Teach yourself statistics

Power of a Hypothesis Test

The probability of not committing a Type II error is called the power of a hypothesis test.

Effect Size

To compute the power of the test, one offers an alternative view about the "true" value of the population parameter, assuming that the null hypothesis is false. The effect size is the difference between the true value and the value specified in the null hypothesis.

Effect size = True value - Hypothesized value

For example, suppose the null hypothesis states that a population mean is equal to 100. A researcher might ask: What is the probability of rejecting the null hypothesis if the true population mean is equal to 90? In this example, the effect size would be 90 - 100, which equals -10.

Factors That Affect Power

The power of a hypothesis test is affected by three factors.

• Sample size ( n ). Other things being equal, the greater the sample size, the greater the power of the test.
• Significance level (α). The lower the significance level, the lower the power of the test. If you reduce the significance level (e.g., from 0.05 to 0.01), the region of acceptance gets bigger. As a result, you are less likely to reject the null hypothesis. This means you are less likely to reject the null hypothesis when it is false, so you are more likely to make a Type II error. In short, the power of the test is reduced when you reduce the significance level; and vice versa.
• The "true" value of the parameter being tested. The greater the difference between the "true" value of a parameter and the value specified in the null hypothesis, the greater the power of the test. That is, the greater the effect size, the greater the power of the test.

Test Your Understanding

Other things being equal, which of the following actions will reduce the power of a hypothesis test?

I. Increasing sample size. II. Changing the significance level from 0.01 to 0.05. III. Increasing beta, the probability of a Type II error.

(A) I only (B) II only (C) III only (D) All of the above (E) None of the above

The correct answer is (C). Increasing sample size makes the hypothesis test more sensitive - more likely to reject the null hypothesis when it is, in fact, false. Changing the significance level from 0.01 to 0.05 makes the region of acceptance smaller, which makes the hypothesis test more likely to reject the null hypothesis, thus increasing the power of the test. Since, by definition, power is equal to one minus beta, the power of a test will get smaller as beta gets bigger.

Suppose a researcher conducts an experiment to test a hypothesis. If she doubles her sample size, which of the following will increase?

I. The power of the hypothesis test. II. The effect size of the hypothesis test. III. The probability of making a Type II error.

The correct answer is (A). Increasing sample size makes the hypothesis test more sensitive - more likely to reject the null hypothesis when it is, in fact, false. Thus, it increases the power of the test. The effect size is not affected by sample size. And the probability of making a Type II error gets smaller, not bigger, as sample size increases.

Statistical Power Calculator

The statistical power is a power of a binary hypothesis test. It is the probability that effectively rejects the null hypothesis value (H 0 ) when the alternative hypothesis value (H 1 ) is true. In this calculator, calculate the statistical power of a test (p = 1 - β) from the beta value.

Null Hypothesis Test

Related Calculators:

• Permutation And Combination Calculator
• Normal Distribution Calculator
• Normal Distribution(PDF)
• Binomial Distribution Calculator
• Ehrenfest Equation For Second Order Phase Transition Calculator
• Spring Resonant Frequency Calculator

Calculators and Converters

• Calculators
• Probability And Distributions

Top Calculators

Popular calculators.

• Derivative Calculator
• Inverse of Matrix Calculator
• Compound Interest Calculator
• Pregnancy Calculator Online

Top Categories

Power and Sample Size Determination

Lisa Sullivan, PhD

Professor of Biosatistics

Boston Univeristy School of Public Health

Introduction

A critically important aspect of any study is determining the appropriate sample size to answer the research question. This module will focus on formulas that can be used to estimate the sample size needed to produce a confidence interval estimate with a specified margin of error (precision) or to ensure that a test of hypothesis has a high probability of detecting a meaningful difference in the parameter.

Studies should be designed to include a sufficient number of participants to adequately address the research question. Studies that have either an inadequate number of participants or an excessively large number of participants are both wasteful in terms of participant and investigator time, resources to conduct the assessments, analytic efforts and so on. These situations can also be viewed as unethical as participants may have been put at risk as part of a study that was unable to answer an important question. Studies that are much larger than they need to be to answer the research questions are also wasteful.

The formulas presented here generate estimates of the necessary sample size(s) required based on statistical criteria. However, in many studies, the sample size is determined by financial or logistical constraints. For example, suppose a study is proposed to evaluate a new screening test for Down Syndrome.  Suppose that the screening test is based on analysis of a blood sample taken from women early in pregnancy. In order to evaluate the properties of the screening test (e.g., the sensitivity and specificity), each pregnant woman will be asked to provide a blood sample and in addition to undergo an amniocentesis. The amniocentesis is included as the gold standard and the plan is to compare the results of the screening test to the results of the amniocentesis. Suppose that the collection and processing of the blood sample costs $250 per participant and that the amniocentesis costs $900 per participant. These financial constraints alone might substantially limit the number of women that can be enrolled. Just as it is important to consider both statistical and clinical significance when interpreting results of a statistical analysis, it is also important to weigh both statistical and logistical issues in determining the sample size for a study.

Learning Objectives

After completing this module, the student will be able to:

• Provide examples demonstrating how the margin of error, effect size and variability of the outcome affect sample size computations.
• Compute the sample size required to estimate population parameters with precision.
• Interpret statistical power in tests of hypothesis.
• Compute the sample size required to ensure high power when hypothesis testing.

Issues in Estimating Sample Size for Confidence Intervals Estimates

The module on confidence intervals provided methods for estimating confidence intervals for various parameters (e.g., μ , p, ( μ 1 - μ 2 ),   μ d , (p 1 -p 2 )). Confidence intervals for every parameter take the following general form:

Point Estimate + Margin of Error

In the module on confidence intervals we derived the formula for the confidence interval for μ as

In practice we use the sample standard deviation to estimate the population standard deviation. Note that there is an alternative formula for estimating the mean of a continuous outcome in a single population, and it is used when the sample size is small (n<30). It involves a value from the t distribution, as opposed to one from the standard normal distribution, to reflect the desired level of confidence. When performing sample size computations, we use the large sample formula shown here. [Note: The resultant sample size might be small, and in the analysis stage, the appropriate confidence interval formula must be used.]

The point estimate for the population mean is the sample mean and the margin of error is

In planning studies, we want to determine the sample size needed to ensure that the margin of error is sufficiently small to be informative. For example, suppose we want to estimate the mean weight of female college students. We conduct a study and generate a 95% confidence interval as follows 125 + 40 pounds, or 85 to 165 pounds. The margin of error is so wide that the confidence interval is uninformative. To be informative, an investigator might want the margin of error to be no more than 5 or 10 pounds (meaning that the 95% confidence interval would have a width (lower limit to upper limit) of 10 or 20 pounds). In order to determine the sample size needed, the investigator must specify the desired margin of error . It is important to note that this is not a statistical issue, but a clinical or a practical one. For example, suppose we want to estimate the mean birth weight of infants born to mothers who smoke cigarettes during pregnancy. Birth weights in infants clearly have a much more restricted range than weights of female college students. Therefore, we would probably want to generate a confidence interval for the mean birth weight that has a margin of error not exceeding 1 or 2 pounds.

The margin of error in the one sample confidence interval for μ can be written as follows:

Our goal is to determine the sample size, n, that ensures that the margin of error, " E ," does not exceed a specified value. We can take the formula above and, with some algebra, solve for n :

First, multipy both sides of the equation by the square root of n . Then cancel out the square root of n from the numerator and denominator on the right side of the equation (since any number divided by itself is equal to 1). This leaves:

Now divide both sides by "E" and cancel out "E" from the numerator and denominator on the left side. This leaves:

Finally, square both sides of the equation to get:

This formula generates the sample size, n , required to ensure that the margin of error, E , does not exceed a specified value. To solve for n , we must input " Z ," " σ ," and " E ."  

• Z is the value from the table of probabilities of the standard normal distribution for the desired confidence level (e.g., Z = 1.96 for 95% confidence)
• E is the margin of error that the investigator specifies as important from a clinical or practical standpoint.
• σ is the standard deviation of the outcome of interest.

Sometimes it is difficult to estimate σ . When we use the sample size formula above (or one of the other formulas that we will present in the sections that follow), we are planning a study to estimate the unknown mean of a particular outcome variable in a population. It is unlikely that we would know the standard deviation of that variable. In sample size computations, investigators often use a value for the standard deviation from a previous study or a study done in a different, but comparable, population. The sample size computation is not an application of statistical inference and therefore it is reasonable to use an appropriate estimate for the standard deviation. The estimate can be derived from a different study that was reported in the literature; some investigators perform a small pilot study to estimate the standard deviation. A pilot study usually involves a small number of participants (e.g., n=10) who are selected by convenience, as opposed to by random sampling. Data from the participants in the pilot study can be used to compute a sample standard deviation, which serves as a good estimate for σ in the sample size formula. Regardless of how the estimate of the variability of the outcome is derived, it should always be conservative (i.e., as large as is reasonable), so that the resultant sample size is not too small.

Sample Size for One Sample, Continuous Outcome

In studies where the plan is to estimate the mean of a continuous outcome variable in a single population, the formula for determining sample size is given below:

where Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%), σ is the standard deviation of the outcome variable and E is the desired margin of error. The formula above generates the minimum number of subjects required to ensure that the margin of error in the confidence interval for μ does not exceed E .  

An investigator wants to estimate the mean systolic blood pressure in children with congenital heart disease who are between the ages of 3 and 5. How many children should be enrolled in the study? The investigator plans on using a 95% confidence interval (so Z=1.96) and wants a margin of error of 5 units. The standard deviation of systolic blood pressure is unknown, but the investigators conduct a literature search and find that the standard deviation of systolic blood pressures in children with other cardiac defects is between 15 and 20. To estimate the sample size, we consider the larger standard deviation in order to obtain the most conservative (largest) sample size. 

In order to ensure that the 95% confidence interval estimate of the mean systolic blood pressure in children between the ages of 3 and 5 with congenital heart disease is within 5 units of the true mean, a sample of size 62 is needed. [ Note : We always round up; the sample size formulas always generate the minimum number of subjects needed to ensure the specified precision.] Had we assumed a standard deviation of 15, the sample size would have been n=35. Because the estimates of the standard deviation were derived from studies of children with other cardiac defects, it would be advisable to use the larger standard deviation and plan for a study with 62 children. Selecting the smaller sample size could potentially produce a confidence interval estimate with a larger margin of error. 

An investigator wants to estimate the mean birth weight of infants born full term (approximately 40 weeks gestation) to mothers who are 19 years of age and under. The mean birth weight of infants born full-term to mothers 20 years of age and older is 3,510 grams with a standard deviation of 385 grams. How many women 19 years of age and under must be enrolled in the study to ensure that a 95% confidence interval estimate of the mean birth weight of their infants has a margin of error not exceeding 100 grams? Try to work through the calculation before you look at the answer.

Sample Size for One Sample, Dichotomous Outcome 

In studies where the plan is to estimate the proportion of successes in a dichotomous outcome variable (yes/no) in a single population, the formula for determining sample size is:

where Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%) and E is the desired margin of error. p is the proportion of successes in the population. Here we are planning a study to generate a 95% confidence interval for the unknown population proportion, p . The equation to determine the sample size for determining p seems to require knowledge of p, but this is obviously this is a circular argument, because if we knew the proportion of successes in the population, then a study would not be necessary! What we really need is an approximate value of p or an anticipated value. The range of p is 0 to 1, and therefore the range of p(1-p) is 0 to 1. The value of p that maximizes p(1-p) is p=0.5. Consequently, if there is no information available to approximate p, then p=0.5 can be used to generate the most conservative, or largest, sample size.

Example 2:  

An investigator wants to estimate the proportion of freshmen at his University who currently smoke cigarettes (i.e., the prevalence of smoking). How many freshmen should be involved in the study to ensure that a 95% confidence interval estimate of the proportion of freshmen who smoke is within 5% of the true proportion?

Because we have no information on the proportion of freshmen who smoke, we use 0.5 to estimate the sample size as follows:

In order to ensure that the 95% confidence interval estimate of the proportion of freshmen who smoke is within 5% of the true proportion, a sample of size 385 is needed.

Suppose that a similar study was conducted 2 years ago and found that the prevalence of smoking was 27% among freshmen. If the investigator believes that this is a reasonable estimate of prevalence 2 years later, it can be used to plan the next study. Using this estimate of p, what sample size is needed (assuming that again a 95% confidence interval will be used and we want the same level of precision)?

An investigator wants to estimate the prevalence of breast cancer among women who are between 40 and 45 years of age living in Boston. How many women must be involved in the study to ensure that the estimate is precise? National data suggest that 1 in 235 women are diagnosed with breast cancer by age 40. This translates to a proportion of 0.0043 (0.43%) or a prevalence of 43 per 10,000 women. Suppose the investigator wants the estimate to be within 10 per 10,000 women with 95% confidence. The sample size is computed as follows:

A sample of size n=16,448 will ensure that a 95% confidence interval estimate of the prevalence of breast cancer is within 0.10 (or to within 10 women per 10,000) of its true value. This is a situation where investigators might decide that a sample of this size is not feasible. Suppose that the investigators thought a sample of size 5,000 would be reasonable from a practical point of view. How precisely can we estimate the prevalence with a sample of size n=5,000? Recall that the confidence interval formula to estimate prevalence is:

Assuming that the prevalence of breast cancer in the sample will be close to that based on national data, we would expect the margin of error to be approximately equal to the following:

Thus, with n=5,000 women, a 95% confidence interval would be expected to have a margin of error of 0.0018 (or 18 per 10,000). The investigators must decide if this would be sufficiently precise to answer the research question. Note that the above is based on the assumption that the prevalence of breast cancer in Boston is similar to that reported nationally. This may or may not be a reasonable assumption. In fact, it is the objective of the current study to estimate the prevalence in Boston. The research team, with input from clinical investigators and biostatisticians, must carefully evaluate the implications of selecting a sample of size n = 5,000, n = 16,448 or any size in between.

Sample Sizes for Two Independent Samples, Continuous Outcome

In studies where the plan is to estimate the difference in means between two independent populations, the formula for determining the sample sizes required in each comparison group is given below:

where n i is the sample size required in each group (i=1,2), Z is the value from the standard normal distribution reflecting the confidence level that will be used and E is the desired margin of error. σ again reflects the standard deviation of the outcome variable. Recall from the module on confidence intervals that, when we generated a confidence interval estimate for the difference in means, we used Sp, the pooled estimate of the common standard deviation, as a measure of variability in the outcome (based on pooling the data), where Sp is computed as follows:

If data are available on variability of the outcome in each comparison group, then Sp can be computed and used in the sample size formula. However, it is more often the case that data on the variability of the outcome are available from only one group, often the untreated (e.g., placebo control) or unexposed group. When planning a clinical trial to investigate a new drug or procedure, data are often available from other trials that involved a placebo or an active control group (i.e., a standard medication or treatment given for the condition under study). The standard deviation of the outcome variable measured in patients assigned to the placebo, control or unexposed group can be used to plan a future trial, as illustrated below.  

Note that the formula for the sample size generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used.  

An investigator wants to plan a clinical trial to evaluate the efficacy of a new drug designed to increase HDL cholesterol (the "good" cholesterol). The plan is to enroll participants and to randomly assign them to receive either the new drug or a placebo. HDL cholesterol will be measured in each participant after 12 weeks on the assigned treatment. Based on prior experience with similar trials, the investigator expects that 10% of all participants will be lost to follow up or will drop out of the study over 12 weeks. A 95% confidence interval will be estimated to quantify the difference in mean HDL levels between patients taking the new drug as compared to placebo. The investigator would like the margin of error to be no more than 3 units. How many patients should be recruited into the study?  

The sample sizes are computed as follows:

A major issue is determining the variability in the outcome of interest (σ), here the standard deviation of HDL cholesterol. To plan this study, we can use data from the Framingham Heart Study. In participants who attended the seventh examination of the Offspring Study and were not on treatment for high cholesterol, the standard deviation of HDL cholesterol is 17.1. We will use this value and the other inputs to compute the sample sizes as follows:

Samples of size n 1 =250 and n 2 =250 will ensure that the 95% confidence interval for the difference in mean HDL levels will have a margin of error of no more than 3 units. Again, these sample sizes refer to the numbers of participants with complete data. The investigators hypothesized a 10% attrition (or drop-out) rate (in both groups). In order to ensure that the total sample size of 500 is available at 12 weeks, the investigator needs to recruit more participants to allow for attrition.  

N (number to enroll) * (% retained) = desired sample size

Therefore N (number to enroll) = desired sample size/(% retained)

N = 500/0.90 = 556

If they anticipate a 10% attrition rate, the investigators should enroll 556 participants. This will ensure N=500 with complete data at the end of the trial.

An investigator wants to compare two diet programs in children who are obese. One diet is a low fat diet, and the other is a low carbohydrate diet. The plan is to enroll children and weigh them at the start of the study. Each child will then be randomly assigned to either the low fat or the low carbohydrate diet. Each child will follow the assigned diet for 8 weeks, at which time they will again be weighed. The number of pounds lost will be computed for each child. Based on data reported from diet trials in adults, the investigator expects that 20% of all children will not complete the study. A 95% confidence interval will be estimated to quantify the difference in weight lost between the two diets and the investigator would like the margin of error to be no more than 3 pounds. How many children should be recruited into the study?  

Again the issue is determining the variability in the outcome of interest (σ), here the standard deviation in pounds lost over 8 weeks. To plan this study, investigators use data from a published study in adults. Suppose one such study compared the same diets in adults and involved 100 participants in each diet group. The study reported a standard deviation in weight lost over 8 weeks on a low fat diet of 8.4 pounds and a standard deviation in weight lost over 8 weeks on a low carbohydrate diet of 7.7 pounds. These data can be used to estimate the common standard deviation in weight lost as follows:

We now use this value and the other inputs to compute the sample sizes:

Samples of size n 1 =56 and n 2 =56 will ensure that the 95% confidence interval for the difference in weight lost between diets will have a margin of error of no more than 3 pounds. Again, these sample sizes refer to the numbers of children with complete data. The investigators anticipate a 20% attrition rate. In order to ensure that the total sample size of 112 is available at 8 weeks, the investigator needs to recruit more participants to allow for attrition.  

N = 112/0.80 = 140

Sample Size for Matched Samples, Continuous Outcome

In studies where the plan is to estimate the mean difference of a continuous outcome based on matched data, the formula for determining sample size is given below:

where Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%), E is the desired margin of error, and σ d is the standard deviation of the difference scores. It is extremely important that the standard deviation of the difference scores (e.g., the difference based on measurements over time or the difference between matched pairs) is used here to appropriately estimate the sample size.    

Sample Sizes for Two Independent Samples, Dichotomous Outcome

In studies where the plan is to estimate the difference in proportions between two independent populations (i.e., to estimate the risk difference), the formula for determining the sample sizes required in each comparison group is:

where n i is the sample size required in each group (i=1,2), Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%), and E is the desired margin of error. p 1 and p 2 are the proportions of successes in each comparison group. Again, here we are planning a study to generate a 95% confidence interval for the difference in unknown proportions, and the formula to estimate the sample sizes needed requires p 1 and p 2 . In order to estimate the sample size, we need approximate values of p 1 and p 2 . The values of p 1 and p 2 that maximize the sample size are p 1 =p 2 =0.5. Thus, if there is no information available to approximate p 1 and p 2 , then 0.5 can be used to generate the most conservative, or largest, sample sizes.    

Similar to the situation for two independent samples and a continuous outcome at the top of this page, it may be the case that data are available on the proportion of successes in one group, usually the untreated (e.g., placebo control) or unexposed group. If so, the known proportion can be used for both p 1 and p 2 in the formula shown above. The formula shown above generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used. Interested readers can see Fleiss for more details. 4

An investigator wants to estimate the impact of smoking during pregnancy on premature delivery. Normal pregnancies last approximately 40 weeks and premature deliveries are those that occur before 37 weeks. The 2005 National Vital Statistics report indicates that approximately 12% of infants are born prematurely in the United States. 5 The investigator plans to collect data through medical record review and to generate a 95% confidence interval for the difference in proportions of infants born prematurely to women who smoked during pregnancy as compared to those who did not. How many women should be enrolled in the study to ensure that the 95% confidence interval for the difference in proportions has a margin of error of no more than 4%?

The sample sizes (i.e., numbers of women who smoked and did not smoke during pregnancy) can be computed using the formula shown above. National data suggest that 12% of infants are born prematurely. We will use that estimate for both groups in the sample size computation.

Samples of size n 1 =508 women who smoked during pregnancy and n 2 =508 women who did not smoke during pregnancy will ensure that the 95% confidence interval for the difference in proportions who deliver prematurely will have a margin of error of no more than 4%.

Is attrition an issue here? 

Issues in Estimating Sample Size for Hypothesis Testing

In the module on hypothesis testing for means and proportions, we introduced techniques for means, proportions, differences in means, and differences in proportions. While each test involved details that were specific to the outcome of interest (e.g., continuous or dichotomous) and to the number of comparison groups (one, two, more than two), there were common elements to each test. For example, in each test of hypothesis, there are two errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true.   In the first step of any test of hypothesis, we select a level of significance, α , and α = P(Type I error) = P(Reject H 0 | H 0 is true). Because we purposely select a small value for α , we control the probability of committing a Type I error. The second type of error is called a Type II error and it is defined as the probability we do not reject H 0 when it is false. The probability of a Type II error is denoted β , and β =P(Type II error) = P(Do not Reject H 0 | H 0 is false). In hypothesis testing, we usually focus on power, which is defined as the probability that we reject H 0 when it is false, i.e., power = 1- β = P(Reject H 0 | H 0 is false). Power is the probability that a test correctly rejects a false null hypothesis. A good test is one with low probability of committing a Type I error (i.e., small α ) and high power (i.e., small β, high power).  

Here we present formulas to determine the sample size required to ensure that a test has high power. The sample size computations depend on the level of significance, aα, the desired power of the test (equivalent to 1-β), the variability of the outcome, and the effect size. The effect size is the difference in the parameter of interest that represents a clinically meaningful difference. Similar to the margin of error in confidence interval applications, the effect size is determined based on clinical or practical criteria and not statistical criteria.  

The concept of statistical power can be difficult to grasp. Before presenting the formulas to determine the sample sizes required to ensure high power in a test, we will first discuss power from a conceptual point of view.  

Suppose we want to test the following hypotheses at aα=0.05:  H 0 : μ = 90 versus H 1 : μ ≠ 90. To test the hypotheses, suppose we select a sample of size n=100. For this example, assume that the standard deviation of the outcome is σ=20. We compute the sample mean and then must decide whether the sample mean provides evidence to support the alternative hypothesis or not. This is done by computing a test statistic and comparing the test statistic to an appropriate critical value. If the null hypothesis is true (μ=90), then we are likely to select a sample whose mean is close in value to 90. However, it is also possible to select a sample whose mean is much larger or much smaller than 90. Recall from the Central Limit Theorem (see page 11 in the module on Probability), that for large n (here n=100 is sufficiently large), the distribution of the sample means is approximately normal with a mean of

If the null hypothesis is true, it is possible to observe any sample mean shown in the figure below; all are possible under H 0 : μ = 90.  

Rejection Region for Test H 0 : μ = 90 versus H 1 : μ ≠ 90 at α =0.05

The areas in the two tails of the curve represent the probability of a Type I Error, α= 0.05. This concept was discussed in the module on Hypothesis Testing.  

Now, suppose that the alternative hypothesis, H 1 , is true (i.e., μ ≠ 90) and that the true mean is actually 94. The figure below shows the distributions of the sample mean under the null and alternative hypotheses.The values of the sample mean are shown along the horizontal axis.  

If the true mean is 94, then the alternative hypothesis is true. In our test, we selected α = 0.05 and reject H 0 if the observed sample mean exceeds 93.92 (focusing on the upper tail of the rejection region for now). The critical value (93.92) is indicated by the vertical line. The probability of a Type II error is denoted β, and β = P(Do not Reject H 0 | H 0 is false), i.e., the probability of not rejecting the null hypothesis if the null hypothesis were true. β is shown in the figure above as the area under the rightmost curve (H 1 ) to the left of the vertical line (where we do not reject H 0 ). Power is defined as 1- β = P(Reject H 0 | H 0 is false) and is shown in the figure as the area under the rightmost curve (H 1 ) to the right of the vertical line (where we reject H 0 ).  

Note that β and power are related to α, the variability of the outcome and the effect size. From the figure above we can see what happens to β and power if we increase α. Suppose, for example, we increase α to α=0.10.The upper critical value would be 92.56 instead of 93.92. The vertical line would shift to the left, increasing α, decreasing β and increasing power. While a better test is one with higher power, it is not advisable to increase α as a means to increase power. Nonetheless, there is a direct relationship between α and power (as α increases, so does power).

β and power are also related to the variability of the outcome and to the effect size. The effect size is the difference in the parameter of interest (e.g., μ) that represents a clinically meaningful difference. The figure above graphically displays α, β, and power when the difference in the mean under the null as compared to the alternative hypothesis is 4 units (i.e., 90 versus 94). The figure below shows the same components for the situation where the mean under the alternative hypothesis is 98.

Notice that there is much higher power when there is a larger difference between the mean under H 0 as compared to H 1 (i.e., 90 versus 98). A statistical test is much more likely to reject the null hypothesis in favor of the alternative if the true mean is 98 than if the true mean is 94. Notice also in this case that there is little overlap in the distributions under the null and alternative hypotheses. If a sample mean of 97 or higher is observed it is very unlikely that it came from a distribution whose mean is 90. In the previous figure for H 0 : μ = 90 and H 1 : μ = 94, if we observed a sample mean of 93, for example, it would not be as clear as to whether it came from a distribution whose mean is 90 or one whose mean is 94.

Ensuring That a Test Has High Power

In designing studies most people consider power of 80% or 90% (just as we generally use 95% as the confidence level for confidence interval estimates). The inputs for the sample size formulas include the desired power, the level of significance and the effect size. The effect size is selected to represent a clinically meaningful or practically important difference in the parameter of interest, as we will illustrate.  

The formulas we present below produce the minimum sample size to ensure that the test of hypothesis will have a specified probability of rejecting the null hypothesis when it is false (i.e., a specified power). In planning studies, investigators again must account for attrition or loss to follow-up. The formulas shown below produce the number of participants needed with complete data, and we will illustrate how attrition is addressed in planning studies.

In studies where the plan is to perform a test of hypothesis comparing the mean of a continuous outcome variable in a single population to a known mean, the hypotheses of interest are:

H 0 : μ = μ 0 and H 1 : μ ≠ μ 0 where μ 0 is the known mean (e.g., a historical control). The formula for determining sample size to ensure that the test has a specified power is given below:

where α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α/2 below it. For example, if α=0.05, then 1- α/2 = 0.975 and Z=1.960. 1- β is the selected power, and Z 1-β is the value from the standard normal distribution holding 1- β below it. Sample size estimates for hypothesis testing are often based on achieving 80% or 90% power. The Z 1-β values for these popular scenarios are given below:

• For 80% power Z 0.80 = 0.84
• For 90% power Z 0.90 =1.282

ES is the effect size , defined as follows:

where μ 0 is the mean under H 0 , μ 1 is the mean under H 1 and σ is the standard deviation of the outcome of interest. The numerator of the effect size, the absolute value of the difference in means | μ 1 - μ 0 |, represents what is considered a clinically meaningful or practically important difference in means. Similar to the issue we faced when planning studies to estimate confidence intervals, it can sometimes be difficult to estimate the standard deviation. In sample size computations, investigators often use a value for the standard deviation from a previous study or a study performed in a different but comparable population. Regardless of how the estimate of the variability of the outcome is derived, it should always be conservative (i.e., as large as is reasonable), so that the resultant sample size will not be too small.

Example 7:  

An investigator hypothesizes that in people free of diabetes, fasting blood glucose, a risk factor for coronary heart disease, is higher in those who drink at least 2 cups of coffee per day. A cross-sectional study is planned to assess the mean fasting blood glucose levels in people who drink at least two cups of coffee per day. The mean fasting blood glucose level in people free of diabetes is reported as 95.0 mg/dL with a standard deviation of 9.8 mg/dL. 7 If the mean blood glucose level in people who drink at least 2 cups of coffee per day is 100 mg/dL, this would be important clinically. How many patients should be enrolled in the study to ensure that the power of the test is 80% to detect this difference? A two sided test will be used with a 5% level of significance.  

The effect size is computed as:

The effect size represents the meaningful difference in the population mean - here 95 versus 100, or 0.51 standard deviation units different. We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.

Therefore, a sample of size n=31 will ensure that a two-sided test with α =0.05 has 80% power to detect a 5 mg/dL difference in mean fasting blood glucose levels.

In the planned study, participants will be asked to fast overnight and to provide a blood sample for analysis of glucose levels. Based on prior experience, the investigators hypothesize that 10% of the participants will fail to fast or will refuse to follow the study protocol. Therefore, a total of 35 participants will be enrolled in the study to ensure that 31 are available for analysis (see below).

N (number to enroll) * (% following protocol) = desired sample size

N = 31/0.90 = 35.

Sample Size for One Sample, Dichotomous Outcome

In studies where the plan is to perform a test of hypothesis comparing the proportion of successes in a dichotomous outcome variable in a single population to a known proportion, the hypotheses of interest are:

where p 0 is the known proportion (e.g., a historical control). The formula for determining the sample size to ensure that the test has a specified power is given below:

where α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α/2 below it. 1- β is the selected power and   Z 1-β is the value from the standard normal distribution holding 1- β below it , and ES is the effect size, defined as follows:

where p 0 is the proportion under H 0 and p 1 is the proportion under H 1 . The numerator of the effect size, the absolute value of the difference in proportions |p 1 -p 0 |, again represents what is considered a clinically meaningful or practically important difference in proportions.  

Example 8:  

A recent report from the Framingham Heart Study indicated that 26% of people free of cardiovascular disease had elevated LDL cholesterol levels, defined as LDL > 159 mg/dL. 9 An investigator hypothesizes that a higher proportion of patients with a history of cardiovascular disease will have elevated LDL cholesterol. How many patients should be studied to ensure that the power of the test is 90% to detect a 5% difference in the proportion with elevated LDL cholesterol? A two sided test will be used with a 5% level of significance.  

We first compute the effect size: 

We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.

A sample of size n=869 will ensure that a two-sided test with α =0.05 has 90% power to detect a 5% difference in the proportion of patients with a history of cardiovascular disease who have an elevated LDL cholesterol level.

A medical device manufacturer produces implantable stents. During the manufacturing process, approximately 10% of the stents are deemed to be defective. The manufacturer wants to test whether the proportion of defective stents is more than 10%. If the process produces more than 15% defective stents, then corrective action must be taken. Therefore, the manufacturer wants the test to have 90% power to detect a difference in proportions of this magnitude. How many stents must be evaluated? For you computations, use a two-sided test with a 5% level of significance. (Do the computation yourself, before looking at the answer.)

In studies where the plan is to perform a test of hypothesis comparing the means of a continuous outcome variable in two independent populations, the hypotheses of interest are:

where μ 1 and μ 2 are the means in the two comparison populations. The formula for determining the sample sizes to ensure that the test has a specified power is:

where n i is the sample size required in each group (i=1,2), α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α /2 below it, and 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it. ES is the effect size, defined as:

where | μ 1 - μ 2 | is the absolute value of the difference in means between the two groups expected under the alternative hypothesis, H 1 . σ is the standard deviation of the outcome of interest. Recall from the module on Hypothesis Testing that, when we performed tests of hypothesis comparing the means of two independent groups, we used Sp, the pooled estimate of the common standard deviation, as a measure of variability in the outcome.

Sp is computed as follows:

If data are available on variability of the outcome in each comparison group, then Sp can be computed and used to generate the sample sizes. However, it is more often the case that data on the variability of the outcome are available from only one group, usually the untreated (e.g., placebo control) or unexposed group. When planning a clinical trial to investigate a new drug or procedure, data are often available from other trials that may have involved a placebo or an active control group (i.e., a standard medication or treatment given for the condition under study). The standard deviation of the outcome variable measured in patients assigned to the placebo, control or unexposed group can be used to plan a future trial, as illustrated.  

 Note also that the formula shown above generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used (see Howell 3 for more details).

An investigator is planning a clinical trial to evaluate the efficacy of a new drug designed to reduce systolic blood pressure. The plan is to enroll participants and to randomly assign them to receive either the new drug or a placebo. Systolic blood pressures will be measured in each participant after 12 weeks on the assigned treatment. Based on prior experience with similar trials, the investigator expects that 10% of all participants will be lost to follow up or will drop out of the study. If the new drug shows a 5 unit reduction in mean systolic blood pressure, this would represent a clinically meaningful reduction. How many patients should be enrolled in the trial to ensure that the power of the test is 80% to detect this difference? A two sided test will be used with a 5% level of significance.  

In order to compute the effect size, an estimate of the variability in systolic blood pressures is needed. Analysis of data from the Framingham Heart Study showed that the standard deviation of systolic blood pressure was 19.0. This value can be used to plan the trial.  

The effect size is:

Samples of size n 1 =232 and n 2 = 232 will ensure that the test of hypothesis will have 80% power to detect a 5 unit difference in mean systolic blood pressures in patients receiving the new drug as compared to patients receiving the placebo. However, the investigators hypothesized a 10% attrition rate (in both groups), and to ensure a total sample size of 232 they need to allow for attrition.  

N = 232/0.90 = 258.

The investigator must enroll 258 participants to be randomly assigned to receive either the new drug or placebo.

An investigator is planning a study to assess the association between alcohol consumption and grade point average among college seniors. The plan is to categorize students as heavy drinkers or not using 5 or more drinks on a typical drinking day as the criterion for heavy drinking. Mean grade point averages will be compared between students classified as heavy drinkers versus not using a two independent samples test of means. The standard deviation in grade point averages is assumed to be 0.42 and a meaningful difference in grade point averages (relative to drinking status) is 0.25 units. How many college seniors should be enrolled in the study to ensure that the power of the test is 80% to detect a 0.25 unit difference in mean grade point averages? Use a two-sided test with a 5% level of significance.  

Answer  

In studies where the plan is to perform a test of hypothesis on the mean difference in a continuous outcome variable based on matched data, the hypotheses of interest are:

where μ d is the mean difference in the population. The formula for determining the sample size to ensure that the test has a specified power is given below:

where α is the selected level of significance and Z 1-α/2 is the value from the standard normal distribution holding 1- α/2 below it, 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it and ES is the effect size, defined as follows:

where μ d is the mean difference expected under the alternative hypothesis, H 1 , and σ d is the standard deviation of the difference in the outcome (e.g., the difference based on measurements over time or the difference between matched pairs).    

Example 10:

An investigator wants to evaluate the efficacy of an acupuncture treatment for reducing pain in patients with chronic migraine headaches. The plan is to enroll patients who suffer from migraine headaches. Each will be asked to rate the severity of the pain they experience with their next migraine before any treatment is administered. Pain will be recorded on a scale of 1-100 with higher scores indicative of more severe pain. Each patient will then undergo the acupuncture treatment. On their next migraine (post-treatment), each patient will again be asked to rate the severity of the pain. The difference in pain will be computed for each patient. A two sided test of hypothesis will be conducted, at α =0.05, to assess whether there is a statistically significant difference in pain scores before and after treatment. How many patients should be involved in the study to ensure that the test has 80% power to detect a difference of 10 units on the pain scale? Assume that the standard deviation in the difference scores is approximately 20 units.    

First compute the effect size:

Then substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.

A sample of size n=32 patients with migraine will ensure that a two-sided test with α =0.05 has 80% power to detect a mean difference of 10 points in pain before and after treatment, assuming that all 32 patients complete the treatment.

Sample Sizes for Two Independent Samples, Dichotomous Outcomes

In studies where the plan is to perform a test of hypothesis comparing the proportions of successes in two independent populations, the hypotheses of interest are:

H 0 : p 1 = p 2 versus H 1 : p 1 ≠ p 2

where p 1 and p 2 are the proportions in the two comparison populations. The formula for determining the sample sizes to ensure that the test has a specified power is given below:

where n i is the sample size required in each group (i=1,2), α is the selected level of significance and Z 1-α/2 is the value from the standard normal distribution holding 1- α/2 below it, and 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it. ES is the effect size, defined as follows: 

where |p 1 - p 2 | is the absolute value of the difference in proportions between the two groups expected under the alternative hypothesis, H 1 , and p is the overall proportion, based on pooling the data from the two comparison groups (p can be computed by taking the mean of the proportions in the two comparison groups, assuming that the groups will be of approximately equal size).  

Example 11: 

An investigator hypothesizes that there is a higher incidence of flu among students who use their athletic facility regularly than their counterparts who do not. The study will be conducted in the spring. Each student will be asked if they used the athletic facility regularly over the past 6 months and whether or not they had the flu. A test of hypothesis will be conducted to compare the proportion of students who used the athletic facility regularly and got flu with the proportion of students who did not and got flu. During a typical year, approximately 35% of the students experience flu. The investigators feel that a 30% increase in flu among those who used the athletic facility regularly would be clinically meaningful. How many students should be enrolled in the study to ensure that the power of the test is 80% to detect this difference in the proportions? A two sided test will be used with a 5% level of significance.  

We first compute the effect size by substituting the proportions of students in each group who are expected to develop flu, p 1 =0.46 (i.e., 0.35*1.30=0.46) and p 2 =0.35 and the overall proportion, p=0.41 (i.e., (0.46+0.35)/2):

We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.  

Samples of size n 1 =324 and n 2 =324 will ensure that the test of hypothesis will have 80% power to detect a 30% difference in the proportions of students who develop flu between those who do and do not use the athletic facilities regularly.

Donor Feces? Really? Clostridium difficile (also referred to as "C. difficile" or "C. diff.") is a bacterial species that can be found in the colon of humans, although its numbers are kept in check by other normal flora in the colon. Antibiotic therapy sometimes diminishes the normal flora in the colon to the point that C. difficile flourishes and causes infection with symptoms ranging from diarrhea to life-threatening inflammation of the colon. Illness from C. difficile most commonly affects older adults in hospitals or in long term care facilities and typically occurs after use of antibiotic medications. In recent years, C. difficile infections have become more frequent, more severe and more difficult to treat. Ironically, C. difficile is first treated by discontinuing antibiotics, if they are still being prescribed. If that is unsuccessful, the infection has been treated by switching to another antibiotic. However, treatment with another antibiotic frequently does not cure the C. difficile infection. There have been sporadic reports of successful treatment by infusing feces from healthy donors into the duodenum of patients suffering from C. difficile. (Yuk!) This re-establishes the normal microbiota in the colon, and counteracts the overgrowth of C. diff. The efficacy of this approach was tested in a randomized clinical trial reported in the New England Journal of Medicine (Jan. 2013). The investigators planned to randomly assign patients with recurrent C. difficile infection to either antibiotic therapy or to duodenal infusion of donor feces. In order to estimate the sample size that would be needed, the investigators assumed that the feces infusion would be successful 90% of the time, and antibiotic therapy would be successful in 60% of cases. How many subjects will be needed in each group to ensure that the power of the study is 80% with a level of significance α = 0.05?

Determining the appropriate design of a study is more important than the statistical analysis; a poorly designed study can never be salvaged, whereas a poorly analyzed study can be re-analyzed. A critical component in study design is the determination of the appropriate sample size. The sample size must be large enough to adequately answer the research question, yet not too large so as to involve too many patients when fewer would have sufficed. The determination of the appropriate sample size involves statistical criteria as well as clinical or practical considerations. Sample size determination involves teamwork; biostatisticians must work closely with clinical investigators to determine the sample size that will address the research question of interest with adequate precision or power to produce results that are clinically meaningful.

The following table summarizes the sample size formulas for each scenario described here. The formulas are organized by the proposed analysis, a confidence interval estimate or a test of hypothesis.

• Buschman NA, Foster G, Vickers P. Adolescent girls and their babies: achieving optimal birth weight. Gestational weight gain and pregnancy outcome in terms of gestation at delivery and infant birth weight: a comparison between adolescents under 16 and adult women. Child: Care, Health and Development. 2001; 27(2):163-171.
• Feuer EJ, Wun LM. DEVCAN: Probability of Developing or Dying of Cancer. Version 4.0 .Bethesda, MD: National Cancer Institute, 1999.
• Howell DC. Statistical Methods for Psychology. Boston, MA: Duxbury Press, 1982.
• Fleiss JL. Statistical Methods for Rates and Proportions. New York, NY: John Wiley and Sons, Inc.,1981.
• National Center for Health Statistics. Health, United States, 2005 with Chartbook on Trends in the Health of Americans. Hyattsville, MD : US Government Printing Office; 2005.  
• Plaskon LA, Penson DF, Vaughan TL, Stanford JL. Cigarette smoking and risk of prostate cancer in middle-aged men. Cancer Epidemiology Biomarkers & Prevention. 2003; 12: 604-609.
• Rutter MK, Meigs JB, Sullivan LM, D'Agostino RB, Wilson PW. C-reactive protein, the metabolic syndrome and prediction of cardiovascular events in the Framingham Offspring Study. Circulation. 2004;110: 380-385.
• Ramachandran V, Sullivan LM, Wilson PW, Sempos CT, Sundstrom J, Kannel WB, Levy D, D'Agostino RB. Relative importance of borderline and elevated levels of coronary heart disease risk factors. Annals of Internal Medicine. 2005; 142: 393-402.
• Wechsler H, Lee JE, Kuo M, Lee H. College Binge Drinking in the 1990s:A Continuing Problem Results of the Harvard School of Public Health 1999 College Health, 2000; 48: 199-210.

Answers to Selected Problems

Answer to birth weight question - page 3.

An investigator wants to estimate the mean birth weight of infants born full term (approximately 40 weeks gestation) to mothers who are 19 years of age and under. The mean birth weight of infants born full-term to mothers 20 years of age and older is 3,510 grams with a standard deviation of 385 grams. How many women 19 years of age and under must be enrolled in the study to ensure that a 95% confidence interval estimate of the mean birth weight of their infants has a margin of error not exceeding 100 grams?

In order to ensure that the 95% confidence interval estimate of the mean birthweight is within 100 grams of the true mean, a sample of size 57 is needed. In planning the study, the investigator must consider the fact that some women may deliver prematurely. If women are enrolled into the study during pregnancy, then more than 57 women will need to be enrolled so that after excluding those who deliver prematurely, 57 with outcome information will be available for analysis. For example, if 5% of the women are expected to delivery prematurely (i.e., 95% will deliver full term), then 60 women must be enrolled to ensure that 57 deliver full term. The number of women that must be enrolled, N, is computed as follows:

                                                        N (number to enroll) * (% retained) = desired sample size

                                                        N (0.95) = 57

                                                        N = 57/0.95 = 60.

 Answer Freshmen Smoking - Page 4

In order to ensure that the 95% confidence interval estimate of the proportion of freshmen who smoke is within 5% of the true proportion, a sample of size 303 is needed. Notice that this sample size is substantially smaller than the one estimated above. Having some information on the magnitude of the proportion in the population will always produce a sample size that is less than or equal to the one based on a population proportion of 0.5. However, the estimate must be realistic.

Answer to Medical Device Problem - Page 7

A medical device manufacturer produces implantable stents. During the manufacturing process, approximately 10% of the stents are deemed to be defective. The manufacturer wants to test whether the proportion of defective stents is more than 10%. If the process produces more than 15% defective stents, then corrective action must be taken. Therefore, the manufacturer wants the test to have 90% power to detect a difference in proportions of this magnitude. How many stents must be evaluated? For you computations, use a two-sided test with a 5% level of significance.

Then substitute the effect size and the appropriate z values for the selected alpha and power to comute the sample size.

A sample size of 364 stents will ensure that a two-sided test with α=0.05 has 90% power to detect a 0.05, or 5%, difference in jthe proportion of defective stents produced.

Answer to Alcohol and GPA - Page 8

An investigator is planning a study to assess the association between alcohol consumption and grade point average among college seniors. The plan is to categorize students as heavy drinkers or not using 5 or more drinks on a typical drinking day as the criterion for heavy drinking. Mean grade point averages will be compared between students classified as heavy drinkers versus not using a two independent samples test of means. The standard deviation in grade point averages is assumed to be 0.42 and a meaningful difference in grade point averages (relative to drinking status) is 0.25 units. How many college seniors should be enrolled in the study to ensure that the power of the test is 80% to detect a 0.25 unit difference in mean grade point averages? Use a two-sided test with a 5% level of significance.

First compute the effect size.

Now substitute the effect size and the appropriate z values for alpha and power to compute the sample size.

Sample sizes of n i =44 heavy drinkers and 44 who drink few fewer than five drinks per typical drinking day will ensure that the test of hypothesis has 80% power to detect a 0.25 unit difference in mean grade point averages.

Answer to Donor Feces - Page 8

We first compute the effect size by substituting the proportions of patients expected to be cured with each treatment, p 1 =0.6 and p 2 =0.9, and the overall proportion, p=0.75:

We now substitute the effect size and the appropriate Z values for the selected a and power to compute the sample size.

Samples of size n 1 =33 and n 2 =33 will ensure that the test of hypothesis will have 80% power to detect this difference in the proportions of patients who are cured of C. diff. by feces infusion versus antibiotic therapy.

In fact, the investigators enrolled 38 into each group to allow for attrition. Nevertheless, the study was stopped after an interim analysis. Of 16 patients in the infusion group, 13 (81%) had resolution of C. difficile–associated diarrhea after the first infusion. The 3 remaining patients received a second infusion with feces from a different donor, with resolution in 2 patients. Resolution of C. difficile infection occurred in only 4 of 13 patients (31%) receiving the antibiotic vancomycin.

Power & Sample Size Calculator

Use this advanced sample size calculator to calculate the sample size required for a one-sample statistic, or for differences between two proportions or means (two independent samples). More than two groups supported for binomial data. Calculate power given sample size, alpha, and the minimum detectable effect (MDE, minimum effect of interest).

Experimental design

Data parameters

Related calculators

• Using the power & sample size calculator

Parameters for sample size and power calculations

Calculator output.

• Why is sample size determination important?
• What is statistical power?

Post-hoc power (Observed power)

• Sample size formula
• Types of null and alternative hypotheses in significance tests
• Absolute versus relative difference and why it matters for sample size determination

    Using the power & sample size calculator

This calculator allows the evaluation of different statistical designs when planning an experiment (trial, test) which utilizes a Null-Hypothesis Statistical Test to make inferences. It can be used both as a sample size calculator and as a statistical power calculator . Usually one would determine the sample size required given a particular power requirement, but in cases where there is a predetermined sample size one can instead calculate the power for a given effect size of interest.

1. Number of test groups. The sample size calculator supports experiments in which one is gathering data on a single sample in order to compare it to a general population or known reference value (one-sample), as well as ones where a control group is compared to one or more treatment groups ( two-sample, k-sample ) in order to detect differences between them. For comparing more than one treatment group to a control group the sample size adjustments based on the Dunnett's correction are applied. These are only approximately accurate and subject to the assumption of about equal effect size in all k groups, and can only support equal sample sizes in all groups and the control. Power calculations are not currently supported for more than one treatment group due to their complexity.

2. Type of outcome . The outcome of interest can be the absolute difference of two proportions (binomial data, e.g. conversion rate or event rate), the absolute difference of two means (continuous data, e.g. height, weight, speed, time, revenue, etc.), or the relative difference between two proportions or two means (percent difference, percent change, etc.). See Absolute versus relative difference for additional information. One can also calculate power and sample size for the mean of just a single group. The sample size and power calculator uses the Z-distribution (normal distribution) .

3. Baseline The baseline mean (mean under H 0 ) is the number one would expect to see if all experiment participants were assigned to the control group. It is the mean one expects to observe if the treatment has no effect whatsoever.

4. Minimum Detectable Effect . The minimum effect of interest, which is often called the minimum detectable effect ( MDE , but more accurately: MRDE, minimum reliably detectable effect) should be a difference one would not like to miss , if it existed. It can be entered as a proportion (e.g. 0.10) or as percentage (e.g. 10%). It is always relative to the mean/proportion under H 0 ± the superiority/non-inferiority or equivalence margin. For example, if the baseline mean is 10 and there is a superiority alternative hypothesis with a superiority margin of 1 and the minimum effect of interest relative to the baseline is 3, then enter an MDE of 2 , since the MDE plus the superiority margin will equal exactly 3. In this case the MDE (MRDE) is calculated relative to the baseline plus the superiority margin, as it is usually more intuitive to be interested in that value.

If entering means data, one needs to specify the mean under the null hypothesis (worst-case scenario for a composite null) and the standard deviation of the data (for a known population or estimated from a sample).

5. Type of alternative hypothesis . The calculator supports superiority , non-inferiority and equivalence alternative hypotheses. When the superiority or non-inferiority margin is zero, it becomes a classical left or right sided hypothesis, if it is larger than zero then it becomes a true superiority / non-inferiority design. The equivalence margin cannot be zero. See Types of null and alternative hypothesis below for an in-depth explanation.

6. Acceptable error rates . The type I error rate, α , should always be provided. Power, calculated as 1 - β , where β is the type II error rate, is only required when determining sample size. For an in-depth explanation of power see What is statistical power below. The type I error rate is equivalent to the significance threshold if one is doing p-value calculations and to the confidence level if using confidence intervals.

The sample size calculator will output the sample size of the single group or of all groups, as well as the total sample size required. If used to solve for power it will output the power as a proportion and as a percentage.

    Why is sample size determination important?

While this online software provides the means to determine the sample size of a test, it is of great importance to understand the context of the question, the "why" of it all.

Estimating the required sample size before running an experiment that will be judged by a statistical test (a test of significance, confidence interval, etc.) allows one to:

• determine the sample size needed to detect an effect of a given size with a given probability
• be aware of the magnitude of the effect that can be detected with a certain sample size and power
• calculate the power for a given sample size and effect size of interest

This is crucial information with regards to making the test cost-efficient. Having a proper sample size can even mean the difference between conducting the experiment or postponing it for when one can afford a sample of size that is large enough to ensure a high probability to detect an effect of practical significance.

For example, if a medical trial has low power, say less than 80% (β = 0.2) for a given minimum effect of interest, then it might be unethical to conduct it due to its low probability of rejecting the null hypothesis and establishing the effectiveness of the treatment. Similarly, for experiments in physics, psychology, economics, marketing, conversion rate optimization, etc. Balancing the risks and rewards and assuring the cost-effectiveness of an experiment is a task that requires juggling with the interests of many stakeholders which is well beyond the scope of this text.

    What is statistical power?

Statistical power is the probability of rejecting a false null hypothesis with a given level of statistical significance , against a particular alternative hypothesis. Alternatively, it can be said to be the probability to detect with a given level of significance a true effect of a certain magnitude. This is what one gets when using the tool in "power calculator" mode. Power is closely related with the type II error rate: β, and it is always equal to (1 - β). In a probability notation the type two error for a given point alternative can be expressed as [1] :

β(T α ; μ 1 ) = P(d(X) ≤ c α ; μ = μ 1 )

It should be understood that the type II error rate is calculated at a given point, signified by the presence of a parameter for the function of beta. Similarly, such a parameter is present in the expression for power since POW = 1 - β [1] :

POW(T α ; μ 1 ) = P(d(X) > c α ; μ = μ 1 )

In the equations above c α represents the critical value for rejecting the null (significance threshold), d(X) is a statistical function of the parameter of interest - usually a transformation to a standardized score, and μ 1 is a specific value from the space of the alternative hypothesis.

One can also calculate and plot the whole power function, getting an estimate of the power for many different alternative hypotheses. Due to the S-shape of the function, power quickly rises to nearly 100% for larger effect sizes, while it decreases more gradually to zero for smaller effect sizes. Such a power function plot is not yet supported by our statistical software, but one can calculate the power at a few key points (e.g. 10%, 20% ... 90%, 100%) and connect them for a rough approximation.

Statistical power is directly and inversely related to the significance threshold. At the zero effect point for a simple superiority alternative hypothesis power is exactly 1 - α as can be easily demonstrated with our power calculator. At the same time power is positively related to the number of observations, so increasing the sample size will increase the power for a given effect size, assuming all other parameters remain the same.

Power calculations can be useful even after a test has been completed since failing to reject the null can be used as an argument for the null and against particular alternative hypotheses to the extent to which the test had power to reject them. This is more explicitly defined in the severe testing concept proposed by Mayo & Spanos (2006).

Computing observed power is only useful if there was no rejection of the null hypothesis and one is interested in estimating how probative the test was towards the null . It is absolutely useless to compute post-hoc power for a test which resulted in a statistically significant effect being found [5] . If the effect is significant, then the test had enough power to detect it. In fact, there is a 1 to 1 inverse relationship between observed power and statistical significance, so one gains nothing from calculating post-hoc power, e.g. a test planned for α = 0.05 that passed with a p-value of just 0.0499 will have exactly 50% observed power (observed β = 0.5).

I strongly encourage using this power and sample size calculator to compute observed power in the former case, and strongly discourage it in the latter.

    Sample size formula

The formula for calculating the sample size of a test group in a one-sided test of absolute difference is:

where Z 1-α is the Z-score corresponding to the selected statistical significance threshold α , Z 1-β is the Z-score corresponding to the selected statistical power 1-β , σ is the known or estimated standard deviation, and δ is the minimum effect size of interest. The standard deviation is estimated analytically in calculations for proportions, and empirically from the raw data for other types of means.

The formula applies to single sample tests as well as to tests of absolute difference between two samples. A proprietary modification is employed when calculating the required sample size in a test of relative difference . This modification has been extensively tested under a variety of scenarios through simulations.

    Types of null and alternative hypotheses in significance tests

When doing sample size calculations, it is important that the null hypothesis (H 0 , the hypothesis being tested) and the alternative hypothesis is (H 1 ) are well thought out. The test can reject the null or it can fail to reject it. Strictly logically speaking it cannot lead to acceptance of the null or to acceptance of the alternative hypothesis. A null hypothesis can be a point one - hypothesizing that the true value is an exact point from the possible values, or a composite one: covering many possible values, usually from -∞ to some value or from some value to +∞. The alternative hypothesis can also be a point one or a composite one.

In a Neyman-Pearson framework of NHST (Null-Hypothesis Statistical Test) the alternative should exhaust all values that do not belong to the null, so it is usually composite. Below is an illustration of some possible combinations of null and alternative statistical hypotheses: superiority, non-inferiority, strong superiority (margin > 0), equivalence.

All of these are supported in our power and sample size calculator.

Careful consideration has to be made when deciding on a non-inferiority margin, superiority margin or an equivalence margin . Equivalence trials are sometimes used in clinical trials where a drug can be performing equally (within some bounds) to an existing drug but can still be preferred due to less or less severe side effects, cheaper manufacturing, or other benefits, however, non-inferiority designs are more common. Similar cases exist in disciplines such as conversion rate optimization [2] and other business applications where benefits not measured by the primary outcome of interest can influence the adoption of a given solution. For equivalence tests it is assumed that they will be evaluated using a two one-sided t-tests (TOST) or z-tests, or confidence intervals.

Note that our calculator does not support the schoolbook case of a point null and a point alternative, nor a point null and an alternative that covers all the remaining values. This is since such cases are non-existent in experimental practice [3][4] . The only two-sided calculation is for the equivalence alternative hypothesis, all other calculations are one-sided (one-tailed) .

    Absolute versus relative difference and why it matters for sample size determination

When using a sample size calculator it is important to know what kind of inference one is looking to make: about the absolute or about the relative difference, often called percent effect, percentage effect, relative change, percent lift, etc. Where the fist is μ 1 - μ the second is μ 1 -μ / μ or μ 1 -μ / μ x 100 (%). The division by μ is what adds more variance to such an estimate, since μ is just another variable with random error, therefore a test for relative difference will require larger sample size than a test for absolute difference. Consequently, if sample size is fixed, there will be less power for the relative change equivalent to any given absolute change.

For the above reason it is important to know and state beforehand if one is going to be interested in percentage change or if absolute change is of primary interest. Then it is just a matter of fliping a radio button.

    References

1 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science . The Netherlands: Elsevier.

2 Georgiev G.Z. (2017) "The Case for Non-Inferiority A/B Tests", [online] https://blog.analytics-toolkit.com/2017/case-non-inferiority-designs-ab-testing/ (accessed May 7, 2018)

3 Georgiev G.Z. (2017) "One-tailed vs Two-tailed Tests of Significance in A/B Testing", [online] https://blog.analytics-toolkit.com/2017/one-tailed-two-tailed-tests-significance-ab-testing/ (accessed May 7, 2018)

4 Hyun-Chul Cho Shuzo Abe (2013) "Is two-tailed testing for directional research hypotheses tests legitimate?", Journal of Business Research 66:1261-1266

5 Lakens D. (2014) "Observed power, and what to do if your editor asks for post-hoc power analyses" [online] http://daniellakens.blogspot.bg/2014/12/observed-power-and-what-to-do-if-your.html (accessed May 7, 2018)

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "Sample Size Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/power-sample-size-calculator.php URL [Accessed Date: 24 Apr, 2024].

Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:

The author of this tool

     Statistical calculators

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Biochem Med (Zagreb)
• v.31(1); 2021 Feb 15

Sample size, power and effect size revisited: simplified and practical approaches in pre-clinical, clinical and laboratory studies

Ceyhan ceran serdar.

1 Medical Biology and Genetics, Faculty of Medicine, Ankara Medipol University, Ankara, Turkey

Murat Cihan

2 Ordu University Training and Research Hospital, Ordu, Turkey

Doğan Yücel

3 Department of Medical Biochemistry, Lokman Hekim University School of Medicine, Ankara, Turkey

Muhittin A Serdar

4 Department of Medical Biochemistry, Acibadem Mehmet Ali Aydinlar University, Istanbul, Turkey

Calculating the sample size in scientific studies is one of the critical issues as regards the scientific contribution of the study. The sample size critically affects the hypothesis and the study design, and there is no straightforward way of calculating the effective sample size for reaching an accurate conclusion. Use of a statistically incorrect sample size may lead to inadequate results in both clinical and laboratory studies as well as resulting in time loss, cost, and ethical problems. This review holds two main aims. The first aim is to explain the importance of sample size and its relationship to effect size (ES) and statistical significance. The second aim is to assist researchers planning to perform sample size estimations by suggesting and elucidating available alternative software, guidelines and references that will serve different scientific purposes.

Introduction

Statistical analysis is a crucial part of a research. A scientific study must include statistical tools in the study, beginning from the planning stage. Developed in the last 20-30 years, information technology, along with evidence-based medicine, increased the spread and applicability of statistical science. Although scientists have understood the importance of statistical analysis for researchers, a significant number of researchers admit that they lack adequate knowledge about statistical concepts and principles ( 1 ). In a study by West and Ficalora, more than two-thirds of the clinicians emphasized that “the level of biostatistics education that is provided to the medical students is not sufficient” ( 2 ). As a result, it was suggested that statistical concepts were either poorly understood or not understood at all ( 3 , 4 ). Additionally, intentionally or not, researchers tend to draw conclusions that cannot be supported by the actual study data, often due to the misuse of statistics tools ( 5 ). As a result, a large number of statistical errors occur affecting the research results.

Although there are a variety of potential statistical errors that might occur in any kind of scientific research, it has been observed that the sources of error have changed due to the use of dedicated software that facilitates statistics in recent years. A summary of main statistical errors frequently encountered in scientific studies is provided below ( 6 - 13 ):

• Flawed and inadequate hypothesis;
• Improper study design;
• Lack of adequate control condition/group;
• Spectrum bias;
• Overstatement of the analysis results;
• Spurious correlations;
• Inadequate sample size;
• Circular analysis (creating bias by selecting the properties of the data retrospectively);
• Utilization of inappropriate statistical studies and fallacious bending of the analyses;
• p-hacking ( i.e. addition of new covariates post hoc to make P values significant);
• Excessive interpretation of limited or insignificant results (subjectivism);
• Confusion (intentionally or not) of correlations, relationships, and causations;
• Faulty multiple regression models;
• Confusion between P value and clinical significance; and
• Inappropriate presentation of the results and effects (erroneous tables, graphics, and figures).

Relationship among sample size, power, P value and effect size

In this review, we will concentrate on the problems associated with the relationships among sample size, power, P value, and effect size (ES). Practical suggestions will be provided whenever possible. In order to understand and interpret the sample size, power analysis, effect size, and P value, it is necessary to know how the hypothesis of the study was formed. It is best to evaluate a study for Type I and Type II errors ( Figure 1 ) through consideration of the study results in the context of its hypotheses ( 14 - 16 ).

Illustration of Type I and Type II errors.

A statistical hypothesis is the researcher’s best guess as to what the result of the experiment will show. It states, in a testable form the proposition the researcher plans to examine in a sample to be able to find out if the proposition is correct in the relevant population. There are two commonly used types of hypotheses in statistics. These are the null hypothesis (H0) and the alternative (H1) hypothesis. Essentially, the H1 is the researcher’s prediction of what will be the situation of the experimental group after the experimental treatment is applied. The H0 expresses the notion that there will be no effect from the experimental treatment.

Prior to the study, in addition to stating the hypothesis, the researcher must also select the alpha (α) level at which the hypothesis will be declared “supported”. The α represents how much risk the researcher is willing to take that the study will conclude H1 is correct when (in the full population) it is not correct (and thus, the null hypothesis is really true). In other words, alpha represents the probability of rejecting H0 when it actually is true. (Thus, the researcher has made an error by reporting that the experimental treatment makes a difference, when in fact, in the full population, that treatment has no effect.)

The most common α level chosen is 0.05, meaning the researcher is willing to take a 5% chance that a result supporting the hypothesis will be untrue in the full population. However, other alpha levels may also be appropriate in some circumstances. For pilot studies, α is often set at 0.10 or 0.20. In studies where it is especially important to avoid concluding a treatment is effective when it actually is not, the alpha may be set at a much lower value; it might be set at 0.001 or even lower. Drug studies are examples for studies that often set the alpha at 0.001 or lower because the consequences of releasing an ineffective drug can be extremely dangerous for patients.

Another probability value is called “the P value”. The P value is simply the obtained statistical probability of incorrectly accepting the alternate hypothesis. The P value is compared to the alpha value to determine if the result is “statistically significant”, meaning that with high probability the result found in the sample will also be true in the full population. If the P value is at or lower than alpha, H1 is accepted. If it is higher than alpha, the H1 is rejected and H0 is accepted instead.

There are actually two types of errors: the error of accepting H1 when it is not true in the population; this is called a Type I error; and is a false positive. The alpha defines the probability of a Type I error. Type I errors can happen for many reasons, from poor sampling that results in an experimental sample quite different from the population, to other mistakes occurring in the design stage or implementation of the research procedures. It is also possible to make an erroneous decision in the opposite direction; by incorrectly rejecting H1 and thus wrongly accepting H0. This is called a Type II error (or a false negative). The β defines the probability of a Type II error. The most common reason for this type of error is small sample size, especially when combined with moderately low or low effect sizes. Both small sample sizes and low effect sizes reduce the power in the study.

Power, which is the probability of rejecting a false null hypothesis, is calculated as 1-β (also expressed as “1 - Type II error probability”). For a Type II error of 0.15, the power is 0.85. Since reduction in the probability of committing a Type II error increases the risk of committing a Type I error (and vice versa ), a delicate balance should be established between the minimum allowed levels for Type I and Type II errors. The ideal power of a study is considered to be 0.8 (which can also be specified as 80%) ( 17 ). Sufficient sample size should be maintained to obtain a Type I error as low as 0.05 or 0.01 and a power as high as 0.8 or 0.9.

However, when power value falls below < 0.8, one cannot immediately conclude that the study is totally worthless. In parallel with this, the concept of “cost-effective sample size” has gained importance in recent years ( 18 ).

Additionally, the traditionally chosen alpha and beta error limits are generally arbitrary and are being used as a convention rather than being based on any scientific validity. Another key issue for a study is the determination, presentation and discussion of the effect size of the study, as will be discussed below in detail.

Although increasing the sample size is suggested to decrease the Type II errors, it will increase the cost of the project and delay the completion of the research activities in a foreseen period of time. In addition, it should not be forgotten that redundant samples may cause ethical problems ( 19 , 20 ).

Therefore, determination of the effective sample size is crucial to enable an efficient study with high significance, increasing the impact of the outcome. Unfortunately, information regarding sample size calculations are not often provided by clinical investigators in most diagnostic studies ( 21 , 22 ).

Calculation of the sample size

Different methods can be utilized before the onset of the study to calculate the most suitable sample size for the specific research. In addition to manual calculation, various nomograms or software can be used. The Figure 2 illustrates one of the most commonly used nomograms for sample size estimation using effect size and power ( 23 ).

Nomogram for sample size and power, for comparing two groups of equal size. Gaussian distributions assumed. Standardized difference (effect size) and aimed power values are initially selected on the nomogram. The line connecting these values cross the significance level region of the nomogram. The intercept at the appropriate significance value presents the required sample size for the study. In the above example, for effect size = 1, power = 0.8 and alpha value = 0.05, the sample size is found to be 30. (Adapted from reference 16 ).

Although manual calculation is preferred by the experts of the subject, it is a bit complicated and difficult for the researchers that are not statistics experts. In addition, considering the variety of the research types and characteristics, it should be noted that a great number of calculations will be required with too many variables ( Table 1 ) ( 16 , 24 - 30 ).

In recent years, numerous software and websites have been developed which can successfully calculate sample size in various study types. Some of the important software and websites are listed in Table 2 and are evaluated based both on the remarks stated in the literature and on our own experience, with respect to the content, ease of use, and cost ( 31 , 32 ). G-Power, R, and Piface stand out among the listed software in terms of being free-to use. G-Power is a free-to use tool that be used to calculate statistical power for many different t-tests, F-tests, χ 2 tests, z-tests and some exact tests. R is an open source programming language which can be tailored to meet individual statistical needs, by adding specific program modules called packages onto a specific base program. Piface is a java application specifically designed for sample size estimation and post-hoc power analysis. The most professional software is PASS (Power Analysis and Sample Size). With PASS, it is possible to analyse sample size and power for approximately 200 different study types. In addition, many websites provide substantial aid in calculating power and sample size, basing their methodology on scientific literature.

The sample size or the power of the study is directly related to the ES of the study. What is this important ES? The ES provides important information on how well the independent variable or variables predict the dependent variable. Low ES means that, independent variables don’t predict well because they are only slightly related to the dependent variable. Strong ES means that, independent variables are very good predictors of the dependent variable. Thus, ES is clinically important for evaluating how efficiently the clinicians can predict outcomes from the independent variables.

The scale of the ES values for different types of statistical tests conducted in different study types are presented in Table 3 .

In order to evaluate the effect of the study and indicate its clinical significance, it is very important to evaluate the effect size along with statistical significance. P value is important in the statistical evaluation of the research. While it provides information on presence/absence of an effect, it will not account for the size of the effect. For comprehensive presentation and interpretation of the studies, both effect size and statistical significance (P value) should be provided and considered.

It would be much easier to understand ES through an example. For example, assume that independent sample t-test is used to compare total cholesterol levels for two groups having normal distribution. Where X, SD and N stands for mean, standard deviation and sample size, respectively. Cohen’s d ES can be calculated as follows:

Mean (X), mmol/L Standard deviation (SD) Sample size (N)

Group 1 6.5 0.5 30

Group 2 5.2 0.8 30

Cohen d ES results represents: 0.8 large, 0.5 medium, 0.2 small effects). The result of 1.94 indicates a very large effect. Means of the two groups are remarkably different.

In the example above, the means of the two groups are largely different in a statistically significant manner. Yet, clinical importance of the effect (whether this effect is important for the patient, clinical condition, therapy type, outcome, etc .) needs to be specifically evaluated by the experts of the topic.

Power, alpha values, sample size, and ES are closely related with each other. Let us try to explain this relationship through different situations that we created using G-Power ( 33 , 34 ).

The Figure 3 shows the change of sample size depending on the ES changes (0.2, 1 and 2.5, respectively) provided that the power remains constant at 0.8. Arguably, case 3 is particularly common in pre-clinical studies, cell culture, and animal studies (usually 5-10 samples in animal studies or 3-12 samples in cell culture studies), while case 2 is more common in clinical studies. In clinical, epidemiological or meta-analysis studies, where the sample size is very large; case 1, which emphasizes the importance of smaller effects, is more commonly observed ( 33 ).

Relationship between effect size and sample size. P – power. ES - effect size. SS - sample size. The required sample size increases as the effect size decreases. In all cases, P value is set to 0.8. The sample sizes (SS) when ES is 0.2, 1, or 2.5; are 788, 34 and 8, respectively. The graphs at the bottom represent the influence of change in the sample size on the power.

In Figure 4 , case 4 exemplifies the change in power and ES values when the sample size is kept constant ( i.e. as low as 8). As can be seen here, in studies with low ES, working with few samples will mean waste of time, redundant processing, or unnecessary use of laboratory animals.

Relationship between effect size and power. Two different cases are schematized where the sample size is kept constant either at 8 or at 30. When the sample size is kept constant, the power of the study decreases as the effect size decreases. When the effect size is 2.5, even 8 samples are sufficient to obtain power = ~0.8. When the effect size is 1, increasing sample size from 8 to 30 significantly increases the power of the study. Yet, even 30 samples are not sufficient to reach a significant power value if effect size is as low as 0.2.

Likewise, case 5 exemplifies the situation where the sample size is kept constant at 30. In this case, it is important to note that when ES is 1, the power of the study will be around 0.8. Some statisticians arbitrarily regard 30 as a critical sample size. However, case 5 clearly demonstrates that it is essential not to underestimate the importance of ES, while deciding on the sample size.

Especially in recent years, where clinical significance or effectiveness of the results has outstripped the statistical significance; understanding the effect size and power has gained tremendous importance ( 35 – 38 ).

Preliminary information about the hypothesis is eminently important to calculate the sample size at intended power. Usually, this is accomplished by determining the effect size from the results of a previous study or a preliminary study. There are software available which can calculate sample size using the effect size

We now want to focus on sample size and power analysis in some of the most common research areas.

Determination of sample size in pre-clinical studies

Animal studies are the most critical studies in terms of sample size. Especially due to ethical concerns, it is vital to keep the sample size at the lowest sufficient level. It should be noted that, animal studies are radically different from human studies because many animal studies use inbred animals having extremely similar genetic background. Thus, far fewer animals are needed in the research because genetic differences that could affect the study results are kept to a minimum ( 39 , 40 ).

Consequently, alternative sample size estimation methodologies were suggested for each study type ( 41 - 44 ). If the effect size is to be determined using the results from previous or preliminary studies, sample size estimation may be performed using G-Power. In addition, Table 4 may also be used for easy estimation of the sample size ( 40 ).

In addition to sample size estimations that may be computed according to Table 4 , formulas stated in Table 1 and the websites mentioned in Table 2 may also be utilized to estimate sample size in animal studies. Relying on previous studies pose certain limitations since it may not always be possible to acquire reliable “pooled standard deviation” and “group mean” values.

Arifin et al. proposed simpler formulas ( Table 5 ) to calculate sample size in animal studies ( 45 ). In group comparison studies, it is possible to calculate the sample size as follows: N = (DF/k)+1 (Eq. 4).

Based on acceptable range of the degrees of freedom (DF), the DF in formulas are replaced with the minimum ( 10 ) and maximum ( 20 ). For example, in an experimental animal study where the use of 3 investigational drugs are tested minimum number of animals that will be required: N = (10/3)+1 = 4.3; rounded up to 5 animals / group, total sample size = 5 x 3 = 15 animals. Maximum number of animals that will be required: N = (20/3)+1 = 7.7; rounded down to 7 animals / group, total sample size = 7 x 3 = 21 animals.

In conclusion, for the recommended study, 5 to 7 animals per group will be required. In other words, a total of 15 to 21 animals will be required to keep the DF within the range of 10 to 20.

In a compilation where Ricci et al. reviewed 15 studies involving animal models, it was noted that the sample size used was 10 in average (between 6 and 18), however, no formal power analysis was reported by any of the groups. It was striking that, all studies included in the review have used parametric analysis without prior normality testing ( i.e. Shapiro-Wilk) to justify their statistical methodology ( 46 ).

It is noteworthy that, unnecessary animal use could be prevented by keeping the power at 0.8 and selecting one-tailed analysis over two-tailed analysis with an accepted 5% risk of making type I error as performed in some pharmacological studies, reducing the number of required animals by 14% ( 47 ).

Neumann et al. proposed a group-sequential design to minimize animal use without a decrease in statistical power. In this strategy, researchers started the experiments with only 30% of the animals that were initially planned to be included in the study. After an interim analysis of the results obtained with 30% of the animals, if sufficient power is not reached, another 30% is included in the study. If results from this initial 60% of the animals provide sufficient statistical power, then the rest of the animals are excused from the study. If not, the remaining animals are also included in the study. This approach was reported to save 20% of the animals in average, without leading to a decrease in statistical power ( 48 ).

Alternative sample size estimation strategies are implemented for animal testing in different countries. As an example, a local authority in southwestern Germany recommended that, in the absence of a formal sample size estimation, less than 7 animals per experimental group should be included in pilot studies and the total number of experimental animals should not exceed 100 ( 48 ).

On the other hand, it should be noted that, for a sample size of 8 to 10 animals per group, statistical significance will not be accomplished unless a large or very large ES (> 2) is expected ( 45 , 46 ). This problem remains as an important limitation for animal studies. Software like G-Power can be used for sample size estimation. In this case, results obtained from a previous or a preliminary study will be required to be used in the calculations. However, even when a previous study is available in literature, using its data for a sample size estimation will still pose an uncertainty risk unless a clearly detailed study design and data is provided in the publication. Although researchers suggested that reliability analyses could be performed by methods such as Markov Chain Monte Carlo, further research is needed in this regard ( 49 ).

The output of the joint workshop held by The National Institutes of Health (NIH), Nature Publishing Group and Science; “Principles and Guidelines for Reporting Preclinical Research” that was published in 2014, has since been acknowledged by many organizations and journals. This guide has shed significant light on studies using biological materials, involving animal studies, and handling image-based data ( 50 ).

Another important point regarding animal studies is the use of technical repetition (pseudo replication) instead of biological repetition. Technical repetition is a specific type of repetition where the same sample is measured multiple times, aiming to probe the noise associated with the measurement method or the device. Here, no matter how many times the same sample is measured, the actual sample size will remain the same. Let us assume a research group is investigating the effect of a therapeutic drug on blood glucose level. If the researchers measure the blood glucose level of 3 mice receiving the actual treatment and 3 mice receiving placebo, this would be a biological repetition. On the other hand, if the blood glucose level of a single mouse receiving the actual treatment and the blood glucose level of a single mouse receiving placebo are each measured 3 times, this would be technical repetition. Both designs will provide 6 data points to calculate P value, yet the P value obtained from the second design would be meaningless since each treatment group will only have one member ( Figure 5 ). Multiple measurements on single mice are pseudo replication; therefore do not contribute to N. No matter how ingenious, no statistical analysis method can fix incorrectly selected replicates at the post-experimental stage; replicate types should be selected accurately at the design stage. This problem is a critical limitation, especially in pre-clinical studies that conduct cell culture experiments. It is very important for critical assessment and evaluation of the published research results ( 51 ). This issue is mostly underestimated, concealed or ignored. It is striking that in some publications, the actual sample size is found to be as low as one. Experiments comparing drug treatments in a patient-derived stem cell line are specific examples for this situation. Although there may be many technical replications for such experiments and the experiment can be repeated several times, the original patient is a single biological entity. Similarly, when six metatarsals are harvested from the front paws of a single mouse and cultured as six individual cultures, another pseudo replication is practiced where the sample size is actually 1, instead of 6 ( 52 ). Lazic et al . suggested that almost half of the studies (46%) had mistaken pseudo replication (technical repeat) for genuine replication, while 32% did not provide sufficient information to enable evaluation of appropriateness of the sample size ( 53 , 54 ).

Technical vs biological repeat.

In studies providing qualitative data (such as electrophoresis, histology, chromatography, electron microscopy), the number of replications (“number of repeats” or “sample size”) should explicitly be stated.

Especially in pre-clinical studies, standard error of the mean (SEM) is frequently used instead of SD in some situations and by certain journals. The SEM is calculated by dividing the SD by the square root of the sample size (N). The SEM will indicate how variable the mean will be if the whole study is repeated many times. Whereas the SD is a measure of how scattered the scores within a set of data are. Since SD is usually higher than SEM, researchers tend to use SEM. While SEM is not a distribution criterion; there is a relation between SEM and 95% confidence interval (CI). For example, when N = 3, 95% CI is almost equal to mean ± 4 SEM, but when N ≥ 10; 95% CI equals to mean ± 2 SEM. Standard deviation and 95% CI can be used to report the statistical analysis results such as variation and precision on the same plot to demonstrate the differences between test groups ( 52 , 55 ).

Given the attrition and unexpected death risk of the laboratory animals during the study, the researchers are generally recommended to increase the sample size by 10% ( 56 ).

Sample size calculation for some genetic studies

Sample size is important for genetic studies as well. In genetic studies, calculation of allele frequencies, calculation of homozygous and heterozygous frequencies based on Hardy-Weinberg principle, natural selection, mutation, genetic drift, association, linkage, segregation, haplotype analysis are carried out by means of probability and statistical models ( 57 - 62 ). While G-Power is useful for basic statistics, substantial amount of analyses can be conducted using genetic power calculator ( http://zzz.bwh.harvard.edu/gpc/ ) ( 61 , 62 ). This calculator, which provides automated power analysis for variance components (VC) quantitative trait locus (QTL) linkage and association tests in sibships, and other common tests, is significantly effective especially for genetics studies analysing complex diseases.

Case-control association studies for single nucleotide polymorphisms (SNPs) may be facilitated using OSSE web site ( http://osse.bii.a-star.edu.sg/ ). As an example, let us assume the minor allele frequencies of an SNP in cases and controls are approximately 15% and 7% respectively. To have a power of 0.8 with 0.05 significance, the study is required to include 239 samples both for cases and controls, adding up to 578 samples in total ( Figure 6 ).

Interface of Online Sample Size Estimator (OSSE) Tool. (Available at: http://osse.bii.a-star.edu.sg/ ).

Hong and Park have proposed tables and graphics in their article for facilitating sample size estimation ( 57 ). With the assumption of 5% disease prevalence, 5% minor allele frequency and complete linkage disequilibrium (D’ = 1), the sample size in a case-control study with a single SNP marker, 1:1 case-to-control ratio, 0.8 statistical power, and 5% type I error rate can be calculated according to the genetic models of inheritance (allelic, additive, dominant, recessive, and co-dominant models) and the odd ratios of heterozygotes/rare homozygotes ( Table 6 ). As demonstrated by Hong and Park among all other types of inheritance, dominant inheritance requires the lowest sample size to achieve 0.8 statistical power. Whereas, testing a single SNP in a recessive inheritance model requires a very large sample size even with a high homozygote ratio, that is practically challenging with a limited budget ( 57 ). The Table 6 illustrates the difficulty in detecting a disease allele following a recessive mode of inheritance with moderate sample size.

Sample size and power analyses in clinical studies

In clinical research, sample size is calculated in line with the hypothesis and study design. The cross-over study design and parallel study design apply different approaches for sample size estimation. Unlike pre-clinical studies, a significant number of clinical journals necessitate sample size estimation for clinical studies.

The basic rules for sample size estimation in clinical trials are as follows ( 63 , 64 ):

• Error level (alpha): It is generally set as < 0.05. The sample size should be increased to compensate for the decrease in the effect size.
• Power must be > 0.8: The sample size should be increased to increase the power of the study. The higher the power, the lower the risk of missing an actual effect.

The relationship among clinical significance, statistical significance, power and effect size. In the example above, in order to provide a clinically significant effect, a treatment is required to trigger at least 0.5 mmol/L decreases in cholesterol levels. Four different scenarios are given for a candidate treatment, each having different mean total cholesterol change and 95% confidence interval. ES - effect size. N – number of participant. Adapted from reference 65 .

• Similarity and equivalence: The sample size required demonstrating similarity and equivalence is very low.

Sample size estimation can be performed manually using the formulas in Table 1 as well as software and websites in Table 2 (especially by G-Power). However, all of these calculations require preliminary results or previous study outputs regarding the hypothesis of interest. Sample size estimations are difficult in complex or mixed study designs. In addition: a) unplanned interim analysis, b) planned interim analysis and

• adjustments for common variables may be required for sample size estimation.

In addition, post-hoc power analysis (possible with G-Power, PASS) following the study significantly facilitates the evaluation of the results in clinical studies.

A number of high-quality journals emphasize that the statistical significance is not sufficient on its own. In fact, they would require evaluation of the results in terms of effect size and clinical effect as well as statistical significance.

In order to fully comprehend the effect size, it would be useful to know the study design in detail and evaluate the effect size with respect to the type of the statistical tests conducted as provided in Table 3 .

Hence, the sample size is one of the critical steps in planning clinical trials, and any negligence or shortcomings in its estimate may lead to rejection of an effective drug, process, or marker. Since statistical concepts have crucial roles in calculating the sample size, sufficient statistical expertise is of paramount importance for these vital studies.

Sample size, effect size and power calculation in laboratory studies

In clinical laboratories, software such as G-Power, Medcalc, Minitab, and Stata can be used for group comparisons (such as t-tests, Mann Whitney U, Wilcoxon, ANOVA, Friedman, Chi-square, etc. ), correlation analyses (Pearson, Spearman, etc .) and regression analyses.

Effect size that can be calculated according to the methods mentioned in Table 3 is important in clinical laboratories as well. However, there are additional important criteria that must be considered while investigating differences or relationships. Especially the guidelines (such as CLSI, RiliBÄK, CLIA, ISO documents) that were established according to many years of experience, and results obtained from biological variation studies provide us with essential information and critical values primarily on effect size and sometimes on sample size.

Furthermore, in addition to the statistical significance (P value interpretation), different evaluation criteria are also important for the assessment of the effect size. These include precision, accuracy, coefficient of variation (CV), standard deviation, total allowable error, bias, biological variation, and standard deviation index, etc . as recommended and elaborated by various guidelines and reference literature ( 66 - 70 ).

In this section, we will assess sample size, effect size, and power for some analysis types used in clinical laboratories.

Sample size in method and device comparisons

Sample size is a critical determinant for Linear, Passing Bablok, and Deming regression studies that are predominantly being used in method comparison studies. Sample size estimations for the Passing-Bablok and Deming method comparison studies are exemplified in Table 7 and Table 8 respectively. As seen in these tables, sample size estimations are based on slope, analytical precision (% CV), and range ratio (c) value ( 66 , 67 ). These tables might seem quite complicated for some researchers that are not familiar with statistics. Therefore, in order to further simplify sample size estimation; reference documents and guidelines have been prepared and published. As stated in CLSI EP09-A3 guideline, the general recommendation for the minimum sample size for validation studies to be conducted by the manufacturer is 100; while the minimum sample size for user-conducted verification is 40 ( 68 ). In addition, these documents clearly explain the requirements that should be considered while collecting the samples for method/device comparison studies. For instance, samples should be homogeneously dispersed covering the whole detection range. Hence, it should be kept in mind that randomly selected 40-100 sample will not be sufficient for impeccable method comparison ( 68 ).

Additionally, comparison studies might be carried out in clinical laboratories for other purposes; such as inter-device, where usage of relatively few samples is suggested to be sufficient. For method comparison studies to be conducted using patient samples; sample size estimation, and power analysis methodologies, in addition to the required number of replicates are defined in CLSI document EP31-A-IR. The critical point here is to know the values of constant difference, within-run standard deviation, and total sample standard deviation ( 69 ). While studies that compare devices having high analytical performance would suffice lower sample size; studies comparing devices with lower analytical performance would require higher sample size.

Lu et al. used maximum allowed differences for calculating sample sizes that would be required in Bland Altman comparison studies. This type of sample size estimation, which is critically important in laboratory medicine, can easily be performed using Medcalc software ( 70 ).

Sample size in lot to lot variation studies

It is acknowledged that lot-to-lot variation may influence the test results. In line with this, method comparison is also recommended to monitor the performance of the kit in use, between lot changes. To aid in the sample size estimation of these studies; CLSI has prepared the EP26-A guideline “User evaluation of between-reagent lot variation; approved guideline”, which provides a methodology like EP31-A-IR ( 71 , 72 ).

The Table 9 presents sample size and power values of a lot-to-lot variation study comparing glucose measurements at 3 different concentrations. In this example, if the difference in the glucose values measured by different lots is > 0.2 mmol/L, > 0.58 mmol/L and > 1.16 mmol/L at analyte concentrations of 2.77 mmol/L, 8.32 mmol/L and 16.65 mmol/L respectively, lots would be confirmed to be different. In a scenario where one sample is used for each concentration; if the lot-to-lot variation results obtained from each of the three different concentrations are lower than the rejection limits (meaning that the precision values for the tested lots are within the acceptance limits), then the lot variation is accepted to lie within the acceptance range. While the example for glucose measurements presented in the guideline suggests that “1 sample” would be sufficient at each analyte concentration, it should be noted that sample size might vary according to the number to devices to be tested, analytical performance results of the devices ( i.e. precision), total allowable error, etc. For different analytes and scenarios ( i.e. for occasions where one sample/concentration is not sufficient), researchers need to refer CLSI EP26-A ( 71 ).

Some researchers find CLSI EP26-A and CLSI EP31 rather complicated for estimating the sample size in lot-to-lot variation and method comparison studies (which are similar to a certain extent). They instead prefer to use the sample size (number of replicates) suggested by Mayo Laboratories. Mayo Laboratories decided that lot-to-lot variation studies may be conducted using 20 human samples where the data are analysed by Passing-Bablok regression and accepted according to the following criteria: a) slope of the regression line will lie between 0.9 and 1.1; b) R2 coefficient of determination will be > 0.95; c) the Y-intercept of the regression line will be < 50% of the lowest reportable concentration, d) difference of the means between reagent lots will be < 10% ( 73 ).

Sample size in verification studies

Acceptance limits should be defined before the verification and validation studies. These could be determined according to clinical cut-off values, biological variation, CLIA criteria, RiliBÄK criteria, criteria defined by the manufacturer, or state of the art criteria. In verification studies, the “sample size” and the “minimum proportion of the observed samples required to lie within the CI limits” are proportional. For instance, for a 50-sample study, 90% of the samples are required to lie within the CI limits for approval of the verification; while for a 200-sample study, 93% is required ( Table 10 ). In an example study whose total allowable error (TAE) is specified as 15%; 50 samples were measured. Results of the 46 samples (92% of all samples) lied within the TAE limit of 15%. Since the proportion of the samples having results within the 15% TAE limit (92% of the samples) exceeds the minimum proportion required to lie within the TAE limits (90% of the samples), the method is verified ( 74 ).

Especially in recent years, researchers tend to use CLSI EP15-A3 or alternative strategies relying on EP15-A3, for verification analyses. While the alternative strategies diverge from each other in many ways, most of them necessitate a sample size of at least 20 ( 75 - 78 ). Yet, for bias studies, especially for the ones involving External Quality Control materials, even lower sample sizes ( i.e. 10) may be observed ( 79 ). Verification still remains to be one of the critical problems for clinical laboratories. It is not possible to find a single criteria and a single verification method that fits all test methods ( i.e. immunological, chemical, chromatographical, etc. ).

While sample size for qualitative laboratory tests may vary according to the reference literature and the experimental context, CLSI EP12 recommends at least 50 positive and 50 negative samples, where 20% of the samples from each group are required to fall within cut-off value +/- 20% ( 80 , 81 ). According to the clinical microbiology validation/verification guideline Cumitech 31A, the minimum number of the samples in positive and negative groups is 100/each group for validation studies, and 10/each group for verification studies ( 82 ).

Sample size in diagnostic and prognostic studies

ROC analysis is the most important statistical analysis in diagnostic and prognostic studies. Although sample size estimation for ROC analyses might be slightly complicated; Medcalc, PASS, and Stata may be used to facilitate the estimation process. Before the actual size estimations, it is a prerequisite for the researcher to calculate potential area under the curve (AUC) using data from previous or preliminary studies. In addition, size estimation may also be calculated manually according to Table 1 , or using sensitivity (or TPF) and 1-specificity (FPF) values according to Table 11 which is adapted from CLSI EP24-A2 ( 83 , 84 ).

As is known, X-axis of the ROC curve is FPF, and Y-axis is TPF. While TPF represents sensitivity, FPF represents 1-specificity. Utilizing Table 11 , for a 0.85 sensitivity, 0.90 specificity and a maximum allowable error of 5% (L = 0.05), 196 positive and 139 negative samples are required. For the scenarios not included in this table, reader should refer to the formulas given under “diagnostic prognostic studies” subsection of Table 1 .

Standards for reporting of diagnostic accuracy studies (STARD) checklist may be followed for diagnostic studies. It is a powerful checklist whose application is explained in detail by Cohen et al. and Flaubaut et al. ( 85 , 86 ). This document suggests that, readers demand to understand the anticipated precision and power of the study and whether authors were successful in recruiting the sufficient number of participants; therefore it is critical for the authors to explain the intended sample size of their study and how it was determined. For this reason, in diagnostic and prognostic studies, sample size and power should clearly be stated.

As can be seen here, the critical parameters for sample size estimation are AUC, specificity and sensitivity, and their 95% CI values. The table 12 demonstrates the relationship of sample size with sensitivity, specificity, negative predictive value (NPV) and positive predictive value (PPV); the lower the sample size, the higher is the 95% CI values, leading to increase in type II errors ( 87 ). As can be seen here, confidence interval is narrowed as the sample size increases, leading to a decrease in type II errors.

Like all sample size calculations, preliminary information is required for sample size estimations in diagnostic and prognostic studies. Yet, variation occurs among sample size estimates that are calculated according to different reference literature or guidelines. This variation is especially prominent depending on the specific requirements of different countries and local authorities.

While sample size calculations for ROC analyses may easily be performed via Medcalc, the method explained by Hanley et al. and Delong et al. may be utilized to calculate sample size in studies comparing different ROC curves ( 88 , 89 ).

Sample size for reference interval determination

Both IFCC working groups and the CLSI guideline C28-A3c offer suggestions regarding sample size estimations in reference interval studies ( 90 - 93 ). These references mainly suggest at least 120 samples should be included for each study sub-group ( i.e., age-group, gender, race, etc. ). In addition, the guideline also states that, at least 20 samples should be studied for verification of the determined reference intervals.

Since extremes of the observed values may under/over-represent the actual percentile values of a population in nonparametric studies, care should be taken not to rely solely on the extreme values while determining the nonparametric 95% reference interval. Reed et al. suggested a minimum sample size of 120 to be used for 90% CI, 146 for 95% CI, and 210 for 99% CI (93). Linnet proposed that up to 700 samples should be obtained for results having highly skewed distributions ( 94 ). The IFCC Committee on Reference Intervals and Decision Limits working group recommends a minimum of 120 reference subjects for nonparametric methods, to obtain results within 90% CI limits ( 90 ).

Due to the inconvenience of the direct method, in addition to the challenges encountered using paediatric and geriatric samples as well as the samples obtained from complex biological fluids ( i.e. cerebrospinal fluid); indirect sample size estimations using patient results has gained significant importance in recent years. Hoffmann method, Bhattacharya method or their modified versions may be used for indirect determination of the reference intervals ( 95 - 101 ). While a specific sample size is not established, sample size between 1000 and 10.000 is recommended for each sub-group. For samples that cannot be easily acquired ( i.e. paediatric and geriatric samples, and complex biological fluids), sample sizes as low as 400 may be used for each sub-group ( 92 , 100 ).

Sample size in survey studies

The formulations given on Table 1 and the websites mentioned on Table 2 will be particularly useful for sample size estimations in survey studies which are dependent primarily on the population size ( 101 ).

Three critical aspects should be determined for sample size determination in survey studies:

• Population size
• Confidence Interval (CI) of 95% means that, when the study is repeated, with 95% probability, the same results will be obtained. Depending on the hypothesis and the study aim, confidence interval may lie between 90% and 99%. Confidence interval below 90% is not recommended.

For a given CI, sample size and ME is inversely proportional; sample size should be increased in order to obtain a narrower ME. On the contrary, for a fixed ME, CI and sample size is directly proportional; in order to obtain a higher CI, the sample size should be increased. In addition, sample size is directly proportional to the population size; higher sample size should be used for a larger population. A variation in ME causes a more drastic change in sample size than a variation in CI. As exemplified in Table 13 , for a population of 10,000 people, a survey with a 95% CI and 5% ME would require at least 370 samples. When CI is changed from 95% to 90% or 99%, the sample size which was 370 initially would change into 264 or 623 respectively. Whereas, when ME is changed from 5% to 10% or 1%; the sample size which was initially 370 would change into 96 or 4900 respectively. For other ME and CI levels, the researcher should refer to the equations and software provided on Table 1 and Table 2 .

The situation is slightly different for the survey studies to be conducted for problem detection. It would be most appropriate to perform a preliminary survey with a small sample size, followed by a power analysis, and completion of the study using the appropriate number of samples estimated based on the power analysis. While 30 is suggested as a minimum sample size for the preliminary studies, the optimal sample size can be determined using the formula suggested in Table 14 which is based on the prevalence value ( 103 ). It is unlikely to reach a sufficient power for revealing of uncommon problems (prevalence 0.02) at small sample sizes. As can be seen on the table, in the case of 0.02 prevalence, a sample size of 30 would yield a power of 0.45. In contrast, frequent problems ( i.e. prevalence 0.30) were discovered with higher power (0.83) even when the sample size was as low as 5. For situations where power and prevalence are known, effective sample size can easily be estimated using the formula in Table 1 .

Does big sample size always increase the impact of a study?

While larger sample size may provide researchers with great opportunities, it may create problems in interpretation of statistical significance and clinical impact. Especially in studies with big sample sizes, it is critically important for the researchers not to rely only on the magnitude of the regression (or correlation) coefficient, and the P value. The study results should be evaluated together with the effect size, study efficiencies ( i.e. basic research, clinical laboratory, and clinical studies) and confidence interval levels. Monte Carlo simulations could be utilized for statistical evaluations of the big data results ( 18 , 104 ).

As a result, sample size estimation is a critical step for scientific studies and may show significant differences according to research types. It is important that sample size estimation is planned ahead of the study, and may be performed through various routes:

• If a similar previous study is available, or preliminary results of the current study are present, their results may be used for sample size estimations via the websites and software mentioned in Table 1 and Table 2 . Some of these software may also be used to calculate effect size and power.
• If the magnitude of the measurand variation that is required for a substantial clinical effect is available ( i.e. significant change is 0.51 mmol/L for cholesterol, 26.5 mmol/L for creatinine, etc. ), it may be used for sample size estimation ( Figure 7 ). Presence of Total Allowable Error, constant and critical differences, biological variations, reference change value (RCV), etc. will further aid in sample size estimation process. Free software (especially G-Power) and web sites presented on Table 2 will facilitate calculations.
• If effect size can be calculated by a preliminary study, sample size estimations may be performed using the effect size ( via G-Power, Table 4 , etc. )
• In the absence of a previous study, if a preliminary study cannot be performed, an effect size may be initially estimated and be used for sample size estimations
• If none of the above is available or possible, relevant literature may be used for sample size estimation.
• For clinical laboratories, especially CLSI documents and guidelines may prove useful for sample size estimation ( Table 9,11 ​ 9,11 ).

Sample size estimations may be rather complex, requiring advanced knowledge and experience. In order to properly appreciate the concept and perform precise size estimation, one should comprehend properties of different study techniques and relevant statistics to certain extend. To assist researchers in different fields, we aimed to compile useful guidelines, references and practical software for calculating sample size and effect size in various study types. Sample size estimation and the relationship between P value and effect size are key points for comprehension and evaluation of biological studies. Evaluation of statistical significance together with the effect size is critical for both basic science, and clinical and laboratory studies. Therefore, effect size and confidence intervals should definitely be provided and its impact on the laboratory/clinical results should be discussed thoroughly.

Potential conflict of interest

None declared.

Statistical power calculators

Power analysis chart.

• next    
• previous    
• Duke NGS Summer Workshop 2015 1.0 documentation »

Hypothesis Testing and Power Calculations ¶

One of things that R is used for is to perform simple testing and power calculations using canned functions. These functions are very simple to run; beign able to use and interpret them correctly is the hard part.

What is covered in this section ¶

• Simple summary statistics
• Functions dealing with probability distributions
• Hypothesis testing
• Power / Sample size calculations
• Tabulating data
• Using simulations to calculate power (use of for and if )
• Customization of graphical plots

Set random see ¶

Estimation ¶.

Often we want to estimate functions of data - for example, the mean or median of a set of numbers.

• 1.2369408226151
• 0.465511274432508
• 0.070684445387072
• 1.42149413805108
• -1.15858605831964
• 0.460407001136643
• -0.625685808667741
• 0.313346968415322
• -1.24274709077289
• -0.945266218602314

Hypothesis testing ¶

Asssume theroy covered in morning statistics lecutres.

Example: Comparing group means ¶

The t-test ¶, what is going on and what does all this actually mean ¶.

The variable result is a list (similar to a hashmap or dictionary in other languages), and named parts can be extracte with the $ method - e.g. result$p.value gives the p-value.

The test firs cacluates a number called a \(t\) statistic that is given by some function of the data. From theoretical anaysis, we know that if the null hypothesis and assumptions of equal vairance and normal distributiono of the data are correct, then the \(t\) random variable will have a \(t\) distribution with 18 degrees of freedom (20 data points minus 2 estimated means).

The formula fot calcualting the \(t\) -statitic is

where \(\bar{x_1}\) and \(\bar{x_2}\) are the sample means, and se (standard error) is

where \(s_1^2\) and \(s_2^2\) are the sample variances.

We will calculate all these values to show what goes on in the sausage factory.

Now we will make use of our knowledge of probability distributions to understan what the p-value is.

We will plot the PDF of the t-distribution with df=18. The x-axis is the value of the t-statistic and the y-axis is the density (you can think of the density as the height of a histogram with total area normalized to sum to 1). The red lines are at the 2.5th and 97.5th quantiles - so for a two-sided test, the t-statistic must be more extreme than these two red lines (i.e. to the right of the 97.5th quantile or to the left of the 2.5th quantile) to reject the null hypothesis. We sse that our \(t\) statisitc (and its symmeetric negative) in dashed green do not meet this requirement - hence the p-value is > 0.05.

The p-value is the areau under the curve more extreme than the green lines. Since the t-statisic is positive, we can find the area to its right as one minus the cumulative density up to the value of the t-statitic. Doubling this (why?) gives us the p-value.

Note that this agrees with the value given by t.test .

The ranksum test ¶

This calculates a test statistic \(W\) that is the sum of the outcomes for all pairwise comparisons of the ranks of the values in \(x\) and \(y\) . Outcomes are 1 if the first item > the second item, 0.5 for a tie and 0 otherwise. This can be simplified to the follwoing formula

where \(R_1\) is the sum of ranks for the values in \(x\) . For large samples, \(W\) can be considered to come from the normal distribution with means aand standard deviations that can be calculated from the data (look up by Googling or any mathematical statitics textbook if interested).

Explicit calculation of statistic ¶

Effect of sample size ¶.

Supppose we measure the weights of 100 people before and after a marathon. We want to know if there is a difference. What is the p-value for an appropirate parametric and non-parametric test?

Example: Comparing proportions ¶

One sample ¶, two samples ¶, test that proportions are equal using z-score (prop.test) ¶, alternative using \(\chi^2\) test ¶.

You find 3 circulating DNA fragments with the following properties

• fragment 1 has length 100 and is 35% CG
• fragment 2 has length 110 and is 40% CG
• fragment 3 has length 120 and is 50% GC

Do you reject the null hypotheses that the percent GC content is the same for all 3 fraemnets?

Sample size calculations ¶

Need some explanation and disclaimers here!

See Qucik-R Power for more examples and more detailed explanation of function parameters.

For simple power calculations, you need 3 out of 4 of the follwoing: - n = number of samples / experimental units - sig.level = what “p-value” you will be using to determine significance - power = fraction of experiments that will reject null hypothesis - d = “effect size” ~ depends on context

Check our understanding of what power means ¶

Note: The code below is an example of a statistical simulation . It can be made more efficient by vectorization, but looping is initially easer to understand and the speed makes no practical differnece for such a small exmaple.

Before running the code - try to answer this question:

If we performed the same experiment 1000 times with n=1879 (from power calucations above), how many experiments would yield a p-value of less than 0.05?

Suppose an investigator proposes to use an unpaired t-test to examine differences between two groups of size 13 and 16. What is the power at the usual 0.05 significance level for effet sizes of 0.1, 0.5 and 1.0.

Page contents

• What is covered in this section
• Set random see
• The ranksum test
• Effect of sample size
• Test that proportions are equal using z-score (prop.test)
• Alternative using \(\chi^2\) test
• Check our understanding of what power means

Previous page

← Grouping and Aggregation

→ Probability distributions and Random Number Genereation

• Show Source

Quick search

Enter search terms or a module, class or function name.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 11 March 2019

Statistical power in genome-wide association studies and quantitative trait locus mapping

• Meiyue Wang 1 &
• Shizhong Xu   ORCID: orcid.org/0000-0001-6789-6655 1  

Heredity volume  123 ,  pages 287–306 ( 2019 ) Cite this article

14k Accesses

49 Citations

10 Altmetric

Metrics details

• Genetic linkage study

Genome-wide association studies

Power calculation prior to a genetic experiment can help investigators choose the optimal sample size to detect a quantitative trait locus (QTL). Without the guidance of power analysis, an experiment may be underpowered or overpowered. Either way will result in wasted resource. QTL mapping and genome-wide association studies (GWAS) are often conducted using a linear mixed model (LMM) with controls of population structure and polygenic background using markers of the whole genome. Power analysis for such a mixed model is often conducted via Monte Carlo simulations. In this study, we derived a non-centrality parameter for the Wald test statistic for association, which allows analytical power analysis. We show that large samples are not necessary to detect a biologically meaningful QTL, say explaining 5% of the phenotypic variance. Several R functions are provided so that users can perform power analysis to determine the minimum sample size required to detect a given QTL with a certain statistical power or calculate the statistical power with given sample size and known values of other population parameters.

You have full access to this article via your institution.

Similar content being viewed by others

Boosting the power of genome-wide association studies within and across ancestries by using polygenic scores

Adrian I. Campos, Shinichi Namba, … Loic Yengo

Emil Uffelmann, Qin Qin Huang, … Danielle Posthuma

A global overview of pleiotropy and genetic architecture in complex traits

Kyoko Watanabe, Sven Stringer, … Danielle Posthuma

Introduction

Genome-wide association studies (GWAS) and quantitative trait locus (QTL) mapping are important tools for gene discovery. The most popular method for GWAS is the Q + K mixed linear model (MLM), first proposed by Yu et al. ( 2006 ) and then modified by numerous authors to improve the computational efficiency (Kang et al. 2008 ; Lippert et al. 2011 ; Listgarten et al. 2012 ; Zhou et al. 2013 ). Note that MLM is called linear mixed model (LMM) in statistics literature, not mixed linear model. In terms of QTL mapping, the current method of choice is still the composite interval mapping, first proposed by Zeng ( 1994 ) and Jansen ( 1994 ) and then modified by Kao et al. ( 1999 ). In the mixed model GWAS, the genomic background effect is captured by the polygene modeled via a marker inferred kinship matrix, while in composite interval mapping the genomic background effect is controlled by selected markers (cofactors) across the whole genome. Recently, Xu ( 2013 a) proposed to fit the genomic background effect in QTL mapping via marker inferred kinship matrix. QTL mapping populations (also called linkage populations) are often homogeneous and thus there are no population structures involved. However, QTL mapping experiments are often replicated spatially and temporally. The systematic environmental effects should be included in the mixed models as fixed effects. These fixed effects are analogous to the population structure effects in GWAS. Methodology-wise, GWAS and QTL are unified under the same LMM framework. As a consequence, the power analysis proposed in this study applies to both GWAS and QTL mapping.

Statistical power is defined as the ability to correctly reject the null hypothesis (Castelloe and O’Brien 2001 ). In GWAS and QTL mapping, the null hypothesis is the absence of an effect for a candidate locus and thus the power is defined as the probability of detecting a true QTL. In interval mapping via the simple regression analysis (Haley and Knott 1992 ) and single marker GWAS implemented via PLINK (Purcell et al. 2007 ), power analysis is very straightforward because standard methods of power calculation in linear models apply (Castelloe and O’Brien 2001 ; Faul et al. 2007 ). The threshold of the test statistic for significance is drawn from the central Chi-square distribution. The power is calculated from the non-central Chi-square distribution with the non-centrality parameter defined from the true parameter values (Castelloe and O’Brien 2001 ). For LMMs, especially for the kinship matrix based GWAS, the non-centrality parameter is difficult to define. Therefore, power analysis in mixed models is primarily conducted via Monte Carlo simulations, in which true parameters are used to simulate the data (Green and MacLeod 2016 ). The SIMR package is available for power analysis via simulation under the generalized LMM (Fulker et al. 1999 ; Spencer et al. 2009 ; Johnson et al. 2015 ; Green and MacLeod 2016 ). The PAMM program (an R package) is a power analysis for random effects in mixed models under the likelihood ratio tests (Martin et al. 2011 ). Power evaluation in classical mixed model association study via simulation can also be found in Shin and Lee ( 2015 ).

In a simulation-based power analysis, the simulation is replicated multiple times. For each replicate, the simulated QTL is either detected or not by a method of interest under a pre-specified genome-wide Type 1 error, say 0.05. The number of replicates that show positive detection against the total number of replicates is declared as the empirical power. For large GWAS data, such a simulation approach is time-consuming. People often use the genotypic data of an existing population to simulate the response variable given a set of true parameters. This approach can save some computational time for not generating the genotypic data, but performing GWAS for the simulated data is still very costly. An explicit method for power calculation in mixed models can save tremendous amount of time, but such a method has not been available yet. Kononoff and Hanford ( 2006 ) proposed to use PROC MIXED in SAS to calculate the non-centrality parameter for an F test in dairy nutritional studies. They provided the true parameters in PROC MIXED and held the initial parameter values. They then extracted the non-centrality parameter from the output. This approach is a short cut method avoiding massive simulations and may be adopted to the mixed model GWAS, assuming users are skilled SAS programmers.

In human linkage and association studies, power calculation often deals with case-control data (Gordon et al. 2002 ; Edwards et al. 2005 ; Skol et al. 2006 ; Klein 2007 ; Kim et al. 2008 ; Spencer et al. 2009 ; Hong and Park 2012 ; Jiang and Yu 2016 ). Software packages are available for case-control power calculation, e.g., the PGA (Power for Genetic Association analyses) program in MatLab with graphic interface (Menashe et al. 2008 ). Genetic power calculator (GPC) (Sham et al. 2000 ; Purcell et al. 2003 ) is an online program for power calculation in linkage and association mapping. The method simultaneously tests between family variance (variance across family means) for association and within family variance for linkage. The package uses likelihood ratio tests. However, this program only deals with full-sib families, case-control study and transmission disequilibrium test (TDT). The combined linkage and association mapping part implemented in GPC was initially proposed by Fulker et al. ( 1999 ) who evaluated the statistical power via simulations. In case-control studies, the test statistic is the typical Chi-square test by comparing the allele frequencies of the case to the control. The non-centrality parameter depends on the sample sizes, genotype frequencies, disease prevalence, and phenotype misclassification probabilities (Edwards et al. 2005 ). In addition to case-control studies, there are identity-by-descent (IBD)-based methods for QTL mapping and GWAS (Amos 1994 ; Xu and Atchley 1995 ; Almasy and Blangero 1998 ), all of which estimate and test variance components. Power calculation can be conducted theoretically using the expected likelihood ratio test as the non-centrality parameter.

Yang et al. ( 2011 , 2014 ) were the first group of people explicitly addressing statistical power for the Q + K mixed model. They used the expectation (average) of the Chi-square test statistics of QTL to indicate the power. Their purpose was to compare the powers of different models, e.g., comparison of powers for LMMs with proximal contamination and without proximal contamination. The authors did not provide the exact power to detect a particular QTL; rather, used the expected Chi-square test to draw a qualitative conclusion about the comparison. In addition, Yang et al. method is a simulation-based method.

The only explicit method of power calculation for GWAS without simulation was developed by Feng et al. ( 2011 ) and Visscher et al. ( 2017 ), where the non-centrality parameter is expressed as a function of QTL size (expressed as QTL heritability). The software package GWAPower is particularly designed for power calculation in GWAS (Feng et al. 2011 ). Unfortunately, the non-centrality parameter proposed there ignores the polygene captured by the kinship matrix. The polygenic control is a fundamental part of the LMM GWAS (Yu et al. 2006 ). It is unclear how the polygene included in the model affect the power. Does the polygene increase the power or decrease the power? How does the overall relatedness of individuals affect the power? Power calculation is an important first step to design QTL mapping and GWAS experiments. In addition to many other factors, sample size and QTL size are the key factors determining the statistical power. Power calculation prior to the experiments can help investigators choose the optimal sample size to detect a biologically meaningful QTL. Without the guidance of power analysis, an experiment may be underpowered or overpowered. Either way will lead to wasted resource in terms of labor, fund, and time. An underpowered experiment will not be able to detect useful QTL and the entire experiment will be wasted. On the other hand, an overpowered experiment will take more resources than necessary to accomplish what is expected to accomplish. This study will derive the non-centrality parameter (thus the statistical power) for the typical Q + K LMM GWAS and QTL mapping. Readers can write their own codes to calculate the power or sample size using the simple formulas developed in the study. They can also use the R functions provided in Supplementary Information of this paper.

Background of statistical power

In hypothesis testing, we typically express the belief that some effect exists in a population by specifying an alternative hypothesis H 1 . We state a null hypothesis H 0 as the assertion that the effect does not exist and we attempt to gather evidence to reject H 0 in favor of H 1 . Evidence is gathered in the form of sampled data, and a statistical test is used to assess H 0 . If H 0 is rejected but there really is no effect, this is called a Type 1 error, which is usually designated “alpha” ( α ), and statistical tests are designed to ensure that α is suitably small (for example, less than 0.05). If there really is an effect in the population but H 0 is not rejected in the statistical test, then a Type 2 error has been made. The Type 2 error is usually designated “beta” ( β ). The probability 1 −  β of avoiding a Type 2 error, that is correctly rejecting H 0 and achieving statistical significance, is called the statistical power. An important goal in study planning is to ensure an acceptably high level of power. Sample size plays a prominent role in power computations because the focus is often on determining a sufficient sample size to achieve a certain power, or assessing the power for a range of different sample sizes.

The relationship between Type 1 error and statistical power is shown in Table 1 . The off-diagonals of the 2 × 2 table (Table 1 ) are the Type 1 and Type 2 errors. The two diagonal elements represent the probabilities of making correct decisions. The second diagonal element is the statistical power (also called sensitivity), as usually defined in statistics. The first diagonal element 1 −  α is called the specificity.

The relationship between the Type 1 and Type 2 errors is more intuitively illustrated in Fig. 1 . The upper panel of Fig. 1 shows the null distribution (left) and the alternative distribution (right), where the upper tail of the null distribution highlighted in light gray represents the Type 1 error and the lower tail of the alternative distribution highlighted in dark gray represents the Type 2 error. The line dividing the Type 1 and Type 2 errors is the critical value of the test statistic. Sliding the critical value towards the left will increase the Type 1 error but decrease the Type 2 error. However, sliding the critical value towards the right will decrease the Type 1 error but increase the Type 2 error. The lower panel of Fig. 1 shows the changes of the Type 1 error, the Type 2 error, and the statistical power. A test statistic that maximizes the distance between the two distributions is the best test. The critical value should be selected as to minimizing both the Type 1 and Type 2 errors.

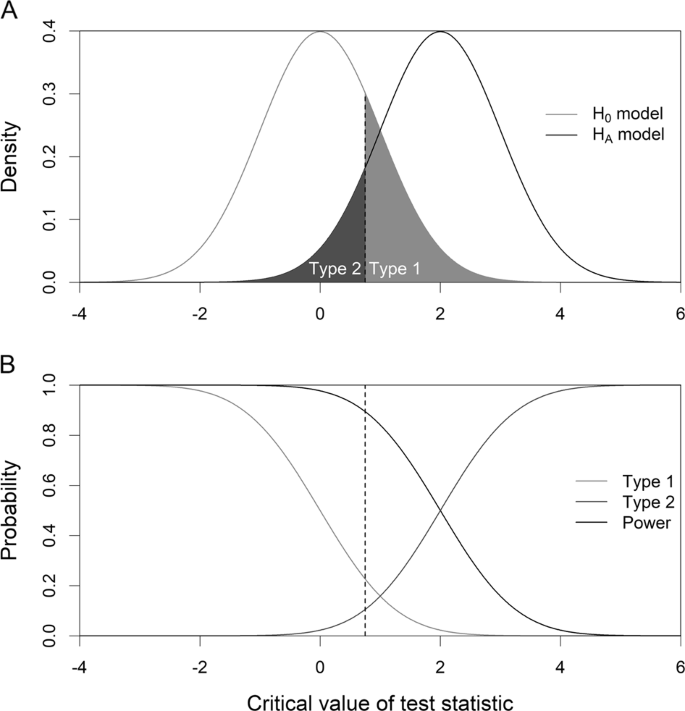
Relationship among the Type 1 and Type 2 errors, and the statistical power. a The null distribution (left) and the alternative distribution (right), where the upper tail of the null distribution highlighted in light gray represents the Type 1 error and the lower tail of the alternative distribution highlighted in dark gray represents the Type 2 error. b Changes of the Type 1 and Type 2 errors, and the statistical power as the critical value (the vertical line) changes

We now use a simple linear regression model to demonstrate the statistical power. Let y be a response variable and Z be an independent variable. The linear model is

where μ is the intercept, γ is the regression coefficient, and e is the residual error vector with an assumed N (0, σ 2 ) distribution for each individual error. The null hypothesis is H 0 : γ  = 0 and the alternative hypothesis is H 1 : γ  ≠ 0. Let \(\hat \gamma\) be the estimated regression coefficient with an estimated variance of

where \(\sigma _Z^2\) is the variance of Z . The Wald test is defined as

When n is sufficiently large, under the null model, the Wald test statistic follows a central Chi-square distribution with 1 degree of freedom (for small n , this test statistic actually follows an F distribution with 1 and n  − 2 degrees of freedom). The assumed Chi-square distribution for the Wald test holds in the ideal situation where the residual error follows a normal distribution. If the normal assumption of the error is violated, power calculation based on the assumed Chi-square distribution will be approximate. However, the approximation will be sufficiently accurate if the sample size is large (Andersen 1970 ). For simplicity, let us use the central χ 2 distribution with 1 degree of freedom as the null distribution. The critical value used to declare significance for the test is \(\chi _{1 - \alpha }^2\) , which is the ( 1 −  α ) × 100 percentile of the χ 2 distribution. If the alternative hypothesis, H 1 : γ  ≠ 0, is true, the Wald-test will follow a non-central Chi-square distribution with a non-centrality parameter

If the independent variable is standardized prior to the analysis, \(\sigma _Z^2 = 1\) and the non-centrality parameter is simply

It is proportional to the product of sample size and the size of the effect (squared regression coefficient relative to the residual error variance).

In terms of QTL mapping with the simple regression model, a more informative way to represent the size of the QTL is

The non-centrality parameter can be rewritten as

The non-centrality parameter will be extended to LMM in the following section. The power and Type 1 error relationship may be different for different test procedures. If the power responds to the change of Type 1 error strongly, the method is considered as a good method. We often use the receiver operating characteristic (ROC) curve to describe the effectiveness of a test procedure. Figure 2 shows three methods (or three sample sizes) having three different patterns of the ROC curves. The curve in red deviates away the most from the diagonal line and thus is the best method. The curve in blue is not as good as the red curve. The curve in purple is closer to the diagonal line and thus is the worst method among the three. If the ROC curve of a method overlaps with the diagonal line, the method is useless.

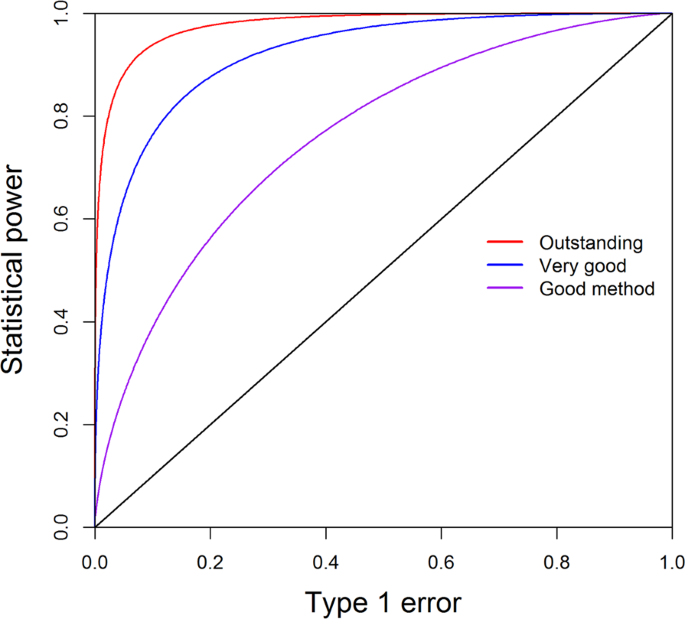
The receiver operating characteristic (ROC) curves of three methods (or different sample sizes). The curve in red deviating away the most from the diagonal line is the best method. The curve in blue is not as good as the red curve. The curve in purple closer to the diagonal line is the worst method among the three

Linear mixed model and Wald test

We first consider the polygenic model ignoring any population structure effects, which will be dealt with in a latter section. Let y be the phenotypic value of a target quantitative trait for QTL mapping or GWAS. The LMM can be written as

where y (an n  × 1 vector) is assumed to be adjusted by any fixed effects, e.g., population structure, year, location, age, and so on, prior to the mixed model analysis, Z k (an n  × 1 vector) is a genotype indicator variable for the locus (candidate gene) under investigation and assumed to be standardized (subtracted by the mean and divided by the standard deviation so that \(\sigma _Z^2 = 1\) ), γ k is the effect of the locus and treated as a fixed effect, ξ is an n  × 1 vector of polygenic effects captured by a marker inferred kinship matrix and is assumed to be \(N(0,K\sigma _\xi ^2)\) distributed where \(\sigma _\xi ^2\) is the polygenic variance, and e  ~  N (0, Iσ 2 ) is a vector of residual errors with a common variance σ 2 .

The marker inferred kinship matrix is calculated based on (VanRaden 2008 )

where Z k ′ is a vector of standardized genotype indicators for marker k ′ and m is the total number of markers used to calculate the kinship matrix. The denominator d is a normalization factor that makes the diagonal elements as close to unity as possible. Typical value of d can take the mean of the diagonal elements of the original un-normalized kinship matrix. Note that normalization of the kinship matrix is recommended in the power study. The number of markers used to calculate K is not necessarily the same as the total number of markers scanned in the study. Essentially, one of the Z k ′ ’s is Z k , so a potential proximal contamination (Listgarten et al. 2012 ) occurs here, but if m is sufficiently large, say m  > 1000, effect of the proximal contamination on the result is negligible (Wang et al. 2016 ; Wei and Xu 2016 ).

The expectation of y is E( y ) =  μ  +  Z k γ k and the variance–covariance matrix of y is

where \(\lambda = \sigma _\xi ^2{\mathrm{/}}\sigma ^2\) is the variance ratio (representing the size of the polygene) and H  =  Kλ  +  I is the covariance structure. The test statistic is the usual Wald test

Under the null hypothesis H 0 : γ k  = 0, the Wald statistic follows approximately the \(\chi _1^2\) distribution. In GWAS, the sample size is often sufficiently large so that the Chi-square distribution is a very safe assumption.

Non-centrality parameter

To evaluate the power of the Wald test, we must assume that all parameters are known so that we can find the distribution of the test statistic under the alternative hypothesis. The parameters include γ k , λ , and σ 2 . The variance of the estimated QTL effects given in Eq. ( 14 ) involves a quadratic form of Z k . If we replace the quadratic form by its expectation, the variance becomes

Note the difference between ( 15 ) and ( 14 ), where one is \(\hat \gamma _k\) and the other is γ k . The non-centrality parameter is obtained by replacing all estimated parameters in the Wald test statistic by the true values and thus

A non-centrality parameter is not supposed to contain the actual data but here we have a kinship matrix ( K ) embedded in matrix H . Let us consider K as a constant when we take the expectation of the quadratic form of Z k . Since Z k is a standardized variable, E( Z k ) = 0 and \({\mathop{\rm{var}}} (Z_k) = I\) , where we assume that the n individuals are not genetically related, i.e., they are independent. Note that being genetically independent does not mean K  =  I because K is not the coancestry matrix but a matrix calculated from markers. The expectation of the quadratic form for Z k can be written in the following form:

because E( Z k ) = 0 and \({\mathop{\rm{var}}} (Z_k) = I\) . Recall that H −1  =  U ( Dλ  +  I ) −1 U T and thus

Therefore, the non-centrality parameter is

If Z k is centered but not scaled and the variance is \(\sigma _Z^2\) , we would have

Therefore, the non-centrality parameter would be

We now define the proportion of phenotypic variance explained by the QTL by

This way of expressing the size of the QTL is more intuitive. The ratio ( γ k / σ ) 2 can be expressed as a function of \(h_{QTL}^2\) , as shown below:

Therefore, the non-centrality parameter can be written as a function of the QTL heritability,

Let us call

the effective sample size, which would be the actual sample size if the polygenic variance were nil ( λ  = 0), as demonstrated below:

The non-centrality parameter of the mixed model would then be identical to the simple regression model, as shown in Eq. ( 8 ). Finally, the non-centrality parameter is simplified into

Type 1 error, Type 2 error, and statistical power

Let α be the Type 1 error chosen by the investigator, let β be the Type 2 error when the Type 1 error is set at α and let ω  = 1 −  β be the statistical power. We define χ 2 ( τ , δ ) as a non-central Chi-square variable with τ degrees of freedom and a non-centrality parameter δ . Therefore, χ 2 (1, 0) is just a central Chi-square variable with 1 degree of freedom. The cumulative distribution function for a non-central Chi-square variable is described by

Given this notation, we define the Type 1 error by

where F ( x |1, 0) is the cumulative distribution function for a central Chi-square variable with 1 degree of freedom. The threshold of the test statistic is obtained via the inverse of the central Chi-square distribution,

The Type 2 error using this threshold is

and thus the power is

The above three equations allow us to calculate the statistical power given the genetic parameters of the population under study.

We now demonstrate that if the Type 1 and Type 2 errors are fixed and the sample size along with the population parameters are known, we can find the minimum detectable QTL. There is another inverse function for the non-central Chi-square distribution, which is called the second non-centrality parameter,

This non-centrality parameter can also be calculated from quantiles of the standardized normal distribution. Let z 1− α /2  = Φ −1 (1 −  α /2) and z 1− β  = Φ −1 (1 −  β ) be the quantiles of the standardized normal distribution. They are the inverses of the normal distribution, also called probit functions. The non-centrality parameter can be expressed as (Xu 2013 b)

Replacing δ in Eq. ( 24 ) by δ β in Eq. ( 34 ) leads to

This equation is all what we need to calculate \(h_{QTL}^2\) given all other parameters, including the Type 1 and Type 2 errors. For example, if α  = 5 × 10 −7 and β  = 0.15 (equivalent to a power of ω  = 0.85), the non-centrality parameter should be

Given λ , n , and d j , we should be able to find \(h_{QTL}^2\) .

A special kinship matrix with the compound symmetry structure

The eigenvalues of a marker inferred kinship matrix depend on the sample size and the LD structure of all markers used to infer the kinship matrix. Evaluation of power must be conducted numerically after we have the kinship matrix (this will be done later in the simulation study). We now simplify the kinship matrix so that a general trend can be found regarding the change of power. We assume that the kinship matrix has the following special structure:

where ρ represents the correlation between any pair of individuals. This structure is close to the compound symmetry (CS) structure (differing by a common factor). Under this assumption, the eigenvalues are d 2  =  d 3  =  ⋯  =  d n  = 1 −  ρ and d 1  =  n  − ( n  − 1)(1 −  ρ ) because \({\sum} {d_j = n}\) (the sum of all eigenvalues of a correlation matrix equals the sample size). These eigenvalues yield

which is the effective sample size. Substituting it into Eq. ( 24 ), we have

Remember that the non-centrality parameter directly relates to the statistical power. We now examine the non-centrality parameter under some special cases. If λ  → 0, the non-centrality parameter becomes

So, the power increases as \(h_{QTL}^2\) and n increase. This is consistent with the simple regression analysis, i.e., interval mapping (Lander and Botstein 1989 ; Haley and Knott 1992 ). If ρ  → 0, the same conclusion is obtained as the situation where λ  → 0, that is

Note that the situation of ρ  = 0 is equivalent to λ not being estimable because the kinship matrix is an identity matrix, explaining why λ  = 0 is the same as ρ  = 0. We now examine the situation when ρ  → 1,

If n is relatively large,

which implies that adding the kinship matrix in GWAS actually helps boost the power by a factor ( λ  + 1).

In reality, the CS assumption of the kinship matrix is not required in power analysis. Given λ , one can directly calculate n 0 using Eq. ( 24 ). The reason to introduce ρ is to identify a general trend of the relationship between the power and the overall relatedness of individuals in the association population.

Power calculation for models including dominance

The power calculation described so far applies to populations with only two possible genotypes per locus or more than two genotypes per locus but only for the additive genetic effect. We will extend the method to populations with arbitrary number of genotypes per locus. For example, an F 2 population derived from the cross of two inbred lines has three possible genotypes per locus. There are two alternative ways to formulate the genotypic model. One is to define an additive indicator ( a ) and a dominance indicator ( d ) for individual j at locus k , such as

Define Z k  = [ Z k ( a )|| Z k ( d )] as an n  × 2 matrix for the genetic effect indicators and \(\gamma _k = \left[ {\begin{array}{*{20}{c}} {\gamma _{1k}} & {\gamma _{2k}} \end{array}} \right]^T\) as the additive ( γ 1 k ) and dominance ( γ 2 k ) effects of marker k . The LMM is

which is exactly the same as Eq. ( 9 ) but here the dimensionalities of Z k and γ k are different from those of the additive model. Let \({\mathop{\rm{var}}} (Z_k) = {\mathrm{\Sigma }}_{ZZ}\) be a 2 × 2 variance matrix for the genotype indicator variables. The non-centrality parameter is defined as

If the genetic effect indicator variables are standardized, Σ ZZ  =  I , so that the non-centrality parameter becomes

where \(\sigma _G^2 = \gamma _{1k}^2 + \gamma _{2k}^2\) is the total genetic variance for the locus of interest. Let us define \(\lambda = \sigma _\xi ^2{\mathrm{/}}\sigma ^2\) and

We now have a non-centrality parameter expressed as a function of QTL size,

Under the null model, \(H_0:\sigma _G^2 = 0\) , the Wald test statistic (obtained by replacing the true values of parameters in δ by the estimated parameters) will follow a Chi-square distribution with 2 degrees of freedom.

To extend the additive plus dominance model to a more generalized genotypic model for arbitrary number of genotypes per locus, e.g., four-way crosses, we code the genotypes as dummy variables like what is done in the general linear model for the analysis of variance (ANOVA). For example, in a four-way cross population, there are four possible genotypes per locus. The dummy variables are represented by an n  × 4 Z k matrix. Each row of Z k has exactly one element being 1 and the remaining three elements being 0. The position where value 1 takes place is the ordered genotype that this individual holds. Let us denote the marker effects for locus k by \(\gamma _k = \left[ {\begin{array}{*{20}{c}} {\gamma _{1k}} & {\gamma _{2k}} & {\gamma _{3k}} & {\gamma _{4k}} \end{array}} \right]^T\) . The variance matrix for Z k is a 4 × 4 matrix Σ ZZ . Supplementary Note S1 shows how to standardize Z k using matrix Σ ZZ . Under the null hypothesis, \(H_0:\sigma _G^2 = 0\) , the Wald test follows a Chi-square distribution with 4 − 1 = 3 degrees of freedom. In general, the degree of freedom is the number of genotypes minus 1.

Population structure

Population structure is often caused by population heterogeneity (or admixture) represented by multiple ethnic groups or subpopulations within the association population (Pritchard et al. 2000 a, 2000 b). The purpose of fitting population structure effects into the LMM is to reduce false positives for loci that are confounded with population structure (Toosi et al. 2018 ). For example, if a locus is fixed to alleles unique to subpopulations and the subpopulations are strongly associated with the trait under study, we do not want to claim the locus as associated with the trait because the association may be caused by subpopulations. Fitting the population structure will prevent such a false positive. Let us review the Q + K mixed model for GWAS (Yu et al. 2006 ),

where Q is the design matrix for population structure (obtained either from principal component analysis or cluster analysis using genome-wide markers), η is a q  × 1 vector of structural effects on the phenotype. If the model is true, the estimated effects of η and γ k are unbiased (best linear unbiased estimates). However, the variance of \(\hat \gamma _k\) with population structure will be increased compared with the variance of estimated γ k when the population structure is absent. The increased variance is formulated as

where \(r_{ZQ_i}^2\) is the squared correlation between the i th column of matrix Q and Z k (under the additive model, Z k is a single column vector). The non-centrality parameter for the Wald test is

If there is a single column of matrix Q , the extra term is simply \(1 - r_{ZQ}^2\) , which is a fraction between 0 and 1. As a result, population structure effects actually reduce the non-centrality parameter and thus lower the power. If the population structure effects are present but ignored in the model, the consequence is a decreased power (if the structure effects are independent of the marker under study) because the structure effects will go to the residual error. An inflated residual error variance will decrease the power. If the structure effects are correlated with the marker under study, failure to incorporate them into the model will violate the model assumption that residual error is not supposed to correlate with the model effects and thus there is no correct way to evaluate the theoretical power. Derivation of the power in the presence of population structure is given in Supplementary Note S2 .

Simulation study to validate the power calculation

Populations.

The purpose of the simulation study is to validate the theoretical powers under several different scenarios. To simplify the simulation, we used marker inferred kinship matrices from three different rice populations as known quantities to generate phenotypic values. The first population consists of 210 recombinant inbred lines (RIL) derived from the hybrid (Shanyou 63) of two elite indica rice varieties (Zhenshan 97 and Minghui 63). The original RIL population was developed by Xing et al. ( 2002 ) and Hua et al. ( 2002 ). The genotypic data were represented by 1619 bins extracted from ~270,000 SNPs and each bin consists of many cosegregating SNPs (Yu et al. 2011 ). We used the 1619 bins to construct a 210 × 210 kinship matrix. Simulation result from this kinship matrix was used to validate power calculation for the simple additive model.

The second rice population consists of 278 hybrids from random pairings of the 210 RILs of the first population with the same number of bins (Hua et al. 2002 ). The bin genotypes of the hybrids were inferred from the genotypes of the 210 parents. Each locus of the hybrid population has three possible genotypes ( A 1 A 1 , A 1 A 2 , and A 2 A 2 ) with expected frequencies of 0.25, 0.5, and 0.25, which mimic the genotypic frequencies of an F 2 population. Since the parents of the hybrids are inbred, the genotypes of a hybrid can be regenerated if needed. Such an F 2 is called an immortalized F 2 (IMF2) (Hua et al. 2002 ). The purpose of this population is to validate power calculation for detection of both additive and dominance effects.

The third rice population consists of a diverse collection of 524 accessions of rice, including both landraces and elite varieties (Chen et al. 2014 ). Genotypes of 180,000 SNPs were selected from a total of more than 6.4 million high-quality SNPs. The selected subset of SNPs were used to build the 524 × 524 kinship matrix. The population contains 293 indica and 231 japonica subspecies. This data set was used to validate power calculation in the presence of population structure. Here, the population structure is represented by two subspecies with indica coded as 1 and japonica coded as 0, i.e., the design matrix Q for population structure contains only one column of a binary variable.

Simulations

Given a kinship matrix (sample size is already known) and a polygenic parameter ( \(\lambda = \sigma _\xi ^2{\mathrm{/}}\sigma ^2\) ), we calculated the effective sample size n 0 , which allows us to calculate the theoretical power under each \(h_{QTL}^2\) . The empirical power from simulation was then compared to the theoretical power. We first simulated data in the absence of population structure under the additive model with n  = 210 recombinant lines (the first population). The kinship matrix for the 210 RILs is provided in Supplementary Data S1 . Recall that the LMM is

where the parameter values were set at μ  = 10, σ 2  = 5, and \(\sigma _\xi ^2 = \left\{ {0,5,10} \right\}\) , so that λ  = {0, 1, 2}. Under the three polygenic levels, the effective sample sizes are n 0  = {210, 303.74, 396.07}. For example, when λ  = 1, the effective sample size is n 0  ≈ 304, much higher than the actual sample size n  = 210. Verbally, we say that we need a sample of 304 for λ  = 0 to reach the same power as a sample of 210 for λ  = 1. We varied \(h_{QTL}^2\) from 0 to 0.06 incremented by 0.001 and generated one sample under each level of \(h_{QTL}^2\) . For each sample, we first generated a Z k vector from a Bernoulli distribution with probability 0.5. The values of Z k mimic the numerical codes of the two possible genotypes for an RIL population. We then standardized Z k so that μ Z  = 0 and \(\sigma _Z^2 = 1\) . Next, given \(h_{QTL}^2\) , we calculated the true value of the QTL effect using

The standardized Z k multiplied by γ k gives the genetic value of the QTL for all individuals. The polygenic effects ξ were generated from a multivariate normal distribution with zero expectation and variance \(K\sigma _\xi ^2\) . We first generated n independent standardized normal variables u n ×1 . We then generated polygenic effects using

where U (an n  ×  n matrix) are the eigenvectors of K and D 1/2 (a diagonal matrix) are the square roots of eigenvalues of K . One can verify that ξ  ~  N (0, K ), as shown below:

Finally, e was simulated from N (0, Iσ 2 ). Once the response variable y was simulated, we called the “mixed” function in R written by our own laboratory (Xu et al. 2014 ) to perform the mixed model analysis and statistical test. The locus was declared as significant if its p -value is smaller than the nominal criterion of 0.05. The experiment was replicated 1000 times and the proportion of samples with significant detection was the empirical statistical power. Alternatively, we could repeat the simulation 1619 times (the number of markers) and compare the p -value of each marker with 0.05/1619 = 0.000030883 (after Bonferroni correction) to calculate the proportion of significant markers. Each experiment consists of 1619 simulations because of 1619 markers. We could then replicate the experiment 1000 times to calculate the average power over 1000 experiments. The alternative approach would take substantially longer time to complete the simulation because it involves 1619 times more work. The empirical power from the alternative approach would be much closer to the true value because it would be equivalent to a simulation experiment replicated 1619 × 1000 times.

For the second population, the kinship matrix was drawn from the genotypes of 1619 bins of n  = 278 hybrids. The parameter values were set at μ  = 10, σ 2  = 5, and \(\sigma _\xi ^2 = \left\{ {0,5,10} \right\}\) , so that λ  = {0, 1, 2}. Under the three levels of polygenic variance, the effective sample sizes are n 0  = 278, n 0  = 402.50, and n 0  = 516.14, respectively. We assumed that the additive and dominance effects contribute equally to the hypothetical trait so that \(\gamma _{1k} = \gamma _{2k} = \sqrt {\sigma _G^2{\mathrm{/}}2}\) , where

Genotypes of the 278 hybrids for the locus of interest were generated from a multinomial distribution with size 1 and probabilities 0.25, 0.5, and 0.25, respectively, for A 1 A 1 , A 1 A 2 , and A 2 A 2 . We then coded the additive indicator Z k ( a ) =  Z 1 k and dominance indicator Z k ( d ) =  Z 2 k from the simulated genotypes. After standardization, the two genetic effect indicators were horizontally concatenated into an n  × 2 matrix Z k . The genetic value of individuals due to the QTL were generated by

The kinship matrix of the 278 hybrids were calculated from the 1619 markers and used to simulate the polygenic effects from \(N(0,K\sigma _\xi ^2)\) distribution. The kinship matrix is given in Supplementary Data S2 . Adding simulated residual errors to the mean value μ  = 10, the simulated QTL effect and the polygenic effects, we generated the simulated phenotypic values for all hybrids. Parameter estimation and statistical tests were conducted using our own mixed function in R. The p -value was calculated from the central Chi-square distribution with 2 degrees of freedom. Nominal 0.05 criterion for the p -value was chosen as the threshold to declare statistical significance. The simulation experiment was replicated 1000 times. The proportion of samples in which significance was claimed was the empirical power.

The third population was used to validate the power calculation in the presence of population structure. The kinship matrix of 524 rice varieties was calculated from 180,000 selected SNPs. This kinship matrix is given in Supplementary Data S3 . The population structure was represented by a single column Q coded by 1 for indica and 0 for japonica (Supplementary Data S4 ). The population parameters were set at μ  = 0, σ 2  = 5, \(\sigma _\xi ^2 = 5\) and λ  = 1. The model with population structure is

where both Q and Z k are standardized and the population structure effect was set at η  = 1. Ignoring the contribution from the QTL, the phenotypic variance contributed by the population structure is \(\eta ^2{\mathrm{/}}(\eta ^2 + \sigma _\xi ^2 + \sigma ^2) = 1{\mathrm{/}}(1 + 5 + 5) = 0.0909\) . Three levels of the correlation between Q and Z k (a single column) was chosen: \(r_{QZ}^{} = \left\{ {0.0,0.5,0.9} \right\}\) . The effect of QTL and the polygenic effect were simulated in the same way as the first population. The genotype indicator Z k was simulated conditional on the population structure. Since both Q and Z k are binary variables, we used a special algorithm to generate Z k . We simulated another vector of binary bits (denoted by ζ ) to indicate whether Z k should be different from Q or not. Given Q and the simulated ζ , we generated

If all values of ζ are 1’s, Z k  = 1 −  Q and the correlation should be −1. However, if all values of ζ are 0’s, Z k  =  Q and the correlation should be 1. The vector of bits ( ζ ) was simulated from a Bernoulli distribution with probability r  = 0.5(1 −  r QZ ) using the following R code

Supplementary Note S3 shows that \({\mathop{\rm{var}}} (Z_k) = {\mathop{\rm{var}}} (Q)\) and

Both Q and simulated Z k were standardized before use to generate the response variable.

Supplementary Note S4 provides several R functions and the scripts to run the R functions. User instruction is also included in this note.

Numerical evaluation of power for some special cases

Let us examine the power under a special case when the sample size is n  = 500, the target QTL contributes \(h_{QTL}^2 = 0.05\) of the phenotypic variance, the genome-wide Type 1 error is α  = 5 × 10 −7 , the polygenic variance to the residual variance ratio is λ  = 1 and the effective correlation between individuals in the kinship matrix is ρ  = 0.5. We assume that the total number of markers scanned is m  = 100k so that the genome-wide Type 1 error is α  = 0.05/100000 = 5 × 10 −7 after Bonferroni correction for multiple tests. Note that λ  = 1 means that the polygene contributes \(h_{\mathrm{POLY}}^2 \approx \lambda {\mathrm{/}}(\lambda + 1) = 0.5\) of the phenotypic variance. Under this special case, the non-centrality parameter is

Substituting δ  = 35.02 into Eq. ( 32 ) yields a statistical power of ω  = 0.8136, which is reasonably high. The parameter values in this special case are treated as default values when we evaluate the change of power against the change of one of the other factors (see next paragraph).

We now evaluate the change of power against the change of one factor with other factors being fixed at the values described above. For example, we can examine the change of power against the change of sample size ( n ) when \(h_{QTL}^2 = 0.05\) , α  = 5 × 10 −7 , λ  = 1, and ρ  = 0.5. Figure 3 shows the changes of power against each of the factors. The polygenic effect can increase the power (Fig. 3a ), starting from ω  = 0.55 when λ  = 0 to ω  = 0.9 when λ  = 2. The curve progressively approaches 1, but very slowly. Sham et al. ( 2000 ) also found the variance of common family effect increases statistical powers in sibship analysis, where the common effect shared by siblings is the polygenic effect plus maternal effect. The effective correlation ρ also increases the statistical power (Fig. 3b ), but the relationship is quite linear until ρ is close to 1. Figure 3c, d shows the changes of power against the sample size and the QTL size, respectively. These changes are consistent with the usual expectation, both the sample size and the QTL size increase the power monotonically.

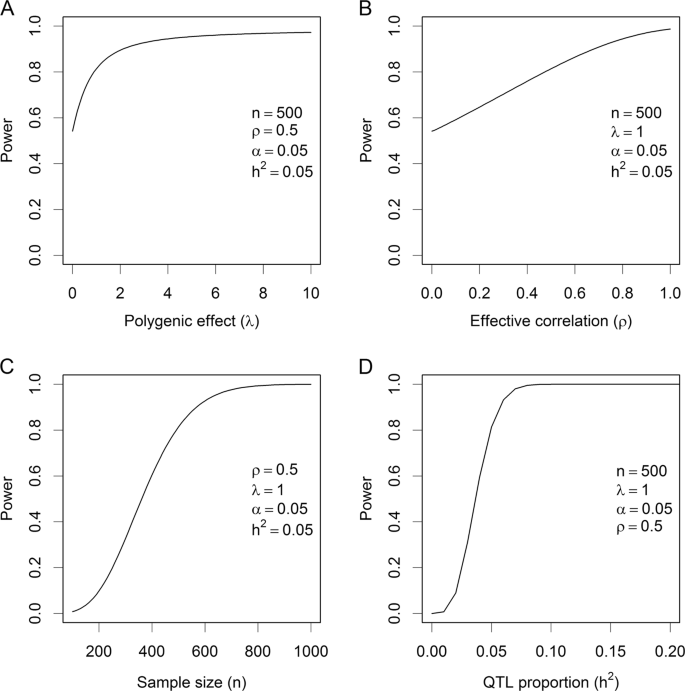
Change of statistical power. a Power changes as the polygenic effect increases in the situation where the sample size is 500, the QTL size is 0.05, the linkage disequilibrium parameter is 0.5 and the nominal Type 1 error is 0.05 (corresponding to 0.05/100,000 after Bonferroni correction for 10k scanned markers). b Power changes as the effective correlation changes in the situation where the polygenic effect size is 1, the sample size is 500, the QTL size is 0.05, and the nominal Type 1 error is 0.05. c Power changes as the sample size increases in the situation where the polygenic effect is 1, the QTL size is 0.05, the linkage disequilibrium parameter is 0.5 and the nominal Type 1 error is 0.05. d Power changes as the QTL size increases in the situation where the polygenic effect is 1, the sample size is 500, the linkage disequilibrium parameter is 0.5 and the nominal Type 1 error is 0.05

Effective correlation coefficient of individuals

The numerical evaluation of statistical power described above was conducted under a special structure of the kinship matrix: the diagonal elements are all unity and off-diagonal element are all the same ( ρ ). We have demonstrated that the power increases as ρ increases. So, a GWAS population with a high ρ tends to be more powerful than a population with a low ρ , assuming that all other factors are fixed. In reality, the diagonal element of the kinship matrix will vary across individuals (not unity), the correlation coefficient will vary across different individual pairs. Equation ( 36 ) shows the link between the effective sample size and ρ . For a given value of λ , we can calculate the effective sample size

If this kinship matrix had a structure of identical off-diagonal element, we should expect to have

Given n 0 , n , and λ , we can solve for ρ . Such an ρ is called the effective correlation between individuals in the GWAS population. The above equation is a quadratic function of ρ and the positive root is the effective ρ . For example, the effective sample size from the kinship matrix of the rice population consisting of 210 RILs ( n  = 210 and assume λ  = 1) is n 0  = 303.7358, which is calculated from Eq. ( 57 ). Substituting n 0 into Eq. ( 58 ) and solving for ρ leads to ρ  = 0.6237.

Sample size and smallest detectable QTL

We generated various population sizes with different marker densities via simulations to show the relationship among the kinship matrix (under some special situations), the effective ρ and the statistical power. We simulated a sample of n  = 1000 with variable number of markers starting from m  = 1000 to m  = 10,000 incremented by 1000. The distance between consecutive markers is 1 cM (equivalent to a recombination fraction of 0.01). We also assumed λ  = 1 so that we can calculate the effective ρ . Supplementary Figure S1 (panel A) shows the change of ρ against the number of markers. Clearly, ρ decreases as the number of markers increases. However, the increase in the number of markers is caused by the increase of genome size because the distance between two consecutive markers is a fixed number. So, 1000 markers correspond to a 10 Morgan of genome size while 10k markers correspond to a genome size 100 Morgan. We then simulated n  = 1000 individuals with a fixed genome size (10 Morgan). This time we varied the marker density from 1 marker per cM to 10 markers per cM. The result is illustrated in Supplementary Figure S1 (panel B). The effective ρ plotted against the marker density appears to be flat, i.e., it does not depend on the marker density but solely depends on the genome size. We then simulated another n  = 1000 individuals with a fixed number of markers ( m  = 1000) but varied the genome size from 10 Morgan to 100 Morgan. The result is demonstrated in Supplementary Figure S1 (panel C), showing that the effective ρ monotonically decreases as the genome size increases. Finally, we fixed the genome size at 10 Morgan with m  = 1000 markers and varied the sample size to see how ρ changes as the sample size changes. Supplementary Figure S1 (panel D), shows the increase of ρ when the sample size changes from n  = 500 to n  = 6500 incremented by 1000. So, large samples will increase the effective ρ and eventually increase the power.

We further simulated n  = 10,000 individuals with m  = 100k markers to construct the kinship matrix. The marker density is one marker per 0.03 cM (equivalent to 33 markers per cM), which corresponds to a genome size of 30 Morgan in length. Such a kinship matrix may be common in GWAS. We also set λ  = 1 (equivalent to 50% of polygenic contribution). From this kinship matrix, we found that the effective sample size is n 0  = 18684.89 and the corresponding effective correlation coefficient is ρ  = 0.9297. Assume that the QTL contributes \(h_{QTL}^2 = 0.05\) of the phenotypic variance, from Eq. ( 37 ), we obtain

At α  = 0.05/100,000 = 5 × 10 −7 , this non-centrality parameter leads to a perfect statistical power (100%). We now let the power be ω  = 1− β  = 0.90 and try to find out the smallest detectable QTL by this sample. The corresponding non-centrality parameter is δ β  = ( z 1− α /2  +  z 1− β ) 2  = 39.79, from which we can find \(h_{QTL}^2\) using

So, with a sample size n  = 10,000 and marker number m  = 100k, we can detect a QTL that explains less than 0.20% of the phenotypic variance with a 90% power. We also extracted the first n  = 1000 individuals from that large sample (with m  = 100k markers) for analysis. Under the same set up as the large sample, i.e., λ  = 1, α  = 5 × 10 −7 and β  = 0.10, we found that, with 90% power, such a population (1000 individuals) can detect a QTL as small as \(h_{QTL}^2 = 0.024\) . If we are not interested in detecting any QTL with size smaller than 0.024, there is no reason to use a sample larger than n  = 1000.

Finally, from the same large simulated population with 100k markers evenly distributed on a 30 Morgan genome, we evaluated the minimum QTL size that can be detected with 90% power at α  = 5 × 10 −7 under several different levels of λ with variable sample size n . We varied λ from 1 to 10 incremented by 1, equivalent to \(h_{\mathrm{POLY}}^2\) changing from 0.5 to 0.9. We varied n from 1000 to 10,000 incremented by 1000, where the first n individuals of the large sample were extracted for the analysis. The minimum detectable QTL size is obtained from Eq. ( 60 ). The results are summarized in Table 2 . In the worst situation where n  = 1000 and λ  = 1, with 90% power, the minimum detectable QTL is 2.389%. In the best situation where n  = 10,000 and λ  = 10, the smallest detectable QTL is 0.045%. Table 2 shows the result when λ changes from 1 to 10. The effective correlation coefficients between individuals that correspond to the 10 different levels of sample size ( n ) and 10 different levels of polygenic contributions ( λ ) are shown in Table 3 . This table is useful for people who are interested in calculating the statistical power for a particular population structure. For example, if one has a population of size 2000 and wants to find the statistical power of detecting a QTL explaining 0.01 of the phenotypic variance, he can choose a ρ value from the second row of Table 3 . Let us assume that the polygenic contribution is λ  = 2, the corresponding effective correlation is ρ  = 0.8815, which leads to

The corresponding non-centrality parameter is

The statistical power is

Tables 2 and 3 only show the results when the population size ( n ) starts from 1000 and the polygenic effect ( λ ) starts from 1. Supplementary Data S5 and S6 show the results when the sample size ranges from 100 to 10,000 and the polygenic effect ( λ ) ranges from 0 to 10. These two supplementary tables provide guidelines for investigators to evaluate the potential effectiveness of their populations.

Interestingly, we compared the minimum detectable QTL under 90% power obtained from GWAPower (Figure 2 of Feng et al. ( 2011 )) and those obtained from our Supplementary Data S5 (the first column of Data S5 when λ  = 0). The comparison is illustrated in Supplementary Figure S2 . The two methods are identical in the situation where λ  = 0, i.e., when the polygenic effect is ignored. This comparison is to show that our powers in the absence of polygenic effects are the same as the powers of the simple fixed model GWAS. When the polygenic effect is present, Feng et al. ( 2011 ) method cannot be used because it does not take into account the kinship matrix. Using the HIV study data (Fellay et al. 2007 ), Feng et al. ( 2011 ) claimed that with a sample size 486, the minimum detectable QTL is \(h_{QTL}^2 = 0.07\) ; with a sample size 2554, the minimum detectable QTL is \(h_{QTL}^2 = 0.014\) . In our study (Supplementary Data S5 ), we show that the minimum detectable QTL sizes are about 0.073 ( n  = 500) and 0.016 ( n  = 2500), respectively, very close to findings of Feng et al. ( 2011 ).

Results of simulation to validate the theoretical powers

Additive model.

For the additive model of the 210 RIL population, we simulated one sample from each combination of λ and \(h_{QTL}^2\) , where λ  = {0, 1, 2} and \(h_{QTL}^2 = \left\{ {0,0.001,0.002, \cdots ,0.06} \right\}\) , a total of 3 × 61 = 183 combinations. Using the 0.05 nominal p -value threshold for one marker per experiment, the statistical powers are shown in Fig. 4 . The simulated powers (open circles) vary slightly around the theoretical powers (smooth curves), which validates the theoretical powers. The powers under the three levels of λ are different, with λ  = 2 having the highest powers and λ  = 0 the lowest powers. The fluctuation of the simulated powers is due to sampling errors because we used the 0.05 nominal p -value as the criterion for detection. In other words, we simulated one marker at a time and compared the p -value of this marker against 0.05 to declare significance for this marker. The simulation was replicated 1000 times. The proportion of samples with significant detection over 1000 replicates is the empirical powers. If we had increased the number of replicates to 10,000, the simulated powers would have been much closer to the theoretical values.

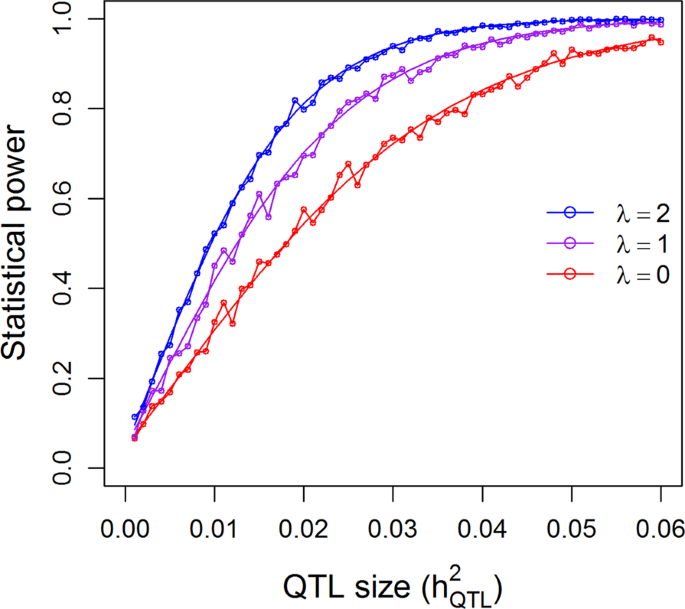
Comparison of the theoretical powers to the empirical powers from simulation studies using the kinship matrix of 210 recombinant inbred lines (RIL) of rice under the additive model. Smooth curves are theoretical power functions and fluctuated curves tagged with open circles are empirical power functions obtained from simulations. The power functions are evaluated under three levels of polygenic contribution represented by the ratios of the polygenic variance to the residual variance ( \(\lambda = \sigma _\xi ^2{\mathrm{/}}\sigma ^2\) )

The choice of the p -value threshold is irrelevant to the comparison of the simulated powers with the theoretical powers. In the following example, we simulated 10 independent markers per genome. The p -value threshold after Bonferroni correction was 0.05/10 = 0.005. For each experiment, we compared the p -values of all 10 markers with 0.005 and recorded the number of significant markers for each experiment. Such an experiment was replicated 1000 times so that an empirical power under each scenario was calculated. The powers are illustrated in Supplementary Figure S3 . The simulated powers (open circles) are much closer to the theoretical powers (smooth curves). However, we actually performed 3 × 61 × 10 × 1000 = 1,830,000 independent simulations here compared with 3 × 61 × 1 × 1000 = 183,000 independent simulations when a single marker was detected at a time using the 0.05 nominal p -value criterion. The shapes of the power functions for 10 markers are different from those of the powers for one marker.

In the 210 RIL rice example, the number of markers is m  = 1619. If we detect 1619 markers in one experiment, the Bonferroni corrected threshold should be 0.05/ m  = 0.00003088. The entire experiment must be done 3 × 61 × 1619 × 1000 = 296,277,000 times. We did not simulate this large number of experiments but only calculated the theoretical power functions, as shown in Supplementary Figure S4 . From this figure, we can easily find the powers to detect a QTL explaining 0.05 of the phenotypic variance under the three λ values, which are roughly 0.20, 0.42, and 0.66 for λ being 0, 1, and 2, respectively. The sample size of the population is not large enough to detect a QTL explaining 0.05 of the phenotypic variance with a reasonable power. The powers would be sufficiently high to detect a QTL with size \(h_{QTL}^2 = 0.10\) .

Genotypic model

The population with 278 hybrids was used to validate the genotypic model (additive plus dominance). The theoretical power functions and empirical powers from simulation are illustrated in Fig. 5 under the 0.05 nominal p -value threshold. Again, the simulated powers vary slightly around the theoretical powers, validating the power calculation for the genotypic model. The theoretical power functions using the 0.05/1619 = 0.00003088 threshold by detecting 1619 bins in one experiment are shown in Supplementary Figure S5 . The powers of this population are higher than the 210 RIL population, either due to the larger population size or the genotypic model or both. When \(h_{QTL}^2\) is 0.05, the powers are 0.27 for λ  = 0, 0.57 for λ  = 1, and 0.78 for λ  = 2. A power of 0.78 is already reasonably high. The power to detect a QTL with \(h_{QTL}^2 = 0.10\) is about 0.88 even for the worst case scenario of λ  = 0.

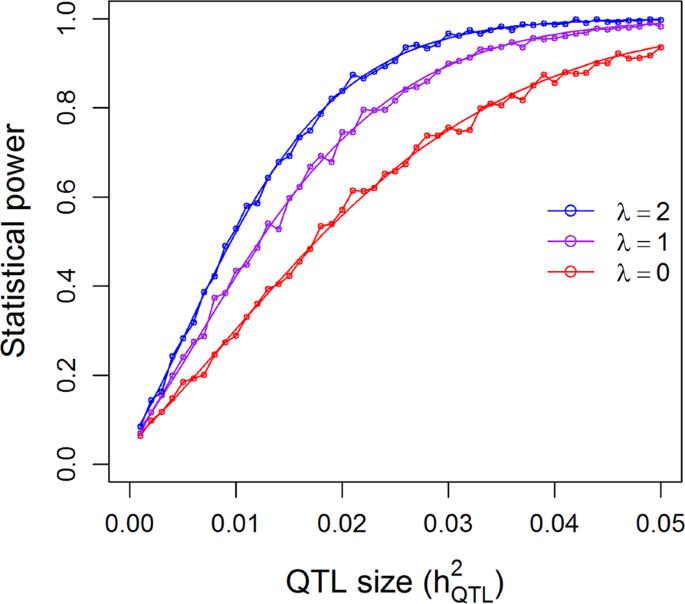
Comparison of the theoretical powers to the empirical powers from simulation studies using the kinship matrix of 278 hybrid rice under the additive plus dominance model. Smooth curves are theoretical power functions and fluctuated curves tagged with open circles are empirical power functions obtained from simulations. The power functions are evaluated under three levels of polygenic contribution represented by the ratios of the polygenic variance to the residual variance ( \(\lambda = \sigma _\xi ^2{\mathrm{/}}\sigma ^2\) )

The population of 524 rice varieties was used to simulate statistical powers in the presence of population structure. Figure 6 shows the theoretical powers and empirical powers from simulations under λ  = 1 and three scenarios of correlation between the population structure and the marker under study. The nominal 0.05 p -value threshold was used since each time only one marker was tested. The simulated powers fluctuated slightly around the theoretical powers, as expected, which validates the power calculation of GWAS for structured populations. Maximum powers occurred when the population structure was not correlated with the marker ( r QZ  = 0). When the correlation was 0.5, a slight reduction of power was observed. As the correlation reached 0.9, the power was substantially reduced. One can imagine that if the correlation is 1.0, the power will be reduced to zero. If we had tested m  = 180,000 markers in one simulation experiment, we would have used the Bonferroni corrected p -value threshold, 0.05/ m  = 2.78 × 10 −7 , as the criterion for significance declaration. Under each combination of \(h_{QTL}^2\) and r QZ , we would need to test m markers. If 1000 replications were done, the entire simulation experiment would have been done 1000 m  = 180,000,000 times just for one combination of \(h_{QTL}^2\) and r QZ . Although it is impossible to simulate such a huge experiment within a reasonable amount of time, we can calculate the theoretical powers in the blink of an eye. Supplementary Figure S6 shows the theoretical powers under λ  = 1 and the three levels of r QZ . When population structure is present but it is ignored, the power will be reduced compared to the power when the population structure effect is included in the model. This can be validated by Fig. 7 , where the correlation between the population structure and the QTL is r QZ  = 0. If r QZ  ≠ 0, one of the assumptions of the linear model will be violated and no theoretical powers are available.

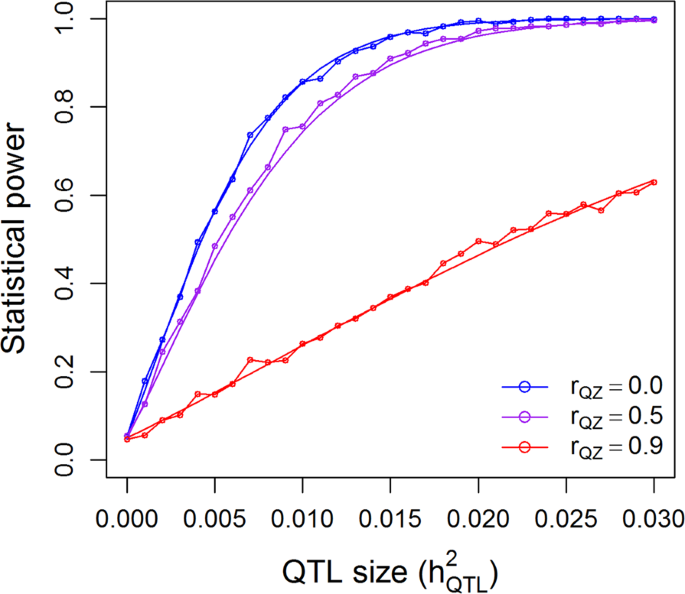
Comparison of the theoretical powers to the empirical powers from simulation studies using the kinship matrix of 524 rice cultivars with correction for population structures ( indica and japonica subspecies). Smooth curves are theoretical power functions and fluctuated curves tagged with open circles are empirical power functions obtained from simulations. The power functions are evaluated under \(\lambda = \sigma _\xi ^2{\mathrm{/}}\sigma ^2 = 1\) and three levels of correlation between population structure ( Q ) and the genotypic indicator variable ( Z )

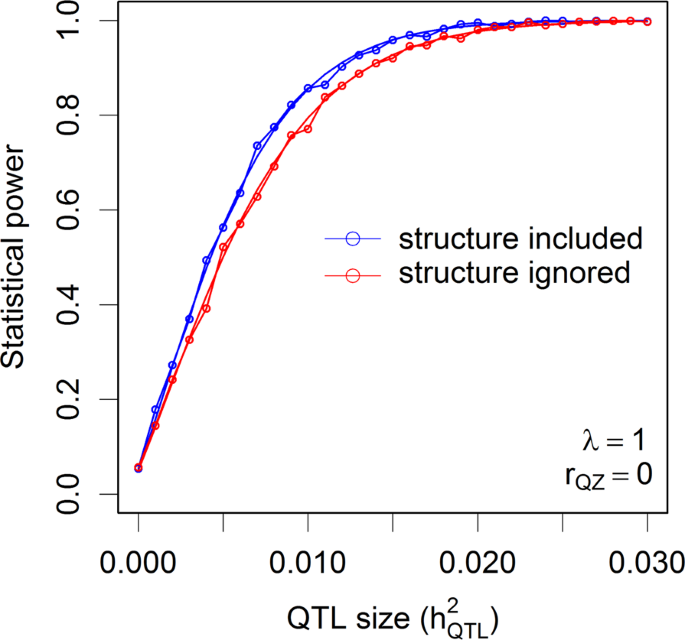
Comparison of the theoretical powers to the empirical powers from simulation studies using the kinship matrix of 524 rice cultivars with and without correction for population structures ( indica and japonica subspecies). Smooth curves are theoretical power functions and fluctuated curves tagged with open circles are empirical power functions obtained from simulations. The power functions are evaluated under \(\lambda = \sigma _\xi ^2{\mathrm{/}}\sigma ^2 = 1\) and the correlation between population structure ( Q ) and the genotypic indicator variable ( Z ) is r QZ  = 0

Powers of QTL mapping using full-sib and half-sib families

Responding to a reviewer’s comment on the effect of relatedness among individuals on the statistic power, we simulated two populations, one consisting of 20 full-sib families and the other consisting of 20 half-sib families. Each family had 25 members and thus each population had 500 individuals. The additive relationship matrices (Supplementary Data S7 and S8 ) were included in the LMM to capture the polygenic effects. Two levels of the polygenic effects were investigated, λ  = 1 and λ  = 2. We expected that the population made of full-sib families would have higher power than the population consisting of half-sib families. Using the nominal p -value threshold of 0.05 to declare statistical significance, we examined the power functions against \(h_{QTL}^2\) that ranges from 0.0 to 0.05. The results are shown in Supplementary Figures S7 and S8 , where the former compares the simulated powers with the theoretical powers and the latter compares the powers of full-sib families with the powers of half-sib families. The conclusions are (1) the simulated powers match the theoretical powers closely and (2) the population of full-sib families is indeed more powerful than the population of half-sib families.

The rapid development of new DNA sequencing technology and the low cost of genotyping make GWAS more popular as tools to detect QTL for quantitative traits of agronomical, behavioral, and medical importance. The samples of GWAS can be as large as more than half million in human (Marouli et al. 2017 ). Typical GWAS samples are in the order of a few hundreds to a few thousands. In this study, we showed that the smallest detectable QTL using a sample of 10,000 individuals ranges from 0.4% to 0.04% of the phenotypic variance (depending on the polygenic contribution), assuming that 100k markers are scanned and used to construct the kinship matrix (see Supplementary Data S5 ). Such small QTL, although statistically significant, are not useful biologically. Therefore, using very large samples for GWAS is not always necessary. If the polygenic contribution is 50% of the phenotypic variance, 500 individuals are sufficient to detect a QTL explaining 5% of the phenotypic variance (see Supplementary Data S5 ). Extremely large samples may be important for detecting rare genetic variants that are often important for rare diseases (Visscher et al. 2017 ). Large sample sizes may also be necessary for QTL mapping and GWAS for discretely distributed traits. These traits are often analyzed using the generalized LMM (Che and Xu 2012 ), in which the Wald test statistic follows the Chi-square distribution only asymptotically. Detecting dominance effects requires a slightly larger sample than detecting additive effects because the dominance indicator variable often has a smaller variance than the additive indicator variable. Detecting epistatic effects (interaction effects between loci) requires even larger samples because (1) the epistatic genotype indicator variables have even smaller variances (they are like rare variants) and (2) more stringent Bonferroni correction (too many epistatic effects to be tested in a single experiment). Large samples may also be useful for determination of the number of loci and prediction of phenotypes via GWAS. However, genomic prediction often requires different statistical methods, not GWAS (Meuwissen et al. 2001 ).

The statistical power developed here is not the empirical power drawn from multiple simulation studies; rather, it is derived based on theoretical distributions of the test statistics (central and non-central Chi-square distributions). The key to evaluate the power is the non-centrality parameter, which is proportional to the product of the sample size ( n ) and the squared effect of the QTL relative to the residual variance. It is important to emphasize that if a QTL is statistically significant, it is true (subject to the controlled Type 1 error), regardless of how small the sample size is. There are many studies being rejected initially by the editors and reviewers due to small sample sizes. The investigators are forced to repeat the experiments using much larger samples. In our opinion, rejection of a study based on small sample sizes is unfair to the investigators. The reason is that the significance test (non-centrality parameter) is the product of the sample size and the QTL size; The sample size has already been taken into account when the test statistic is calculated. If the test is significant in a small sample, the effect must be very large to compensate for the small sample size. Such a QTL should be more important than a very small QTL detected in an extremely large sample. Unfortunately, many editors and reviewers often favor the latter and criticize the former. One particular comment against small samples is the “Beavis’ effect” in small samples, i.e., small samples lead to upward bias in estimated QTL effect (Beavis 1994 ; Xu 2003 ). This is an abuse or misinterpretation of the Beavis’ effect. In the original simulation study, Beavis ( 1994 ) claimed that the average reported QTL size from multiple studies is biased upward for small samples. The reason for such a bias is due to selective reports of QTL mapping results. Only statistically significant QTL are reported and those studies with non-significant detection are left out of the report (Xu 2003 ). For a single study, regardless of the sample size, a significant QTL is still significant and there is no bias of the estimated effect, if the method itself is unbiased. Although we encourage investigators to use large samples for QTL mapping to increase the probability of detecting more QTL; but if the investigators are lucky enough and have already detected QTLs using small samples, there is no reason to reject their studies. What is the reason for doing statistical tests?

The mixed model in GWAS is a special case in LMM where the covariance structure is modeled by a marker inferred kinship matrix. Compared with its fixed model counterpart, the mixed model power calculation requires a given kinship matrix, which depends on marker data. This has complicated the power calculation for mixed models. Here, we assume that the marker genotype indicator (variable Z ) has been standardized (with mean zero and variance 1). In reality, the variance of Z often varies from marker to marker, especially when many rare variants are present. This way of power calculation seems to have ignored the rare variant issue. However, standardization of Z will not affect the power calculation because we defined the QTL size as the proportion of the phenotypic variance contributed by the QTL, denoted by \(h_{QTL}^2\) . In the original scale of Z , the genetic variance contributed by the QTL is \(\sigma _G^2 = \sigma _Z^2\gamma ^2\) and \(\sigma _G^2\) is known, regardless of the scale of Z . When we standardize Z , \(\sigma _G^2 = (\gamma ^ \ast )^2\) . Therefore, \((\gamma ^ \ast )^2 = \sigma _Z^2\gamma ^2\) and γ  =  γ * / σ Z . For a rare variant, σ Z is extremely small, leading to a very large QTL effect ( γ ) to compensate for the small σ Z and produce the same \(h_{QTL}^2\) as a common variant. Therefore, rare variants are hard to detect because the effect must be huge to produce a QTL with a detectable \(h_{QTL}^2\) and the sample size to detect rare variants must be very large (Bush and Moore 2012 ).

Statistical powers and Type 1 errors are concepts depending on known genetic parameters, population structures, and sample sizes. In real data analysis, the genetic parameters (effects of QTL) are not known. Therefore, there are no such things as powers and Type 1 errors in real data analysis. We often see reports that compare the test statistics of two methods, one method generating test statistics higher than the other method, and the authors then claim that the first method has higher power than the second method. In real populations, we really do not know whether the detected QTL are real or just false positives. Therefore, power analysis must be conducted either in theory or with multiple replicated data simulated under the alternative model. In GWAS, the population is often large and the marker density is often very high, making multiple simulation experiments very costly in terms of computational time. Therefore, theoretical evaluation is necessary. This study is the first theoretical evaluation of statistical power under the Q + K mixed model. If an investigator has already collected the marker data, he can just build the kinship matrix and calculate the eigenvalues of the kinship matrix and calculate the effective sample size n 0 , from which a power can be computed.

In addition to cryptic relatedness, population structure is another factor that needs to be controlled in GWAS (Pritchard et al. 2000 b). Effects of population structure on the powers of GWAS have been investigated via Monte Carlo simulations (Atwell et al. 2010 ; Platt et al. 2010 ; Korte and Farlow 2013 ; Shin and Lee 2015 ; Toosi et al. 2018 ). A consensus conclusion is that proper control of population structure can reduce false positive rate. If an association population consists of several subpopulations (in human) or several different breeds and their hybrids (in animals), many private alleles (unique to the subpopulations) may exist and the allele frequencies of many loci may be significantly different across subpopulations. If the trait of interest is also associated with the population structures due to historical and geographical reasons, the loci associated with population structures are often detected as associated with the trait, although they may not be the causal loci (Atwell et al. 2010 ). When the population structure effects are included in the mixed model, the association signals of these loci will be reduced. This explains why fitting population structure effects can reduce false positives. However, population differentiation is most likely caused by natural selection or domestication and loci associated with traits under selection pressure may be the causal loci. As a result, fitting population structure may not be appropriate in GWAS for adaptation-related traits. A well-studied area in evolutionary genomics is to detect selection signatures (Baldwin-Brown et al. 2014 ; Xu and Garland 2017 ). The loci associated with population structures are the very loci of interests in evolutionary genomics. Assuming that we do not want to claim loci associated with population structure as significant in GWAS and fitting population structure is necessary, this study is the first to theoretically evaluate the effects of population structures on the statistical powers. The conclusions are consistent with the empirical observations from simulation studies (Toosi et al. 2018 ). However, if population structural effects are present but ignored in the mixed model, the statistical power will be reduced compared to that if they are taken into account (see Fig. 7 ), which is due to the increased residual error variance. However, the same phenomenon can be stated alternatively as “Incorporating population structure effects will increase power compared with that if they are ignored.” The alternative statement appears to contradict with the consensus conclusion about population structure. One needs to be careful when interpreting the effects of population structure on statistical power. We also quantified the effect of population structure on power as a function of the correlation coefficient between population structure ( Q ) and genotype indicator of the locus under study ( Z k ), the higher the correlation, the lower the power (see Fig. 6 and Supplementary Figure S6 ).

The power formula derived in this study assumes that the QTL is in perfect LD with a marker. If this is not true, then the calculated power will be lower than the actual power. Let r be the correlation coefficient between Z and the true genotype indicator of the QTL, the power reduction is represented by a reduced QTL effect represented by the ratio of the square of the genetic effect to the residual error variance, r 2 ( γ k / σ ) 2 , where γ k is the effect of the true QTL and r 2 is the linkage disequilibrium parameter. This power reduction can be compensated by an increased marker density. Under the common disease/common variate hypothesis, 500k to a million markers are required (Bush and Moore 2012 ). Compared with sample size, marker density is less important. Klein ( 2007 ) stated that genotyping more individuals with fewer markers is better than genotyping fewer individuals with more markers.

Finally, theoretical power calculation depends on known parameters and the distributions of the test statistics under both the null model and the alternative model. For the usual quantitative trait GWAS and QTL mapping, the residual errors are often normally distributed, resulting in normally distributed estimated QTL effects. The Wald test is a quadratic form of the estimated QTL effects; it is well known that the quadratic form of normal variables ( y T Ay ) follows a Chi-square distribution if the symmetric matrix in the middle ( A ) is the inverse of the variance matrix of the normal variables. It should be cautious to calculate power for GWAS and QTL mapping with discrete traits, e.g., binary and ordinal traits, because the Wald test statistic follows a Chi-square distribution only asymptotically. Therefore, the sample size for discrete traits should be sufficiently large to ensure the normality of estimated QTL effects and thus the required Chi-square distribution of the test statistic.

Data and R code

Several R functions are available. The R codes and examples to call the functions for power analysis are provided in Supplementary Note S4 . A sample kinship matrix with n  = 210 individuals used to demonstrate the application is provided in Supplementary Data S1 .

Almasy L, Blangero J (1998) Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Human Genet 62:1198–1211

Article   CAS   Google Scholar  

Amos CI (1994) Robust variance-components approach for assessing genetic linkage in pedigrees. Am J Human Genet 54:535–543

CAS   Google Scholar  

Andersen EB (1970) Asymptotic properties of conditional maximum likelihood estimators. J R Stat Soc B 32:283–301

Google Scholar  

Atwell S, Huang YS, Vilhjálmsson BJ, Willems G, Horton M, Li Y, Meng D, Platt A, Tarone AM, Hu TT et al. (2010) Genome-wide association study of 107 phenotypes in Arabidopsis thaliana inbred lines. Nature 465:627

Article   CAS   PubMed   PubMed Central   Google Scholar  

Baldwin-Brown JG, Long AD, Thornton KR (2014) The power to detect quantitative trait loci using resequenced, experimentally evolved populations of diploid, sexual organisms. Mol Biol Evol 31:1040–1055

Beavis WD (1994) The power and deceit of QTL experiments: lessons from comparitive QTL studies. In: Proceedings of the forty-ninth annual corn & sorghum industry research conference. American Seed Trade Association, Washington, D.C., pp 250–266

Bush WS, Moore JH (2012) Chapter 11: genome-wide association studies. PLoS Comput Biol 8:e1002822

Castelloe JM, O’Brien RG (2001) Power and sample size determination for linear models. In: SAS (ed) The twenty-sixth annual SAS users group international conference. SAS Institute Inc., Cary, NC

Che X, Xu S (2012) Generalized linear mixed models for mapping multiple quantitative trait loci. Heredity 109:41

Chen W, Gao Y, Xie W, Gong L, Lu K, Wang W, Li Y, Liu X, Zhang H, Dong H et al. (2014) Genome-wide association analyses provide genetic and biochemical insights into natural variation in rice metabolism. Nat Genet 46:714

Article   CAS   PubMed   Google Scholar  

Edwards BJ, Haynes C, Levenstien MA, Finch SJ, Gordon D (2005) Power and sample size calculations in the presence of phenotype errors for case/control genetic association studies. BMC Genet 6:18

Article   PubMed   PubMed Central   Google Scholar  

Faul F, Erdfelder E, Lang A-G, Buchner A (2007) G*Power 3: a flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav Res Methods 39:175–191

Article   PubMed   Google Scholar  

Fellay J, Shianna KV, Ge D, Colombo S, Ledergerber B, Weale M, Zhang K, Gumbs C, Castagna A, Cossarizza A et al. (2007) A whole-genome association study of major determinants for host control of HIV-1. Science 317:944–947

Feng S, Wang S, Chen C-C, Lan L (2011) GWAPower: a statistical power calculation software for genome-wide association studies with quantitative traits. BMC Genet 12:12

Fulker DW, Cherny SS, Sham PC, Hewitt JK (1999) Combined linkage and association sib-pair analysis for quantitative traits. Am J Hum Genet 64:259–267

Gordon D, Finch SJ, Nothnagel M, Ott J (2002) Power and sample size calculations for case-control genetic association tests when errors are present: application to single nucleotide polymorphisms. Hum Hered 54:22–33

Green P, MacLeod CJ (2016) SIMR: an R package for power analysis of generalized linearmixed models by simulation. Methods Ecol Evol 7:493–498

Article   Google Scholar  

Haley CS, Knott SA (1992) A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity 69:315–324

Hong EP, Park JW (2012) Sample size and statistical power calculation in genetic association studies. Genomics Inform 10:117–122

Hua JP, Xing YZ, Xu CG, Sun XL, Yu SB, Zhang Q (2002) Genetic dissection of an elite rice hybrid revealed that heterozygotes are not always advantageous for performance. Genetics 162:1885–1895

CAS   PubMed   PubMed Central   Google Scholar  

Jansen RC (1994) Controlling the type I and type II errors in mapping quantitative trait loci. Genetics 138:871–881

Jiang W, Yu W (2016) Power estimation and sample size determination for replication studies of genome-wide association studies. BMC Genomics 17:19

Johnson PCD, Barry SJE, Ferguson HM, Muller P (2015) Power analysis for generalized linear mixed models in ecology and evolution. Methods Ecol Evol 6:133–142

Kang HM, Zaitlen NA, Wade CM, Kirby A, Heckerman D, Daly MJ, Eskin E (2008) Efficient control of population structure in model organism association mapping. Genetics 178:1709–1723

Kao CH, Zeng ZB, Teasdale RD (1999) Multiple interval mapping for quantitative trait loci. Genetics 152:1203–1216

Kim W, Gordon D, Sebat J, Ye KQ, Finch SJ (2008) Computing power and sample size for case-control association studies with copy number polymorphism: application of mixture-based likelihood ratio test. PLoS ONE 3:e3475

Klein RJ (2007) Power analysis for genome-wide association studies. BMC Genet 8:58

Kononoff PJ, Hanford KJ (2006) Technical note: estimating statistical power of mixed models used in dairy nutrition experiments. J Dairy Sci 89:3968–3971

Korte A, Farlow A (2013) The advantages and limitations of trait analysis with GWAS: a review. Plant Methods 9:29

Lander ES, Botstein D (1989) Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121:185–199

Lippert C, Listgarten J, Liu Y, Kadie CM, Davidson RI, Heckerman D (2011) FaST linear mixed models for genome-wide association studies. Nat Methods 8:833–835

Listgarten J, Lippert C, Kadie CM, Davidson RI, Eskin E, Heckerman D (2012) Improved linear mixed models for genome-wide association studies. Nat Methods 9:525–526

Marouli E, Graff M, Medina-Gomez C, Lo KS, Wood AR, Kjaer TR, Fine RS, Lu Y, Schurmann C, Highland HM et al. (2017) Rare and low-frequency coding variants alter human adult height. Nature 542:186

Martin JGA, Nussey DH, Wilson AJ, Reale D (2011) Measuring individual differences in reaction norms in field and experimental studies: a power analysis of random regression models. Methods Ecol Evol 2:362–374

Menashe I, Rosenberg PS, Chen BE (2008) PGA: power calculator for case-control genetic association analyses. BMC Genet 9:36–36

Meuwissen THE, Hayes BJ, Goddard ME (2001) Prediction of total genetic value using genome-wide dense marker maps. Genetics 157:1819–1829

Platt A, Vilhjálmsson BJ, Nordborg M (2010) Conditions under which genome-wide association studies will be positively misleading. Genetics 186:1045–1052

Pritchard JK, Stephens M, Donnelly P (2000a) Inference of population structure using multilocus genotype data. Genetics 155:945–959

Pritchard JK, Stephens M, Rosenberg NA, Donnelly P (2000b) Association mapping in structured populations. Am J Hum Genet 67:170–181

Purcell S, Cherny SS, Sham PC (2003) Genetic power calculator: design of linkage and association genetic mapping studies of complex traits. Bioinformatics 19:149–150

Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, de Bakker PIW, Daly MJ et al. (2007) PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 81:559–575

Sham PC, Cherny SS, Purcell S, Hewitt JK (2000) Power of linkage versus association analysis of quantitative traits, by use of variance-components models, for sibship data. Am J Hum Genet 66:1616–1630

Shin J, Lee C (2015) Statistical power for identifying nucleotide markers associated with quantitative traits in genome-wide association analysis using a mixed model. Genomics 105:1–4

Skol AD, Scott LJ, Abecasis GR, Boehnke M (2006) Joint analysis is more efficient than replication-based analysis for two-stage genome-wide association studies. Nat Genet 38:209

Spencer CCA, Su Z, Donnelly P, Marchini J (2009) Designing genome-wide association studies: sample size, power, imputation, and the choice of genotyping chip. PLoS Genet 5:e1000477

Toosi A, Fernando RL, Dekkers JCM (2018) Genome-wide mapping of quantitative trait loci in admixed populations using mixed linear model and Bayesian multiple regression analysis. Genet Sel Evol 50:32

VanRaden PM (2008) Efficient methods to compute genomic predictions. J Dairy Sci 91:4414–4423

Visscher PM, Wray NR, Zhang Q, Sklar P, McCarthy MI, Brown MA, Yang J (2017) 10 Years of GWAS discovery: biology, function, and translation. Am J Hum Genet 101:5–22

Wang Q, Wei J, Pan Y, Xu S (2016) An efficient empirical Bayes method for genomewide association studies. J Anim Breed Genet 133:253–263

Wei J, Xu S (2016) A random model approach to QTL mapping in multi-parent advanced generation inter-cross (MAGIC) populations. Genetics 202:471–486

Xing YZ, Tan YF, Hua JP, Sun XL, Xu CG (2002) Characterization of the main effects, epistatic effects and their environmental interactions of QTLs on the genetic basis of yield traits in rice. Theor Appl Genet 105:248–257

Xu S (2003) Theoretical basis of the Beavis effect. Genetics 165:2259–2268

PubMed   PubMed Central   Google Scholar  

Xu S (2013a) Mapping quantitative trait loci by controlling polygenic background effects. Genetics 195:1209–1222

Xu S (2013b) Principles of statistical genomics. Springer, New York

Book   Google Scholar  

Xu S, Atchley WR (1995) A random model approach to interval mapping of quantitative trait loci. Genetics 141:1189–1197

Xu S, Garland T (2017) A mixed model approach to genome-wide association studies for selection signatures, with application to mice bred for voluntary exercise. Behav Genet 207:785–799

Xu S, Zhu D, Zhang Q (2014) Predicting hybrid performance in rice using genomic best linear unbiased prediction. Proc Natl Acad Sci USA 111:12456–12461

Yang J, Weedon MN, Purcell S, Lettre G, Estrada K, Willer CJ, Smith AV, Ingelsson E, O’Connell JR, Mangino M et al. (2011) Genomic inflation factors under polygenic inheritance. Eur J Hum Genet 19:807

Yang J, Zaitlen NA, Goddard ME, Visscher PM, Price AL (2014) Advantages and pitfalls in the application of mixed-model association methods. Nat Genet 46:100

Yu H, Xie W, Wang J, Xing Y, Xu C, Li X, Xiao J, Zhang Q (2011) Gains in QTL detection using an ultra-high density SNP map based on population sequencing relative to traditional RFLP/SSR markers. PLoS ONE 6:e17595

Yu J, Pressoir G, Briggs WH, Vroh Bi I, Yamasaki M, Doebley JF, McMullen MD, Gaut BS, Nielsen DM, Holland JB et al. (2006) A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet 38:203–208

Zeng Z-B (1994) Precision mapping of quantitative trait loci. Genetics 136:1457–1468

Zhou X, Carbonetto P, Stephens M (2013) Polygenic modeling with Bayesian sparse linear mixed models. PLoS Genet 9:e1003264

Download references

Acknowledgements

The authors are grateful to the associate editor and two anonymous reviewers for their constructive suggestions for improvement of the first draft of the manuscript. The project was supported by the United States National Science Foundation Collaborative Research Grant 473 DBI-1458515 to SX.

Author information

Authors and affiliations.

Department of Botany and Plant Sciences, University of California, Riverside, CA, 92521, USA

Meiyue Wang & Shizhong Xu

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Shizhong Xu .

Ethics declarations

Conflict of interest.

The authors declare that they have no conflict of interest.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supporting information legends., supplementary note s1., supplementary note s2., supplementary note s3., supplementary note s4., supplementary figures., supplementary figure 1., supplementary figure 2., supplementary figure 3., supplementary figure 4., supplementary figure 5., supplementary figure 6., supplementary figure 7., supplementary figure 8., supplementary dataset 1., supplementary dataset 2., supplementary dataset 3., supplementary dataset 4., supplementary dataset 5., supplementary dataset 6., supplementary dataset 7., supplementary dataset 8., rights and permissions.

Reprints and permissions

About this article

Cite this article.

Wang, M., Xu, S. Statistical power in genome-wide association studies and quantitative trait locus mapping. Heredity 123 , 287–306 (2019). https://doi.org/10.1038/s41437-019-0205-3

Download citation

Received : 19 October 2018

Revised : 22 February 2019

Accepted : 24 February 2019

Published : 11 March 2019

Issue Date : September 2019

DOI : https://doi.org/10.1038/s41437-019-0205-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Genomic dissection of additive and non-additive genetic effects and genomic prediction in an open-pollinated family test of japanese larch.

• Leiming Dong
• Xiaomei Sun

BMC Genomics (2024)

Genome-wide association study of drought tolerance in wheat (Triticum aestivum L.) identifies SNP markers and candidate genes

• Sina Nouraei
• Md Sultan Mia

Molecular Genetics and Genomics (2024)

GWAS determined genetic loci associated with callus induction in oil palm tissue culture

• Yin Min Htwe

Plant Cell Reports (2024)

Mining genes regulating root system architecture in maize based on data integration analysis

• Lixing Yuan

Theoretical and Applied Genetics (2023)

Robust markers associated with floral traits in roses are suitable for marker-assisted selection across gene pools

• Dietmar Schulz
• Marcus Linde
• Thomas Debener

Molecular Breeding (2023)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies