problem solving using arithmetic sequence

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.2: Problem Solving with Arithmetic Sequences

• Last updated
• Save as PDF
• Page ID 83159

• Jennifer Freidenreich
• Diablo Valley College

Arithmetic sequences, introduced in Section 8.1, have many applications in mathematics and everyday life. This section explores those applications.

Example 8.2.1

A water tank develops a leak. Each week, the tank loses \(5\) gallons of water due to the leak. Initially, the tank is full and contains \(1500\) gallons.

• How many gallons are in the tank \(20\) weeks later?
• How many weeks until the tank is half-full?
• How many weeks until the tank is empty?

This problem can be viewed as either a linear function or as an arithmetic sequence. The table of values give us a few clues towards a formula.

The problem allows us to begin the sequence at whatever \(n\)−value we wish. It’s most convenient to begin at \(n = 0\) and set \(a_0 = 1500\).

Therefore, \(a_n = −5n + 1500\)

Since the leak is first noticed in week one, \(20\) weeks after the initial week corresponds with \(n = 20\). Use the formula where \(\textcolor{red}{n = 20}\):

\(a_{20} = −5(\textcolor{red}{20}) + 1500 = −100 + 1500 = 1400\)

Therefore, \(20\) weeks later, the tank contains \(1400\) gallons of water.

• How many weeks until the tank is half-full? A half-full tank would be \(750\) gallons. We need to find \(n\) when \(\textcolor{red}{a_n = 750}\).

\(\begin{array} &750 &= −5n + 1500 &\text{Substitute \(a_n = 750\) into the general term.} \\ 750 − 1500 &= −5n + 1505 − 1500 &\text{Subtract \(1500\) from each side of the equation.} \\ −750 &= −5n &\text{Simplify each side of the equation.} \\ \dfrac{−750}{−5} &= \dfrac{−5n}{−5} &\text{Divide both sides by \(−5\).} \\ 150 &= n & \end{array}\)

Since \(n\) is the week-number, this answer tells us that on week \(150\), the tank is half full. However, most people would better understand the answer if stated in the following way, “The tank is half full after 150 weeks.” This answer sounds more natural and is preferred.

• How many weeks until the tank is empty? The tank is empty when \(a_n = 0\) gallons. Find \(n\) such that \(\textcolor{red}{a_n = 0}\).

\(\begin{array}& 0 &= −5n + 1500 &\text{Substitute \(a_n=0\) into the general term.} \\ 0 − 1500 &= −5n + 1500 − 1500 &\text{Subtract \(1500\) from each side of the equation.} \\ −1500 &= −5n &\text{Simplify.} \\ \dfrac{−1500}{−5} &= \dfrac{−5n}{−5} &\text{Divide both sides by \(−5\).} \\ 300 &= n & \end{array}\)

Since \(n\) is the week-number, this answer tells us that on week \(300\), the tank is empty. However, most people would better understand the answer if stated in the following way, “ The tank is empty after 300 weeks. ” This answer sounds more natural and is preferred.

Example 8.2.2

Three stages of a pattern are shown below, using matchsticks. Each stage requires a certain number of matchsticks. If we keep up the pattern…

• How many matchsticks are required to make the figure in stage \(34\)?
• What stage would require \(220\) matchsticks?

Let’s create a table of values. Let \(n =\) stage number, and let \(a_n =\) the number of matchsticks used in that stage. Then note the common difference.

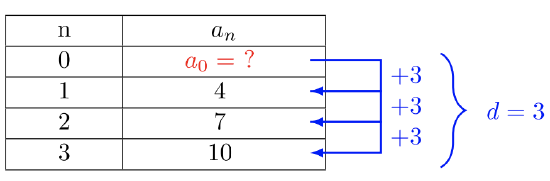
Find the value \(a_0\):

\(\begin{array} &a_0 + 3 &= 4 \\ a_0 + 3 − 3 &= 4 − 3 \\ a_0 &= 1 \end{array}\)

The general term of the sequence is:

\(a_n = 3n + 1\)

• Compute \(a_{34}\) to find the number of matchsticks in stage \(34\):

\(a_{34} = 3(\textcolor{red}{34}) + 1 = 103\).

There are \(103\) matchsticks in stage \(34\).

• What stage would require \(220\) matchsticks? We are looking for the stage-number, given the number of matchsticks. Find \(n\) if \(a_n = 220\).

\(\begin{array} &220 &= 3n + 1 \\ 219 &= 3n \\ 73 &= n \end{array}\)

Answer Stage \(73\) would require \(220\) matchsticks.

Example 8.2.3

Cory buys \(5\) items at the grocery store with prices \(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\) which is an arithmetic sequence. The least expensive item is \($1.89\), while the total cost of the \(5\) items is \($12.95\). What is the cost of each item?

Put the \(5\) items in order of expense: least to most and left to right. Because it is an arithmetic sequence, each item is \(d\) more dollars than the previous item. Each item’s price can be written in terms of the price of the least expensive item, \(a_1\), and \(a_1 = $1.89\).

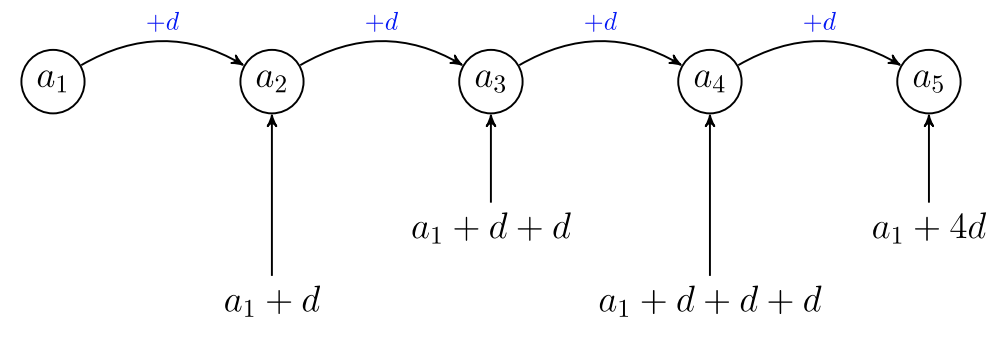
The diagram above gives \(5\) expressions for the costs of the \(5\) items in terms of \(a_1\) and the common difference is \(d\).

\(\begin{array} &a_1 + a_2 + a_3 + a_4 + a_5 &= 12.95 &\text{Total cost of \(5\) items is \($12.95\).} \\ a_1 + (a_1 + d) + (a_1 + 2d) + (a_1 + 3d) + (a_1 + 4d) &= 12.95 &\text{See diagram for substitutions.} \\ 5s_1 + 10d &= 12.95 &\text{Gather like terms.} \\ 5(1.89) + 10d &= 12.95 &a_1 = 1.89. \\ 9.45 + 10d &= 12.95 &\text{Simplify.} \\ 9.45 + 10d − 9.45 &= 12.95 − 9.45 &\text{Subtract \(9.45\) from each side of equation.} \\ 10d &= 3.50 &\text{Simplify. Then divide both sides by \(10\).} \\ d &= 0.35 &\text{The common difference is \($0.35\).} \end{array}\)

Now that we know the common difference, \(d = $0.35\), we can answer the question.

The price of each item is as follows: \($1.89, $2.24, $2.59, $2.94, $3.29\).

Try It! (Exercises)

1. ZKonnect cable company requires customers sign a \(2\)-year contract to use their services. The following describes the penalty for breaking contract: Your services are subject to a minimum term agreement of \(24\) months. If the contract is terminated before the end of the \(24\)-month contract, an early termination fee is assessed in the following manner: \($230\) termination fee is assessed if contract is terminated in the first \(30\) days of service. Thereafter, the termination fee decreases by \($10\) per month of contract.

• If Jack enters contract with ZKonnect on April 1 st of \(2021\), but terminates the service on January 10 th of \(2022\), what are Jack’s early termination fees?
• The general term \(a_n\) describes the termination fees for the stated contract. Describe the meaning of the variable \(n\) in the context of this problem. Find the general term \(a_n\).
• Is the early termination fee a finite sequence or an infinite sequence? Explain.
• Find the value of \(a_{13}\) and interpret its meaning in words.

2. A drug company has manufactured \(4\) million doses of a vaccine to date. They promise additional production at a rate of \(1.2\) million doses/month over the next year.

• How many doses of the vaccine, in total, will have been produced after a year?
• The general term \(a_n\) describes the total number of doses of the vaccine produced. Describe the meaning of the variable \(n\) in the context of this problem. Find the general term\(a_n\).
• Find the value of \(a_8\) and interpret its meaning in words.

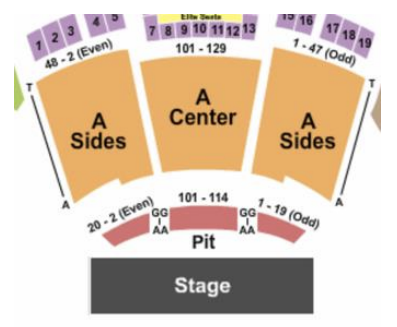
3. The theater shown at right has \(22\) seats in the first row of the “A Center” section. Each row behind the first row gains two additional seats.

• Let \(a_n = 22 + 2n\), starting with \(n = 0\). Give the first \(10\) values of this sequence.
• Using \(a_n = 22 + 2n\), Find the value of \(a_{10}\) and interpret its meaning in words in the context of this problem. Careful! Does \(n=\) row number?
• How many seats, in total, are in “A Center” section if there are \(12\) rows in the section?

4) Logs are stacked in a pile with \(48\) logs on the bottom row and \(24\) on the top row. Each row decreases by three logs.

• The stack, as described, has how many rows of logs?
• Write the general term \(a_n\) to describe the number of logs in a row in two different ways. Each general term should produce the same sequence, regardless of its starting \(n\)-value.

i. Start with \(n = 0\).

ii. Start with \(n = 1\).

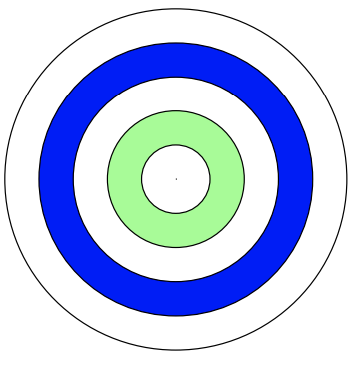
5) The radii of the target circle are an arithmetic sequence. If the area of the innermost circle is \(\pi \text{un}^2\) and the area of the entire target is \(49 \pi \text{un}^2\), what is the area of the blue ring? [The formula for area of a circle is \(A = \pi r^2\)].

6) Three stages of a pattern are shown below, using matchsticks. Each stage adds another triangle and requires a certain number of matchsticks. If we keep up the pattern…

• What stage would require \(325\) matchsticks?

7) Three stages of a pattern are shown below, using matchsticks. Each stage requires a certain number of matchsticks. If we keep up the pattern…

• How many matchsticks are required to make the figure in stage \(22\)?
• What stage would require \(424\) matchsticks?

Arithmetic Sequences Problems with Solutions

Arithmetic sequences are used throughout mathematics and applied to engineering, sciences, computer sciences, biology and finance problems. A set of problems and exercises involving arithmetic sequences, along with detailed solutions are presented.

Review of Arithmetic Sequences

The formula for the n th term a n of an arithmetic sequence with a common difference d and a first term a 1 is given by \[ a_n = a_1 + (n - 1) d \] The sum s n of the first n terms of an arithmetic sequence is defined by \[ s_n = a_1 + a_2 + a_3 + ... + a_n \] and is is given by \[ s_n = \dfrac{n (a_1 + a_n)}{2} \] Arithmetic Series Online Calculator . An online calculator to calculate the sum of the terms in an arithmetic sequence.

Problems with Solutions

The first term of an arithmetic sequence is equal to 6 and the common difference is equal to 3. Find a formula for the n th term and the value of the 50 th term Solution to Problem 1: Use the value of the common difference d = 3 and the first term a 1 = 6 in the formula for the n th term given above \( a_n = a_1 + (n - 1) d \\ = 6 + 3 (n - 1) \\ = 3 n + 3 \) The 50 th term is found by setting n = 50 in the above formula. \[ a_{50} = 3 (50) + 3 = 153 \]

The first term of an arithmetic sequence is equal to 200 and the common difference is equal to -10. Find the value of the 20 th term Solution to Problem 2: Use the value of the common difference d = -10 and the first term a 1 = 200 in the formula for the n th term given above and then apply it to the 20 th term a 20 = 200 + (-10) (20 - 1 ) = 10

An arithmetic sequence has a common difference equal to 10 and its 6 th term is equal to 52. Find its 15 th term. Solution to Problem 3: We use the n th term formula for the 6 th term, which is known, to write a 6 = 52 = a 1 + 10 (6 - 1 ) The above equation allows us to calculate a 1 . a 1 = 2 Now that we know the first term and the common difference, we use the n th term formula to find the 15 th term as follows. a 15 = 2 + 10 (15 - 1) = 142

An arithmetic sequence has a its 5 th term equal to 22 and its 15 th term equal to 62. Find its 100 th term. Solution to Problem 4: We use the n th term formula for the 5 th and 15 th terms to write a 5 = a 1 + (5 - 1 ) d = 22 a 15 = a 1 + (15 - 1 ) d = 62 We obtain a system of 2 linear equations where the unknown are a 1 and d. Subtract the right and left term of the two equations to obtain 62 - 22 = 14 d - 4 d Solve for d. d = 4 Now use the value of d in one of the equations to find a 1 . a 1 + (5 - 1 ) 4 = 22 Solve for a 1 to obtain. a 1 = 6 Now that we have calculated a 1 and d we use them in the n th term formula to find the 100 th formula. a 100 = 6 + 4 (100 - 1 )= 402

Find the sum of all the integers from 1 to 1000. Solution to Problem 5: The sequence of integers starting from 1 to 1000 is given by 1 , 2 , 3 , 4 , ... , 1000 The above sequence has 1000 terms. The first term is 1 and the last term is 1000 and the common difference is equal to 1. We have the formula that gives the sum of the first n terms of an arithmetic sequence knowing the first and last term of the sequence and the number of terms (see formula above). s 1000 = 1000 (1 + 1000) / 2 = 500500

Find the sum of the first 50 even positive integers. Solution to Problem 6: The sequence of the first 50 even positive integers is given by 2 , 4 , 6 , ... The above sequence has a first term equal to 2 and a common difference d = 2. We use the n th term formula to find the 50 th term a 50 = 2 + 2 (50 - 1) = 100 We now the first term and last term and the number of terms in the sequence, we now find the sum of the first 50 terms s 50 = 50 (2 + 100) / 2 = 2550

Find the sum of all positive integers, from 5 to 1555 inclusive, that are divisible by 5. Solution to Problem 7: The first few terms of a sequence of positive integers divisible by 5 is given by 5 , 10 , 15 , ... The above sequence has a first term equal to 5 and a common difference d = 5. We need to know the rank of the term 1555. We use the formula for the n th term as follows 1555 = a 1 + (n - 1 )d Substitute a 1 and d by their values 1555 = 5 + 5(n - 1 ) Solve for n to obtain n = 311 We now know that 1555 is the 311 th term, we can use the formula for the sum as follows s 311 = 311 (5 + 1555) / 2 = 242580

Find the sum S defined by \[ S = \sum_{n=1}^{10} (2n + 1 / 2) \] Solution to Problem 8: Let us first decompose this sum as follows \( S = \sum_{n=1}^{10} (2n + 1 / 2) \) \( = 2 \sum_{n=1}^{10} n + \sum_{n=1}^{10} (1/2) \) The term ∑ n is the sum of the first 10 positive integers. The 10 first positive integers make an arirhmetic sequence with first term equal to 1, it has n = 10 terms and its 10 th term is equal to 10. This sum is obtained using the formula s n = n (a 1 + a n ) / 2 as follows 10(1+10)/2 = 55 The term ∑ (1 / 2) is the addition of a constant term 10 times and is given by 10(1/2) = 5 The sum S is given by S = 2(55) + 5 = 115

Answer the following questions related to arithmetic sequences: a) Find a 20 given that a 3 = 9 and a 8 = 24 b) Find a 30 given that the first few terms of an arithmetic sequence are given by 6,12,18,... c) Find d given that a 1 = 10 and a 20 = 466 d) Find s 30 given that a 10 = 28 and a 20 = 58 e) Find the sum S defined by \[ S = \sum_{n=1}^{20}(3n - 1 / 2) \] f) Find the sum S defined by \[ S = \sum_{n=1}^{20}0.2 n + \sum_{j=21}^{40} 0.4 j \]

Solutions to Above Exercises

a) a 20 = 60 b) a 30 = 180 c) d = 24 d) s 30 = 1335 e) 1380 f) 286

More References and links

• Geometric Sequences Problems with Solutions
• math problems with detailed solutions
• Math Tutorials and Problems

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Arithmetic Sequence Problems with Solutions – Mastering Series Challenges

JUMP TO TOPIC

Arithmetic Sequences Practice Problems and Solutions

Calculating terms in an arithmetic sequence, solving problems involving arithmetic sequences.

An arithmetic sequence is a series where each term increases by a constant amount, known as the common difference . I’ve always been fascinated by how this simple pattern appears in many mathematical problems and real-world situations alike.

Understanding this concept is fundamental for students as it not only enhances their problem-solving skills but also introduces them to the systematic approach of sequences in math .

The first term of an arithmetic sequence sets the stage, while the common difference dictates the incremental steps that each subsequent term will follow. This can be mathematically expressed as $a_n = a_1 + (n – 1)d$.

Whether I’m calculating the nth term or the sum of terms within a sequence , these formulas are the tools that uncover solutions to countless arithmetic sequence problems. Join me in unraveling the beauty and simplicity of arithmetic sequences ; together, we might just discover why they’re considered the building blocks in the world of mathematics .

When I work with arithmetic sequences , I always keep in mind that they have a unique feature: each term is derived by adding a constant value, known as the common difference , to the previous term. Let’s explore this concept through a few examples and problems.

Example 1: Finding a Term in the Sequence

Given the first term, $a_1$ of an arithmetic sequence is 5 and the common difference ( d ) is 3, what is the 10th term $a_{10}$?

Here’s how I determine it: $a_{10} = a_1 + (10 – 1)d ] [ a_{10} = 5 + 9 \times 3 ] [ a_{10} = 5 + 27 ] [ a_{10} = 32$

So, the 10th term is 32.

Sequence A: If $a_1 = 2 $and ( d = 4 ), find $a_5$.

Sequence B: For $a_3 = 7 $ and $a_7 = 19$, calculate the common difference ( d ).

I calculate $a_5$ by using the formula: $a_n = a_1 + (n – 1)d $ $ a_5 = 2 + (5 – 1) \times 4 $ $a_5 = 2 + 16 $ $a_5 = 18$

To find ( d ), I use the formula: $a_n = a_1 + (n – 1)d$ Solving for ( d ), I rearrange the terms from $a_3$ and $a_7$: $d = \frac{a_7 – a_3}{7 – 3}$ $d = \frac{19 – 7}{4}$ $d = \frac{12}{4}$ [ d = 3 ]

Here’s a quick reference table summarizing the properties of arithmetic sequences :

Remember these properties to solve any arithmetic sequence problem effectively!

In an arithmetic sequence , each term after the first is found by adding a constant, known as the common difference ( d ), to the previous term. I find that a clear understanding of the formula helps immensely:

$a_n = a_1 + (n – 1)d$

Here, $a_n$ represents the $n^{th}$term, $a_1$ is the first term, and ( n ) is the term number.

Let’s say we need to calculate the fourth and fifth terms of a sequence where the first term $a_1 $ is 8 and the common difference ( d ) is 2. The explicit formula for this sequence would be $ a_n = 8 + (n – 1)(2) $.

To calculate the fourth term $a_4 $: $a_4 = 8 + (4 – 1)(2) = 8 + 6 = 14$

For the fifth term ( a_5 ), just add the common difference to the fourth term: $a_5 = a_4 + d = 14 + 2 = 16$

Here’s a table to illustrate these calculations:

Remember, the formula provides a direct way to calculate any term in the sequence, known as the explicit or general term formula. Just insert the term number ( n ) and you’ll get the value for $a_n$. I find this methodical approach simplifies the process and avoids confusion.

When I approach arithmetic sequences , I find it helpful to remember that they’re essentially lists of numbers where each term is found by adding a constant to the previous term. This constant is called the common difference, denoted as ( d ). For example, in the sequence 3, 7, 11, 15, …, the common difference is ( d = 4 ).

To articulate the ( n )th term of an arithmetic sequence, $a_n $, I use the fundamental formula:

$a_n = a_1 + (n – 1)d $

In this expression, $a_1$ represents the first term of the sequence.

If I’m solving a specific problem—let’s call it Example 1—I might be given $a_1 = 5 $and ( d = 3 ), and asked to find $a_4 $. I’d calculate it as follows:

$a_4 = 5 + (4 – 1) \times 3 = 5 + 9 = 14$

In applications involving arithmetic series, such as financial planning or scheduling tasks over weeks, the sum of the first ( n ) terms often comes into play. To calculate this sum, ( S_n ), I rely on the formula:

$S_n = \frac{n}{2}(a_1 + a_n)$

Now, if I’m asked to work through Example 3, where I need the sum of the first 10 terms of the sequence starting with 2 and having a common difference of 5, the process looks like this:

$a_{10} = 2 + (10 – 1) \times 5 = 47$ $S_{10} = \frac{10}{2}(2 + 47) = 5 \times 49 = 245$

Linear functions and systems of equations sometimes bear a resemblance to arithmetic sequences, such as when I need to find the intersection of sequence A and sequence B. This would involve setting the nth terms equal to each other and solving the resulting linear equation.

Occasionally, arithmetic sequences can be mistaken for geometric sequences , where each term is found by multiplying by a constant. It’s important to differentiate between them based on their definitions.

For exercises, it’s beneficial to practice finding nth terms, and sums , and even constructing sequences from given scenarios. This ensures a robust understanding when faced with a variety of problems involving arithmetic sequences .

In exploring the realm of arithmetic sequences , I’ve delved into numerous problems and their corresponding solutions. The patterns in these sequences—where the difference between consecutive terms remains constant—allow for straightforward and satisfying problem-solving experiences.

For a sequence with an initial term of $a_1 $ and a common difference of ( d ), the $n^{th}$term is given by $a_n = a_1 + (n – 1)d $.

I’ve found that this formula not only assists in identifying individual terms but also in predicting future ones. Whether calculating the $50^{th}$term or determining the sum of the first several terms, the process remains consistent and is rooted in this foundational equation.

In educational settings, arithmetic sequences serve as an excellent tool for reinforcing the core concepts of algebra and functions. Complexity varies from basic to advanced problems, catering to a range of skill levels. These sequences also reflect practical real-world applications, such as financial modeling and computer algorithms, highlighting the relevance beyond classroom walls.

Through practicing these problems, the elegance and power of arithmetic sequences in mathematical analysis become increasingly apparent. They exemplify the harmony of structure and progression in mathematics —a reminder of how simple rules can generate infinitely complex and fascinating patterns.

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

12.2 Arithmetic Sequences

Learning objectives.

By the end of this section, you will be able to:

• Determine if a sequence is arithmetic
• Find the general term ( n n th term) of an arithmetic sequence
• Find the sum of the first n n terms of an arithmetic sequence

Be Prepared 12.4

Before you get started, take this readiness quiz.

Evaluate 4 n − 1 4 n − 1 for the integers 1, 2, 3, and 4. If you missed this problem, review Example 1.6 .

Be Prepared 12.5

Solve the system of equations: { x + y = 7 3 x + 4 y = 23 . { x + y = 7 3 x + 4 y = 23 . If you missed this problem, review Example 4.9 .

Be Prepared 12.6

If f ( n ) = n 2 ( 3 n + 5 ) , f ( n ) = n 2 ( 3 n + 5 ) , find f ( 1 ) + f ( 20 ) . f ( 1 ) + f ( 20 ) . If you missed this problem, review Example 3.49 .

Determine if a Sequence is Arithmetic

The last section introduced sequences and now we will look at two specific types of sequences that each have special properties. In this section we will look at arithmetic sequences and in the next section, geometric sequences.

An arithmetic sequence is a sequence where the difference between consecutive terms is constant. The difference between consecutive terms in an arithmetic sequence, a n − a n − 1 , a n − a n − 1 , is d , the common difference , for n greater than or equal to two.

Arithmetic Sequence

An arithmetic sequence is a sequence where the difference between consecutive terms is always the same.

The difference between consecutive terms, a n − a n − 1 , a n − a n − 1 , is d , the common difference , for n greater than or equal to two.

In each of these sequences, the difference between consecutive terms is constant, and so the sequence is arithmetic.

Example 12.13

Determine if each sequence is arithmetic. If so, indicate the common difference.

ⓐ 5 , 9 , 13 , 17 , 21 , 25 , … 5 , 9 , 13 , 17 , 21 , 25 , …

ⓑ 4 , 9 , 12 , 17 , 20 , 25 , … 4 , 9 , 12 , 17 , 20 , 25 , …

ⓒ 10 , 3 , −4 , −11 , −18 , −25 , … 10 , 3 , −4 , −11 , −18 , −25 , …

To determine if the sequence is arithmetic, we find the difference of the consecutive terms shown.

Try It 12.25

ⓐ 9 , 20 , 31 , 42 , 53 , 64 , … 9 , 20 , 31 , 42 , 53 , 64 , … ⓑ 12 , 6 , 0 , −6 , −12 , −18 , … 12 , 6 , 0 , −6 , −12 , −18 , … ⓒ 7 , 1 , 10 , 4 , 13 , 7 , … 7 , 1 , 10 , 4 , 13 , 7 , …

Try It 12.26

ⓐ −4 , 4 , 2 , 10 , 8 , 16 , … −4 , 4 , 2 , 10 , 8 , 16 , … ⓑ −3 , −1 , 1 , 3 , 5 , 7 , … −3 , −1 , 1 , 3 , 5 , 7 , … ⓒ 7 , 2 , −3 , −8 , −13 , −18 , … 7 , 2 , −3 , −8 , −13 , −18 , …

If we know the first term, a 1 , a 1 , and the common difference, d , we can list a finite number of terms of the sequence.

Example 12.14

Write the first five terms of the sequence where the first term is 5 and the common difference is d = −6 . d = −6 .

We start with the first term and add the common difference. Then we add the common difference to that result to get the next term, and so on.

The sequence is 5 , −1 , −7 , −13 , −19 , … 5 , −1 , −7 , −13 , −19 , …

Try It 12.27

Write the first five terms of the sequence where the first term is 7 and the common difference is d = −4 . d = −4 .

Try It 12.28

Write the first five terms of the sequence where the first term is 11 and the common difference is d = −8 . d = −8 .

Find the General Term ( n th Term) of an Arithmetic Sequence

Just as we found a formula for the general term of a sequence, we can also find a formula for the general term of an arithmetic sequence.

Let’s write the first few terms of a sequence where the first term is a 1 a 1 and the common difference is d . We will then look for a pattern.

As we look for a pattern we see that each term starts with a 1 a 1 .

The first term adds 0 d to the a 1 a 1 , the second term adds 1 d , the third term adds 2 d , the fourth term adds 3 d , and the fifth term adds 4 d . The number of d s that were added to a 1 a 1 is one less than the number of the term. This leads us to the following

General Term ( n th term) of an Arithmetic Sequence

The general term of an arithmetic sequence with first term a 1 a 1 and the common difference d is

We will use this formula in the next example to find the 15 th term of a sequence.

Example 12.15

Find the fifteenth term of a sequence where the first term is 3 and the common difference is 6.

Try It 12.29

Find the twenty-seventh term of a sequence where the first term is 7 and the common difference is 9.

Try It 12.30

Find the eighteenth term of a sequence where the first term is 13 and the common difference is −7 −7 .

Sometimes we do not know the first term and we must use other given information to find it before we find the requested term.

Example 12.16

Find the twelfth term of a sequence where the seventh term is 10 and the common difference is −2 −2 . Give the formula for the general term.

Try It 12.31

Find the eleventh term of a sequence where the ninth term is 8 and the common difference is −3 . −3 . Give the formula for the general term.

Try It 12.32

Find the nineteenth term of a sequence where the fifth term is 1 and the common difference is −4 . −4 . Give the formula for the general term.

Sometimes the information given leads us to two equations in two unknowns. We then use our methods for solving systems of equations to find the values needed.

Example 12.17

Find the first term and common difference of a sequence where the fifth term is 19 and the eleventh term is 37. Give the formula for the general term.

Since we know two terms, we can make a system of equations using the formula for the general term.

Try It 12.33

Find the first term and common difference of a sequence where the fourth term is 17 and the thirteenth term is 53. Give the formula for the general term.

Try It 12.34

Find the first term and common difference of a sequence where the third term is 2 and the twelfth term is −25 . −25 . Give the formula for the general term.

Find the Sum of the First n Terms of an Arithmetic Sequence

As with the general sequences, it is often useful to find the sum of an arithmetic sequence. The sum, S n , S n , of the first n n terms of any arithmetic sequence is written as S n = a 1 + a 2 + a 3 + ... + a n . S n = a 1 + a 2 + a 3 + ... + a n . To find the sum by merely adding all the terms can be tedious. So we can also develop a formula to find the sum of a sequence using the first and last term of the sequence.

We can develop this new formula by first writing the sum by starting with the first term, a 1 , a 1 , and keep adding a d to get the next term as:

We can also reverse the order of the terms and write the sum by starting with a n a n and keep subtracting d to get the next term as

If we add these two expressions for the sum of the first n terms of an arithmetic sequence, we can derive a formula for the sum of the first n terms of any arithmetic series.

Because there are n sums of ( a 1 + a n ) ( a 1 + a n ) on the right side of the equation, we rewrite the right side as n ( a 1 + a n ) . n ( a 1 + a n ) .

We divide by two to solve for S n . S n .

This gives us a general formula for the sum of the first n terms of an arithmetic sequence.

Sum of the First n Terms of an Arithmetic Sequence

The sum, S n , S n , of the first n terms of an arithmetic sequence is

where a 1 a 1 is the first term and a n a n is the n th term.

We apply this formula in the next example where the first few terms of the sequence are given.

Example 12.18

Find the sum of the first 30 terms of the arithmetic sequence: 8, 13, 18, 23, 28, …

To find the sum, we will use the formula S n = n 2 ( a 1 + a n ) . S n = n 2 ( a 1 + a n ) . We know a 1 = 8 a 1 = 8 , d = 5 d = 5 and n = 30 , n = 30 , but we need to find a n a n in order to use the sum formula.

Try It 12.35

Find the sum of the first 30 terms of the arithmetic sequence: 5, 9, 13, 17, 21, …

Try It 12.36

Find the sum of the first 30 terms of the arithmetic sequence: 7, 10, 13, 16, 19, …

In the next example, we are given the general term for the sequence and are asked to find the sum of the first 50 terms.

Example 12.19

Find the sum of the first 50 terms of the arithmetic sequence whose general term is a n = 3 n − 4 . a n = 3 n − 4 .

To find the sum, we will use the formula S n = n 2 ( a 1 + a n ) . S n = n 2 ( a 1 + a n ) . We know n = 50 , n = 50 , but we need to find a 1 a 1 and a n a n in order to use the sum formula.

Try It 12.37

Find the sum of the first 50 terms of the arithmetic sequence whose general term is a n = 2 n − 5 . a n = 2 n − 5 .

Try It 12.38

Find the sum of the first 50 terms of the arithmetic sequence whose general term is a n = 4 n + 3 . a n = 4 n + 3 .

In the next example we are given the sum in summation notation. To add all the terms would be tedious, so we extract the information needed to use the formula to find the sum of the first n terms.

Example 12.20

Find the sum: ∑ i = 1 25 ( 4 i + 7 ) . ∑ i = 1 25 ( 4 i + 7 ) .

To find the sum, we will use the formula S n = n 2 ( a 1 + a n ) . S n = n 2 ( a 1 + a n ) . We know n = 25 , n = 25 , but we need to find a 1 a 1 and a n a n in order to use the sum formula.

Try It 12.39

Find the sum: ∑ i = 1 30 ( 6 i − 4 ) . ∑ i = 1 30 ( 6 i − 4 ) .

Try It 12.40

Find the sum: ∑ i = 1 35 ( 5 i − 3 ) . ∑ i = 1 35 ( 5 i − 3 ) .

Access these online resources for additional instruction and practice with arithmetic sequences

• Arithmetic Sequences
• Arithmetic Sequences: A Formula for the ‘n-th’ Term
• Arithmetic Series

Section 12.2 Exercises

Practice makes perfect.

In the following exercises, determine if each sequence is arithmetic, and if so, indicate the common difference.

4 , 12 , 20 , 28 , 36 , 44 , … 4 , 12 , 20 , 28 , 36 , 44 , …

−7 , −2 , 3 , 8 , 13 , 18 , … −7 , −2 , 3 , 8 , 13 , 18 , …

−15 , −16 , 3 , 12 , 21 , 30 , … −15 , −16 , 3 , 12 , 21 , 30 , …

11 , 5 , −1 , −7 − 13 , −19 , … 11 , 5 , −1 , −7 − 13 , −19 , …

8 , 5 , 2 , −1 , −4 , −7 , … 8 , 5 , 2 , −1 , −4 , −7 , …

15 , 5 , −5 , −15 , −25 , −35 , … 15 , 5 , −5 , −15 , −25 , −35 , …

In the following exercises, write the first five terms of each sequence with the given first term and common difference.

a 1 = 11 a 1 = 11 and d = 7 d = 7

a 1 = 18 a 1 = 18 and d = 9 d = 9

a 1 = −7 a 1 = −7 and d = 4 d = 4

a 1 = −8 a 1 = −8 and d = 5 d = 5

a 1 = 14 a 1 = 14 and d = −9 d = −9

a 1 = −3 a 1 = −3 and d = −3 d = −3

In the following exercises, find the term described using the information provided.

Find the twenty-first term of a sequence where the first term is three and the common difference is eight.

Find the twenty-third term of a sequence where the first term is six and the common difference is four.

Find the thirtieth term of a sequence where the first term is −14 −14 and the common difference is five.

Find the fortieth term of a sequence where the first term is −19 −19 and the common difference is seven.

Find the sixteenth term of a sequence where the first term is 11 and the common difference is −6 . −6 .

Find the fourteenth term of a sequence where the first term is eight and the common difference is −3 . −3 .

Find the twentieth term of a sequence where the fifth term is −4 −4 and the common difference is −2 . −2 . Give the formula for the general term.

Find the thirteenth term of a sequence where the sixth term is −1 −1 and the common difference is −4 . −4 . Give the formula for the general term.

Find the eleventh term of a sequence where the third term is 19 and the common difference is five. Give the formula for the general term.

Find the fifteenth term of a sequence where the tenth term is 17 and the common difference is seven. Give the formula for the general term.

Find the eighth term of a sequence where the seventh term is −8 −8 and the common difference is −5 . −5 . Give the formula for the general term.

Find the fifteenth term of a sequence where the tenth term is −11 −11 and the common difference is −3 . −3 . Give the formula for the general term.

In the following exercises, find the first term and common difference of the sequence with the given terms. Give the formula for the general term.

The second term is 14 and the thirteenth term is 47.

The third term is 18 and the fourteenth term is 73.

The second term is 13 and the tenth term is −51 . −51 .

The third term is four and the tenth term is −38 −38 .

The fourth term is −6 −6 and the fifteenth term is 27.

The third term is −13 −13 and the seventeenth term is 15.

In the following exercises, find the sum of the first 30 terms of each arithmetic sequence.

11 , 14 , 17 , 20 , 23 , … 11 , 14 , 17 , 20 , 23 , …

12 , 18 , 24 , 30 , 36 , … 12 , 18 , 24 , 30 , 36 , …

8 , 5 , 2 , −1 , −4 , … 8 , 5 , 2 , −1 , −4 , …

16 , 10 , 4 , −2 , −8 , … 16 , 10 , 4 , −2 , −8 , …

−17 , −15 , −13 , −11 , −9 , … −17 , −15 , −13 , −11 , −9 , …

−15 , −12 , −9 , −6 , −3 , … −15 , −12 , −9 , −6 , −3 , …

In the following exercises, find the sum of the first 50 terms of the arithmetic sequence whose general term is given.

a n = 5 n − 1 a n = 5 n − 1

a n = 2 n + 7 a n = 2 n + 7

a n = −3 n + 5 a n = −3 n + 5

a n = −4 n + 3 a n = −4 n + 3

In the following exercises, find each sum.

∑ i = 1 40 ( 8 i − 7 ) ∑ i = 1 40 ( 8 i − 7 )

∑ i = 1 45 ( 7 i − 5 ) ∑ i = 1 45 ( 7 i − 5 )

∑ i = 1 50 ( 3 i + 6 ) ∑ i = 1 50 ( 3 i + 6 )

∑ i = 1 25 ( 4 i + 3 ) ∑ i = 1 25 ( 4 i + 3 )

∑ i = 1 35 ( −6 i − 2 ) ∑ i = 1 35 ( −6 i − 2 )

∑ i = 1 30 ( −5 i + 1 ) ∑ i = 1 30 ( −5 i + 1 )

Writing Exercises

In your own words, explain how to determine whether a sequence is arithmetic.

In your own words, explain how the first two terms are used to find the tenth term. Show an example to illustrate your explanation.

In your own words, explain how to find the general term of an arithmetic sequence.

In your own words, explain how to find the sum of the first n n terms of an arithmetic sequence without adding all the terms.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/12-2-arithmetic-sequences

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Arithmetic Sequence

The arithmetic sequence is the sequence where the common difference remains constant between any two successive terms. Let us recall what is a sequence. A sequence is a collection of numbers that follow a pattern. For example, the sequence 1, 6, 11, 16, … is an arithmetic sequence because there is a pattern where each number is obtained by adding 5 to its previous term. We have two arithmetic sequence formulas.

• The formula for finding n th term of an arithmetic sequence
• The formula to find the sum of first n terms of an arithmetic sequence

If we want to find any term in the arithmetic sequence then we can use the arithmetic sequence formula. Let us learn the definition of an arithmetic sequence and arithmetic sequence formulas along with derivations and a lot more examples for a better understanding.

What is an Arithmetic Sequence?

An arithmetic sequence is defined in two ways. It is a "sequence where the differences between every two successive terms are the same" (or) In an arithmetic sequence, "every term is obtained by adding a fixed number (positive or negative or zero) to its previous term". The following is an arithmetic sequence as every term is obtained by adding a fixed number 4 to its previous term.

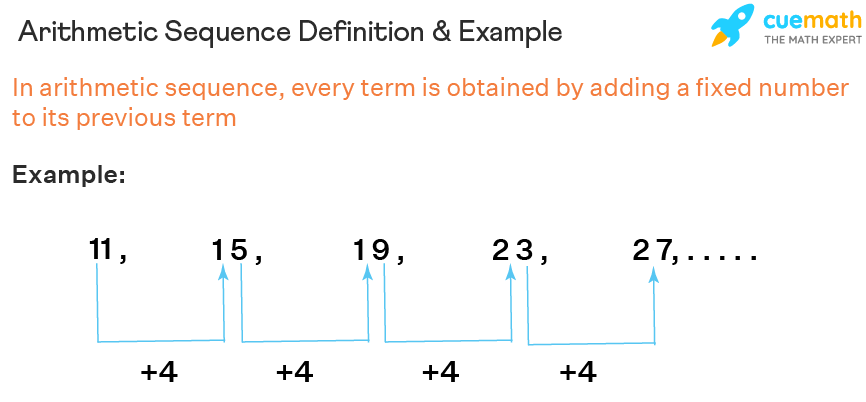
Arithmetic Sequence Example

Consider the sequence 3, 6, 9, 12, 15, .... is an arithmetic sequence because every term is obtained by adding a constant number (3) to its previous term.

• The first term, a = 3
• The common difference, d = 6 - 3 = 9 - 6 = 12 - 9 = 15 - 12 = ... = 3

Thus, an arithmetic sequence can be written as a, a + d, a + 2d, a + 3d, .... Let us verify this pattern for the above example.

a, a + d, a + 2d, a + 3d, a + 4d, ... = 3, 3 + 3, 3 + 2(3), 3 + 3(3), 3 + 4(3),... = 3, 6, 9, 12,15,....

A few more examples of an arithmetic sequence are:

• 5, 8, 11, 14, ...
• 80, 75, 70, 65, 60, ...
• π/2, π, 3π/2, 2π, ....
• -√2, -2√2, -3√2, -4√2, ...

Arithmetic Sequence Formula

The first term of an arithmetic sequence is a, its common difference is d, n is the number of terms. The general form of the AP is a, a+d, a+2d, a+3d,......up to n terms. We have different formulas associated with an arithmetic sequence used to calculate the n th term, the sum of n terms of an AP, or the common difference of a given arithmetic sequence.

The arithmetic sequence formula is given as,

• N th Term: a n = a + (n-1)d
• S n = (n/2) [2a + (n - 1)d]
• d = a n - a n-1

Nth Term of Arithmetic Sequence

The n th term of an arithmetic sequence a 1 , a 2 , a 3 , ... is given by a n = a 1 + (n - 1) d . This is also known as the general term of the arithmetic sequence. This directly follows from the understanding that the arithmetic sequence a 1 , a 2 , a 3 , ... = a 1 , a 1 + d, a 1 + 2d, a 1 + 3d,... The following table shows some arithmetic sequences along with the first term, the common difference, and the n th term.

Arithmetic Sequence Recursive Formula

The above formula for finding the n t h term of an arithmetic sequence is used to find any term of the sequence when the values of 'a 1 ' and 'd' are known. There is another formula to find the n th term which is called the " recursive formula of an arithmetic sequence " and is used to find a term (a n ) of the sequence when its previous term (a n-1 ) and 'd' are known. It says

a n = a n-1 + d

This formula just follows the definition of the arithmetic sequence.

Example: Find a 21 of an arithmetic sequence if a 19 = -72 and d = 7.

By using the recursive formula,

a 20 = a 19 + d = -72 + 7 = -65

a 21 = a 20 + d = -65 + 7 = -58

Therefore, a 21 = -58.

Arithmetic Series

The sum of the arithmetic sequence formula is used to find the sum of its first n terms. Note that the sum of terms of an arithmetic sequence is known as arithmetic series. Consider an arithmetic series in which the first term is a 1 (or 'a') and the common difference is d. The sum of its first n terms is denoted by S n . Then

• When the n th term is NOT known: S n = n/2 [2a 1 + (n-1) d]
• When the n th term is known: S n = n/2 [a 1 + a n ]

Ms. Natalie earns $200,000 per annum and her salary increases by $25,000 per annum. Then how much does she earn at the end of the first 5 years?

The amount earned by Ms. Natalie for the first year is, a = 2,00,000. The increment per annum is, d = 25,000. We have to calculate her earnings in the first 5 years. Hence n = 5. Substituting these values in the sum sum of arithmetic sequence formula,

S n = n/2 [2a 1 + (n-1) d]

⇒ S n = 5/2(2(200000) + (5 - 1)(25000))

= 5/2 (400000 +100000)

= 5/2 (500000)

She earns $1,250,000 in 5 years. We can use this formula to be more helpful for larger values of 'n'.

Sum of Arithmetic Sequence

Let us take an arithmetic sequence that has its first term to be a 1 and the common difference to be d. Then the sum of the first 'n' terms of the sequence is given by

S n = a 1 + (a 1 + d) + (a 1 + 2d) + … + a n ... (1)

Let us write the same sum from right to left (i.e., from the n th term to the first term).

S n = a n + (a n – d) + (a n – 2d) + … + a 1 ... (2)

Adding (1) and (2), all terms with 'd' get canceled.

2S n = (a 1 + a n ) + (a 1 + a n ) + (a 1 + a n ) + … + (a 1 + a n )

2S n = n (a 1 + a n )

S n = [n(a 1 + a n )]/2

By substituting a n = a 1 + (n – 1)d into the last formula, we have

S n = n/2 [a 1 + a 1 + (n – 1)d] (or)

S n = n/2 [2a 1 + (n – 1)d]

Thus, we have derived both formulas for the sum of the arithmetic sequence.

Difference Between Arithmetic Sequence and Geometric Sequence

Here are the differences between arithmetic and geometric sequence :

Important Notes on Arithmetic Sequence:

• In arithmetic sequences, the difference between every two successive numbers is the same.
• The common difference of an arithmetic sequence a 1 , a 2 , a 3 , ... is, d = a 2 - a 1 = a 3 - a 2 = ...
• The n th term of an arithmetic sequence is a n = a 1 + (n−1)d.
• The sum of the first n terms of an arithmetic sequence is S n = n/2[2a 1 + (n − 1)d].
• The common difference between arithmetic sequences can be either positive or negative or zero.

☛ Related Topics:

• Sequence Calculator
• Series Calculator
• Arithmetic Sequence Calculator
• Geometric Sequence Calculator

Arithmetic Sequence Examples

Example 1: Find the n th term of the arithmetic sequence -5, -7/2, -2, ....

The given sequence is -5, -7/2, -2, ...

Here, the first term is a = -5, and the common difference is, d = -(7/2) - (-5) = -2 - (-7/2) = ... = 3/2.

The n th term of an arithmetic sequence is given by

a n = a 1 + (n−1)d

a n = -5 +(n - 1) (3/2)

= -5+ (3/2)n - 3/2

= 3n/2 - 13/2

Answer: The n th term of the given arithmetic sequence is, a n = 3n/2 - 13/2.

Example 2: Which term of the arithmetic sequence -3, -8, -13, -18,... is -248?

The given arithmetic sequence is -3, -8, -13, -18,...

The first term is, a = -3

The common difference is, d = -8 - (-3) = -13 - (-8) = ... = -5.

It is given that the n th term is, a n = -248.

Substitute all these values in the n th term of an arithmetic sequence formula,

a n = a 1 + (n−1)d ⇒ -248 = -3 + (-5)(n - 1) ⇒ -248 = -3 -5n + 5 ⇒ -248 = 2 - 5n ⇒ -250 = -5n ⇒ n = 50

Answer: -248 is the 50 th term of the given sequence.

Example 3: Find the sum of the arithmetic sequence -3, -8, -13, -18,.., -248.

This sequence is the same as the one that is given in Example 2 .

There we found that a = -3, d = -5, and n = 50.

So we have to find the sum of the 50 terms of the given arithmetic series.

S n = n/2[a 1 + a n ]

S 50 = [50 (-3 - 248)]/2 = -6275

Answer: The sum of the given arithmetic sequence is -6275.

go to slide go to slide go to slide

Book a Free Trial Class

Arithmetic Sequence Questions

go to slide go to slide

FAQs on Arithmetic Sequence

What is an arithmetic sequence in algebra.

An arithmetic sequence in algebra is a sequence of numbers where the difference between every two consecutive terms is the same. Generally, the arithmetic sequence is written as a, a+d, a+2d, a+3d, ..., where a is the first term and d is the common difference.

What are Arithmetic Sequence Formulas?

Here are the formulas related to an arithmetic sequence where a₁ (or a) is the first term and d is a common difference:

• The common difference, d = a n - a n-1 .
• n th term of sequence is, a n = a + (n - 1)d
• Sum of n terms of sequence is , S n = [n(a 1 + a n )]/2 (or) n/2 (2a + (n - 1)d)

What is the Definition of an Arithmetic Sequence?

A sequence of numbers in which every term (except the first term) is obtained by adding a constant number to the previous term is called an arithmetic sequence . For example, 1, 3, 5, 7, ... is an arithmetic sequence as every term is obtained by adding 2 (a constant number) to its previous term.

How to Identify An Arithmetic Sequence?

If the difference between every two consecutive terms of a sequence is the same then it is an arithmetic sequence. For example, 3, 8, 13, 18 ... is arithmetic because the consecutive terms have a fixed difference.

• 18-13 = 5 and so on.

What is the n th term of an Arithmetic Sequence?

The n th term of arithmetic sequences is given by a n = a + (n – 1) × d. Here 'a' represents the first term and 'd' represents the common difference.

What is an Arithmetic Series?

An arithmetic series is a sum of an arithmetic sequence where each term is obtained by adding a fixed number to each previous term.

What is the Arithmetic Series Formula?

The sum of the first n terms of an arithmetic sequence (arithmetic series ) with the first term 'a' and common difference 'd' is denoted by Sₙ and we have two formulas to find it.

• S n = n/2[2a + (n - 1)d]
• S n = n/2[a + a n ].

What is the Formula to Find the Common Difference in Arithmetic sequence?

The common difference of an arithmetic sequence, as its name suggests, is the difference between every two of its successive (or consecutive) terms. The formula for finding the common difference of an arithmetic sequence is, d = a n - a n-1 .

How to Find n in Arithmetic Sequence?

When we have to find the number of terms (n) in arithmetic sequences, some of the information about a, d, a n or S n might have been given in the problem. We will just substitute the given values in the formulas of a n or S n and solve it for n.

How To Find the First Term in Arithmetic sequence?

The first term of an arithmetic sequence is the number that occurs in the first position from the left. It is denoted by 'a'. If 'a' is NOT given in the problem, then some information about d (or) a n (or) S n might be given in the problem. We will just substitute the given values in the formulas of a n or S n and solve it for 'a'.

What is the Difference Between Arithmetic Sequence and Arithmetic Series?

An arithmetic sequence is a collection of numbers in which all the differences between every two consecutive numbers are equal to a constant whereas an arithmetic series is the sum of a few or more terms of an arithmetic sequence.

What are the Types of Sequences?

There are mainly 3 types of sequences in math. They are:

• Arithmetic sequence
• Geometric sequence
• Harmonic sequence

What are the Applications of Arithmetic Sequence?

Here are some applications: the salary of a person which is increased by a constant amount by each year, the rent of a taxi which charges per mile, the number of fishes in a pond that increase by a constant number each month, etc.

How to Find the n th Term in Arithmetic Sequence?

Here are the steps for finding the n th term of arithmetic sequences:

• Identify its first term, a
• Common difference , d
• Identify which term you want. i.e., n
• Substitute all these into the formula a n = a + (n – 1) × d.

How to Find the Sum of n Terms of Arithmetic Sequence?

To find the sum of the first n terms of arithmetic sequences,

• Identify its first term (a)
• Common difference (d)
• Identify which term you want (n)
• Substitute all these into the formula S n = (n/2)(2a + (n - 1)d)

Arithmetic Sequences and Sums

A Sequence is a set of things (usually numbers) that are in order.

Each number in the sequence is called a term (or sometimes "element" or "member"), read Sequences and Series for more details.

Arithmetic Sequence

In an Arithmetic Sequence the difference between one term and the next is a constant .

In other words, we just add the same value each time ... infinitely.

Example: 1, 4, 7, 10, 13, 16, 19, 22, 25, ...

This sequence has a difference of 3 between each number. The pattern is continued by adding 3 to the last number each time, like this:

In General we could write an arithmetic sequence like this:

{a, a+d, a+2d, a+3d, ... }

• a is the first term, and
• d is the difference between the terms (called the "common difference" )

Example (continued): 1, 4, 7, 10, 13, 16, 19, 22, 25, ...

• a = 1 (the first term)
• d = 3 (the "common difference" between terms)

And we get:

{1, 1+3, 1+2×3, 1+3×3, ... }

{1, 4, 7, 10, ... }

We can write an Arithmetic Sequence as a rule :

x n = a + d(n−1)

(We use "n−1" because d is not used in the 1st term).

Example: Write a rule, and calculate the 9th term, for this Arithmetic Sequence:

3, 8, 13, 18, 23, 28, 33, 38, ...

This sequence has a difference of 5 between each number.

The values of a and d are:

• a = 3 (the first term)
• d = 5 (the "common difference")

Using the Arithmetic Sequence rule:

So the 9 th term is:

x 9 = 5× 9 − 2 = 43

Is that right? Check for yourself!

Arithmetic Sequences are sometimes called Arithmetic Progressions (A.P.’s)

Advanced Topic : Summing an Arithmetic Series

To sum up the terms of this arithmetic sequence:

a + (a+d) + (a+2d) + (a+3d) + ...

use this formula:

What is that funny symbol? It is called Sigma Notation

And below and above it are shown the starting and ending values:

It says "Sum up n where n goes from 1 to 4. Answer= 10

Here is how to use it:

Example: Add up the first 10 terms of the arithmetic sequence:

{ 1, 4, 7, 10, 13, ... }

The values of a , d and n are:

• n = 10 (how many terms to add up)

= 5(2+9·3) = 5(29) = 145

Check: why don't you add up the terms yourself, and see if it comes to 145

Footnote: Why Does the Formula Work?

Let's see why the formula works, because we get to use an interesting "trick" which is worth knowing.

First , we will call the whole sum "S" :

Next , rewrite S in reverse order:

Now add those two, term by term:

Each term is the same! And there are "n" of them so ...

Now, just divide by 2 and we get:

S = n 2 (2a + (n−1)d)

Which is our formula:

• Daily Games
• Strategy and Puzzles
• Vocabulary Games
• Junior Edition Games
• All problems
• High School Math
• MAML Problems
• Calculus Problems
• Loony Physics
• Pro Problems
• Getting Started
• Pro Control Panel
• Virtual Classroom
• Play My Favorites
• Select My Favorites

Arithmetic Sequence Problems

There are many problems we can solve if we keep in mind that the  n th term of an arithmetic sequence can be written in the following way: a n  = a 1 +(n - 1)d Where a 1  is the first term, and  d  is the common difference. For example, if we are told that the first two terms add up to the fifth term, and that the common difference is 8 less than the first term we can take this equation: a 1  + a 2  = a 5 and rewrite it as follows: a 1  + [a 1  + d] = [a 1  + 4d] This leads to a 1  = 3d. Combine this with d = a 1  - 8, and we have: a 1  = 3(a 1  - 8) or a 1  = 12. This leads to d = 4, and from this information, we can find any other term of the sequence.

Blogs on This Site

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Patterns and Sequences Short Problems

Pattern Snake

This pattern repeats every 12 dots. Can you work out what a later piece will be?

What a Coincidence!

Consider two arithmetic sequences: 1998, 2005, 2012,... and 1996, 2005, 2014,... Which numbers will appear in both?

Suit Sequence

A pattern repeats every six symbols. What are the 100th and 101st symbols?

Knights and Knaves

Knights always tell the truth. Knaves always lie. Can you catch these knights and knaves out?

Doubly Consecutive Sums

How many numbers less than 2017 are both the sum of two consecutive integers and the sum of five consecutive integers?

Expanding Pattern

How many squares are needed to continue this pattern?

Fibonacci Deduction

Leonard writes down a sequence of numbers. Can you find a formula to predict the seventh number in his sequence?

Hexagon Line

How many hexagons are required for the perimeter of the whole shape to have length 1002cm?

Street Lamps

Walking up a steep hill, I pass 10 equally spaced street lamps. How long do I take to walk from the first lamp to the last?

Fruit Line-up

This grocer wants to arrange his fruit in a particular order, can you help him?

Triangular Clock

Trinni rearanges numbers on a clock face so each adjacent pair add up to a triangle number... What number did she put where 6 would usually be?

Printing Error

Every third page number in this book has been omitted. Can you work out what number will be on the last page?

Sliding Robot

A robot moves along the number line. Where will it be after 2011 slides?

Many Matildas

MatildaMatildaMatil... What is the 1000th letter?

How Many Rectangles?

By drawing 5 horizontal and four vertical lines, one can form 12 rectangles. What is the greatest number of rectangles that can be formed by drawing 15 lines?

Night Watchmen

Grannie's watch gains 30 minutes every hour, whilst Grandpa's watch loses 30 minutes every hour. What is the correct time when their watches next agree?

Weekly Problem 51 - 2016 Pegs numbered 1 to 50 are placed in a row. Alternate pegs are knocked down, and this process is repeated. What is the number of the last peg to be knocked down?

If a number is even, halve it; if odd, treble it and add 1. If a sequence starts at 13, what will be the value of the 2008th term?

Repeat a pattern of numbers to form a larger number. Can you find the sum of all the digits?

Collatz-ish

A sequence is generated using these rules. For which values of n is the nth term equal to n?

Can you work out which number will appear directly below 400 in this pattern?

Trolley Park

In a supermarket, there are two lines of tightly packed trolleys. What is the length of one trolley?

Alternating Sum

Given that the number 2008 is the correct answer to a sum, can you find n?

Arithmetic Sequence Calculator

Find indices, sums and common diffrence of an arithmetic sequence step-by-step.

• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems

Frequently Asked Questions (FAQ)

How do you calculate an arithmetic sequence.

• The formula for the nth term of an arithmetic sequence is a_n = a_1 + (n-1)d, where a_1 is the first term of the sequence, a_n is the nth term of the sequence, and d is the common difference.

What is an arithmetic Sequence?

• An arithmetic sequence is a sequence of numbers in which each term is obtained by adding a fixed number to the previous term. It is represented by the formula a_n = a_1 + (n-1)d, where a_1 is the first term of the sequence, a_n is the nth term of the sequence, and d is the common difference, which is obtained by subtracting the previous term from the current term.

How do you know if a sequence is arithmetic or geometric?

• An arithmetic sequence has a constant difference between consecutive terms, while a geometric sequence has a constant ratio between consecutive terms.

arithmetic-sequence-calculator

Related Symbolab blog posts

Please add a message.

Message received. Thanks for the feedback.