radical equations and problem solving

Radical Equations

Solving radical equations.

Learning how to solve radical equations requires a lot of practice and familiarity of the different types of problems. In this lesson, the goal is to show you detailed worked solutions of some problems with varying levels of difficulty.

What is a Radical Equation?

An equation wherein the variable is contained inside a radical symbol or has a rational exponent. In particular, we will deal with the square root which is the consequence of having an exponent of [latex]\Large{1 \over 2}[/latex].

Key Steps to Solve Radical Equations:

1) Isolate the radical symbol on one side of the equation

2) Square both sides of the equation to eliminate the radical symbol

3) Solve the equation that comes out after the squaring process

4) Check your answers with the original equation to avoid extraneous values or solutions

Examples of How to Solve Radical Equations

Example 1 : Solve the radical equation

The radical is by itself on one side so it is fine to square both sides of the equations to get rid of the radical symbol. Then proceed with the usual steps in solving linear equations.

You must ALWAYS check your answers to verify if they are “truly” the solutions. Some answers from your calculations may be extraneous. Substitute x = 16 back into the original radical equation to see whether it yields a true statement.

Yes, it checks, so x = 16 is a solution.

Example 2 : Solve the radical equation

The setup looks good because the radical is again isolated on one side. So I can square both sides to eliminate that square root symbol. Be careful dealing with the right side when you square the binomial (x−1). You must apply the FOIL method correctly.

We move all the terms to the right side of the equation and then proceed with factoring out the trinomial. Applying the Zero-Product Property, we obtain the values of x = 1 and x = 3 .

Caution: Always check your calculated values from the original radical equation to make sure that they are true answers and not extraneous or “false” answers.

Looks good for both of our solved values of x after checking, so our solutions are x = 1 and x = 3 .

Example 3 : Solve the radical equation

We need to recognize the radical symbol is not isolated just yet on the left side. It means we have to get rid of that −1 before squaring both sides of the equation. A simple step of adding both sides by 1 should take care of that problem. After doing so, the “new” equation is similar to the ones we have gone over so far.

Our possible solutions are x = −2 and x = 5 . Notice I use the word “possible” because it is not final until we perform our verification process of checking our values against the original radical equation.

Since we arrive at a false statement when x = -2, therefore that value of x is considered to be extraneous  so we disregard it! Leaving us with one true answer, x = 5 .

Example 4 : Solve the radical equation

The left side looks a little messy because there are two radical symbols. But it is not that bad! Always remember the key steps suggested above. Since both of the square roots are on one side that means it’s definitely ready for the entire radical equation to be squared.

So for our first step, let’s square both sides and see what happens.

It is perfectly normal for this type of problem to see another radical symbol after the first application of squaring. The good news coming out from this is that there’s only one left. From this point, try to isolate again the single radical on the left side, which should force us to relocate the rest to the opposite side.

As you can see, that simplified radical equation is definitely familiar . Proceed with the usual way of solving it and make sure that you always verify the solved values of x against the original radical equation.

I will leave it to you to check that indeed x = 4 is a solution.

Example 5 : Solve the radical equation

This problem is very similar to example 4. The only difference is that this time around both of the radicals has binomial expressions. The approach is also to square both sides since the radicals are on one side, and simplify. But we need to perform the second application of squaring to fully get rid of the square root symbol.

The solution is x = 2 . You may verify it by substituting the value back into the original radical equation and see that it yields a true statement.

Example 6 : Solve the radical equation

It looks like our first step is to square both sides and observe what comes out afterward. Don’t forget to combine like terms every time you square the sides. If it happens that another radical symbol is generated after the first application of squaring process, then it makes sense to do it one more time. Remember, our goal is to get rid of the radical symbols to free up the variable we are trying to solve or isolate.

Well, it looks like we will need to square both sides again because of the newly generated radical symbol. But we must isolate the radical first on one side of the equation before doing so. I will keep the square root on the left, and that forces me to move everything to the right.

Looking good so far! Now it’s time to square both sides again to finally eliminate the radical.

Be careful though in squaring the left side of the equation. You must also square that −2 to the left of the radical.

What we have now is a quadratic equation in the standard form. The best way to solve for x is to use the Quadratic Formula where a = 7, b = 8, and c = −44.

So the possible solutions are [latex]x = 2[/latex], and [latex]x = {{ – 22} \over 7}[/latex].

I will leave it to you to check those two values of “x” back into the original radical equation. I hope you agree that x = 2 is the only solution while the other value is an extraneous solution, so disregard it!

Example 7 : Solve the radical equation

There are two ways to approach this problem. I could immediately square both sides to get rid of the radicals or multiply the two radicals first then square. Both procedures should arrive at the same answers when properly done. For this, I will use the second approach.

Next, move everything to the left side and solve the resulting Quadratic equation.  You can use the Quadratic formula to solve it, but since it is easily factorable I will just factor it out.

The possible solutions then are [latex]x = {{ – 5} \over 2}[/latex] and [latex]x = 3[/latex] .

I will leave it to you to check the answers. The only answer should be [latex]x = 3[/latex] which makes the other one an extraneous solution.

You may also be interested in these related math lessons or tutorials:

Simplifying Radical Expressions Adding and Subtracting Radical Expressions Multiplying Radical Expressions Rationalizing the Denominator

8.6 Solve Radical Equations

Learning objectives.

By the end of this section, you will be able to:

• Solve radical equations
• Solve radical equations with two radicals
• Use radicals in applications

Be Prepared 8.16

Before you get started, take this readiness quiz.

Simplify: ( y − 3 ) 2 . ( y − 3 ) 2 . If you missed this problem, review Example 5.31 .

Be Prepared 8.17

Solve: 2 x − 5 = 0 . 2 x − 5 = 0 . If you missed this problem, review Example 2.2 .

Be Prepared 8.18

Solve n 2 − 6 n + 8 = 0 . n 2 − 6 n + 8 = 0 . If you missed this problem, review Example 6.45 .

Solve Radical Equations

In this section we will solve equations that have a variable in the radicand of a radical expression. An equation of this type is called a radical equation .

Radical Equation

An equation in which a variable is in the radicand of a radical expression is called a radical equation .

As usual, when solving these equations, what we do to one side of an equation we must do to the other side as well. Once we isolate the radical, our strategy will be to raise both sides of the equation to the power of the index. This will eliminate the radical.

Solving radical equations containing an even index by raising both sides to the power of the index may introduce an algebraic solution that would not be a solution to the original radical equation. Again, we call this an extraneous solution as we did when we solved rational equations.

In the next example, we will see how to solve a radical equation. Our strategy is based on raising a radical with index n to the n th power. This will eliminate the radical.

Example 8.56

How to solve a radical equation.

Solve: 5 n − 4 − 9 = 0 . 5 n − 4 − 9 = 0 .

Try It 8.111

Solve: 3 m + 2 − 5 = 0 . 3 m + 2 − 5 = 0 .

Try It 8.112

Solve: 10 z + 1 − 2 = 0 . 10 z + 1 − 2 = 0 .

Solve a radical equation with one radical.

• Step 1. Isolate the radical on one side of the equation.
• Step 2. Raise both sides of the equation to the power of the index.
• Step 3. Solve the new equation.
• Step 4. Check the answer in the original equation.

When we use a radical sign, it indicates the principal or positive root. If an equation has a radical with an even index equal to a negative number, that equation will have no solution.

Example 8.57

Solve: 9 k − 2 + 1 = 0 . 9 k − 2 + 1 = 0 .

Because the square root is equal to a negative number, the equation has no solution.

Try It 8.113

Solve: 2 r − 3 + 5 = 0 . 2 r − 3 + 5 = 0 .

Try It 8.114

Solve: 7 s − 3 + 2 = 0 . 7 s − 3 + 2 = 0 .

If one side of an equation with a square root is a binomial, we use the Product of Binomial Squares Pattern when we square it.

Binomial Squares

Don’t forget the middle term!

Example 8.58

Solve: p − 1 + 1 = p . p − 1 + 1 = p .

Try It 8.115

Solve: x − 2 + 2 = x . x − 2 + 2 = x .

Try It 8.116

Solve: y − 5 + 5 = y . y − 5 + 5 = y .

When the index of the radical is 3, we cube both sides to remove the radical.

Example 8.59

Solve: 5 x + 1 3 + 8 = 4 . 5 x + 1 3 + 8 = 4 .

Try It 8.117

Solve: 4 x − 3 3 + 8 = 5 4 x − 3 3 + 8 = 5

Try It 8.118

Solve: 6 x − 10 3 + 1 = −3 6 x − 10 3 + 1 = −3

Sometimes an equation will contain rational exponents instead of a radical. We use the same techniques to solve the equation as when we have a radical. We raise each side of the equation to the power of the denominator of the rational exponent. Since ( a m ) n = a m · n , ( a m ) n = a m · n , we have for example,

Remember, x 1 2 = x x 1 2 = x and x 1 3 = x 3 . x 1 3 = x 3 .

Example 8.60

Solve: ( 3 x − 2 ) 1 4 + 3 = 5 . ( 3 x − 2 ) 1 4 + 3 = 5 .

Try It 8.119

Solve: ( 9 x + 9 ) 1 4 − 2 = 1 . ( 9 x + 9 ) 1 4 − 2 = 1 .

Try It 8.120

Solve: ( 4 x − 8 ) 1 4 + 5 = 7 . ( 4 x − 8 ) 1 4 + 5 = 7 .

Sometimes the solution of a radical equation results in two algebraic solutions, but one of them may be an extraneous solution !

Example 8.61

Solve: r + 4 − r + 2 = 0 . r + 4 − r + 2 = 0 .

Try It 8.121

Solve: m + 9 − m + 3 = 0 . m + 9 − m + 3 = 0 .

Try It 8.122

Solve: n + 1 − n + 1 = 0 . n + 1 − n + 1 = 0 .

When there is a coefficient in front of the radical, we must raise it to the power of the index, too.

Example 8.62

Solve: 3 3 x − 5 − 8 = 4 . 3 3 x − 5 − 8 = 4 .

Try It 8.123

Solve: 2 4 a + 4 − 16 = 16 . 2 4 a + 4 − 16 = 16 .

Try It 8.124

Solve: 3 2 b + 3 − 25 = 50 . 3 2 b + 3 − 25 = 50 .

Solve Radical Equations with Two Radicals

If the radical equation has two radicals, we start out by isolating one of them. It often works out easiest to isolate the more complicated radical first.

In the next example, when one radical is isolated, the second radical is also isolated.

Example 8.63

Solve: 4 x − 3 3 = 3 x + 2 3 . 4 x − 3 3 = 3 x + 2 3 .

Try It 8.125

Solve: 5 x − 4 3 = 2 x + 5 3 . 5 x − 4 3 = 2 x + 5 3 .

Try It 8.126

Solve: 7 x + 1 3 = 2 x − 5 3 . 7 x + 1 3 = 2 x − 5 3 .

Sometimes after raising both sides of an equation to a power, we still have a variable inside a radical. When that happens, we repeat Step 1 and Step 2 of our procedure. We isolate the radical and raise both sides of the equation to the power of the index again.

Example 8.64

Solve: m + 1 = m + 9 . m + 1 = m + 9 .

Try It 8.127

Solve: 3 − x = x − 3 . 3 − x = x − 3 .

Try It 8.128

Solve: x + 2 = x + 16 . x + 2 = x + 16 .

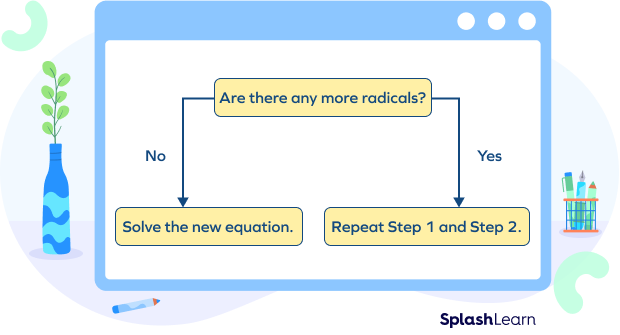
We summarize the steps here. We have adjusted our previous steps to include more than one radical in the equation This procedure will now work for any radical equations.

Solve a radical equation.

• Step 1. Isolate one of the radical terms on one side of the equation.
• Step 3. Are there any more radicals? If yes, repeat Step 1 and Step 2 again. If no, solve the new equation.

Be careful as you square binomials in the next example. Remember the pattern is ( a + b ) 2 = a 2 + 2 a b + b 2 ( a + b ) 2 = a 2 + 2 a b + b 2 or ( a − b ) 2 = a 2 − 2 a b + b 2 . ( a − b ) 2 = a 2 − 2 a b + b 2 .

Example 8.65

Solve: q − 2 + 3 = 4 q + 1 . q − 2 + 3 = 4 q + 1 .

Try It 8.129

Solve: x − 1 + 2 = 2 x + 6 x − 1 + 2 = 2 x + 6

Try It 8.130

Solve: x + 2 = 3 x + 4 x + 2 = 3 x + 4

Use Radicals in Applications

As you progress through your college courses, you’ll encounter formulas that include radicals in many disciplines. We will modify our Problem Solving Strategy for Geometry Applications slightly to give us a plan for solving applications with formulas from any discipline.

Use a problem solving strategy for applications with formulas.

• Step 1. Read the problem and make sure all the words and ideas are understood. When appropriate, draw a figure and label it with the given information.
• Step 2. Identify what we are looking for.
• Step 3. Name what we are looking for by choosing a variable to represent it.
• Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
• Step 5. Solve the equation using good algebra techniques.
• Step 6. Check the answer in the problem and make sure it makes sense.
• Step 7. Answer the question with a complete sentence.

One application of radicals has to do with the effect of gravity on falling objects. The formula allows us to determine how long it will take a fallen object to hit the gound.

Falling Objects

On Earth, if an object is dropped from a height of h feet, the time in seconds it will take to reach the ground is found by using the formula

For example, if an object is dropped from a height of 64 feet, we can find the time it takes to reach the ground by substituting h = 64 h = 64 into the formula.

It would take 2 seconds for an object dropped from a height of 64 feet to reach the ground.

Example 8.66

Marissa dropped her sunglasses from a bridge 400 feet above a river. Use the formula t = h 4 t = h 4 to find how many seconds it took for the sunglasses to reach the river.

Try It 8.131

A helicopter dropped a rescue package from a height of 1,296 feet. Use the formula t = h 4 t = h 4 to find how many seconds it took for the package to reach the ground.

Try It 8.132

A window washer dropped a squeegee from a platform 196 feet above the sidewalk Use the formula t = h 4 t = h 4 to find how many seconds it took for the squeegee to reach the sidewalk.

Police officers investigating car accidents measure the length of the skid marks on the pavement. Then they use square roots to determine the speed , in miles per hour, a car was going before applying the brakes.

Skid Marks and Speed of a Car

If the length of the skid marks is d feet, then the speed, s , of the car before the brakes were applied can be found by using the formula

Example 8.67

After a car accident, the skid marks for one car measured 190 feet. Use the formula s = 24 d s = 24 d to find the speed of the car before the brakes were applied. Round your answer to the nearest tenth.

Try It 8.133

An accident investigator measured the skid marks of the car. The length of the skid marks was 76 feet. Use the formula s = 24 d s = 24 d to find the speed of the car before the brakes were applied. Round your answer to the nearest tenth.

Try It 8.134

The skid marks of a vehicle involved in an accident were 122 feet long. Use the formula s = 24 d s = 24 d to find the speed of the vehicle before the brakes were applied. Round your answer to the nearest tenth.

Access these online resources for additional instruction and practice with solving radical equations.

• Solving an Equation Involving a Single Radical
• Solving Equations with Radicals and Rational Exponents
• Solving Radical Equations
• Radical Equation Application

Section 8.6 Exercises

Practice makes perfect.

In the following exercises, solve.

5 x − 6 = 8 5 x − 6 = 8

4 x − 3 = 7 4 x − 3 = 7

5 x + 1 = −3 5 x + 1 = −3

3 y − 4 = −2 3 y − 4 = −2

2 x 3 = −2 2 x 3 = −2

4 x − 1 3 = 3 4 x − 1 3 = 3

2 m − 3 − 5 = 0 2 m − 3 − 5 = 0

2 n − 1 − 3 = 0 2 n − 1 − 3 = 0

6 v − 2 − 10 = 0 6 v − 2 − 10 = 0

12 u + 1 − 11 = 0 12 u + 1 − 11 = 0

4 m + 2 + 2 = 6 4 m + 2 + 2 = 6

6 n + 1 + 4 = 8 6 n + 1 + 4 = 8

2 u − 3 + 2 = 0 2 u − 3 + 2 = 0

5 v − 2 + 5 = 0 5 v − 2 + 5 = 0

u − 3 + 3 = u u − 3 + 3 = u

v − 10 + 10 = v v − 10 + 10 = v

r − 1 = r − 1 r − 1 = r − 1

s − 8 = s − 8 s − 8 = s − 8

6 x + 4 3 = 4 6 x + 4 3 = 4

11 x + 4 3 = 5 11 x + 4 3 = 5

4 x + 5 3 − 2 = −5 4 x + 5 3 − 2 = −5

9 x − 1 3 − 1 = −5 9 x − 1 3 − 1 = −5

( 6 x + 1 ) 1 2 − 3 = 4 ( 6 x + 1 ) 1 2 − 3 = 4

( 3 x − 2 ) 1 2 + 1 = 6 ( 3 x − 2 ) 1 2 + 1 = 6

( 8 x + 5 ) 1 3 + 2 = −1 ( 8 x + 5 ) 1 3 + 2 = −1

( 12 x − 5 ) 1 3 + 8 = 3 ( 12 x − 5 ) 1 3 + 8 = 3

( 12 x − 3 ) 1 4 − 5 = −2 ( 12 x − 3 ) 1 4 − 5 = −2

( 5 x − 4 ) 1 4 + 7 = 9 ( 5 x − 4 ) 1 4 + 7 = 9

x + 1 − x + 1 = 0 x + 1 − x + 1 = 0

y + 4 − y + 2 = 0 y + 4 − y + 2 = 0

z + 100 − z = −10 z + 100 − z = −10

w + 25 − w = −5 w + 25 − w = −5

3 2 x − 3 − 20 = 7 3 2 x − 3 − 20 = 7

2 5 x + 1 − 8 = 0 2 5 x + 1 − 8 = 0

2 8 r + 1 − 8 = 2 2 8 r + 1 − 8 = 2

3 7 y + 1 − 10 = 8 3 7 y + 1 − 10 = 8

3 u + 7 = 5 u + 1 3 u + 7 = 5 u + 1

4 v + 1 = 3 v + 3 4 v + 1 = 3 v + 3

8 + 2 r = 3 r + 10 8 + 2 r = 3 r + 10

10 + 2 c = 4 c + 16 10 + 2 c = 4 c + 16

5 x − 1 3 = x + 3 3 5 x − 1 3 = x + 3 3

8 x − 5 3 = 3 x + 5 3 8 x − 5 3 = 3 x + 5 3

2 x 2 + 9 x − 18 3 = x 2 + 3 x − 2 3 2 x 2 + 9 x − 18 3 = x 2 + 3 x − 2 3

x 2 − x + 18 3 = 2 x 2 − 3 x − 6 3 x 2 − x + 18 3 = 2 x 2 − 3 x − 6 3

a + 2 = a + 4 a + 2 = a + 4

r + 6 = r + 8 r + 6 = r + 8

u + 1 = u + 4 u + 1 = u + 4

x + 1 = x + 2 x + 1 = x + 2

a + 5 − a = 1 a + 5 − a = 1

−2 = d − 20 − d −2 = d − 20 − d

2 x + 1 = 1 + x 2 x + 1 = 1 + x

3 x + 1 = 1 + 2 x − 1 3 x + 1 = 1 + 2 x − 1

2 x − 1 − x − 1 = 1 2 x − 1 − x − 1 = 1

x + 1 − x − 2 = 1 x + 1 − x − 2 = 1

x + 7 − x − 5 = 2 x + 7 − x − 5 = 2

x + 5 − x − 3 = 2 x + 5 − x − 3 = 2

In the following exercises, solve. Round approximations to one decimal place.

Landscaping Reed wants to have a square garden plot in his backyard. He has enough compost to cover an area of 75 square feet. Use the formula s = A s = A to find the length of each side of his garden. Round your answer to the nearest tenth of a foot.

Landscaping Vince wants to make a square patio in his yard. He has enough concrete to pave an area of 130 square feet. Use the formula s = A s = A to find the length of each side of his patio. Round your answer to the nearest tenth of a foot.

Gravity A hang glider dropped his cell phone from a height of 350 feet. Use the formula t = h 4 t = h 4 to find how many seconds it took for the cell phone to reach the ground.

Gravity A construction worker dropped a hammer while building the Grand Canyon skywalk, 4000 feet above the Colorado River. Use the formula t = h 4 t = h 4 to find how many seconds it took for the hammer to reach the river.

Accident investigation The skid marks for a car involved in an accident measured 216 feet. Use the formula s = 24 d s = 24 d to find the speed of the car before the brakes were applied. Round your answer to the nearest tenth.

Accident investigation An accident investigator measured the skid marks of one of the vehicles involved in an accident. The length of the skid marks was 175 feet. Use the formula s = 24 d s = 24 d to find the speed of the vehicle before the brakes were applied. Round your answer to the nearest tenth.

Writing Exercises

Explain why an equation of the form x + 1 = 0 x + 1 = 0 has no solution.

ⓐ Solve the equation r + 4 − r + 2 = 0 . r + 4 − r + 2 = 0 . ⓑ Explain why one of the “solutions” that was found was not actually a solution to the equation.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/8-6-solve-radical-equations

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Solving Radical Equations

How to solve equations with square roots, cube roots, etc.

Radical Equations

We can get rid of a square root by squaring (or cube roots by cubing, etc).

Warning: this can sometimes create "solutions" which don't actually work when we put them into the original equation. So we need to Check!

Follow these steps:

• isolate the square root on one side of the equation
• square both sides of the equation

Then continue with our solution!

Example: solve √(2x+9) − 5 = 0

Now it should be easier to solve!

Check: √(2·8+9) − 5 = √(25) − 5 = 5 − 5 = 0

That one worked perfectly.

More Than One Square Root

What if there are two or more square roots? Easy! Just repeat the process for each one.

It will take longer (lots more steps) ... but nothing too hard.

Example: solve √(2x−5) − √(x−1) = 1

We have removed one square root.

Now do the "square root" thing again:

We have now successfully removed both square roots.

Let us continue on with the solution.

It is a Quadratic Equation! So let us put it in standard form.

Using the Quadratic Formula (a=1, b=−14, c=29) gives the solutions:

2.53 and 11.47 (to 2 decimal places)

Let us check the solutions:

There is really only one solution :

Answer: 11.47 (to 2 decimal places)

See? This method can sometimes produce solutions that don't really work!

The root that seemed to work, but wasn't right when we checked it, is called an "Extraneous Root"

So checking is important.

Forgot password? New user? Sign up

Existing user? Log in

Solving Radical Equations

Already have an account? Log in here.

A radical equation is an equation that contains at least one radical sign that includes a variable. For an example you can consider the following equation:

\(\qquad \qquad \qquad \qquad \sqrt{x+2}=x-3\).

Solving radical equations requires applying the rules of exponents and following some basic algebraic principles. In some cases, it also requires looking out for errors generated by raising unknown quantities to an even power .

Introduction

Problem solving.

A radical is an exponential number where the exponent is a fraction . For an example, consider \( \sqrt[n]{x^m} = x ^ { m/n } \). A radical equation contains at least one radical sign that includes a variable.

A square root \(\left( \sqrt{x} \right)\) is simplified, when the radicand (value inside the square root sign, which is \(x\) in this case) has no square factors. This can be done effectively by factorizing the radicand first, to know what terms to pull out.

Here is a problem based on the basics of radicals.

True or False:

For all real numbers \(y \),

\[\Large y = \sqrt{y^2}\]

The leading step of solving a radical equation is to eliminate the radical exponent to obtain a polynomial equation and check whether the obtained roots satisfy the original equation to escape from extraneous roots.

Following are the steps to solve a radical equation:

Eliminate the radicals or rational exponents and obtain a polynomial equation. The key step is to raise each side of the equation to the same power. If \(a = b,\) then \(a^n = b^n\). [Powers property of equality] Then solve the new equation using standard procedures. Before raising each side of an equation to the same power, you should isolate the radical expression on one side of the equation. However, this is not it. When solving radical equations we must always be cautious of extraneous roots . An extraneous root is a root that satisfies the polynomial obtained by squaring, but does not satisfy the original radical equation.

Question: Why do extraneous roots appear?

Answer: Suppose we are solving the radical equation \(A=\sqrt{B},\) where \(A\) and \(B\) are both polynomials. Squaring both sides gives \(A^2=B,\) solving which would give solutions to both \(A=\sqrt{B}\) and \(A=-\sqrt{B}.\) The roots that satisfy \(A=-\sqrt{B}\) are not what we were looking for. Therefore we must never forget to check if the roots we obtained satisfy the original radical equation.

However, we will most often encounter radical equations that contain square roots. The way to solve such equations is simple. Just put the square root on one side of the equation and the non-radicals on the other. Then square both sides and we get a polynomial we can solve!

For demonstration we will take the following example and solve it using the above stated steps:

Solve the equation \(\sqrt{x+3}=x+1.\) Step 1: Squaring both sides (which will get rid of the square root) gives \(x+3=x^2+2x+1.\) Step 2: Rearranging terms, we have \[x^2+x-2=(x+2)(x-1)=0 \Rightarrow x=-2 \text{ or } x=1.\] Step 3: Observe that \(x=-2\) is an extraneous root because \[\text{LHS}=\sqrt{(-2)+3}=1 \ne (-2)+1=\text{ RHS}.\] Then since \[\text{LHS}=\sqrt{(1)+3}=2=(1)+1=\text{ RHS},\] the solution to the equation \(\sqrt{x+3}=x+1\) is \(x=1.\) \( _\square \)

Try to solve the following problems using the above steps.

No problem found with slug "real-ly"

\[ \sqrt{x+1} - \sqrt{x-1} = \sqrt{4x-1}, \ \ x = ? \]

This section is dedicated to enhance the problem solving skills through several examples and problems to try.

Solve the equation \(x-2=\sqrt{2x+31}.\) Squaring both sides gives \(x^2-4x+4=2x+31.\) Rearranging terms, we have \[x^2-6x-27=(x+3)(x-9)=0 \Rightarrow x=-3 \text{ or } x=9.\] Observe that \(x=-3\) is an extraneous root because \[\text{LHS}=(-3)-2 = -5 \ne \sqrt{2\cdot (-3)+31}=\text{ RHS}.\] Then since \[\text{LHS}=(9)-2=7= \sqrt{2\cdot (9)+31}=\text{ RHS},\] the solution to the equation \(x-2=\sqrt{2x+31}\) is \(x=9.\) \( _\square \)

Solve the equation \(\sqrt{2x^2+7}+1=2x.\) The equation \(\sqrt{2x^2+7}+1=2x\) is equivalent to \(\sqrt{2x^2+7}=2x-1.\) Squaring both sides gives \(2x^2+7=4x^2-4x+1.\) Rearranging terms, we have \[2x^2-4x-6=2(x^2-2x-3)=2(x+1)(x-3)=0 \Rightarrow x=-1 \text{ or } x=3.\] Observe that \(x=-1\) is an extraneous root since \[\text{LHS}=\sqrt{2\cdot(-1)^2+7}=3 \ne 2\cdot (-1)-1=\text{ RHS}.\] Then since \[\text{LHS}=\sqrt{2\cdot (3)^2+7}=5=2\cdot (3)-1=\text{ RHS},\] the solution to the equation \(\sqrt{2x^2+7}+1=2x\) is \(x=3.\) \( _\square \)

Here are the problems for you try.

Find the only integral value of \(x\) in the equation

\[\sqrt[3]{x-9}+\sqrt[4]{x+8}=7.\]

\[ \dfrac{ \sqrt{3x} + \sqrt{2x+1} }{\sqrt{3x} - \sqrt{2x+1}} = 5 \]

Find the value of \(x\) satisfying the equation above.

\[\] Clarification: For this question, we are working over the complex numbers.

\(\big(\sqrt{x+1}+1\big)\big(\sqrt{x+16}+4\big)-\big(\sqrt{x+4}+2\big)\big(\sqrt{x+9}+3\big)=0\)

How many real value(s) of \(x\) satisfy the above equation?

If \[\Large {\color{blue}{x}}^{\color{blue}{x}}= 2015,\] then which answer is equivalent to \[\Huge \color{blue}{x^{x^{x^x}}}?\]

Find the integer value of \(x\) satisfying the equation below.

\[ \sqrt{10 + \sqrt{x^3 + 100}} = 10 - \sqrt{x^3 + 100} \]

Find the domain of all real numbers \(x\) such that

\[ \sqrt{ x + 6 - 4 \sqrt{ x+2} } + \sqrt{ x+11 - 6 \sqrt{x+2}} = 1. \]

Systems of Equations

Quadratic Equations

Functional Equations

Problem Loading...

Note Loading...

Set Loading...

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Roots and Radicals

Solve Radical Equations

Learning Objectives

By the end of this section, you will be able to:

• Solve radical equations
• Solve radical equations with two radicals
• Use radicals in applications

Before you get started, take this readiness quiz.

In this section we will solve equations that have a variable in the radicand of a radical expression. An equation of this type is called a radical equation .

An equation in which a variable is in the radicand of a radical expression is called a radical equation .

As usual, when solving these equations, what we do to one side of an equation we must do to the other side as well. Once we isolate the radical, our strategy will be to raise both sides of the equation to the power of the index. This will eliminate the radical.

Solving radical equations containing an even index by raising both sides to the power of the index may introduce an algebraic solution that would not be a solution to the original radical equation. Again, we call this an extraneous solution as we did when we solved rational equations.

In the next example, we will see how to solve a radical equation. Our strategy is based on raising a radical with index n to the n th power. This will eliminate the radical.

• Isolate the radical on one side of the equation.
• Raise both sides of the equation to the power of the index.
• Solve the new equation.
• Check the answer in the original equation.

When we use a radical sign, it indicates the principal or positive root. If an equation has a radical with an even index equal to a negative number, that equation will have no solution.

Because the square root is equal to a negative number, the equation has no solution.

If one side of an equation with a square root is a binomial, we use the Product of Binomial Squares Pattern when we square it.

Don’t forget the middle term!

When the index of the radical is 3, we cube both sides to remove the radical.

Sometimes the solution of a radical equation results in two algebraic solutions, but one of them may be an extraneous solution !

When there is a coefficient in front of the radical, we must raise it to the power of the index, too.

Solve Radical Equations with Two Radicals

If the radical equation has two radicals, we start out by isolating one of them. It often works out easiest to isolate the more complicated radical first.

In the next example, when one radical is isolated, the second radical is also isolated.

Sometimes after raising both sides of an equation to a power, we still have a variable inside a radical. When that happens, we repeat Step 1 and Step 2 of our procedure. We isolate the radical and raise both sides of the equation to the power of the index again.

We summarize the steps here. We have adjusted our previous steps to include more than one radical in the equation This procedure will now work for any radical equations.

• Isolate one of the radical terms on one side of the equation.

If yes, repeat Step 1 and Step 2 again.

Use Radicals in Applications

As you progress through your college courses, you’ll encounter formulas that include radicals in many disciplines. We will modify our Problem Solving Strategy for Geometry Applications slightly to give us a plan for solving applications with formulas from any discipline.

• Read the problem and make sure all the words and ideas are understood. When appropriate, draw a figure and label it with the given information.
• Identify what we are looking for.
• Name what we are looking for by choosing a variable to represent it.
• Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
• Solve the equation using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

One application of radicals has to do with the effect of gravity on falling objects. The formula allows us to determine how long it will take a fallen object to hit the gound.

On Earth, if an object is dropped from a height of h feet, the time in seconds it will take to reach the ground is found by using the formula

It would take 2 seconds for an object dropped from a height of 64 feet to reach the ground.

Police officers investigating car accidents measure the length of the skid marks on the pavement. Then they use square roots to determine the speed , in miles per hour, a car was going before applying the brakes.

If the length of the skid marks is d feet, then the speed, s , of the car before the brakes were applied can be found by using the formula

Access these online resources for additional instruction and practice with solving radical equations.

• Solving an Equation Involving a Single Radical
• Solving Equations with Radicals and Rational Exponents
• Solving Radical Equations
• Radical Equation Application

Key Concepts

Practice Makes Perfect

In the following exercises, solve.

no solution

In the following exercises, solve. Round approximations to one decimal place.

Writing Exercises

Answers will vary.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

Intermediate Algebra Copyright © 2017 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Solving Radical Equations: Steps, Definition, Examples

What are radical equations, radical equations definition, how to solve radical equations, solved examples on radical equations, practice problems on radical equations, frequently asked questions about radical equations.

Radical equations are equations in which a variable is under a radical symbol.

Before we explore the concept of radical equations, let’s quickly take a look at the important terminologies that will be helpful.

Radical symbol: The symbol “⎷” that we use to denote square root, cube root, or nth root (like $\sqrt{},\; ^3\sqrt{},\; ^4\sqrt{}$, etc.) is called a “radical symbol.”  

The horizontal line at the top is called the vinculum.

In the radical symbol, $(\sqrt{}$ or $^2\sqrt{}),\; ^3\sqrt{},\; ^4\sqrt{}$, etc., the numbers 2, 3, and 4 written in the little dent represent the “index.”

If the index is not written, it is considered to be 2.

Radical expression: A radical expression is the expression that has an n th root (usually a square root).

Radicand: A number or expression inside the radical symbol.

Important Note: The square root of a number in an exponent form is the number raised to the power of $\frac{1}{2}$.

$\sqrt{x} = x^\frac{1}{2}$

The n th root of x can be written as $^n\sqrt{x} = x^\frac{1}{n}$.

The n th root of xm can be written as $^n\sqrt{x}^m = x^\frac{m}{n}$

Examples: $^3\sqrt{x^2} = (x^2)\frac{1}{3} = x^\frac{2}{3}$

       $^3\sqrt{x^4} = x^\frac{4}{3}$

      $^2\sqrt{x^5} = x^\frac{5}{2}$ etc.

A radical equation is an equation in which a variable is in the radicand of the expression. 

At least one radical sign of a radical equation includes a variable. 

In other words, a radical equation has a variable with a rational exponent. 

Examples of Radical Equations: $\sqrt{a} + 4 = 13,\; \sqrt{x\;-\;1} = 5$ 

Related Worksheets

Solving a radical equation simply means finding the value of the variable. The variable in a radical equation is under the radical sign. Thus, exponent rules and fundamental algebraic principles must be followed in order to solve radical equations. A square root can be eliminated by squaring, and cube roots can be eliminated by cubing, etc. 

Note that the solutions obtained by solving a radical equation must be verified.

The binomial square formulas are extremely useful when solving a radical equation where a binomial term is present on one side of the radical equation.

• $(a + b)^2 = a^2 + 2ab + b^2$
• $(a\;-\;b)^2 = a^2\;-\;2ab + b^2$

Let’s discuss the steps to solving radical equations with two cases.

I. Solving Radical Equation With One Radical

II. Solving Radical Equations with Two Radicals 

Solving Radical Equation with One Radical

Step 1: Isolate the radical symbol on one side of the equation.

Step 2: Eliminate the radical symbol by raising both sides of the equation to the power of the index. If it is a square root, then square both sides; if it is a cube root, cube both sides; and so on.

Step 3: Solve the obtained equation using the following formula:

For $x \gt 0$, we have $(^n\sqrt{x})^n = x$

Step 4: Verify by substituting the answer in the original equation.

(Note: The principal square root of a number can only be positive. A radical sign indicates a positive root. So, an equation will not have a solution if its radical has an even index equal to a negative number.)

Example: Solve $\sqrt{2x + 3} \;-\; 5 = 0$ .

Step 1: Isolate the radical symbol. 

Add 5 on both sides. Use the addition property of equality .

$\sqrt{2x + 3} = 5$

Step 2: Eliminate the radical symbol. 

To eliminate the radicals, square both sides.

$(\sqrt{2x + 3})^2 = 5^2$

$\Rightarrow 2x + 3 = 25$

Step 3: Solve the obtained equation.

$2x = 25\;-\;3 = 22$

$\Rightarrow x = \frac{22}{2} = 11$

Step 4: Verify the answer. 

Substitute $x = 11$ in the given equation, we get

L.H.S. $= \sqrt{2 \times 11 + 3} \;-\; 5 = \sqrt{25} \;-\; 5 = 5 \;-\; 5 = 0 =$ R.H.S.

Hence, $x = 11$ is the solution of the given equation.

Solving Radical Equations with Two Radicals

If there are two in the radical equation, we begin by isolating one of the two radicals. Isolating the more complicated radical first often works best.

Step 1: Isolate one of the radical terms on one side of the equation.

Step 2: Eliminate the radicals by raising both sides of the equation to the power of the index. This means that if it is a square root, then square both sides; if it is a cube root, cube both sides; etc.

Step 3: Solve the obtained equation once the radical signs are eliminated.

Step 4: Verify the answer in the original equation and check whether it is satisfying or not.

Let’s use this concept to solve an example.

Example: Solve $\sqrt{x + 5} \;-\; \sqrt{x} = 2$ .

$\sqrt{x + 5} = 2 + \sqrt{x}$

Step 2: Eliminate the radicals.

$(\sqrt{x+5})^2 = (2 + \sqrt{x})^2$

$\Rightarrow x + 5 = 4 + 4 \sqrt{x} + x$ 

$\Rightarrow 1 = 4 \sqrt{x}$ 

Since a radical is still present in the obtained equation, square both sides again.

$x = \frac{1}{16}$

Substitute x=116 in the given equation, and we get

L.H.S. $\sqrt{\frac{1}{16} + 5} \;-\; \sqrt{\frac{1}{16}} = \sqrt{\frac{81}{16}}\;-\; \sqrt{\frac{1}{16}} = \frac{9}{4}\;-\; \frac{1}{4}=2 =$ R.H.S.

Hence, $x = \frac{1}{16}$ is the solution of the given equation.

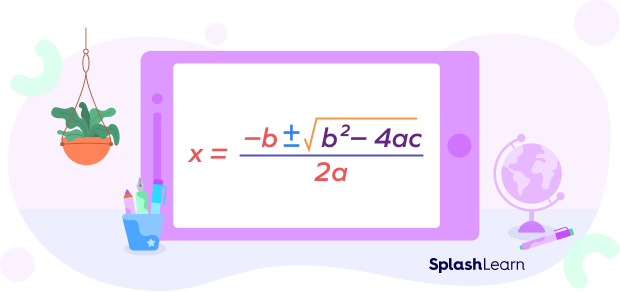
Note: A quadratic equation of the form $ax^2 + bx + c = 0$ obtained in the process of solving a radical equation can also be solved using the quadratic formula .

Facts about Radical Equations

• The modern radical sign, “√” was first introduced by a German mathematician Christoff Rudolff.
• European paper sizes are a good illustration of how a radical is used in the real world. The measurements of an A4-sized sheet of paper are $8.27 \times 11.67$ inches. The ratio of the lengths of the longer and shorter side of an A4 paper is approximately $\sqrt{2}$.
• When you square a radical equation, you sometimes get solutions to the squared equation which may not satisfy the original equation. Such a solution is called an extraneous solution . Thus, if you raise both sides of an equation by some power, then you have to verify your solutions to eliminate the extraneous solutions. 

In this article, we have discussed the radicals, methods, and steps for solving radical equations. Let’s solve a few examples and practice problems.

• Solve $\sqrt{3x^2\;-\;12x} = 6$ .

Given, $\sqrt{3x^2\;-\;12x} =6$

To eliminate the radical sign, square both sides.

$\bigg(\sqrt{3x^2\;-\;12x}\bigg)^2 = 6^2$

$\Rightarrow 3x^2\;-\;12x = 36$

$\Rightarrow 3x^2\;-\;12x\;-\;36 = 0$

$\Rightarrow 3(x^2\;-\;4x\;-\;12) = 0$

$\Rightarrow x^2\;-\;4x\;-\;12 = 0$

$\Rightarrow x^2\;-\;6x + 2x\;-\;12 = 0$

$\Rightarrow x(x\;-\;6) + 2(x\;-\;6) = 0$

$\Rightarrow (x + 2) (x\;-\;6)=0$

$x=\;-\;2,\; 6$

Verification: 

For $x = \;-2$

L.H.S. $\sqrt{3(\;-\;2)^2\;-\;12(\;-\;2)} = \sqrt{12+24} = \sqrt{36} = 6 =$ R.H.S.

For $x = 6$

L.H.S. $= \sqrt{3(6)^2\;-\;12(6)} = \sqrt{108\;-\;72} = \sqrt{36} = 6 =$ R.H.S.

Hence, the solution of the given equation is $x = \;-\;2,\; 6$.

• Solve:  $^3sqrt{x\;-\;1} = 3$ .

$^3\sqrt{x\;-\;1} = 3$

To eliminate the radical, cube both sides.

$(^3\sqrt{x\;-\;1})^3 = 3^3$

$\Rightarrow x\;-\;1 = 27$

For $x = 28$

L.H.S. $= ^3\sqrt{x\;-\;1} = ^3\sqrt{28\;-\;1} = ^3\sqrt{27} = 3 =$ R.H.S.

Hence, the solution of the given equation is $x = 28$.

• Solve $^3\sqrt{2x + 4} + 8 = 4$ .

Given, $^3\sqrt{2x + 4} + 8 = \;-4$

Here, the radical is not isolated, so first isolate the radical on one side.

$^3\sqrt{2x + 4} =\; -4$

To eliminate the radicals, cube both sides.

$(^3\sqrt{2x+4})^3 =(-4)^3$

$\Rightarrow 2x + 4 =\; -64$

$\Rightarrow 2x = \;-64\;-\;4$

$\Rightarrow 2x= \;-68$

$\Rightarrow x = \frac{-68}{2} =\; -34$

Verification:

For $x = \;-34$

L.H.S. $= ^3\sqrt{2(\;-\;34)+4} + 8 = ^3\sqrt{\;-\;68+4} + 8 = ^3\sqrt{\;-\;64} + 8= \;-4 + 8 = 4 =$ R.H.S.

Hence, the solution of the given equation is $x = \;-34$.

• Solve $\sqrt{x\;-\;2} + \sqrt{x\;-\;1} = 1$ .

Given, $\sqrt{x\;-\;2} + \sqrt{x\;-\;1} = 1$

$\sqrt{x \;-\; 2} = 1\;-\; \sqrt{x\;-\;1}$

$(\sqrt{x-2})^2 = (1-\sqrt{x\;-\;1})^2$

$\Rightarrow x\;-\;2 = 1\;-\;2 \sqrt{x\;-\;1} + x\;-\;1$

$\Rightarrow \;-\;2 = \;-\;2\sqrt{x\;-\;1}$

$\Rightarrow 1 = \sqrt{x\;-\;1}$

Squaring both sides again, we get

$1 = x\;-\;1$

For $x = 2$

L.H.S. $= \sqrt{x\;-\;2} + \sqrt{x\;-\;1} = \sqrt{2\;-\;2} + \sqrt{2\;-\;1} = 0 + 1 = 1 =$ R.H.S.

Hence, the solution of the given equation is $x = 2$.

• $\sqrt{x + 4} =x \;-\; 2$

Solution: 

$sqrt{x + 4} = x – 2$

Squaring both sides:

$x + 4 = (x\;-\;2)^2$

$x + 4 = x^2\;-\;4x + 4$

$x^2\;-\;5x = 0$

$x (x\;-\;5) = 0$

$x = 0 ; x = 5$

Put $x = 0$

L.H.S. $= \sqrt{0+4} = \sqrt{4} = 2$ 

R.H.S. $= 0 \;-\; 2 $

L.H.S. $\neq$ R.H.S.

Thus, $x = 0$ is not the solution.

Put $x = 5$

L.H.S. $= \sqrt{5 + 4} = \sqrt{9} = 3$

R.H.S. $= 5\;-\;2 = 3$

L.H.S. $=$ R.H.S.

Thus, $x = 5$ is the solution.

Attend this quiz & Test your knowledge.

The radicand of the expression $7^3\sqrt{9}$ is equal to____.

The index of the radical number $^5\sqrt{4^3}$ is equal to____., solve the radical equation: $\sqrt{x }\;-\;1 = 2$, what is the value of “x” in the radical equation $\sqrt{2x} = 4$ , what is the value of “m” in the radical equation $^3\sqrt{m} = 3$ , the equation $\sqrt{a\;-\;1} = \;-3$ has.

What is the radical equation in math?

An equation in which a variable is under a radical symbol (i.e.,$\sqrt{} ,\;^3\sqrt{},\; ^4\sqrt{}$, etc.) is called a radical equation. For example, $\sqrt{x} + 2 = 4$.

What are the n th root radicals?

The radical symbol $^n\sqrt{x}$,or $x^\frac{1}{n}$ , is called the n th root radical. The index for n th root radicals is n.

What is the formula for simplifying radicals?

The general formula for simplifying radicals is  $^n\sqrt{x}^m = x^\frac{m}{n}$.

What is the use of radicals in real life?

European paper sizes are a good example of how a radical is used in real life. The ratio of the lengths of the longer and shorter sides of A4 paper is approximate $\sqrt{2}$.

What are surds?

If the square root (or the cube root/the n th root) of a number cannot be simplified into a whole number (W) or a rational number (𝕫), we call it a surd. Examples: $\sqrt{2},\; \sqrt{3},\; ^3\sqrt{11}$

RELATED POSTS

• Direct Variation: Definition, Formula, Equation, Examples, FAQs
• Types of Angles – Definition with Examples
• Right Circular Cone – Definition, Properties, Formulas, Examples
• Pythagorean Triples
• Australian Dollar to USD Calculator

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Module 10: Rational and Radical Functions

Applications with radical equations, learning outcomes.

Applications with radical equations

• Solve an application using a formula containing a radical expression

Radical Equations

Radical equations in real-life applications may contain two or more variables. Solving such an equation involves isolating the unknown variable, which may be contained within a radical such as a square or cube root, while substituting known values for the remaining variables.

[latex]S=\sqrt{\dfrac{x}{32}}\qquad \qquad T=2\sqrt{L}\qquad \qquad r=\sqrt{\dfrac{V}{h\pi}}[/latex]

Each of the above equations is an example of a radical equation. Use the examples given in the situations below to practice solving applications involving radical equations.

Kinetic Energy

One way to measure the amount of energy that a moving object (such as a car or roller coaster) possesses is by finding its Kinetic Energy. The Kinetic Energy ([latex]E_{k}[/latex], measured in Joules) of an object depends on the object’s mass ( m , measured in kg) and velocity ( v , measured in meters per second), and can be written as [latex] v=\sqrt{\frac{2{{E}_{k}}}{m}}[/latex].

What is the Kinetic Energy of an object with a mass of [latex]1,000[/latex] kilograms that is traveling at [latex]30[/latex] meters per second?

[latex]\begin{array}{l}E_{k}=\text{unknown}\\\,\,m=1000\\\,\,\,\,v=30\end{array}[/latex]

Substitute values into the formula.

[latex] 30=\sqrt{\frac{2{{E}_{k}}}{1,000}}[/latex]

Solve the radical equation for   E k .

[latex] \begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{\left( 30 \right)}^{2}}={{\left( \sqrt{\frac{2{{E}_{k}}}{1,000}} \right)}^{2}}\\\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,900=\frac{2{{E}_{k}}}{1,000}\\\\900\cdot 1,000=\frac{2{{E}_{k}}}{1,000}\cdot 1,000\\\\\,\,\,\,\,\,\,\,900,000=2{{E}_{k}}\\\\\,\,\,\,\,\,\,\,\frac{900,000}{2}=\frac{2{{E}_{k}}}{2}\\\\\,\,\,\,\,\,\,\,\,\,450,000={{E}_{k}}\end{array}[/latex]

Now check the solution by substituting it into the original equation.

[latex] \begin{array}{l}30=\sqrt{\frac{2\cdot 450,000}{1,000}}\\30=\sqrt{\frac{900,000}{1,000}}\\30=\sqrt{900}\\30=30\end{array}[/latex]

The Kinetic Energy is [latex]450,000[/latex] Joules.

Here is another example of finding the kinetic energy of an object in motion.

Harvester ants found in the southwest of the U.S. create a vast interlocking network of tunnels for their nests. As a result of all this excavation, a very common above-ground hallmark of a harvester ant nest is a conical mound of small gravel or sand  [1]

The radius of  a cone whose height is is equal to twice it’s radius is given as: [latex]r=\sqrt[3]{\frac{3V}{2\pi }}[/latex].

A mound of gravel is in the shape of a cone with the height equal to twice the radius. Calculate the volume of such a mound of gravel whose radius is [latex]3.63[/latex] ft. Use [latex]\pi =3.14[/latex].

The radius of a cone given it’s volume can be found with the following formula: [latex]r=\sqrt[3]{\frac{3V}{2\pi }}[/latex], [latex]r\ge 0[/latex]

Cube both sides to eliminate the cube root.

Therefore, the volume is about 100 cubic feet.

[latex]V\approx{100}\frac{\text{cu}}{ft}[/latex]

Here is another example of finding Volume given the radius of a cone.

When you drop an object from a height, the only force acting on it is gravity (and some air friction) and it is said to be in free-fall. We can use math to describe the height of an object in free fall after a given time because we know how to quantify the force of the earth pulling on us – the force of gravity.

An object dropped from a height of 600 feet has a height, h, in feet after t  seconds have elapsed, such that [latex]h=600 - 16{t}^{2}[/latex]. In our next example we will find the time at which the object is at a given height by first solving for t.

Find the time is takes to reach a height of 400 feet by first finding an expression for t.

We are asked two things.  First, we will solve the height equation for t, then we will find how long it takes for the object’s height above the ground to be 400 feet.

Solve for t:

[latex]\begin{array}{ccc}h=600 - 16{t}^{2}\\h-600=-16t^2\\\frac{h-600}{-16}=t^2\\\pm\sqrt{\frac{h-600}{-16}}=t\end{array}[/latex]

At this point, let’s stop and talk about whether it makes sense to include both [latex]\pm\sqrt{\frac{h-600}{-16}}[/latex].  We want time to be only positive since we are talking about a measurable quantity, so we will restrict our answers to just [latex]+\sqrt{\frac{h-600}{-16}}[/latex]

We want to know at what time the height will be 400 ft., so we can substitute 400 for h.

[latex]\begin{array}{ccc}\sqrt{\frac{400-600}{-16}}=t\\\sqrt{\frac{-200}{-16}}=t\\\sqrt{12.5}=t\\3.54=t\end{array}[/latex]

It takes [latex]3.54[/latex] seconds for the object to be at a height of [latex]400[/latex] ft.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \sqrt{3+x}=-2
• \sqrt{x-1}-x=-7
• \sqrt{x}\sqrt{x-7}=12
• \sqrt{17x-\sqrt{x^2-5}}=7
• (2x-5)^{\frac{1}{3}}=3
• \sqrt{x-3}=3+\sqrt{x}
• How do you solve a radical equation?
• To solve a radical equation, isolate the radical on one side of the equation, raise both sides to a power that will eliminate the radical and solve the equation. Check you answer.
• What is a radical equation?
• A radical equation is an equation that involves a radical of an expression containing a varaible.
• How do I simplify a radical?
• To simplify a radical, factor the number inside the radical and pull out any perfect square factors as a power of the radical.
• How do you multiply two radicals?
• To multiply two radicals, multiply the numbers inside the radicals (the radicands) and leave the radicals unchanged. √a x √b = √(a x b)

radical-equation-calculator

• High School Math Solutions – Radical Equation Calculator Radical equations are equations involving radicals of any order. We will show examples of square roots; higher...

Please add a message.

Message received. Thanks for the feedback.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Solving Harder Radical Equations

Concepts Simple Eqns Harder Eqns Painful Eqns Higher-Index Eqns

Moving on from the simplest radical equations, we encounter equations in which the radical is not isolated. Sometimes, all we'll need to do is move a constant; other times, the solution will get rather messy.

Solve: katex.render("\\boldsymbol{\\color{green}{\\small{ \\sqrt{x\\,} - 2 = 5 }}}", typed01);

I could square both sides of the equation right away, but the radical isn't isolated on the left-hand side (because there's a 2 subtracted from it), so the result of squaring both sides at this stage won't be very helpful.

Here's what I get if I try squaring now:

Content Continues Below

MathHelp.com

Solving Radical Equations

Advertisement

I think I've made things worse! Rather than getting rid of the radical, I now have a radical term, plus a variable term outside of any radical. What now?

While squaring both sides at this point was not "wrong", it arguably wasn't much "right". (To complete the solution, I'd need to isolate the radical term, and then square both sides again.)

Instead of squaring right away, it will be more useful first to move the constant term 2 from the left-hand side of the equation over to the right-hand side. In this way, the radical will be isolated on the left:

I've isolated the square root, so now squaring both sides will work better:

Checking my solution, I find:

The solution checks, so my answer is:

Some radical equations can be simplified by first isolating the radical. But sometimes that won't be possible.

Find the solution: katex.render("\\boldsymbol{\\color{green}{\\small{ \\sqrt{x - 3\\,} - \\sqrt{x\\,} = 3 }}}", typed06);

This equation is a bit more messy than what we've seen before. I cannot isolate the radical because there are actually two radical terms. So how can I solve this algebraically? I'll have to square both sides twice . Here's what that looks like:

(sqrt[ x − 3] − sqrt[ x ]) 2 = (3) 2

( x − 3) − 2×sqrt[ x 2 − 3 x ] + ( x ) = 9

2 x − 12 = 2×sqrt[ x 2 − 3 x ]

x − 6 = sqrt[ x 2 − 3 x ]

At this point, having finishing squaring once, I have managed to get the radical isolated on the right-hand side of the equation. Now I'll square for the second time:

( x − 6) 2 = (sqrt[ x 2 − 3 x ]) 2

x 2 − 12 x + 36 = x 2 − 3 x     ⋆⋆

−9 x + 36 = 0

Checking my solution, I get:

LHS ≠ RHS

Hmm... All that work, and the only solution doesn't work in the original equation? Can that be right? I'll check the graph of the two lines corresponding to the two sides of the original equation to see if there appears to be an intersection point:

y 1 = sqrt[ x − 3] − sqrt[ x ]

According to the graph, no, it does not appear that these lines ever intersect (and calculus techniques can prove this). So my answer is:

no solution

Why did it appear that there was a solution to that equation? Let's look at the graphs after the second squaring of the radicals (starred above, and repeated below):

y 1 = x 2 − 12 x + 36

y 2 = x 2 − 3 x

By squaring (twice, in this case), I had accidentally created a solution that hadn't existed for the original equation. Because I checked that solution in the original equation, I was able to see that the actual answer was that the equation had no solution.

Because these exercises are so lengthy to solve, your book or instructor may not provide many examples. Try not to be misled by the small sample sizes. Yes, the above equation with two radicals had no solution. But, no, this will not always be the case for equations with two radicals.

Find the solution: katex.render("\\boldsymbol{\\color{green}{\\small{ \\sqrt{x - 3\\,} + \\sqrt{x\\,} = 3 }}}", typed30);

This is the same as the previous equation, except that the sign between the radicals has been reversed. If I turn the left-hand and right-hand sides of this equation into their own functions, I get:

Graphing them, I get:

So this equation does have a solution, which appears to be around x  = 4 . To know the answer for sure, I have to do the algebra:

...and here's the check of my solution:

Since the solution works in the original equation, then the solution is valid, and the answer is:

URL: https://www.purplemath.com/modules/solverad3.htm

Page 1 Page 2 Page 3 Page 4 Page 5

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

16.3.1: Solving Radical Equations

• Last updated
• Save as PDF
• Page ID 73009

• The NROC Project

Learning Objectives

• Solve equations containing radicals.
• Recognize extraneous solutions.
• Solve application problems that involve radical equations as part of the solution.

Introduction

An equation that contains a radical expression is called a radical equation . Solving radical equations requires applying the rules of exponents and following some basic algebraic principles. In some cases, it also requires looking out for errors generated by raising unknown quantities to an even power.

Squaring Both Sides

A basic strategy for solving radical equations is to isolate the radical term first, and then raise both sides of the equation to a power to remove the radical. (The reason for using powers will become clear in a moment.) This is the same type of strategy you used to solve other, non-radical equations: rearrange the expression to isolate the variable you want to know, and then solve the resulting equation.

There are two key ideas that you will be using to solve radical equations. The first is that if \(\ a=b\), then \(\ a^{2}=b^{2}\). (This property allows you to square both sides of an equation and remain certain that the two sides are still equal.) The second is that if the square root of any nonnegative number \(\ x\) is squared, then you get \(\ x\): \(\ (\sqrt{x})^{2}=x\). (This property allows you to “remove” the radicals from your equations.)

Let’s start with a radical equation that you can solve in a few steps: \(\ \sqrt{x}-3=5\).

Solve. \(\ \sqrt{x}-3=5\)

\(\ x=64\) is the solution to \(\ \sqrt{x}-3=5\).

To check your solution, you can substitute 64 in for \(\ x\) in the original equation. Does \(\ \sqrt{64}-3=5\)? Yes—the square root of 64 is 8, and \(\ 8-3=5\).

Notice how you combined like terms and then squared both sides of the equation in this problem. This is a standard method for removing a radical from an equation. It is important to isolate a radical on one side of the equation and simplify as much as possible before squaring. The fewer terms there are before squaring, the fewer additional terms will be generated by the process of squaring.

In the example above, only the variable \(\ x\) was underneath the radical. Sometimes you will need to solve an equation that contains multiple terms underneath a radical. Follow the same steps to solve these, but pay attention to a critical point: square both sides of an equation, not individual terms . Watch how the next two problems are solved.

Solve. \(\ \sqrt{x+8}=3\)

\(\ x=1\) is the solution to \(\ \sqrt{x+8}=3\).

Solve. \(\ 1+\sqrt{2 x+3}=6\)

\(\ x=11\) is the solution for \(\ 1+\sqrt{2 x+3}=6\).

Solving Radical Equations

Follow the four steps to solve radical equations.

• Isolate the radical expression.
• Square both sides of the equation: If \(\ x=y\) then \(\ x^{2}=y^{2}\).
• Once the radical is removed, solve for the unknown.
• Check all answers.

Solve. \(\ \sqrt{3 x+22}=4\)

• \(\ x=\frac{16}{3}\)
• Incorrect. Check your answer. If you substitute \(\ x=2\) into the equation, you get \(\ \sqrt{3(2)+22}=4\), or \(\ \sqrt{28}=4\). This is not correct. Remember to square both sides and then solve for \(\ x\). The correct answer is \(\ x=-2\).
• Incorrect. It looks like you squared both sides but ignored the \(\ +22\) underneath the radical. Remember to include the entire binomial when you square both sides; then solve for \(\ x\). The correct answer is \(\ x=-2\).
• Correct. Squaring both sides, you find \(\ (\sqrt{3 x+22})^{2}=(4)^{2}\) becomes \(\ 3 x+22=16\), so \(\ 3 x=-6\) and \(\ x=-2\).
• Incorrect. It looks like you only squared the left side of the equation. Remember to square both sides: \(\ (\sqrt{3 x+22})^{2}=(4)^{2}\), which becomes \(\ 3 x+22=16\). Now solve for \(\ x\). The correct answer is \(\ x=-2\).

Extraneous Solutions

Following rules is important, but so is paying attention to the math in front of you, especially when solving radical equations. Take a look at this next problem that demonstrates a potential pitfall of squaring both sides to remove the radical.

Solve. \(\ \sqrt{a-5}=-2\)

No solution.

The answer \(\ a=9\) does not produce a true statement when substituted back into the original equation. What happened?

Check the original problem: \(\ \sqrt{a-5}=-2\). Notice that the radical is set equal to -2, and recall that the principal square root of a number can only be positive . This means that no value for \(\ a\) will result in a radical expression whose positive square root is -2! You might have noticed that right away and concluded that there were no solutions for \(\ a\). But why did the process of squaring create an answer, \(\ a=9\), that proved to be incorrect?

The answer lies in the process of squaring itself. When you raise a number to an even power, whether it is the second, fourth, or 50 th power, you can introduce a false solution because the result of an even power is always a positive number. Think about it: \(\ 3^{2}\) and \(\ (-3)^{2}\) are both 9, and \(\ 2^{4}\) and \(\ (-2)^{4}\) are both 16. So when you squared -2 and got 4 in this problem, you artificially turned the quantity positive. This is why you were still able to find a value for \(\ a\); you solved the problem as if you were solving \(\ \sqrt{a-5}=2\)! (The correct solution to \(\ \sqrt{a-5}=-2\) is actually “no solution.”)

Incorrect values of the variable, such as those that are introduced as a result of the squaring process are called extraneous solutions . Extraneous solutions may look like the real solution, but you can identify them because they will not create a true statement when substituted back into the original equation. This is one of the reasons why checking your work is so important. If you do not check your answers by substituting them back into the original equation, you may be introducing extraneous solutions into the problem.

Have a look at the following problem. Notice how the original problem is \(\ x+4=\sqrt{x+10}\), but after both sides are squared, it becomes \(\ x^{2}+8 x+16=x+10\). Squaring both sides may have introduced an extraneous solution.

Solve. \(\ x+4=\sqrt{x+10}\)

\(\ x=-1\) is the only solution

It may be difficult to understand why extraneous solutions exist at all. Thinking about extraneous solutions by graphing the equation may help you make sense of what is going on.

You can graph \(\ x+4=\sqrt{x+10}\) on a coordinate plane by breaking it into a system of two equations: \(\ y=x+4\) and \(\ y=\sqrt{x+10}\). The graph is shown below. Notice how the two graphs intersect at one point, when the value of \(\ x\) is -1. This is the value of \(\ x\) that satisfies both equations, so it is the solution to the system.

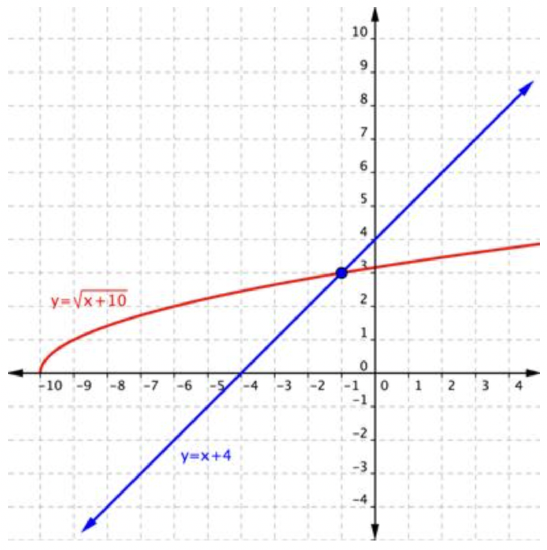
Now, following the work we did in the example problem, let’s square both of the expressions to remove the variable from the radical. Instead of solving the equation \(\ x+4=\sqrt{x+10}\) we are now solving the equation \(\ (x+4)^{2}=(\sqrt{x+10})^{2}\), or \(\ x^{2}+8 x+16=x+10\). The graphs of \(\ y=x^{2}+8 x+16\) and \(\ y=x+10\) are plotted below. Notice how the two graphs intersect at two points, when the values of \(\ x\) are -1 and -6.

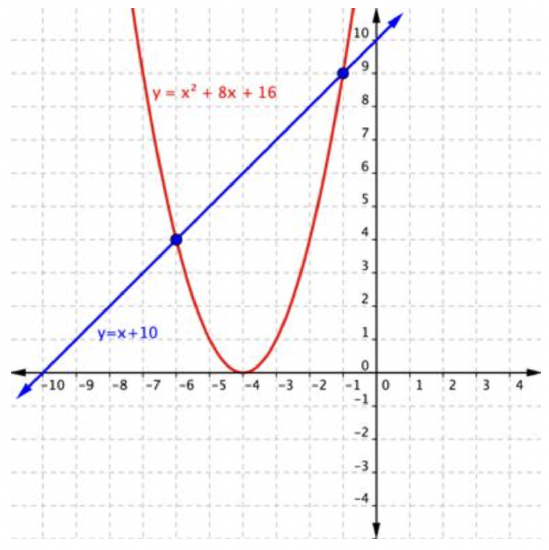
Although \(\ x=-1\) is shown as a solution in both graphs, squaring both sides of the equation had the effect of adding an extraneous solution, \(\ x=-6\). Again, this is why it is so important to check your answers when solving radical equations!

Solve. \(\ 4+\sqrt{x+2}=x\)

\(\ x=7\) is the only solution.

Solve. \(\ x-3=\sqrt{4 x+9}\)

• \(\ x=3,0\)
• \(\ x=0,10\)
• Incorrect. To solve the equation, square both sides and then solve the resulting equation \(\ x^{2}-6 x+9=4 x+9\). The correct answer is: \(\ x=10\).
• Incorrect. You solved the equation \(\ x^{2}-6 x+9=4 x+9\) correctly, but you forgot to evaluate both values for \(\ x\) in the original equation. \(\ x=0\) is an extraneous solution since it doesn't make the original equation true! The correct answer is: \(\ x=10\)
• Incorrect. When you square both sides and then solve the resulting equation, \(\ x^{2}-6 x+9=4 x+9\), you do get \(\ x=0\) as a possible solution. However, \(\ x=0\) is an extraneous solution since it does not make the original equation true! The correct answer is: \(\ x=10\)
• Correct. Solving the equation, you find that squaring both sides results in \(\ x^{2}-6 x+9=4 x+9\), which simplifies to \(\ x^{2}-10 x=0\). Although this equation produces \(\ x\) values of 0 or 10, 0 is extraneous since it does not make the original equation true.

Solving Application Problems with Radical Equations

Radical equations play a significant role in science, engineering, and even music. Sometimes you may need to use what you know about radical equations to solve for different variables in these types of problems.

One way to measure the amount of energy that a moving object (such as a car) possesses is by finding its Kinetic Energy. The Kinetic Energy (\(\ E_{k}\), measured in Joules) of an object depends on the object’s mass (\(\ m\), measured in kg) and velocity (\(\ v\), measured in meters per second) and can be written as \(\ v=\sqrt{\frac{2 E_{k}}{m}}\).

What is the Kinetic Energy of an object with a mass of 1,000 kilograms that is traveling at 30 meters per second?

The Kinetic Energy is 450,000 Joules.

A common method for solving radical equations is to raise both sides of an equation to whatever power will eliminate the radical sign from the equation. But be careful: when both sides of an equation are raised to an even power, the possibility exists that extraneous solutions will be introduced. When solving a radical equation, it is important to always check your answer by substituting the value back into the original equation. If you get a true statement, then that value is a solution; if you get a false statement, then that value is not a solution.