homework 9 standard form of a circle

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

Standard Form of a Circle

The equation of a circle is written using the radius and center of the circle.

The equation of the circle is shown with the center and radius of the circle. With this information, we can sketch the graph of the circle.

Related Topics

• How to Find the Area and Circumference of Circles
• How to Find the Center and the Radius of Circles

Step by Step Guide to Write the Standard Form of a Circle

• The Standard form of a circle is \((x- h)^2+( y-k)^2= r^2\), where \(r\) is the radius and \((h, k)\) is the center. By knowing the center and radius of the circle we can write the standard form of a circle.

Standard form of a Circle – Example 1:

Write the standard form equation of circle with center: \((0, 5)\) , radius: \(3\)

The Standard form of a circle is \((x- h)^2+( y-k)^2= r^2\), where \(r\) is the radius and \((h, k)\) is the center.

In this case, the center is \((0, 5)\) and the radius is \(3\) : \((h, k)=(0, 5), r=3\)

Then: \((x- 0)^2+( y-5)^2= 3^2 → x^2+( y-5)^2= 9 \)

Standard form of a Circle – Example 2:

Write the standard form equation of the circle \(x^2+y^2-6x+2y= 6\).

Group \(x\)-variables and \(y\)-variables together: \((x^2-6x)+( y^2+2y)= 6\)

Convert \(x\) to square form: \((x^2-6x+9)+( y^2+2y)= 6+9 → (x-3)^2+( y^2+2y)=6+9\)

Convert \(y\) to square form: \((x-3)^2+( y^2+2y+1)= 6+9+1 → (x-3)^2+(y+1)^2=6+9+1\)

Then: \((x-3)^2+(y+1)^2=4^2\)

Exercises for Writing Standard form of a Circle

Write the standard form equation of each circle with the given information..

• \(\color{blue}{Center: (0, 4)}, \color{blue}{Radius: 2}\)
• \(\color{blue}{Center: (-1, 2)}\), \(\color{blue}{Radius: 5}\)
• \(\color{blue}{x^2+y^2-6x+8y=0}\)
• \(\color{blue}{x^2+y^2-2x+8y=0}\)
• \(\color{blue}{x^2+(y-4)^2=2^2}\)
• \(\color{blue}{(x+1)^2+(y-2)^2=5^2}\)
• \(\color{blue}{(x-5)^2+y^2=4^2}\)
• \(\color{blue}{(x-1)^2+(y+4)^2=5^2}\)

by: Effortless Math Team about 2 years ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

• Best Blue Light Glasses for Teachers and Students
• Top 10 TSI Math Test-taking Tips
• How to Solve Word Problems: Guessing and Checking
• How to Define Limits Analytically Using Correct Notation?
• DAT Quantitative Reasoning Math FREE Sample Practice Questions
• How to Evaluate Two Variables? (+FREE Worksheet!)
• Function Values of Special Angles
• Full-Length 8th Grade Common Core Math Practice Test
• Linear, Quadratic, and Exponential Models
• Top 10 Math Books for Grade 4: Empowering Young Minds to Discover Numbers

What people say about "Standard Form of a Circle - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

10 Full Length PSSA Grade 7 Math Practice Tests The Practice You Need to Ace the PSSA Grade 7 Math Test

Ged math workbook comprehensive math practices and solutions the ultimate test prep book with two full-length practice tests, calculus for beginners the ultimate step by step guide to acing calculus, statistics for beginners the ultimate step by step guide to acing statistics, ged math test prep in 30 days complete study guide and test tutor for ged mathematics. the ultimate book for beginners and pros + two practice tests, 10 full length gre math practice tests the practice you need to ace the gre math test, basic mathematics for beginners the ultimate step by step guide and a comprehensive basic math refresher, gre math for beginners the ultimate step by step guide to preparing for the gre math test, a comprehensive math workbook for grade 2, ged math made easy study guide to ace your test with key points, examples, and practices, the ultimate high school math bundle from algebra i to pre-calculus, the ultimate middle school math bundle grades 6-8, the ultimate elementary school math bundle grade 3-5, ap pre-calculus for beginners the ultimate step by step guide to acing ap precalculus, grade 7 pre-algebra the ultimate step by step guide to acing 7th grade math.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos
• Google Play
• Apple Store

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Standard Form of a Circle

Instructions: Use this calculator to compute the standard form of the circle, showing all the steps. Please type in the radius of the circle as well as the coordinates of the center in the form below.

More on the standard form equation of a circle

This calculator will allow you to calculate the standard form of the equation of the circle, showing all the steps. You need to provide a valid expression for the radius and the coordinates of the center. They can be any valid expression, with the only restriction that the radius must be positive.

Once valid data are provided, you need to click on the "Calculate" button, and all the steps of the process will be shown to you on how the circle is put in standard form.

In general terms, computing the standard form is fairly straightforward when you know the radius and the center, as we will see in the following sections.

What is the standard form of a circle?

As it happens frequently in math, commonly used math objects can be expressed in different ways. For example, for lines we have the standard form of the line and the slope-intercept form . For circles, something similar happens. A circle is in standard form if it is expressed in the following form:

In this case, we know that \(r\) is the radius of the circle and \((x_0, y_0)\) is the center of the circle.

What are the steps for finding the standard form of the circle?

• Step 1: Identify what information you have available. The process will depend on whether you have the radius and center, or whether you have an equation in general form
• Step 2: If you have the radius r and the center, all you need to do is plug them in to the the equation: \(\displaystyle (x-x_0)^2 + (y-y_0)^2 = r^2\)
• Step 3: If you have a general equation of the circle, you reach the standard form by conducting a completing the square process , for both variables x and y

Then, you will proceed to compute the circle equation subject to the kind of information you have available. Most commonly you will have a radius and a center provided, and this is the easier case. But it is not uncommon to need to complete squares from a general equation.

Difficulties in finding the standard equation of a circle

Like we mentioned before, the easy case is when the radius and the center are provided, but that is not always the case, as often times you will start with a general quadratic equation and will need to complete the squares to get to the standard equation of the circle.

How to go to general to standard form for a circle?

• Step 1: You need to conduct a completing the squares process for each of the variables x and y. Start by grouping together terms with x and terms with y
• Step 2: For each variable, say x, you identify which terms goes with x^2, and factor it out
• Step 3: Force create a term like 2*"something"*x, and the add and subtract "something" you found

For more details, check this completing the squares calculator .

Why would care about the standard form of a circle?

The standard form will tell you all you need to know about a circle, because you can visually see, directly from the equation what the radius is and what the center is.

This is unlike the case of the expanded equation of a circle , where at first sight, you cannot tell anything about the radius or center.

Example: Calculating the standard form equation of a circle

Obtained the standard equation of a circle given that its radius is r = 3/4, and it is centered at (2, 1).

Solution: We need to find the standard form of a circle, where the provided radius is \(r = \displaystyle \frac{3}{4}\), and the center that has been provided is \((\displaystyle 2, 1)\).

The equation of the circle in standard form has the following structure:

where \(x_0\) and \(y_0\) are the corresponding x and y coordinates of the center, and \(r\) is the radius. Therefore, all we need to do in order to fully determine the standard form of the circle is to clearly identify the center and radius, and plug them into the above formula.

In this case, from the information provided we already know that \(x_0 = \displaystyle 2\) and \(y_0 = \displaystyle 1\), and \(r = \frac{3}{4}\). Plugging this in we obtain:

This concludes the calculation. We have found that the equation of the circle in standard form is \(\displaystyle \left(x-2\right)^2+\left(y-1\right)^2=\frac{9}{16} \)

Example: Standard form equation of a circle calculation

Assume that a circle is centered at the origin, and its radius is 5/4. Find the standard form of its equation

Solution: We need to find the standard form of a circle, where the provided radius is \(r = \displaystyle \frac{5}{4}\), and the center that has been provided is \((\displaystyle 0, 0)\).

In this case, from the information provided we already know that \(x_0 = \displaystyle 0\) and \(y_0 = \displaystyle 0\), and \(r = \frac{5}{4}\). Plugging this in we obtain:

This concludes the calculation. We have found that the equation of the circle in standard form is \(\displaystyle x^2+y^2=\frac{25}{16} \)

More circle calculators

Circles represent one of the key elements in Algebra, but it goes way beyond that. Circles and their symmetry contribute to most fields in science.

We know a lot about circles, we know how to compute their areas and circumference , and we know how to deal with angles and angle conversions , as well as dealing with areas of sectors and their interpretation.

Related Calculators

log in to your account

Reset password.

Chapter 1: Functions and Relations

Section 1.2: circles, learning outcomes.

• Write the equation of a circle in standard form
• Graph a circle

DEFINITION OF A CIRCLE

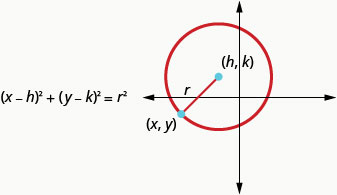
A circle is all points in a plane that are a fixed distance from a given point in the plane.  The given point is called the center, [latex](h,k)[/latex], and the fixed distance is called the radius , [latex]r[/latex], of the circle.

DERIVING THE STANDARD FORM OF A CIRCLE

To derive the equation of a circle, we can use the distance formula with the points [latex](h,k)[/latex], [latex](x,y)[/latex], and the distance [latex]r[/latex].

Substitute the values.

Square both sides.

STANDARD FORM OF A CIRCLE

The standard form of a circle is as follows:

[latex]{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}=r^{2}[/latex]

Write the Equation of a Circle in Standard Form

Example 1: write the standard form equation of a circle.

Write the standard form of a circle with radius [latex]3[/latex] and center [latex](0,0)[/latex].

Use the standard form of a circle.

Substitute in the values [latex]r=3, h=0, k=0[/latex].

  [latex]{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}=3^{2}[/latex]

[latex]{x}^{2}+{y}^{2}=9[/latex]

Example 2: WRITE THE STANDARD FORM equation OF A CIRCLE

Write the standard form of a circle with radius [latex]2[/latex] and center [latex](-1,3)[/latex].

Substitute in the values [latex]r=2, h=-1, k=3[/latex].

  [latex]{\left(x-(-1)\right)}^{2}+{\left(y-3\right)}^{2}=2^{2}[/latex]

[latex]{\left(x+1\right)}^{2}+{\left(y-3\right)}^{2}=4[/latex]

Example 3: finding the center and radius

Find the center and radius, then graph the circle: [latex]{\left(x+2\right)}^{2}+{\left(y-1\right)}^{2}=9[/latex].

Identify the center [latex](h,k)[/latex], and radius [latex]r[/latex].

  [latex]{\left(x-(-2)\right)}^{2}+{\left(y-1\right)}^{2}=3^{2}[/latex]

The center is [latex](-2,1)[/latex], and the radius is [latex]3[/latex].

Now graph the circle.  Plot the center first and then go up, down, left, and right 2 places.

Example 4: finding the center and radius

Find the center and radius, then graph the circle: [latex]{4x}^{2}+{4y}^{2}=64[/latex].

Divide each side by 4.

[latex]{x}^{2}+{y}^{2}=16[/latex]

  [latex]{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}=4^{2}[/latex]

The center is [latex](0,0)[/latex], and the radius is [latex]4[/latex].

Now graph the circle.  Plot the center first and then go up, down, left, and right 4 places.

GENERAL FORM OF A CIRCLE

The general form of a circle is as follows:

[latex]{x}^{2}+{y}^{2}+ax+by+c=0[/latex]

Example 5: WRITE THE STANDARD FORM Equation OF A CIRCLE

Find the center and radius, then graph: [latex]{x}^{2}+{y}^{2}-4x-6y+4=0[/latex].

We need to rewrite this general form into standard form in order to find the center and radius.

[latex]{x}^{2}+{y}^{2}-4x-6y+4=0[/latex]

Group the x-terms and y-terms.  Collect the constants on the right right side.

  [latex]{x}^{2}-4x+{y}^{2}-6y=-4[/latex]

Complete the squares.

[latex]{x}^{2}-4x+4+{y}^{2}-6y+9=-4+4+9[/latex]

Rewrite as binomial squares.

[latex]{\left(x-2\right)}^{2}+{\left(y-3\right)}^{2}=9[/latex]

The center is [latex](2,3)[/latex], and the radius is [latex]3[/latex].

Now graph the circle.  Plot the center first and then go up, down, left, and right 3 places.

Example 6: WRITE THE STANDARD FORM Equation OF A CIRCLE

Find the center and radius, then graph: [latex]{x}^{2}+{y}^{2}+8y=0[/latex].

[latex]{x}^{2}+{y}^{2}+8y=0[/latex]

Group the x-terms and y-terms.

  [latex]{x}^{2}+{y}^{2}+8y=0[/latex]

[latex]{x}^{2}+{y}^{2}+8y+16=0+16[/latex]

[latex]{\left(x-0\right)}^{2}+{\left(y+4\right)}^{2}=16[/latex]

The center is [latex](0,-4)[/latex], and the radius is [latex]4[/latex].

Example 7: APPLYING THE DISTANCE AND MIDPOINT FORMULAS TO A CIRCLE EQUATION

The diameter of a circle has endpoints [latex](-1,-4)[/latex] and [latex](7,2)[/latex]. Find the center and radius of the circle and also write its standard form equation.

The center of a circle is the center, or midpoint, of its diameter.  Thus the midpoint formula will yield the center point.

[latex]M=\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2}\right)[/latex]

  [latex]=\left(\frac{-1+7}{2},\frac{-4+2}{2}\right)[/latex]

[latex]=\left(\frac{6}{2},\frac{-2}{2}\right)[/latex]

[latex]=(3,-1)[/latex]

The center is [latex](3,-1)[/latex].  The distance formula will be used to find the distance from the center to one of the points on the circle.  This will yield the radius:

[latex]d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}[/latex]

[latex]d=\sqrt{(7-3)^{2}+(2-(-1))^{2}}[/latex]

[latex]d=\sqrt{4^{2}+3^{2}}=5[/latex]

The distance from the center to a point on the circle is 5.  Therefore the radius is 5.  The center and radius can now be used to find the standard form of the circle:

Start with the standard form of a circle.

Substitute in the values [latex]r=5, h=3, k=-1[/latex].

  [latex]{\left(x-3\right)}^{2}+{\left(y-(-1)\right)}^{2}=5^{2}[/latex]

[latex]{\left(x-3\right)}^{2}+{\left(y+1\right)}^{2}=25[/latex]

Example 8: Finding the Center of a Circle

The diameter of a circle has endpoints [latex]\left(-1,-4\right)[/latex] and [latex]\left(5,-4\right)[/latex]. Find the center of the circle.

The center of a circle is the center or midpoint of its diameter. Thus, the midpoint formula will yield the center point.

Key Concepts

• A circle is all points in a plane that are a fixed distance from a given point on the plane.  The given point is called the center, and the fixed distance is called the radius.
• The standard form of the equation of a circle with center [latex](h,k)[/latex] and radius [latex]r[/latex] is [latex]{\left(x-h\right)}^{2}{+}{\left(y-k\right)}^{2}=r^{2}[/latex]

Section 1.2 Homework Exercises

For the following exercises, write the standard form of the equation of the circle with the given radius and center [latex](0,0)[/latex].

1. Radius: [latex]7[/latex]

2. Radius: [latex]9[/latex]

3. Radius: [latex]\sqrt{2}[/latex]

4. Radius: [latex]\sqrt{5}[/latex]

In the following exercises, write the standard form of the equation of the circle with the given radius and center.

5. Radius: [latex]1[/latex], center: [latex](3,5)[/latex]

6. Radius: [latex]10[/latex], center: [latex](-2,6)[/latex]

7. Radius: [latex]2.5[/latex], center: [latex](1.5,-3.5)[/latex]

8. Radius: [latex]1.5[/latex], center: [latex](-5.5,-6.5)[/latex]

For the following exercises, write the standard form of the equation of the circle with the given center and point on the circle.

9. Center: [latex](3,-2)[/latex] with point [latex](3,6)[/latex]

10. Center: [latex](6,-6)[/latex] with point [latex](2,-3)[/latex]

11. Center: [latex](4,4)[/latex] with point [latex](2,2)[/latex]

12. Center: [latex](-5,6)[/latex] with point [latex](-2,3)[/latex]

In the following exercises, find the center and radius and then graph each circle.

13. [latex]{\left(x+5\right)}^{2}+{\left(y+3\right)}^{2}=1[/latex]

14. [latex]{\left(x-2\right)}^{2}+{\left(y-3\right)}^{2}=9[/latex]

15. [latex]{\left(x-4\right)}^{2}+{\left(y+2\right)}^{2}=16[/latex]

16. [latex]{\left(x+2\right)}^{2}+{\left(y-5\right)}^{2}=4[/latex]

17. [latex]x^{2}+{\left(y+2\right)}^{2}=25[/latex]

18. [latex]{\left(x-1\right)}^{2}+{y}^{2}=36[/latex]

19. [latex]{\left(x-1.5\right)}^{2}+{\left(y-2.5\right)}^{2}=0.25[/latex]

20. [latex]{\left(x-1\right)}^{2}+{\left(y-3\right)}^{2}=\frac{9}{4}[/latex]

21. [latex]x^{2}+y^{2}=64[/latex]

22. [latex]x^{2}+y^{2}=49[/latex]

23. [latex]2x^{2}+2y^{2}=8[/latex]

24. [latex]6x^{2}+6y^{2}=216[/latex]

In the following exercises, identify the center and radius and graph.

25. [latex]x^{2}+y^{2}+2x+6y+9=0[/latex]

26. [latex]x^{2}+y^{2}-6x-8y=0[/latex]

27. [latex]x^{2}+y^{2}-4x+10y-7=0[/latex]

28. [latex]x^{2}+y^{2}+12x-14y+21=0[/latex]

29. [latex]x^{2}+y^{2}+6y+5=0[/latex]

30. [latex]x^{2}+y^{2}-10y=0[/latex]

31. [latex]x^{2}+y^{2}+4x=0[/latex]

32. [latex]x^{2}+y^{2}-14x+13=0[/latex]

33. Explain the relationship between the distance formula and the equation of a circle.

34. In your own words, state the definition of a circle.

35. In your own words, explain the steps you would take to change the general form of the equation of a circle to the standard form.

Equation of a Circle

Learn about the equation of a circle., equation of a circle lesson, common forms of a circle's equation.

Let's take a look together through three common forms of a circle's equation ( standard form , general form , and polar coordinates ), so we can become more comfortable working with circles in algebra.

Standard Form for the Equation of a Circle

The standard form equation of a circle is given as:

(x - a) 2 + (y - b) 2 = r 2

Where a is x-coordinate of the circle's center, b is the y-coordinate of the circle's center, and r is the radius of the circle.

Let's look at a circle defined by the equation (x - 1) 2 + (y - 2) 2 = 25. The center of this circle is located at the point (1, 2) since a = 1 and b = 2. The circle's radius is 5 since r 2 = 25 and r = 5.

General Form for the Equation of a Circle

The general form equation of a circle is given as:

x 2 + y 2 + Ax + By + C = 0

Where A , B , and C are constants.

The general form equation is not formatted to give us a quick glimpse of circle location and radius like the standard form equation is. However, general form can be converted to standard form by using the algebraic process known as completing the square .

Polar Coordinates Equation of a Circle

The standard form and general form of a circle's equation are expressed in the Cartesian coordinate system. When dealing with circles, using the polar coordinate system is simpler than the Cartesian coordinate system.

In polar coordinates, the equation of a circle centered over the origin is:

r = radius of the circle

If the circle is not centered over the origin but lies on the x-axis, the equation is:

Where a is the x-coordinate of the circle's center.

If the circle is not centered over the origin but lies on the y-axis, the equation is:

Where b is the y-coordinate of the circle's center.

Learning math has never been easier. Get unlimited access to more than 168 personalized lessons and 73 interactive calculators. Join Voovers+ Today 100% risk free. Cancel anytime.

Insert/edit link

Enter the destination URL

Or link to existing content

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.2: Distance and Midpoint Formulas and Circles

• Last updated
• Save as PDF
• Page ID 5188

Learning Objectives

By the end of this section, you will be able to:

Use the Distance Formula

Use the midpoint formula.

• Write the equation of a circle in standard form
• Graph a circle

Before you get started, take this readiness quiz.

• Find the length of the hypotenuse of a right triangle whose legs are \(12\) and \(16\) inches. If you missed this problem, review Example 2.34.
• Factor: \(x^{2}-18 x+81\). If you missed this problem, review Example 6.24.
• Solve by completing the square: \(x^{2}-12 x-12=0\). If you missed this problem, review Example 9.22.

In this chapter we will be looking at the conic sections, usually called the conics, and their properties. The conics are curves that result from a plane intersecting a double cone—two cones placed point-to-point. Each half of a double cone is called a nappe.

There are four conics—the circle , parabola , ellipse , and hyperbola . The next figure shows how the plane intersecting the double cone results in each curve.

Each of the curves has many applications that affect your daily life, from your cell phone to acoustics and navigation systems. In this section we will look at the properties of a circle.

We have used the Pythagorean Theorem to find the lengths of the sides of a right triangle. Here we will use this theorem again to find distances on the rectangular coordinate system. By finding distance on the rectangular coordinate system, we can make a connection between the geometry of a conic and algebra—which opens up a world of opportunities for application.

Our first step is to develop a formula to find distances between points on the rectangular coordinate system. We will plot the points and create a right triangle much as we did when we found slope in Graphs and Functions. We then take it one step further and use the Pythagorean Theorem to find the length of the hypotenuse of the triangle—which is the distance between the points.

Example \(\PageIndex{1}\)

Use the rectangular coordinate system to find the distance between the points \((6,4)\) and \((2,1)\).

Exercise \(\PageIndex{1}\)

Use the rectangular coordinate system to find the distance between the points \((6,1)\) and \((2,-2)\).

Exercise \(\PageIndex{2}\)

Use the rectangular coordinate system to find the distance between the points \((5,3)\) and \((-3,-3)\).

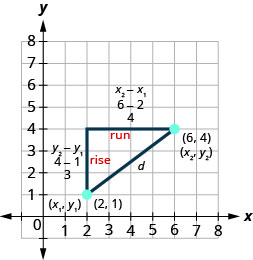
The method we used in the last example leads us to the formula to find the distance between the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\).

When we found the length of the horizontal leg we subtracted \(6−2\) which is \(x_{2}-x_{1}\).

When we found the length of the vertical leg we subtracted \(4−1\) which is \(y_{2}-y_{1}\).

If the triangle had been in a different position, we may have subtracted \(x_{1}-x_{2}\) or \(y_{1}-y_{2}\). The expressions \(x_{2}-x_{1}\) and \(x_{1}-x_{2}\) vary only in the sign of the resulting number. To get the positive value-since distance is positive- we can use absolute value. So to generalize we will say \(\left|x_{2}-x_{1}\right|\) and \(\left|y_{2}-y_{1}\right|\).

In the Pythagorean Theorem, we substitute the general expressions \(\left|x_{2}-x_{1}\right|\) and \(\left|y_{2}-y_{1}\right|\) rather than the numbers.

\(\begin{array}{l c}{} & {a^{2}+b^{2}=c^{2}} \\ {\text {Substitute in the values. }}&{(|x_{2}-x_{1}|)^{2}+(|y_{2}-y_{1}|)^{2}=d^{2}} \\ {\text{Squaring the expressions makes}}&{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}} \\ \text{them positive, so we eliminate} \\\text{the absolute value bars.}\\ {\text{Use the Square Root Property.}}&{d=\pm\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\ {\text{Distance is positive, so eliminate}}&{d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\\text{the negative value.}\end{array}\)

This is the Distance Formula we use to find the distance \(d\) between the two points \((x_{1},y_{1})\) and \((x_{2}, y_{2})\).

Definition \(\PageIndex{1}\)

Distance Formula

The distance \(d\) between the two points \((x_{1},y_{1})\) and \((x_{2}, y_{2})\) is

\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Example \(\PageIndex{2}\)

Use the Distance Formula to find the distance between the points \((-5,-3)\) and \((7,2)\).

Write the Distance Formula.

Label the points, \(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-3}\end{array}\right)\), \(\left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) and substitute.

\(d=\sqrt{(7-(-5))^{2}+(2-(-3))^{2}}\)

\(d=\sqrt{12^{2}+5^{2}}\) \(d=\sqrt{144+25}\) \(d=\sqrt{169}\) \(d=13\)

Exercise \(\PageIndex{3}\)

Use the Distance Formula to find the distance between the points \((-4,-5)\) and \((5,7)\).

Exercise \(\PageIndex{4}\)

Use the Distance Formula to find the distance between the points \((-2,-5)\) and \((-14,-10)\).

Example \(\PageIndex{3}\)

Use the Distance Formula to find the distance between the points \((10,−4)\) and \((−1,5)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

Label the points, \(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {10,-4}\end{array}\right)\), \(\left( \begin{array}{c}{x_{2}, y_{2}} \\ {-1,5}\end{array}\right)\) and substitute.

\(d=\sqrt{(-1-10)^{2}+(5-(-4))^{2}}\)

\(d=\sqrt{(-11)^{2}+9^{2}}\) \(d=\sqrt{121+81}\) \(d=\sqrt{202}\)

Since \(202\) is not a perfect square, we can leave the answer in exact form or find a decimal approximation.

\(d=\sqrt{202}\) or \(d \approx 14.2\)

Exercise \(\PageIndex{5}\)

Use the Distance Formula to find the distance between the points \((−4,−5)\) and \((3,4)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

\(d=\sqrt{130}, d \approx 11.4\)

Exercise \(\PageIndex{6}\)

Use the Distance Formula to find the distance between the points \((−2,−5)\) and \((−3,−4)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

\(d=\sqrt{2}, d \approx 1.4\)

It is often useful to be able to find the midpoint of a segment. For example, if you have the endpoints of the diameter of a circle, you may want to find the center of the circle which is the midpoint of the diameter. To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints.

Definition \(\PageIndex{2}\)

Midpoint Formula

The midpoint of the line segment whose endpoints are the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is

\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints.

Example \(\PageIndex{4}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−5,−4)\) and \((7,2)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

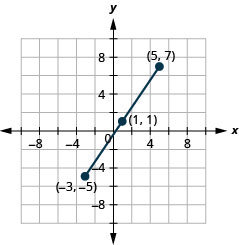
Exercise \(\PageIndex{7}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−3,−5)\) and \((5,7)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

Exercise \(\PageIndex{8}\)

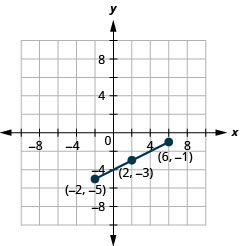
Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−2,−5)\) and \((6,−1)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

Both the Distance Formula and the Midpoint Formula depend on two points, \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\). It is easy to confuse which formula requires addition and which subtraction of the coordinates. If we remember where the formulas come from, is may be easier to remember the formulas.

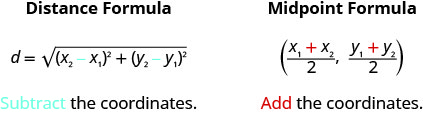
Write the Equation of a Circle in Standard Form

As we mentioned, our goal is to connect the geometry of a conic with algebra. By using the coordinate plane, we are able to do this easily.

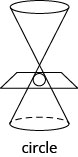
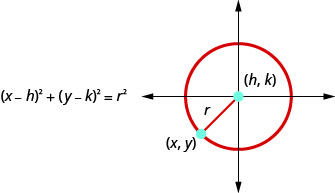
We define a circle as all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius , \(r\), of the circle.

Definition \(\PageIndex{3}\)

A circle is all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center , \((h,k)\), and the fixed distance is called the radius , \(r\), of the circle.

This is the standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\).

Definition \(\PageIndex{4}\)

The standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\), is

Example \(\PageIndex{5}\)

Write the standard form of the equation of the circle with radius \(3\) and center \((0,0)\).

Exercise \(\PageIndex{9}\)

Write the standard form of the equation of the circle with a radius of \(6\) and center \((0,0)\).

\(x^{2}+y^{2}=36\)

Exercise \(\PageIndex{10}\)

Write the standard form of the equation of the circle with a radius of \(8\) and center \((0,0)\).

\(x^{2}+y^{2}=64\)

In the last example, the center was \((0,0)\). Notice what happened to the equation. Whenever the center is \((0,0)\), the standard form becomes \(x^{2}+y^{2}=r^{2}\).

Example \(\PageIndex{6}\)

Write the standard form of the equation of the circle with radius \(2\) and center \((−1,3)\).

Exercise \(\PageIndex{11}\)

Write the standard form of the equation of the circle with a radius of \(7\) and center \((2,−4)\).

\((x-2)^{2}+(y+4)^{2}=49\)

Exercise \(\PageIndex{12}\)

Write the standard form of the equation of the circle with a radius of \(9\) and center \((−3,−5)\).

\((x+3)^{2}+(y+5)^{2}=81\)

In the next example, the radius is not given. To calculate the radius, we use the Distance Formula with the two given points.

Example \(\PageIndex{7}\)

Write the standard form of the equation of the circle with center \((2,4)\) that also contains the point \((−2,1)\).

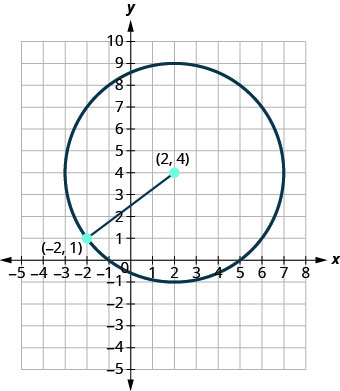
The radius is the distance from the center to any point on the circle so we can use the distance formula to calculate it. We will use the center \((2,4)\) and point \((−2,1)\)

Use the Distance Formula to find the radius.

\(r=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Substitute the values. \(\left( \begin{array}{l}{x_{1}, y_{1}} \\ {2,4}\end{array}\right), \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-2,1}\end{array}\right)\)

\(r=\sqrt{(-2-2)^{2}+(1-4)^{2}}\)

\(r=\sqrt{(-4)^{2}+(-3)^{2}}\) \(r=\sqrt{16+9}\) \(r=\sqrt{25}\) \(r=5\)

Now that we know the radius, \(r=5\), and the center, \((2,4)\), we can use the standard form of the equation of a circle to find the equation.

Use the standard form of the equation of a circle.

\((x-h)^{2}+(y-k)^{2}=r^{2}\)

Substitute in the values.

\((x-2)^{2}+(y-4)^{2}=5^{2}\)

\((x-2)^{2}+(y-4)^{2}=25\)

Exercise \(\PageIndex{13}\)

Write the standard form of the equation of the circle with center \((2,1)\) that also contains the point \((−2,−2)\).

\((x-2)^{2}+(y-1)^{2}=25\)

Exercise \(\PageIndex{14}\)

Write the standard form of the equation of the circle with center \((7,1)\) that also contains the point \((−1,−5)\).

\((x-7)^{2}+(y-1)^{2}=100\)

Graph a Circle

Any equation of the form \((x-h)^{2}+(y-k)^{2}=r^{2}\) is the standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\) . We can then graph the circle on a rectangular coordinate system.

Note that the standard form calls for subtraction from \(x\) and \(y\). In the next example, the equation has \(x+2\), so we need to rewrite the addition as subtraction of a negative.

Example \(\PageIndex{8}\)

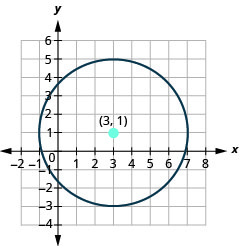
Find the center and radius, then graph the circle: \((x+2)^{2}+(y-1)^{2}=9\).

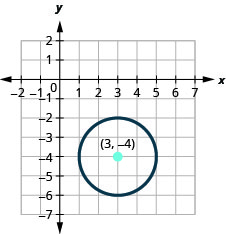
Exercise \(\PageIndex{15}\)

• Find the center and radius, then
• Graph the circle: \((x-3)^{2}+(y+4)^{2}=4\).
• The circle is centered at \((3,-4)\) with a radius of \(2\).

Exercise \(\PageIndex{16}\)

• Graph the circle: \((x-3)^{2}+(y-1)^{2}=16\).
• The circle is centered at \((3,1)\) with a radius of \(4\).

To find the center and radius, we must write the equation in standard form. In the next example, we must first get the coefficient of \(x^{2}, y^{2}\) to be one.

Example \(\PageIndex{9}\)

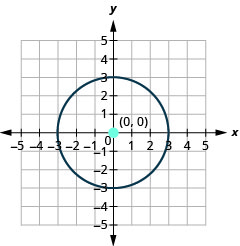
Find the center and radius and then graph the circle, \(4 x^{2}+4 y^{2}=64\).

Exercise \(\PageIndex{17}\)

• Graph the circle: \(3 x^{2}+3 y^{2}=27\)
• The circle is centered at \((0,0)\) with a radius of \(3\).

Exercise \(\PageIndex{18}\)

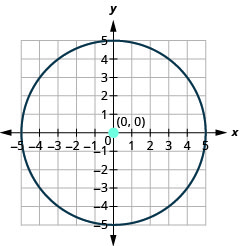
• Graph the circle: \(5 x^{2}+5 y^{2}=125\)
• The circle is centered at \((0,0)\) with a radius of \(5\).

If we expand the equation from Example 11.1.8, \((x+2)^{2}+(y-1)^{2}=9\), the equation of the circle looks very different.

\((x+2)^{2}+(y-1)^{2}=9\)

Square the binomials.

\(x^{2}+4 x+4+y^{2}-2 y+1=9\)

Arrange the terms in descending degree order, and get zero on the right

\(x^{2}+y^{2}+4 x-2 y-4=0\)

This form of the equation is called the general form of the equation of the circle .

Definition \(\PageIndex{5}\)

The general form of the equation of a circle is

\(x^{2}+y^{2}+a x+b y+c=0\)

If we are given an equation in general form, we can change it to standard form by completing the squares in both \(x\) and \(y\). Then we can graph the circle using its center and radius.

Example \(\PageIndex{10}\)

• Graph the circle: \(x^{2}+y^{2}-4 x-6 y+4=0\)

We need to rewrite this general form into standard form in order to find the center and radius.

Exercise \(\PageIndex{19}\)

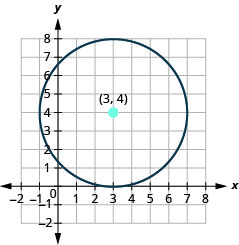
• Graph the circle: \(x^{2}+y^{2}-6 x-8 y+9=0\).
• The circle is centered at \((3,4)\) with a radius of \(4\).

Exercise \(\PageIndex{20}\)

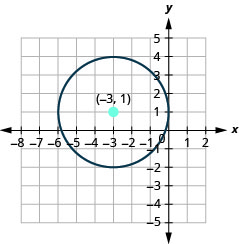
• Graph the circle: \(x^{2}+y^{2}+6 x-2 y+1=0\)
• The circle is centered at \((-3,1)\) with a radius of \(3\).

In the next example, there is a \(y\)-term and a \(y^{2}\)-term. But notice that there is no \(x\)-term, only an \(x^{2}\)-term. We have seen this before and know that it means \(h\) is \(0\). We will need to complete the square for the \(y\) terms, but not for the \(x\) terms.

Example \(\PageIndex{11}\)

• Graph the circle: \(x^{2}+y^{2}+8 y=0\)

Exercise \(\PageIndex{21}\)

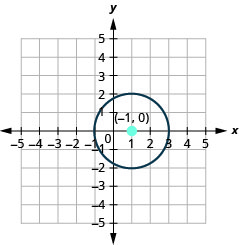
• Graph the circle: \(x^{2}+y^{2}-2 x-3=0\).
• The circle is centered at \((-1,0)\) with a radius of \(2\).

Exercise \(\PageIndex{22}\)

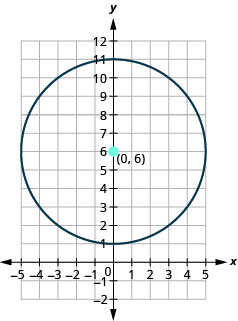
• Graph the circle: \(x^{2}+y^{2}-12 y+11=0\).
• The circle is centered at \((0,6)\) with a radius of \(5\).

Access these online resources for additional instructions and practice with using the distance and midpoint formulas, and graphing circles.

• Distance-Midpoint Formulas and Circles
• Finding the Distance and Midpoint Between Two Points
• Completing the Square to Write Equation in Standard Form of a Circle

Key Concepts

• Circle: A circle is all points in a plane that are a fixed distance from a fixed point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius, \(r\), of the circle.
• Standard Form of the Equation a Circle: The standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\) , is