hypothesis testing graded questions

Understanding Hypothesis Testing

In the last two modules, you learned about the following topics:

Exploratory data analysis: Exploring data for insights and patterns

Inferential statistics: Making inferences about the population using the sample data

Now, these methods help you formulate a basic idea or conclusion about the population. Such assumptions are called “hypotheses”.

basic difference between inferential statistics and hypothesis testing.

Inferential statistics is used to find some population parameter (mostly population mean) when you have no initial number to start with. So, you start with the sampling activity and find out the sample mean. Then, you estimate the population mean from the sample mean using the confidence interval.

Hypothesis testing is used to confirm your conclusion (or hypothesis) about the population parameter (which you know from EDA or your intuition). Through hypothesis testing, you can determine whether there is enough evidence to conclude if the hypothesis about the population parameter is true or not.

Q - Null and Alternate Hypotheses Government regulatory bodies have specified that the maximum permissible amount of lead in any food product is 2.5 parts per million or 2.5 ppm.

If you conduct tests on randomly chosen Maggi Noodles samples from the market, what would be the null hypothesis in this case?

The average lead content is equal to 2.5 ppm

The average lead content is less than or equal to 2.5 ppm

• Feedback: The null hypothesis is the status quo, i.e. the average lead content is within the allowed limit of 2.5 ppm.
• The average lead content is more than or equal to 2.5 ppm

Q - Government regulatory bodies have specified that the maximum permissible amount of lead in any food product is 2.5 parts per million or 2.5 ppm.

What would be the alternate hypothesis in the same case, when you conduct tests on randomly chosen Maggi Noodles samples from the market?

The average lead content is more than 2.5 ppm

• Feedback: The alternate hypothesis is the opposite of the null hypothesis. Since the null hypothesis is that the average lead content is less than or equal to 2.5 ppm, the alternate hypothesis would be that the average lead content is more than 2.5 ppm.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6.6 - confidence intervals & hypothesis testing.

Confidence intervals and hypothesis tests are similar in that they are both inferential methods that rely on an approximated sampling distribution. Confidence intervals use data from a sample to estimate a population parameter. Hypothesis tests use data from a sample to test a specified hypothesis. Hypothesis testing requires that we have a hypothesized parameter. 

The simulation methods used to construct bootstrap distributions and randomization distributions are similar. One primary difference is a bootstrap distribution is centered on the observed sample statistic while a randomization distribution is centered on the value in the null hypothesis. 

In Lesson 4, we learned confidence intervals contain a range of reasonable estimates of the population parameter. All of the confidence intervals we constructed in this course were two-tailed. These two-tailed confidence intervals go hand-in-hand with the two-tailed hypothesis tests we learned in Lesson 5. The conclusion drawn from a two-tailed confidence interval is usually the same as the conclusion drawn from a two-tailed hypothesis test. In other words, if the the 95% confidence interval contains the hypothesized parameter, then a hypothesis test at the 0.05 \(\alpha\) level will almost always fail to reject the null hypothesis. If the 95% confidence interval does not contain the hypothesize parameter, then a hypothesis test at the 0.05 \(\alpha\) level will almost always reject the null hypothesis.

Example: Mean Section  

This example uses the Body Temperature dataset built in to StatKey for constructing a  bootstrap confidence interval and conducting a randomization test . 

Let's start by constructing a 95% confidence interval using the percentile method in StatKey:

The 95% confidence interval for the mean body temperature in the population is [98.044, 98.474].

Now, what if we want to know if there is enough evidence that the mean body temperature is different from 98.6 degrees? We can conduct a hypothesis test. Because 98.6 is not contained within the 95% confidence interval, it is not a reasonable estimate of the population mean. We should expect to have a p value less than 0.05 and to reject the null hypothesis.

\(H_0: \mu=98.6\)

\(H_a: \mu \ne 98.6\)

\(p = 2*0.00080=0.00160\)

\(p \leq 0.05\), reject the null hypothesis

There is evidence that the population mean is different from 98.6 degrees. 

Selecting the Appropriate Procedure Section  

The decision of whether to use a confidence interval or a hypothesis test depends on the research question. If we want to estimate a population parameter, we use a confidence interval. If we are given a specific population parameter (i.e., hypothesized value), and want to determine the likelihood that a population with that parameter would produce a sample as different as our sample, we use a hypothesis test. Below are a few examples of selecting the appropriate procedure. 

Example: Cheese Consumption Section  

Research question: How much cheese (in pounds) does an average American adult consume annually? 

What is the appropriate inferential procedure? 

Cheese consumption, in pounds, is a quantitative variable. We have one group: American adults. We are not given a specific value to test, so the appropriate procedure here is a  confidence interval for a single mean .

Example: Age Section  

Research question:  Is the average age in the population of all STAT 200 students greater than 30 years?

There is one group: STAT 200 students. The variable of interest is age in years, which is quantitative. The research question includes a specific population parameter to test: 30 years. The appropriate procedure is a  hypothesis test for a single mean .

Try it! Section  

For each research question, identify the variables, the parameter of interest and decide on the the appropriate inferential procedure.

Research question:  How strong is the correlation between height (in inches) and weight (in pounds) in American teenagers?

There are two variables of interest: (1) height in inches and (2) weight in pounds. Both are quantitative variables. The parameter of interest is the correlation between these two variables.

We are not given a specific correlation to test. We are being asked to estimate the strength of the correlation. The appropriate procedure here is a  confidence interval for a correlation . 

Research question:  Are the majority of registered voters planning to vote in the next presidential election?

The parameter that is being tested here is a single proportion. We have one group: registered voters. "The majority" would be more than 50%, or p>0.50. This is a specific parameter that we are testing. The appropriate procedure here is a  hypothesis test for a single proportion .

Research question:  On average, are STAT 200 students younger than STAT 500 students?

We have two independent groups: STAT 200 students and STAT 500 students. We are comparing them in terms of average (i.e., mean) age.

If STAT 200 students are younger than STAT 500 students, that translates to \(\mu_{200}<\mu_{500}\) which is an alternative hypothesis. This could also be written as \(\mu_{200}-\mu_{500}<0\), where 0 is a specific population parameter that we are testing. 

The appropriate procedure here is a  hypothesis test for the difference in two means .

Research question:  On average, how much taller are adult male giraffes compared to adult female giraffes?

There are two groups: males and females. The response variable is height, which is quantitative. We are not given a specific parameter to test, instead we are asked to estimate "how much" taller males are than females. The appropriate procedure is a  confidence interval for the difference in two means .

Research question:  Are STAT 500 students more likely than STAT 200 students to be employed full-time?

There are two independent groups: STAT 500 students and STAT 200 students. The response variable is full-time employment status which is categorical with two levels: yes/no.

If STAT 500 students are more likely than STAT 200 students to be employed full-time, that translates to \(p_{500}>p_{200}\) which is an alternative hypothesis. This could also be written as \(p_{500}-p_{200}>0\), where 0 is a specific parameter that we are testing. The appropriate procedure is a  hypothesis test for the difference in two proportions.

Research question:  Is there is a relationship between outdoor temperature (in Fahrenheit) and coffee sales (in cups per day)?

There are two variables here: (1) temperature in Fahrenheit and (2) cups of coffee sold in a day. Both variables are quantitative. The parameter of interest is the correlation between these two variables.

If there is a relationship between the variables, that means that the correlation is different from zero. This is a specific parameter that we are testing. The appropriate procedure is a  hypothesis test for a correlation . 

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: Introduction to Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 10211

• Kyle Siegrist
• University of Alabama in Huntsville via Random Services

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Basic Theory

Preliminaries.

As usual, our starting point is a random experiment with an underlying sample space and a probability measure \(\P\). In the basic statistical model, we have an observable random variable \(\bs{X}\) taking values in a set \(S\). In general, \(\bs{X}\) can have quite a complicated structure. For example, if the experiment is to sample \(n\) objects from a population and record various measurements of interest, then \[ \bs{X} = (X_1, X_2, \ldots, X_n) \] where \(X_i\) is the vector of measurements for the \(i\)th object. The most important special case occurs when \((X_1, X_2, \ldots, X_n)\) are independent and identically distributed. In this case, we have a random sample of size \(n\) from the common distribution.

The purpose of this section is to define and discuss the basic concepts of statistical hypothesis testing . Collectively, these concepts are sometimes referred to as the Neyman-Pearson framework, in honor of Jerzy Neyman and Egon Pearson, who first formalized them.

A statistical hypothesis is a statement about the distribution of \(\bs{X}\). Equivalently, a statistical hypothesis specifies a set of possible distributions of \(\bs{X}\): the set of distributions for which the statement is true. A hypothesis that specifies a single distribution for \(\bs{X}\) is called simple ; a hypothesis that specifies more than one distribution for \(\bs{X}\) is called composite .

In hypothesis testing , the goal is to see if there is sufficient statistical evidence to reject a presumed null hypothesis in favor of a conjectured alternative hypothesis . The null hypothesis is usually denoted \(H_0\) while the alternative hypothesis is usually denoted \(H_1\).

An hypothesis test is a statistical decision ; the conclusion will either be to reject the null hypothesis in favor of the alternative, or to fail to reject the null hypothesis. The decision that we make must, of course, be based on the observed value \(\bs{x}\) of the data vector \(\bs{X}\). Thus, we will find an appropriate subset \(R\) of the sample space \(S\) and reject \(H_0\) if and only if \(\bs{x} \in R\). The set \(R\) is known as the rejection region or the critical region . Note the asymmetry between the null and alternative hypotheses. This asymmetry is due to the fact that we assume the null hypothesis, in a sense, and then see if there is sufficient evidence in \(\bs{x}\) to overturn this assumption in favor of the alternative.

An hypothesis test is a statistical analogy to proof by contradiction, in a sense. Suppose for a moment that \(H_1\) is a statement in a mathematical theory and that \(H_0\) is its negation. One way that we can prove \(H_1\) is to assume \(H_0\) and work our way logically to a contradiction. In an hypothesis test, we don't prove anything of course, but there are similarities. We assume \(H_0\) and then see if the data \(\bs{x}\) are sufficiently at odds with that assumption that we feel justified in rejecting \(H_0\) in favor of \(H_1\).

Often, the critical region is defined in terms of a statistic \(w(\bs{X})\), known as a test statistic , where \(w\) is a function from \(S\) into another set \(T\). We find an appropriate rejection region \(R_T \subseteq T\) and reject \(H_0\) when the observed value \(w(\bs{x}) \in R_T\). Thus, the rejection region in \(S\) is then \(R = w^{-1}(R_T) = \left\{\bs{x} \in S: w(\bs{x}) \in R_T\right\}\). As usual, the use of a statistic often allows significant data reduction when the dimension of the test statistic is much smaller than the dimension of the data vector.

The ultimate decision may be correct or may be in error. There are two types of errors, depending on which of the hypotheses is actually true.

Types of errors:

• A type 1 error is rejecting the null hypothesis \(H_0\) when \(H_0\) is true.
• A type 2 error is failing to reject the null hypothesis \(H_0\) when the alternative hypothesis \(H_1\) is true.

Similarly, there are two ways to make a correct decision: we could reject \(H_0\) when \(H_1\) is true or we could fail to reject \(H_0\) when \(H_0\) is true. The possibilities are summarized in the following table:

Of course, when we observe \(\bs{X} = \bs{x}\) and make our decision, either we will have made the correct decision or we will have committed an error, and usually we will never know which of these events has occurred. Prior to gathering the data, however, we can consider the probabilities of the various errors.

If \(H_0\) is true (that is, the distribution of \(\bs{X}\) is specified by \(H_0\)), then \(\P(\bs{X} \in R)\) is the probability of a type 1 error for this distribution. If \(H_0\) is composite, then \(H_0\) specifies a variety of different distributions for \(\bs{X}\) and thus there is a set of type 1 error probabilities.

The maximum probability of a type 1 error, over the set of distributions specified by \( H_0 \), is the significance level of the test or the size of the critical region.

The significance level is often denoted by \(\alpha\). Usually, the rejection region is constructed so that the significance level is a prescribed, small value (typically 0.1, 0.05, 0.01).

If \(H_1\) is true (that is, the distribution of \(\bs{X}\) is specified by \(H_1\)), then \(\P(\bs{X} \notin R)\) is the probability of a type 2 error for this distribution. Again, if \(H_1\) is composite then \(H_1\) specifies a variety of different distributions for \(\bs{X}\), and thus there will be a set of type 2 error probabilities. Generally, there is a tradeoff between the type 1 and type 2 error probabilities. If we reduce the probability of a type 1 error, by making the rejection region \(R\) smaller, we necessarily increase the probability of a type 2 error because the complementary region \(S \setminus R\) is larger.

The extreme cases can give us some insight. First consider the decision rule in which we never reject \(H_0\), regardless of the evidence \(\bs{x}\). This corresponds to the rejection region \(R = \emptyset\). A type 1 error is impossible, so the significance level is 0. On the other hand, the probability of a type 2 error is 1 for any distribution defined by \(H_1\). At the other extreme, consider the decision rule in which we always rejects \(H_0\) regardless of the evidence \(\bs{x}\). This corresponds to the rejection region \(R = S\). A type 2 error is impossible, but now the probability of a type 1 error is 1 for any distribution defined by \(H_0\). In between these two worthless tests are meaningful tests that take the evidence \(\bs{x}\) into account.

If \(H_1\) is true, so that the distribution of \(\bs{X}\) is specified by \(H_1\), then \(\P(\bs{X} \in R)\), the probability of rejecting \(H_0\) is the power of the test for that distribution.

Thus the power of the test for a distribution specified by \( H_1 \) is the probability of making the correct decision.

Suppose that we have two tests, corresponding to rejection regions \(R_1\) and \(R_2\), respectively, each having significance level \(\alpha\). The test with region \(R_1\) is uniformly more powerful than the test with region \(R_2\) if \[ \P(\bs{X} \in R_1) \ge \P(\bs{X} \in R_2) \text{ for every distribution of } \bs{X} \text{ specified by } H_1 \]

Naturally, in this case, we would prefer the first test. Often, however, two tests will not be uniformly ordered; one test will be more powerful for some distributions specified by \(H_1\) while the other test will be more powerful for other distributions specified by \(H_1\).

If a test has significance level \(\alpha\) and is uniformly more powerful than any other test with significance level \(\alpha\), then the test is said to be a uniformly most powerful test at level \(\alpha\).

Clearly a uniformly most powerful test is the best we can do.

\(P\)-value

In most cases, we have a general procedure that allows us to construct a test (that is, a rejection region \(R_\alpha\)) for any given significance level \(\alpha \in (0, 1)\). Typically, \(R_\alpha\) decreases (in the subset sense) as \(\alpha\) decreases.

The \(P\)-value of the observed value \(\bs{x}\) of \(\bs{X}\), denoted \(P(\bs{x})\), is defined to be the smallest \(\alpha\) for which \(\bs{x} \in R_\alpha\); that is, the smallest significance level for which \(H_0\) is rejected, given \(\bs{X} = \bs{x}\).

Knowing \(P(\bs{x})\) allows us to test \(H_0\) at any significance level for the given data \(\bs{x}\): If \(P(\bs{x}) \le \alpha\) then we would reject \(H_0\) at significance level \(\alpha\); if \(P(\bs{x}) \gt \alpha\) then we fail to reject \(H_0\) at significance level \(\alpha\). Note that \(P(\bs{X})\) is a statistic . Informally, \(P(\bs{x})\) can often be thought of as the probability of an outcome as or more extreme than the observed value \(\bs{x}\), where extreme is interpreted relative to the null hypothesis \(H_0\).

Analogy with Justice Systems

There is a helpful analogy between statistical hypothesis testing and the criminal justice system in the US and various other countries. Consider a person charged with a crime. The presumed null hypothesis is that the person is innocent of the crime; the conjectured alternative hypothesis is that the person is guilty of the crime. The test of the hypotheses is a trial with evidence presented by both sides playing the role of the data. After considering the evidence, the jury delivers the decision as either not guilty or guilty . Note that innocent is not a possible verdict of the jury, because it is not the point of the trial to prove the person innocent. Rather, the point of the trial is to see whether there is sufficient evidence to overturn the null hypothesis that the person is innocent in favor of the alternative hypothesis of that the person is guilty. A type 1 error is convicting a person who is innocent; a type 2 error is acquitting a person who is guilty. Generally, a type 1 error is considered the more serious of the two possible errors, so in an attempt to hold the chance of a type 1 error to a very low level, the standard for conviction in serious criminal cases is beyond a reasonable doubt .

Tests of an Unknown Parameter

Hypothesis testing is a very general concept, but an important special class occurs when the distribution of the data variable \(\bs{X}\) depends on a parameter \(\theta\) taking values in a parameter space \(\Theta\). The parameter may be vector-valued, so that \(\bs{\theta} = (\theta_1, \theta_2, \ldots, \theta_n)\) and \(\Theta \subseteq \R^k\) for some \(k \in \N_+\). The hypotheses generally take the form \[ H_0: \theta \in \Theta_0 \text{ versus } H_1: \theta \notin \Theta_0 \] where \(\Theta_0\) is a prescribed subset of the parameter space \(\Theta\). In this setting, the probabilities of making an error or a correct decision depend on the true value of \(\theta\). If \(R\) is the rejection region, then the power function \( Q \) is given by \[ Q(\theta) = \P_\theta(\bs{X} \in R), \quad \theta \in \Theta \] The power function gives a lot of information about the test.

The power function satisfies the following properties:

• \(Q(\theta)\) is the probability of a type 1 error when \(\theta \in \Theta_0\).
• \(\max\left\{Q(\theta): \theta \in \Theta_0\right\}\) is the significance level of the test.
• \(1 - Q(\theta)\) is the probability of a type 2 error when \(\theta \notin \Theta_0\).
• \(Q(\theta)\) is the power of the test when \(\theta \notin \Theta_0\).

If we have two tests, we can compare them by means of their power functions.

Suppose that we have two tests, corresponding to rejection regions \(R_1\) and \(R_2\), respectively, each having significance level \(\alpha\). The test with rejection region \(R_1\) is uniformly more powerful than the test with rejection region \(R_2\) if \( Q_1(\theta) \ge Q_2(\theta)\) for all \( \theta \notin \Theta_0 \).

Most hypothesis tests of an unknown real parameter \(\theta\) fall into three special cases:

Suppose that \( \theta \) is a real parameter and \( \theta_0 \in \Theta \) a specified value. The tests below are respectively the two-sided test , the left-tailed test , and the right-tailed test .

• \(H_0: \theta = \theta_0\) versus \(H_1: \theta \ne \theta_0\)
• \(H_0: \theta \ge \theta_0\) versus \(H_1: \theta \lt \theta_0\)
• \(H_0: \theta \le \theta_0\) versus \(H_1: \theta \gt \theta_0\)

Thus the tests are named after the conjectured alternative. Of course, there may be other unknown parameters besides \(\theta\) (known as nuisance parameters ).

Equivalence Between Hypothesis Test and Confidence Sets

There is an equivalence between hypothesis tests and confidence sets for a parameter \(\theta\).

Suppose that \(C(\bs{x})\) is a \(1 - \alpha\) level confidence set for \(\theta\). The following test has significance level \(\alpha\) for the hypothesis \( H_0: \theta = \theta_0 \) versus \( H_1: \theta \ne \theta_0 \): Reject \(H_0\) if and only if \(\theta_0 \notin C(\bs{x})\)

By definition, \(\P[\theta \in C(\bs{X})] = 1 - \alpha\). Hence if \(H_0\) is true so that \(\theta = \theta_0\), then the probability of a type 1 error is \(P[\theta \notin C(\bs{X})] = \alpha\).

Equivalently, we fail to reject \(H_0\) at significance level \(\alpha\) if and only if \(\theta_0\) is in the corresponding \(1 - \alpha\) level confidence set. In particular, this equivalence applies to interval estimates of a real parameter \(\theta\) and the common tests for \(\theta\) given above .

In each case below, the confidence interval has confidence level \(1 - \alpha\) and the test has significance level \(\alpha\).

• Suppose that \(\left[L(\bs{X}, U(\bs{X})\right]\) is a two-sided confidence interval for \(\theta\). Reject \(H_0: \theta = \theta_0\) versus \(H_1: \theta \ne \theta_0\) if and only if \(\theta_0 \lt L(\bs{X})\) or \(\theta_0 \gt U(\bs{X})\).
• Suppose that \(L(\bs{X})\) is a confidence lower bound for \(\theta\). Reject \(H_0: \theta \le \theta_0\) versus \(H_1: \theta \gt \theta_0\) if and only if \(\theta_0 \lt L(\bs{X})\).
• Suppose that \(U(\bs{X})\) is a confidence upper bound for \(\theta\). Reject \(H_0: \theta \ge \theta_0\) versus \(H_1: \theta \lt \theta_0\) if and only if \(\theta_0 \gt U(\bs{X})\).

Pivot Variables and Test Statistics

Recall that confidence sets of an unknown parameter \(\theta\) are often constructed through a pivot variable , that is, a random variable \(W(\bs{X}, \theta)\) that depends on the data vector \(\bs{X}\) and the parameter \(\theta\), but whose distribution does not depend on \(\theta\) and is known. In this case, a natural test statistic for the basic tests given above is \(W(\bs{X}, \theta_0)\).

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability   >   unit 12, simple hypothesis testing.

• Idea behind hypothesis testing
• Examples of null and alternative hypotheses
• Writing null and alternative hypotheses
• P-values and significance tests
• Comparing P-values to different significance levels
• Estimating a P-value from a simulation
• Estimating P-values from simulations
• Using P-values to make conclusions

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Hypothesis Testing: Questions and Answers (Biostatistics Notes)

(1). what is hypothesis.

A hypothesis is a statement or an assumption about a phenomenon or a relationship between variables. It is a proposed explanation for a set of observations or an answer to a research question.

In research, hypotheses are tested through experiments or data analysis using a test statistic . The aim of hypothesis testing is to determine if the evidence supports or rejects the hypothesis. If the evidence supports the hypothesis, it provides evidence for the validity of the hypothesis. If the evidence does not support the hypothesis, it may need to be revised or rejected and a new hypothesis may be proposed.

Learn more: Testing of Hypothesis: Theory and Steps

They hypotheses may be directional or non-directional . Directional hypotheses specify the direction of the relationship between the variables , whereas the non-directional hypotheses only state the presence of a relationship without specifying the direction.

(2). What is Hypothesis Testing in Statistics?

It is a method used to make a decision about the validity of the hypothesis concerning a population parameter based on a random sample from that population. It involves the calculation of a test statistic, and the comparison of this test statistic to a critical value determined from the distribution of that test statistic. The decision is made by comparing the p-value (p-value is described below) with a significance level, typically 0.05. If the p-value is less than the significance level, the null hypothesis is rejected and the alternative hypothesis is accepted.

Learn more: Graphical Representation of Data

(3). What is Test-Statistic?

A test statistic is a numerical value calculated from the sample data. It is used to test the hypothesis about a population parameter. Test-statistic summarizes the sample information in to a single value and helps to determine the significance of the results. The choice of test statistic depends on the specific hypothesis test being conducted and the type of data. Commonly used test statistics are t-statistic (t-test), z-statistic (z-test), F-statistic (F-test) and the chi-squared statistic ( Chi-square test ). The test statistic is used in conjunction with a critical value and a p-value to make inferences about the population parameter and determine whether the null hypothesis should be rejected or not.

(4). What is null hypothesis?

The null hypothesis is a statement in statistical testing that assumes no significant difference exists between the tested variables or parameters. It is usually denoted as H0 and serves as a starting point for statistical analysis. The null hypothesis is tested against an alternative hypothesi s, which is the opposite of the null hypothesis and represents the researchers’ research question or prediction of an effect. The aim of statistical testing is to determine whether the evidence in the sample data supports the rejection of the null hypothesis in favor of the alternative hypothesis. If the null hypothesis can’t be rejected, it doesn’t mean it’s proven to be true, it just means that the data do not provide enough evidence to support the alternative hypothesis.

(5). What is alternate hypothesis?

The alternative hypothesis is a statement in statistical testing that contradicts or negates the null hypothesis and represents the researchers’ research hypothesis. Alternate hypothesis is denoted as H1 or Ha .  The alternative hypothesis is what the researcher is hoping to prove through the statistical analysis. If the results of the analysis provide strong evidence, the null hypothesis is rejected in favor of the alternative hypothesis. The alternative hypothesis typically represents a non-zero difference or a relationship between variables, whereas the null hypothesis assumes no difference or relationship.

(6). What is Level of Significance in Statistics?

The level of significance in statistics refers to the threshold of probability or p-value below which a result or finding is considered statistically significant. It means that, it is unlikely to have occurred by chance. Level of significance is usually set at 5% (0.05) and indicates the maximum probability of accepting the null hypothesis when it is actually false (Type I error).

Learn more: Difference between Type-I and Type-II Errors

(7). What are statistical errors?

Statistical errors are mistakes can occur during the process of statistical analysis. There are two types of statistical errors: Type I errors and Type II errors.

(8). What is type-I error in statistics?

The type I error, also known as a false positive, is a statistical error that occurs when the null hypothesis is rejected when it is actually true. In other words, a Type I error occurs when a significant result is obtained by chance, leading to the incorrect conclusion that there is a real effect or relationship present.

In hypothesis testing, the level of significance (alpha) is used to control the probability of making a Type I error. A level of significance of 0.05, for example, means that there is a 5% chance of rejecting the null hypothesis when it is actually true. The level of significance is a threshold that is used to determine whether the observed result is significant enough to reject the null hypothesis. Minimizing Type I errors is important in statistical analysis because a false positive can lead to incorrect conclusions and misguided decisions.

(9). How to reduce the chance of committing a type-I error?

There are several ways to reduce the chance of committing a Type I error, they are:

Ø   Increasing the sample size: Increasing the sample size increases the precision and power of the statistical test. High sample size reduces the probability of observing a significant result by chance.

Ø   Decreasing the level of significance (alpha) : Decreasing the level of significance reduces the probability of rejecting the null hypothesis when it is actually true. A lower level of significance increases the threshold for rejecting the null hypothesis, making it less likely that a Type I error will occur.

Ø   Conducting a replication study : Replicating the study with a new sample of data helps to confirm or refute the results and reduces the chance of observing a false positive result by chance.

Ø   Using more stringent statistical methods : More sophisticated statistical methods, such as Bayesian analysis, can provide additional information to help reduce the probability of making a Type I error.

Ø   Careful interpretation of results : Proper interpretation of results and thorough understanding of the underlying statistical methods used can also help reduce the chance of making a Type I error.

It is very important have a balance in reducing Type I errors with the risk of increasing the chance of making a Type II error. The statistical analysis implemented with an aim of reducing the chance of a Type I error may also the chance of a Type II error.

(10). What is type-II error in statistics?

Type II error, also known as a false negative , is a statistical error that occurs when the null hypothesis is not rejected when it is actually false. In other words, a Type II error occurs when a significant difference or relationship is not detected in the data, despite its existence in the population.

In hypothesis testing, the probability of making a Type II error is represented by beta ( beta error ) and is related to the sample size and the magnitude of the effect being tested. The larger the sample size or the larger the effect, the lower the probability of making a Type II error.

Minimizing Type II errors is important because a false negative can lead to incorrect conclusions and missed opportunities for discovery. To reduce the probability of a Type II error, researchers may use larger sample sizes, increase the level of significance (alpha), or use more powerful statistical methods.

(11). How to reduce the chance of committing the type-II error in statistics?

There are several ways to reduce the chance of committing a Type II error in statistics, they are:

Ø   Increasing the sample size : Increasing the sample size increases the precision and power of the statistical test. Increased sample size reduces the probability of failing to detect a significant result.

Ø   Increasing the level of significance (alpha): Increasing the level of significance reduces the probability of failing to reject the null hypothesis when it is actually false. A higher level of significance decreases the threshold for rejecting the null hypothesis, making it more likely that a significant result will be detected.

Ø   Using a more powerful statistical test : More powerful statistical tests, such as a two-sample t-test or ANOVA, can increase the ability to detect a significant difference or relationship in the data.

Ø   Increasing the magnitude of the effect being tested: A larger effect size makes it more likely that a significant result will be detected, reducing the probability of a Type II error.

Ø   Conducting a pilot study: A pilot study can provide an estimate of the sample size needed for the main study, increasing the ability to detect a significant result.

It’s important to balance reducing the probability of a Type II error with the risk of increasing the chance of making a Type I error. A statistical analysis that offers to reduce the chance of a Type II error may also increase the chance of a Type I error.

(12). What is p-value?

The p-value is a statistical measure that represents the probability of obtaining a result as extreme or more extreme than the one observed, given that the null hypothesis is true. In other words, the p-value is the probability of observing the data if the null hypothesis is true.

In hypothesis testing, the p-value is compared to the level of significance (alpha) to determine whether the null hypothesis should be rejected in favor of the alternative hypothesis. If the p-value is less than the level of significance, the null hypothesis is rejected, and the result is considered statistically significant. A small p-value indicates that it is unlikely that the result was obtained by chance, and provides evidence against the null hypothesis.

It’s important to note that the p-value does not indicate the magnitude of the effect or the likelihood of the alternative hypothesis being true. It only provides information about the strength of the evidence against the null hypothesis. A low p-value is not proof of the alternative hypothesis, but it does provide evidence against the null hypothesis and supports the conclusion that the effect or relationship is real.

(13). What is the importance of hypothesis testing in research?

Hypothesis testing is an important tool in research as it allows researchers to test their ideas and make inferences about a population based on a sample of data. It provides a systematic and objective approach for evaluating the evidence and making decisions about the validity of a claim.

Evaluating claims : Hypothesis testing provides a way to evaluate claims and determine if they are supported by the data. By testing hypotheses and comparing the results to a predetermined level of significance, researchers can determine if their ideas are supported by the data.

Making decisions : Hypothesis testing helps researchers make decisions about the validity of their ideas and the direction of their research. It provides a way to determine if a claim is supported by the data.

Enhancing the quality of research : Hypothesis testing ensures that research is conducted in a systematic and rigorous manner, which enhances the quality and validity of the research findings. By using a hypothesis testing framework, researchers can ensure that their results are not due to chance and that their conclusions are based on valid evidence.

Understanding the phenomena : By testing hypotheses and evaluating the evidence, hypothesis testing helps researchers gain a better understanding of the phenomena they are studying. It provides a way to determine if a claim is supported by the data and to gain insights into the underlying relationships and patterns in the data.

(14). What are the different types of hypothesis testing tools (test-statistics) available in statistics?

There are several different types of hypothesis testing tools available in statistics which are summarized below. The choice of which tool to use depends on the research question, the type of data being analyzed, and the underlying assumptions of the test.

Z-test: A Z-test is used to test the mean of a population when the population standard deviation is known. It is commonly used to test the difference between two means.

t-test: A t-test is used to test the mean of a population when the population standard deviation is unknown. It is commonly used to test the difference between two means. t-test is performed when the sample size is small (n<30).

ANOVA : Analysis of Variance (ANOVA) is a hypothesis testing tool used to test the equality of means for two or more groups. It is used to determine if there are significant differences among the means of multiple groups. Here comparison between and within groups are done to find out the significance.

Chi-Square Test : The Chi-Square Test the discrepancies between the observed and expected data. It is used to test the independence of two categorical variables. It is commonly used to test if there is a relationship between two categorical variables.

F-test: F-test is variance ratio test. An F-test is used to test the equality of variances for two or more groups. It is commonly used in ANOVA to determine if the variances of the groups are equal.

Non-Parametric Tests : Non-parametric tests are hypothesis tests that do not assume a normal distribution of the data. Examples include the Wilcoxon rank-sum test, the Kruskal-Wallis test, and the Mann-Whitney U test.

(15). What is statistical power?

Statistical power is the probability of correctly rejecting a false null hypothesis in a statistical hypothesis test. It is the complement of the probability of making a type II error, which is failing to reject a false null hypothesis.

The power of a hypothesis test is determined by several factors such as sample size, the effect size, the level of significance and the variability of the data. Increasing the sample size, reducing the variability of the data, or increasing the effect size will generally increase the power of the test.

The power of a hypothesis test is an important consideration in the design of experiments and the selection of sample sizes, as it affects the ability of the test to detect meaningful differences between groups or to reject false null hypotheses. It is also important to consider the trade-off between the power of the test and the level of significance, as increasing the power of the test typically requires a decrease in the level of significance.

Learn more: Principles of Experimental Designs

Learn More : Different Types of Experimental Designs

(16). What is one-tailed and two-tailed test in statistics?

A one-tailed test and a two-tailed test are two types of statistical hypothesis tests used to determine if there is a significant difference between two groups or if a relationship exists between two variables.

A one-tailed test is a hypothesis test that tests the direction of the relationship between two variables. For example, if a researcher wants to determine if a new drug is better than a placebo, a one-tailed test would be used. In a one-tailed test, the alternative hypothesis specifies the direction of the difference, either the new drug is better than the placebo or it is not.

A two-tailed test , on the other hand, does not specify the direction of the difference between the two groups or variables. It only tests if there is a significant difference between the two groups or variables in either direction. For example, if a researcher wants to determine if a new drug is different from a placebo, a two-tailed test would be used. In a two-tailed test, the alternative hypothesis states that the new drug is different from the placebo but does not specify in which direction the difference lies (example- the efficiency may be less or more).

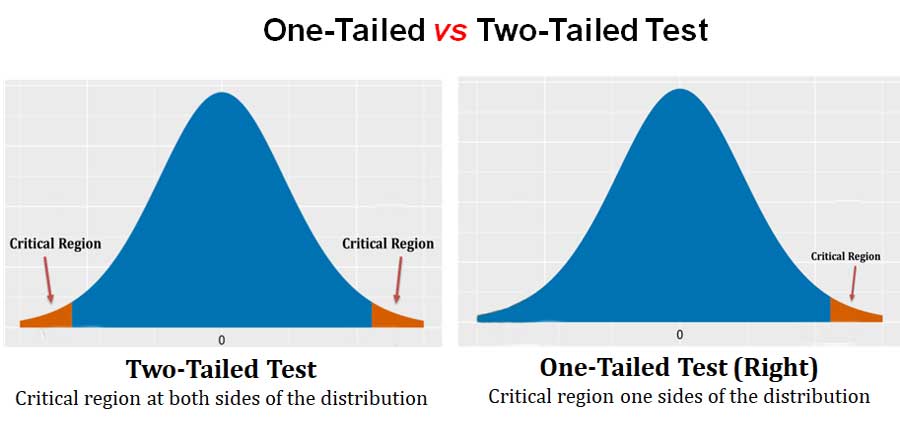
The choice between a one-tailed and a two-tailed test depends on the research question, the data, and the underlying assumptions of the test. One-tailed tests are typically used when the direction of the difference is already known or when the research question is very specific, while two-tailed tests are used when the direction of the difference is not known or when the research question is more general.

(17). What is critical region?

In statistical hypothesis testing, a critical region is the set of values of a test statistic for which the null hypothesis is rejected. The critical region is determined by the level of significance, which is the probability of making a type I error, or incorrectly rejecting a true null hypothesis.

The critical region is often defined as the region of the distribution of the test statistic that is beyond a certain threshold. The threshold is determined by the level of significance and the type of test being conducted (one-tailed or two-tailed). If the calculated test statistic falls within the critical region, the null hypothesis is rejected and the alternative hypothesis is accepted. If the calculated test statistic falls outside of the critical region, the null hypothesis is not rejected. Thus, the critical region is a key component of hypothesis testing, as it determines the decision rule for accepting or rejecting the null hypothesis.

<<< Back to Biostatistics Notes Page

Dear readers

I hope you have enjoyed reading this article and finding the content informative. We believe that this article helped you to understand the Hypothesis Testing Questions and Answers . I would like to take this opportunity to request your COMMENTS on the topics I have covered. Whether you have a suggestion, a question about the topic, or simply want to share your thoughts, I would love to hear from you. Your comments provide me with the opportunity to engage in meaningful discussion and continue to write with the best possible content in Biology.

So, please don’t hesitate to leave a comment below. I appreciate your support and look forward to hearing from you. Best regards, [Admin, EasyBiologyClass]

Related posts:

• Hypothesis Testing in Statistics – Short Notes + PPT
• Graphical Representation of Data (Frequency Polygon, Frequency Curve, Ogive and Pie Diagram)
• What is Data in Statistics?
• Principles of Experimental Designs in Statistics – Replication, Randomization & Local Control
• Types of Experimental Designs in Statistics (RBD, CRD, LSD, Factorial Designs)

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Privacy Overview

Concepts of Hypothesis Testing - I

Understanding hypothesis testing.

Null and Alternate Hypotheses In the Maggi Noodles example, if you fail to reject the null hypothesis, what can you conclude from this statement?

Maggi Noodles contain excess lead

Maggi Noodles do not contain excess lead ✓ Correct

Types of Hypotheses The null and alternative hypotheses divide all possibilities into:

2 sets that overlap

2 non-overlapping sets ✓ Correct