graphical representation of a linear polynomial

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.1: Graphs of Polynomials

• Last updated
• Save as PDF
• Page ID 119155

• Carl Stitz & Jeff Zeager
• Lakeland Community College & Lorain County Community College

Prerequisite Skillbuilders

The following topics are assumed knowledge prior to going through this material or the homework. If you find you are stuck on a concept, you might find the necessary remediation within these videos.

• What is a polynomial function?

Math 370 Learning Objectives

• Applications Involving Polynomial Functions: Develop models involving polynomial functions and use them to investigate and optimize values.
• End Behavior of Monomials: Review the end behavior of monomials.
• End Behavior of Polynomials: Review the end behavior of polynomials and how they are related to the end behavior of monomials.
• Middle Behavior of Polynomials: Review zeros of polynomials and how to find them.
• Sketching Graphs of Polynomials: Review basic techniques for sketching the graph of a polynomial function.

Introduction to Polynomial Functions

Three of the families of functions studied thus far – constant, linear, and quadratic – belong to a much larger group of functions called polynomials . We begin our formal study of general polynomials with a definition and some examples.

Definition: Polynomial Function

A polynomial function is a function of the form

\[f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{2} x^{2}+a_{1} x+a_{0},\label{PolyFunc} \]

where \(a_0\), \(a_{1}\), …, \(a_{n}\) are real numbers and \(n \geq 1\) is a natural number. The domain of a polynomial function is \((-\infty, \infty)\).

There are several things about the definition of a polynomial function that may be off-putting or downright frightening. The best thing to do is look at an example. Consider

\[f(x) = 4x^5 - 3x^2 + 2x - 5.\nonumber \]

Is this a polynomial function? We can re-write the formula for \(f\) as

\[f(x)= 4x^5 + 0 x^{4} + 0 x^{3} + (-3)x^2 + 2 x + (-5).\nonumber \]

Comparing this with Equation \( \ref{PolyFunc} \), we identify \(n=5\), \(a_{5} = 4\), \(a_{4} = 0\), \(a_{3} = 0\), \(a_{2} = -3\), \(a_{1} = 2\) and \(a_0 = -5\). In other words, \(a_{5}\) is the coefficient of \(x^{5}\), \(a_{4}\) is the coefficient of \(x^{4}\), and so forth; the subscript on the \(a\)’s merely indicates to which power of \(x\) the coefficient belongs. The business of restricting \(n\) to be a natural number lets us focus on well-behaved algebraic animals,

Example \( \PageIndex{1} \)

Determine if the following functions are polynomials. Explain your reasoning.

• \(g(x) = \dfrac{4+x^3}{x}\)
• \(p(x) = \dfrac{4x+x^3}{x}\)
• \(q(x) = \dfrac{4x+x^3}{x^2+4}\)
• \(f(x) =\sqrt[3]{x}\)
• \(h(x) = |x|\)
• \(z(x) = 0\)
• We note directly that the domain of \(g(x) = \dfrac{x^3+4}{x}\) is \(x \neq 0\). By definition, a polynomial has all real numbers as its domain. Hence, \(g\) can’t be a polynomial.
• Even though \(p(x) = \dfrac{x^3+4x}{x}\) simplifies to \(p(x) = x^2+4\), which certainly looks like the form given in Equation \( \ref{PolyFunc} \), the domain of \(p\), which, as you may recall, we determine before we simplify, excludes \(0\). Alas, \(p\) is not a polynomial function for the same reason \(g\) isn’t.
• After what happened with \(p\) in the previous part, you may be a little shy about simplifying \(q(x) = \dfrac{x^3+4x}{x^2+4}\) to \(q(x) = x\), which certainly fits Equation \( \ref{PolyFunc} \). If we look at the domain of \(q\) before we simplified, we see that it is, indeed, all real numbers. A function which can be written in the form of Equation \( \ref{PolyFunc}  \) whose domain is all real numbers is, in fact, a polynomial. Therefore, this  is  a polynomial!
• We can rewrite \(f(x) =\sqrt[3]{x}\) as \(f(x) = x^{\dfrac{1}{3}}\). Since \(\dfrac{1}{3}\) is not a natural number, \(f\) is not a polynomial.
• The function \(h(x) = |x|\) isn’t a polynomial, since it can’t be written as a combination of powers of \(x\) even though it can be written as a piecewise function involving polynomials. As we shall see in this section, graphs of polynomials possess a quality that the graph of \(h\) does not.
• There’s nothing in the definition of a polynomial function which prevents all the coefficients \(a_{n}\), etc., from being \(0\). Hence, \(z(x) = 0\), is an honest-to-goodness polynomial.

Definition: Degree, Leading Term, Leading Coefficient, and Constant Term of a Polynomial Function

Suppose \(f\) is a polynomial function.

• The natural number \(n\) is called the degree of the polynomial \(f\).
• The term \(a_{n} x^{n}\) is called the leading term of the polynomial \(f\).
• The real number \(a_{n}\) is called the leading coefficient of the polynomial \(f\).
• The real number \(a_0\) is called the constant term of the polynomial \(f\).
• If \(f(x) = a_0\), and \(a_0 \neq 0\), we say \(f\) has degree \(0\).
• If \(f(x) = 0\), we say \(f\) has no degree.

The reader may wonder why we have chosen to separate off constant functions from the other polynomials in our defintion above. Why not just lump them all together and, instead of forcing \(n\) to be a natural number, \(n = 1, 2, \ldots\), allow \(n\) to be a whole number, \(n = 0, 1, 2, \ldots\)? We could unify all of the cases, since, after all, isn’t \(a_0x^{0} = a_0\)?

The answer is "yes, as long as \(x\neq 0\)."

The functions \(f(x) = 3\) and \(g(x) = 3x^{0}\) are different, because their domains are different. The number \(f(0) = 3\) is defined, whereas \(g(0) = 3(0)^{0}\) is not. 1  Indeed, much of the theory we will develop in this chapter doesn’t include the constant functions, so we might as well treat them as outsiders from the start. One good thing that comes from our definition above is that we can now think of linear functions as degree \(1\) (or "first-degree") polynomial functions and quadratic functions as degree \(2\) (or "second-degree") polynomial functions.

Example \( \PageIndex{2} \)

Find the degree, leading term, leading coefficient and constant term of the following polynomial functions.

• \(f(x) = 4x^5 - 3x^2 + 2x - 5\)
• \(g(x) = 12x +x^3\)
• \(h(x) = \dfrac{4-x}{5}\)
• \(p(x) = (2x-1)^{3}(x-2)(3x+2)\)
• There are no surprises with \(f(x) = 4x^5 - 3x^2 + 2x - 5\). It is written in the form of Equation \( \ref{PolyFunc} \), and we see that the degree is \(5\), the leading term is \(4x^5\), the leading coefficient is \(4\) and the constant term is \(-5\).
• The form given in Equation \( \ref{PolyFunc} \) has the highest power of \(x\) first. To that end, we re-write \(g(x) = 12x +x^3 = x^3+12x\), and see that the degree of \(g\) is \(3\), the leading term is \(x^3\), the leading coefficient is \(1\) and the constant term is \(0\).
• We need to rewrite the formula for \(h\) so that it resembles the form given in Equation \( \ref{PolyFunc} \): \[h(x) = \dfrac{4-x}{5} = \dfrac{4}{5} - \dfrac{x}{5} = -\dfrac{1}{5} x + \dfrac{4}{5}. \nonumber \]The degree of \(h\) is \(1\), the leading term is \(-\dfrac{1}{5} x\), the leading coefficient is \(-\dfrac{1}{5}\) and the constant term is \(\dfrac{4}{5}\).
• It may seem that we have some work ahead of us to get \(p\) in the form of Equation \( \ref{PolyFunc} \). However, it is possible to glean the information requested about \(p\) without multiplying out the entire expression \((2x-1)^{3}(x-2)(3x+2)\). The leading term of \(p\) will be the term which has the highest power of \(x\). The way to get this term is to multiply the terms with the highest power of \(x\) from each factor together - in other words, the leading term of \(p(x)\) is the product of the leading terms of the factors of \(p(x)\). Hence, the leading term of \(p\) is \((2x)^3(x)(3x) = 24x^5\). b  This means that the degree of \(p\) is \(5\) and the leading coefficient is \(24\). As for the constant term, we can perform a similar trick. The constant term is obtained by multiplying the constant terms from each of the factors \((-1)^3(-2)(2) = 4\). 2

Subsection Footnotes

1  Technically, \( 0^0 \) is an indeterminate form, which is a special case of being undefined. The authors realize this is beyond pedantry, but we wouldn’t mention it if we didn’t feel it was necessary.

2  Whatever you do, please please please do not think we are saying \( (2x - 1)^3 = (2x)^2 - (1)^3 \). This is  absolutely not true ! In fact, \[ (2x - 1)^3 =  (2x - 1)(2x - 1)(2x - 1) = (2x - 1)(4x^2 -4x +1) = 8x^3 -16x^2 + 6x - 1. \nonumber \]We hope you see the difference.

Applications Involving Polynomial Functions

Our next example shows how polynomials of higher-degree arise "naturally" in even the most basic geometric applications. 3

Example \( \PageIndex{3} \)

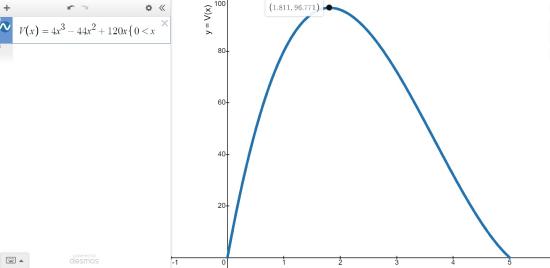
A box with no top is to be fashioned from a \(10\) inch \(\times\) \(12\) inch piece of cardboard by cutting out congruent squares from each corner of the cardboard and then folding the resulting tabs. Let \(x\) denote the length of the side of the square which is removed from each corner (see Figure \( \PageIndex{1} \)).

• Find the volume \(V\) of the box as a function of \(x\). Include an appropriate applied domain.
• Use graphing technology to graph \(y=V(x)\) on the domain you found in part 1 and approximate the dimensions of the box with maximum volume to two decimal places. What is the maximum volume?
• From Geometry, we know that \[\mbox{Volume} = \mbox{width} \times \mbox{height} \times \mbox{depth}.\nonumber\]The key is to find each of these quantities in terms of \(x\). From the Figure \( \PageIndex{1} \), we see that the height of the box is \(x\) itself. The cardboard piece is initially \(10\) inches wide. Removing squares with a side length of \(x\) inches from each corner leaves \(10-2x\) inches for the width. 4  As for the depth, the cardboard is initially \(12\) inches long, so after cutting out \(x\) inches from each side, we would have \(12-2x\) inches remaining. As a function of \(x\), 5 the volume is \[V(x) = x(10-2x)(12-2x) = 4x^3-44x^2+120x.\nonumber\]To find a suitable applied domain, we note that to make a box at all we need \(x > 0\). Also the shorter of the two dimensions of the cardboard is \(10\) inches, and since we are removing \(2x\) inches from this dimension, we also require \(10 - 2x > 0\) or \(x < 5\). Hence, our applied domain is \(0 < x < 5\).
• Using Desmos, we see that the graph of \(y=V(x)\) has a relative maximum. For \(0 < x < 5\), this is also the absolute maximum. Clicking on the curve in Desmos, we find that this maximum occurs at approximately \( (1.811, 96.771)\). This yields a height of \(x \approx 1.81\) inches, a width of \(10 - 2x \approx 6.38\) inches, and a depth of \(12 - 2x \approx 8.38\) inches. The \(y\)-coordinate is the maximum volume, which is approximately \(96.77\) cubic inches (also written \(\mbox{in}^3\)).

3  We understand that "naturally" is a  very  dangerous word in Mathematics.

4  There’s no harm in taking an extra step here and making sure this makes sense. If we chopped out a \(1\) inch square from each side, then the width would be \(8\) inches, so chopping out \(x\) inches would leave \(10−2x\) inches.

5  When we write \(V(x)\), it is in the context of function notation, not the volume \(V\) times the quantity \(x\).

End Behavior of Monomials

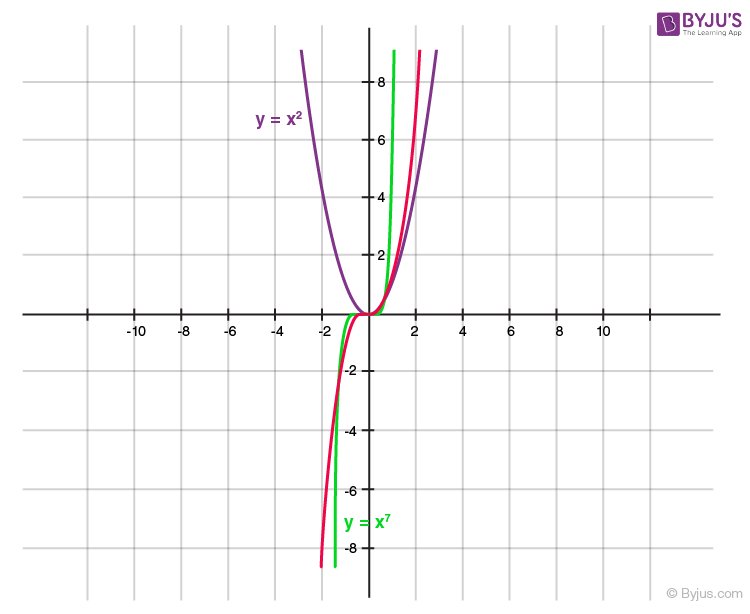
In order to solve Example \( \PageIndex{3} \), we made good use of the graph of the polynomial \(y=V(x)\), so we ought to turn our attention to graphs of polynomials in general. Figure \( \PageIndex{3} \) shows the graphs of \(y=x^2\), \(y=x^4\), and \(y=x^6\), side-by-side. We have omitted the axes to allow you to see that as the exponent increases, the "bottom" becomes "flatter" and the "sides" become "steeper." If you take the the time to graph these functions by hand, you will see why. 6

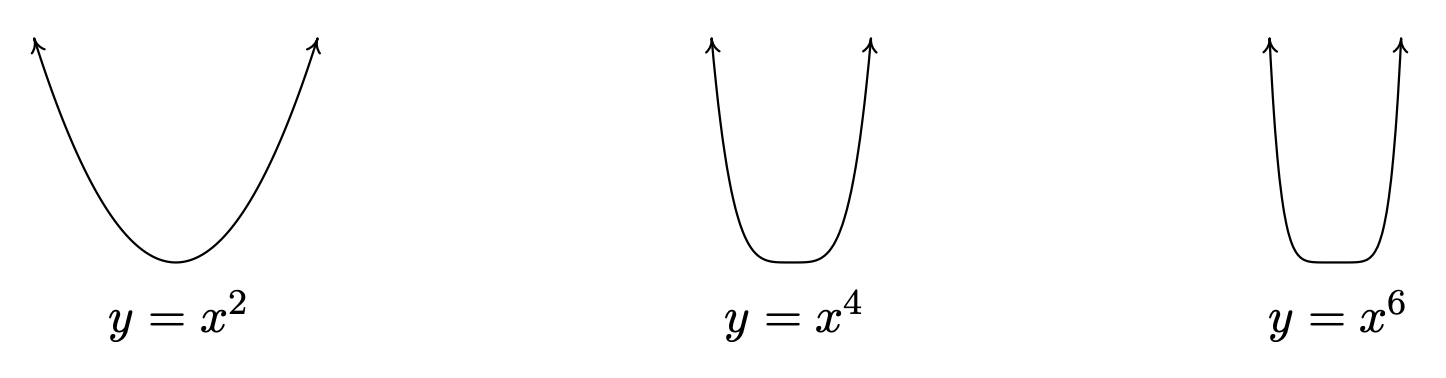
All of these functions are even, 7 and it is exactly because the exponent is even. 8  This symmetry is important, but we want to explore a different yet equally important feature of these functions which can be seen graphically – their end behavior .

The end behavior of a function is a way to describe what is happening to the function values (the \(y\)-values) as the \(x\)-values approach the "ends" of the \(x\)-axis. 9  That is, what happens to \(y\) as \(x\) becomes negatively large without bound (written \(x \to -\infty\)) and, on the flip side, as \(x\) becomes positively large without bound (written \(x \to \infty\)).

For example, given \(f(x) = x^2\), as \(x \to -\infty\), we imagine substituting \(x=-100\), \(x=-1000\), etc., into \(f\) to get \(f(-100)=10000\), \(f(-1000)=1000000\), and so on. Thus the function values are becoming larger and larger positive numbers (without bound). To describe this behavior, we write: as \(x \to -\infty\), \(f(x) \to \infty\). If we study the behavior of \(f\) as \(x \to \infty\), we see that in this case, too, \(f(x) \to \infty\). (We told you that the symmetry was important!) The same can be said for any function of the form \(f(x) = x^n\) where \(n\) is an even natural number. If we generalize just a bit to include vertical scalings and reflections across the \(x\)-axis, we have the following theorem.

Theorem \(\PageIndex{1}\): End Behavior of \( f(x) = x^n \), where \( n \) is Even

Suppose \(f(x) = a x^{n}\) where \(a \neq 0\) is a real number and \(n\) is an even natural number. The end behavior of the graph of \(y=f(x)\) matches one of the following:

• for \(a > 0\), as \(x \to -\infty\), \(f(x) \to \infty\) and as \(x \to \infty\), \(f(x) \to \infty\)
• for \(a < 0\), as \(x \to -\infty\), \(f(x) \to -\infty\) and as \(x \to \infty\), \(f(x) \to -\infty\)

Graphically:

We now turn our attention to functions of the form \(f(x) = x^{n}\) where \(n \geq 3\) is an odd natural number. (We ignore the case when \(n=1\), since the graph of \(f(x)=x\) is a line and doesn’t fit the general pattern of higher-degree odd polynomials.) The graphs of \(y=x^3\), \(y=x^5\), and \(y=x^7\) are shown in Figure \( \PageIndex{4} \). The "flattening" and "steepening" that we saw with the even powers presents itself here as well, and, it should come as no surprise that all of these functions are odd. 10  The end behavior of these functions is all the same, with \(f(x) \to -\infty\) as \(x \to -\infty\) and \(f(x) \to \infty\) as \(x \to \infty\).

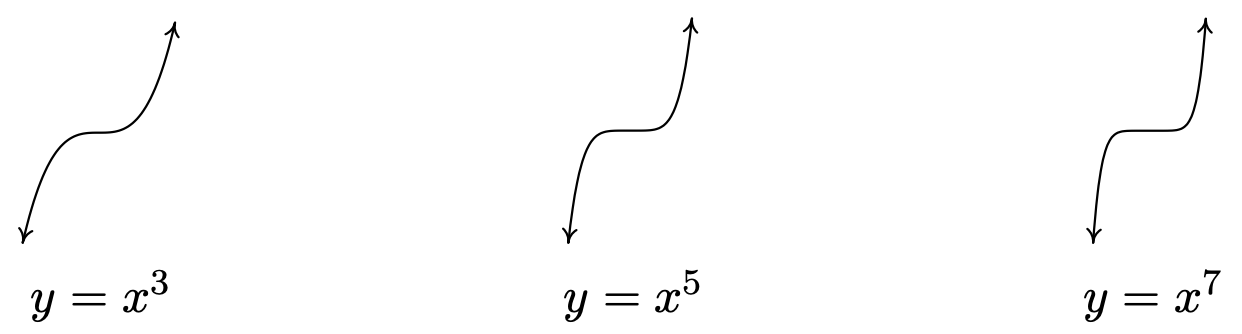
As with the even degreed functions we studied earlier, we can generalize their end behavior.

Theorem \(\PageIndex{2}\): End Behavior of \( f(x) = x^n \), where \( n \) is Odd

Suppose \(f(x) = a x^{n}\) where \(a \neq 0\) is a real number and \(n \geq 3\) is an odd natural number. The end behavior of the graph of \(y=f(x)\) matches one of the following:

• for \(a > 0\), as \(x \to -\infty\), \(f(x) \to -\infty\) and as \(x \to \infty\), \(f(x) \to \infty\)
• for \(a < 0\), as \(x \to -\infty\), \(f(x) \to \infty\) and as \(x \to \infty\), \(f(x) \to -\infty\)

6  Make sure you choose some \(x\)-values between \(−1\) and \(1\).

7  It's a good idea to review how to show a function is even or odd. This skill comes in very handy in calculus.

8  Herein lies one of the possible origins of the term "even" when applied to functions.

9  Of course, there are no ends to the \(x\)-axis.

10  And are, perhaps, the inspiration for the moniker "odd function."

The Intermediate Value Theorem

Despite having different end behavior, all functions of the form \(f(x) = ax^{n}\) for natural numbers \(n\) share two properties which help distinguish them from other animals in the algebra zoo: they are continuous and smooth . While these concepts are formally defined using Calculus, 11  informally, graphs of continuous functions have no "breaks" or "holes" in them, and the graphs of smooth functions have no "sharp turns." It turns out that these traits are preserved when functions are added together, so general polynomial functions inherit these qualities.

Figure \( \PageIndex{6}A \) shows the graph of a function which is neither smooth nor continuous, and Figure \( \PageIndex{6}B \) shows the graph of a polynomial, for comparison. The function in \( \PageIndex{6}A \) fails to be continuous where it has a "break" or "hole" in the graph; everywhere else, the function is continuous. The function is continuous at the "corner" and the "cusp," but we consider these "sharp turns," so these are places where the function fails to be smooth. Apart from these four places, the function is smooth and continuous. Polynomial functions are smooth and continuous everywhere, as exhibited in Figure \( \PageIndex{6}B \).

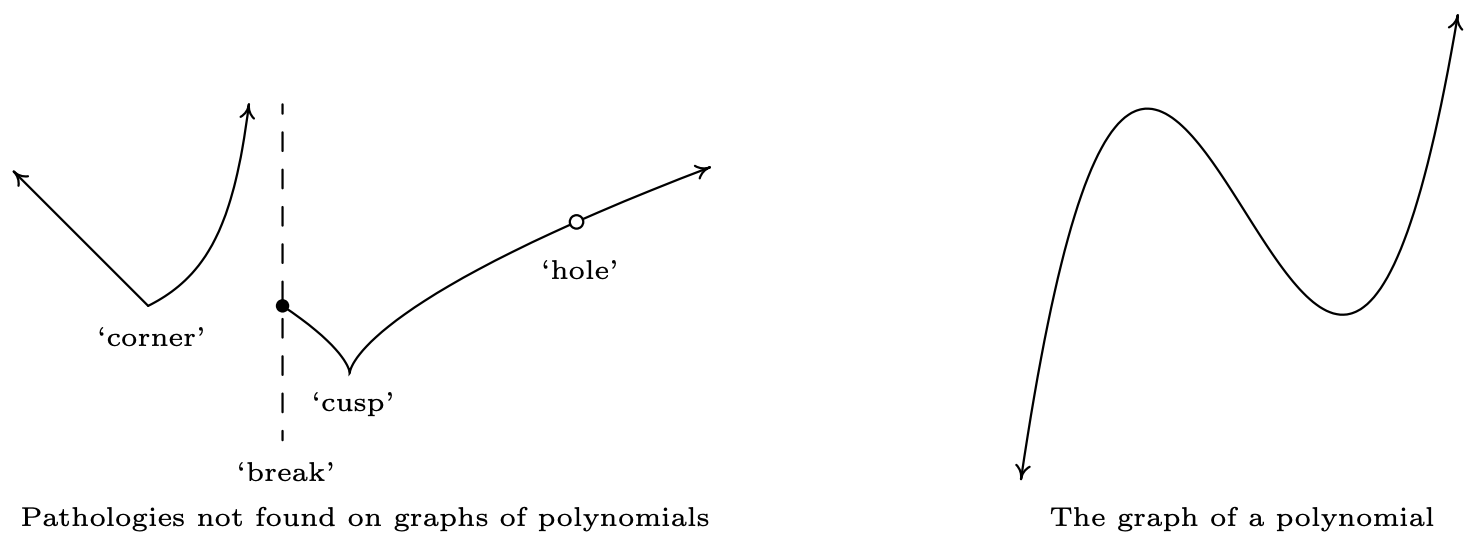
The notion of smoothness is what tells us graphically that, for example, \(f(x) = |x|\), whose graph is the characteristic "\(\vee\)" shape, cannot be a polynomial. The notion of continuity is what allowed us to construct the sign diagram for quadratic inequalities as we did in Section 2.4 . This last result is formalized in the following theorem.

Theorem \(\PageIndex{2}\): Intermediate Value Theorem

Suppose \(f\) is a continuous function on an interval containing \(x=a\) and \(x=b\) with \(a<b\). If \(f(a)\) and \(f(b)\) have different signs, then \(f\) has at least one zero between \(x = a\) and \(x = b\); that is, for at least one real number \(c\) such that \(a < c < b\), we have \(f(c) = 0\).

The version of the Intermediate Value Theorem presented here is sometimes called the "Zero Version" due to the fact that it guarantees a continuous function that switches signs on the closed interval \( \left[ a, b \right] \) must have a zero on the open interval \( \left( a, b \right) \).

The Intermediate Value Theorem is extremely profound; it gets to the heart of what it means to be a real number, and is one of the most often used and underappreciated theorems in Mathematics. With that being said, most students see the result as common sense since it says, geometrically, that the graph of a polynomial function cannot be above the \(x\)-axis at one point and below the \(x\)-axis at another point without crossing the \(x\)-axis somewhere in between. The following example uses the Intermediate Value Theorem to establish a fact that that most students take for granted. Many students, and sadly some instructors, will find it silly.

Example \( \PageIndex{4} \)

Use the Intermediate Value Theorem to establish that \(\sqrt{2}\) is a real number.

Consider the polynomial function \[f(x) = x^2 - 2.\nonumber \]Then \(f(1) = -1\) and \(f(3) = 7\). Since \(f(1)\) and \(f(3)\) have different signs, the Intermediate Value Theorem guarantees us a real number \(c\) between \(1\) and \(3\) with \(f(c) = 0\). If \(c^2 - 2 = 0\) then \(c = \pm \sqrt{2}\). Since \(c\) is between \(1\) and \(3\), \(c\) is positive, so \(c = \sqrt{2}\) and, therefore, \( \sqrt{2} \) must be a real number.

11  In fact, if you take Calculus, you’ll find that smooth functions are automatically continuous, so that saying "polynomials are continuous and smooth" is redundant.

End Behavior of Polynomials

Our primary use of the Intermediate Value Theorem is in the construction of sign diagrams, as in Section 2.4 , since it guarantees us that polynomial functions are always positive \((+)\) or always negative \((-)\) on intervals which do not contain any of its zeros. The next example illustrates the procedure.

Example \( \PageIndex{5} \)

Construct a sign diagram for \(f(x) = x^3 (x-3)^2 (x+2) \left(x^2+1\right)\). Use it to give a rough sketch of the graph of \(y=f(x)\).

First, we find the zeros of \(f\) by solving \(x^3 (x-3)^2 (x+2)\left(x^2+1\right)=0\). We get \(x=0\), \(x=3\) and \(x=-2\). (The equation \(x^2+1=0\) produces no real solutions.) These three points divide the real number line into four intervals: \[(-\infty, -2), (-2,0), (0,3), \text{ and } (3,\infty).\nonumber \]We select the test values \(x=-3\), \(x=-1\), \(x=1\) and \(x=4\), and find that \(f(-3)\) is \((+)\), \(f(-1)\) is \((-)\) and \(f(1)\) is \((+)\) as is \(f(4)\). Wherever \(f\) is \((+)\), its graph is above the \(x\)-axis; wherever \(f\) is \((-)\), its graph is below the \(x\)-axis. The \(x\)-intercepts of the graph of \(f\) are \((-2,0)\), \((0,0)\) and \((3,0)\). Knowing \(f\) is smooth and continuous allows us to sketch its graph.

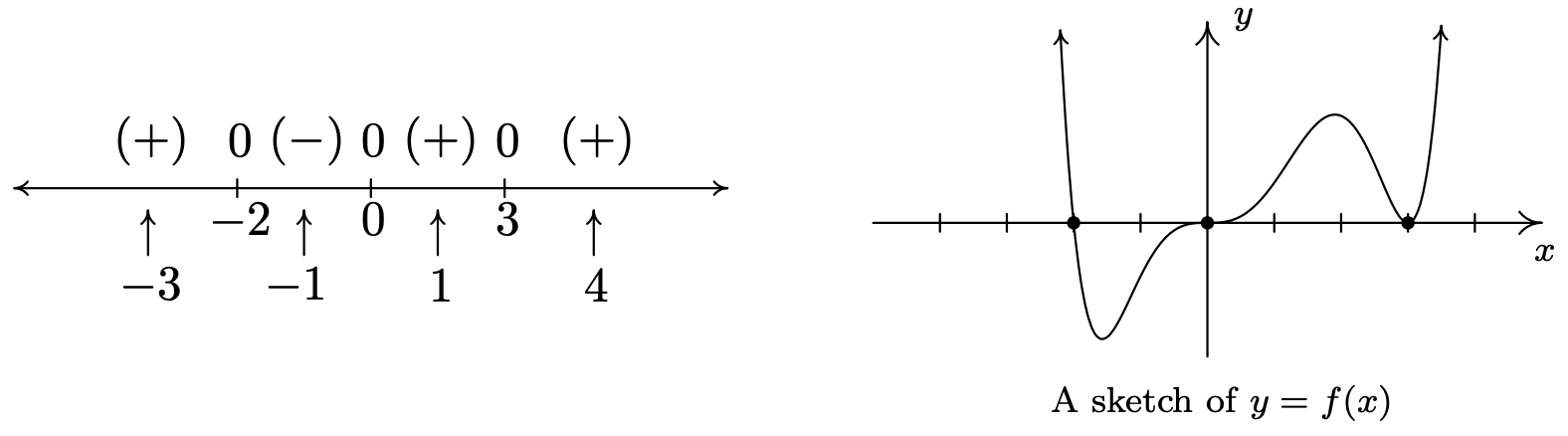
A couple of notes about Example \( \PageIndex{5} \) are in order. First, note that we purposefully did not label the \(y\)-axis in the sketch of the graph of \(y=f(x)\). This is because the sign diagram gives us the zeros and the relative position of the graph - it doesn’t give us any information as to how high or low the graph strays from the \(x\)-axis. Furthermore, as we have mentioned earlier in the text, without Calculus, the values of the relative maximum and minimum can only be found approximately using a calculator. If we took the time to find the leading term of \(f\), we would find it to be \(x^8\). Looking at the end behavior of \(f\), we notice that it matches the end behavior of \(y=x^8\). This is no accident, as we find out in the next theorem.

Theorem \(\PageIndex{3}\): End Behavior of Polynomial Functions

The end behavior of a polynomial \(f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{2} x^{2}+a_{1} x+a_{0} \text { with } a_{n} \neq 0\) matches the end behavior of \(y = a_{n} x^{n}\).

To see why Theorem \( \PageIndex{3} \) is true, let’s first look at a specific example. Consider \(f(x) = 4x^3 - x + 5\). If we wish to examine end behavior, we look to see the behavior of \(f\) as \(x \to \pm \infty\). Since we’re concerned with \(x\)’s far down the \(x\)-axis, we are far away from \(x=0\) so can rewrite \(f(x)\) for these values of \(x\) as

\[f(x) = 4x^3 \left( 1 - \dfrac{1}{4x^2} + \dfrac{5}{4x^3}\right) \nonumber \]

As \(x\) becomes unbounded (in either direction), the terms \(\dfrac{1}{4x^2}\) and \(\dfrac{5}{4x^3}\) become closer and closer to \(0\), as the table below indicates.

\[\begin{array}{|r||r|r|} \hline x & \dfrac{1}{4x^2} & \dfrac{5}{4x^3} \vphantom{\dfrac{a}{a}} \\[4pt] \hline -1000 & 0.00000025 & -0.00000000125 \\ \hline -100 & 0.000025 & -0.00000125 \\ \hline -10 & 0.0025 & -0.00125 \\ \hline 10 & 0.0025 & 0.00125 \\ \hline 100 & 0.000025 & 0.00000125 \\ \hline 1000 & 0.00000025 & 0.00000000125 \\ \hline \end{array}\nonumber \]

In other words, as \(x \to \pm \infty\), \(f(x) \approx 4x^3\left( 1 - 0 +0\right) = 4x^3\), which is the leading term of \(f\). The formal proof of Theorem \( \PageIndex{3} \) works in much the same way. Factoring out the leading term leaves

\[f(x) = a_{n} x^{n} \left( 1 + \dfrac{a_{n - 1}}{a_{n} x}+ \ldots + \dfrac{a_2}{a_{n} x^{n-2}} + \dfrac{a_1}{a_{n} x^{n-1}}+\dfrac{a_0}{a_{n} x^{n}}\right)\nonumber \]

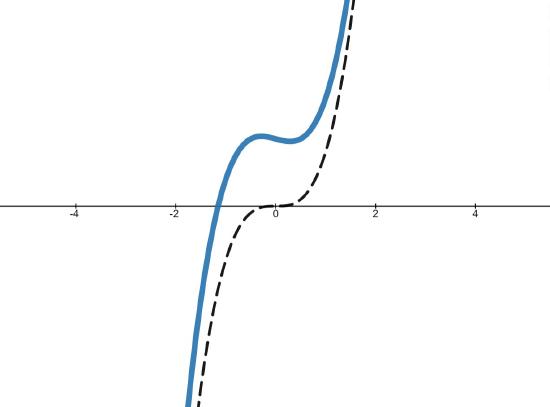
As \(x \to \pm \infty\), any term with an \(x\) in the denominator becomes closer and closer to \(0\), and we have \(f(x) \approx a_{n} x^{n}\). Geometrically, Theorem \( \PageIndex{3} \) says that if we graph \(y=f(x)\) using graphing technology, and continue to "zoom out," the graph of it and its leading term become indistinguishable. Figure \( \PageIndex{8} \) shows the graphs of \(y=4x^3-x+5\) (the solid blue line) and \(y=4x^3\) (the dashed black line) in two different windows.

Middle Behavior of Polynomials

Let’s return to the function in Example \( \PageIndex{5} \), \(f(x) = x^3 (x-3)^2 (x+2)\left(x^2+1\right)\), whose sign diagram and graph are reproduced in Figure \( \PageIndex{9} \) below for reference. Theorem \( \PageIndex{3} \) tells us that the end behavior is the same as that of its leading term, \(x^{8}\). This tells us that the graph of \(y=f(x)\) starts and ends above the \(x\)-axis. In other words, \(f(x)\) is \((+)\) as \(x \to \pm \infty\), and as a result, we no longer need to evaluate \(f\) at the test values \(x=-3\) and \(x=4\).

Is there a way to eliminate the need to evaluate \(f\) at the other test values? What we would really need to know is how the function behaves near its zeros - does it cross through the \(x\)-axis at these points, as it does at \(x=-2\) and \(x=0\), or does it simply touch and rebound like it does at \(x=3\). From the sign diagram, the graph of \(f\) will cross the \(x\)-axis whenever the signs on either side of the zero switch (like they do at \(x=-2\) and \(x=0\)); it will touch when the signs are the same on either side of the zero (as is the case with \(x=3\)). What we need to determine is the reason behind whether or not the sign change occurs.

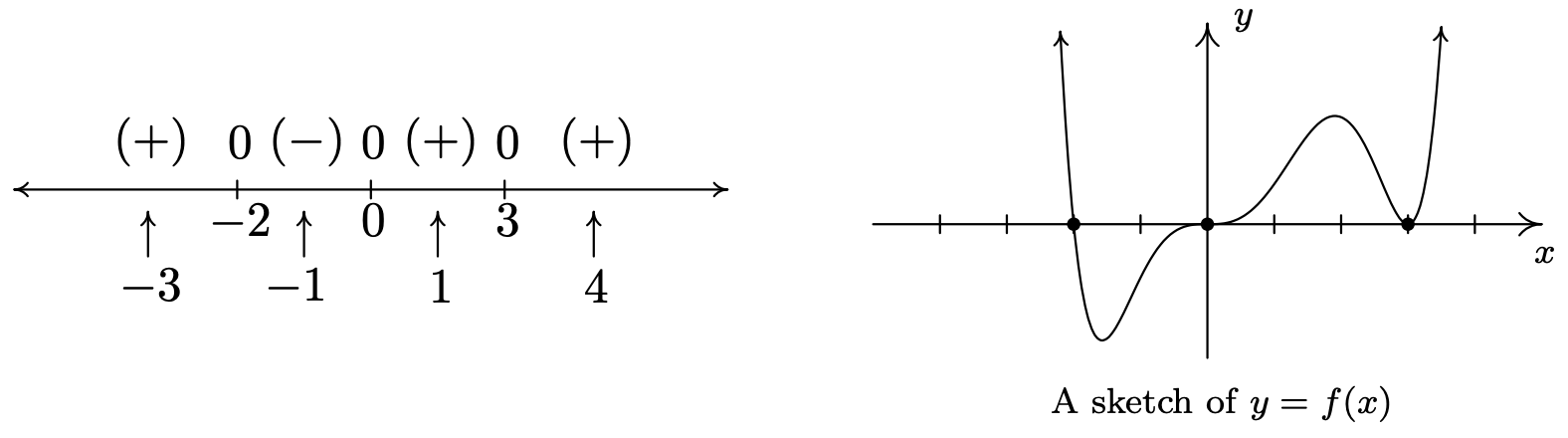
Fortunately, \(f\) was given to us in factored form: \(f(x) = x^3 (x-3)^2 (x+2)\). When we attempt to determine the sign of \(f(-4)\), we are attempting to find the sign of the number \((-4)^3 (-7)^2 (-2)\), which works out to be \((-)(+)(-)\) which is \((+)\). If we move to the other side of \(x=-2\), and find the sign of \(f(-1)\), we are determining the sign of \((-1)^3 (-4)^2 (+1)\), which is \((-)(+)(+)\) which gives us the \((-)\). Notice that signs of the first two factors in both expressions are the same in \(f(-4)\) and \(f(-1)\). The only factor which switches sign is the third factor, \((x+2)\), precisely the factor which gave us the zero \(x=-2\). If we move to the other side of \(0\) and look closely at \(f(1)\), we get the sign pattern \((+1)^3(-2)^2(+3)\) or \((+)(+)(+)\) and we note that, once again, going from \(f(-1)\) to \(f(1)\), the only factor which changed sign was the first factor, \(x^3\), which corresponds to the zero \(x=0\). Finally, to find \(f(4)\), we substitute to get \((+4)^3(+2)^2(+5)\) which is \((+)(+)(+)\) or \((+)\). The sign didn’t change for the middle factor \((x-3)^2\). Even though this is the factor which corresponds to the zero \(x=3\), the fact that the quantity is squared kept the sign of the middle factor the same on either side of \(3\).

If we look back at the exponents on the factors \((x+2)\) and \(x^3\), we see that they are both odd, so as we substitute values to the left and right of the corresponding zeros, the signs of the corresponding factors change which results in the sign of the function value changing. This is the key to the behavior of the function near the zeros. We need a definition and then a theorem.

Definition: Multiplicity

Suppose \(f\) is a polynomial function and \(m\) is a natural number. If \((x-c)^{m}\) is a factor of \(f(x)\) but \((x-c)^{m+1}\) is not, then we say \(x=c\) is a zero of multiplicity \(m\).

Hence, rewriting \[f(x) = x^3 (x-3)^2 (x+2)\nonumber \] as \[f(x) = (x-0)^3 (x-3)^2 (x-(-2))^{1},\nonumber \]we see that \(x=0\) is a zero of multiplicity \(3\), \(x=3\) is a zero of multiplicity \(2\) and \(x=-2\) is a zero of multiplicity \(1\).

Theorem \(\PageIndex{4}\): Basic Behavior of a Polynomial Graph Near a Zero of Multiplicity \( m \)

Suppose \(f\) is a polynomial function and \(x=c\) is a zero of multiplicity \(m\).

• If \(m\) is even, the graph of \(y=f(x)\) touches and rebounds from the \(x\)-axis at \((c,0)\).
• If \(m\) is odd, the graph of \(y=f(x)\) crosses through the \(x\)-axis at \((c,0)\).

Example \(\PageIndex{6}\)

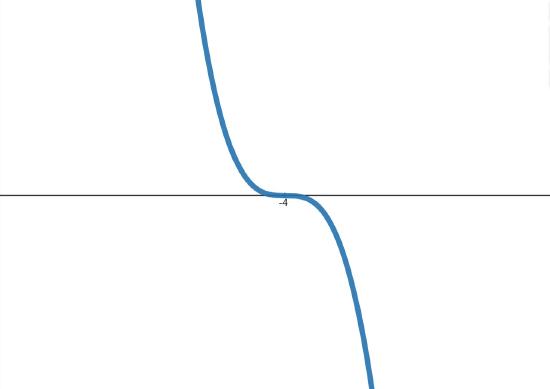
Determine the zeros, their associated multiplicities, and the basic behavior for the function near the zeros if

\[ f(x) = 3x^2 (x - 2) (x + 4)^3 (x - 8)^{10}. \nonumber \]

Luckily, \( f \) has already been "prefactored" for us. Making a table of the zeros, their associated multiplicities, and the corresponding behavior of the graph at those zeros, we get

\[ \begin{array}{|c||c|c|} \hline \text{Zero} & \text{Multiplicity} & \text{Basic Behavior} \\ \hline -4 & 3 & \text{crosses} \\ \hline 0 & 2 & \text{bounces} \\ \hline 2 & 1 & \text{crosses} \\ \hline 8 & 10 & \text{bounces} \\ \hline \end{array} \nonumber \]

The graph of \( f(x) \) near each zero is shown in Figure \( \PageIndex{9} \).

Looking at Figure \( \PageIndex{9} \) in Example \( \PageIndex{6} \), we can see that there is more to "local behavior" near the zero of a function than just "crossing" or "bouncing." The following theorem completes our investigation into the graphs of polynomials.

Theorem \(\PageIndex{5}\): Exact Behavior of a Polynomial Graph Near a Zero of Multiplicity \( m \)

Suppose \(f\) is a polynomial function and \(x=c\) is a zero of multiplicity \(m\). The "local behavior" of the graph of \( f \) near \( x = c \) is that of either \( y = (x - c)^m \) or \( y = -(x - c)^m \).

 Determining if it is \( + \) or \( - \) in the equation \( y = \pm (x - c)^m \) comes from starting the graph of the function. An example is very useful here.

Example \(\PageIndex{7}\)

Determine the zeros, their associated multiplicities, and the exact behavior for the function near the zeros if

\[ f(x) = 3x^2 (x - 2) (x + 4)^3 (x - 8)^{10} \nonumber \]

We first note that the overall degree of this polynomial is \( 2 + 1 + 3 + 10 = 16 \), which is even. Moreover, the leading coefficient would be positive (in fact, it would be \( +3 \)). These two pieces of information alone tell us that \( f(x) \to \infty \) as \( x \to \pm \infty \).

The zeros for the polynomial are \( x = 0 \) (multiplicity \( 2 \)), \( x = 2 \) (multiplicity \( 1 \)), \( x = -4 \) (multiplicity \( 3 \)), and \( x = 8 \) (multiplicity \( 10 \)); however, listing these in numerical order will be helpful, so we begin our table.

\[ \begin{array}{|c||c|c|} \hline \text{Zero} & \text{Multiplicity} & \text{Behavior} \\ \hline -4 & 3 &  \\ \hline 0 & 2 &  \\ \hline 2 & 1 &  \\ \hline 8 & 10 &  \\ \hline \end{array} \nonumber \]

We then use the multiplicities to fill in the "exact" behavior.

\[ \begin{array}{|c||c|c|} \hline \text{Zero} & \text{Multiplicity} & \text{Behavior} \\ \hline -4 & 3 &  (x + 4)^3 \\ \hline 0 & 2 &  x^2 \\ \hline 2 & 1 &  x - 2 \\ \hline 8 & 10 & (x - 8)^{10} \\ \hline \end{array} \nonumber \]

Notice that I don't list whether the local behavior is like \( +(x - c)^m \) or \( -(x - c)^m \). This is because that behavior will show itself during the graphing process naturally. The following animation displays the graphing behavior from left-to-right.

Sketching Graphs of Polynomials

We have finally arrived at our goal - to accurately graph a polynomial function. 12 Our last example shows how end behavior and multiplicity allow us to sketch a decent graph without appealing to a sign diagram.

Example \( \PageIndex{8} \)

Sketch the graph of \(f(x) = -3.1(2x-1)^5(x+1)^2\) using end behavior and the multiplicity of its zeros.

The end behavior of the graph of \(f\) will match that of its leading term. To find the leading term, we multiply by the leading terms of each factor to get \((-3.1)(2x)(x)^2 = -6.2x^3\). 13 This tells us that the graph will start above the \(x\)-axis, in Quadrant II, and finish below the \(x\)-axis, in Quadrant IV.

Next, we find the zeros of \(f\). Fortunately for us, \(f\) is factored. 14  Listing the zeros, their multiplicities, and their local behaviors, we get the following table.

\[ \begin{array}{|c||c|c|} \hline \text{Zero} & \text{Multiplicity} & \text{Behavior} \\ \hline -1 & 2 &  (x + 1)^2 \\ \hline \dfrac{1}{2} & 5 &  \left(x - \dfrac{1}{2}\right)^5 \\ \hline \end{array} \nonumber \]

Though we’re not asked to, we can find the \(y\)-intercept by finding \(f(0) = -3.1(2(0)-1)^5(0+1)^2 = 3.1\). Thus \((0,3.1)\) is an additional point on the graph. 15 Putting this together gives us the graph in Figure \( \PageIndex{10} \).

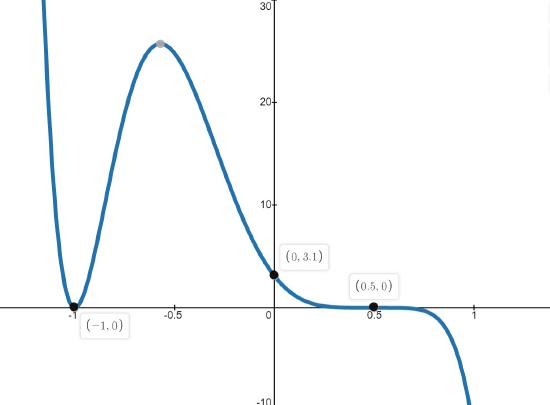
12  In reality, we still need Calculus to determine where the maximums and minimums occur, but we have developed everything we can  without  the use of Calculus to get a fairly decent sketch.

13  In truth, there is no need to worry about the \( 3.1 \) or \( 2 \) in this product. The important part is the  sign .

14  Obtaining the factored form of a polynomial is the main focus of the next few sections.

15  Finding the \( y \)-intercept in polynomial functions can either be simple (if the powers are low enough), or disastrously horrid (if the powers are large). You need to develop an intuitive sense of when finding the \( y \)-intercept is fruitful. Often, it's much better to just find the  sign  of the \( y \)-intercept so you can check that your polynomial graph is properly oriented.

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

How to Graph Polynomials – A Step-by-Step Beginner’s Guide

JUMP TO TOPIC

Steps Involved in Graphing Polynomials

Advanced concepts, real-world applications.

To graph polynomials, I always begin by identifying the polynomial function and its degree. The degree gives me valuable insight into the overall shape of the graph.

For instance, if I have a second-degree polynomial like $(f(x) = ax^2 + bx + c)$ , I know the graph is a parabola. When graphing higher-degree polynomials, such as $(f(x) = ax^n + … + k)$, where (n) is a positive integer, I look for turning points, which are one less than the degree of the polynomial.

My next step involves finding the roots of the polynomial, which are the values of (x) that make (f(x) = 0) . These correspond to the x-intercepts of the graph on a Cartesian plane.

Factoring the polynomial helps to find these roots easily. If the polynomial cannot be factored, I use numerical methods or graphing tools to estimate them.

By sketching a rough outline based on the degree and roots, I consider the leading coefficient to determine the end behavior of the graph . This tells me where the arms of the polynomial go at extreme values of (x); that is, as (x) approaches positive or negative infinity.

Graphing polynomials is a straightforward process when you follow these steps.

I’ll detail how to sketch the graph of a polynomial function by hand.

Determine the Degree and Leading Coefficient

• Find the degree of the polynomial . It’s the highest power of the variable in the equation .
• Identify the leading coefficient (the coefficient of the term with the highest power).

Analyze End Behavior

• Use the degree and the leading coefficient to predict the end behavior of the function. If the degree is odd and the leading coefficient is positive, the graph starts low and ends high.

Find the X- and Y-intercepts

• Solve the equation (f(x)=0) to find the x-intercepts or zeros .
• Substitute (x=0) to find the y-intercept .

Plot the Intercepts

• Place the intercepts on the graph . Remember, for zeros of even multiplicity , the graph touches the x-axis , and for zeros of odd multiplicity , it crosses the x-axis .

Draw and Refine the Graph

• Knowing that a polynomial function is continuous , draw a smooth curve through the intercepts , respecting the end behavior .
• Check for symmetry if applicable; an even degree may indicate the graph is symmetrical about the y-axis .

Remember, while graphing , keep the curve smooth since polynomial functions do not have breaks or sharp turns.

In graphing polynomials , one of my key considerations is identifying turning points .

These are points where the graph changes direction, and they’re essential for understanding the local behavior of the function. I use calculus to find turning points by setting the first derivative to zero and solving for the x -values.

Symmetry plays a role, too. If a function is even, its graph is symmetric about the y-axis, and if it’s odd, it’s symmetric about the origin. To check for symmetry, I substitute $-x$ for $x$ and see if I get the original function or its negative.

When I utilize technology like graphing calculators or computer software, I can quickly visualize the function and its properties. This is incredibly useful when dealing with complex polynomials that are not easily graphed by hand.

Here’s a quick table summarizing the checks for symmetry in polynomials:

When modeling real-world scenarios with polynomials, I ensure that my polynomial function accurately represents the data. For example, if I’m given a table of values, I can derive a polynomial that passes through those points using methods like polynomial interpolation.

In summary, graphing polynomials involves pinpointing turning points, assessing symmetry, utilizing technology for visualization, and ensuring the model suits the given data. By understanding these advanced concepts, I can unlock a deeper comprehension of polynomial behavior.

When I explore real-world applications of polynomials, their versatility truly shines. For instance, imagine a cable company determining its expected revenue for the upcoming years. Polynomials allow this company to create a model that predicts financial outcomes.

The shape of the graph of a revenue polynomial provides insights that are crucial for business planning.

For example, consider a polynomial representing revenue in millions of dollars against time in years. The x-values can represent the year , and the output gives the projected revenue.

Let’s say a revenue function is modeled as ( R(t) = -0.037t^4 + 1.414t^3 – 19.777t^2 + 118.696t – 205.332 ), where ( R ) represents the revenue in millions of dollars and ( t ) is the year with ( t = 6 ) corresponding to 2006.

By graphing this polynomial, I can identify the years of high and low revenue and plan accordingly.

Further, the visual representation aids in understanding at which points revenue increases or decreases, which can signal when to invest in marketing or expansion.

Understanding these patterns is valuable to both business strategists and economists who regularly employ polynomials to analyze and predict economic growth trends.

In graphing polynomial functions , my approach has been systematic, emphasizing the importance of understanding the core concepts such as zeros , multiplicities , end behavior , and intercepts .

Remember that zeros of odd multiplicity mean the graph will intersect and pass through the x-axis at those points, whereas even multiplicity indicates a touch and turn at the axis without crossing.

Identifying the degree of the polynomial is crucial because it influences the end behavior of the graph. A fundamental concept to remember is that the degree of the polynomial indicates the maximum number of turns the graph can take.

As a brief recap, for a polynomial function $ f(x) $ , the end behavior is determined by the leading coefficient and the degree of the function. If the degree is odd and the leading coefficient is positive, as $ x \rightarrow \infty $ , $ f(x) \rightarrow \infty $ and as $ x \rightarrow -\infty $ , $ f(x) \rightarrow -\infty $ .

Make use of the Intermediate Value Theorem to understand how polynomial functions behave between given points. This is especially useful to verify the existence of roots or zeros within certain intervals.

As you continue to practice and apply these principles in graphing polynomials , I trust you’ll find a growing confidence in interpreting and sketching these functions on your own.

The coherence between the algebraic form and graphical representation of polynomials is a powerful tool in the study and application of mathematics.

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

• Math Article
• Polynomial For Class 10

Polynomial Class 10 Notes: Chapter 2

Cbse class 10 maths notes polynomial:- download pdf here, class 10 maths chapter 2 polynomial notes.

CBSE Class 10 Maths Chapter 2 Polynomial Notes are provided here in detail. Here, we are going to discuss the complete explanation of what is polynomial and its types, algebraic expressions, degree of a polynomial expression, graphical representation of the polynomial equations, factorization, relationship between zeroes and coefficient of a polynomial, and so on with many examples.

Students can refer to the short notes and MCQ questions along with separate solution pdf of this chapter for quick revision from the links below:

• Polynomials Short Notes
• Polynomials MCQ Practice Questions
• Polynomials MCQ Practice Solutions

Algebraic Expressions

An algebraic expression is an expression made up of variables and constants along with mathematical operators. An algebraic expression is a sum of terms, which are considered to be building blocks for expressions.

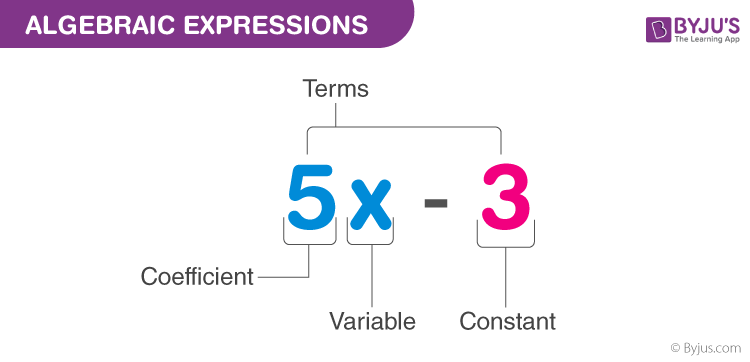
A term is a product of variables and constants. A term can be an algebraic expression in itself. Examples of a term – 3, which is just a constant. – 2x, which is the product of constant ‘2’ and the variable ‘x’ – 4xy, which is the product of the constant ‘4’ and the variables ‘x’ and ‘y’. – 5x 2 y, which is the product of 5, x, x and y.

The constant in each term is referred to as the coefficient.

Example of an algebraic expression: 3x 2 y+4xy+5x+6 which is the sum of four terms: 3x2y, 4xy, 5x and 6.

An algebraic expression can have any number of terms . The coefficient in each term can be any real number . There can be any number of variables in an algebraic expression. The exponent on the variables, however, must be rational numbers.

To know more about Algebraic Expressions, visit here .

An algebraic expression can have exponents that are rational numbers. However, a polynomial is an algebraic expression in which the exponent on any variable is a whole number.

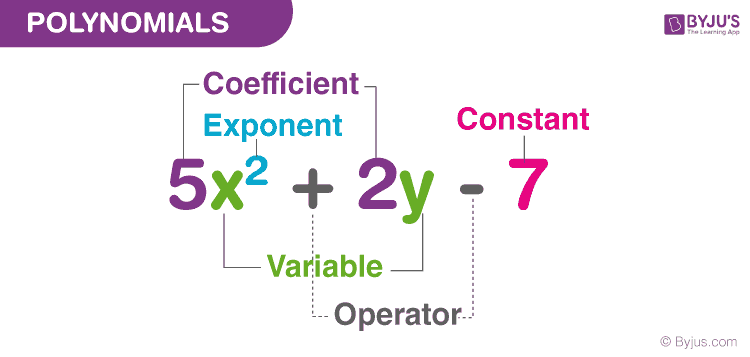
Let us consider a few more examples, 5x 3 +3x+1 is an example of a polynomial. It is an algebraic expression as well.

2x+3√x is an algebraic expression but not a polynomial. – since the exponent on x is 1/2, which is not a whole number.

To know more about polynomials, visit here .

Degree of a Polynomial

For a polynomial in one variable – the highest exponent on the variable in a polynomial is the degree of the polynomial.

Example: The degree of the polynomial x 2 +2x+3 is 2, as the highest power of x in the given expression is x 2 . Consider another example, the degree of the polynomial x 8 + 2x 6 – 3x + 9 is 8 since the greatest power in the given expression is 8.

Types Of Polynomials

Polynomials can be classified based on the following. a) Number of terms b) Degree of the polynomial.

Types of Polynomials Based on the Number of Terms

a) Monomial – A polynomial with just one term. Example: 2x, 6x 2 , 9xy

b) Binomial – A polynomial with two unlike terms. Example: 4x 2 +x, 5x+4

a) Trinomial – A polynomial with three unlike terms. Example: x 2 +3x+4

Types of Polynomials based on Degree

Linear Polynomial

A polynomial whose degree is one is called a linear polynomial. For example, 2x+1 is a linear polynomial.

Quadratic Polynomial

A polynomial of degree two is called a quadratic polynomial. For example, 3x 2 +8x+5 is a quadratic polynomial.

To know more about the types of polynomials, click here .

For more information on Quadratic Polynomials, watch the below video

Cubic Polynomial

A polynomial of degree three is called a cubic polynomial . For example, 2x 3 +5x 2 +9x+15 is a cubic polynomial.

Graphical Representations

Let us learn here how to represent polynomial equations on the graph.

Representing Equations on a Graph

Any equation can be represented as a graph on the Cartesian plane, where each point on the graph represents the x and y coordinates of the point that satisfies the equation. An equation can be seen as a constraint placed on the x and y coordinates of a point, and any point that satisfies that constraint will lie on the curve.

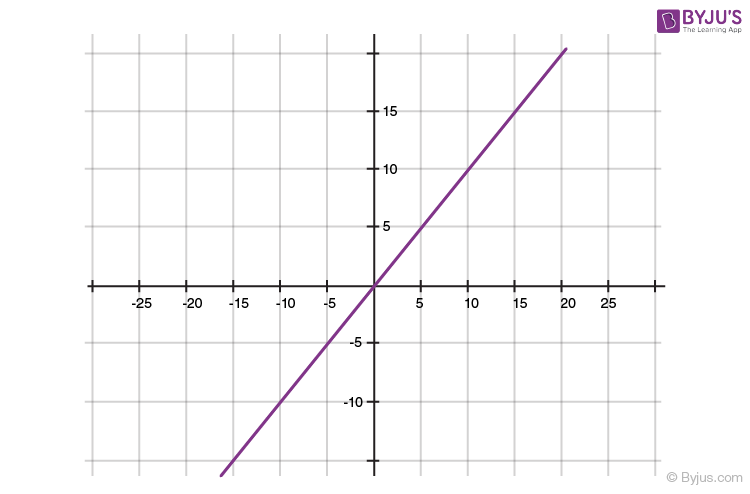
Geometrical Representation of a Linear Polynomial

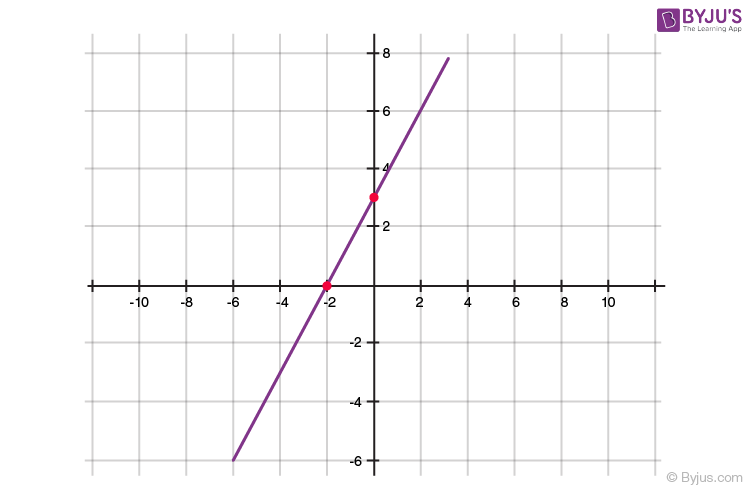
Geometrical Representation of a Quadratic Polynomial

• The graph of a quadratic polynomial is a parabola
• It looks like a U, which either opens upwards or opens downwards depending on the value of ‘a’ in ax 2 +bx+c
• If ‘a’ is positive, then parabola opens upwards and if ‘a’ is negative then it opens downwards
• It can cut the x-axis at 0, 1 or two points

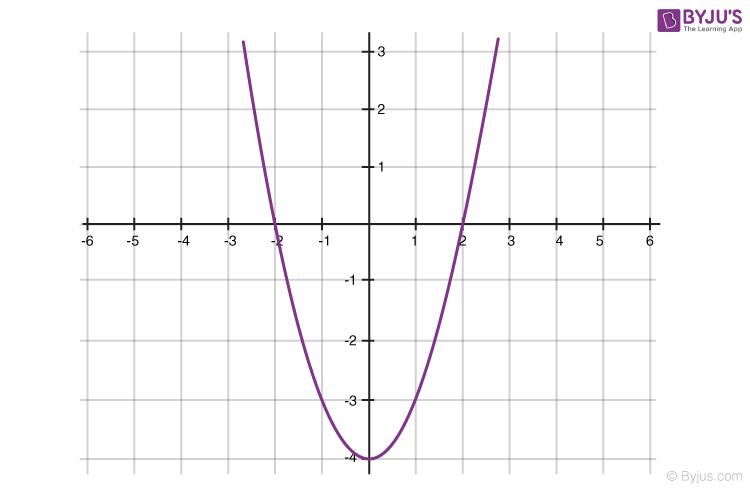
Graph of the Polynomial x^n

For a polynomial of the form y=x n where n is a whole number:

• as n increases, the graph becomes steeper or draws closer to the Y-axis
• If n is odd, the graph lies in the first and third quadrants
• If n is even, the graph lies in the first and second quadrants
• The graph of y=−x n is the reflection of the graph of y=x n on the x-axis

Zeroes of a Polynomial

A zero of a polynomial p(x) is the value of x for which the value of p(x) is 0. If k is a zero of p(x), then p(k)=0.

For example, consider a polynomial p(x)=x 2 −3x+2.

When x=1, the value of p(x) will be equal to

p(1)=12−3×1+2

Since p(x)=0 at x=1, we say that 1 is a zero of the polynomial x 2 −3x+2

Video Lesson on Zeroes of Polynomials

To know more about Zeroes of a Polynomial, visit here .

Geometrical Meaning of Zeros of a Polynomial

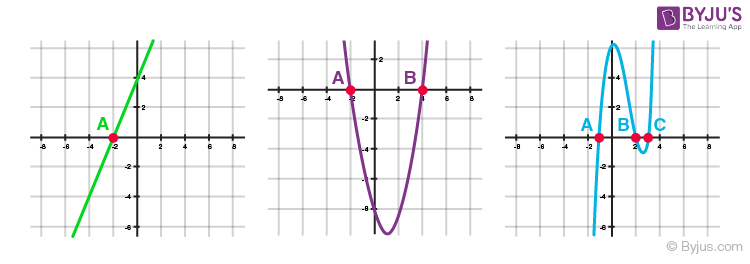
Here A, B and C correspond to the zeros of the polynomial represented by the graphs.

Number of Zeros

In general, a polynomial of degree n has at most n zeros.

• A linear polynomial has one zero,
• A quadratic polynomial has at most two zeros.
• A cubic polynomial has at most 3 zeros.

Factorisation of Polynomials

Quadratic polynomials can be factorized by splitting the middle term.

For example, consider the polynomial 2x 2 −5x+3

Splitting the middle term:

The middle term in the polynomial 2x 2 −5x+3 is -5x. This must be expressed as a sum of two terms such that the product of their coefficients is equal to the product of 2 and 3 (coefficient of x 2 and the constant term)

−5 can be expressed as (−2)+(−3), as −2×−3=6=2×3

Thus, 2x 2 −5x+3=2x 2 −2x−3x+3

Now, identify the common factors in individual groups

2x 2 −2x−3x+3=2x(x−1)−3(x−1)

Taking (x−1) as the common factor, this can be expressed as:

2x(x−1)−3(x−1)=(x−1)(2x−3)

For more information on Factorisation Of Quadratic Polynomials, watch the below video

To know more about Factorisation of Polynomials, visit here .

Relationship between Zeroes and Coefficients of a Polynomial

For Quadratic Polynomial: If α and β are the roots of a quadratic polynomial ax 2 +bx+c, then,

α +  β = -b/a

Sum of zeroes = -coefficient of x /coefficient of x 2

Product of zeroes = constant term / coefficient of x 2

For Cubic Polynomial

If α,β and γ are the roots of a cubic polynomial ax 3 +bx 2 +cx+d, then

α+β+γ = -b/a

αβ +βγ +γα = c/a

Calculate the sum of the zeroes and the product of the zeroes of the polynomial 9x 2 – 16x + 20.

Given polynomial: 9x 2 – 16x + 20

The given polynomial is a quadratic polynomial, as the degree of the polynomial is 2.

We know that the standard form of a quadratic polynomial is ax 2 + bx + c.

By comparing the given polynomial and the standard form, we can write.

By using the relationship between zeroes and the coefficients of the polynomial, we can get the following:

For a quadratic polynomial,

The sum of zeroes = -coefficient of x /coefficient of x 2

Now, substitute the values in the formula, we get

Sum of zeroes = -(-16)/9 = 16/9.

Similarly, Product of zeroes = constant term / coefficient of x 2

Plugging the values in the above formula, we get

Product of zeroes = 20/9

Hence, 16/9 and 20/9 are the sum and the product of the zeroes of the polynomial 9x 2 – 16x + 20.

To know more about Relationship between Zeroes and Coefficients of a Polynomial, visit here .

Division Algorithm

Let us assume that P(x) and G(x) are the two polynomials, such that G(x)≠ 0, then the division algorithm states the formula to find Q(x) and R(x) of the polynomial.

Here, P(x) denotes dividend polynomial

G(x) denotes divisor polynomial

Q(x) denotes quotient polynomial

R(x) denotes the remainder polynomial.

Thus, the formula stated by division algorithm is:

P(x) = G(x) × Q(x) + R(x)

To divide one polynomial by another, follow the steps given below.

Step 1: Arrange the terms of the dividend and the divisor in the decreasing order of their degrees.

Step 2: To obtain the first term of the quotient, divide the highest degree term of the dividend by the highest degree term of the divisor  Then carry out the division process.

Step 3: The remainder from the previous division becomes the dividend for the next step. Repeat this process until the degree of the remainder is less than the degree of the divisor.

Algebraic Identities

1. (a+b) 2 =a 2 +2ab+b 2

2. (a−b) 2 =a 2 −2ab+b 2

3. (x+a)(x+b)=x 2 +(a+b)x+ab

4. a 2 −b 2 =(a+b)(a−b)

5. a 3 −b 3 =(a−b)(a 2 +ab+b 2 )

6. a 3 +b 3 =(a+b)(a 2 −ab+b 2 )

7. (a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3

8. (a−b) 3 =a 3 −3a 2 b+3ab 2 −b 3

For more information on Algebraic Identities, watch the below videos

To know more about Algebraic Identities, visit here .

Polynomials for Class 10 Examples

Determine the quadratic polynomial, whose zeroes are 5-3√2 and 5+3√2.

Given zeroes: 5-3√2 and 5+3√2.

Finding sum of zeroes:

Sum of zeroes = (5-3√2)+(5+3√2)

Sum of zeroes = 5+5 = 10.

Finding product of zeroes:

Product of zeroes = (5-3√2)(5+3√2)

We know that a 2 -b 2 = (a+b)(a-b).

Hence, (5) 2 – (3√2) 2 = (5-3√2)(5+3√2).

Therefore, product of zeroes = 25 – [9(2)]= 25 – 18 = 7

Thus, the required quadratic polynomial is:

P(x)= x 2 -(sum of zeroes)x + product of zeroes

P(x) = x 2 -10x+7.

Hence, the required quadratic polynomial is x 2 -10x+7.

Find the zeroes of the quadratic polynomial 6x 2 -3-7x. Also, verify the relationship between the zeroes and the coefficient of a polynomial.

Given quadratic polynomial: 6x 2 -3-7x.

Let P(x) = 6x 2 -3-7x.

We know that zero of a polynomial is a value of x, when P(x) = 0.

Hence, 6x 2 -7x-3 = 0

Now, factorize the above polynomial equation to find the value of x.

Thus, 6x 2 -7x – 3 = 0 is also written as:

6x 2 -9x+2x-3 = 0

3x(2x-3)+1(2x-3) = 0

(3x+1) (2x-3) =0

Thus, 3x+1 = 0 and 2x-3 =0

⇒3x+1 = 0

⇒2x-3 = 0

⇒x = 3/2.

Hence, the zeroes of the quadratic polynomial 6x 2 – 7x-3 are -1/3 and 3/2.

Thus, α = -1/3 and β = 3/2 are the zeroes of the polynomial.

Now, comparing P(x) = 6x 2 -7x-3 with ax 2 +bx+c.

Hence, a = 6, b=-7 and c = -3.

Verifying the Relationship Between Zeroes and Coefficient of Polynomial:

Sum of zeroes:

We know that the sum of zeroes = – coefficient of x/Coefficient of x 2 .

Thus, α+β = -b/a

Now, substitute the values, we get

(-1/3)+(3/2) = -(-7)/6

(-2+9)/6 = 7/6

Hence, LHS = RHS.

Product of Zeroes:

We know that the product of zeroes = Constant term/Coefficient of x 2 .

Therefore, αβ = c/a

On substituting the values, we get

(-1/3)(3/2) = (-3/6)

-1/2 = -1/2

Therefore, the relationship between the zeroes and coefficients of the polynomial 6x 2 -7x-3 is verified.

Stay tuned with BYJU’S – The Learning App and download the app to learn all class-wise concepts easily by exploring more videos.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

it was very useful

This notes helped me a lot.

Very helpful and best material ever!!!!!!!!!!!1111

nice its helpful

really it will help me in board exams

I learnt a lot of formulas through these notes

it is very useful for me

it has many useful questions related to class 10 exams .

I test myself in quiz thanks a lot

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

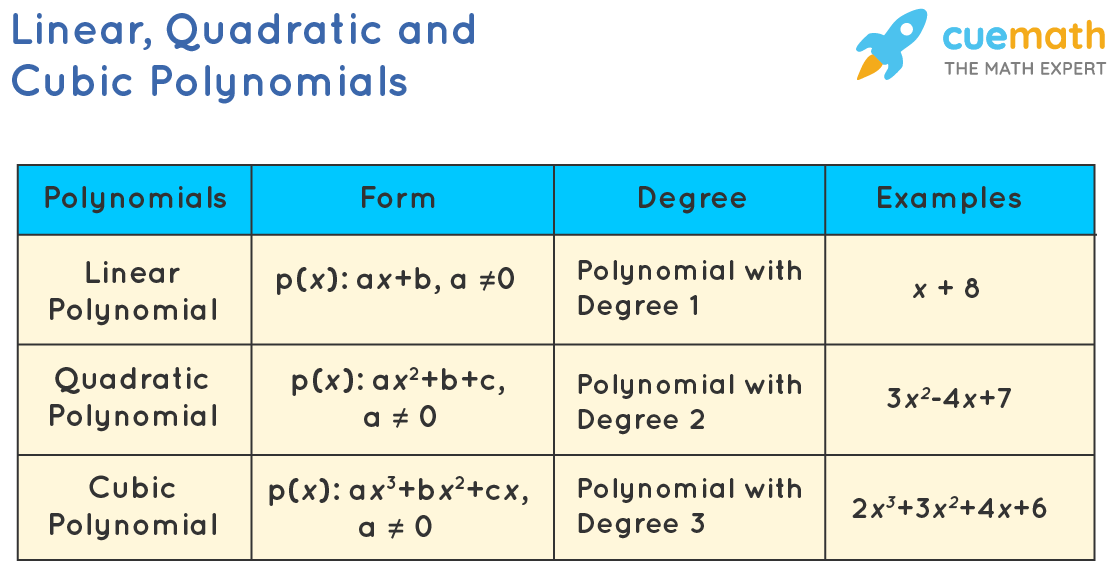
Linear, Quadratic and Cubic Polynomials

Polynomials are one of the significant concepts of mathematics, and so are the types of polynomials that are determined by the degree of polynomials, which further determines the maximum number of solutions a function could have and the number of times a function will cross the x-axis when graphed. Let's learn in detail about linear, quadratic, and cubic polynomials .

What are Linear, Quadratic and Cubic Polynomials?

Each of the polynomials has a specific degree and based on that they have been assigned a specific name and are thus referred to as different types of polynomials. Let's know about linear, quadratic, and cubic polynomials.

Linear Polynomials

A linear polynomial is a polynomial of degree one, i.e., the highest exponent of the variable is one, defined by an equation of the form: p(x): ax + b, a≠0.

Given below are a few examples of linear polynomials:

• p(x): 2x + 3
• q(y): πy + √2
• r(z): z + √5

We note that a linear polynomial in one variable can have at the most two terms. The constraint that a should not be equal to 0 is required because if a is 0, then this becomes a constant polynomial.

Example: Is 1/x a linear polynomial?

Solution: In general form, we can write it as 1/x -1 + 0. Clearly, the degree of this polynomial is not one, it is not a linear polynomial.

Quadratic Polynomials

A quadratic polynomial is a polynomial of degree two, i.e., the highest exponent of the variable is two. In general, a quadratic polynomial will be of the form: p(x): ax 2 + bx + c, a≠0

Given below are a few examples of quadratic polynomials:

• p(x): 3x 2 + 2x + 1
• q(y): y 2 − 1
• r(z): √2z 2

We observe that a quadratic polynomial can have at the most three terms. The constraint that a should not be equal to 0 is required because if a is 0, then this becomes a linear polynomial.

Example: Which of the following are quadratic polynomials?

• πx 2 /2 + x

Solution: In (1) and (3), the degree of polynomial is two. But In (2), the exponent of term 2/x is not a whole number. So, (1) and (3) are quadratic polynomials, and (2) are not even polynomial.

Cubic Polynomials

A cubic polynomial is a polynomial of degree three, i.e., the highest exponent of the variable is three. A cubic polynomial, in general, will be of the form p(x): ax 3 + bx 2 + cx + d, a≠0

Given below are a few examples of cubic polynomials:

• p(x): x 3 − 6x 2 + 11x − 6
• q(y): 27y 3 − 1
• r(z): πz 3 + (√2) 10

We observe that a cubic polynomial can have at the most four terms. Once again, the constraint that a should not be equal to 0 is required because if a is 0, then this becomes a quadratic rather than a cubic polynomial.

Tips and Tricks

• After converting any expression into the general form, if the exponent of the variable in any term is not a whole number , then it's not a polynomial either.
• For any polynomial of positive order, there are a maximum number of zeros equal to its order.

Important Notes

• Why do we use the adjective linear ? It turns out that when we draw the graph corresponding to a linear polynomial, we will get a straight line – hence the name linear.
• A polynomial of degree n will have n number of zeros or roots.
• A polynomial can have any number of terms, but never infinite.
• Zeros correspond to expressions, and roots correspond to equations.
• A linear polynomial has only one zero.
• A quadratic polynomial can have at most two zeros, whereas a cubic polynomial can have at most 3 zeros.

Related Topics

• Factors of a Polynomial
• Factorization of Quadratic Polynomials
• What are Roots in Polynomial Expression
• Zeroes of a Cubic Polynomial
• Zeroes of a Quadratic Polynomial
• Zeroes of a Linear Polynomial
• nth-Degree Polynomial
• Degree of the Remainder Polynomial
• Quadratic Equations
• Variables, Constants, and Expressions
• Polynomial Expressions
• Types of Polynomials
• Multiplication of Polynomials

Examples on Linear, Quadratic, and Cubic Polynomials

Example 1: Classify the given polynomials as linear, quadratic or cubic polynomials:

p(x): 5x 2 + 6x + 1 p(x): 2x + 3 q(z): z 2 − 1 r(z): z 2 + (√2) 9 r(z): √5z 2 s(x): 10x p(y): y 3 − 6y 2 + 11y − 6 q(y): 81y 3 − 1 r(z): z + 3

The given polynomials can be classified as follows:

Example 2: Verify whether the 1 and 0 are the zeros of the given polynomials:

27x 3 − 1 x + 2 2x 2 + x - 3

p(x) = 27x 3 − 1, p(0) = 27(0) 3 - 1 = - 1, p(1) = 27(1) 3 - 1 = 26. Therefore, 0 and 1 are not the zeros of the polynomial 27x 3 − 1 p(x) = x + 2, p(0) = (0) + 2 = 2, p(1) = (1) + 2 = 3. Therefore, 0 and 1 are not the zeros of the polynomial x + 2 p(x) = 2x 2 + x - 3, p(0) = 2(0) 2 + (0) - 3 = -3, p(1) = 2(1) 2 + (1) - 3 = 0. Therefore, 0 is the zero of the polynomial 2x 2 + x - 3 but 1 is not.

go to slide go to slide

Book a Free Trial Class

Practice Questions on Linear, Quadratic, and Cubic Polynomials

Faqs on linear, quadratic, and cubic polynomials, how do you know if a polynomial is linear.

A polynomial of degree one is called the linear polynomial. That is, the highest exponent of the variable is one, then the polynomial is said to be a linear polynomial.

How to Classify Linear, Quadratic, and Cubic Polynomials?

Linear, quadratic and cubic polynomials can be classified on the basis of their degrees.

• A polynomial of degree one is a linear polynomial. For example, 5x + 3
• A polynomial of degree two is a quadratic polynomial. For example, 2x 2 + x + 5
• A polynomial of degree three is a cubic polynomial. For example, y 3 − 6y 2 + 11y − 6

How to Solve Cubic Polynomials?

The most commonly used strategy for solving a cubic equation is

• Step 1: Reduce a cubic polynomial to a quadratic equation.
• Step 2: Solve the quadratic equation using the quadratic formula .

What is the Equation for Cubic Polynomials?

A cubic equation is an algebraic equation of degree three and is of the form ax 3 + bx 2 + cx + d = 0, where a, b and c are the coefficients and d is the constant.

How to Factor Quadratic Polynomials?

Factorization of cubic polynomials can be done by the following methods:

• Common Factor Method: In this method, we have to look at all the terms and determine the common terms. If there is a common term in the equation, we will factor it out for the polynomial.
• Sum of Difference Method: The sum and the difference of two terms is most likely used when the two factors match exactly, except one term involves addition and the other is a difference.
• Product Sum Method: In the product sum method for factoring polynomials, we use trinomials (ax 2 +bx+c), where the value of a is 1. This method is probably used the most for factoring polynomials.
• Factor by Grouping Method: Factor by grouping means that we have to group all the terms with common factors before factoring.
• Perfect Square Trinomials Method: The method of converting any trinomial into the perfect square is known as the perfect square trinomial method.

Talk to our experts

1800-120-456-456

• Geometrical Meaning of Zeroes of the Polynomial

Geometrical Meaning of Zeroes of the Polynomial : A Detailed Summary

Expression consists of variables, coefficients, and arithmetic operations . An expression may consist of more than one variable , and the variable's power is any real number.

Let’s understand polynomials definition with example ; a polynomial is an expression of one variable. The power of variables of a polynomial must be a natural number. A polynomial represented by P(x), where x is the variable of the polynomial. For example P(x) = \[2x^3+5x+3\].

Degree of a Polynomial

The degree of a polynomial is the highest power of the variable of the polynomial. The degree of linear polynomials is 1 because the highest degree of the polynomial is 1. The degree of a quadratic polynomial is 2 because the highest degree of the polynomial is 2. The degree of a cubic polynomial is 3 because the highest degree of the polynomial is 3.

Types of Polynomials

The type of polynomial depends on the degree of the polynomial.

The general form of a polynomial is \[P(x) = a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_1x+a_{0}\]

Constant polynomial: If \[a_{n}=a_{n-1}=\cdots =a_2=a_{1}=0\] and \[a_{0}\ne 0\], then the polynomial is known as a constant polynomial. For example: P(x) =3.

Zero polynomial: If \[a_{n}=a_{n-1}=\cdots =a_2=a_{1}=a_{0}= 0\], then the polynomial is known as a zero polynomial .

Linear polynomial: If \[a_{n}=a_{n-1} = a_2 = 0\] and \[a_{1}\ne 0\], then the polynomial is known as linear polynomial.

Quadratic polynomial: If \[a_{n}=a_{n-1} =\cdots =a_3=0\] and \[a_{2}\ne 0\], then the polynomial is known as quadratic polynomial.

Cubic polynomial: If \[a_{n}=a_{n-1} =\cdots0= a_4\] and \[a_{3}\ne 0\], then the polynomial is known as quadratic polynomial.

Zeroes of the Polynomial Definition

The zero of a polynomial is the value of the variable for which the value of the polynomial becomes zero.

The polynomial P(x) has a zero at x = a. This means the value of P(x) at x = a is zero that is P(a) = 0.

Assume a polynomial, \[ P(x)=2x+4\]

Now equate P(x) with zero.

\[\Rightarrow 2x+4=0\]

\[\Rightarrow 2x=-4\]

\[\Rightarrow x=-2\]

The zero of the polynomial P(x)=2x+4 is x = -2.

Number of Zeros of a Polynomial

The degree of a linear polynomial is 1. Thus the number of zeros of a linear polynomial is at most 1.

The degree of a quadratic polynomial is 2. Thus the number of zeros of a linear polynomial is at most 2.

The degree of a cubic polynomial is 3. Thus the number of zeros of a linear polynomial is at most 3.

How to Obtain the Zero of a Linear Polynomial Geometrically?

The degree of a polynomial is the highest power of the variable of the polynomial. The degree of a linear polynomial is 1. Thus the number of zeros of the polynomial is 1.

To get a zero of linear polynomials geometrically, we will find the point where the given linear polynomial cuts the x-axis. Suppose the polynomial cuts the x-axis at x = a, then the zero of the polynomial is a.

For Example,

Assume an equation of a linear polynomial P(x) = x+4.

The graphical representation of a linear polynomial is shown below:

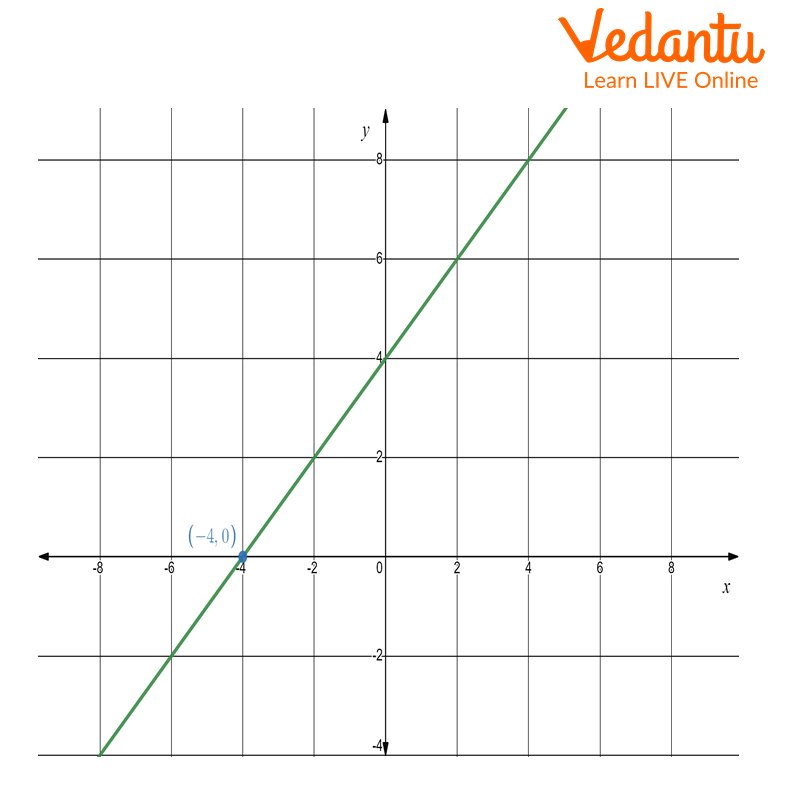
Linear polynomial

The linear polynomial P(x) cuts the x-axis at (-4,0). Thus the zero of the polynomial is -4. It means P(-4) = 0. The zero of the polynomial P(x) = x+4 is -4.

Since the given polynomial is a linear polynomial, thus it intersects the x-axis at a point.

Geometrical Meaning of the Zeros of a Polynomial

The number of zeros of a polynomial is dependent on the degree of that polynomial. The number of zeros of a polynomial is less than or equal to the degree of the polynomial. The number of zeros of a polynomial is equal x-intercepts of the polynomials.

Geometrical Representation of Zeros

The number of zeros is equal to the number of the x-intercept of the polynomial graph. Below we have the geometrical meaning of zeroes of polynomials with examples

Linear polynomial: The number of the x-intercepts is 1. Thus, the number of zeros is 1 for the linear polynomial.

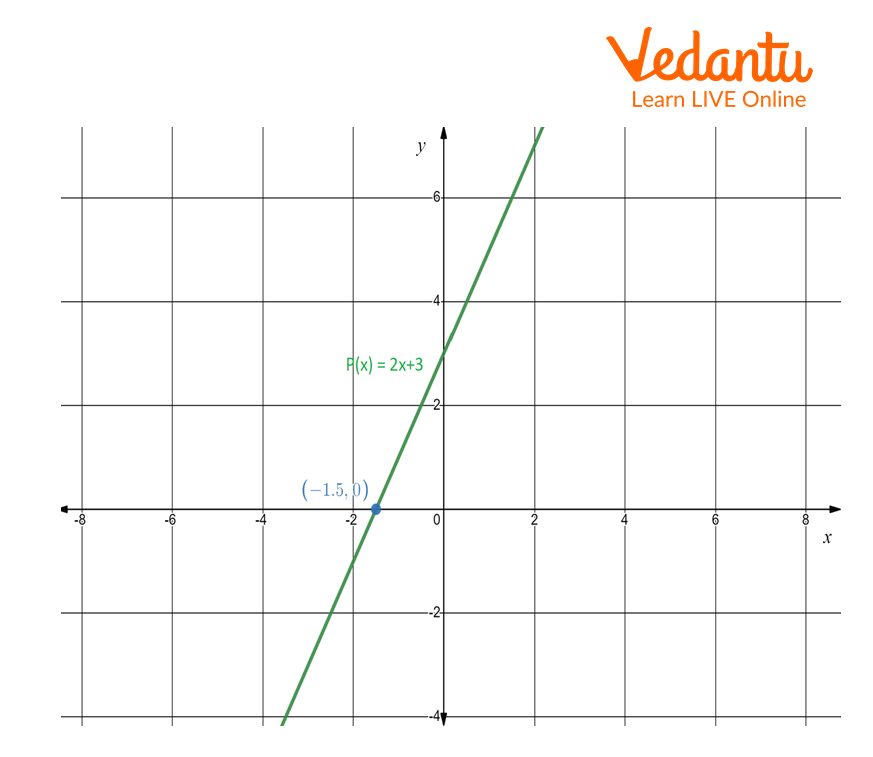
Graph of a linear polynomial

Quadratic polynomial: The quadratic polynomial has at most 2 zeros. Thus, the graph of quadratic polynomial intercepts at two points.

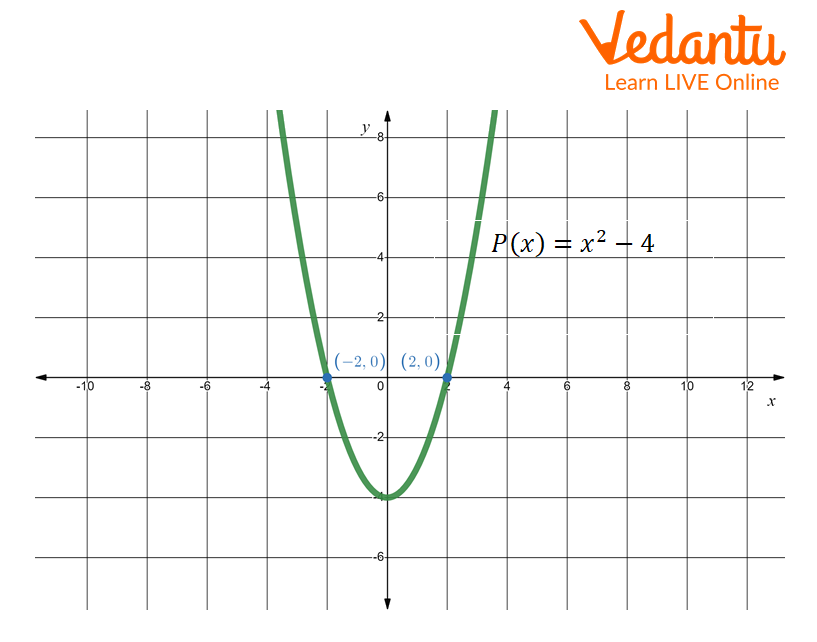
Graph of the quadratic polynomial

Cubic polynomial: The cubic polynomial has at most 3 zeros. Thus, the graph of cubic polynomial intercepts at three points.

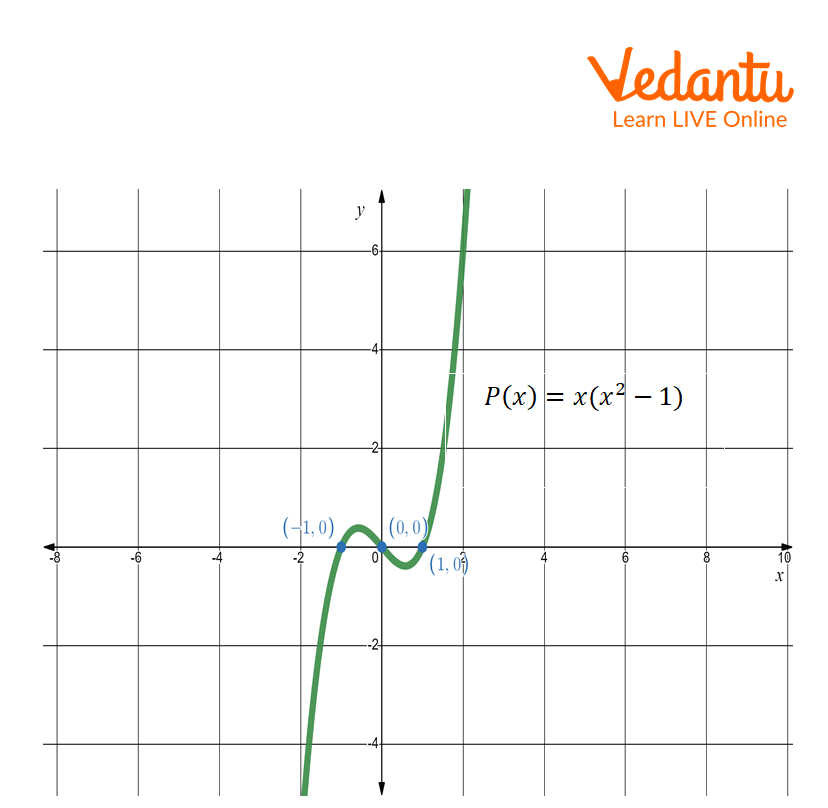
Graph of a cubic polynomial

Solved Problems

Q1 Find the number of zeroes of the polynomial in a given graph.

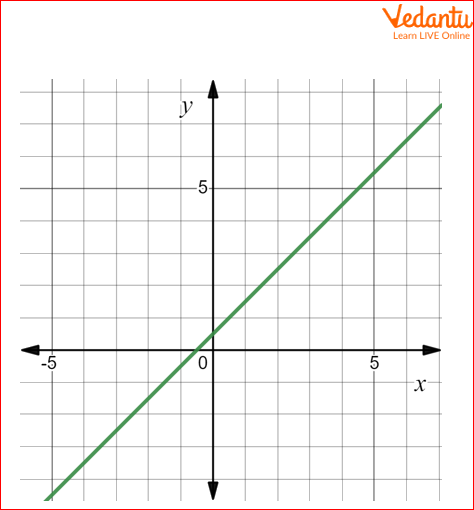
Solution 1: From the above geometrical presentation we can see that the straight line intersects the x-axis at one time , therefore the number of zeros in the given polynomial is one.

Q2 Find the zeros of the polynomial \[P(x) =4x^{2}-16\].

Solution 2: Given polynomial is \[P(x) =4x^{2}-16\].

Equate P(x) with zero:

\[4x^{2}-16=0\]

\[\Rightarrow 4x^{2}=16\]

Divide both sides by 4:

\[\Rightarrow x^{2}=4\]

Take square root both sides

\[\Rightarrow x=\pm 4\]

The zeros of the polynomial are \[\pm 4\].

Q3 Find out the zero of the polynomial y=x+1 geometrically.

Solution3: First we make the table for y=x+1

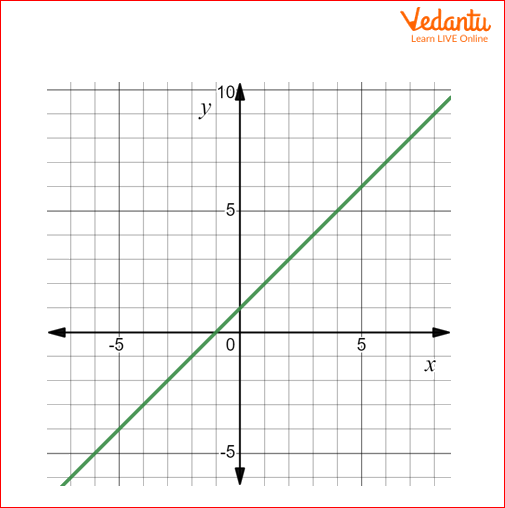
Graph for given table

We can see that at x=-1, given straight line intersecting the x-axis, therefore x=-1 is zero of the given polynomial.

Interesting Facts

If the zeros of a quadratic polynomial are the same, then the graph of the quadratic polynomial touches the x-axis at a point.

If the zeros of a cubic polynomial are the same, then the graph of the cubic polynomial cuts the x-axis at a point.

The number of zeros of a polynomial depends on the degree of the polynomial. The number of zeros of a polynomial equals the number of x-intercepts of the polynomial. If P(a) = 0, then a is a zero of the polynomial P(x). A linear polynomial has at most 1 zero. A quadratic polynomial has at most 2 zeros and a cubic polynomial has at most 3 zeros.

Practice Problem

Q1 Write the type of the given polynomial (1) 2x+3 (2) \[2x^{2}+3\]

Solution: (1) linear polynomial (2) Quadratic polynomial

Q2 From the given table find the zero of the polynomial.

Solution: The zero is X = 2

FAQs on Geometrical Meaning of Zeroes of the Polynomial

1. What are the parts of a polynomial?

The different parts of a polynomial are:

Terms: Each monomial is part of the polynomial.

Coefficients: The numbers that accompany each term of the polynomial.

Degree: The largest exponent to which the polynomial variable is raised.

Variable: It is the letter that has the polynomial.

2. What is the difference between zero of the polynomial and zero polynomial ?

A zero of a polynomial is the value where the polynomial becomes zero. 

For example: The zero of the polynomial P(x) = 4x + 2 is \[ - \dfrac{1}{2}\] , because \[P\left( { - \dfrac{1}{2}} \right) = 0\] .

The zero polynomial is a special type of polynomial where the coefficient of \[{x^n}\] is always zero, where n is a whole number.

For example P(x) = 0 is known as a zero polynomial.

3. Is it possible that 0 is a zero of a polynomial?

Assume a quadratic polynomial \[P\left( x \right) = {x^2} - 4x\] . Equate the polynomial with zero to find the zeros of the polynomial.

\[{x^2} - 4x = 0\]

Solving the above equation

\[x\left( {x - 4} \right) = 0\]

Either,              or,

\[x = 0\]                   \[x - 4 = 0\]

The zeros of the polynomial are 0 and 4.

Thus, 0 can be a zero of a polynomial.