multiple assignment problem

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

One of the most well-known combinatorial optimization problems is the assignment problem . Here's an example: suppose a group of workers needs to perform a set of tasks, and for each worker and task, there is a cost for assigning the worker to the task. The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost.

You can visualize this problem by the graph below, in which there are four workers and four tasks. The edges represent all possible ways to assign workers to tasks. The labels on the edges are the costs of assigning workers to tasks.

An assignment corresponds to a subset of the edges, in which each worker has at most one edge leading out, and no two workers have edges leading to the same task. One possible assignment is shown below.

The total cost of the assignment is 70 + 55 + 95 + 45 = 265 .

The next section shows how solve an assignment problem, using both the MIP solver and the CP-SAT solver.

Other tools for solving assignment problems

OR-Tools also provides a couple of other tools for solving assignment problems, which can be faster than the MIP or CP solvers:

• Linear sum assignment solver
• Minimum cost flow solver

However, these tools can only solve simple types of assignment problems. So for general solvers that can handle a wide variety of problems (and are fast enough for most applications), we recommend the MIP and CP-SAT solvers.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

Multiple Optimal Solutions: Assignment Problem

Sometimes, it is possible to cross out all the zeros in the reduced matrix in two or more ways.

If you can choose a zero cell arbitrarily, then there will be multiple optimal solutions with the same total pay-off for assignments made. In such a case, the management may select that set of optimal assignments, which is more suited to their requirement.

• Maximization Problem
• Unbalanced Assignment Problem

Example: Multiple Optimal Solutions

Consider the following assignment problem : The Spicy Spoon restaurant has four payment counters. There are four persons available for service. The cost of assigning each person to each counter is given in the following table.

Assign one person to one counter to minimize the total cost.

After applying steps 1 to 3 of the Hungarian Method, we obtain the following matrix.

Use Horizontal Scrollbar to View Full Table Calculation.

Now by applying the usual procedure, we get the following matrix.

The resulting matrix suggest the alternative optimal solutions as shown in the following tables.

The persons B & C may be assigned either to job 2 or 3. The two alternative assignments are:

Share This Article

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

www.springer.com The European Mathematical Society

• StatProb Collection
• Recent changes
• Current events
• Random page
• Project talk
• Request account
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• View source

Assignment problem

The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :

maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $

$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$

(origins or supply),

$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$

(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.

If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).

In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.

The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.

In turn, the transportation problem is a special case of the network optimization problem.

A totally different assignment problem is the pole assignment problem in control theory.

• This page was last edited on 5 April 2020, at 18:48.
• Privacy policy
• About Encyclopedia of Mathematics
• Disclaimers
• Impressum-Legal

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

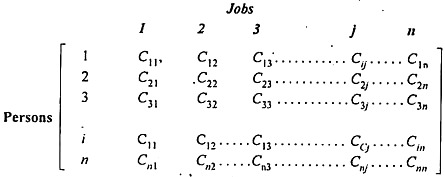
Unbalanced Assignment Problem: Definition, Formulation, and Solution Methods

Table of Contents

Are you familiar with the assignment problem in Operations Research (OR)? This problem deals with assigning tasks to workers in a way that minimizes the total cost or time needed to complete the tasks. But what if the number of tasks and workers is not equal? In this case, we face the Unbalanced Assignment Problem (UAP). This blog will help you understand what the UAP is, how to formulate it, and how to solve it.

What is the Unbalanced Assignment Problem?

The Unbalanced Assignment Problem is an extension of the Assignment Problem in OR, where the number of tasks and workers is not equal. In the UAP, some tasks may remain unassigned, while some workers may not be assigned any task. The objective is still to minimize the total cost or time required to complete the assigned tasks, but the UAP has additional constraints that make it more complex than the traditional assignment problem.

Formulation of the Unbalanced Assignment Problem

To formulate the UAP, we start with a matrix that represents the cost or time required to assign each task to each worker. If the matrix is square, we can use the Hungarian algorithm to solve the problem. But when the matrix is not square, we need to add dummy tasks or workers to balance the matrix. These dummy tasks or workers have zero costs and are used to make the matrix square.

Once we have a square matrix, we can apply the Hungarian algorithm to find the optimal assignment. However, we need to be careful in interpreting the results, as the assignment may include dummy tasks or workers that are not actually assigned to anything.

Solutions for the Unbalanced Assignment Problem

Besides the Hungarian algorithm, there are other methods to solve the UAP, such as the transportation algorithm and the auction algorithm. The transportation algorithm is based on transforming the UAP into a transportation problem, which can be solved with the transportation simplex method. The auction algorithm is an iterative method that simulates a bidding process between the tasks and workers to find the optimal assignment.

In summary, the Unbalanced Assignment Problem is a variant of the traditional Assignment Problem in OR that deals with assigning tasks to workers when the number of tasks and workers is not equal. To solve the UAP, we need to balance the matrix by adding dummy tasks or workers and then apply algorithms such as the Hungarian algorithm, the transportation algorithm, or the auction algorithm. Understanding the UAP can help businesses and organizations optimize their resource allocation and improve their operational efficiency.

How useful was this post?

Click on a star to rate it!

Average rating 1 / 5. Vote count: 1

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

Knapsack Problems pp 285–316 Cite as

Multiple Knapsack Problems

• Hans Kellerer 3 ,
• Ulrich Pferschy 3 &
• David Pisinger 4  

5273 Accesses

5 Citations

The multiple knapsack problem is a generalization of the standard knapsack problem (KP) from a single knapsack to m knapsacks with (possibly) different capacities. The objective is to assign each item to at most one of the knapsacks such that none of the capacity constraints are violated and the total profit of the items put into knapsacks is maximized.

This is a preview of subscription content, log in via an institution .

Buying options

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Unable to display preview.  Download preview PDF.

Author information

Authors and affiliations.

Department of Statistics and Operations Research, University of Graz, Universitätsstr. 15, A-8010, Graz, Austria

Prof. Hans Kellerer & Prof. Ulrich Pferschy

DIKU, Department of Computer Science, University of Copenhagen, Universitetsparken 1, DK-2100, Copenhagen, Denmark

Prof. David Pisinger

You can also search for this author in PubMed   Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

© 2004 Springer-Verlag Berlin Heidelberg

About this chapter

Cite this chapter.

Kellerer, H., Pferschy, U., Pisinger, D. (2004). Multiple Knapsack Problems. In: Knapsack Problems. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-24777-7_10

Download citation

DOI : https://doi.org/10.1007/978-3-540-24777-7_10

Publisher Name : Springer, Berlin, Heidelberg

Print ISBN : 978-3-642-07311-3

Online ISBN : 978-3-540-24777-7

eBook Packages : Springer Book Archive

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Introduction to Assignment Methods in Tracking Systems

In a multiple target tracking (MTT) system, one or more sensors generate multiple detections from multiple targets in a scan. To track these targets, one essential step is to assign these detections correctly to the targets or tracks maintained in the tracker so that these detections can be used to update these tracks. If the number of targets or detections is large, or there are conflicts between different assignment hypotheses, assigning detections is challenging.

Depending on the dimension of the assignment, assignment problems can be categorized into:

2-D assignment problem – assigns n targets to m observations. For example, assign 5 tracks to 6 detections generated from one sensor at one time step.

S-D assignment problem – assigns n targets to a set ( m 1 , m 2 , m 3 , …) of observations. For example, assign 5 tracks to 6 detections from one sensor, and 4 detections from another sensor at the same time. This example is a typical 3-D assignment problem.

To illustrate the basic idea of an assignment problem, consider a simple 2-D assignment example. One company tries to assign 3 jobs to 3 workers. Because of the different experience levels of the workers, not all workers are able to complete each job with the same effectiveness. The cost (in hours) of each worker to finish each job is given by the cost matrix shown in the table. An assignment rule is that each worker can only take one job, and one job can only be taken by one worker. To guarantee efficiency, the object of this assignment is to minimize the total cost.

Since the numbers of workers and jobs are both small in this example, all the possible assignments can be obtained by enumeration, and the minimal cost solution is highlighted in the table with assignment pairs (1, 3), (2, 2) and (3, 1). In practice, as the size of the assignment becomes larger, the optimal solution is difficult to obtain for 2-D assignment. For an S-D assignment problem, the optimal solution may not be obtainable in practice.

2-D Assignment in Multiple Target Tracking

In the 2-D MTT assignment problem, a tracker tries to assign multiple tracks to multiple detections. Other than the dimensionality challenge mentioned above, a few other factors can significantly change the complexity of the assignment:

Target or detection distribution — If targets are sparsely distributed, associating a target to its corresponding detection is relatively easy. However, if targets or detections are densely distributed, assignments become ambiguous because assigning a target to a detection or another nearby detection rarely makes any differences on the cost.

Probability of detection ( P d ) of the sensor — P d describes the probability that a target is detected by the sensor if the target is within the field of view of the sensor. If the P d of a sensor is small, then the true target may not give rise to any detection during a sensor scan. As a result, the track represented by the true target may steal detections from other tracks.

Sensor resolution — Sensor resolution determines the sensor’s ability to distinguish the detections from two targets. If the sensor resolution is low, then two targets in proximity may only give rise to one detection. This violates the common assumption that each detection can only be assigned to one track and results in unresolvable assignment conflicts between tracks.

Clutter or false alarm rate of the sensor — False alarms introduce additional possible assignments and therefore increase the complexity of data assignment.

The complexity of the assignment task can determine which assignment methods to apply. In Sensor Fusion and Tracking Toolbox™ toolbox, three 2-D assignment approaches are employed corresponding to three different trackers:

trackerGNN — adopts a global nearest data assignment approach

trackerJPDA — adopts a joint probability data association approach

trackerTOMHT — adopts a tracker-oriented multiple hypothesis tracking approach

Note that each tracker processes the data from sensors sequentially, meaning that each tracker only deals with the assignment problem with the detections of one sensor at a time. Even with this treatment, there may still be too many assignment pairs. To reduce the number of track and detection pairs considered for assignment, the gating technique is frequently used.

Gating is a screening mechanism to determine which observations are valid candidates to update existing tracks and eliminate unlikely detection-to-track pairs using the distribution information of the predicted tracks. To establish the validation gate for a track at the current scan, the estimated track for the current step is predicted from the previous step.

For example, a tracker confirms a track at time t k and receives several detections at time t k +1 . To form a validation gate at time t k +1 , the tracker first needs to obtain the predicted measurement as:

y ^ k + 1 = h ( x ^ k + 1 | k )

where x ^ k + 1 | k is the track estimate predicted from time t k and h ( x ^ k + 1 | k ) is the measurement model that outputs the expected measurement given the track state. The observation residual vector is

y ˜ = y k + 1 − y ^ k + 1

where y k +1 is the actual measurement. To establish the boundary of the gate, the detection residual covariance S is used to form an ellipsoidal validation gate. The ellipsoidal gate that establishes a spatial ellipsoidal region in the measurement space is defined in Mahalanobis distance as:

d 2 ( y k + 1 ) = y ˜ T S − 1 y ˜ ≤ G

where G is the gating threshold which you can specify based on the assignment requirement. Increasing the threshold can incorporate more detections into the gate.

After the assignment gate is established for each track, the gating status of each detection y i ( i = 1,…, n ) can be determined by comparing its Mahalanobis distance d 2 ( y i ) with the gating threshold G . If d 2 ( y i ) < G , then detection y i is inside the gate of the track and will be considered for association. Otherwise, the possibility of the detection associated with the track is removed. In Figure 1, T 1 represents a predicted track estimate, and O 1 – O 6 are six detections. Based on the gating result, O 1 , O 2 , and O 3 are within the validation gate in the figure.

Global Nearest Neighbor (GNN) Method

The GNN method is a single hypothesis assignment method. For each new data set, the goal is to assign the global nearest observations to existing tracks and to create new track hypotheses for unassigned detections.

The GNN assignment problem can be easily solved if there are no conflicts of association between tracks. The tracker only needs to assign a track to its nearest neighbor. However, conflict situations (see Figure 2) occur when there is more than one observation within a track’s validation gate or an observation is in the gates of more than one track. To resolve these conflicts, the tracker must evaluate a cost matrix.

The elements of a cost matrix for the GNN method includes the distance from tracks to detections and other factors you might want to consider. For example, one approach is to define a generalized statistical distance between observation j to track i as:

C i j = d i j + ln ( | S i j | )

where d ij is the Mahalanobis distance and ln(| S ij |), the logarithm of the determinant of the residual covariance matrix, is used to penalize tracks with greater prediction uncertainty.

For the assignment problem given in Figure 2, the following table shows a hypothetical cost matrix. The nonallowed assignments, which failed the gating test, are denoted by X. (In practice, the costs of nonallowed assignments can be denoted by large values, such as 1000.)

For this problem, the highlighted optimal solution can be found by enumeration. Detection O 3 is unassigned, so the tracker will use it to create a new tentative track. For more complicated GNN assignment problems, more accurate formulations and more efficient algorithms to obtain the optimal or suboptimal solution are required.

A general 2-D assignment problem can be formed as following. Given the cost matrix element C ij , find an assignment Z = { z ij } that minimizes

J = ∑ i = 0 n ∑ j = 0 m C i j z i j

subject to two constraints:

∑ i = 0 m z i j = 1 , ∀ j ∑ j = 0 n z i j = 1 , ∀ i

If track i is assigned to observation j , then z ij = 1. Otherwise, z ij = 0. z i 0 = 1 represents the hypothesis that track i is not assigned to any detection. Similarly, z 0 j = 1 represents the hypothesis that observation j is not assigned to any track. The first constraint means each detection can be assigned to no more than one track. The second constraint means each track can be assigned to no more than one detection.

Sensor Fusion and Tracking Toolbox provides multiple functions to solve 2-D GNN assignment problems:

assignmunkres – Uses the Munkres algorithm, which guarantees an optimal solution but may require more calculation operations.

assignauction – Uses the auction algorithm, which requires fewer operations but can possibly converge on an optimal or suboptimal solution.

assignjv – Uses the Jonker-Volgenant algorithm, which also converges on an optimal or suboptimal solution but usually with a faster converging speed.

In trackerGNN , you can select the assignment algorithm by specifying the Assignment property.

K Best Solutions to the 2-D Assignment Problem

Because of the uncertainty nature of assignment problems, only obtaining a solution (optimal or suboptimal) may not be sufficient. To account for multiple hypotheses about the assignment between tracks and detections, multiple suboptimal solutions are required. These suboptimal solutions are called K best solutions to the assignment problem.

The K best solutions are usually obtained by varying the solution obtained by any of the previously mentioned assignment functions. Then, at the next step, the K best solution algorithm removes one track-to-detection pair in the original solution and finds the next best solution. For example, for this cost matrix:

[ 10 5 8 9 7 × 20 × × × 21 1 5 × 17 × × × × 1 6 22 ]

each row represents the cost associated with a track, and each column represents the cost associated with a detection. As highlighted, the optimal solution is (7,15,16, 9) with a cost of 47. In the next step, remove the first pair (corresponding to 7), and the next best solution is (10,15, 20, 22) with a cost of 67. After that, remove the second pair (corresponding to 15), and the next best solution is (7, 5,16, 9) with a cost of 51. After a few steps, the five best solutions are:

See the Find Five Best Solutions Using Assignkbest example, which uses the assignkbest function to find the K best solutions.

Joint Probability Data Association (JPDA) Method

While the GNN method makes a rigid assignment of a detection to a track, the JPDA method applies a soft assignment so that detections within the validation gate of a track can all make weighted contributions to the track based on their probability of association.

For example, for the gating results shown in Figure 1, a JPDA tracker calculates the possibility of association between track T 1 and observations O 1 , O 2 , and O 3 . Assume the association probability of these three observations are p 11 , p 12 , and p 13 , and their residuals relative to track T 1 are y ˜ 11 , y ˜ 12 , and y ˜ 13 , respectively. Then the weighted sum of the residuals associated with track T 1 is:

y ˜ 1 = ∑ j = 1 3 p 1 j y ˜ 1 j

In the tracker, the weighted residual is used to update track T 1 in the correction step of the tracking filter. In the filter, the probability of unassignment, p 10 , is also required to update track T 1 . For more details, see JPDA Correction Algorithm for Discrete Extended Kalman Filter .

The JPDA method requires one more step when there are conflicts between assignments in different tracks. For example, in the following figure, track T 2 conflicts with T 1 on the assignment of observation O 3 . Therefore, to calculate the association probability p 13 , the joint probability that T 2 is not assigned to O 3 (that is T 2 is assigned to O 6 or unassigned) must be accounted for.

Track-Oriented Multiple Hypothesis Tracking (TOMHT) Method

Unlike the JPDA method, which combines all detections within the validation gate using a weighted sum, the TOMHT method generates multiple hypotheses or branches of the tracks based on the detections within the gate and propagates high-likelihood branches between scan steps. After propagation, these hypotheses can be tested and pruned based on the new set of detections.

For example, for the gating scenario shown in Figure 1, a TOMHT tracker considers the following four hypotheses:

Assign no detection to T 1 resulting in hypothesis T 10

Assign O 1 to T 1 resulting in hypothesis T 11

Assign O 2 to T 1 resulting in hypothesis T 12

Assign O 3 to T 1 resulting in hypothesis T 13

Given the assignment threshold, the tracker will calculate the possibility of each hypothesis and discard hypotheses with probability lower than the threshold. Hypothetically, if only p 10 and p 11 are larger than the threshold, then only T 10 and T 11 are propagated to the next step for detection update.

S-D Assignment in Multiple Target Tracking

In an S-D assignment problem, the dimension of assignment S is larger than 2. Note that all three trackers ( trackerGNN , trackerJPDA , and trackerTOMHT ) process detections from each sensor sequentially, which results in a 2-D assignment problem. However, some applications require a tracker that processes simultaneous observations from multiple sensor scans all at once, which requires solving an S-D assignment problem. Meanwhile, the S-D assignment is widely used in tracking applications such as static data fusion, which preprocesses the detection data before fed to a tracker.

An S-D assignment problem for static data fusion has S scans of a surveillance region from multiple sensors simultaneously, and each scan consists of multiple detections. The detection sources can be real targets or false alarms. The object is to detect an unknown number of targets and estimate their states. For example, as shown in the Figure 4, three sensor scans produce six detections. The detections in the same color belong to the same scan. Since each scan generates two detections, there are probably two targets in the region of surveillance. To choose between different assignment or association possibilities, evaluate the cost matrix.

The calculation of the cost can depend on many factors, such as the distance between detections and the covariance distribution of each detection. To illustrate the basic concept, the assignment costs for a few hypotheses are hypothetically given in the table [1] .

In the table, 0 denotes a track is associated with no detection in that scan. Assume the hypotheses not shown in the table are truncated by gating or neglected because of high costs. To concisely represent each track, use c ijk to represent the cost for association of observation i in scan 1, j in scan 2, and k in scan 3. For example, for the assignment hypothesis 1, c 011 = -10.2. Several track hypotheses conflict with other in the table. For instance, the two most likely assignments, c 111 and c 121 are incompatible because they share the same observation in scans 1 and 3.

The goal of solving an S-D assignment problem is to find the most likely compatible assignment hypothesis accounting for all the detections. When S ≥ 3, however, the problem is known to scale with the number of tracks and detections at an exponential rate (NP-hard). The Lagrangian relaxation method is commonly used to obtain the optimal or sub-optimal solution for an S-D assignment problem efficiently.

Brief Introduce to the Lagrangian Relaxation Method for 3-D Assignment

Three scans of data have a number of M 1 , M 2 , and M 3 observations, respectively. Denote an observation of scan 1, 2, and 3 as i , j , and k , respectively. For example, i = 1, 2, …, M 1 . Use z ijk to represent the track formation hypothesis of O 1 i , O 2 j , and O 3 k . If the hypothesis is valid, then z ijk = 1; otherwise, z ijk = 0. As mentioned, c ijk is used to represent the cost of z ijk association. c ijk is 0 for false alarms and negative for possible associations. The S-D optimization problem can be formulated as:

J ( z ) = min i , j , k ∑ i = 0 M 1 ∑ j = 0 M 2 ∑ k = 0 M 3 c i j k z i j k

subject to three constraints:

∑ i = 0 M 1 ∑ j = 0 M 2 z i j k = 1 , ∀ k = 1 , 2 , … , M 3 ∑ i = 0 M 1 ∑ k = 0 M 3 z i j k = 1 , ∀ j = 1 , 2 , … , M 2 ∑ j = 0 M 2 ∑ k = 0 M 3 z i j k = 1 , ∀ i = 1 , 2 , … , M 1

The optimization function chooses associations to minimize the total cost. The three constraints ensure that each detection is accounted for (either included in an assignment or treated as false alarm).

The Lagrangian relaxation method approaches this 3-D assignment problem by relaxing the first constraint using Lagrange multipliers. Define a new function L ( λ ) :

L ( λ ) = ∑ k = 0 M 3 λ k [ ∑ i = 0 M 1 ∑ j = 0 M 2 z i j k − 1 ]

where λ k , k = 1, 2, …, M 3 are Lagrange multipliers. Subtract L from the original object function J ( z ) to get a new object function, and the first constraint in k is relaxed. Therefore, the 3-D assignment problem reduces to a 2-D assignment problem, which can be solved by any of the 2-D assignment method. For more details, see [1] .

The Lagrangian relaxation method allows the first constraint to be mildly violated, and therefore can only guarantee a suboptimal solution. For most applications, however, this is sufficient. To specify the solution accuracy, the method uses the solution gap, which defines the difference between the current solution and the potentially optimistic solution. The gap is nonnegative, and a smaller solution gap corresponds to a solution closer to the optimal solution.

Sensor Fusion and Tracking Toolbox provides assignsd to solve for S-D assignment using the Lagrangian relaxation method. Similar to the K best 2-D assignment solver assignkbest , the toolbox also provides a K best S-D assignment solver, assignkbestsd , which is used to provide multiple suboptimal solutions for an S-D assignment problem.

See Tracking Using Distributed Synchronous Passive Sensors for the application of S-D assignment in static detection fusion.

assignTOMHT | assignauction | assignjv | assignkbest | assignkbestsd | assignmunkres | assignsd | trackerGNN | trackerJPDA | trackerTOMHT

[1] Blackman, S., and R. Popoli. Design and Analysis of Modern Tracking Systems. Artech House Radar Library, Boston, 1999.

[2] Musicki, D., and R. Evans. "Joint Integrated Probabilistic Data Association: JIPDA." IEEE Transactions on Aerospace and Electronic Systems. Vol. 40, Number 3, 2004, pp 1093 –1099.

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

Help | Advanced Search

Computer Science > Artificial Intelligence

Title: ita-ecbs: a bounded-suboptimal algorithm for combined target-assignment and path-finding problem.

Abstract: Multi-Agent Path Finding (MAPF), i.e., finding collision-free paths for multiple robots, plays a critical role in many applications. Sometimes, assigning a specific target to each agent also presents a challenge. The Combined Target-Assignment and Path-Finding (TAPF) problem, a variant of MAPF, requires simultaneously assigning targets to agents and planning collision-free paths. Several algorithms, including CBM, CBS-TA, and ITA-CBS, can optimally solve the TAPF problem, with ITA-CBS being the leading method of flowtime. However, the only existing suboptimal method ECBS-TA, is derived from CBS-TA rather than ITA-CBS, and adapting the optimal ITA-CBS method to its bounded-suboptimal variant is a challenge due to the variability of target assignment solutions in different search nodes. We introduce ITA-ECBS as the first bounded-suboptimal variant of ITA-CBS. ITA-ECBS employs focal search to enhance efficiency and determines target assignments based on a new lower bound matrix. We show that ITA-ECBS outperforms the baseline method ECBS-TA in 87.42% of 54,033 test cases.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .