hypothesis testing statistical inference

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base
• Inferential Statistics | An Easy Introduction & Examples

Inferential Statistics | An Easy Introduction & Examples

Published on September 4, 2020 by Pritha Bhandari . Revised on June 22, 2023.

While descriptive statistics summarize the characteristics of a data set, inferential statistics help you come to conclusions and make predictions based on your data.

When you have collected data from a sample , you can use inferential statistics to understand the larger population from which the sample is taken.

Inferential statistics have two main uses:

• making estimates about populations (for example, the mean SAT score of all 11th graders in the US).
• testing hypotheses to draw conclusions about populations (for example, the relationship between SAT scores and family income).

Table of contents

Descriptive versus inferential statistics, estimating population parameters from sample statistics, hypothesis testing, other interesting articles, frequently asked questions about inferential statistics.

Descriptive statistics allow you to describe a data set, while inferential statistics allow you to make inferences based on a data set.

• Descriptive statistics

Using descriptive statistics, you can report characteristics of your data:

• The distribution concerns the frequency of each value.
• The central tendency concerns the averages of the values.
• The variability concerns how spread out the values are.

In descriptive statistics, there is no uncertainty – the statistics precisely describe the data that you collected. If you collect data from an entire population, you can directly compare these descriptive statistics to those from other populations.

Inferential statistics

Most of the time, you can only acquire data from samples, because it is too difficult or expensive to collect data from the whole population that you’re interested in.

While descriptive statistics can only summarize a sample’s characteristics, inferential statistics use your sample to make reasonable guesses about the larger population.

With inferential statistics, it’s important to use random and unbiased sampling methods . If your sample isn’t representative of your population, then you can’t make valid statistical inferences or generalize .

Sampling error in inferential statistics

Since the size of a sample is always smaller than the size of the population, some of the population isn’t captured by sample data. This creates sampling error , which is the difference between the true population values (called parameters) and the measured sample values (called statistics).

Sampling error arises any time you use a sample, even if your sample is random and unbiased. For this reason, there is always some uncertainty in inferential statistics. However, using probability sampling methods reduces this uncertainty.

Prevent plagiarism. Run a free check.

The characteristics of samples and populations are described by numbers called statistics and parameters :

• A statistic is a measure that describes the sample (e.g., sample mean ).
• A parameter is a measure that describes the whole population (e.g., population mean).

Sampling error is the difference between a parameter and a corresponding statistic. Since in most cases you don’t know the real population parameter, you can use inferential statistics to estimate these parameters in a way that takes sampling error into account.

There are two important types of estimates you can make about the population: point estimates and interval estimates .

• A point estimate is a single value estimate of a parameter. For instance, a sample mean is a point estimate of a population mean.
• An interval estimate gives you a range of values where the parameter is expected to lie. A confidence interval is the most common type of interval estimate.

Both types of estimates are important for gathering a clear idea of where a parameter is likely to lie.

Confidence intervals

A confidence interval uses the variability around a statistic to come up with an interval estimate for a parameter. Confidence intervals are useful for estimating parameters because they take sampling error into account.

While a point estimate gives you a precise value for the parameter you are interested in, a confidence interval tells you the uncertainty of the point estimate. They are best used in combination with each other.

Each confidence interval is associated with a confidence level. A confidence level tells you the probability (in percentage) of the interval containing the parameter estimate if you repeat the study again.

A 95% confidence interval means that if you repeat your study with a new sample in exactly the same way 100 times, you can expect your estimate to lie within the specified range of values 95 times.

Although you can say that your estimate will lie within the interval a certain percentage of the time, you cannot say for sure that the actual population parameter will. That’s because you can’t know the true value of the population parameter without collecting data from the full population.

However, with random sampling and a suitable sample size, you can reasonably expect your confidence interval to contain the parameter a certain percentage of the time.

Your point estimate of the population mean paid vacation days is the sample mean of 19 paid vacation days.

Hypothesis testing is a formal process of statistical analysis using inferential statistics. The goal of hypothesis testing is to compare populations or assess relationships between variables using samples.

Hypotheses , or predictions, are tested using statistical tests . Statistical tests also estimate sampling errors so that valid inferences can be made.

Statistical tests can be parametric or non-parametric. Parametric tests are considered more statistically powerful because they are more likely to detect an effect if one exists.

Parametric tests make assumptions that include the following:

• the population that the sample comes from follows a normal distribution of scores
• the sample size is large enough to represent the population
• the variances , a measure of variability , of each group being compared are similar

When your data violates any of these assumptions, non-parametric tests are more suitable. Non-parametric tests are called “distribution-free tests” because they don’t assume anything about the distribution of the population data.

Statistical tests come in three forms: tests of comparison, correlation or regression.

Comparison tests

Comparison tests assess whether there are differences in means, medians or rankings of scores of two or more groups.

To decide which test suits your aim, consider whether your data meets the conditions necessary for parametric tests, the number of samples, and the levels of measurement of your variables.

Means can only be found for interval or ratio data , while medians and rankings are more appropriate measures for ordinal data .

Correlation tests

Correlation tests determine the extent to which two variables are associated.

Although Pearson’s r is the most statistically powerful test, Spearman’s r is appropriate for interval and ratio variables when the data doesn’t follow a normal distribution.

The chi square test of independence is the only test that can be used with nominal variables.

Regression tests

Regression tests demonstrate whether changes in predictor variables cause changes in an outcome variable. You can decide which regression test to use based on the number and types of variables you have as predictors and outcomes.

Most of the commonly used regression tests are parametric. If your data is not normally distributed, you can perform data transformations.

Data transformations help you make your data normally distributed using mathematical operations, like taking the square root of each value.

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Confidence interval
• Measures of central tendency
• Correlation coefficient

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

Descriptive statistics summarize the characteristics of a data set. Inferential statistics allow you to test a hypothesis or assess whether your data is generalizable to the broader population.

A statistic refers to measures about the sample , while a parameter refers to measures about the population .

A sampling error is the difference between a population parameter and a sample statistic .

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bhandari, P. (2023, June 22). Inferential Statistics | An Easy Introduction & Examples. Scribbr. Retrieved April 16, 2024, from https://www.scribbr.com/statistics/inferential-statistics/

Is this article helpful?

Pritha Bhandari

Other students also liked, parameter vs statistic | definitions, differences & examples, descriptive statistics | definitions, types, examples, hypothesis testing | a step-by-step guide with easy examples, what is your plagiarism score.

Forgot password? New user? Sign up

Existing user? Log in

Hypothesis Testing

Already have an account? Log in here.

A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators . In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population.

The test considers two hypotheses: the null hypothesis , which is a statement meant to be tested, usually something like "there is no effect" with the intention of proving this false, and the alternate hypothesis , which is the statement meant to stand after the test is performed. The two hypotheses must be mutually exclusive ; moreover, in most applications, the two are complementary (one being the negation of the other). The test works by comparing the \(p\)-value to the level of significance (a chosen target). If the \(p\)-value is less than or equal to the level of significance, then the null hypothesis is rejected.

When analyzing data, only samples of a certain size might be manageable as efficient computations. In some situations the error terms follow a continuous or infinite distribution, hence the use of samples to suggest accuracy of the chosen test statistics. The method of hypothesis testing gives an advantage over guessing what distribution or which parameters the data follows.

Definitions and Methodology

Hypothesis test and confidence intervals.

In statistical inference, properties (parameters) of a population are analyzed by sampling data sets. Given assumptions on the distribution, i.e. a statistical model of the data, certain hypotheses can be deduced from the known behavior of the model. These hypotheses must be tested against sampled data from the population.

The null hypothesis \((\)denoted \(H_0)\) is a statement that is assumed to be true. If the null hypothesis is rejected, then there is enough evidence (statistical significance) to accept the alternate hypothesis \((\)denoted \(H_1).\) Before doing any test for significance, both hypotheses must be clearly stated and non-conflictive, i.e. mutually exclusive, statements. Rejecting the null hypothesis, given that it is true, is called a type I error and it is denoted \(\alpha\), which is also its probability of occurrence. Failing to reject the null hypothesis, given that it is false, is called a type II error and it is denoted \(\beta\), which is also its probability of occurrence. Also, \(\alpha\) is known as the significance level , and \(1-\beta\) is known as the power of the test. \(H_0\) \(\textbf{is true}\)\(\hspace{15mm}\) \(H_0\) \(\textbf{is false}\) \(\textbf{Reject}\) \(H_0\)\(\hspace{10mm}\) Type I error Correct Decision \(\textbf{Reject}\) \(H_1\) Correct Decision Type II error The test statistic is the standardized value following the sampled data under the assumption that the null hypothesis is true, and a chosen particular test. These tests depend on the statistic to be studied and the assumed distribution it follows, e.g. the population mean following a normal distribution. The \(p\)-value is the probability of observing an extreme test statistic in the direction of the alternate hypothesis, given that the null hypothesis is true. The critical value is the value of the assumed distribution of the test statistic such that the probability of making a type I error is small.

Methodologies: Given an estimator \(\hat \theta\) of a population statistic \(\theta\), following a probability distribution \(P(T)\), computed from a sample \(\mathcal{S},\) and given a significance level \(\alpha\) and test statistic \(t^*,\) define \(H_0\) and \(H_1;\) compute the test statistic \(t^*.\) \(p\)-value Approach (most prevalent): Find the \(p\)-value using \(t^*\) (right-tailed). If the \(p\)-value is at most \(\alpha,\) reject \(H_0\). Otherwise, reject \(H_1\). Critical Value Approach: Find the critical value solving the equation \(P(T\geq t_\alpha)=\alpha\) (right-tailed). If \(t^*>t_\alpha\), reject \(H_0\). Otherwise, reject \(H_1\). Note: Failing to reject \(H_0\) only means inability to accept \(H_1\), and it does not mean to accept \(H_0\).

Assume a normally distributed population has recorded cholesterol levels with various statistics computed. From a sample of 100 subjects in the population, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is larger than 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the \(p\)-value approach with significance level \(\alpha=0.05:\) Define \(H_0\): \(\mu=200\). Define \(H_1\): \(\mu>200\). Since our values are normally distributed, the test statistic is \(z^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{100}}}\approx 3.09\). Using a standard normal distribution, we find that our \(p\)-value is approximately \(0.001\). Since the \(p\)-value is at most \(\alpha=0.05,\) we reject \(H_0\). Therefore, we can conclude that the test shows sufficient evidence to support the claim that \(\mu\) is larger than \(200\) mg/dL.

If the sample size was smaller, the normal and \(t\)-distributions behave differently. Also, the question itself must be managed by a double-tail test instead.

Assume a population's cholesterol levels are recorded and various statistics are computed. From a sample of 25 subjects, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is not equal to 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the \(p\)-value approach with significance level \(\alpha=0.05\) and the \(t\)-distribution with 24 degrees of freedom: Define \(H_0\): \(\mu=200\). Define \(H_1\): \(\mu\neq 200\). Using the \(t\)-distribution, the test statistic is \(t^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{25}}}\approx 1.54\). Using a \(t\)-distribution with 24 degrees of freedom, we find that our \(p\)-value is approximately \(2(0.068)=0.136\). We have multiplied by two since this is a two-tailed argument, i.e. the mean can be smaller than or larger than. Since the \(p\)-value is larger than \(\alpha=0.05,\) we fail to reject \(H_0\). Therefore, the test does not show sufficient evidence to support the claim that \(\mu\) is not equal to \(200\) mg/dL.

The complement of the rejection on a two-tailed hypothesis test (with significance level \(\alpha\)) for a population parameter \(\theta\) is equivalent to finding a confidence interval \((\)with confidence level \(1-\alpha)\) for the population parameter \(\theta\). If the assumption on the parameter \(\theta\) falls inside the confidence interval, then the test has failed to reject the null hypothesis \((\)with \(p\)-value greater than \(\alpha).\) Otherwise, if \(\theta\) does not fall in the confidence interval, then the null hypothesis is rejected in favor of the alternate \((\)with \(p\)-value at most \(\alpha).\)

• Statistics (Estimation)
• Normal Distribution
• Correlation
• Confidence Intervals

Problem Loading...

Note Loading...

Set Loading...

• Comprehensive Learning Paths
• 150+ Hours of Videos
• Complete Access to Jupyter notebooks, Datasets, References.

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

• September 21, 2023

Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:

• What is Hypothesis Testing?
• Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
• Example : Testing a new drug.
• Example in python

1. What is Hypothesis Testing?

In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.

Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.

2. Steps in Hypothesis Testing

• Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
• Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
• Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
• p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
• Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.

2.1. Set up Hypotheses: Null and Alternative

Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.

For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”

2.2. Choose a Significance Level (α)

When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.

The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.

In other words, it’s the risk you’re willing to take of making a Type I error (false positive).

Type I Error (False Positive) :

• Symbolized by the Greek letter alpha (α).
• Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
• The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
• Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.

Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.

Type II Error (False Negative) :

• Symbolized by the Greek letter beta (β).
• Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
• The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.

Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.

Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.

It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.

2.3. Calculate a test statistic and P-Value

Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.

P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.

2.4. Make a Decision

Relationship between $α$ and P-Value

When conducting a hypothesis test:

We then calculate the p-value from our sample data and the test statistic.

Finally, we compare the p-value to our chosen $α$:

• If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
• If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.

3. Example : Testing a new drug.

Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.

Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.

• Set up Hypotheses : Before starting, you make a prediction:
• Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
• Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.

Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.

For instance, let’s say:

• The average healing time in the Drug Group is 2 hours.
• The average healing time in the Placebo Group is 3 hours.

The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.

Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”

For instance:

• P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
• P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
• If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
• If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.

4. Example in python

For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:

Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”

5. Conclusion

Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.

More Articles

Correlation – connecting the dots, the role of correlation in data analysis, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

Statistical Inference via Data Science

Chapter 9 Hypothesis Testing

Now that we’ve studied confidence intervals in Chapter 8 , let’s study another commonly used method for statistical inference: hypothesis testing. Hypothesis tests allow us to take a sample of data from a population and infer about the plausibility of competing hypotheses. For example, in the upcoming “promotions” activity in Section 9.1 , you’ll study the data collected from a psychology study in the 1970s to investigate whether gender-based discrimination in promotion rates existed in the banking industry at the time of the study.

The good news is we’ve already covered many of the necessary concepts to understand hypothesis testing in Chapters 7 and 8 . We will expand further on these ideas here and also provide a general framework for understanding hypothesis tests. By understanding this general framework, you’ll be able to adapt it to many different scenarios.

The same can be said for confidence intervals. There was one general framework that applies to all confidence intervals and the infer package was designed around this framework. While the specifics may change slightly for different types of confidence intervals, the general framework stays the same.

We believe that this approach is much better for long-term learning than focusing on specific details for specific confidence intervals using theory-based approaches. As you’ll now see, we prefer this general framework for hypothesis tests as well.

If you’d like more practice or you’re curious to see how this framework applies to different scenarios, you can find fully-worked out examples for many common hypothesis tests and their corresponding confidence intervals in Appendix B. We recommend that you carefully review these examples as they also cover how the general frameworks apply to traditional theory-based methods like the \(t\) -test and normal-theory confidence intervals. You’ll see there that these traditional methods are just approximations for the computer-based methods we’ve been focusing on. However, they also require conditions to be met for their results to be valid. Computer-based methods using randomization, simulation, and bootstrapping have much fewer restrictions. Furthermore, they help develop your computational thinking, which is one big reason they are emphasized throughout this book.

Needed packages

Let’s load all the packages needed for this chapter (this assumes you’ve already installed them). Recall from our discussion in Section 4.4 that loading the tidyverse package by running library(tidyverse) loads the following commonly used data science packages all at once:

• ggplot2 for data visualization
• dplyr for data wrangling
• tidyr for converting data to “tidy” format
• readr for importing spreadsheet data into R
• As well as the more advanced purrr , tibble , stringr , and forcats packages

If needed, read Section 1.3 for information on how to install and load R packages.

9.1 Promotions activity

Let’s start with an activity studying the effect of gender on promotions at a bank.

9.1.1 Does gender affect promotions at a bank?

Say you are working at a bank in the 1970s and you are submitting your résumé to apply for a promotion. Will your gender affect your chances of getting promoted? To answer this question, we’ll focus on data from a study published in the Journal of Applied Psychology in 1974. This data is also used in the OpenIntro series of statistics textbooks.

To begin the study, 48 bank supervisors were asked to assume the role of a hypothetical director of a bank with multiple branches. Every one of the bank supervisors was given a résumé and asked whether or not the candidate on the résumé was fit to be promoted to a new position in one of their branches.

However, each of these 48 résumés were identical in all respects except one: the name of the applicant at the top of the résumé. Of the supervisors, 24 were randomly given résumés with stereotypically “male” names, while 24 of the supervisors were randomly given résumés with stereotypically “female” names. Since only (binary) gender varied from résumé to résumé, researchers could isolate the effect of this variable in promotion rates.

While many people today (including us, the authors) disagree with such binary views of gender, it is important to remember that this study was conducted at a time where more nuanced views of gender were not as prevalent. Despite this imperfection, we decided to still use this example as we feel it presents ideas still relevant today about how we could study discrimination in the workplace.

The moderndive package contains the data on the 48 applicants in the promotions data frame. Let’s explore this data by looking at six randomly selected rows:

The variable id acts as an identification variable for all 48 rows, the decision variable indicates whether the applicant was selected for promotion or not, while the gender variable indicates the gender of the name used on the résumé. Recall that this data does not pertain to 24 actual men and 24 actual women, but rather 48 identical résumés of which 24 were assigned stereotypically “male” names and 24 were assigned stereotypically “female” names.

Let’s perform an exploratory data analysis of the relationship between the two categorical variables decision and gender . Recall that we saw in Subsection 2.8.3 that one way we can visualize such a relationship is by using a stacked barplot.

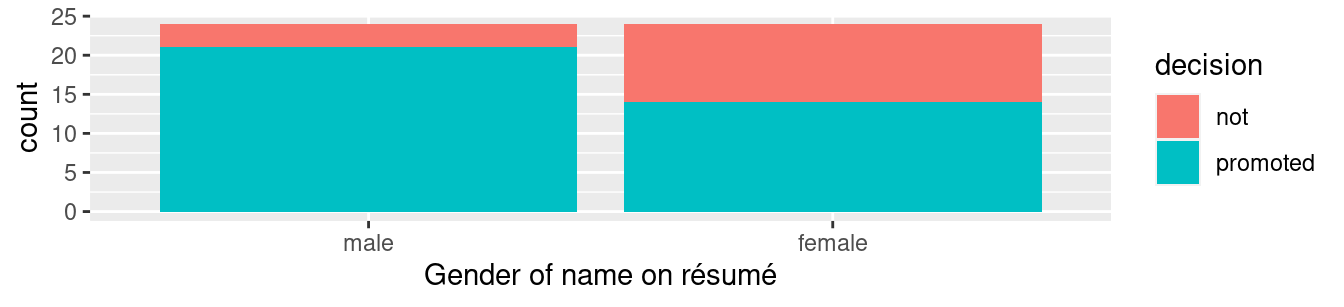
FIGURE 9.1: Barplot relating gender to promotion decision.

Observe in Figure 9.1 that it appears that résumés with female names were much less likely to be accepted for promotion. Let’s quantify these promotion rates by computing the proportion of résumés accepted for promotion for each group using the dplyr package for data wrangling. Note the use of the tally() function here which is a shortcut for summarize(n = n()) to get counts.

So of the 24 résumés with male names, 21 were selected for promotion, for a proportion of 21/24 = 0.875 = 87.5%. On the other hand, of the 24 résumés with female names, 14 were selected for promotion, for a proportion of 14/24 = 0.583 = 58.3%. Comparing these two rates of promotion, it appears that résumés with male names were selected for promotion at a rate 0.875 - 0.583 = 0.292 = 29.2% higher than résumés with female names. This is suggestive of an advantage for résumés with a male name on it.

The question is, however, does this provide conclusive evidence that there is gender discrimination in promotions at banks? Could a difference in promotion rates of 29.2% still occur by chance, even in a hypothetical world where no gender-based discrimination existed? In other words, what is the role of sampling variation in this hypothesized world? To answer this question, we’ll again rely on a computer to run simulations .

9.1.2 Shuffling once

First, try to imagine a hypothetical universe where no gender discrimination in promotions existed. In such a hypothetical universe, the gender of an applicant would have no bearing on their chances of promotion. Bringing things back to our promotions data frame, the gender variable would thus be an irrelevant label. If these gender labels were irrelevant, then we could randomly reassign them by “shuffling” them to no consequence!

To illustrate this idea, let’s narrow our focus to 6 arbitrarily chosen résumés of the 48 in Table 9.1 . The decision column shows that 3 résumés resulted in promotion while 3 didn’t. The gender column shows what the original gender of the résumé name was.

However, in our hypothesized universe of no gender discrimination, gender is irrelevant and thus it is of no consequence to randomly “shuffle” the values of gender . The shuffled_gender column shows one such possible random shuffling. Observe in the fourth column how the number of male and female names remains the same at 3 each, but they are now listed in a different order.

Again, such random shuffling of the gender label only makes sense in our hypothesized universe of no gender discrimination. How could we extend this shuffling of the gender variable to all 48 résumés by hand? One way would be by using standard deck of 52 playing cards, which we display in Figure 9.2 .

FIGURE 9.2: Standard deck of 52 playing cards.

Since half the cards are red (diamonds and hearts) and the other half are black (spades and clubs), by removing two red cards and two black cards, we would end up with 24 red cards and 24 black cards. After shuffling these 48 cards as seen in Figure 9.3 , we can flip the cards over one-by-one, assigning “male” for each red card and “female” for each black card.

FIGURE 9.3: Shuffling a deck of cards.

We’ve saved one such shuffling in the promotions_shuffled data frame of the moderndive package. If you compare the original promotions and the shuffled promotions_shuffled data frames, you’ll see that while the decision variable is identical, the gender variable has changed.

Let’s repeat the same exploratory data analysis we did for the original promotions data on our promotions_shuffled data frame. Let’s create a barplot visualizing the relationship between decision and the new shuffled gender variable and compare this to the original unshuffled version in Figure 9.4 .

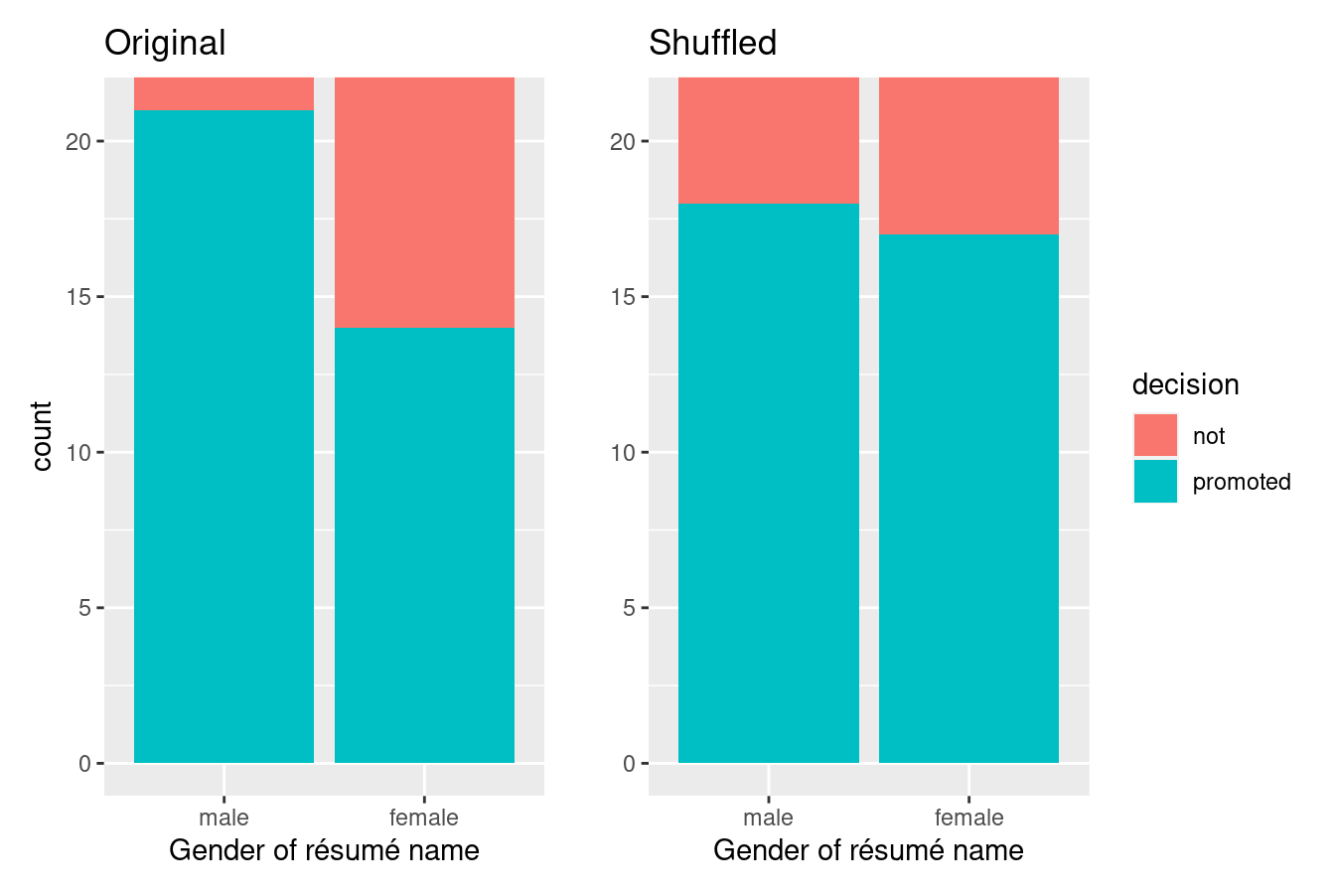
FIGURE 9.4: Barplots of relationship of promotion with gender (left) and shuffled gender (right).

It appears the difference in “male names” versus “female names” promotion rates is now different. Compared to the original data in the left barplot, the new “shuffled” data in the right barplot has promotion rates that are much more similar.

Let’s also compute the proportion of résumés accepted for promotion for each group:

So in this hypothetical universe of no discrimination, \(18/24 = 0.75 = 75\%\) of “male” résumés were selected for promotion. On the other hand, \(17/24 = 0.708 = 70.8\%\) of “female” résumés were selected for promotion.

Let’s next compare these two values. It appears that résumés with stereotypically male names were selected for promotion at a rate that was \(0.75 - 0.708 = 0.042 = 4.2\%\) different than résumés with stereotypically female names.

Observe how this difference in rates is not the same as the difference in rates of 0.292 = 29.2% we originally observed. This is once again due to sampling variation . How can we better understand the effect of this sampling variation? By repeating this shuffling several times!

9.1.3 Shuffling 16 times

We recruited 16 groups of our friends to repeat this shuffling exercise. They recorded these values in a shared spreadsheet ; we display a snapshot of the first 10 rows and 5 columns in Figure 9.5 .

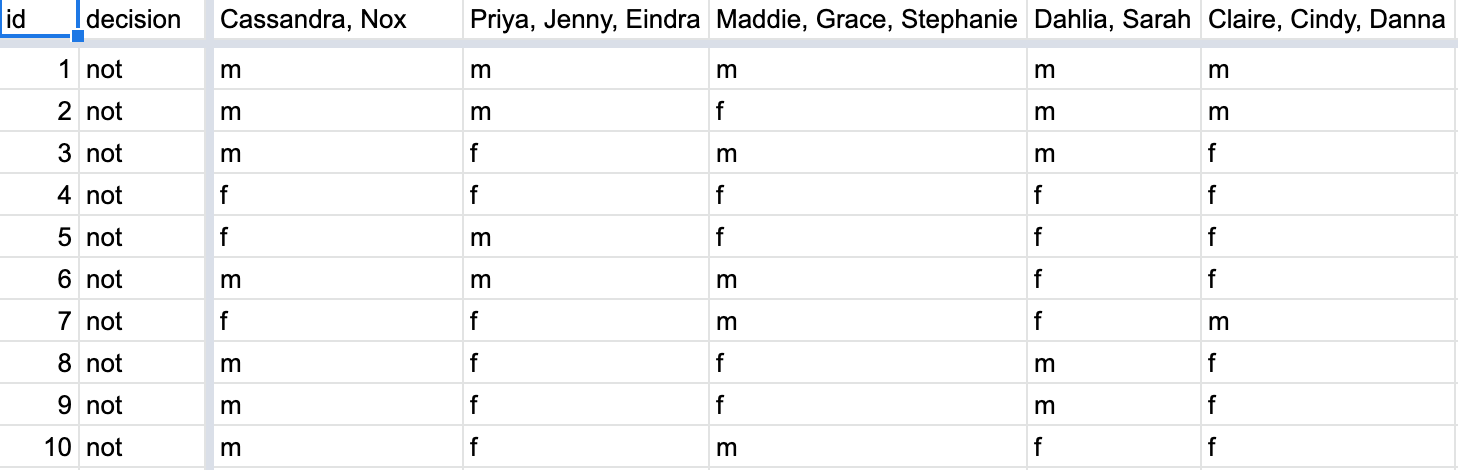
FIGURE 9.5: Snapshot of shared spreadsheet of shuffling results (m for male, f for female).

For each of these 16 columns of shuffles , we computed the difference in promotion rates, and in Figure 9.6 we display their distribution in a histogram. We also mark the observed difference in promotion rate that occurred in real life of 0.292 = 29.2% with a dark line.

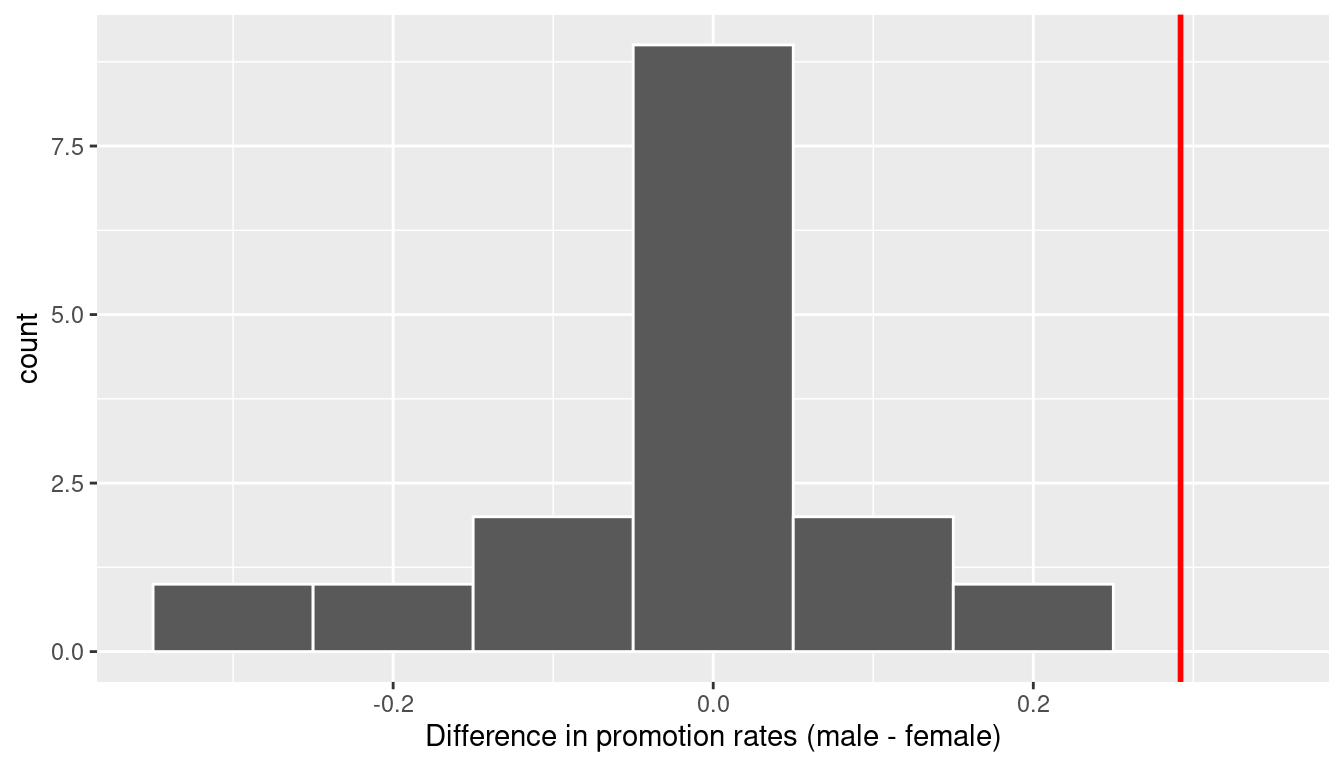
FIGURE 9.6: Distribution of shuffled differences in promotions.

Before we discuss the distribution of the histogram, we emphasize the key thing to remember: this histogram represents differences in promotion rates that one would observe in our hypothesized universe of no gender discrimination.

Observe first that the histogram is roughly centered at 0. Saying that the difference in promotion rates is 0 is equivalent to saying that both genders had the same promotion rate. In other words, the center of these 16 values is consistent with what we would expect in our hypothesized universe of no gender discrimination.

However, while the values are centered at 0, there is variation about 0. This is because even in a hypothesized universe of no gender discrimination, you will still likely observe small differences in promotion rates because of chance sampling variation . Looking at the histogram in Figure 9.6 , such differences could even be as extreme as -0.292 or 0.208.

Turning our attention to what we observed in real life: the difference of 0.292 = 29.2% is marked with a vertical dark line. Ask yourself: in a hypothesized world of no gender discrimination, how likely would it be that we observe this difference? While opinions here may differ, in our opinion not often! Now ask yourself: what do these results say about our hypothesized universe of no gender discrimination?

9.1.4 What did we just do?

What we just demonstrated in this activity is the statistical procedure known as hypothesis testing using a permutation test . The term “permutation” is the mathematical term for “shuffling”: taking a series of values and reordering them randomly, as you did with the playing cards.

In fact, permutations are another form of resampling , like the bootstrap method you performed in Chapter 8 . While the bootstrap method involves resampling with replacement, permutation methods involve resampling without replacement.

Think of our exercise involving the slips of paper representing pennies and the hat in Section 8.1 : after sampling a penny, you put it back in the hat. Now think of our deck of cards. After drawing a card, you laid it out in front of you, recorded the color, and then you did not put it back in the deck.

In our previous example, we tested the validity of the hypothesized universe of no gender discrimination. The evidence contained in our observed sample of 48 résumés was somewhat inconsistent with our hypothesized universe. Thus, we would be inclined to reject this hypothesized universe and declare that the evidence suggests there is gender discrimination.

Recall our case study on whether yawning is contagious from Section 8.6 . The previous example involves inference about an unknown difference of population proportions as well. This time, it will be \(p_{m} - p_{f}\) , where \(p_{m}\) is the population proportion of résumés with male names being recommended for promotion and \(p_{f}\) is the equivalent for résumés with female names. Recall that this is one of the scenarios for inference we’ve seen so far in Table 9.2 .

So, based on our sample of \(n_m\) = 24 “male” applicants and \(n_w\) = 24 “female” applicants, the point estimate for \(p_{m} - p_{f}\) is the difference in sample proportions \(\widehat{p}_{m} -\widehat{p}_{f}\) = 0.875 - 0.583 = 0.292 = 29.2%. This difference in favor of “male” résumés of 0.292 is greater than 0, suggesting discrimination in favor of men.

However, the question we asked ourselves was “is this difference meaningfully greater than 0?”. In other words, is that difference indicative of true discrimination, or can we just attribute it to sampling variation ? Hypothesis testing allows us to make such distinctions.

9.2 Understanding hypothesis tests

Much like the terminology, notation, and definitions relating to sampling you saw in Section 7.3 , there are a lot of terminology, notation, and definitions related to hypothesis testing as well. Learning these may seem like a very daunting task at first. However, with practice, practice, and more practice, anyone can master them.

First, a hypothesis is a statement about the value of an unknown population parameter. In our résumé activity, our population parameter of interest is the difference in population proportions \(p_{m} - p_{f}\) . Hypothesis tests can involve any of the population parameters in Table 7.5 of the five inference scenarios we’ll cover in this book and also more advanced types we won’t cover here.

Second, a hypothesis test consists of a test between two competing hypotheses: (1) a null hypothesis \(H_0\) (pronounced “H-naught”) versus (2) an alternative hypothesis \(H_A\) (also denoted \(H_1\) ).

Generally the null hypothesis is a claim that there is “no effect” or “no difference of interest.” In many cases, the null hypothesis represents the status quo or a situation that nothing interesting is happening. Furthermore, generally the alternative hypothesis is the claim the experimenter or researcher wants to establish or find evidence to support. It is viewed as a “challenger” hypothesis to the null hypothesis \(H_0\) . In our résumé activity, an appropriate hypothesis test would be:

\[ \begin{aligned} H_0 &: \text{men and women are promoted at the same rate}\\ \text{vs } H_A &: \text{men are promoted at a higher rate than women} \end{aligned} \]

Note some of the choices we have made. First, we set the null hypothesis \(H_0\) to be that there is no difference in promotion rate and the “challenger” alternative hypothesis \(H_A\) to be that there is a difference. While it would not be wrong in principle to reverse the two, it is a convention in statistical inference that the null hypothesis is set to reflect a “null” situation where “nothing is going on.” As we discussed earlier, in this case, \(H_0\) corresponds to there being no difference in promotion rates. Furthermore, we set \(H_A\) to be that men are promoted at a higher rate, a subjective choice reflecting a prior suspicion we have that this is the case. We call such alternative hypotheses one-sided alternatives . If someone else however does not share such suspicions and only wants to investigate that there is a difference, whether higher or lower, they would set what is known as a two-sided alternative .

We can re-express the formulation of our hypothesis test using the mathematical notation for our population parameter of interest, the difference in population proportions \(p_{m} - p_{f}\) :

\[ \begin{aligned} H_0 &: p_{m} - p_{f} = 0\\ \text{vs } H_A&: p_{m} - p_{f} > 0 \end{aligned} \]

Observe how the alternative hypothesis \(H_A\) is one-sided with \(p_{m} - p_{f} > 0\) . Had we opted for a two-sided alternative, we would have set \(p_{m} - p_{f} \neq 0\) . To keep things simple for now, we’ll stick with the simpler one-sided alternative. We’ll present an example of a two-sided alternative in Section 9.5 .

Third, a test statistic is a point estimate/sample statistic formula used for hypothesis testing. Note that a sample statistic is merely a summary statistic based on a sample of observations. Recall we saw in Section 3.3 that a summary statistic takes in many values and returns only one. Here, the samples would be the \(n_m\) = 24 résumés with male names and the \(n_f\) = 24 résumés with female names. Hence, the point estimate of interest is the difference in sample proportions \(\widehat{p}_{m} - \widehat{p}_{f}\) .

Fourth, the observed test statistic is the value of the test statistic that we observed in real life. In our case, we computed this value using the data saved in the promotions data frame. It was the observed difference of \(\widehat{p}_{m} -\widehat{p}_{f} = 0.875 - 0.583 = 0.292 = 29.2\%\) in favor of résumés with male names.

Fifth, the null distribution is the sampling distribution of the test statistic assuming the null hypothesis \(H_0\) is true . Ooof! That’s a long one! Let’s unpack it slowly. The key to understanding the null distribution is that the null hypothesis \(H_0\) is assumed to be true. We’re not saying that \(H_0\) is true at this point, we’re only assuming it to be true for hypothesis testing purposes. In our case, this corresponds to our hypothesized universe of no gender discrimination in promotion rates. Assuming the null hypothesis \(H_0\) , also stated as “Under \(H_0\) ,” how does the test statistic vary due to sampling variation? In our case, how will the difference in sample proportions \(\widehat{p}_{m} - \widehat{p}_{f}\) vary due to sampling under \(H_0\) ? Recall from Subsection 7.3.2 that distributions displaying how point estimates vary due to sampling variation are called sampling distributions . The only additional thing to keep in mind about null distributions is that they are sampling distributions assuming the null hypothesis \(H_0\) is true .

In our case, we previously visualized a null distribution in Figure 9.6 , which we re-display in Figure 9.7 using our new notation and terminology. It is the distribution of the 16 differences in sample proportions our friends computed assuming a hypothetical universe of no gender discrimination. We also mark the value of the observed test statistic of 0.292 with a vertical line.

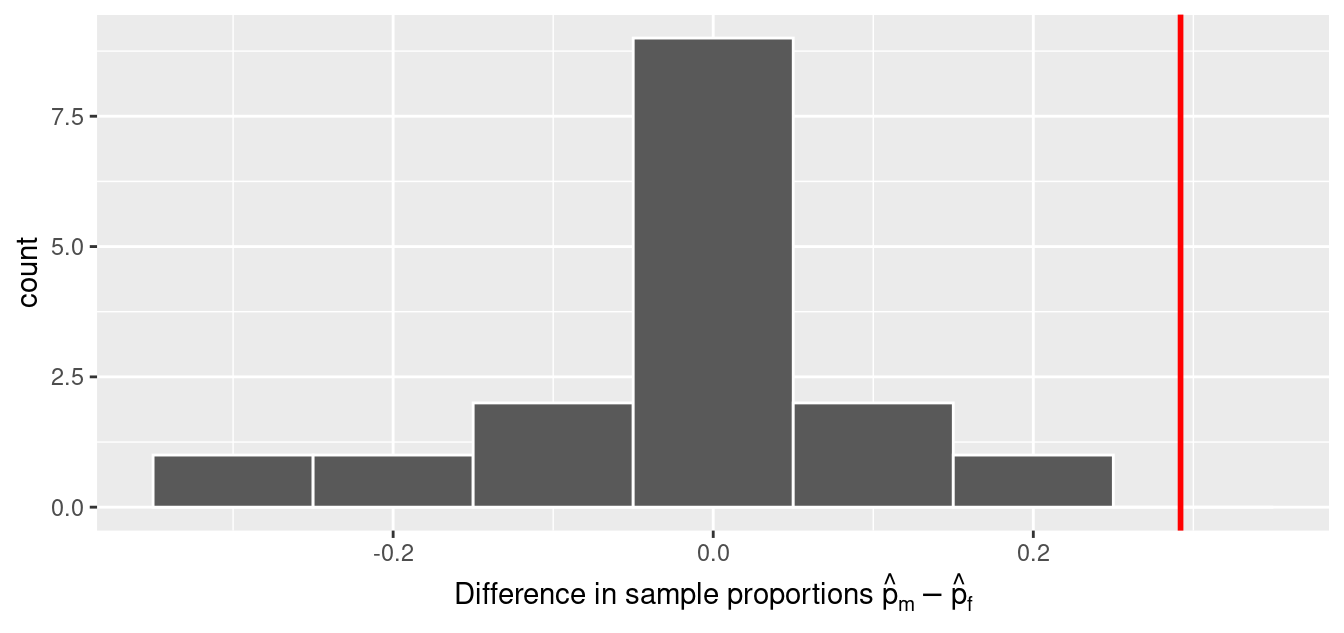
FIGURE 9.7: Null distribution and observed test statistic.

Sixth, the \(p\) -value is the probability of obtaining a test statistic just as extreme or more extreme than the observed test statistic assuming the null hypothesis \(H_0\) is true . Double ooof! Let’s unpack this slowly as well. You can think of the \(p\) -value as a quantification of “surprise”: assuming \(H_0\) is true, how surprised are we with what we observed? Or in our case, in our hypothesized universe of no gender discrimination, how surprised are we that we observed a difference in promotion rates of 0.292 from our collected samples assuming \(H_0\) is true? Very surprised? Somewhat surprised?

The \(p\) -value quantifies this probability, or in the case of our 16 differences in sample proportions in Figure 9.7 , what proportion had a more “extreme” result? Here, extreme is defined in terms of the alternative hypothesis \(H_A\) that “male” applicants are promoted at a higher rate than “female” applicants. In other words, how often was the discrimination in favor of men even more pronounced than \(0.875 - 0.583 = 0.292 = 29.2\%\) ?

In this case, 0 times out of 16, we obtained a difference in proportion greater than or equal to the observed difference of 0.292 = 29.2%. A very rare (in fact, not occurring) outcome! Given the rarity of such a pronounced difference in promotion rates in our hypothesized universe of no gender discrimination, we’re inclined to reject our hypothesized universe. Instead, we favor the hypothesis stating there is discrimination in favor of the “male” applicants. In other words, we reject \(H_0\) in favor of \(H_A\) .

Seventh and lastly, in many hypothesis testing procedures, it is commonly recommended to set the significance level of the test beforehand. It is denoted by the Greek letter \(\alpha\) (pronounced “alpha”). This value acts as a cutoff on the \(p\) -value, where if the \(p\) -value falls below \(\alpha\) , we would “reject the null hypothesis \(H_0\) .”

Alternatively, if the \(p\) -value does not fall below \(\alpha\) , we would “fail to reject \(H_0\) .” Note the latter statement is not quite the same as saying we “accept \(H_0\) .” This distinction is rather subtle and not immediately obvious. So we’ll revisit it later in Section 9.4 .

While different fields tend to use different values of \(\alpha\) , some commonly used values for \(\alpha\) are 0.1, 0.01, and 0.05; with 0.05 being the choice people often make without putting much thought into it. We’ll talk more about \(\alpha\) significance levels in Section 9.4 , but first let’s fully conduct the hypothesis test corresponding to our promotions activity using the infer package.

9.3 Conducting hypothesis tests

In Section 8.4 , we showed you how to construct confidence intervals. We first illustrated how to do this using dplyr data wrangling verbs and the rep_sample_n() function from Subsection 7.2.3 which we used as a virtual shovel. In particular, we constructed confidence intervals by resampling with replacement by setting the replace = TRUE argument to the rep_sample_n() function.

We then showed you how to perform the same task using the infer package workflow. While both workflows resulted in the same bootstrap distribution from which we can construct confidence intervals, the infer package workflow emphasizes each of the steps in the overall process in Figure 9.8 . It does so using function names that are intuitively named with verbs:

• specify() the variables of interest in your data frame.
• generate() replicates of bootstrap resamples with replacement.
• calculate() the summary statistic of interest.
• visualize() the resulting bootstrap distribution and confidence interval.

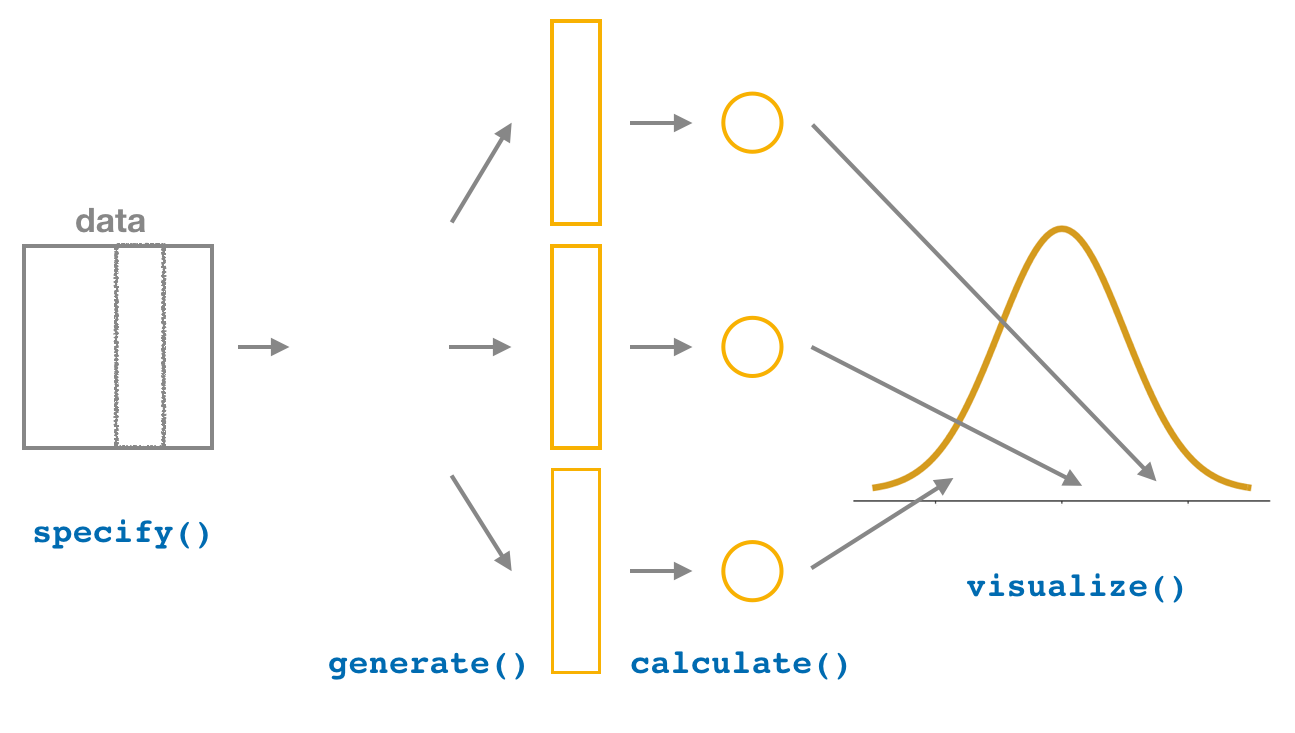
FIGURE 9.8: Confidence intervals with the infer package.

In this section, we’ll now show you how to seamlessly modify the previously seen infer code for constructing confidence intervals to conduct hypothesis tests. You’ll notice that the basic outline of the workflow is almost identical, except for an additional hypothesize() step between the specify() and generate() steps, as can be seen in Figure 9.9 .

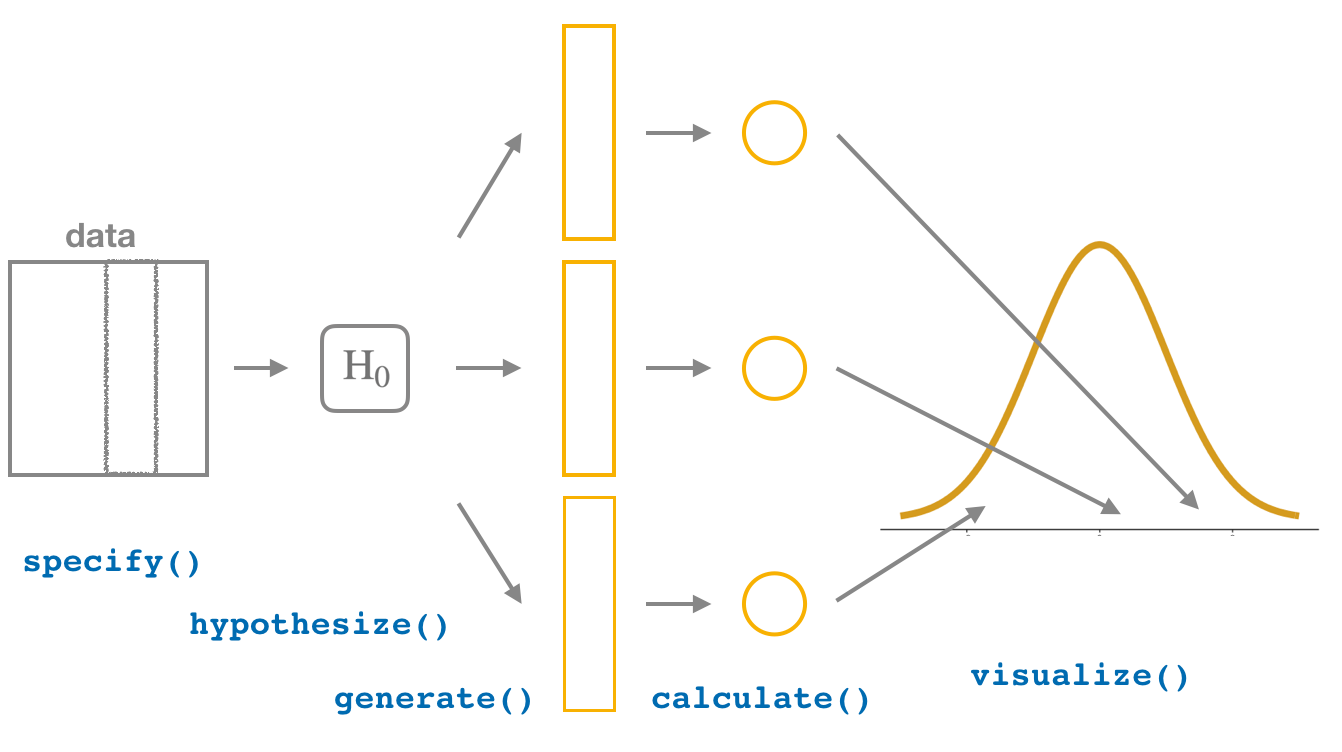
FIGURE 9.9: Hypothesis testing with the infer package.

Furthermore, we’ll use a pre-specified significance level \(\alpha\) = 0.05 for this hypothesis test. Let’s leave discussion on the choice of this \(\alpha\) value until later on in Section 9.4 .

9.3.1 infer package workflow

1. specify variables.

Recall that we use the specify() verb to specify the response variable and, if needed, any explanatory variables for our study. In this case, since we are interested in any potential effects of gender on promotion decisions, we set decision as the response variable and gender as the explanatory variable. We do so using formula = response ~ explanatory where response is the name of the response variable in the data frame and explanatory is the name of the explanatory variable. So in our case it is decision ~ gender .

Furthermore, since we are interested in the proportion of résumés "promoted" , and not the proportion of résumés not promoted, we set the argument success to "promoted" .

Again, notice how the promotions data itself doesn’t change, but the Response: decision (factor) and Explanatory: gender (factor) meta-data do. This is similar to how the group_by() verb from dplyr doesn’t change the data, but only adds “grouping” meta-data, as we saw in Section 3.4 .

2. hypothesize the null

In order to conduct hypothesis tests using the infer workflow, we need a new step not present for confidence intervals: hypothesize() . Recall from Section 9.2 that our hypothesis test was

\[ \begin{aligned} H_0 &: p_{m} - p_{f} = 0\\ \text{vs. } H_A&: p_{m} - p_{f} > 0 \end{aligned} \]

In other words, the null hypothesis \(H_0\) corresponding to our “hypothesized universe” stated that there was no difference in gender-based discrimination rates. We set this null hypothesis \(H_0\) in our infer workflow using the null argument of the hypothesize() function to either:

• "point" for hypotheses involving a single sample or
• "independence" for hypotheses involving two samples.

In our case, since we have two samples (the résumés with “male” and “female” names), we set null = "independence" .

Again, the data has not changed yet. This will occur at the upcoming generate() step; we’re merely setting meta-data for now.

Where do the terms "point" and "independence" come from? These are two technical statistical terms. The term “point” relates from the fact that for a single group of observations, you will test the value of a single point. Going back to the pennies example from Chapter 8 , say we wanted to test if the mean year of all US pennies was equal to 1993 or not. We would be testing the value of a “point” \(\mu\) , the mean year of all US pennies, as follows

\[ \begin{aligned} H_0 &: \mu = 1993\\ \text{vs } H_A&: \mu \neq 1993 \end{aligned} \]

The term “independence” relates to the fact that for two groups of observations, you are testing whether or not the response variable is independent of the explanatory variable that assigns the groups. In our case, we are testing whether the decision response variable is “independent” of the explanatory variable gender that assigns each résumé to either of the two groups.

3. generate replicates

After we hypothesize() the null hypothesis, we generate() replicates of “shuffled” datasets assuming the null hypothesis is true. We do this by repeating the shuffling exercise you performed in Section 9.1 several times. Instead of merely doing it 16 times as our groups of friends did, let’s use the computer to repeat this 1000 times by setting reps = 1000 in the generate() function. However, unlike for confidence intervals where we generated replicates using type = "bootstrap" resampling with replacement, we’ll now perform shuffles/permutations by setting type = "permute" . Recall that shuffles/permutations are a kind of resampling, but unlike the bootstrap method, they involve resampling without replacement.

Observe that the resulting data frame has 48,000 rows. This is because we performed shuffles/permutations for each of the 48 rows 1000 times and \(48,000 = 1000 \cdot 48\) . If you explore the promotions_generate data frame with View() , you’ll notice that the variable replicate indicates which resample each row belongs to. So it has the value 1 48 times, the value 2 48 times, all the way through to the value 1000 48 times.

4. calculate summary statistics

Now that we have generated 1000 replicates of “shuffles” assuming the null hypothesis is true, let’s calculate() the appropriate summary statistic for each of our 1000 shuffles. From Section 9.2 , point estimates related to hypothesis testing have a specific name: test statistics . Since the unknown population parameter of interest is the difference in population proportions \(p_{m} - p_{f}\) , the test statistic here is the difference in sample proportions \(\widehat{p}_{m} - \widehat{p}_{f}\) .

For each of our 1000 shuffles, we can calculate this test statistic by setting stat = "diff in props" . Furthermore, since we are interested in \(\widehat{p}_{m} - \widehat{p}_{f}\) we set order = c("male", "female") . As we stated earlier, the order of the subtraction does not matter, so long as you stay consistent throughout your analysis and tailor your interpretations accordingly.

Let’s save the result in a data frame called null_distribution :

Observe that we have 1000 values of stat , each representing one instance of \(\widehat{p}_{m} - \widehat{p}_{f}\) in a hypothesized world of no gender discrimination. Observe as well that we chose the name of this data frame carefully: null_distribution . Recall once again from Section 9.2 that sampling distributions when the null hypothesis \(H_0\) is assumed to be true have a special name: the null distribution .

What was the observed difference in promotion rates? In other words, what was the observed test statistic \(\widehat{p}_{m} - \widehat{p}_{f}\) ? Recall from Section 9.1 that we computed this observed difference by hand to be 0.875 - 0.583 = 0.292 = 29.2%. We can also compute this value using the previous infer code but with the hypothesize() and generate() steps removed. Let’s save this in obs_diff_prop :

5. visualize the p-value

The final step is to measure how surprised we are by a promotion difference of 29.2% in a hypothesized universe of no gender discrimination. If the observed difference of 0.292 is highly unlikely, then we would be inclined to reject the validity of our hypothesized universe.

We start by visualizing the null distribution of our 1000 values of \(\widehat{p}_{m} - \widehat{p}_{f}\) using visualize() in Figure 9.10 . Recall that these are values of the difference in promotion rates assuming \(H_0\) is true. This corresponds to being in our hypothesized universe of no gender discrimination.

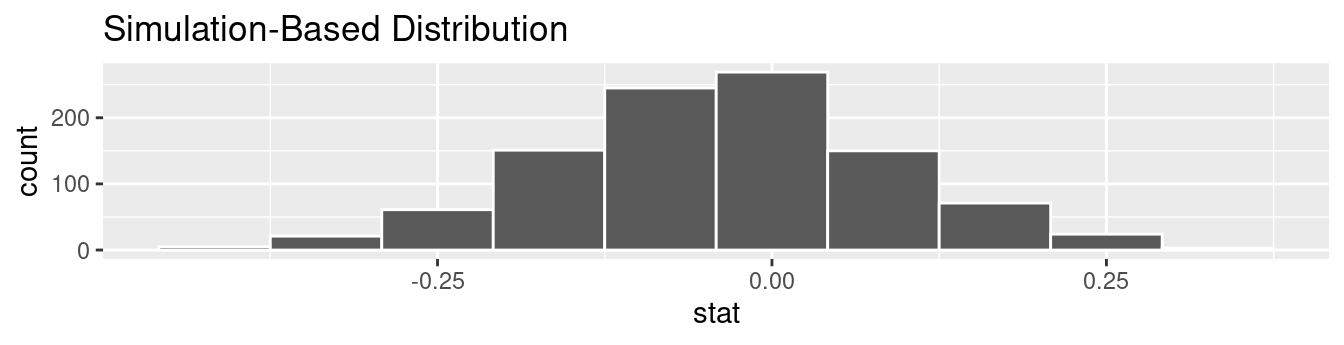
FIGURE 9.10: Null distribution.

Let’s now add what happened in real life to Figure 9.10 , the observed difference in promotion rates of 0.875 - 0.583 = 0.292 = 29.2%. However, instead of merely adding a vertical line using geom_vline() , let’s use the shade_p_value() function with obs_stat set to the observed test statistic value we saved in obs_diff_prop .

Furthermore, we’ll set the direction = "right" reflecting our alternative hypothesis \(H_A: p_{m} - p_{f} > 0\) . Recall our alternative hypothesis \(H_A\) is that \(p_{m} - p_{f} > 0\) , stating that there is a difference in promotion rates in favor of résumés with male names. “More extreme” here corresponds to differences that are “bigger” or “more positive” or “more to the right.” Hence we set the direction argument of shade_p_value() to be "right" .

On the other hand, had our alternative hypothesis \(H_A\) been the other possible one-sided alternative \(p_{m} - p_{f} < 0\) , suggesting discrimination in favor of résumés with female names, we would’ve set direction = "left" . Had our alternative hypothesis \(H_A\) been two-sided \(p_{m} - p_{f} \neq 0\) , suggesting discrimination in either direction, we would’ve set direction = "both" .

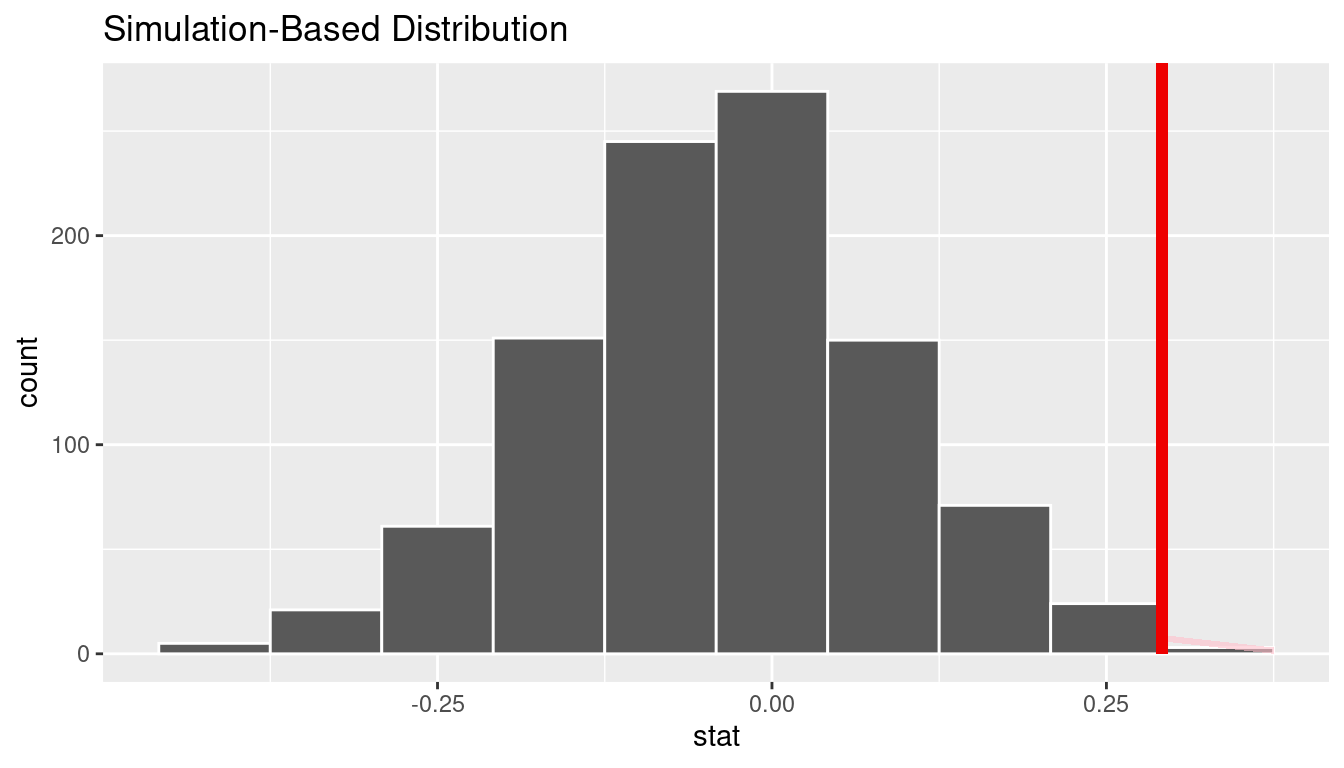
FIGURE 9.11: Shaded histogram to show \(p\) -value.

In the resulting Figure 9.11 , the solid dark line marks 0.292 = 29.2%. However, what does the shaded-region correspond to? This is the \(p\) -value . Recall the definition of the \(p\) -value from Section 9.2 :

A \(p\) -value is the probability of obtaining a test statistic just as or more extreme than the observed test statistic assuming the null hypothesis \(H_0\) is true .

So judging by the shaded region in Figure 9.11 , it seems we would somewhat rarely observe differences in promotion rates of 0.292 = 29.2% or more in a hypothesized universe of no gender discrimination. In other words, the \(p\) -value is somewhat small. Hence, we would be inclined to reject this hypothesized universe, or using statistical language we would “reject \(H_0\) .”

What fraction of the null distribution is shaded? In other words, what is the exact value of the \(p\) -value? We can compute it using the get_p_value() function with the same arguments as the previous shade_p_value() code:

Keeping the definition of a \(p\) -value in mind, the probability of observing a difference in promotion rates as large as 0.292 = 29.2% due to sampling variation alone in the null distribution is 0.027 = 2.7%. Since this \(p\) -value is smaller than our pre-specified significance level \(\alpha\) = 0.05, we reject the null hypothesis \(H_0: p_{m} - p_{f} = 0\) . In other words, this \(p\) -value is sufficiently small to reject our hypothesized universe of no gender discrimination. We instead have enough evidence to change our mind in favor of gender discrimination being a likely culprit here. Observe that whether we reject the null hypothesis \(H_0\) or not depends in large part on our choice of significance level \(\alpha\) . We’ll discuss this more in Subsection 9.4.3 .

9.3.2 Comparison with confidence intervals

One of the great things about the infer package is that we can jump seamlessly between conducting hypothesis tests and constructing confidence intervals with minimal changes! Recall the code from the previous section that creates the null distribution, which in turn is needed to compute the \(p\) -value:

To create the corresponding bootstrap distribution needed to construct a 95% confidence interval for \(p_{m} - p_{f}\) , we only need to make two changes. First, we remove the hypothesize() step since we are no longer assuming a null hypothesis \(H_0\) is true. We can do this by deleting or commenting out the hypothesize() line of code. Second, we switch the type of resampling in the generate() step to be "bootstrap" instead of "permute" .

Using this bootstrap_distribution , let’s first compute the percentile-based confidence intervals, as we did in Section 8.4 :

Using our shorthand interpretation for 95% confidence intervals from Subsection 8.5.2 , we are 95% “confident” that the true difference in population proportions \(p_{m} - p_{f}\) is between (0.044, 0.539). Let’s visualize bootstrap_distribution and this percentile-based 95% confidence interval for \(p_{m} - p_{f}\) in Figure 9.12 .

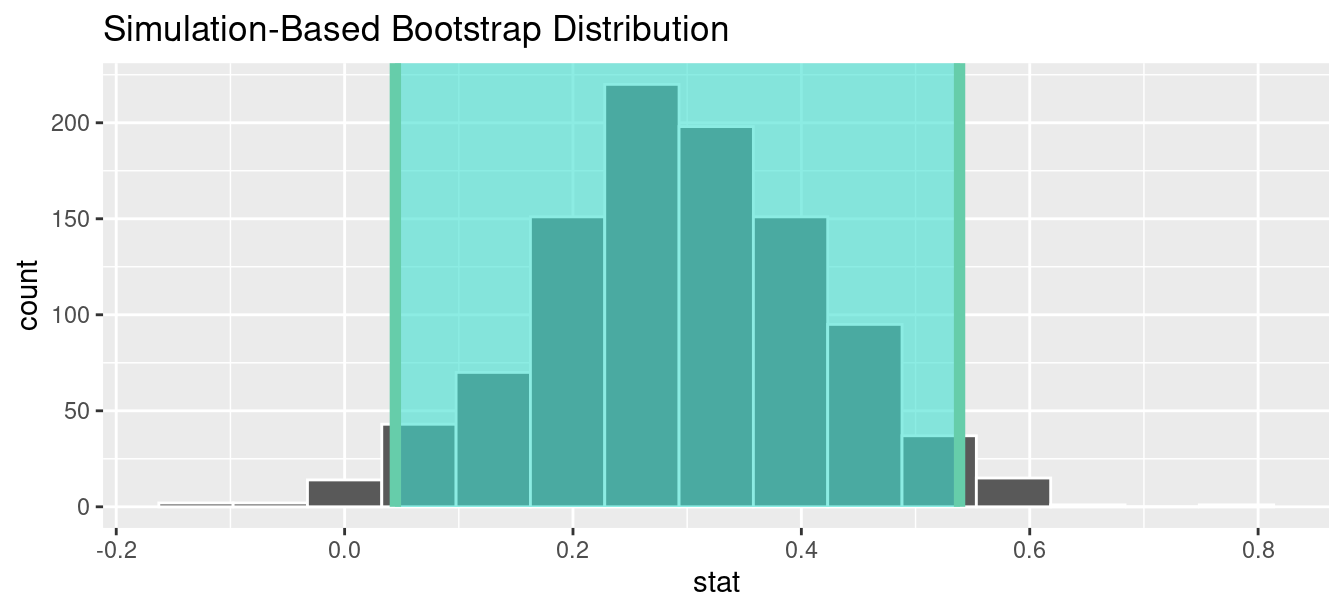
FIGURE 9.12: Percentile-based 95% confidence interval.

Notice a key value that is not included in the 95% confidence interval for \(p_{m} - p_{f}\) : the value 0. In other words, a difference of 0 is not included in our net, suggesting that \(p_{m}\) and \(p_{f}\) are truly different! Furthermore, observe how the entirety of the 95% confidence interval for \(p_{m} - p_{f}\) lies above 0, suggesting that this difference is in favor of men.

Since the bootstrap distribution appears to be roughly normally shaped, we can also use the standard error method as we did in Section 8.4 . In this case, we must specify the point_estimate argument as the observed difference in promotion rates 0.292 = 29.2% saved in obs_diff_prop . This value acts as the center of the confidence interval.

Let’s visualize bootstrap_distribution again, but now the standard error based 95% confidence interval for \(p_{m} - p_{f}\) in Figure 9.13 . Again, notice how the value 0 is not included in our confidence interval, again suggesting that \(p_{m}\) and \(p_{f}\) are truly different!

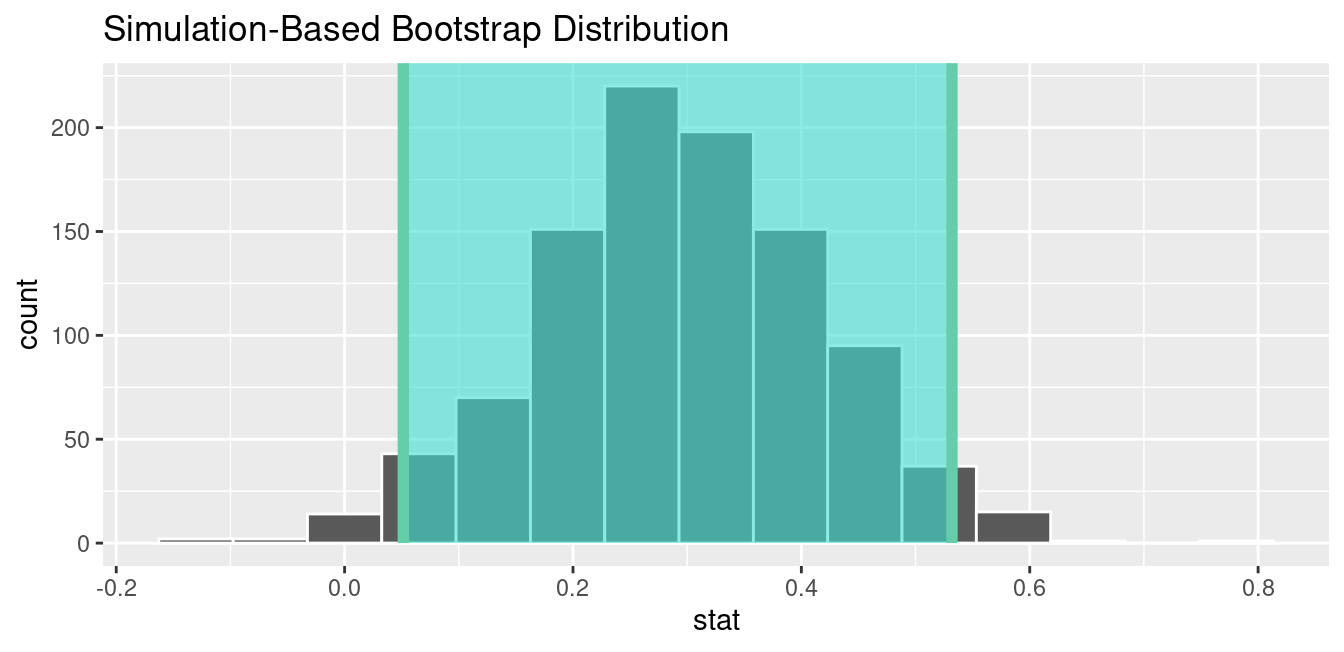
FIGURE 9.13: Standard error-based 95% confidence interval.

Learning check

(LC9.1) Why does the following code produce an error? In other words, what about the response and predictor variables make this not a possible computation with the infer package?

(LC9.2) Why are we relatively confident that the distributions of the sample proportions will be good approximations of the population distributions of promotion proportions for the two genders?

(LC9.3) Using the definition of p-value , write in words what the \(p\) -value represents for the hypothesis test comparing the promotion rates for males and females.

9.3.3 “There is only one test”

Let’s recap the steps necessary to conduct a hypothesis test using the terminology, notation, and definitions related to sampling you saw in Section 9.2 and the infer workflow from Subsection 9.3.1 :

• hypothesize() the null hypothesis \(H_0\) . In other words, set a “model for the universe” assuming \(H_0\) is true.
• generate() shuffles assuming \(H_0\) is true. In other words, simulate data assuming \(H_0\) is true.
• calculate() the test statistic of interest, both for the observed data and your simulated data.
• visualize() the resulting null distribution and compute the \(p\) -value by comparing the null distribution to the observed test statistic.

While this is a lot to digest, especially the first time you encounter hypothesis testing, the nice thing is that once you understand this general framework, then you can understand any hypothesis test. In a famous blog post, computer scientist Allen Downey called this the “There is only one test” framework, for which he created the flowchart displayed in Figure 9.14 .

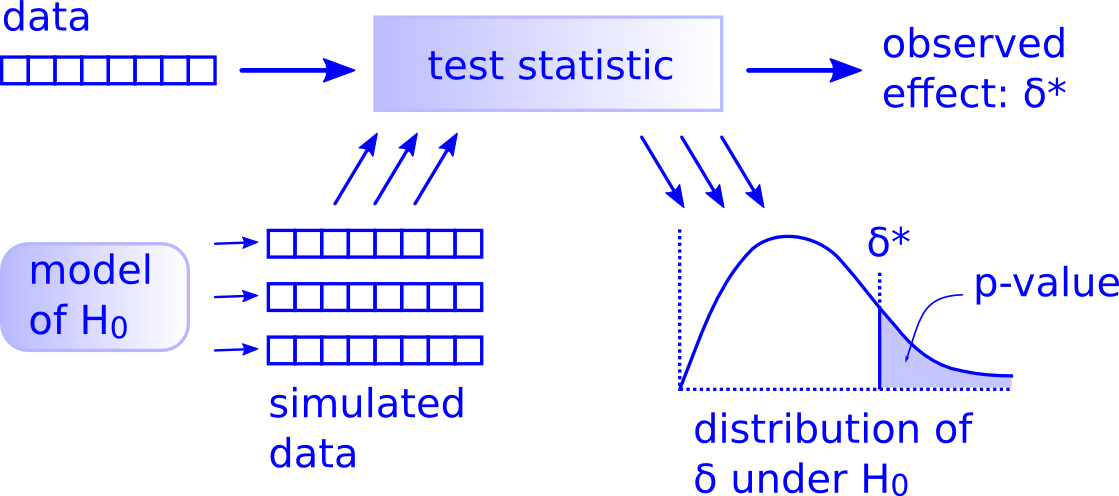
FIGURE 9.14: Allen Downey’s hypothesis testing framework.

Notice its similarity with the “hypothesis testing with infer ” diagram you saw in Figure 9.9 . That’s because the infer package was explicitly designed to match the “There is only one test” framework. So if you can understand the framework, you can easily generalize these ideas for all hypothesis testing scenarios. Whether for population proportions \(p\) , population means \(\mu\) , differences in population proportions \(p_1 - p_2\) , differences in population means \(\mu_1 - \mu_2\) , and as you’ll see in Chapter 10 on inference for regression, population regression slopes \(\beta_1\) as well. In fact, it applies more generally even than just these examples to more complicated hypothesis tests and test statistics as well.

(LC9.4) Describe in a paragraph how we used Allen Downey’s diagram to conclude if a statistical difference existed between the promotion rate of males and females using this study.

9.4 Interpreting hypothesis tests

Interpreting the results of hypothesis tests is one of the more challenging aspects of this method for statistical inference. In this section, we’ll focus on ways to help with deciphering the process and address some common misconceptions.

9.4.1 Two possible outcomes

In Section 9.2 , we mentioned that given a pre-specified significance level \(\alpha\) there are two possible outcomes of a hypothesis test:

• If the \(p\) -value is less than \(\alpha\) , then we reject the null hypothesis \(H_0\) in favor of \(H_A\) .
• If the \(p\) -value is greater than or equal to \(\alpha\) , we fail to reject the null hypothesis \(H_0\) .

Unfortunately, the latter result is often misinterpreted as “accepting the null hypothesis \(H_0\) .” While at first glance it may seem that the statements “failing to reject \(H_0\) ” and “accepting \(H_0\) ” are equivalent, there actually is a subtle difference. Saying that we “accept the null hypothesis \(H_0\) ” is equivalent to stating that “we think the null hypothesis \(H_0\) is true.” However, saying that we “fail to reject the null hypothesis \(H_0\) ” is saying something else: “While \(H_0\) might still be false, we don’t have enough evidence to say so.” In other words, there is an absence of enough proof. However, the absence of proof is not proof of absence.

To further shed light on this distinction, let’s use the United States criminal justice system as an analogy. A criminal trial in the United States is a similar situation to hypothesis tests whereby a choice between two contradictory claims must be made about a defendant who is on trial:

• The defendant is truly either “innocent” or “guilty.”
• The defendant is presumed “innocent until proven guilty.”
• The defendant is found guilty only if there is strong evidence that the defendant is guilty. The phrase “beyond a reasonable doubt” is often used as a guideline for determining a cutoff for when enough evidence exists to find the defendant guilty.
• The defendant is found to be either “not guilty” or “guilty” in the ultimate verdict.

In other words, not guilty verdicts are not suggesting the defendant is innocent , but instead that “while the defendant may still actually be guilty, there wasn’t enough evidence to prove this fact.” Now let’s make the connection with hypothesis tests:

• Either the null hypothesis \(H_0\) or the alternative hypothesis \(H_A\) is true.
• Hypothesis tests are conducted assuming the null hypothesis \(H_0\) is true.
• We reject the null hypothesis \(H_0\) in favor of \(H_A\) only if the evidence found in the sample suggests that \(H_A\) is true. The significance level \(\alpha\) is used as a guideline to set the threshold on just how strong of evidence we require.
• We ultimately decide to either “fail to reject \(H_0\) ” or “reject \(H_0\) .”

So while gut instinct may suggest “failing to reject \(H_0\) ” and “accepting \(H_0\) ” are equivalent statements, they are not. “Accepting \(H_0\) ” is equivalent to finding a defendant innocent. However, courts do not find defendants “innocent,” but rather they find them “not guilty.” Putting things differently, defense attorneys do not need to prove that their clients are innocent, rather they only need to prove that clients are not “guilty beyond a reasonable doubt”.

So going back to our résumés activity in Section 9.3 , recall that our hypothesis test was \(H_0: p_{m} - p_{f} = 0\) versus \(H_A: p_{m} - p_{f} > 0\) and that we used a pre-specified significance level of \(\alpha\) = 0.05. We found a \(p\) -value of 0.027. Since the \(p\) -value was smaller than \(\alpha\) = 0.05, we rejected \(H_0\) . In other words, we found needed levels of evidence in this particular sample to say that \(H_0\) is false at the \(\alpha\) = 0.05 significance level. We also state this conclusion using non-statistical language: we found enough evidence in this data to suggest that there was gender discrimination at play.

9.4.2 Types of errors

Unfortunately, there is some chance a jury or a judge can make an incorrect decision in a criminal trial by reaching the wrong verdict. For example, finding a truly innocent defendant “guilty”. Or on the other hand, finding a truly guilty defendant “not guilty.” This can often stem from the fact that prosecutors don’t have access to all the relevant evidence, but instead are limited to whatever evidence the police can find.

The same holds for hypothesis tests. We can make incorrect decisions about a population parameter because we only have a sample of data from the population and thus sampling variation can lead us to incorrect conclusions.

There are two possible erroneous conclusions in a criminal trial: either (1) a truly innocent person is found guilty or (2) a truly guilty person is found not guilty. Similarly, there are two possible errors in a hypothesis test: either (1) rejecting \(H_0\) when in fact \(H_0\) is true, called a Type I error or (2) failing to reject \(H_0\) when in fact \(H_0\) is false, called a Type II error . Another term used for “Type I error” is “false positive,” while another term for “Type II error” is “false negative.”

This risk of error is the price researchers pay for basing inference on a sample instead of performing a census on the entire population. But as we’ve seen in our numerous examples and activities so far, censuses are often very expensive and other times impossible, and thus researchers have no choice but to use a sample. Thus in any hypothesis test based on a sample, we have no choice but to tolerate some chance that a Type I error will be made and some chance that a Type II error will occur.

To help understand the concepts of Type I error and Type II errors, we apply these terms to our criminal justice analogy in Figure 9.15 .

FIGURE 9.15: Type I and Type II errors in criminal trials.

Thus a Type I error corresponds to incorrectly putting a truly innocent person in jail, whereas a Type II error corresponds to letting a truly guilty person go free. Let’s show the corresponding table in Figure 9.16 for hypothesis tests.

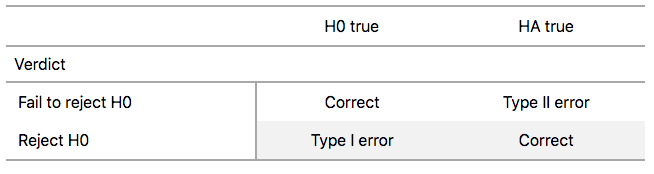
FIGURE 9.16: Type I and Type II errors in hypothesis tests.

9.4.3 How do we choose alpha?

If we are using a sample to make inferences about a population, we run the risk of making errors. For confidence intervals, a corresponding “error” would be constructing a confidence interval that does not contain the true value of the population parameter. For hypothesis tests, this would be making either a Type I or Type II error. Obviously, we want to minimize the probability of either error; we want a small probability of making an incorrect conclusion:

• The probability of a Type I Error occurring is denoted by \(\alpha\) . The value of \(\alpha\) is called the significance level of the hypothesis test, which we defined in Section 9.2 .
• The probability of a Type II Error is denoted by \(\beta\) . The value of \(1-\beta\) is known as the power of the hypothesis test.

In other words, \(\alpha\) corresponds to the probability of incorrectly rejecting \(H_0\) when in fact \(H_0\) is true. On the other hand, \(\beta\) corresponds to the probability of incorrectly failing to reject \(H_0\) when in fact \(H_0\) is false.

Ideally, we want \(\alpha = 0\) and \(\beta = 0\) , meaning that the chance of making either error is 0. However, this can never be the case in any situation where we are sampling for inference. There will always be the possibility of making either error when we use sample data. Furthermore, these two error probabilities are inversely related. As the probability of a Type I error goes down, the probability of a Type II error goes up.

What is typically done in practice is to fix the probability of a Type I error by pre-specifying a significance level \(\alpha\) and then try to minimize \(\beta\) . In other words, we will tolerate a certain fraction of incorrect rejections of the null hypothesis \(H_0\) , and then try to minimize the fraction of incorrect non-rejections of \(H_0\) .

So for example if we used \(\alpha\) = 0.01, we would be using a hypothesis testing procedure that in the long run would incorrectly reject the null hypothesis \(H_0\) one percent of the time. This is analogous to setting the confidence level of a confidence interval.

So what value should you use for \(\alpha\) ? Different fields have different conventions, but some commonly used values include 0.10, 0.05, 0.01, and 0.001. However, it is important to keep in mind that if you use a relatively small value of \(\alpha\) , then all things being equal, \(p\) -values will have a harder time being less than \(\alpha\) . Thus we would reject the null hypothesis less often. In other words, we would reject the null hypothesis \(H_0\) only if we have very strong evidence to do so. This is known as a “conservative” test.

On the other hand, if we used a relatively large value of \(\alpha\) , then all things being equal, \(p\) -values will have an easier time being less than \(\alpha\) . Thus we would reject the null hypothesis more often. In other words, we would reject the null hypothesis \(H_0\) even if we only have mild evidence to do so. This is known as a “liberal” test.

(LC9.5) What is wrong about saying, “The defendant is innocent.” based on the US system of criminal trials?

(LC9.6) What is the purpose of hypothesis testing?

(LC9.7) What are some flaws with hypothesis testing? How could we alleviate them?

(LC9.8) Consider two \(\alpha\) significance levels of 0.1 and 0.01. Of the two, which would lead to a more liberal hypothesis testing procedure? In other words, one that will, all things being equal, lead to more rejections of the null hypothesis \(H_0\) .

9.5 Case study: Are action or romance movies rated higher?

Let’s apply our knowledge of hypothesis testing to answer the question: “Are action or romance movies rated higher on IMDb?”. IMDb is a database on the internet providing information on movie and television show casts, plot summaries, trivia, and ratings. We’ll investigate if, on average, action or romance movies get higher ratings on IMDb.

9.5.1 IMDb ratings data

The movies dataset in the ggplot2movies package contains information on 58,788 movies that have been rated by users of IMDb.com.

We’ll focus on a random sample of 68 movies that are classified as either “action” or “romance” movies but not both. We disregard movies that are classified as both so that we can assign all 68 movies into either category. Furthermore, since the original movies dataset was a little messy, we provide a pre-wrangled version of our data in the movies_sample data frame included in the moderndive package. If you’re curious, you can look at the necessary data wrangling code to do this on GitHub .

The variables include the title and year the movie was filmed. Furthermore, we have a numerical variable rating , which is the IMDb rating out of 10 stars, and a binary categorical variable genre indicating if the movie was an Action or Romance movie. We are interested in whether Action or Romance movies got a higher rating on average.

Let’s perform an exploratory data analysis of this data. Recall from Subsection 2.7.1 that a boxplot is a visualization we can use to show the relationship between a numerical and a categorical variable. Another option you saw in Section 2.6 would be to use a faceted histogram. However, in the interest of brevity, let’s only present the boxplot in Figure 9.17 .

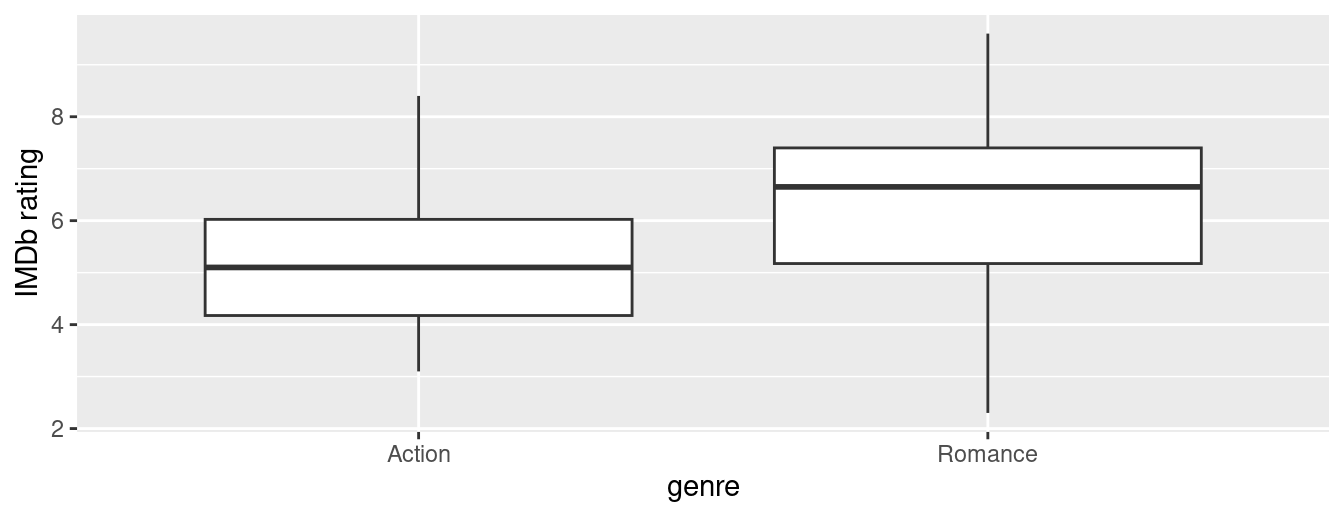
FIGURE 9.17: Boxplot of IMDb rating vs. genre.

Eyeballing Figure 9.17 , romance movies have a higher median rating. Do we have reason to believe, however, that there is a significant difference between the mean rating for action movies compared to romance movies? It’s hard to say just based on this plot. The boxplot does show that the median sample rating is higher for romance movies.

However, there is a large amount of overlap between the boxes. Recall that the median isn’t necessarily the same as the mean either, depending on whether the distribution is skewed.

Let’s calculate some summary statistics split by the binary categorical variable genre : the number of movies, the mean rating, and the standard deviation split by genre . We’ll do this using dplyr data wrangling verbs. Notice in particular how we count the number of each type of movie using the n() summary function.

Observe that we have 36 movies with an average rating of 6.322 stars and 32 movies with an average rating of 5.275 stars. The difference in these average ratings is thus 6.322 - 5.275 = 1.047. So there appears to be an edge of 1.047 stars in favor of romance movies. The question is, however, are these results indicative of a true difference for all romance and action movies? Or could we attribute this difference to chance sampling variation ?

9.5.2 Sampling scenario

Let’s now revisit this study in terms of terminology and notation related to sampling we studied in Subsection 7.3.1 . The study population is all movies in the IMDb database that are either action or romance (but not both). The sample from this population is the 68 movies included in the movies_sample dataset.

Since this sample was randomly taken from the population movies , it is representative of all romance and action movies on IMDb. Thus, any analysis and results based on movies_sample can generalize to the entire population. What are the relevant population parameter and point estimates ? We introduce the fourth sampling scenario in Table 9.3 .

So, whereas the sampling bowl exercise in Section 7.1 concerned proportions , the pennies exercise in Section 8.1 concerned means , the case study on whether yawning is contagious in Section 8.6 and the promotions activity in Section 9.1 concerned differences in proportions , we are now concerned with differences in means .

In other words, the population parameter of interest is the difference in population mean ratings \(\mu_a - \mu_r\) , where \(\mu_a\) is the mean rating of all action movies on IMDb and similarly \(\mu_r\) is the mean rating of all romance movies. Additionally the point estimate/sample statistic of interest is the difference in sample means \(\overline{x}_a - \overline{x}_r\) , where \(\overline{x}_a\) is the mean rating of the \(n_a\) = 32 movies in our sample and \(\overline{x}_r\) is the mean rating of the \(n_r\) = 36 in our sample. Based on our earlier exploratory data analysis, our estimate \(\overline{x}_a - \overline{x}_r\) is \(5.275 - 6.322 = -1.047\) .

So there appears to be a slight difference of -1.047 in favor of romance movies. The question is, however, could this difference of -1.047 be merely due to chance and sampling variation? Or are these results indicative of a true difference in mean ratings for all romance and action movies on IMDb? To answer this question, we’ll use hypothesis testing.

9.5.3 Conducting the hypothesis test

We’ll be testing:

\[ \begin{aligned} H_0 &: \mu_a - \mu_r = 0\\ \text{vs } H_A&: \mu_a - \mu_r \neq 0 \end{aligned} \]

In other words, the null hypothesis \(H_0\) suggests that both romance and action movies have the same mean rating. This is the “hypothesized universe” we’ll assume is true. On the other hand, the alternative hypothesis \(H_A\) suggests that there is a difference. Unlike the one-sided alternative we used in the promotions exercise \(H_A: p_m - p_f > 0\) , we are now considering a two-sided alternative of \(H_A: \mu_a - \mu_r \neq 0\) .

Furthermore, we’ll pre-specify a low significance level of \(\alpha\) = 0.001. By setting this value low, all things being equal, there is a lower chance that the \(p\) -value will be less than \(\alpha\) . Thus, there is a lower chance that we’ll reject the null hypothesis \(H_0\) in favor of the alternative hypothesis \(H_A\) . In other words, we’ll reject the hypothesis that there is no difference in mean ratings for all action and romance movies, only if we have quite strong evidence. This is known as a “conservative” hypothesis testing procedure.

Let’s now perform all the steps of the infer workflow. We first specify() the variables of interest in the movies_sample data frame using the formula rating ~ genre . This tells infer that the numerical variable rating is the outcome variable, while the binary variable genre is the explanatory variable. Note that unlike previously when we were interested in proportions, since we are now interested in the mean of a numerical variable, we do not need to set the success argument.

Observe at this point that the data in movies_sample has not changed. The only change so far is the newly defined Response: rating (numeric) and Explanatory: genre (factor) meta-data .

We set the null hypothesis \(H_0: \mu_a - \mu_r = 0\) by using the hypothesize() function. Since we have two samples, action and romance movies, we set null to be "independence" as we described in Section 9.3 .

After we have set the null hypothesis, we generate “shuffled” replicates assuming the null hypothesis is true by repeating the shuffling/permutation exercise you performed in Section 9.1 .

We’ll repeat this resampling without replacement of type = "permute" a total of reps = 1000 times. Feel free to run the code below to check out what the generate() step produces.

Now that we have 1000 replicated “shuffles” assuming the null hypothesis \(H_0\) that both Action and Romance movies on average have the same ratings on IMDb, let’s calculate() the appropriate summary statistic for these 1000 replicated shuffles. From Section 9.2 , summary statistics relating to hypothesis testing have a specific name: test statistics . Since the unknown population parameter of interest is the difference in population means \(\mu_{a} - \mu_{r}\) , the test statistic of interest here is the difference in sample means \(\overline{x}_{a} - \overline{x}_{r}\) .

For each of our 1000 shuffles, we can calculate this test statistic by setting stat = "diff in means" . Furthermore, since we are interested in \(\overline{x}_{a} - \overline{x}_{r}\) , we set order = c("Action", "Romance") . Let’s save the results in a data frame called null_distribution_movies :

Observe that we have 1000 values of stat , each representing one instance of \(\overline{x}_{a} - \overline{x}_{r}\) . The 1000 values form the null distribution , which is the technical term for the sampling distribution of the difference in sample means \(\overline{x}_{a} - \overline{x}_{r}\) assuming \(H_0\) is true. What happened in real life? What was the observed difference in promotion rates? What was the observed test statistic \(\overline{x}_{a} - \overline{x}_{r}\) ? Recall from our earlier data wrangling, this observed difference in means was \(5.275 - 6.322 = -1.047\) . We can also achieve this using the code that constructed the null distribution null_distribution_movies but with the hypothesize() and generate() steps removed. Let’s save this in obs_diff_means :

Lastly, in order to compute the \(p\) -value, we have to assess how “extreme” the observed difference in means of -1.047 is. We do this by comparing -1.047 to our null distribution, which was constructed in a hypothesized universe of no true difference in movie ratings. Let’s visualize both the null distribution and the \(p\) -value in Figure 9.18 . Unlike our example in Subsection 9.3.1 involving promotions, since we have a two-sided \(H_A: \mu_a - \mu_r \neq 0\) , we have to allow for both possibilities for more extreme , so we set direction = "both" .

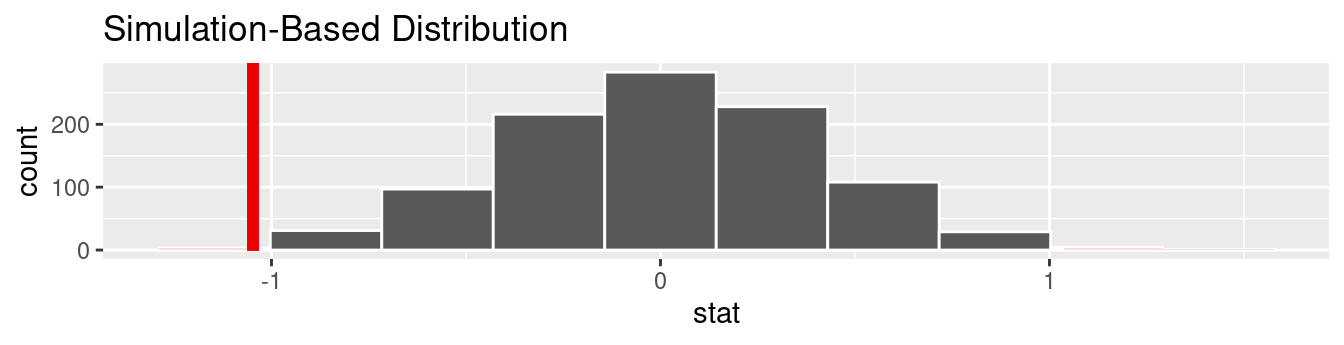
FIGURE 9.18: Null distribution, observed test statistic, and \(p\) -value.

Let’s go over the elements of this plot. First, the histogram is the null distribution . Second, the solid line is the observed test statistic , or the difference in sample means we observed in real life of \(5.275 - 6.322 = -1.047\) . Third, the two shaded areas of the histogram form the \(p\) -value , or the probability of obtaining a test statistic just as or more extreme than the observed test statistic assuming the null hypothesis \(H_0\) is true .

What proportion of the null distribution is shaded? In other words, what is the numerical value of the \(p\) -value? We use the get_p_value() function to compute this value:

This \(p\) -value of 0.004 is very small. In other words, there is a very small chance that we’d observe a difference of 5.275 - 6.322 = -1.047 in a hypothesized universe where there was truly no difference in ratings.

But this \(p\) -value is larger than our (even smaller) pre-specified \(\alpha\) significance level of 0.001. Thus, we are inclined to fail to reject the null hypothesis \(H_0: \mu_a - \mu_r = 0\) . In non-statistical language, the conclusion is: we do not have the evidence needed in this sample of data to suggest that we should reject the hypothesis that there is no difference in mean IMDb ratings between romance and action movies. We, thus, cannot say that a difference exists in romance and action movie ratings, on average, for all IMDb movies.

(LC9.9) Conduct the same analysis comparing action movies versus romantic movies using the median rating instead of the mean rating. What was different and what was the same?

(LC9.10) What conclusions can you make from viewing the faceted histogram looking at rating versus genre that you couldn’t see when looking at the boxplot?

(LC9.11) Describe in a paragraph how we used Allen Downey’s diagram to conclude if a statistical difference existed between mean movie ratings for action and romance movies.

(LC9.12) Why are we relatively confident that the distributions of the sample ratings will be good approximations of the population distributions of ratings for the two genres?

(LC9.13) Using the definition of \(p\) -value, write in words what the \(p\) -value represents for the hypothesis test comparing the mean rating of romance to action movies.

(LC9.14) What is the value of the \(p\) -value for the hypothesis test comparing the mean rating of romance to action movies?

(LC9.15) Test your data wrangling knowledge and EDA skills:

• Use dplyr and tidyr to create the necessary data frame focused on only action and romance movies (but not both) from the movies data frame in the ggplot2movies package.
• Make a boxplot and a faceted histogram of this population data comparing ratings of action and romance movies from IMDb.
• Discuss how these plots compare to the similar plots produced for the movies_sample data.

9.6 Conclusion

9.6.1 theory-based hypothesis tests.

Much as we did in Subsections 7.6.2 and 8.7.2 when we showed you theory-based methods for compututing standard errors and constructing confidence intervals that involved mathematical formulas, we now present an example of a traditional theory-based method to conduct hypothesis tests. This method relies on probability models, probability distributions, and a few assumptions to construct the null distribution. This is in contrast to the approach we’ve been using throughout this book where we relied on computer simulations to construct the null distribution.

These traditional theory-based methods have been used for decades mostly because researchers didn’t have access to computers that could run thousands of calculations quickly and efficiently. Now that computing power is much cheaper and more accessible, simulation-based methods are much more feasible. However, researchers in many fields continue to use theory-based methods. Hence, we make it a point to include an example here.

As we’ll show in this section, any theory-based method is ultimately an approximation to the simulation-based method. The theory-based method we’ll focus on is known as the two-sample \(t\) -test for testing differences in sample means. However, the test statistic we’ll use won’t be the difference in sample means \(\overline{x}_1 - \overline{x}_2\) , but rather the related two-sample \(t\) -statistic . The data we’ll use will once again be the movies_sample data of action and romance movies from Section 9.5 .

Two-sample t-statistic

A common task in statistics is the process of “standardizing a variable.” By standardizing different variables, we make them more comparable. For example, say you are interested in studying the distribution of temperature recordings from Portland, Oregon, USA and comparing it to that of the temperature recordings in Montreal, Quebec, Canada. Given that US temperatures are generally recorded in degrees Fahrenheit and Canadian temperatures are generally recorded in degrees Celsius, how can we make them comparable? One approach would be to convert degrees Fahrenheit into Celsius, or vice versa. Another approach would be to convert them both to a common “standardized” scale, like Kelvin units of temperature.

One common method for standardizing a variable from probability and statistics theory is to compute the \(z\) -score:

\[z = \frac{x - \mu}{\sigma}\]

where \(x\) represents one value of a variable, \(\mu\) represents the mean of that variable, and \(\sigma\) represents the standard deviation of that variable. You first subtract the mean \(\mu\) from each value of \(x\) and then divide \(x - \mu\) by the standard deviation \(\sigma\) . These operations will have the effect of re-centering your variable around 0 and re-scaling your variable \(x\) so that they have what are known as “standard units.” Thus for every value that your variable can take, it has a corresponding \(z\) -score that gives how many standard units away that value is from the mean \(\mu\) . \(z\) -scores are normally distributed with mean 0 and standard deviation 1. This curve is called a “ \(z\) -distribution” or “standard normal” curve and has the common, bell-shaped pattern from Figure 9.19 discussed in Appendix A.2 .

FIGURE 9.19: Standard normal z curve.

Bringing these back to the difference of sample mean ratings \(\overline{x}_a - \overline{x}_r\) of action versus romance movies, how would we standardize this variable? By once again subtracting its mean and dividing by its standard deviation. Recall two facts from Subsection 7.3.3 . First, if the sampling was done in a representative fashion, then the sampling distribution of \(\overline{x}_a - \overline{x}_r\) will be centered at the true population parameter \(\mu_a - \mu_r\) . Second, the standard deviation of point estimates like \(\overline{x}_a - \overline{x}_r\) has a special name: the standard error.

Applying these ideas, we present the two-sample \(t\) -statistic :

\[t = \dfrac{ (\bar{x}_a - \bar{x}_r) - (\mu_a - \mu_r)}{ \text{SE}_{\bar{x}_a - \bar{x}_r} } = \dfrac{ (\bar{x}_a - \bar{x}_r) - (\mu_a - \mu_r)}{ \sqrt{\dfrac{{s_a}^2}{n_a} + \dfrac{{s_r}^2}{n_r}} }\]

Oofda! There is a lot to try to unpack here! Let’s go slowly. In the numerator, \(\bar{x}_a-\bar{x}_r\) is the difference in sample means, while \(\mu_a - \mu_r\) is the difference in population means. In the denominator, \(s_a\) and \(s_r\) are the sample standard deviations of the action and romance movies in our sample movies_sample . Lastly, \(n_a\) and \(n_r\) are the sample sizes of the action and romance movies. Putting this together under the square root gives us the standard error \(\text{SE}_{\bar{x}_a - \bar{x}_r}\) .

Observe that the formula for \(\text{SE}_{\bar{x}_a - \bar{x}_r}\) has the sample sizes \(n_a\) and \(n_r\) in them. So as the sample sizes increase, the standard error goes down. We’ve seen this concept numerous times now, in particular (1) in our simulations using the three virtual shovels with \(n\) = 25, 50, and 100 slots in Figure 7.15 , (2) in Subsection 8.5.3 where we studied the effect of using larger sample sizes on the widths of confidence intervals, and (3) in Subsection 7.6.2 where we studied the formula-based approximation to the standard error of the sample proportion \(\widehat{p}\) .

So how can we use the two-sample \(t\) -statistic as a test statistic in our hypothesis test? First, assuming the null hypothesis \(H_0: \mu_a - \mu_r = 0\) is true, the right-hand side of the numerator (to the right of the \(-\) sign), \(\mu_a - \mu_r\) , becomes 0.

Second, similarly to how the Central Limit Theorem from Subsection 7.5 states that sample means follow a normal distribution, it can be mathematically proven that the two-sample \(t\) -statistic follows a \(t\) distribution with degrees of freedom “roughly equal” to \(df = n_a + n_r - 2\) . To better understand this concept of degrees of freedom , we next display three examples of \(t\) -distributions in Figure 9.20 along with the standard normal \(z\) curve.

FIGURE 9.20: Examples of t-distributions and the z curve.

Begin by looking at the center of the plot at 0 on the horizontal axis. As you move up from the value of 0, follow along with the labels and note that the bottom curve corresponds to 1 degree of freedom, the curve above it is for 3 degrees of freedom, the curve above that is for 10 degrees of freedom, and lastly the dotted curve is the standard normal \(z\) curve.

Observe that all four curves have a bell shape, are centered at 0, and that as the degrees of freedom increase, the \(t\) -distribution more and more resembles the standard normal \(z\) curve. The “degrees of freedom” measures how different the \(t\) distribution will be from a normal distribution. \(t\) -distributions tend to have more values in the tails of their distributions than the standard normal \(z\) curve.

This “roughly equal” statement indicates that the equation \(df = n_a + n_r - 2\) is a “good enough” approximation to the true degrees of freedom. The true formula is a bit more complicated than this simple expression, but we’ve found the formula to be beyond the reach of those new to statistical inference and it does little to build the intuition of the \(t\) -test.

The message to retain, however, is that small sample sizes lead to small degrees of freedom and thus small sample sizes lead to \(t\) -distributions that are different than the \(z\) curve. On the other hand, large sample sizes correspond to large degrees of freedom and thus produce \(t\) distributions that closely align with the standard normal \(z\) -curve.

So, assuming the null hypothesis \(H_0\) is true, our formula for the test statistic simplifies a bit:

\[t = \dfrac{ (\bar{x}_a - \bar{x}_r) - 0}{ \sqrt{\dfrac{{s_a}^2}{n_a} + \dfrac{{s_r}^2}{n_r}} } = \dfrac{ \bar{x}_a - \bar{x}_r}{ \sqrt{\dfrac{{s_a}^2}{n_a} + \dfrac{{s_r}^2}{n_r}} }\]

Let’s compute the values necessary for this two-sample \(t\) -statistic. Recall the summary statistics we computed during our exploratory data analysis in Section 9.5.1 .

Using these values, the observed two-sample \(t\) -test statistic is

\[ \dfrac{ \bar{x}_a - \bar{x}_r}{ \sqrt{\dfrac{{s_a}^2}{n_a} + \dfrac{{s_r}^2}{n_r}} } = \dfrac{5.28 - 6.32}{ \sqrt{\dfrac{{1.36}^2}{32} + \dfrac{{1.61}^2}{36}} } = -2.906 \]

Great! How can we compute the \(p\) -value using this theory-based test statistic? We need to compare it to a null distribution, which we construct next.

Null distribution

Let’s revisit the null distribution for the test statistic \(\bar{x}_a - \bar{x}_r\) we constructed in Section 9.5 . Let’s visualize this in the left-hand plot of Figure 9.21 .

The infer package also includes some built-in theory-based test statistics as well. So instead of calculating the test statistic of interest as the "diff in means" \(\bar{x}_a - \bar{x}_r\) , we can calculate this defined two-sample \(t\) -statistic by setting stat = "t" . Let’s visualize this in the right-hand plot of Figure 9.21 .

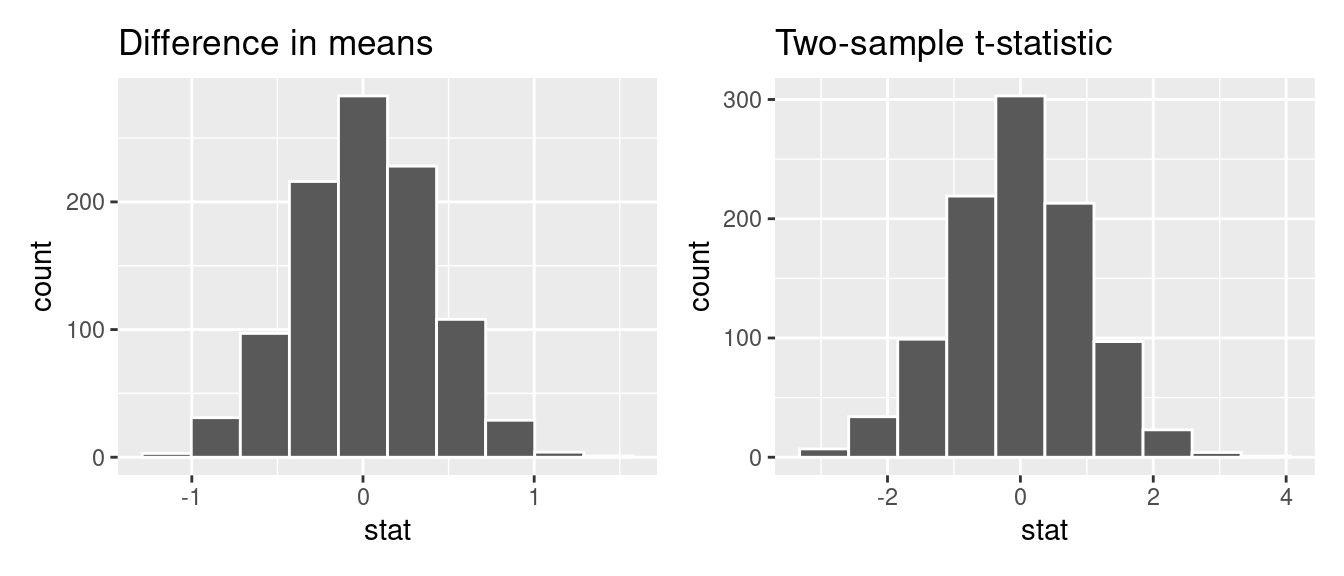
FIGURE 9.21: Comparing the null distributions of two test statistics.

Observe that while the shape of the null distributions of both the difference in means \(\bar{x}_a - \bar{x}_r\) and the two-sample \(t\) -statistics are similar, the scales on the x-axis are different. The two-sample \(t\) -statistic values are spread out over a larger range.

However, a traditional theory-based \(t\) -test doesn’t look at the simulated histogram in null_distribution_movies_t , but instead it looks at the \(t\) -distribution curve with degrees of freedom equal to roughly 65.85. This calculation is based on the complicated formula referenced previously, which we approximated with \(df = n_a + n_r - 2 = 32 + 36 - 2 = 66\) . Let’s overlay this \(t\) -distribution curve over the top of our simulated two-sample \(t\) -statistics using the method = "both" argument in visualize() .

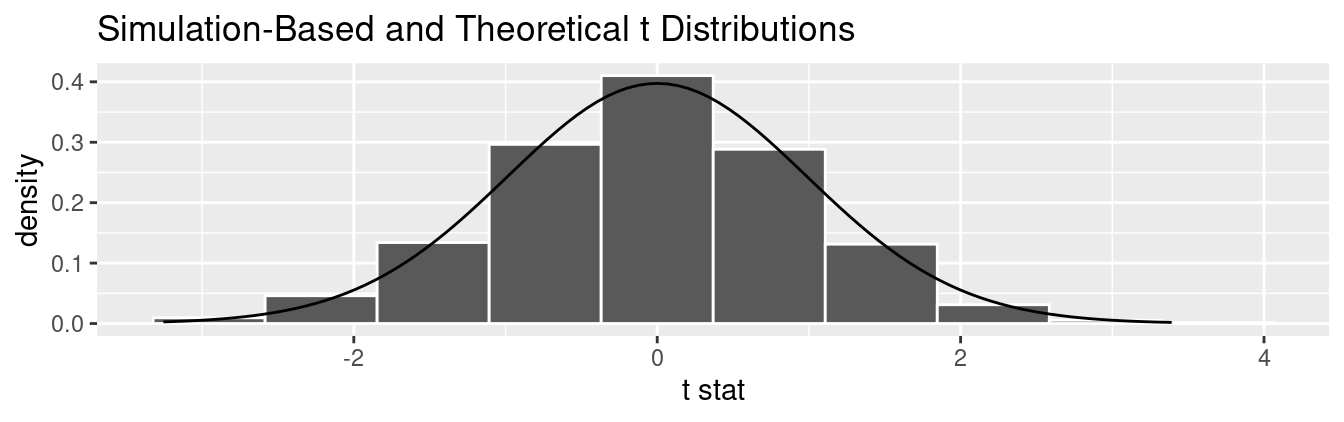
FIGURE 9.22: Null distribution using t-statistic and t-distribution.

Observe that the curve does a good job of approximating the histogram here. To calculate the \(p\) -value in this case, we need to figure out how much of the total area under the \(t\) -distribution curve is at or “more extreme” than our observed two-sample \(t\) -statistic. Since \(H_A: \mu_a - \mu_r \neq 0\) is a two-sided alternative, we need to add up the areas in both tails.

We first compute the observed two-sample \(t\) -statistic using infer verbs. This shortcut calculation further assumes that the null hypothesis is true: that the population of action and romance movies have an equal average rating.

We want to find the percentage of values that are at or below obs_two_sample_t \(= -2.906\) or at or above -obs_two_sample_t \(= 2.906\) . We use the shade_p_value() function with the direction argument set to "both" to do this:

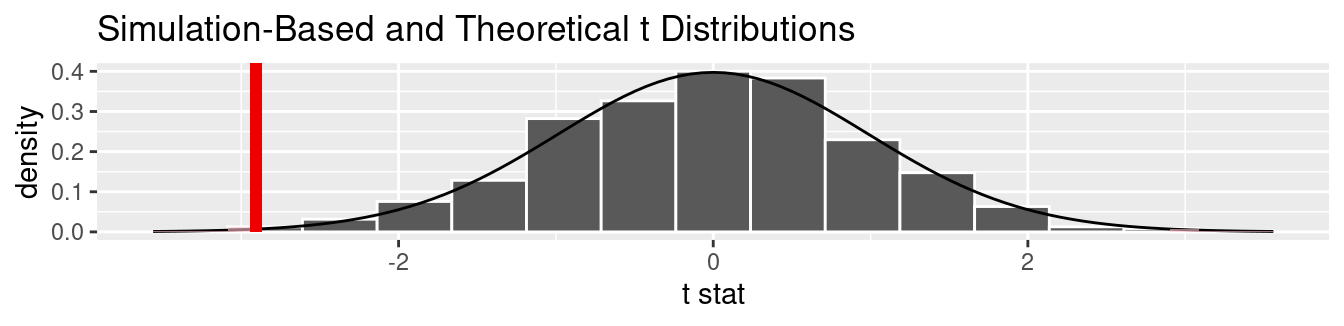
FIGURE 9.23: Null distribution using t-statistic and t-distribution with \(p\) -value shaded.

(We’ll discuss this warning message shortly.) What is the \(p\) -value? We apply get_p_value() to our null distribution saved in null_distribution_movies_t :

We have a very small \(p\) -value, and thus it is very unlikely that these results are due to sampling variation . Thus, we are inclined to reject \(H_0\) .

Let’s come back to that earlier warning message: Check to make sure the conditions have been met for the theoretical method. {infer} currently does not check these for you. To be able to use the \(t\) -test and other such theoretical methods, there are always a few conditions to check. The infer package does not automatically check these conditions, hence the warning message we received. These conditions are necessary so that the underlying mathematical theory holds. In order for the results of our two-sample \(t\) -test to be valid, three conditions must be met:

• Nearly normal populations or large sample sizes. A general rule of thumb that works in many (but not all) situations is that the sample size \(n\) should be greater than 30.
• Both samples are selected independently of each other.
• All observations are independent from each other.

Let’s see if these conditions hold for our movies_sample data:

• This is met since \(n_a\) = 32 and \(n_r\) = 36 are both larger than 30, satisfying our rule of thumb.
• This is met since we sampled the action and romance movies at random and in an unbiased fashion from the database of all IMDb movies.
• Unfortunately, we don’t know how IMDb computes the ratings. For example, if the same person rated multiple movies, then those observations would be related and hence not independent.

Assuming all three conditions are roughly met, we can be reasonably certain that the theory-based \(t\) -test results are valid. If any of the conditions were clearly not met, we couldn’t put as much trust into any conclusions reached. On the other hand, in most scenarios, the only assumption that needs to be met in the simulation-based method is that the sample is selected at random. Thus, in our experience, we prefer simulation-based methods as they have fewer assumptions, are conceptually easier to understand, and since computing power has recently become easily accessible, they can be run quickly. That being said since much of the world’s research still relies on traditional theory-based methods, we also believe it is important to understand them.

You may be wondering why we chose reps = 1000 for these simulation-based methods. We’ve noticed that after around 1000 replicates for the null distribution and the bootstrap distribution for most problems you can start to get a general sense for how the statistic behaves. You can change this value to something like 10,000 though for reps if you would like even finer detail but this will take more time to compute. Feel free to iterate on this as you like to get an even better idea about the shape of the null and bootstrap distributions as you wish.

9.6.2 When inference is not needed

We’ve now walked through several different examples of how to use the infer package to perform statistical inference: constructing confidence intervals and conducting hypothesis tests. For each of these examples, we made it a point to always perform an exploratory data analysis (EDA) first; specifically, by looking at the raw data values, by using data visualization with ggplot2 , and by data wrangling with dplyr beforehand. We highly encourage you to always do the same. As a beginner to statistics, EDA helps you develop intuition as to what statistical methods like confidence intervals and hypothesis tests can tell us. Even as a seasoned practitioner of statistics, EDA helps guide your statistical investigations. In particular, is statistical inference even needed?

Let’s consider an example. Say we’re interested in the following question: Of all flights leaving a New York City airport, are Hawaiian Airlines flights in the air for longer than Alaska Airlines flights? Furthermore, let’s assume that 2013 flights are a representative sample of all such flights. Then we can use the flights data frame in the nycflights13 package we introduced in Section 1.4 to answer our question. Let’s filter this data frame to only include Hawaiian and Alaska Airlines using their carrier codes HA and AS :

There are two possible statistical inference methods we could use to answer such questions. First, we could construct a 95% confidence interval for the difference in population means \(\mu_{HA} - \mu_{AS}\) , where \(\mu_{HA}\) is the mean air time of all Hawaiian Airlines flights and \(\mu_{AS}\) is the mean air time of all Alaska Airlines flights. We could then check if the entirety of the interval is greater than 0, suggesting that \(\mu_{HA} - \mu_{AS} > 0\) , or, in other words suggesting that \(\mu_{HA} > \mu_{AS}\) . Second, we could perform a hypothesis test of the null hypothesis \(H_0: \mu_{HA} - \mu_{AS} = 0\) versus the alternative hypothesis \(H_A: \mu_{HA} - \mu_{AS} > 0\) .

However, let’s first construct an exploratory visualization as we suggested earlier. Since air_time is numerical and carrier is categorical, a boxplot can display the relationship between these two variables, which we display in Figure 9.24 .

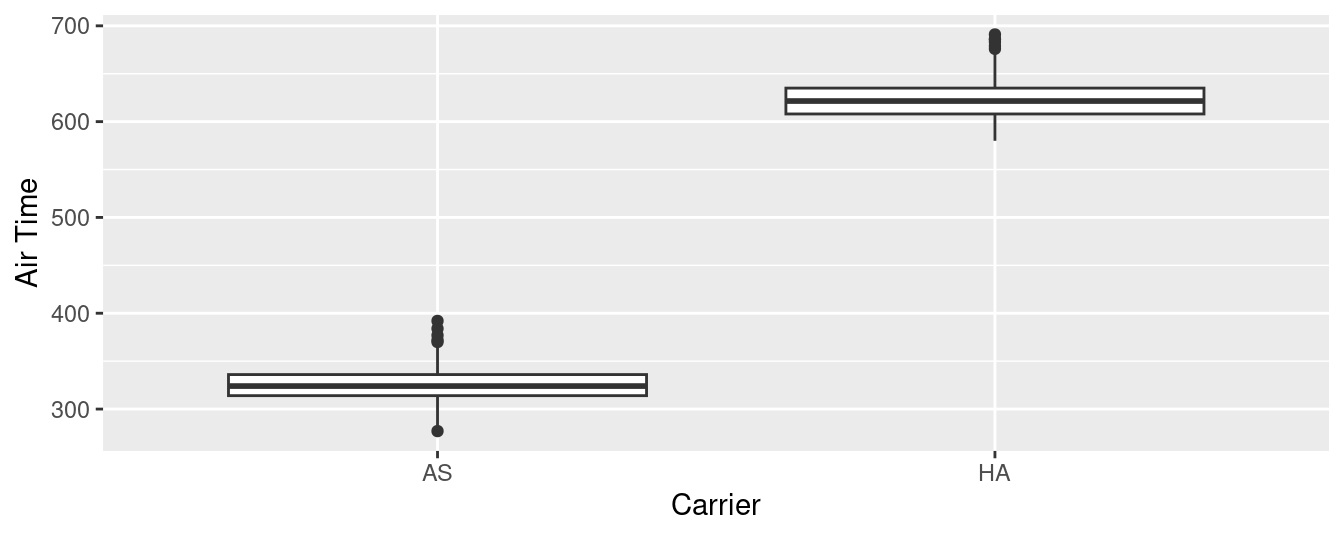
FIGURE 9.24: Air time for Hawaiian and Alaska Airlines flights departing NYC in 2013.

This is what we like to call “no PhD in Statistics needed” moments. You don’t have to be an expert in statistics to know that Alaska Airlines and Hawaiian Airlines have significantly different air times. The two boxplots don’t even overlap! Constructing a confidence interval or conducting a hypothesis test would frankly not provide much more insight than Figure 9.24 .

Let’s investigate why we observe such a clear cut difference between these two airlines using data wrangling. Let’s first group by the rows of flights_sample not only by carrier but also by destination dest . Subsequently, we’ll compute two summary statistics: the number of observations using n() and the mean airtime:

It turns out that from New York City in 2013, Alaska only flew to SEA (Seattle) from New York City (NYC) while Hawaiian only flew to HNL (Honolulu) from NYC. Given the clear difference in distance from New York City to Seattle versus New York City to Honolulu, it is not surprising that we observe such different ( statistically significantly different , in fact) air times in flights.

This is a clear example of not needing to do anything more than a simple exploratory data analysis using data visualization and descriptive statistics to get an appropriate conclusion. This is why we highly recommend you perform an EDA of any sample data before running statistical inference methods like confidence intervals and hypothesis tests.

9.6.3 Problems with p-values

On top of the many common misunderstandings about hypothesis testing and \(p\) -values we listed in Section 9.4 , another unfortunate consequence of the expanded use of \(p\) -values and hypothesis testing is a phenomenon known as “p-hacking.” p-hacking is the act of “cherry-picking” only results that are “statistically significant” while dismissing those that aren’t, even if at the expense of the scientific ideas. There are lots of articles written recently about misunderstandings and the problems with \(p\) -values. We encourage you to check some of them out:

• Misunderstandings of \(p\) -values
• What a nerdy debate about \(p\) -values shows about science - and how to fix it
• Statisticians issue warning over misuse of \(P\) values
• You Can’t Trust What You Read About Nutrition
• A Litany of Problems with p-values

Such issues were getting so problematic that the American Statistical Association (ASA) put out a statement in 2016 titled, “The ASA Statement on Statistical Significance and \(P\) -Values,” with six principles underlying the proper use and interpretation of \(p\) -values. The ASA released this guidance on \(p\) -values to improve the conduct and interpretation of quantitative science and to inform the growing emphasis on reproducibility of science research.

We as authors much prefer the use of confidence intervals for statistical inference, since in our opinion they are much less prone to large misinterpretation. However, many fields still exclusively use \(p\) -values for statistical inference and this is one reason for including them in this text. We encourage you to learn more about “p-hacking” as well and its implication for science.

9.6.4 Additional resources

An R script file of all R code used in this chapter is available here .

If you want more examples of the infer workflow for conducting hypothesis tests, we suggest you check out the infer package homepage, in particular, a series of example analyses available at https://infer.netlify.app/articles/ .

9.6.5 What’s to come

We conclude with the infer pipeline for hypothesis testing in Figure 9.25 .

FIGURE 9.25: infer package workflow for hypothesis testing.

Now that we’ve armed ourselves with an understanding of confidence intervals from Chapter 8 and hypothesis tests from this chapter, we’ll now study inference for regression in the upcoming Chapter 10 .

We’ll revisit the regression models we studied in Chapter 5 on basic regression and Chapter 6 on multiple regression. For example, recall Table 5.2 (shown again here in Table 9.4 ), corresponding to our regression model for an instructor’s teaching score as a function of their “beauty” score.

We previously saw in Subsection 5.1.2 that the values in the estimate column are the fitted intercept \(b_0\) and fitted slope for “beauty” score \(b_1\) . In Chapter 10 , we’ll unpack the remaining columns: std_error which is the standard error, statistic which is the observed standardized test statistic to compute the p_value , and the 95% confidence intervals as given by lower_ci and upper_ci .

Data Science Central

• Author Portal
• 3D Printing
• AI Data Stores
• AI Hardware
• AI Linguistics
• AI User Interfaces and Experience
• AI Visualization
• Cloud and Edge
• Cognitive Computing
• Containers and Virtualization
• Data Science
• Data Security
• Digital Factoring
• Drones and Robot AI
• Internet of Things
• Knowledge Engineering
• Machine Learning
• Quantum Computing
• Robotic Process Automation
• The Mathematics of AI
• Tools and Techniques
• Virtual Reality and Gaming
• Blockchain & Identity
• Business Agility
• Business Analytics
• Data Lifecycle Management
• Data Privacy
• Data Strategist
• Data Trends
• Digital Communications
• Digital Disruption
• Digital Professional
• Digital Twins
• Digital Workplace
• Marketing Tech
• Sustainability
• Agriculture and Food AI
• AI and Science
• AI in Government
• Autonomous Vehicles
• Education AI
• Energy Tech
• Financial Services AI
• Healthcare AI
• Logistics and Supply Chain AI
• Manufacturing AI
• Mobile and Telecom AI
• News and Entertainment AI
• Smart Cities
• Social Media and AI
• Functional Languages
• Other Languages
• Query Languages
• Web Languages
• Education Spotlight
• Newsletters
• O’Reilly Media

An introduction to Statistical Inference and Hypothesis testing

• March 22, 2020 at 10:22 am

In a previous blog ( The difference between statistics and data science ), I discussed the significance of statistical inference. In this section, we expand on these ideas  

The goal of statistical inference is to make a statement about something that is not observed within a certain level of uncertainty. Inference is difficult because it is based on a sample i.e. the objective is to understand the population based on the sample . The population is a collection of objects that we want to study/test. For example, if you are studying quality of products from an assembly line for a given day, then the whole production for that day is the population. In the real world, it may be hard to test every product – hence we draw a sample from the population and infer the results based on the sample for the whole population. 

In this sense, the statistical model provides an abstract representation of the population and how the elements of the population relate to each other. Parameters are numbers that represent features or associations of the population. We estimate the value of the parameters from the data.  A  parameter represents a s ummary description of a fixed characteristic or measure of the target population. It represents the true value that would be obtained as if we had taken a census (instead of a sample). Examples of parameters include Mean (μ), Variance (σ²), Standard Deviation (σ), Proportion (π). These values are individually called a statistic. A Sampling Distribution is a probability distribution of a statistic obtained through a large number of samples drawn from the population. In sampling, the confidence interval provides a more continuous measure of un-certainty. The confidence interval proposes a range of plausible values for an unknown parameter (for example, the mean). In other words, the confidence interval represents a range of values we are fairly sure our true value lies in. For example, for a given sample group, the mean height is 175 cms and if the confidence interval is 95%, then it means, 95% of similar experiments will include the true mean, but 5% will not contain the sample.

Image source and reference: An introduction to confidence intervals

Hypothesis testing

Having understood sampling and inference, let us now explore hypothesis testing. Hypothesis testing enables us to make claims about the distribution of data or whether one set of results are different from another set of results. Hypothesis testing allows us to interpret or draw conclusions about the population using sample data. In a hypothesis test, we evaluate two mutually exclusive statements about a population to determine which statement is best supported by the sample data. The Null Hypothesis(H0) is a statement of no change and is assumed to be true unless evidence indicates otherwise. The Null hypothesis is the one we want to disprove. The Alternative Hypothesis: (H1 or Ha) is the opposite of the null hypothesis, represents the claim that is being testing. We are trying to collect evidence in favour of the alternative hypothesis. The Probability value (P-Value) represents the probability that the null hypothesis is true based on the current sample or one that is more extreme than the current sample. The Significance Level (α) defines a cut-off p-value for how strongly a sample contradicts the null hypothesis of the experiment. If P-Value < α, then there is sufficient evidence to reject the null hypothesis and accept the alternative hypothesis. If P-Value > α, we fail to reject the null hypothesis.

Central limit theorem

The central limit theorem is at the heart of hypothesis testing. Given a sample where the statistics of the population is unknowable, we need a way to infer statistics across the population. For example, if we want to know the average weight of all the dogs in the world, it is not possible to weigh up each dog and compute the mean. So, we use the central limit theorem and the confidence interval which enables to infer the mean of the population within a certain margin.

So, if we take multiple samples – say the first sample of 40 dogs and compute of the mean for that sample. Again, we take a next sample of say 50 dogs and do the same. We repeat the process by getting a large number of random samples which are independent of each other – then the ‘mean of the means’ of these samples will give the approximate mean of the whole population as per the central limit theorem. Also, the histogram of the means will represent the bell curve as per the central limit theorem. The central limit theorem is significant because this idea applies to an unknown distribution (ex: Binomial or even a completely random distribution) – which means techniques like hypothesis testing can apply to any distribution (not just the normal distribution) 

Image source: minitab .

Related Content

We are in the process of writing and adding new material (compact eBooks) exclusively available to our members, and written in simple English, by world leading experts in AI, data science, and machine learning.

Welcome to the newly launched Education Spotlight page! View Listings

Statistical Inference I: Randomization Methods for Hypothesis Testing

• First Online: 06 May 2023

Cite this chapter

• Bruce Blaine 2  

725 Accesses

In the previous four chapters, we focused on using statistics to summarize and explore X-Y relationships in various statistical models. In that data analytic mode, we used effect size statistics to describe the direction and strength of a relationship. While descriptive analysis is important to understand relationships between variables, scientists and analysts are often interested in two further issues: Is an observed X-Y relationship “statistically significant”? And, can we use sample findings to estimate unknown quantities in the population? Both of these data analytic questions require that we shift our focus to using statistics to make inferences from sample data. These different roles of statistics—to describe and to infer—are bound up with the relationship between sample and population. Let’s work through the dynamics of that relationship first (see Fig. 7.1).

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Author information

Authors and affiliations.

Statistics Program, University of Rochester, Rochester, NY, USA

Bruce Blaine

You can also search for this author in PubMed   Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this chapter

Blaine, B. (2023). Statistical Inference I: Randomization Methods for Hypothesis Testing. In: Introductory Applied Statistics. Springer, Cham. https://doi.org/10.1007/978-3-031-27741-2_7

Download citation

DOI : https://doi.org/10.1007/978-3-031-27741-2_7

Published : 06 May 2023

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-27740-5

Online ISBN : 978-3-031-27741-2

eBook Packages : Mathematics and Statistics Mathematics and Statistics (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6b.5 - statistical inference - hypothesis testing.

Statisticians construct the null hypothesis and the alternative hypothesis for statistical hypothesis testing such that the research hypothesis is the alternative hypothesis:

\(H_0: \left\{ \text{non-equivalence}\right\} \text{ vs. } H_1: \left\{ \text{equivalence}\right\} \)

\(H_0: \left\{ \text{inferiority}\right\} \text{ vs. } H_1: \left\{ \text{non-inferiority}\right\} \)

In terms of the population means, the hypotheses for testing equivalence are expressed as:

\(H_0: \left\{ \mu_{E} - \mu_{A} \le -\Psi \text{ or } \mu_{E} - \mu_{A} \ge \Psi \right\}\)

\(H_1: \left\{-\Psi < \mu_{E} - \mu_{A}< \Psi \right\}\)

also expressed as

\(H_0: \left\{|\mu_{E} - \mu_{A}| \ge \Psi \right\} \text{ vs. } H_1: \left\{|\mu_{E} - \mu_{A}| < \Psi \right\}\)

In terms of the population means, the hypotheses for testing non-inferiority are expressed as

\(H_0: \left\{\mu_{E} - \mu_{A} \le -\Psi \right\} \text{ vs. } H_1: \left\{\mu_{E} - \mu_{A} > -\Psi \right\}\)

The null and alternative hypotheses for an equivalence trial can be decomposed into two distinct hypothesis testing problems, one for non-inferiority:

\(H_{01}: \left\{\mu_{E} - \mu_{A} \le -\Psi \right\} \text{ vs. } H_{11}: \left\{\mu_{E} - \mu_{A} > -\Psi \right\}\)

and one for non-superiority

\(H_{02}: \left\{\mu_{E} - \mu_{A} \ge \Psi \right\} \text{ vs. } H_{12}: \left\{\mu_{E} - \mu_{A} <\Psi \right\}\)

The null hypothesis of non-equivalence is rejected if and only if the null hypothesis of non-inferiority \(\left(H_{01}\right)\) is rejected AND the null hypothesis of non-superiority \(\left(H_{02}\right)\) is rejected.

This rationale leads to what is called two one-sided testing (TOST). If the data are approximately normally distributed, then two-sample t tests can be applied. If normality is suspect, then Wilcoxon rank-sum tests can be applied.

With respect to two-sample t tests, reject the null hypothesis of inferiority if:

\( t_{inf}= \left(\bar{Y}_E - \bar{Y}_A + \Psi \right) / s \sqrt{\frac {1}{n_E}+\frac {1}{n_Z}}>t_{n_{E}+n_{A}-2, 1-\alpha}\)

and reject the null hypothesis of superiority if:

\( t_{sup}= \left(\bar{Y}_E - \bar{Y}_A + \Psi \right) / s \sqrt{\frac {1}{n_E}+\frac {1}{n_A}}< -t_{n_{E}+n_{A}-2, 1-\alpha}\)

where s is the pooled sample estimate of the standard deviation, calculated as the square-root of the pooled sample estimate of the variance:

\( s^2 = \left(\sum_{i=1}^{n_E}\left(Y_{Ei}-\bar{Y}_E\right)^2+\sum_{j=1}^{n_A}\left(Y_{Aj}-\bar{Y}_A\right)^2\right) / \left(n_E + n_A -2\right) \)

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, a complete guide on hypothesis testing in statistics, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.

All You Need to Know About Bias in Statistics

A Complete Guide to Get a Grasp of Time Series Analysis

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is hypothesis testing in statistics types and examples.

Lesson 10 of 24 By Avijeet Biswal

Table of Contents

In today’s data-driven world , decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life - 

• A teacher assumes that 60% of his college's students come from lower-middle-class families.
• A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternate Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average. 

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

 We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps of Hypothesis Testing

Step 1: specify your null and alternate hypotheses.

It is critical to rephrase your original research hypothesis (the prediction that you wish to study) as a null (Ho) and alternative (Ha) hypothesis so that you can test it quantitatively. Your first hypothesis, which predicts a link between variables, is generally your alternate hypothesis. The null hypothesis predicts no link between the variables of interest.

Step 2: Gather Data

For a statistical test to be legitimate, sampling and data collection must be done in a way that is meant to test your hypothesis. You cannot draw statistical conclusions about the population you are interested in if your data is not representative.

Step 3: Conduct a Statistical Test

Other statistical tests are available, but they all compare within-group variance (how to spread out the data inside a category) against between-group variance (how different the categories are from one another). If the between-group variation is big enough that there is little or no overlap between groups, your statistical test will display a low p-value to represent this. This suggests that the disparities between these groups are unlikely to have occurred by accident. Alternatively, if there is a large within-group variance and a low between-group variance, your statistical test will show a high p-value. Any difference you find across groups is most likely attributable to chance. The variety of variables and the level of measurement of your obtained data will influence your statistical test selection.

Step 4: Determine Rejection Of Your Null Hypothesis

Your statistical test results must determine whether your null hypothesis should be rejected or not. In most circumstances, you will base your judgment on the p-value provided by the statistical test. In most circumstances, your preset level of significance for rejecting the null hypothesis will be 0.05 - that is, when there is less than a 5% likelihood that these data would be seen if the null hypothesis were true. In other circumstances, researchers use a lower level of significance, such as 0.01 (1%). This reduces the possibility of wrongly rejecting the null hypothesis.

Step 5: Present Your Results 

The findings of hypothesis testing will be discussed in the results and discussion portions of your research paper, dissertation, or thesis. You should include a concise overview of the data and a summary of the findings of your statistical test in the results section. You can talk about whether your results confirmed your initial hypothesis or not in the conversation. Rejecting or failing to reject the null hypothesis is a formal term used in hypothesis testing. This is likely a must for your statistics assignments.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

Chi-Square 

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

• The null hypothesis is (H0 <= 90) or less change.
• A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true]. 

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Level of Significance

The alpha value is a criterion for determining whether a test statistic is statistically significant. In a statistical test, Alpha represents an acceptable probability of a Type I error. Because alpha is a probability, it can be anywhere between 0 and 1. In practice, the most commonly used alpha values are 0.01, 0.05, and 0.1, which represent a 1%, 5%, and 10% chance of a Type I error, respectively (i.e. rejecting the null hypothesis when it is in fact correct).

Future-Proof Your AI/ML Career: Top Dos and Don'ts

A p-value is a metric that expresses the likelihood that an observed difference could have occurred by chance. As the p-value decreases the statistical significance of the observed difference increases. If the p-value is too low, you reject the null hypothesis.

Here you have taken an example in which you are trying to test whether the new advertising campaign has increased the product's sales. The p-value is the likelihood that the null hypothesis, which states that there is no change in the sales due to the new advertising campaign, is true. If the p-value is .30, then there is a 30% chance that there is no increase or decrease in the product's sales.  If the p-value is 0.03, then there is a 3% probability that there is no increase or decrease in the sales value due to the new advertising campaign. As you can see, the lower the p-value, the chances of the alternate hypothesis being true increases, which means that the new advertising campaign causes an increase or decrease in sales.

Why is Hypothesis Testing Important in Research Methodology?

Hypothesis testing is crucial in research methodology for several reasons:

• Provides evidence-based conclusions: It allows researchers to make objective conclusions based on empirical data, providing evidence to support or refute their research hypotheses.
• Supports decision-making: It helps make informed decisions, such as accepting or rejecting a new treatment, implementing policy changes, or adopting new practices.
• Adds rigor and validity: It adds scientific rigor to research using statistical methods to analyze data, ensuring that conclusions are based on sound statistical evidence.
• Contributes to the advancement of knowledge: By testing hypotheses, researchers contribute to the growth of knowledge in their respective fields by confirming existing theories or discovering new patterns and relationships.

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

• It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
• Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
• Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
• Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore Simplilearn’s Post Graduate Program in Data Science.

If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is hypothesis testing and its types?

Hypothesis testing is a statistical method used to make inferences about a population based on sample data. It involves formulating two hypotheses: the null hypothesis (H0), which represents the default assumption, and the alternative hypothesis (Ha), which contradicts H0. The goal is to assess the evidence and determine whether there is enough statistical significance to reject the null hypothesis in favor of the alternative hypothesis.

Types of hypothesis testing:

• One-sample test: Used to compare a sample to a known value or a hypothesized value.
• Two-sample test: Compares two independent samples to assess if there is a significant difference between their means or distributions.
• Paired-sample test: Compares two related samples, such as pre-test and post-test data, to evaluate changes within the same subjects over time or under different conditions.
• Chi-square test: Used to analyze categorical data and determine if there is a significant association between variables.
• ANOVA (Analysis of Variance): Compares means across multiple groups to check if there is a significant difference between them.

3. What are the steps of hypothesis testing?

The steps of hypothesis testing are as follows:

• Formulate the hypotheses: State the null hypothesis (H0) and the alternative hypothesis (Ha) based on the research question.
• Set the significance level: Determine the acceptable level of error (alpha) for making a decision.
• Collect and analyze data: Gather and process the sample data.
• Compute test statistic: Calculate the appropriate statistical test to assess the evidence.
• Make a decision: Compare the test statistic with critical values or p-values and determine whether to reject H0 in favor of Ha or not.
• Draw conclusions: Interpret the results and communicate the findings in the context of the research question.

4. What are the 2 types of hypothesis testing?

• One-tailed (or one-sided) test: Tests for the significance of an effect in only one direction, either positive or negative.
• Two-tailed (or two-sided) test: Tests for the significance of an effect in both directions, allowing for the possibility of a positive or negative effect.

The choice between one-tailed and two-tailed tests depends on the specific research question and the directionality of the expected effect.

5. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

• Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
• Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
• Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

• Math Article

Statistical Inference

Statistics is a branch of Mathematics, that deals with the collection, analysis, interpretation, and the presentation of the numerical data. In other words, it is defined as the collection of quantitative data. The main purpose of Statistics is to make an accurate conclusion using a limited sample about a greater population.

Types of Statistics

Statistics can be classified into two different categories. The two different types of Statistics are:

• Descriptive Statistics
• Inferential Statistics

In Statistics, descriptive statistics describe the data, whereas inferential statistics help you make predictions from the data. In inferential statistics, the data are taken from the sample and allows you to generalize the population. In general, inference means “guess”, which means making inference about something. So, statistical inference means, making inference about the population. To take a conclusion about the population, it uses various statistical analysis techniques. In this article, one of the types of statistics called inferential statistics is explained in detail. Now, you are going to learn the proper definition of statistical inference, types, solutions, and examples.

Statistical Inference Definition

Statistical inference is the process of analysing the result and making conclusions from data subject to random variation. It is also called inferential statistics. Hypothesis testing and confidence intervals are the applications of the statistical inference. Statistical inference is a method of making decisions about the parameters of a population, based on random sampling. It helps to assess the relationship between the dependent and independent variables. The purpose of statistical inference to estimate the uncertainty or sample to sample variation. It allows us to provide a probable range of values for the true values of something in the population. The components used for making statistical inference are:

• Sample Size
• Variability in the sample
• Size of the observed differences

Types of Statistical Inference

There are different types of statistical inferences that are extensively used for making conclusions. They are:

• One sample hypothesis testing
• Confidence Interval
• Pearson Correlation
• Bi-variate regression
• Multi-variate regression
• Chi-square statistics and contingency table
• ANOVA or T-test

Statistical Inference Procedure

The procedure involved in inferential statistics are:

• Begin with a theory
• Create a research hypothesis
• Operationalize the variables
• Recognize the population to which the study results should apply
• Formulate a null hypothesis for this population
• Accumulate a sample from the population and continue the study
• Conduct statistical tests to see if the collected sample properties are adequately different from what would be expected under the null hypothesis to be able to reject the null hypothesis

Statistical Inference Solution

Statistical inference solutions produce efficient use of statistical data relating to groups of individuals or trials. It deals with all characters, including the collection, investigation and analysis of data and organizing the collected data. By statistical inference solution, people can acquire knowledge after starting their work in diverse fields. Some statistical inference solution facts are:

• It is a common way to assume that the observed sample is of independent observations from a population type like Poisson or normal
• Statistical inference solution is used to evaluate the parameter(s) of the expected model like normal mean or binomial proportion

Importance of Statistical Inference

Inferential Statistics is important to examine the data properly. To make an accurate conclusion, proper data analysis is important to interpret the research results. It is majorly used in the future prediction for various observations in different fields. It helps us to make inference about the data. The statistical inference has a wide range of application in different fields, such as:

• Business Analysis
• Artificial Intelligence
• Financial Analysis
• Fraud Detection
• Machine Learning
• Share Market
• Pharmaceutical Sector

Statistical Inference Examples

An example of statistical inference is given below.

Question: From the shuffled pack of cards, a card is drawn. This trial is repeated for 400 times, and the suits are given below:

While a card is tried at random, then what is the probability of getting a

• Diamond cards
• Black cards
• Except for spade

By statistical inference solution,

Total number of events = 400

i.e.,90+100+120+90=400

(1) The probability of getting diamond cards:

Number of trials in which diamond card is drawn = 90

Therefore, P(diamond card) = 90/400 = 0.225

(2) The probability of getting black cards:

Number of trials in which black card showed up = 90+100 =190

Therefore, P(black card) = 190/400 = 0.475

(3) Except for spade

Number of trials other than spade showed up = 90+100+120 =310

Therefore, P(except spade) = 310/400 = 0.775

Stay tuned with BYJU’S – The Learning App for more Maths-related concepts and download the app for more personalized videos.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Search Cornell

Class Roster

Section menu.

• Toggle Navigation
• Summer 2024
• Spring 2024
• Winter 2024
• Archived Rosters

Last Updated

• Schedule of Classes - April 15, 2024 7:36PM EDT
• Course Catalog - April 15, 2024 7:06PM EDT

MATH 6740 Mathematical Statistics II

Course description.

Course information provided by the Courses of Study 2023-2024 . Courses of Study 2024-2025 is scheduled to publish mid-June.

Focuses on the foundations of statistical inference, with an emphasis on asymptotic methods and the minimax optimality criterion. In the first part, the solution of the classical problem of justifying Fisher's information bound in regular statistical models will be presented. This solution will be obtained applying the concepts of contiguity, local asymptotic normality and asymptotic minimaxity. The second part will be devoted to nonparametric estimation, taking a Gaussian regression model as a paradigmatic example. Key topics are kernel estimation and local polynomial approximation, optimal rates of convergence at a point and in global norms, and adaptive estimation. Optional topics may include irregular statistical models, estimation of functionals and nonparametric hypothesis testing.

When Offered Fall.

Prerequisites/Corequisites Prerequisite: MATH 6710 (measure theoretic probability) and STSCI 6730/MATH 6730, or permission of instructor.

View Enrollment Information

  Regular Academic Session.   Combined with: STSCI 6740

Credits and Grading Basis

3 Credits Stdnt Opt (Letter or S/U grades)

Class Number & Section Details

 5814 MATH 6740   LEC 001

Meeting Pattern

• TR 11:40am - 12:55pm To Be Assigned
• Aug 26 - Dec 9, 2024

Instructors

Nussbaum, M

To be determined. There are currently no textbooks/materials listed, or no textbooks/materials required, for this section. Additional information may be found on the syllabus provided by your professor.

For the most current information about textbooks, including the timing and options for purchase, see the Cornell Store .

Additional Information

Instruction Mode: In Person

Or send this URL:

Available Syllabi

About the class roster.

The schedule of classes is maintained by the Office of the University Registrar . Current and future academic terms are updated daily . Additional detail on Cornell University's diverse academic programs and resources can be found in the Courses of Study . Visit The Cornell Store for textbook information .

Please contact [email protected] with questions or feedback.

If you have a disability and are having trouble accessing information on this website or need materials in an alternate format, contact [email protected] for assistance.

Cornell University ©2024