problem solving about algebraic expressions

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game New
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve an Algebraic Expression

Last Updated: April 6, 2024 Fact Checked

This article was co-authored by David Jia . David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math. There are 10 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 488,938 times.

An algebraic expression is a mathematical phrase that contains numbers and/or variables. Though it cannot be solved because it does not contain an equals sign (=), it can be simplified. You can, however, solve algebraic equations , which contain algebraic expressions separated by an equals sign. If you want to know how to master this mathematical concept, then see Step 1 to get started.

Understanding the Basics

• Algebraic expression : 4x + 2
• Algebraic equation : 4x + 2 = 100

• 3x 2 + 5 + 4x 3 - x 2 + 2x 3 + 9 =
• 3x 2 - x 2 + 4x 3 + 2x 3 + 5 + 9 =
• 2x 2 + 6x 3 + 14

• You can see that each coefficient can be divisible by 3. Just "factor out" the number 3 by dividing each term by 3 to get your simplified equation.
• 3x/3 + 15/3 = 9x/3 + 30/3 =
• x + 5 = 3x + 10

• (3 + 5) 2 x 10 + 4
• First, follow P, the operation in the parentheses:
• = (8) 2 x 10 + 4
• Then, follow E, the operation of the exponent:
• = 64 x 10 + 4
• Next, do multiplication:
• And last, do addition:

• 5x + 15 = 65 =
• 5x/5 + 15/5 = 65/5 =
• x + 3 = 13 =

Joseph Meyer

To solve an equation for a variable like "x," you need to manipulate the equation to isolate x. Use techniques like the distributive property, combining like terms, factoring, adding or subtracting the same number, and multiplying or dividing by the same non-zero number to isolate "x" and find the answer.

Solve an Algebraic Equation

• 4x + 16 = 25 -3x =
• 4x = 25 -16 - 3x
• 4x + 3x = 25 -16 =
• 7x/7 = 9/7 =

• First, subtract 12 from both sides.
• 2x 2 + 12 -12 = 44 -12 =
• Next, divide both sides by 2.
• 2x 2 /2 = 32/2 =
• Solve by taking the square root of both sides, since that will turn x 2 into x.
• √x 2 = √16 =
• State both answers:x = 4, -4

• First, cross multiply to get rid of the fraction. You have to multiply the numerator of one fraction by the denominator of the other.
• (x + 3) x 3 = 2 x 6 =
• Now, combine like terms. Combine the constant terms, 9 and 12, by subtracting 9 from both sides.
• 3x + 9 - 9 = 12 - 9 =
• Isolate the variable, x, by dividing both sides by 3 and you've got your answer.
• 3x/3 = 3/3 =

• First, move everything that isn't under the radical sign to the other side of the equation:
• √(2x+9) = 5
• Then, square both sides to remove the radical:
• (√(2x+9)) 2 = 5 2 =
• Now, solve the equation as you normally would by combining the constants and isolating the variable:
• 2x = 25 - 9 =

• |4x +2| - 6 = 8 =
• |4x +2| = 8 + 6 =
• |4x +2| = 14 =
• 4x + 2 = 14 =
• Now, solve again by flipping the sign of the term on the other side of the equation after you've isolated the absolute value:
• 4x + 2 = -14
• 4x = -14 -2
• 4x/4 = -16/4 =
• Now, just state both answers: x = -4, 3

Community Q&A

• The degree of a polynomial is the highest power within the terms. Thanks Helpful 9 Not Helpful 1
• Once you're done, replace the variable with the answer, and solve the sum to see if it makes sense. If it does, then, congratulations! You just solved an algebraic equation! Thanks Helpful 7 Not Helpful 3
• To cross-check your answer, visit wolfram-alpha.com. They give the answer and often the two steps. Thanks Helpful 8 Not Helpful 5

You Might Also Like

• ↑ https://www.math4texas.org/Page/527
• ↑ https://www.khanacademy.org/math/cc-sixth-grade-math/cc-6th-expressions-and-variables/cc-6th-combining-like-terms/v/combining-like-terms-2
• ↑ https://www.mathsisfun.com/algebra/factoring.html
• ↑ https://www.mathsisfun.com/operation-order-pemdas.html
• ↑ https://sciencing.com/tips-for-solving-algebraic-equations-13712207.html
• ↑ https://www.mathsisfun.com/algebra/equations-solving.html
• ↑ https://tutorial.math.lamar.edu/Classes/Alg/SolveExpEqns.aspx
• ↑ https://www.mathsisfun.com/algebra/fractions-algebra.html
• ↑ https://math.libretexts.org/Courses/Coastline_College/Math_C045%3A_Beginning_and_Intermediate_Algebra_(Chau_Duc_Tran)/10%3A_Roots_and_Radicals/10.07%3A_Solve_Radical_Equations
• ↑ https://www.mathplanet.com/education/algebra-1/linear-inequalitites/solving-absolute-value-equations-and-inequalities

About This Article

If you want to solve an algebraic expression, first understand that expressions, unlike equations, are mathematical phrase that can contain numbers and/or variables but cannot be solved. For example, 4x + 2 is an expression. To reduce the expression, combine like terms, for example everything with the same variable. After you've done that, factor numbers by finding the lowest common denominator. Then, use the order of operations, which is known by the acronym PEMDAS, to reduce or solve the problem. To learn how to solve algebraic equations, keep scrolling! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Marie Taufa

May 27, 2018

Did this article help you?

Sep 16, 2023

Vickram Bheemsain

May 5, 2016

Imran Ahmed

Nov 1, 2018

Veer Gaudani

Feb 21, 2017

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Get all the best how-tos!

Sign up for wikiHow's weekly email newsletter

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.4: Algebraic Expressions and Formulas

• Last updated
• Save as PDF
• Page ID 6229

Learning Objectives

• Identify the parts of an algebraic expression.
• Apply the distributive property.
• Evaluate algebraic expressions.
• Use formulas that model common applications.

Algebraic Expressions and the Distributive Property

In algebra, letters called variables are used to represent numbers. Combinations of variables and numbers along with mathematical operations form algebraic expressions 87 , or just expressions . The following are some examples of expressions with one variable, \(x\):

Terms 88 in an algebraic expression are separated by addition operators and factors 89 are separated by multiplication operators. The numerical factor of a term is called the coefficient 90 . For example, the algebraic expression \(x^{2} y^{2} + 6xy − 3\) can be thought of as \(x^{2} y^{2} + 6xy + (−3)\) and has three terms. The first term, \(x^{2} y^{2}\), represents the quantity \(1x^{2} y^{2} = 1 ⋅ x ⋅ x ⋅ y ⋅ y\) where \(1\) is the coefficient and x and y are the variables. All of the variable factors with their exponents form the variable part of a term 91 . If a term is written without a variable factor, then it is called a constant term 92 . Consider the components of \(x^{2} y^{2} + 6xy − 3\),

The third term in this expression, \(−3\), is called a constant term because it is written without a variable factor. While a variable represents an unknown quantity and may change, the constant term does not change.

Example \(\PageIndex{1}\):

List all coefficients and variable parts of each term: \(10a^{2}−5ab−b^{2}\).

We want to think of the third term in this example \(−b^{2}\) as  \(−1b^{2}\).

Answer : Coefficients: \(\{−5, −1, 10\}\); Variable parts: \(\{a^{2},  ab,  b^{2}\}\)

In our study of algebra, we will encounter a wide variety of algebraic expressions. Typically, expressions use the two most common variables, \(x\) and \(y\). However, expressions may use any letter (or symbol) for a variable, even Greek letters, such as alpha (\(\alpha\)) and beta (\(\beta\)). Some letters and symbols are reserved for constants, such as \(π ≈ 3.14159\) and \(e ≈ 2.71828\). Since there is only a limited number of letters, you will also use subscripts, \(x_{1} , x_{2} , x_{3} , x_{4} , …,\) to indicate different variables.

The properties of real numbers are important in our study of algebra because a variable is simply a letter that represents a real number. In particular, the distributive property 93 states that if given any real numbers \(a, b\) and \(c\), then,

\(\color{Cerulean}{a}\) \( ( b + c ) = \color{Cerulean}{a}\)\(b + \color{Cerulean}{a}\)\(c\)

This property is one that we apply often when simplifying algebraic expressions. To demonstrate how it will be used, we simplify \(2(5 − 3)\) in two ways, and observe the same correct result.

Certainly, if the contents of the parentheses can be simplified we should do that first. On the other hand, when the contents of parentheses cannot be simplified any further, we multiply every term within it by the factor outside of it using the distributive property. Applying the distributive property allows us to multiply and remove the parentheses.

Example \(\PageIndex{2}\):

Simplify: \(5(−2a+5b)−2c\).

Multiply only the terms grouped within the parentheses for which we are applying the distributive property.

\(=\color{Cerulean}{5}\)\(⋅(−2a)+\color{Cerulean}{5}\)\(⋅5b−2c\)

\(=−10a+25b−2c\)

Answer : \(−10a+25b−2c\)

Recall that multiplication is commutative and therefore we can write the distributive property in the following manner, \((b + c) a = ba + ca\).

Example \(\PageIndex{3}\):

Simplify:  \((3x−4y+1)⋅3\).

Multiply all terms within the parenthesis by \(3\).

\((3x−4y+1)⋅3=3x\color{Cerulean}{⋅3}\)\(−4y\color{Cerulean}{⋅3}\)\(+1\color{Cerulean}{⋅3}\)

\(=9x−12y+3\)

Answer : \(9x−12y+3\)

Terms whose variable parts have the same variables with the same exponents are called like terms 94 , or similar terms 95 . Furthermore, constant terms are considered to be like terms. If an algebraic expression contains like terms, apply the distributive property as follows:

\(5 \color{Cerulean}{x}\)\( + 7 \color{Cerulean}{x}\)\( = ( 5 + 7 ) \color{Cerulean}{x}\)\( = 12 \color{Cerulean}{x}\)

\(4 \color{Cerulean}{x ^ { 2 }}\)\( + 5 \color{Cerulean}{x ^ { 2 }}\)\( - 7 \color{Cerulean}{x ^ { 2 }}\)\( = ( 4 + 5 - 7 ) \color{Cerulean}{x ^ { 2 }}\)\( = 2 \color{Cerulean}{x ^ { 2 }}\)

In other words, if the variable parts of terms are exactly the same, then we can add or subtract the coefficients to obtain the coefficient of a single term with the same variable part. This process is called combining like terms 96 . For example,

\(12 x ^ { 2 } y ^ { 3 } + 3 x ^ { 2 } y ^ { 3 } = 15 x ^ { 2 } y ^ { 3 }\)

Notice that the variable factors and their exponents do not change. Combining like terms in this manner, so that the expression contains no other similar terms, is called simplifying the expression 97 . Use this idea to simplify algebraic expressions with multiple like terms.

Example \(\PageIndex{4}\):

\(x ^ { 2 } - 10 x + 8 + 5 x ^ { 2 } - 6 x - 1\).

Identify the like terms and add the corresponding coefficients.

\(\color{Cerulean}{\underline{1x^{2}}}\) \( - \color{OliveGreen}{\underline{\underline{10x}}}\)\( + \underline{\underline{\underline{8}}} + \color{Cerulean}{\underline{5 x ^ { 2 }}}\)\( -\color{OliveGreen}{\underline{\underline{6x}}}\)\( - \underline{\underline{\underline{1}}}\) \(\color{Cerulean}{Combine\: like\: terms.}\)

\(= 6 x ^ { 2 } - 16 x + 7\)

Answer : \(6 x ^ { 2 } - 16 x + 7\)

Example \(\PageIndex{5}\):

Simplify: \(a ^ { 2 } b ^ { 2 } - a b - 2 \left( 2 a ^ { 2 } b ^ { 2 } - 5 a b + 1 \right)\).

Distribute \(−2\) and then combine like terms.

\(\begin{aligned} a ^ { 2 } b ^ { 2 } - a b - 2 \left( 2 a ^ { 2 } b ^ { 2 } - 5 a b + 1 \right) & = a ^ { 2 } b ^ { 2 } - a b - 4 a ^ { 2 } b ^ { 2 } + 10 a b - 2 \\ & = - 3 a ^ { 2 } b ^ { 2 } + 9 a b - 2 \end{aligned}\)

Answer : \(- 3 a ^ { 2 } b ^ { 2 } + 9 a b - 2\)

Evaluating Algebraic Expressions

An algebraic expression can be thought of as a generalization of particular arithmetic operations. Performing these operations after substituting given values for variables is called evaluating 98 . In algebra, a variable represents an unknown value. However, if the problem specifically assigns a value to a variable, then you can replace that letter with the given number and evaluate using the order of operations.

Example \(\PageIndex{6}\):

• \(5x − 2\) where \(x =\frac{2}{3}\)
• \(y^{2} − y − 6\) where \(y = −4\)

To avoid common errors, it is a best practice to first replace all variables with parentheses, and then replace, or substitute 99 , the appropriate given value.

\(\begin{aligned} 5 x - 2 & = 5 (\:\: ) - 2 \\ & = 5 \left(\color{OliveGreen}{ \frac { 2 } { 3 }} \right) - 2 \\ & = \frac { 10 } { 3 } - \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 3 } { 3 }} \\ & = \frac { 10 - 6 } { 3 } \\ & = \frac { 4 } { 3 } \end{aligned}\)

\(y ^ { 2 } - y - 6 = (\:\: ) ^ { 2 } - (\:\: ) - 6\)

\(= ( \color{OliveGreen}{- 4}\)\( ) ^ { 2 } - ( \color{OliveGreen}{- 4}\)\( ) - 6\)

\(\begin{array} { l } { = 16 + 4 - 6 } \\ { = 14 } \end{array}\)

a. \(\frac{4}{3}\)

Often algebraic expressions will involve more than one variable.

Example \(\PageIndex{7}\):

Evaluate \(a ^ { 3 } - 8 b ^ { 3 }\) where \(a = −1\) and \(b = \frac{1}{2}\).

After substituting in the appropriate values, we must take care to simplify using the correct order of operations.

\(a ^ { 3 } - 8 b ^ { 3 } = (\:\: ) ^ { 3 } - 8 (\:\: ) ^ { 3 } \color{Cerulean}{Replace\: variables\: with\: parentheses.}\)

\(= ( \color{OliveGreen}{- 1}\) \( )^{3} -8(\color{OliveGreen}{\frac{1}{2}}\)\()^{3} \color{Cerulean}{Substitute\: in\: the\: appropriate\: values.}\)

\(= - 1 - 8 \left( \frac { 1 } { 8 } \right) \color{Cerulean}{Simplify.}\)

\(\begin{array} { l } { = - 1 - 1 } \\ { = - 2 } \end{array}\)

Answer : \(-2\)

Example \(\PageIndex{8}\):

Evaluate \(\frac { x ^ { 2 } - y ^ { 2 } } { 2 x - 1 }\) where \(x = −\frac{3}{2}\) and \(y = −3\).

\(\frac { x ^ { 2 } - y ^ { 2 } } { 2 x - 1 } = \frac { (\:\: ) ^ { 2 } - ( \:\:) ^ { 2 } } { 2 ( \:\:) - 1 }\)

\(= \frac { \left( \color{OliveGreen}{- \frac { 3 } { 2 }} \right) ^ { 2 } - ( \color{OliveGreen}{- 3} \color{Black}{) ^ { 2 } }} { 2 \left( - \color{OliveGreen}{\frac { 3 } { 2 }} \right) - 1 }\)

\(= \frac { \frac { 9 } { 4 } - 9 } { - 3 - 1 }\)

At this point we have a complex fraction. Simplify the numerator and then multiply by the reciprocal of the denominator.

\(\begin{aligned} & = \frac { \frac { 9 } { 4 } - \frac { 9 } { 1 } \cdot \color{Cerulean}{\frac { 4 } { 4 } }} { - 4 } \\ & = \frac { \frac { - 27 } { 4 } } { { \frac { - 4 } { 1 } } } \\ & = \frac { - 27 } { 4 } \left( - \frac { 1 } { 4 } \right) \\ & = \frac { 27 } { 16 } \end{aligned}\)

Answer : \(\frac { 27 } { 16 }\)

The answer to the previous example can be written as a mixed number, \(\frac { 27 } { 16 } = 1 \frac { 11 } { 16 }\). Unless the original problem has mixed numbers in it, or it is an answer to a realworld application, solutions will be expressed as reduced improper fractions.

Example \(\PageIndex{9}\):

Evaluate \(\sqrt { b ^ { 2 } - 4 a c }\) where \(a = −1, b = −7\), and \(c = \frac{1}{4}\).

Substitute in the appropriate values and then simplify.

\(\sqrt { b ^ { 2 } - 4 a c } = \sqrt { ( \:\: ) ^ { 2 } - 4 ( \:\: ) \:\:(\:\:) }\)

\( = \sqrt { ( \color{OliveGreen}{- 7}\color{Black}{ ) ^ { 2 } - 4 (}\color{OliveGreen}{ - 1}\color{Black}{ ) (}\color{OliveGreen}{ \frac { 1 } { 4 }}\color{Black}{)} } \)

\(\begin{aligned} & =\sqrt { 49 + 4(\frac{1}{4}) } \\ & = \sqrt { 49 + 1 } \\ & =\sqrt{50} \\& = \sqrt { 25 \cdot 2 } \\ & = 5 \sqrt { 2 } \end{aligned}\)

Aligned : \(5 \sqrt { 2 }\)

Exercise \(\PageIndex{1}\)

Evaluate \(\frac { \sqrt { 3 \pi V h } } { \pi h }\) where \(V = 25\pi\) and \(h = 3\).

www.youtube.com/v/Y4RCMceThu4

Using Formulas

The main difference between algebra and arithmetic is the organized use of variables. This idea leads to reusable formulas 100 , which are mathematical models using algebraic expressions to describe common applications. For example, the volume of a right circular cone depends on its radius \(r\) and height \(h\) and is modeled by the formula:

\(V = \frac { 1 } { 3 } \pi r ^ { 2 } h\)

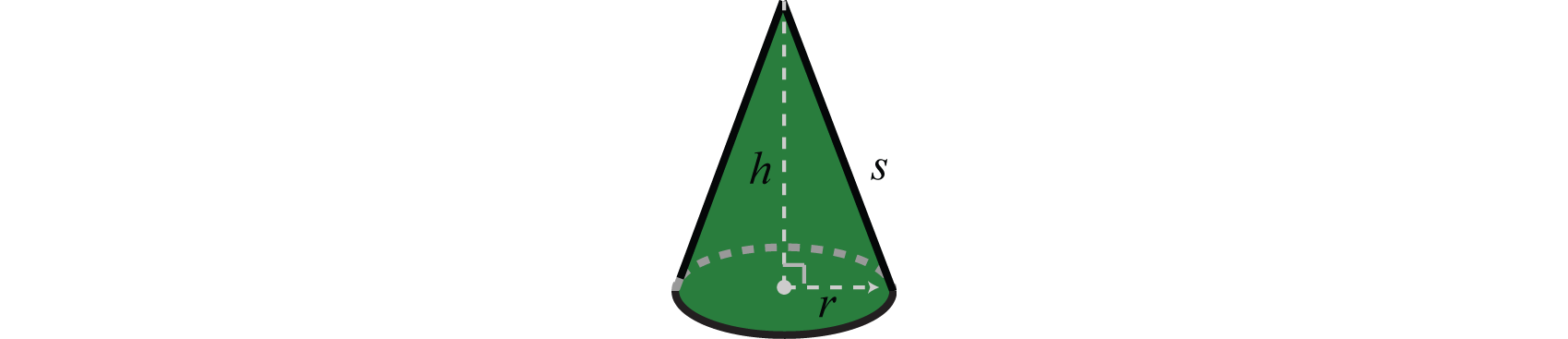
In this equation, variables and constants are used to describe the relationship between volume and the length of the base and height. If the radius of the base measures \(3\) meters and the height measures \(5\) meters, then the volume can be calculated using the formula as follows:

\(\begin{aligned} V & = \frac { 1 } { 3 } \pi r ^ { 2 } h \\ & = \frac { 1 } { 3 } \pi ( 3 m ) ^ { 2 } ( 5 m ) \\ & = \frac { 1 } {\bcancel {3}} \pi \cdot \stackrel{\color{Cerulean}{3}}{\bcancel{9}} \cdot 5 m ^ { 3 } \\ & = 15 \pi \mathrm { m } ^ { 3 } \end{aligned}\)

Using \(π ≈ 3.14\), we can approximate the volume: \(V ≈ 15 (3.14) = 47.1\) cubic meters.

A list of formulas that describe the area and perimeter of common plane figures follows. The letter P represents perimeter and is measured in linear units. The letter A represents area and is measured in square units.

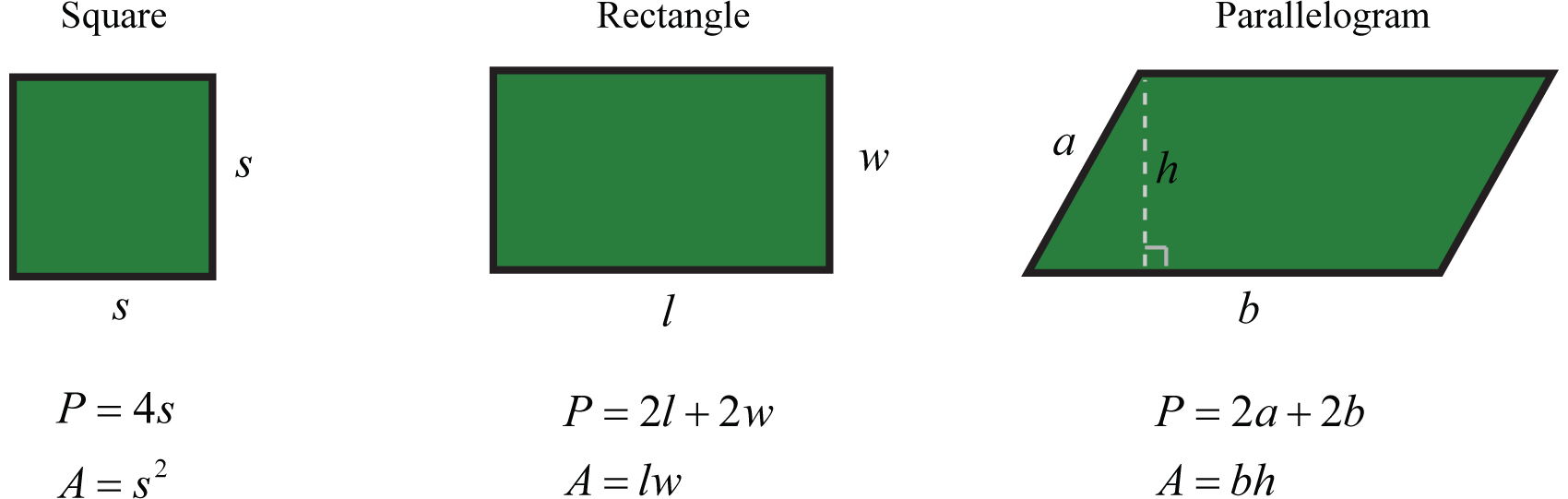
A list of formulas that describe the surface area and volume of common figures follows. Here SA represents surface area and is measured in square units. The letter V represents volume and is measured in cubic units.

Example \(\PageIndex{10}\):

The diameter of a spherical balloon is \(10\) inches. Determine the volume rounded off to the nearest hundredth.

The formula for the volume of a sphere is

\(V = \frac { 4 } { 3 } \pi r ^ { 3 }\)

This formula gives the volume in terms of the radius, \(r\). Therefore, divide the diameter by \(2\) and then substitute into the formula. Here, \(r = \frac{10}{2} = 5\) inches and we have

\(\begin{aligned} V & = \frac { 4 } { 3 } \pi r ^ { 3 } \\ & = \frac { 4 } { 3 } \pi ( 5 \mathrm { in } ) ^ { 3 } \\ & = \frac { 4 } { 3 } \pi \cdot 125 \mathrm { in } ^ { 3 } \\ & = \frac { 500 \pi } { 3 } \mathrm { in } ^ { 3 } \approx 523.60 \mathrm { in } ^ { 3 } \end{aligned}\)

Answer : The volume of the balloon is approximately \(523.60\) cubic inches.

Formulas can be found in a multitude of subjects. For example, uniform motion 101 is modeled by the formula \(D = rt\), which expresses distance \(D\), in terms of the average rate, or speed, \(r\) and the time traveled at that rate, \(t\). This formula, \(D = rt\), is used often and is read, “ distance equals rate times time .”

Example \(\PageIndex{11}\):

Jim’s road trip took \(2\:\frac{1}{2}\) hours at an average speed of \(66\) miles per hour. How far did he travel?

Substitute the appropriate values into the formula and then simplify.

\(\begin{aligned} D & = r \cdot t \\ & = ( \color{Cerulean}{66 \frac { \mathrm { mi } } { \mathrm { hr } }}\color{Black}{ ) \cdot (}\color{Cerulean}{ 2 \frac { 1 } { 2 } \mathrm { hr }}\color{Black}{)} \\ & = \frac { 66 } { 1 } \cdot \frac { 5 } { 2 } \mathrm { mi } \\ & = 33 \cdot 5 \mathrm { mi } \\ & = 165 \mathrm { mi } \end{aligned}\)

Answer : Jim traveled \(165\) miles.

Simple interest 102 \(I\) is given by the formula \(I = prt\), where \(p\) represents the principal amount invested at an annual interest rate \(r\) for \(t\) years.

Example \(\PageIndex{12}\):

Calculate the simple interest earned on a \(2\)-year investment of \($1,250\) at an annual interest rate of \(3\:\frac{3}{4} %\).

Convert \(3\:\frac{3}{4}%\) to a decimal number before using it in the formula.

\(r = 3 \frac { 3 } { 4 } \% = 3.75 \% = 0.0375\)

Use this and the fact that \(p = $1,250\) and \(t = 2\) years to calculate the simple interest.

\(\begin{aligned} I & = p r t \\ & = ( \color{Cerulean}{1,250}\color{Black}{ ) (}\color{Cerulean}{ 0.0375}\color{Black}{ ) (}\color{Cerulean}{ 2}\color{Black}{ )} \\ & = 93.75 \end{aligned}\)

Answer : The simple interest earned is \($93.75\).

Key Takeaways

• Think of algebraic expressions as generalizations of common arithmetic operations that are formed by combining numbers, variables, and mathematical operations.
• The distributive property \(a (b + c) = ab + ac\), is used when multiplying grouped algebraic expressions. Applying the distributive property allows us to remove parentheses.
• Combine like terms, or terms whose variable parts have the same variables with the same exponents, by adding or subtracting the coefficients to obtain the coefficient of a single term with the same variable part. Remember that the variable factors and their exponents do not change.
• To avoid common errors when evaluating, it is a best practice to replace all variables with parentheses and then substitute the appropriate values.
• The use of algebraic expressions allows us to create useful and reusable formulas that model common applications.

Exercise \(\PageIndex{2}\)

List all of the coefficients and variable parts of each term.

• \(−5x^{2} + x − 1\)
• \(y^{2} − 9y + 3\)
• \(5x^{2} − 3xy + y^{2}\)
• \(a^{2}b^{2} + 2ab − 4\)
• \(x^{2}y + xy^{2} − 3xy + 9\)
• \(x^{4} − x^{3} + x^{2} − x + 2\)

1. Coefficients: \(\{−5, 1, −1\}\) ; variable parts: \(\{x^{2} , x\}\)

3. Coefficients: \(\{5, −3, 1\}\) ; variable parts: \(\{x^{2} , xy, y^{2} \}\)

5. Coefficients: \(\{1, −3, 9\}\) ; variable parts: \(\{x^{2}y, xy^{2} , xy\}\)

Exercise \(\PageIndex{3}\)

• \(5 (3x − 5) \)
• \(3 (4x − 1) \)
• \(−2 (2x^{2} − 5x + 1) \)
• \(−5 (6x^{2} − 3x − 1)\)
• \(\frac{2}{3} (9y^{2} + 12y − 3)\)
• \(−\frac{3}{4} (8y^{2} + 20y + 4)\)
• \(12(\frac{1}{3} a^{2} − \frac{5}{6} a + \frac{7}{12} )\)
• \(−9 (\frac{1}{9} a^{2} − \frac{5}{3} a + 1 )\)
• \(9 (a^{2} − 2b^{2} )\)
• \(−5 (3x^{2} − y^{2} )\)
• \((5a^{2} − 3ab + b^{2} ) ⋅ 6\)
• \((a^{2}b^{2} − 9ab − 3) ⋅ 7\)
• \(− (5x^{2} − xy + y^{2} )\)
• \(− (x^{2}y^{2} − 6xy − 1)\)

1. \(15x − 25\)

3. \(−4x^{2} + 10x − 2\)

5. \(6y^{2} + 8y − 2\)

7. \(4a^{2} − 10a + 7\)

9. \(9a^{2} − 18b^{2}\)

11. \(30a^{2} − 18ab + 6b^{2}\)

13. \(−5x^{2} + xy − y^{2}\)

Exercise \(\PageIndex{4}\)

Combine like terms.

• \(18x − 5x + 3x\)
• \(30x − 50x + 10x\)
• \(3y − 4 + 2y − 12\)
• \(12y + 7 − 15y − 6\)
• \(2x^{2} − 3x + 2 + 5x^{2} − 6x + 1\)
• \(9x^{2} + 7x − 5 − 10x^{2} − 8x + 6\)
• \(\frac{3}{5} a^{2} − \frac{1}{2} + \frac{1}{3} a^{2} + \frac{4}{5}\)
• \(\frac{1}{6} a^{2} + \frac{2}{3} − \frac{4}{3} a^{2} − \frac{1}{9}\)
• \(\frac{1}{2} y^{2} + \frac{2}{3} y − 3 + \frac{3}{5} y^{2} + \frac{1}{3} y − \frac{7}{3}\)
• \(\frac{5}{6} x^{2} + \frac{1}{8} x − 1 − \frac{1}{2} x^{2} + \frac{3}{4} x − \frac{4}{5}\)
• \(a^{2}b^{2} + 5ab − 2 + 7a^{2}b^{2} − 6ab + 12\)
• \(a^{2} − 12ab + 4b^{2} − 6a^{2} + 10ab − 5b^{2}\)
• \(3x^{2}y + 12xy − 5xy^{2} + 5xy − 8x^{2}y + 2xy^{2}\)
• \(10x^{2}y + 2xy − 4xy^{2} + 2x^{2}y − 8xy + 5xy^{2}\)
• \(7m^{2}n − 9mn + mn^{2} − 6m^{2}n + mn − 2mn^{2}\)
• \(m^{2}n − 5mn + 5mn^{2} − 3m^{2}n + 5mn + 2mn^{2}\)
• \(x^{2n} − 3x^{n} + 5 + 2x^{2n} − 4x^{n} − 3\)
• \(5y^{2n} − 3y^{n} + 1 − 3y^{2n} − 2y^{n} − 1\)

3. \(5y − 16\)

5. \(7x^{2} − 9x + 3\)

7. \(\frac{14}{15}a^{2} + \frac{3}{10}\)

9. \(\frac{11}{10} y^{2} + y − \frac{16}{3}\)

11. \(8a^{2}b^{2} − ab + 10\)

13. \(−5x^{2}y + 17xy − 3xy^{2}\)

15. \(m^{2}n − 8mn − mn^{2}\)

17. \(3x^{2n} − 7x^{n} + 2\)

Exercise \(\PageIndex{5}\)

• \(5 − 2 (4x + 8)\)
• \(8 − 6 (2x − 1)\)
• \(2 (x^{2} − 7x + 1) + 3x − 7\)
• \(−5 (x^{2} + 4x − 1) + 8x^{2} − 5\)
• \(5ab − 4 (ab + 5)\)
• \(5 (7 − ab) + 2ab\)
• \(2 − a^{2} + 3 (a^{2} + 4)\)
• \(7 − 3y + 2 (y^{2} − 3y − 2)\)
• \(8x^{2} − 3x − 5 (x^{2} + 4x − 1)\)
• \(2 − 5y − 6 (y^{2} − y + 2)\)
• \(a^{2}b^{2} − 5 + 3 (a^{2}b^{2} − 3ab + 2)\)
• \(a^{2} − 3ab − 2 (a^{2} − ab + 1)\)
• \(10y^{2} + 6 − (3y^{2} + 2y + 4)\)
• \(4m^{2} − 3mn − (m^{2} − 3mn + n^{2} )\)
• \(x^{2n} − 3x^{n} + 5 (x^{2n} − x^{n} + 1)\)
• \(−3 (y^{2n} − 2y^{n} + 1) + 4y^{2n} − 5\)

1. \(−8x − 11\)

3. \(2x^{2} − 11x − 5\)

5. \(ab − 20\)

7. \(2a^{2} + 14\)

9. \(3x^{2} − 23x + 5\)

11. \(4a^{2}b^{2} − 9ab + 1\)

13. \(7y^{2} − 2y + 2\)

15. \(6x^{2n} − 8x^{n} + 5\)

Exercise \(\PageIndex{6}\)

• \(−2x + 3\) where \(x = −2\)
• \(8x − 5\) where \(x = −1\)
• \(x^{2} − x + 5\) where \(x = −5\)
• \(2x^{2} − 8x + 1\) where \(x = 3\)
• \(\frac { x ^ { 2 } - x + 2 } { 2 x - 1 }\) where \(x = -\frac{1}{2}\)
• \(\frac { 9 x ^ { 2 } + x - 2 } { 3 x - 4 }\) where \(x = -\frac{2}{3}\)
• \(( 3 y - 2 ) ( y + 5 )\) where \(y = \frac { 2 } { 3 }\)
• \((3x + 2) (5x + 1)\) where \(x = −\frac{1}{5}\)
• \((3x − 1) (x − 8)\) where \(x = −1\)
• \((7y + 5) (y + 1)\) where \(y = −2\)
• \(y^{6} − y^{3} + 2\) where \(y = −1\)
• \(y^{5} + y^{3} − 3\) where \(y = −2\)
• \(a^{2} − 5b^{2}\) where \(a = −2\) and \(b = −1\)
• \(a^{3} − 2b^{3}\) where \(a = −3\) and \(b = 2\)
• \((x − 2y) (x + 2y)\) where \(x = 2\) and \(y = −5\)
• \((4x − 3y) (x − y)\) where \(x = −4\) and \(y = −3\)
• \(a^{2} − ab + b^{2}\) where \(a = −1\) and \(b = −2\)
• \(x^{2}y^{2} − xy + 2\) where \(x = −3\) and \(y = −2\)
• \(a^{4} − b^{4}\) where \(a = −2\) and \(b = −3\)
• \(a^{6} − 2a^{3}b^{3} − b^{6}\) where \(a = 2\) and \(b = −1\)

5. \(−\frac{11}{8}\)

13. \(−1\)

15. \(−96\)

19. \(−65\)

Exercise \(\PageIndex{7}\)

Evaluate \(\sqrt { b ^ { 2 } - 4 a c }\) given the following values.

• \(a = 6, b = 1\) and \(c = −1\)
• \(a = 15, b = 4\) and \(c = −4\)
• \(a = \frac{3}{4} , b = −2\) and \(c = −4\)
• \(a = \frac{1}{2} , b = −2\) and \(c = −30\)
• \(a = 1, b = 2\) and \(c = −1\)
• \(a = 1, b = −4\) and \(c = −50\)
• \(a = 1, b = −1\) and \(c = −\frac{1}{16}\)
• \(a = −2, b = −\frac{1}{3}\) and \(c = 1\)

5. \(2\sqrt{2}\)

7. \(\frac { \sqrt { 5 } } { 2 }\)

Exercise \(\PageIndex{8}\)

Convert the following temperatures to degrees Celsius given \(C = \frac{5}{9} (F − 32)\), where F represents degrees Fahrenheit.

• \(95°\)F
• \(86°\)F
• \(32°\)F
• \(−40°\)F

1. \(35°\)C

3. \(0°\)C

Exercise \(\PageIndex{9}\)

• Calculate the perimeter and area of a rectangle with dimensions \(12\) feet by \(5\) feet.
• Calculate the perimeter and area of a rectangle with dimensions \(5\) meters by \(1\) meter.
• Calculate the surface area and volume of a sphere with radius \(6\) centimeters.
• The radius of the base of a right circular cylinder measures \(4\) inches and the height measures \(10\) inches. Calculate the surface area and volume.
• Calculate the volume of a sphere with a diameter of \(18\) centimeters.
• The diameter of the base of a right circular cone measures \(6\) inches. If the height is \(1\:\frac{1}{2}\) feet, then calculate its volume.
• Given that the height of a right circular cylinder is equal to the radius of the base, derive a formula for the surface area in terms of the radius of the base.
• Given that the area of the base of a right circular cylinder is \(25π\) square inches, find the volume if the height is \(1\) foot.
• Jose was able to drive from Tucson to Phoenix in \(2\) hours at an average speed of \(58\) mph. How far is Phoenix from Tucson?
• If a bullet train can average \(152\) mph, then how far can it travel in \(\frac{3}{4}\) of an hour?
• Margaret traveled for \(1\:\frac{3}{4}\) hour at an average speed of \(68\) miles per hour. How far did she travel?
• The trip from Flagstaff, AZ to the Grand Canyon national park took \(1\:\frac{1}{2}\) hours at an average speed of \(54\) mph. How far is the Grand Canyon national park from Flagstaff?
• Calculate the simple interest earned on a \(3\)-year investment of \($2,500\) at an annual interest rate of \(5\:\frac{1}{4} \)%.
• Calculate the simple interest earned on a \(1\)-year investment of \($5,750\) at an annual interest rate of \(2\:\frac{5}{8} \)%.
• What is the simple interest earned on a \(5\)-year investment of \($20,000\) at an annual interest rate of \(6\)%?
• What is the simple interest earned on a \(1\)-year investment of \($50,000\) at an annual interest rate of \(4.5\)%?
• The time \(t\) in seconds an object is in free fall is given by the formula \(t = \frac { \sqrt { s } } { 4 }\), where s represents the distance in feet the object has fallen. How long does it take an object to fall \(32\) feet? (Give the exact answer and the approximate answer to the nearest hundredth.)
• The current \(I\) measured in amperes, is given by the formula \(I = \sqrt { \frac { P } { R } }\), where \(P\) is the power usage measured in watts, and \(R\) is the resistance measured in ohms. If a light bulb uses \(60\) watts of power and has \(240\) ohms of resistance, then how many amperes of current are required?

1. \(P = 34\) feet; \(A = 60\) square feet

3. \(SA = 144π\) square centimeters; \(V = 288π\) cubic centimeters

5. \(972π\) cubic centimeters

7. \(SA = 4πr^{2}\)

9. \(116\) miles

11. \(119\) miles

13. \($393.75\)

15. \($6,000\)

17. \(\sqrt { 2 } \approx 1.41\) seconds

Exercise \(\PageIndex{10}\)

• Find and post a useful mathematical model. Demonstrate its use with some values.
• Research and discuss the history of the variable. What can we use if we run out of letters?
• Find and post a link to a useful resource describing the Greek alphabet.
• Given the algebraic expression \(5 − 3 (9x − 1)\), explain why we do not subtract \(5\) and \(3\) first.
• Do we need a separate distributive property for more than two terms? For example, \(a (b + c + d) = ab + ac + ad\). Explain.
• How can we check to see if we have simplified an expression correctly?

1. Answer may vary

3. Answer may vary

5. Answer may vary

87 Combinations of variables and numbers along with mathematical operations used to generalize specific arithmetic operations.

88 Components of an algebraic expression separated by addition operators.

89 Components of a term separated by multiplication operators.

90 The numerical factor of a term.

91 All the variable factors with their exponents.

92 A term written without a variable factor.

93 Given any real numbers \(a, b,\) and \(c, a (b + c) = ab + ac\) or \((b + c) a = ba + ca\).

94 Constant terms or terms whose variable parts have the same variables with the same exponents.

95 Used when referring to like terms.

96 Adding or subtracting like terms within an algebraic expression to obtain a single term with the same variable part.

97 The process of combining like terms until the expression contains no more similar terms.

98 The process of performing the operations of an algebraic expression for given values of the variables.

99 The act of replacing a variable with an equivalent quantity.

100 A reusable mathematical model using algebraic expressions to describe a common application.

101 The distance \(D\) after traveling at an average rate \(r\) for some time \(t\) can be calculated using the formula \(D = rt\).

102 Modeled by the formula \(I = prt\), where \(p\) represents the principal amount invested at an annual interest rate \(r\) for \(t\) years.

Algebraic Expressions

Algebraic expressions are the mathematical statement that we get when operations such as addition, subtraction, multiplication, division, etc. are operated upon on variables and constants. For example, let us assume that James and Natalie were playing with matchsticks and thought of forming number patterns using them. James took four matchsticks and formed the number 4. Natalie added three more matchsticks to form a pattern with two 4's. They realized that they can keep on adding 3 matchsticks in each round to make one extra "four". From this, they concluded that they need 4+ 3(n-1) sticks, in general, to make a pattern with n number of 4's. Here, 4+ 3(n-1) is called an algebraic expression.

Let us learn more about algebraic expressions along with their types and operations on them.

What are Algebraic Expressions?

An algebraic expression (or) a variable expression is a combination of terms by the operations such as addition, subtraction, multiplication, division, etc. For example, let us have a look at the expression 5x + 7. Thus, we can say that 5x + 7 is an example of an algebraic expression. Here are more examples:

• 5x + 4y + 10
• 2x 2 y - 3xy 2
• (-a + 4b) 2 + 6ab

Variables, Constants, Terms, and Coefficients

There are different components of an algebraic expression. Let us have a look at the image given below in order to understand the concept of Variables, Constants, Terms, and Coefficients of any algebraic expression.

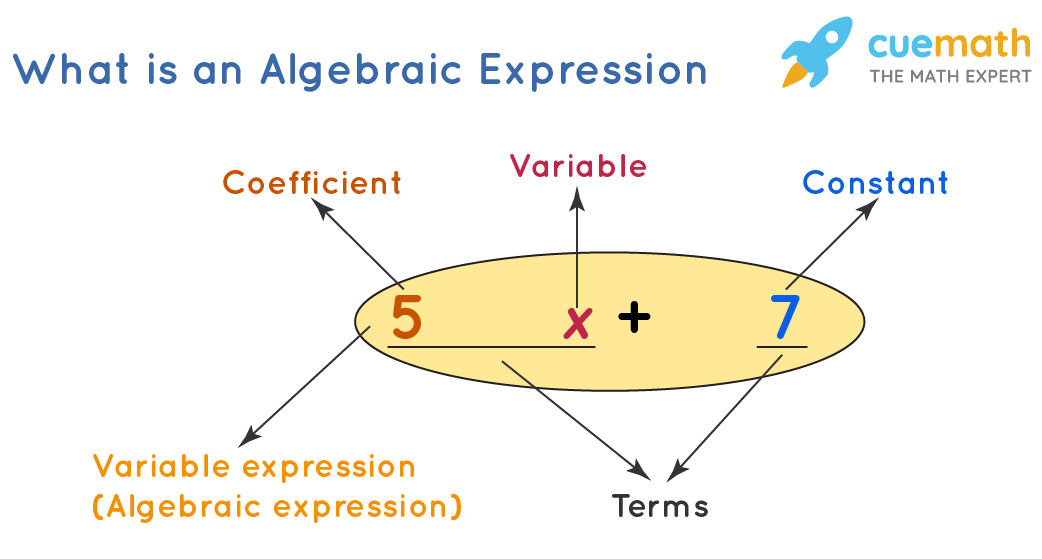
In mathematics,

• a symbol that doesn't have a fixed value is called a variable . It can take any value. In the above example that involved matchsticks, n is a variable and in this case, it can take the values 1,2,3,... Some examples of variables in Math are a,b, x, y, z, m, etc.
• On the other hand, a symbol that has a fixed numerical value is called a constant . All numbers are constants. Some examples of constants are 3, 6, -(1/2), √5, etc.
• A term is a variable alone (or) a constant alone (or) it can be a combination of variables and constants by the operation of multiplication or division. Some examples of terms are 3x 2 , -(2y/3), √(5x), etc.
• Here, the numbers that are multiplying the variables are 3, -2/3, and 5. These numbers are called coefficients.

Simplifying Algebraic Expressions

To simplify an algebraic expression , we just combine the like terms. Hence, the like variables will be combined together. Now, out of the like variables, the same powers will be combined together. For example, let us take an algebraic expression and try to reduce it to its lowest form in order to understand the concept better. Let our expression be:

x 3 + 3x 2 − 2x 3 + 2x − x 2 + 3 − x

= (x 3 − 2x 3 ) + (3x 2 − x 2 ) + (2x − x) + 3

= −x 3 + 2x 2 + x + 3

Hence, the algebraic expression x 3 + 3x 2 − 2x 3 + 2x − x 2 + 3 − x simplifies to −x 3 + 2x 2 + x + 3.

Adding Algebraic Expressions

Here are some examples for adding algebraic expressions :

• (x 2 + 2x + 3) + (2x 2 - 3x) = (x 2 + 2x 2 ) + (2x + (-3x)) + 3 = 3x 2 - x + 3
• (1.5ab + 3) + (2.5ab - 2) = (1.5ab + 2.5ab) + (3 + (-2)) = 4ab + 1

Subtracting Algebraic Expressions

To subtract two algebraic expressions, we add the additive inverse of the second expression to the first expression. Here are some examples for subtracting algebraic expressions :

• (3x 2 - 5x) - (x 2 - 2x + 2) = (3x 2 - 5x) + (-x 2 + 2x - 2) = (3x 2 - x 2 ) + (-5x + 2x) - 2 = 2x 2 - 3x - 2
• (3ab + 4) - (2ab - 4) = (3ab + 4) + (-2ab + 4) = (3ab - 2ab) + (4 + 4) = ab + 8

Multiplying Algebraic Expressions

To multiply two algebraic expressions, we multiply every term of the first expression with every term of the second expression and combine all the products. Here are some examples of multiplying algebraic expressions .

• ab (2ab + 3) = 2a 2 b 2 + 3ab
• (x + 1) (x + 2) = x 2 + x + 2x + 2 = x 2 + 3x + 2

Dividing Algebraic Expressions

To divide two algebraic expressions, we factor the numerator and the denominator, cancel the possible terms, and simplify the rest. Here are some examples of dividing algebraic expressions .

• 2x 2 / (2x 2 + 4x) = (2x 2 ) / [2x (x + 2)] = x / (x + 2)
• (x 2 + 5x + 4) / (x + 1) = [ (x + 4) (x + 1) ] / (x + 1) = x + 4

Algebraic Expression Formulas

Algebraic formulas are the derived short formulas that help us in solving the equations easily. They are just a rearrangement of the given terms in order to create a better expression that is easy to memorize. Find below a list of some of the basic formulas that are being used widely. Have a look at this page in order to understand the algebraic formulas better.

• (a + b) 2 = a 2 + 2ab + b 2
• (a - b) 2 = a 2 - 2ab + b 2
• (a + b)(a - b) = a 2 - b 2
• (x + a)(x + b) = x 2 + x(a + b) + ab
• (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
• (a - b) 3 = a 3 - 3a 2 b + 3ab 2 - b 3
• a 3 + b 3 = (a + b) (a 2 - ab + b 2 )

Types of Algebraic Expressions

The types of algebraic expressions are based on the variables found in that particular expression, the number of the terms of that expression, and the values of the exponents of the variables in each expression. Given below is a table that divides the algebraic expressions into five different categories. Let us have a look at the table.

☛ Related Topics :

• Simplifying Rational Expressions
• Simplifying Algebraic Expressions Calculator
• Inequalities

Algebraic Expressions Examples

Example 1: There are 25 oranges in a bag. Write the algebraic expression for the number of oranges in x number of bags.

The number of oranges in one bag = 25. The number of bags = x. So the number of oranges in x bags = 25x.

Answer: Required Algebraic Expression = 25x

Example 2: What type of algebraic expression is 4x + 5?

4x + 5 has two monomials 4x and 5 and hence it is a binomial. Every binomial is a polynomial as well. So 4x+5 is a polynomial as well. So the correct answers are: binomial and polynomial.

Answer: 4x + 5 is a polynomial/binomial.

Example 3: Is 12y/x a monomial expression? Justify your answer.

The expression has a single non-zero term, but the denominator of the expression is a variable.

Answer: The expression 12y/x is not a monomial.

Example 4: Add the following algebraic expressions: 3x + 2 and 4y + 2z.

We combine the like terms to add two algebraic expressions. But the given expressions have no like terms. Hence their sum is 3x + 2 + 4y + 2z.

If we rearrange the terms, we get the sum = 3x + 4y + 2z + 2.

Answer: sum = 3x + 4y + 2z + 2.

go to slide go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Algebraic Expressions

go to slide go to slide go to slide go to slide go to slide

FAQs on Algebraic Expressions

How do you describe an algebraic expression.

An algebraic expression is a variable expression described using its terms, and operations on the terms. For example, x + 3 can be described as "3 more than x". While a + b - 7 can be described as "7 less than the sum of a and b".

How Many Terms are There in an Algebraic Expression?

A term is a variable alone (or) a constant alone (or) it can be a combination of variables and constants by the operation of multiplication or division . We apply this definition to identify the terms in an algebraic expression. After we identify the terms, we can just count them.

Why are Algebraic Expressions Useful?

The algebraic expressions use variables (which take multiple multiples ) in order to describe a real-life scenario. Instead of saying "The cost of 3 pens and 4 pencils", it is simple to say 3x+4y where x and y are the costs of each pen and pencil respectively. Also, writing a real-life scenario as an expression helps to perform mathematical calculations.

How do you Identify an Algebraic Expression?

An algebraic expression is a combination of variables and constants . However, no equalities should be present in it. Otherwise, it will become an algebraic equation .

How to Simplify an Algebraic Expression?

To simplify an algebraic expression, we just combine the like terms and solve further to get a simplified form of the expression.

Is 7 an Algebraic Expression?

Yes, 7 is an algebraic expression, because it can be considered as a monomial.

What are Algebraic Expression and Equation?

An algebraic expression is any number , variable, or different operations combined together, while an equation is two different algebraic expressions combined together with an equal sign .

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

7.3 Simple Algebraic Equations and Word Problems

An algebraic equation is a mathematical sentence expressing equality between two algebraic expressions (or an algebraic expression and a number).

When two expressions are joined by an equal (=) sign, it indicates that the expression to the left of the equal sign is identical in value to the expression to the right of the equal sign.

For example, when two algebraic expressions, such as [latex]5x + 7[/latex] and [latex]x + 19[/latex], are equal, the two expressions are joined by an equal (=) sign and the equation is written as:

[latex]5x + 7 = x + 19[/latex]

‘Left side’ (LS) = ‘Right side’ (RS)

The solution to the equation is the value of the variable that makes the left side (LS) evaluate to the same number as the right side (RS).

Note: You need an equation to solve for an unknown variable – you cannot solve for a variable in an algebraic expression that is not part of an equation.

• If you have an expression , it needs to be simplified .
• If you have an equation , it needs to be solved .

In algebra, there are a variety of equations. In this section, we will learn one equation category, linear equations with one variable .

Examples of linear equations with one variable are:

[latex]2x = 8[/latex],   [latex]3x + 5 = 14[/latex],   [latex]5x + 7 = x + 19[/latex]

An equation is either true or false depending on the value of the variable.

For example, consider the equation [latex]2x = 8[/latex]:

• If [latex]x = 4[/latex],   LS = 2(4) = 8, RS = 8; therefore, the equation is true.
• If [latex]x = 3[/latex],   LS = 2(3) = 6, RS = 8; therefore, the equation is false.

Equations may be classified into the following three types:

• Conditional equation: these equations are only true when the variable has a specific value. For example, [latex]2x = 8[/latex] is a conditional equation, true if and only if [latex]x = 4[/latex].
• Identity: these equations are true for any value for the variable. For example, [latex]2x + 10 = 2(x + 5)[/latex] is an identity, true for any value of [latex]x[/latex].
• Contradiction: these equations are not true for any value of the variable. For example, [latex]x + 5 = x + 4[/latex] is a contradiction, not true for any value of [latex]x[/latex].

Equivalent Equations

Equations with the same solutions are called equivalent equations .

For example, [latex]2x + 5 = 9[/latex] and [latex]2x = 4[/latex] are equivalent equations because the solution [latex]x = 2[/latex] satisfies each equation.

Similarly, [latex]3x - 4 = 5[/latex], [latex]2x = x + 3[/latex], and [latex]x + 1 = 4[/latex] are equivalent equations because the solution [latex]x = 3[/latex] satisfies each equation.

Properties of Equality

If [latex]a = b[/latex], then,

These properties are used to solve equations.

Equations with Fractional Coefficients

If an equation contains fractional coefficients, then the fractional coefficients can be changed to whole numbers by multiplying both sides of the equation by the least common denominator (LCD) of all the fractions, using the Multiplication Property.

For example,

[latex]\displaystyle{\frac{2}{3}x = \frac{5}{2} + 4}[/latex] Since the LCD of the denominators 3 and 2 is 6, multiply both sides of the equation by 6.

[latex]\displaystyle{6\left(\frac{2}{3}x\right) = 6\left(\frac{5}{2} + 4\right)}[/latex] This is the same as multiplying each term by the LCD of 6.

[latex]\displaystyle{6\left(\frac{2}{3}x\right) = 6\left(\frac{5}{2}\right) + 6(4)}[/latex] Simplifying, [latex]4x = 15 + 24[/latex] Now, the equation has only whole number coefficients [latex]4x = 39[/latex].

Equations with Decimal Coefficients

If an equation contains decimal coefficients, then the decimal coefficients can be changed to whole numbers by multiplying both sides of the equation by an appropriate power of 10, using the Multiplication Property.

[latex]\underline{1.25}x = \underline{0.2} + 4[/latex] Since there is at most 2 decimal places in any of the coefficients or constants, multiply both sides of the equation by [latex]10^2 = 100[/latex].

[latex]100(1.25x) = 100(0.2 + 4)[/latex] This is the same as multiplying each term by 100. [latex]100(1.25x) = 100(0.2) + 100(4)[/latex] Simplifying, [latex]125x = 20 + 400[/latex] Now, the equation has only whole number coefficients [latex]125x = 420[/latex].

Steps to Solve Algebraic Equations with One Variable

If the equation contains fraction and/or decimal coefficients, it is possible to work with them as they are – in that case, proceed to Step 2. Alternatively, as explained earlier, the equation may be rewritten in whole numbers to make calculations and rearrangements easier.

If present, expand and clear brackets in the equation by following the order of arithmetic operations (BEDMAS).

Use the addition and subtraction properties to collect and group all variable terms on the left side of the equation and all constants on the right side . Then, simplify both sides.

Note: If it is more convenient to gather all the variable terms on the right side and the constants on the left side, you may do so, and then use the symmetric property and switch the sides of the equation to bring the variables over to the left side and the constants to the right side.

Use the division and multiplication properties to ensure that the coefficient of the variable is +1.

After completing Step 4, there should be a single variable with a coefficient of +1 on the left side and a single constant term on the right side – that constant term is the solution to the equation.

Verify the answer by substituting the solution from Step 5 back into the original problem.

State the answer.

Example 7.3-a: Solving Equations Using the Addition and Subtraction Properties

Solve the following equations and verify the solutions:

• [latex]x - 11 = 4[/latex]
• [latex]8 + x = 20[/latex]
• [latex]x - 11 = 4[/latex] Adding 11 to both sides, [latex]x - 11 + 11 = 4 + 11[/latex] [latex]x = 15[/latex] Verify by substituting [latex]x = 15[/latex]: LS [latex]= x - 11 = 15 - 11 = 4[/latex]     RS [latex]= 4[/latex] LS = RS Therefore, the solution is [latex]x = 15[/latex].
• [latex]8 + x = 20[/latex] Subtracting 8 from both sides, [latex]8 - 8 + x = 20 - 8[/latex] [latex]x = 12[/latex] Verify by substituting [latex]x = 12[/latex]: LS [latex]= 8 + x = 8 + 12 = 20[/latex]   RS [latex]= 20[/latex] LS = RS Therefore, the solution is [latex]x = 12[/latex].

Example 7.3-b: Solving Equations Using the Multiplication and Division Properties

• [latex]5x = 20[/latex]
• [latex]\displaystyle{\frac{3}{8}x = 12}[/latex]
• [latex]5x = 20[/latex] Dividing both sides by 5 , [latex]\displaystyle{\frac{5x}{5} = \frac{20}{5}}[/latex] [latex]x = 4[/latex] Verify by substituting [latex]x = 4[/latex]: LS [latex]= 5x = 5(4) = 20[/latex]   RS [latex]= 20[/latex] LS = RS Therefore, the solution is [latex]x = 4[/latex].
• [latex]\displaystyle{\frac{3}{8}x = 12}[/latex] Multiplying both sides by [latex]\displaystyle{\frac{8}{3}}[/latex] (the reciprocal of [latex]\displaystyle{\frac{3}{8}}[/latex]), [latex]\displaystyle{\left(\frac{8}{3}\right) \cdot \frac{3}{8}x = \left(\frac{8}{3}\right) \cdot 12}[/latex] [latex]x = 8 \times 4[/latex] [latex]x = 32[/latex]   or  [latex]\displaystyle{\frac{3}{8}x = 12}[/latex] Multiplying both sides by 5 , [latex]\displaystyle{(8) \cdot \frac{3}{8}x = (8) \cdot 12}[/latex] [latex]3x = 96[/latex]Dividing both sides by 3 , [latex]\displaystyle{\frac{3x}{3} = \cdot \frac{96}{3}}[/latex][latex]x = 32[/latex]Verify by substituting [latex]x = 32[/latex]:LS [latex]\displaystyle{= \frac{3}{8}x = \frac{3}{8} \times 32 = 12}[/latex]RS [latex]= 12[/latex]LS = RSTherefore, the solution is [latex]x = 32[/latex].

Example 7.3-c: Solving Equations with Variables on Both Sides

• [latex]3x - 8 = 12 - 2x[/latex]
• [latex]15 + 6x - 4 = 3x + 31 - x[/latex]
• [latex]3x - 8 = 12 - 2x[/latex] Adding 2x to both sides,[latex]3x + 2x - 8 = 12 - 2x + 2x[/latex] [latex]5x - 8 = 12[/latex] Adding 8 to both sides,[latex]5x - 8 + 8 = 12 + 8[/latex] [latex]5x = 20[/latex] Dividing both sides by 5 , [latex]\displaystyle{\frac{5x}{5} = \frac{20}{5}}[/latex] [latex]x = 4[/latex] Verify by substituting [latex]x = 4[/latex]: LS [latex]= 3x - 8 = 3(4) - 8 = 12 - 8 = 4[/latex]RS [latex]= 12 - 2x = 12 - 2(4) = 12 - 8 = 4[/latex]LS = RSTherefore, the solution is [latex]x = 4[/latex].
• [latex]15 + 6x - 4 = 3x + 31 - x[/latex] Combining like terms (LS: [latex]15 - 4 = 11[/latex], and RS: [latex]3x - x = 2x[/latex]), [latex]11 + 6x = 2x + 31[/latex]   Subtracting [latex]2x[/latex] from both sides, [latex]11 + 6x - 2x = 2x - 2x + 31[/latex] [latex]11 + 4x = 31[/latex] Subtracting 11 from both sides, [latex]11 - 11 + 4x = 31 - 11[/latex] [latex]4x = 20[/latex] Dividing both sides by 4 , [latex]\displaystyle{\frac{4x}{4} = \frac{20}{4}}[/latex] [latex]x = 5[/latex] Verify by substituting [latex]x = 5[/latex] back into the original equation:LS [latex]= 15 + 6x - 4 = 15 + 6(5) - 4 = 15 + 30 - 4 = 41[/latex]RS [latex]= 3x + 31 - x = 3(5) + 31 - 5 = 15 + 31 - 5 = 41[/latex]LS = RSTherefore, the solution is [latex]x = 5[/latex].

Example 7.3-d: Solving Equations with Fractions

Solve the following equation and verify the solution:

[latex]\displaystyle{\frac{x}{3} - \frac{1}{12} = \frac{1}{6} + \frac{x}{4}}[/latex]

[latex]\displaystyle{\frac{x}{3} - \frac{1}{12} = \frac{1}{6} + \frac{x}{4}}[/latex] LCD of 3, 4, 6, and 12 is 12.

Multiplying each term by 12 ,

[latex]\displaystyle{12\left(\frac{x}{3}\right) - 12\left(\frac{1}{12}\right) = 12\left(\frac{1}{6}\right) + 12\left(\frac{x}{4}\right)}[/latex]

[latex]4x - 1 = 2 + 3x[/latex]

Subtracting [latex]3x[/latex] from both sides,

[latex]4x - 3x - 1 = 2 + 3x - 3x[/latex]

[latex]x - 1 = 2[/latex]

Adding 1 to both sides,

[latex]x - 1 + 1 = 2 + 1[/latex]

[latex]x = 3[/latex]

Verify by substituting [latex]x = 3[/latex] back into the original equation:

LS [latex]\displaystyle{= \frac{x}{3} - \frac{1}{12} = \frac{3}{3} - \frac{1}{12} = \frac{12}{12} - \frac{1}{12} = \frac{11}{12}}[/latex]

RS [latex]\displaystyle{= \frac{1}{6} + \frac{x}{4} = \frac{1}{6} + \frac{3}{4} = \frac{2}{12} + \frac{9}{12} = \frac{11}{12}}[/latex]

Therefore, the solution is [latex]x = 3[/latex].

Example 7.3-e: Solving Equations with Decimals

[latex]0.15x + 1.2 = 0.4x - 0.8[/latex]

[latex]0.15x + 1.2 = 0.4x - 0.8[/latex] Greatest number of decimal places is 2 (i.e., hundredths).

Multiplying all the terms by [latex]10^2 = 100[/latex],

[latex]100(0.15x) + 100(1.2) = 100(0.4x) - 100(0.8)[/latex]

[latex]15x + 120 = 40x - 80[/latex]

Interchanging the LS and RS using the Symmetric Property to have the larger x term on the LS,

[latex]40x - 80 = 15x + 120[/latex]

Subtracting [latex]15x[/latex] from both sides,

[latex]40x - 15x - 80 = 15x - 15x + 120[/latex]

[latex]25x - 80 = 120[/latex]

Adding 80 to both sides,

[latex]25x - 80 + 80 = 120 + 80[/latex]

[latex]25x = 200[/latex]

Dividing both sides by 25 ,

[latex]\displaystyle{\frac{25x}{25} = \frac{200}{25}}[/latex]

[latex]x = 8[/latex]

Verify by substituting [latex]x = 8[/latex] back into the original equation:

LS [latex]= 0.15x + 1.2 = 0.15(8) + 1.2 = 1.2 + 1.2 = 2.4[/latex]

RS [latex]= 0.4x - 0.8 = 0.4(8) - 0.8 = 3.2 - 0.8 = 2.4[/latex]

Therefore, the solution is [latex]x = 8[/latex].

Note: For the rest of the examples in this section, we will not show the verification by substitution step.

Example 7.3-f: Solving Equations Using All the Properties

Solve the following equations by using the properties of equality, and express the answer as a fraction in its lowest terms, or as a mixed number, wherever applicable:

• [latex]8x + 7 - 3x = -6x - 15 + x[/latex]
• [latex]2(3x - 7) = 28 - 3(x + 1)[/latex]
• [latex]\displaystyle{\frac{1}{4}(x + \frac{2}{3}) = \frac{1}{2}(x - 3) + x}[/latex]
• [latex]0.45(2x + 3) - 2.55 = 0.6(3x - 5)[/latex]
• [latex]\displaystyle{\frac{x + 2}{3} = \frac{5 - 2x}{7}}[/latex]
• [latex]8x + 7 - 3x = -6x - 15 + x[/latex] Grouping like terms on both sides, [latex]8x - 3x + 7 = -6x + x - 15[/latex] [latex]5x + 7 = -5x - 15[/latex] Adding 5 to both sides, [latex]5x + 5x + 7 = -5x + 5x - 15[/latex] [latex]10x + 7 = -15[/latex] Subtracting 7 from both sides, [latex]10x + 7 - 7 = -15 - 7[/latex] [latex]10x = -22[/latex] Dividing both sides by 10 , [latex]\displaystyle{\frac{10x}{10} = -\frac{22}{10}}[/latex] [latex]\displaystyle{x = -\frac{11}{5} = -2\frac{1}{5}}[/latex]
• [latex]2(3x - 7) = 28 - 3(x + 1)[/latex] Expanding both sides,[latex]6x - 14 = 28 - 3x - 3[/latex]   Grouping like terms,[latex]6x - 14 = 28 - 3 - 3x[/latex] [latex]6x - 14 = 25 - 3x[/latex] Adding [latex]3x[/latex] to both sides,[latex]6x + 3x - 14 = 25 - 3x + 3x[/latex] [latex]9x - 14 = 25[/latex] Adding 14 to both sides, [latex]9x - 14 + 14 = 25 + 14[/latex] [latex]9x = 39[/latex] Dividing both sides by 9 ,[latex]\displaystyle{\frac{9x}{9} = \frac{39}{9}}[/latex] [latex]\displaystyle{x = \frac{13}{3} = 4\frac{1}{3}}[/latex]
• [latex]\displaystyle{\frac{1}{4}(x + \frac{2}{3}) = \frac{1}{2}(x - 3) + x}[/latex] Expanding both sides, [latex]\displaystyle{\frac{1}{4}x + \frac{1}{6} = \frac{1}{2}x - \frac{3}{2} + x}[/latex] Multiplying each term by the LCD 12 , [latex]\displaystyle{12\left(\frac{1}{4}x\right) + 12\left(\frac{1}{6}\right) = 12\left(\frac{1}{2}x\right) - 12\left(\frac{3}{2}\right) + 12(x)}[/latex] [latex]3x + 2 = 6x - 18 + 12x[/latex] Grouping like terms,[latex]3x + 2 = 6x + 12x - 18[/latex] [latex]3x + 2 = 18x - 18[/latex] Interchanging the LS and RS using the Symmetric Property to have the larger x term on the LS, [latex]18x 18 = 3x + 2[/latex]   Subtracting [latex]3x[/latex] from both sides, [latex]18x - 3x - 18 = 3x - 3x + 2[/latex] [latex]15x - 18 = 2[/latex] Adding 18 to both sides, [latex]15x - 18 + 18 = 2 + 18[/latex] [latex]15x = 20[/latex] Dividing both sides by 15 , [latex]\displaystyle{\frac{15x}{15} = \frac{20}{15}}[/latex][latex]\displaystyle{x = \frac{4}{3} = 1\frac{1}{3}}[/latex]
• [latex]0.45(2x + 3) - 2.55 = 0.6(3x - 5)[/latex] Expanding both sides, [latex]0.90x + 1.35 - 2.55 = 1.8x - 3.0[/latex] Greatest number of decimal places is 2 (i.e., hundredths). Multiplying all the terms by [latex]10^2 = 100[/latex],   [latex]100(0.90x) + 100(1.35) - 100(2.55) = 100(1.8x) - 100(3.0)[/latex] [latex]90x + 135 - 255 = 180x - 300[/latex] Grouping like terms,[latex]90x 120 = 180x 300[/latex] Interchanging the LS and RS using the Symmetric Property to have the larger x term on the LS,   [latex]180x - 300 = 90x - 120[/latex] Subtracting [latex]90x[/latex] from both sides,  [latex]180x - 90x - 300 = 90x - 90x - 120[/latex] [latex]90x - 300 = -120[/latex] Adding 300 to both sides,  [latex]90x - 300 + 300 = -120 + 300[/latex] [latex]90x = 180[/latex] Dividing both sides by 90 ,  [latex]\displaystyle{\frac{90x}{90} = \frac{180}{90}}[/latex] [latex]x = 2[/latex]
• [latex]\displaystyle{\frac{x + 2}{3} = \frac{5 - 2x}{7}}[/latex] Cross-multiplying,  [latex]7(x + 2) = 3(5 - 2x)[/latex] Expanding both sides,[latex]7x + 14 = 15 - 6x[/latex] Adding [latex]6x[/latex] to both sides,  [latex]7x + 6x + 14 = 15 - 6x + 6x[/latex] [latex]13x + 14 = 15[/latex] Subtracting 14 from both sides, [latex]13x + 14 - 14 = 15 - 14[/latex] [latex]13x = 1[/latex] Dividing both sides by 13 ,  [latex]\displaystyle{\frac{13x}{13} = \frac{1}{13}}[/latex] [latex]\displaystyle{x = \frac{1}{13}}[/latex]

Steps to Solve Word Problems

Read the entire problem and ensure you understand the situation.

Identify the given information and the question to be answered.

Look for keywords. Some words indicate certain mathematical operations (see Table 7.1).

Choose a variable to represent the unknown(s) and state what that variable represents, including the unit of measure.

Note: For now, if there is more than one unknown, try to identify all the unknowns in terms of one variable, as all the questions in this chapter can be solved with only one variable.

Where necessary, draw a simple sketch to identify the information. This helps with envisioning the question more clearly.

Create an equation (or set of equations) to describe the relationship between the variables and the constants in the question.

Group like terms, isolate the variable and solve for the unknown(s).

State the solution to the given problem.

Example 7.3-g: Solving a Word Problem Using Algebraic Equations

If Harry will be 65 years old in 5 years, how old is he today?

Let Harry’s age today be x years.

Therefore, in 5 years, Harry’s age will be:

[latex]x + 5 = 65[/latex]   Solving for [latex]x[/latex],

[latex]x = 65 - 5 = 60[/latex]

Therefore, Harry is 60 years old today.

Example 7.3-h: Solving a Geometry Problem Using Algebraic Equations

The perimeter of a rectangular garden is 50 metres. The length is 5 metres more than the width. Find the dimensions of the garden.

Hint: Perimeter = 2(length) + 2(width)

Let the width be [latex]w[/latex] metres.

Therefore, the length is (w + 5) metres.

Perimeter = 2(length) + 2(width)

[latex]50 = 2(w + 5) + 2w[/latex]

[latex]50 = 2w + 10 + 2w[/latex]

[latex]2w + 10 + 2w = 50[/latex]

[latex]4w + 10 = 50[/latex]

[latex]4w = 50 - 10[/latex]

[latex]4w = 40[/latex]

[latex]\displaystyle{w = \frac{40}{4}}[/latex]

[latex]w = 10[/latex]

Therefore, the width of the garden is 10 metres and the length is (10 + 5) = 15 metres.

Example 7.3-i: Solving a Finance Problem Using Algebraic Equations

A TV costs $190 more than a Blu-ray player. The total cost of the TV and the Blu-ray player is $688. Calculate the cost of the TV and the cost of the Blu-ray player.

Let the cost of the Blu-ray player be [latex]\$x[/latex].

Therefore, the cost of the TV is [latex]\$(x + 190.00)[/latex].

The total cost is $688.00.

[latex]x + (x + 190.00) = 688.00[/latex]

[latex]x + x + 190.00 = 688.00[/latex]

[latex]2x + 190.00 = 688.00[/latex]

[latex]2x = 688.00 - 190.00[/latex]

[latex]2x = 498.00[/latex]

[latex]\displaystyle{x = \frac{498.00}{2}}[/latex]

[latex]x = \$249.00[/latex]

Therefore, the cost of the Blu-ray player is $249.00 and the cost of the TV is (249.00 + 190.00) = $439.00.

Example 7.3-j: Solving a Mixture Problem Using Algebraic Equations

How many litres of water need to be added to 30 litres of a 15% saline solution to make a saline solution that is 10% saline?

From the last column, we get the equation for the saline mix. The number of litres of saline in the 15% solution must be the same as the number of litres in the final 10% solution, as only water is being added, which does not contribute any additional saline to the solution. Therefore,

[latex]4.5 = 0.10 \times (30 + x)[/latex]

[latex]4.5 = 3 + 0.10x[/latex]

[latex]1.5 = 0.10x[/latex]

[latex]x = 15[/latex]

Therefore, 15 litres of water need to be added to the 15% saline solution to make the solution 10% saline.

7.3 Exercises

Answers to the odd-numbered problems are available at the end of the textbook .

For problems 1 to 8, simplify and evaluate the expressions.

• The sum of a number and six is ten.
• A number decreased by fifteen is five.
• Six times a number is seventy-two.
• The product of a number and four is twenty-eight.
• A number divided by five is four.
• A number divided by three is three.
• Two-thirds of a number is twelve.
• Two-fifths of a number is six.

For problems 9 to 30, solve the algebraic equations using the properties of equality, and express the answer as a fraction in its lowest terms or as a mixed number, wherever applicable.

• [latex]x - 20 = 10[/latex]
• [latex]x - 25 = 17[/latex]
• [latex]22 = 40 - x[/latex]
• [latex]54 = 23 - x[/latex]
• [latex]21 + x = 4[/latex]
• [latex]50 + x = 45[/latex]
• [latex]16 + x = 22[/latex]
• [latex]12 + x = 38[/latex]
• [latex]11x + 4 = 17[/latex]
• [latex]7x - 16 = 22[/latex]
• [latex]\displaystyle{x - \frac{4}{5} = \frac{3}{5}}[/latex]
• [latex]\displaystyle{x - \frac{1}{6} = 1}[/latex]
• [latex]\displaystyle{\frac{10}{15} = x - \frac{4}{3}}[/latex]
• [latex]\displaystyle{\frac{x}{7} + 15 = 24}[/latex]
• [latex]\displaystyle{x + \frac{2}{5} = \frac{1}{4}}[/latex]
• [latex]\displaystyle{2x - \frac{2}{3} = \frac{5}{6}}[/latex]
• [latex]4x = 24[/latex]
• [latex]\displaystyle{\frac{2x}{3} + 1 = \frac{5x}{8} + 2}[/latex]
• [latex]\displaystyle{\frac{x}{2} - \frac{1}{6} = \frac{1}{3} + \frac{3x}{5}}[/latex]
• [latex]\displaystyle{\frac{7x}{8} - 4 = \frac{x}{4} + 6}[/latex]
• [latex]\displaystyle{\frac{8x}{3} - 5 = \frac{x}{3} + 2}[/latex]

For problems 31 to 54, solve the algebraic equations using the properties of equality, and round the answer to 2 decimal places, wherever applicable.

• [latex]10y - 0.09y = 17[/latex]
• [latex]x + 0.13x = 70[/latex]
• [latex]0.3x - 3.2 = 0.4 - 0.6x[/latex]
• [latex]4 + 0.2x = 0.7x - 0.5[/latex]
• [latex]0.4x - 1.38 = 0.3x - 1.2[/latex]
• [latex]1.2 - 0.7x = 2.7 - 0.5x[/latex]
• [latex]0.43x + 0.25 = 0.29x - 0.03[/latex]
• [latex]0.6x - 1.2 = 0.9 - 1.5x[/latex]
• [latex]x - 2 - 4x = -3x - 8 + 5x[/latex]
• [latex]4(2x - 5) = 32 - 4(x - 2)[/latex]
• [latex](4 + 6)(2 + 4x) = 45 - 2.5(x + 3)[/latex]
• [latex](5 + 0.5x)(1 + 3) = -1.2(2x + 4) + 25[/latex]
• [latex]15 + 5(x - 10) = 3(x - 1)[/latex]
• [latex]2(x - 3) + 3(x - 5) = 4[/latex]
• [latex]4(y + 7) - 2(y - 4) = 3(y - 2)[/latex]
• [latex]8(2y + 4) - 6(3y + 7) = 3y[/latex]
• [latex]\displaystyle{\frac{x - 7}{2} + \frac{x + 2}{3} = 41}[/latex]
• [latex]\displaystyle{\frac{7}{12}(2x + 1) + \frac{3}{4}(x + 1) = 3}[/latex]
• [latex]\displaystyle{\frac{5}{y + 4} = \frac{3}{y - 2}}[/latex]
• [latex]\displaystyle{\frac{3}{x + 1} = \frac{2}{x - 3}}[/latex]
• [latex]\displaystyle{\frac{7}{5x - 3} = \frac{5}{4x}}[/latex]
• [latex]\displaystyle{\frac{5}{y + 2} = \frac{3}{y}}[/latex]

For problems 55 to 76, solve the word problems using algebraic equations.

• If three times a number plus twenty is seven times that number, what is the number?
• Fifteen less than three times a number is twice that number. What is the number?
• A 25-metre-long wire is cut into two pieces. One piece is 7 metres longer than the other. Find the length of each piece.
• A 9-metre-long pipe is cut into two pieces. One piece is twice the length of the other piece. Find the length of each piece.
• $500 is shared between Andy and Becky. Andy’s share is $150 less than Becky’s share. Calculate the amount of each of their shares.
• $200 is shared between Bill and Ann. Ann’s share is $50 more than Bill’s share. Calculate the size of each of their shares.
• Movie tickets that were sold to each child were $3 cheaper than those sold to each adult. If a family of two adults and two children paid $34 to watch a movie at the cinema, what was the price of each adult ticket and each child ticket?
• Giri had twice the number of quarters (25 cents) in his bag than dimes (10 cents). If he had a total of 54 coins, how many of them were quarters? What was the total dollar value of these coins?
• A square garden, with sides of length x metres, is widened by 4 metres and lengthened by 3 metres. Write the equation for the area (A) of the expanded garden. If each side was originally 10 metres in length, find the new area. (Hint: Area of a Rectangle = Length × Width)
• A square garden, with sides of length x metres, has had its width reduced by 4 metres and its length reduced by 2 metres. Write the equation for the Area (A) of the smaller garden. If each side was originally 20 metres in length, find the new area.
• Aran bought a shirt and a pair of pants for $34.75. The pair of pants cost $9.75 more than the shirt. Calculate the cost of the shirt.
• Mythili bought a schoolbag and a toy for $30.45. The school bag cost $5.45 more than the toy. Calculate the cost of the school bag.
• Sam is paid $720 a week. He worked 9 hours of overtime last week and he received $954. Calculate his overtime rate per hour.
• Lisa is paid $840 a week. Her overtime rate is $28 per hour. Last week she received $1,036. How many hours of overtime did she work last week?
• The sum of the three angles of any triangle is 180°. If [latex]3x[/latex], [latex]7x[/latex], and [latex]8x[/latex] are the measures of the three angles of a triangle, calculate the measure of each angle of the triangle.
• The sum of the three angles of any triangle is 180°. If [latex]3x[/latex], [latex]4x[/latex], and [latex]5x[/latex] are the measures of the three angles of a triangle, calculate the measure of each angle of the triangle.
• The perimeter of a triangle is the sum of the lengths of the three sides of the triangle. The perimeter of a triangle with sides [latex]x[/latex] cm, [latex](x + 10)[/latex] cm, and [latex]2x[/latex] cm is 70 cm. Calculate the length of each side of the triangle.
• The perimeter of a triangle is the sum of the lengths of the three sides of the triangle. The perimeter of a triangle with sides [latex]x + 10[/latex], [latex]2x + 10[/latex], and [latex]3x[/latex] is 110 cm. Calculate the length of each side of the triangle.
• After completing a weight-loss program, a patient weighs 160 lb. His dietician observes that the patient has lost 15% of his original weight. What was the patient’s starting weight?
• A beaker in a chemistry lab contains 3 litres of water. While conducting an experiment, the chemistry professor removes three-fifths of the water from the beaker. He then adds three-fifths of the remaining volume to the beaker. How much water is left in the beaker at the end of the experiment?
• A researcher wants to make 4 L of a 7% acid solution. She has a beaker of 15% acid solution in stock. How much of the 15% solution does she need to use and how much water must she add in order to prepare her desired solution?
• A chemist wants to make a 10% acid solution. She has 5 L of 25% acid solution. How many litres of water should she add to the 25% solution in order to prepare her desired solution?

Unless otherwise indicated, this chapter is an adaptation of the eTextbook  Foundations of Mathe matics  (3 rd  ed.) by Thambyrajah Kugathasan, published by  Vretta-Lyryx Inc ., with permission. Adaptations include supplementing existing material and reordering chapters.

Fundamentals of Business Math Copyright © 2023 by Lisa Koster and Tracey Chase is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Algebraic Sentences Problems

Algebraic sentences word problems.

An algebraic sentence when written in equation form involves algebraic expressions (which contain variables such as letters in the alphabet), constants, and an equal symbol. Each algebraic sentence may contain a combination of algebraic expressions and constants, or with just two or more algebraic expressions. Almost always, the word “is” in an algebraic sentence denotes the symbol of equality.

In our example above, the algebraic sentence, “ Five more than twice a number is forty-three “, is translated and written into its equation form: [latex]2x + 5 = 43[/latex].

But before we delve into solving word problems that involve algebraic sentences, it’s crucial that we become familiar with how to translate and write algebraic expressions.

Algebraic Expressions

Learning how to write and translate algebraic expressions is the foundation in writing algebraic sentences. Eventually, we will use this knowledge to write algebraic equations where we solve for the value of the unknown variable.

What is an algebraic expression?

Think of an algebraic expression as the equivalent of a phrase in the English language. It does not convey a complete thought but is an important building block in constructing a sentence. Algebraic expressions consist of numbers, variables, and arithmetic operations.

Let’s take a quick look at some math phrases that were translated and written into algebraic expressions.

• the sum of a number and [latex]8[/latex] [latex]\large{\,\,\, \to \,\,\,\, {\color{red}{c + 8}}}[/latex]
• [latex]3[/latex] less than a number [latex]\large{\,\,\, \to \,\,\,\, {\color{red}{y – 3}}}[/latex]
• the product of [latex]45[/latex] and [latex]m[/latex] [latex]\large{\,\,\, \to \,\,\,\,{\color{red}{45m}}}[/latex]
• a number divided by [latex]2[/latex] [latex]\large{\,\,\, \to \,\,\,\,\Large {\color{red}{x \over 2}}}[/latex]

Translating and Writing Algebraic Sentences

Once you know how to translate math phrases into algebraic expressions, it’ll be easy for you to translate and write algebraic sentences in an equation form as well.

For instance, how do you write “ the difference of 16 and k is seven ” into an algebraic equation?

Let’s deconstruct this algebraic sentence.

You may notice that we translated “the difference of [latex]16[/latex] and [latex]k[/latex]” into an algebraic expression, [latex]16-k[/latex], then used the equal symbol ([latex]=[/latex]) in place of the word “is”.

As I mentioned at the beginning of this lesson, the word “is” in an algebraic sentence, most of the time, signifies the equality symbol which is the case in this example.

Therefore, we can write this algebraic sentence in equation form as [latex]16 – k = 7[/latex].

Now that we are confident in translating algebraic sentences and writing them in an equation format, it’s time for us to take one step further. We will not only translate and write algebraic sentences into algebraic equations but also proceed to solve them.

Examples of Algebraic Sentences Word Problems

The main key when solving word problems with algebraic sentences is to accurately translate the algebraic expressions then set up and write each algebraic equation correctly. In doing so, we can ensure that we are solving the right equation and as a result, will get the correct answer for each word problem.

Example 1: Six more than seven times a number is thirty-four. Find the number.

First, let’s deconstruct the algebraic sentence. It’s important that we identify and separate the algebraic expressions from the constants as well as determine if the problem suggests equality between the terms.

For the unknown value, we’ll use [latex]\large{x}[/latex] as our variable.

Note: Since addition is commutative, changing the order of the addends on the left side of the equation does not change the sum. Therefore, we may also write the algebraic expression as [latex]7x+6[/latex] or the algebraic equation as [latex]7x + 6 = 34[/latex] instead.

However, for our discussion, we will use [latex]6 + 7x = 34[/latex] as our equation.

The original problem asks us to find the number which in this case is [latex]\large{x}[/latex]. So our next step is to solve for [latex]\large{x}[/latex] in our equation, [latex]6 + 7x = 34[/latex].

Now, we’ll evaluate the value of [latex]\large{x = 4}[/latex] to verify if the number we found satisfies the original algebraic sentence.

Remember that we are asked to find the identity of “the number” in our algebraic sentence and NOT the value of the variable [latex]\large{x}[/latex]. Therefore, it will be incorrect to say that [latex]\large{x=4}[/latex] is the answer. This is a common mistake that we always need to pay attention to.

We’ll replace the variable [latex]\large{x}[/latex] with the number [latex]4[/latex] to see if the algebraic expression on the left side of the equation also results to [latex]34[/latex].

Yes, it does! This means that number 4 is the answer .

Example 2: The difference between three times a number and five is sixteen. Find the number.

Right away, the word “difference” in our algebraic sentence gives us a clue that we will be using the subtraction operation. But, unlike, in addition, the order of the terms within an expression matters in subtraction. So we have to make sure that the terms in our algebraic expression are set up in the correct order.

Another keyword is “times”, which suggests that [latex]3[/latex] is being multiplied to a number whose value is currently unknown.

This time, let’s use [latex]\large{g}[/latex] as our variable. Start by translating the algebraic expression correctly then continue to write the equation.

Now that we have our equation, let’s find out what the unknown value is by solving for the variable, [latex]\large{g}[/latex].

As discussed in our first example, it is important that we verify if the result of our solution makes the algebraic equation true. For this one, I will leave it up to you to evaluate the value of [latex]\large{g = 7}[/latex]. Remember to replace the unknown value of the variable [latex]\large{g}[/latex] with the number [latex]7[/latex] to see if the left side of the equation is also equal to [latex]16[/latex].

Since the original algebraic sentence requires us to find the number, then the answer is number 7 .

Example 3: A number decreased by half of the number is four. Find the number.

This algebraic sentence is quite interesting because we don’t just have one unknown value, but two! First, we have the “number” (the unknown) then the “half of the number”, which means one-half of the unknown.

The keyword “half of” also indicates multiplying something by one-half while the “decreased by” tells us that we will be subtracting one term from the other.

To organize our thoughts, let’s deconstruct this algebraic sentence into its meat and potatoes.

Being able to break apart our algebraic sentence into its basic parts allows us to read the sentence thoroughly and understand the relationship between its quantities.

After setting up our algebraic equation, our next step is to solve it for [latex]\large{m}[/latex].

We need to evaluate the value of [latex]\large{m = 8}[/latex] to check if the number we got makes our algebraic equation true.

Great! The values on both sides of the equation are equal to each other. Therefore, the number 8 is the correct answer to our original algebraic sentence.

Example 4: Four times the sum of twice a number and six is thirty-two. Find the number.

Looking closely, we see a few keywords that would help us in translating this algebraic sentence into an equation.

• times – means that we’ll be multiplying [latex]4[/latex] by the quantity, “sum of twice a number and six”
• sum – means that we need to add the terms, “ twice a number ” and six
• twice – means that a number (the unknown value) is multiplied by [latex]2[/latex]

With these in mind, let’s write our algebraic equation.

Notice that we used the variable [latex]\large{d}[/latex] in our equation to stand for our unknown value. Let’s now proceed and solve for [latex]\large{d}[/latex] and afterward, check if the value we get indeed makes the equation true.

Evaluate the value of [latex]\large{d = 1}[/latex]:

Looks like everything checks out, so the answer to our algebraic sentence is the number 1 .

Example 5: Two-thirds of the sum of three times a number and six is ten. What is the number?

This problem involves a fraction and an algebraic expression as you can tell. The keyword “of” indicates multiplication, so it tells us that we need to multiply the fraction [latex]\large{2 \over 3}[/latex] by the sum of the two given quantities (“three times a number” and six).

Let’s move on and write our algebraic equation. We’ll use the variable [latex]\large{y}[/latex] as the placeholder for our “number” whose value is currently unknown.

Awesome! We are able to translate our algebraic sentence into an equation. It’s time for us to solve for [latex]\large{y}[/latex] then I’ll leave it up to you to do a check if the number we find as the value of [latex]\large{y}[/latex] makes the algebraic equation true.

Once you evaluate [latex]\large{y = 3}[/latex], you’ll see that the answer to our word problem is indeed the number 3 .

Example 6: Twice the difference of a number and three is four more than the number. Find the number.

We have an example here that is a little different from the word problems we’ve covered so far. In this algebraic sentence, both sides of the equation contain an algebraic expression. However, the keywords present will help us translate it correctly into an equation so there’s nothing to worry about.

• twice – means that we will multiply the quantity (difference of a number and three) by [latex]2[/latex]
• difference – tells us to use the subtraction operation between our unknown value (“number”) and three
• more than – means that we need to add four to our unknown value

Let’s solve for our unknown value, [latex]\large{a}[/latex], then verify that our result makes the algebraic equation true.

Evaluate the value of [latex]\large{a = 10}[/latex]:

Perfect! The value we got for [latex]\large{a}[/latex] which is [latex]10[/latex], made our equation equal on both sides. Thus, the answer is the number 10 .

You may also be interested in these related math lessons or tutorials:

Algebraic Expressions Worked Examples

Algebraic Expressions and Word Problems

Related Topics: More Lessons for Grade 7 Math Worksheets

Examples, solutions, videos, worksheets, games and activities to help Algebra 1 or grade 7 students learn how to write algebraic expressions from word problems.

Beginning Algebra & Word Problem Steps

• Name what x is.
• Define everything in the problem in terms of x.
• Write the equation.
• Solve the equation.
• Kevin’s age is 3 years more than twice Jane’s age. The sum of their ages is 39. How old is Kevin and Jane?
• The difference between two numbers is 7. Find the two numbers if the larger number is three times the smaller.
• Mary and Jim collect baseball cards, Mary has 5 more than 3 times as many cards as Jim. The total number of cards they both have is 253. How many cards does Mary have?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Simple Algebra Problems – Easy Exercises with Solutions for Beginners

JUMP TO TOPIC

Understanding Algebraic Expressions

Breaking down algebra problems, solving algebraic equations, tackling algebra word problems, types of algebraic equations, algebra for different grades.

For instance, solving the equation (3x = 7) for (x) helps us understand how to isolate the variable to find its value.

I always find it fascinating how algebra serves as the foundation for more advanced topics in mathematics and science. Starting with basic problems such as ( $(x-1)^2 = [4\sqrt{(x-4)}]^2$ ) allows us to grasp key concepts and build the skills necessary for tackling more complex challenges.

So whether you’re refreshing your algebra skills or just beginning to explore this mathematical language, let’s dive into some examples and solutions to demystify the subject. Trust me, with a bit of practice, you’ll see algebra not just as a series of problems, but as a powerful tool that helps us solve everyday puzzles.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• -x+3\gt 2x+1
• (x+5)(x-5)\gt 0
• 10^{1-x}=10^4
• \sqrt{3+x}=-2
• 6+11x+6x^2+x^3=0
• factor\:x^{2}-5x+6
• simplify\:\frac{2}{3}-\frac{3}{2}+\frac{1}{4}
• x+2y=2x-5,\:x-y=3
• How do you solve algebraic expressions?
• To solve an algebraic expression, simplify the expression by combining like terms, isolate the variable on one side of the equation by using inverse operations. Then, solve the equation by finding the value of the variable that makes the equation true.
• What are the basics of algebra?
• The basics of algebra are the commutative, associative, and distributive laws.
• What are the 3 rules of algebra?
• The basic rules of algebra are the commutative, associative, and distributive laws.
• What is the golden rule of algebra?
• The golden rule of algebra states Do unto one side of the equation what you do to others. Meaning, whatever operation is being used on one side of equation, the same will be used on the other side too.
• What are the 5 basic laws of algebra?
• The basic laws of algebra are the Commutative Law For Addition, Commutative Law For Multiplication, Associative Law For Addition, Associative Law For Multiplication, and the Distributive Law.

algebra-calculator

• Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series. Over the next few weeks, we'll be showing how Symbolab...

Please add a message.

Message received. Thanks for the feedback.

Grade 7 Mathematics Module: Solving Problems Involving Algebraic Expressions

This Self-Learning Module (SLM) is prepared so that you, our dear learners, can continue your studies and learn while at home. Activities, questions, directions, exercises, and discussions are carefully stated for you to understand each lesson.

Each SLM is composed of different parts. Each part shall guide you step-by-step as you discover and understand the lesson prepared for you.

Pre-tests are provided to measure your prior knowledge on lessons in each SLM. This will tell you if you need to proceed on completing this module or if you need to ask your facilitator or your teacher’s assistance for better understanding of the lesson. At the end of each module, you need to answer the post-test to self-check your learning. Answer keys are provided for each activity and test. We trust that you will be honest in using these.

Please use this module with care. Do not put unnecessary marks on any part of this SLM. Use a separate sheet of paper in answering the exercises and tests. And read the instructions carefully before performing each task.

If you have any questions in using this SLM or any difficulty in answering the tasks in this module, do not hesitate to consult your teacher or facilitator.

In this lesson, we will use algebraic expression to find the values of the things or unknown in real life situations.

This module was designed and written with you in mind. It is here to help you master Solving Problems Involving Algebraic Expressions. The scope of this module permits it to be used in many different learning situations. The language used recognizes the diverse vocabulary level of students. The lessons are arranged to follow the standard sequence of the course. But the order in which you read them can be changed to correspond with the textbook you are now using.

The module is comprised of only one lesson:

• Solving Problems Involving Algebraic Expressions

After going through this module, you are expected to:

• solve problems involving algebraic expressions.

Grade 7 Mathematics Quarter 2 Self-Learning Module: Solving Problems Involving Algebraic Expressions

Can't find what you're looking for.

We are here to help - please use the search box below.

Leave a Comment Cancel reply

Modeling, Functions, and Graphs

Katherine Yoshiwara

Section A.3 Algebraic Expressions and Problem Solving

Example a.17 ..

• Choose a variable for the number of hours Loren works per week.
• Write an algebraic expression for the amount of Loren’s weekly earnings.
• Let \(h\) stand for the number of hours Loren works per week.
• The amount Loren earns is given by \begin{equation*} \blert{6\times (\text{number of hours Loren worked})} \end{equation*} or \(6\cdot h\text{.}\) Loren’s weekly earnings can be expressed as \(6h\text{.}\)

Example A.18 .

Example a.19 ..

• Choose variables to represent the unknown quantities and write an algebraic expression for April’s weekly income in terms of her sales.
• Find April’s income for a week in which she sells $ \(350\) worth of cleaning products.
• Let \(I\) represent April’s total income for the week, and let \(S\) represent the total amount of her sales. We translate the information from the problem into mathematical language as follows: \begin{gather*} \blert{\text{Her income consists of }\$200 . . .\text{ plus }. . . 9\% \text{ of her sales}} \\ I \hphantom{consists of}= \hphantom{of}200 \hphantom{plus+}+ \hphantom{....}0.09 \hphantom{of her}S \end{gather*} Thus, \(I = 200 + 0.09S\text{.}\)
• We want to evaluate our expression from part (a) with \(S = 350\text{.}\) We substitute \(\alert{350}\) for \(S\) to find \begin{equation*} I = 200 + 0.09(\alert{350}) \end{equation*} Following the order of operations, we perform the multiplication before the addition. Thus, we begin by computing \(0.09(350)\text{.}\) \begin{align*} I \amp = 200 + 0.09(350)\amp\amp\blert{\text{Multiply }0.09 (350) \text{ first.}}\\ \amp = 200 + 31.5\\ \amp = 231.50 \end{align*} April’s income for the week is $ \(231.50\text{.}\)

Remark A.20 . Calculator Tip.

Example a.21 ..

• Choose variables to represent the unknown quantities and write an expression for the cost of shipping Andrew’s painting.
• Find the shipping cost if Andrew uses \(2.9\) pounds of packing material.
• Let \(C\) stand for the shipping cost and let \(w\) stand for the weight of the packing material. Andrew must find the total weight of his package first, then multiply by the shipping charge. The total weight of the package is \(8.3 + w\) pounds. We use parentheses around this expression to show that it should be computed first, and the sum should be multiplied by the shipping charge of $ \(2.80\) per pound. Thus, \begin{equation*} C = 2.80(8.3 + w) \end{equation*}
• Evaluate the formula from part (a) with \(w = \alert{2.9}\text{.}\) \begin{align*} C \amp = 2.80(8.3 + \alert{2.9})\amp\amp\blert{\text{Add inside parentheses.}}\\ \amp = 2.80(11.2)\amp\amp\blert{\text{Multiply.}}\\ \amp = 31.36 \end{align*} The cost of shipping the painting is $ \(31.36\text{.}\)

Remark A.22 . Calculator Tip.

Caution a.23 ., subsection problem solving, guidelines for problem solving..

• Identify the unknown quantity and assign a variable to represent it.
• Find some quantity that can be expressed in two different ways and write an equation.
• Solve the equation.
• Interpret your solution to answer the question in the problem.

Subsection Supply and Demand

Example a.24 ..

• We are looking for the equilibrium price, \(p\text{.}\)
• The Coffee Connection would like the demand for its coffee to equal its supply. We equate the expressions for supply and for demand to obtain the equation \begin{equation*} 800 - 60p = 175 + 40p \end{equation*}
• Solve the equation. To get all terms containing the variable, \(p\text{,}\) on one side of the equation, we add \(60p\) to both sides and subtract \(175\) from both sides to obtain \begin{align*} 800 - 60p + \alert{60p - 175} \amp= 175 + 40p + \alert{60p - 175}\\ 625 \amp = 100p \amp\amp\blert{\text{Divide both sides by }100.}\\ 6.25 \amp = p \end{align*}
• The Coffee Connection should charge $ \(6.25\) per pound for its coffee.

Subsection Percent Problems

Percent formula., example a.25 ..

• Let \(c\) represent the cost of the house last year.
• Express the current price of the house in two different ways. During the past year, the price of the house increased by \(4\%\text{,}\) or \(0.04c\text{.}\) Its current price is thus \begin{equation*} \stackrel{\text{Original cost}}{(1)c} + \stackrel{\text{Price increase}}{0.04c} = c(1 + 0.04) = 1.04c \end{equation*} This expression is equal to the value given for current price of the house: \begin{equation*} 1.04c = 100,000 \end{equation*}
• To solve this equation, we divide both sides by \(1.04\) to find \begin{equation*} c = \frac{100,000}{1.04}= 96,153.846 \end{equation*}
• To the nearest cent, the cost of the house last year was $ \(96,153.85\text{.}\)

Caution A.26 .

Subsection weighted averages, example a.27 ..

• Let \(x\) represent the final exam score Kwan needs.
• Kwan’s grade is the weighted average of his test, homework, and final exam scores. \begin{equation*} \frac{\alert{0.50}(84) + \alert{0.20}(92) + \alert{0.30}x}{1.00}=90 \end{equation*} (The sum of the weights is 1.00, or 100% of Kwan’s grade.) Multiply both sides of the equation by \(1.00\) to get \begin{equation*} 0.50(84) + 0.20(92) + 0.30x = 1.00(90) \end{equation*}
• Solve the equation. Simplify the left side first. \begin{align*} 60.4 + 0.30x \amp = 90\amp\amp\blert{\text{Subtract 60.4 from both sides.}}\\ 0.30x \amp = 29.6\amp\amp\blert{\text{Divide both sides by 0.30.}}\\ x \amp = 98.7 \end{align*}
• Kwan needs a score of \(98.7\) on the final exam to earn a grade of \(90\text{.}\)

Weighted Average.

Example a.28 ..

• Let \(p\) represent the number of pounds of LeanMeal needed.
• Simplify each side of the equation, using the distributive law on the right side, then solve. \begin{align*} 7.5 + 0.05p \amp = 4 + 0.08p \amp\amp\blert{\text{Subtract}~4+0.05p~\text{from both sides.}}\\ 3.5 \amp = 0.03p \amp\amp \blert{\text{Divid both sides by}~ 0.03.}\\ p \amp = 116.\overline{6} \end{align*}
• Delbert should mix \(116\frac{2}{3}\) pounds of LeanMeal with \(50\) pounds of JuicyBits to make a mixture that is \(8\%\) fat.

Subsection Section Summary

Subsubsection vocabulary.

• Weighted average
• Equilibrium price
• Algebraic expression
• Evaluate an expression

Subsubsection SKILLS

• Write an algebraic expression: #1–12
• Evaluate an algebraic expression: #1–12
• Write and solve an equation to solve a problem: #13–28

Exercises Exercises A.3

Exercise group..

• Write an expression for Jim’s age in terms of Ana’s age.
• Use your expression to find Jim’s age when ana is 22 years old.
• Write an expression for the total cost of new wheels in terms of the number of wheels Rani must replace.
• Use your expression to find the total cost if Rani must replace 8 wheels.
• Write an expression for the total number of hours Helen must drive in terms of her average driving speed.
• Use your expression to find how long Helen must drive if she averages 45 miles per hour.
• Write an expression for the number of years before Ben gets his inheritance in terms of his present age.
• Use your expression to find how many more years Ben must wait after he turns 13 years old.
• Write an expression for the area of a circle in terms of its radius.
• Find the area of a circle whose radius is 5 centimeters.
• Write an expression for the volume of a sphere in terms of its radius.
• Find the volume of a sphere whose radius is 5 centimeters.
• Write an expression for the total bill for an item (price plus tax) in terms of the price of the item.
• Find the total bill for an item whose price is $490.
• Write an expression for the balance (initial deposit plus interest) in the account after one year in terms of the amount deposited.
• Find the total amount in the account after one year if $350 was deposited.
• Write an expression for the cost of a long-distance phone call in terms of the number of minutes of the call.
• Find the cost of a 27-minute phone call.
• Write an expression for the cost of the flight in terms of Mr. Owlsley’s weight.
• Find the cost if Mr. Owsley weights 162 pounds.
• Write an expression for the amount of rice Juan has consumed in terms of the number of weeks since he bought the bag.
• Write an expression for the amount of rice Juan has left in terms of the number of weeks since he bought the bag.
• Find the amount of rice Juan has left after 6 weeks.
• Write an expression for the elevation that Trinh has lost in terms of the distance she has cycled.
• Write an expression for Trinh’s elevation in terms of the number of miles she has cycled.
• Find Trinh’s elevation after she has cycled 9 miles.
• What are we asked to find in this problem? Assign a variable to represent it.
• Write an expression in terms of your variable for the distance Roger’s wife drives.
• Write an expression in terms of your variable for the distance Roger has cycled.
• Write an equation and solve it.
• Write an expression in terms of your variable for the distance Kate and Julie sailed.
• Write an expression in terms of your variable for the distance their father traveled.
• Write an expression in terms of your variable for the total cost incurred by each machine.
• Write an expression in terms of your variable for the total cost incurred by each refrigerator.
• Assuming the same rate of growth, what do you predict for the population of Midland next year?
• What was the population of Midland last year?
• Assuming the same rate of inflation, what do you predict for the price of a steak dinner next year?
• What did a steak dinner cost last year?
• Write algebraic expressions in terms of your variable for the amounts of each fertilizer the horticulturist uses. Use the table.
• Write expressions for the amount of potash in each batch of fertilizer.
• Write two different expressions for the amount of potash in the mixture. Now write an equation and solve it.
• Write algebraic expressions in terms of your variable for the amounts of each alloy the sculptor uses. Use the table.
• Write expressions for the amount of copper in each batch of alloy.
• Write two different expressions for the amount of copper in the mixture. Now write an equation and solve it.
• Write algebraic expressions for the total amounts Lacy’s pays its managers, its department heads, and its clerks.
• Write two different expressions for the total amount Lacy’s pays in salaries each year.
• Write algebraic expressions for the number of trucks and the number of cars that will meet emission standards.
• Write two different expressions for the total number of vehicles that will meet the standards.

• Math Article

Algebra Problems

Algebra problems are not only based on algebraic expressions but also on various types of equations in Maths where a quantity or variable is unknown to us. Many of us are familiar with the word problem, but are we aware of the fact and problems related to variables and constants? When we say 5 it means a number but what if we say x=5 or 5y or something like that?

This is where algebra came into existence algebra is that branch of mathematics which not only deals with numbers but also variable and alphabets. The versatility of Algebra is very deep and very conceptual, all the non-numeric character represents variable and numeric as constants. Let us solve some problems based algebra with solutions which will cover the syllabus for class 6, 7, 8. Below are some of the examples of algebraic expressions .

For example.

Algebra Word Problems deal with real-time situations and solutions which can be solved using algebra.

Basic Algebra Identities

• (a + b) 2  = a 2 + b 2 + 2ab
• (a – b) 2 = a 2  + b 2 – 2ab
• a 2 – b 2 = (a + b)(a – b)
• a 2 + b 2 = (a + b) 2 – 2ab = (a – b) 2 + 2ab
• a 3 + b 3 = (a + b)(a 2 – ab + b 2 )
• a 3 – b 3 = (a – b)(a 2 + ab + b 2 )
• (a + b) 3 = a 3 + 3ab(a + b) + b 3
• (a – b) 3 = a 3 – 3ab(a – b) – b 3

Algebra problems With Solutions

Example 1: Solve, (x-1) 2 = [4√(x-4)] 2 Solution: x 2 -2x+1 = 16(x-4)

x 2 -2x+1 = 16x-64

x 2 -18x+65 = 0

(x-13) (x-5) = 0

Hence, x = 13 and x = 5.

Algebra Problems for Class 6

In class 6, students will be introduced with an algebra concept. Here, you will learn how the unknown values are represented in terms of variables.  The given expression can be solved only if we know the value of unknown variable. Let us see some examples.

Example: Solve, 4x + 5 when, x = 3.

Solution: Given, 4x + 5

Now putting the value of x=3, we get;

4 (3) + 5 = 12 + 5 = 17.

Example: Give expressions for the following cases:

(i) 12 added to 2x

(ii) 6 multiplied by y

(iii) 25 subtracted from z

(iv) 17 times of m 

(i) 12 + 2x

Algebra Problems for Class 7

In class 7, students will deal with algebraic expressions like x+y, xy, 32x 2 -12y 2 , etc. There are different kinds of the terminology used in case algebraic equations such as;

• Coefficient

Let us understand these terms with an example. Suppose 4x + 5y is an algebraic expression, then 4x and 5y are the terms. Since here the variables used are x and y, therefore, x and y are the factors of 4x + 5y. And the numerical factor attached to the variables are the coefficient such as 4 and 5 are the coefficient of x and y in the given expression.

Any expression with one or more terms is called a polynomial. Specifically, a one-term expression is called a monomial; a two-term expression is called a binomial, and a three-term expression is called a trinomial.

Terms which have the same algebraic factors are like terms . Terms which have different algebraic factors are unlike terms . Thus, terms 4xy and – 3xy are like terms; but terms 4xy and – 3x are not like terms.

Example: Add 3x + 5x

Solution: Since 3x and 5x have the same algebraic factors, hence, they are like terms and can be added by their coefficient.

3x + 5x = 8x

Example: Collect like terms and simplify the expression: 12x 2 – 9x + 5x – 4x 2 – 7x + 10.

Solution: 12x 2 – 9x + 5x – 4x 2 – 7x + 10

= (12 – 4)x 2 – 9x + 5x – 7x + 10

=  8x 2 – 11x + 10

Algebra Problems for Class 8

Here, students will deal with algebraic identities. See the examples.

Example: Solve (2x+y) 2

Solution: Using the identity: (a+b) 2  = a 2 + b 2 + 2 ab, we get;

(2x+y) = (2x) 2 + y 2 + 2.2x.y = 4x 2 + y 2 + 4xy

Example: Solve (99) 2 using algebraic identity.

Solution: We can write, 99 = 100 -1

Therefore, (100 – 1 ) 2

= 100 2 + 1 2 – 2 x 100 x 1  [By identity: (a -b) 2 = a 2 + b 2 – 2ab

= 10000 + 1 – 200

Algebra Word Problems

Question 1: There are 47 boys in the class. This is three more than four times the number of girls. How many girls are there in the class?

Solution: Let the number of girls be x

As per the given statement,

4 x + 3 = 47

4x = 47 – 3

Question 2: The sum of two consecutive numbers is 41. What are the numbers?

Solution: Let one of the numbers be x.

Then the other number will x+1

Now, as per the given questions,

x + x + 1 = 41

2x + 1 = 41

So, the first number is 20 and second number is 20+1 = 21

Linear Algebra Problems

There are various methods For Solving the Linear Equations

• Cross multiplication method
• Replacement method or Substitution method
• Hit and trial method

There are Variety of different Algebra problem present and are solved depending upon their functionality and state. For example, a linear equation problem can’t be solved using a quadratic equation formula and vice verse for, e.g., x+x/2=7 then solve for x is an equation in one variable for x which can be satisfied by only one value of x. Whereas x 2 +5x+6 is a quadratic equation which is satisfied for two values of x the domain of algebra is huge and vast so for more information. Visit BYJU’S. where different techniques are explained different algebra problem.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Advertisement

Deciphering 'Greater Than,' 'Less Than' and 'Equal To' Symbols

• Share Content on Facebook
• Share Content on LinkedIn
• Share Content on Flipboard
• Share Content on Reddit
• Share Content via Email

Greater than, less than , equal to: These terms are mathematical expressions that allow the user to compare two numbers or equations. Once you've become familiar with these terms — and the symbols used to represent them — you'll be able to apply them to various math problems.

What Are Inequality Symbols?

Examples of inequalities, 3 ways to remember greater than and less than symbols, 3 more symbols in math inequalities, how to know when to use greater than or less than signs, greater than and less than symbols in algebraic equations.

The relevant symbols we'll be discussing are defined through negation. Unlike the classic, familiar equal sign (=), which denotes two values that are equal, an inequality symbol tells us that two numbers are not or may not be equal.

There are a few different inequality symbols, but we'll start with the two most common: greater than (>) and less than (<).

These are both about as straightforward as you can get. Greater than means that the number that precedes the symbol (>) is greater than the number that follows it. In the same way, the less than sign (<) means that the number before it is of smaller value than the number after it.

These mathematical expressions are ways to relate meaning without using words. Unlike some of the more advanced math symbols, they can be easily translated to standard English , as the below examples illustrate. Since we read from left to right, substituting the symbols for the words is simple.

When you do the arithmetic in that last example, you can see that 73 + 54 is 127, and 148 – 15 is 133. Thus, 127 < 133 (127 is less than 133).

While the concept is straightforward, if you're not used to the greater than and less than symbols, it can be tricky to recall which one means which. Fortunately, there are some simple, easy-to-remember tricks that can help identify which symbols fits in a given context.

1. The Alligator Method

This trick has a nice visual component. If you think of the greater than or less than symbols as the open mouth of an alligator, you can imagine that the alligator's mouth is going to be open towards the bigger number, as if it's about to eat the greater value. Take the following example:

Here, the alligator mouth is open wide towards the second number, clearly indicating that 83 is greater than 41.

2. The L Method

If you rotate the less than symbol slightly, you get a capital letter "L." This makes the translation into spoken English very easy, since it tells you how to read the inequality.

This example can be read as "15 is less than 33." If you look at the less than sign as a tilted or squashed L, you can see how the sentence ought to read. The second number is the greater number, and the first number is has the smaller value.

3. The Crescendo Method

This method is for the musically inclined. You may have noticed that the greater than and less than symbols resemble the decrescendo and crescendo symbols you'll find on sheet music.

In math, the symbol widens toward the larger value, just as the (de)crescendo symbols widen toward the louder volume.

This example can be read as "612 is less than 680." If you look at the less than sign as you would in music, you remember that the arrow in this direction means the volume will grow louder — or in this case, it will grow larger, towards the bigger number.

There are other symbols that can be used in these kinds of problems. Sometimes, what's called for isn't simply an equal sign, greater than or less than symbol.

1. Greater Than or Equal To: ≥

This sign is used between two numbers that are, as the name suggests, either equal, or where the first number is greater than the second.

Here, we don't know the exact value of y , but the inequality symbol tells us that it can be equal to 1 or any value greater than that.

2. Less Than or Equal To: ≤

On the flip side, this symbol is used between two numbers where the first number is less than or equal to the second.

Again, we don't know the exact value of x , but this sign tells us that it could any number equal to or less than 54.

3. Not Equal To: ≠

This symbol means "not equal to" and can be thought of as the opposite of an equal sign.

If you were to use a traditional equal sign, you'd need to show the same number on each side of the symbol, such as 72 = 72 , or 64 = 64 .

In most of the examples so far, it isn't hard to compare two numbers and decide which sign to use. Sometimes, however, greater than and less than aren't so obvious. Take the example of negative numbers . Is -50 greater than -35?

In this case, it can be helpful to look at, or even to imagine, a number line . In this case, the number of greater value will be the point on the number line that is closer to zero . Since -35 is closer to zero than -50, the inequality would read:

Sometimes, math inequalities will involve variables, such as in algebra. More than one step must be taken to solve the inequality, and you might not get a single value.

But if all that needs to be done is determine which side of the problem has a greater value, you can express the solution using the greater than and less than symbols.

Please copy/paste the following text to properly cite this HowStuffWorks.com article: