distance speed time problem solving

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 8: Rational Expressions

8.8 Rate Word Problems: Speed, Distance and Time

Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance .

[latex]r\cdot t=d[/latex]

For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h)(4h) = 120 km.

The problems to be solved here will have a few more steps than described above. So to keep the information in the problem organized, use a table. An example of the basic structure of the table is below:

The third column, distance, will always be filled in by multiplying the rate and time columns together. If given a total distance of both persons or trips, put this information in the distance column. Now use this table to set up and solve the following examples.

Example 8.8.1

Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?

The distance travelled by both is 30 km. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \\ \hline &&&&\dfrac{6r}{6}&=&\dfrac{24}{6} \\ \\ &&&&r&=&4 \text{ km/h} \end{array}[/latex]

This means that Natasha walks at 4 km/h and Joey walks at 6 km/h.

Example 8.8.2

Nick and Chloe left their campsite by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. After how much time did the campers turn around downstream?

The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:

[latex]\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \hline \dfrac{16t}{16}&=&\dfrac{4}{16}&& \\ \\ t&=&0.25&& \end{array}[/latex]

This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling back.

Example 8.8.3

Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h later on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?

The distance travelled by both is the same. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \hline \dfrac{-60t}{-60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}[/latex]

This means that Terry travels for 8 h and Sally only needs 2 h to catch up to him.

Example 8.8.4

On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the car travel 40 km/h?

[latex]\begin{array}{rrrrrrr} 55(t)&+&40(2.5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ &-&100&&&&-100 \\ \hline &&&&\dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{array}[/latex]

This means that the time spent travelling at 40 km/h was 0.5 h.

Distance, time and rate problems have a few variations that mix the unknowns between distance, rate and time. They generally involve solving a problem that uses the combined distance travelled to equal some distance or a problem in which the distances travelled by both parties is the same. These distance, rate and time problems will be revisited later on in this textbook where quadratic solutions are required to solve them.

For Questions 1 to 8, find the equations needed to solve the problems. Do not solve.

• A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long will it be before the automobiles meet?
• Two automobiles are 276 kilometres apart and start to travel toward each other at the same time. They travel at rates differing by 5 km/h. If they meet after 6 h, find the rate of each.
• Two trains starting at the same station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon will they be 195 kilometres apart?
• Two bike messengers, Jerry and Susan, ride in opposite directions. If Jerry rides at the rate of 20 km/h, at what rate must Susan ride if they are 150 kilometres apart in 5 hours?
• A passenger and a freight train start toward each other at the same time from two points 300 kilometres apart. If the rate of the passenger train exceeds the rate of the freight train by 15 km/h, and they meet after 4 hours, what must the rate of each be?
• Two automobiles started travelling in opposite directions at the same time from the same point. Their rates were 25 and 35 km/h, respectively. After how many hours were they 180 kilometres apart?
• A man having ten hours at his disposal made an excursion by bike, riding out at the rate of 10 km/h and returning on foot at the rate of 3 km/h. Find the distance he rode.
• A man walks at the rate of 4 km/h. How far can he walk into the country and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?

Solve Questions 9 to 22.

• A boy rides away from home in an automobile at the rate of 28 km/h and walks back at the rate of 4 km/h. The round trip requires 2 hours. How far does he ride?
• A motorboat leaves a harbour and travels at an average speed of 15 km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of 5 hours?
• A family drove to a resort at an average speed of 30 km/h and later returned over the same road at an average speed of 50 km/h. Find the distance to the resort if the total driving time was 8 hours.
• As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was 90 km/h, and the average speed returning was 120 km/h. Find the distance between the two airports if the total flying time was 7 hours.
• Sam starts travelling at 4 km/h from a campsite 2 hours ahead of Sue, who travels 6 km/h in the same direction. How many hours will it take for Sue to catch up to Sam?
• A man travels 5 km/h. After travelling for 6 hours, another man starts at the same place as the first man did, following at the rate of 8 km/h. When will the second man overtake the first?
• A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small island. Two hours later, a cabin cruiser leaves the same harbour and travels at an average speed of 16 km/h toward the same island. How many hours after the cabin cruiser leaves will it be alongside the motorboat?
• A long distance runner started on a course, running at an average speed of 6 km/h. One hour later, a second runner began the same course at an average speed of 8 km/h. How long after the second runner started will they overtake the first runner?
• Two men are travelling in opposite directions at the rate of 20 and 30 km/h at the same time and from the same place. In how many hours will they be 300 kilometres apart?
• Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres apart at the end of 4 hours, what is the rate of each?
• Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours, they are 72 kilometres apart. Find the rate of each cyclist.
• Two small planes start from the same point and fly in opposite directions. The first plane is flying 25 km/h slower than the second plane. In two hours, the planes are 430 kilometres apart. Find the rate of each plane.
• On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of 2.5 hours. For how long did the car travel at 40 km/h?
• Running at an average rate of 8 m/s, a sprinter ran to the end of a track and then jogged back to the starting point at an average of 3 m/s. The sprinter took 55 s to run to the end of the track and jog back. Find the length of the track.

Answer Key 8.8

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Real World Algebra by Edward Zaccaro

Algebra is often taught abstractly with little or no emphasis on what algebra is or how it can be used to solve real problems. Just as English can be translated into other languages, word problems can be "translated" into the math language of algebra and easily solved. Real World Algebra explains this process in an easy to understand format using cartoons and drawings. This makes self-learning easy for both the student and any teacher who never did quite understand algebra. Includes chapters on algebra and money, algebra and geometry, algebra and physics, algebra and levers and many more. Designed for children in grades 4-9 with higher math ability and interest but could be used by older students and adults as well. Contains 22 chapters with instruction and problems at three levels of difficulty.

Solving Problems Involving Distance, Rate, and Time

• Pre Algebra & Algebra
• Math Tutorials
• Exponential Decay
• Worksheets By Grade

In math, distance, rate, and time are three important concepts you can use to solve many problems if you know the formula. Distance is the length of space traveled by a moving object or the length measured between two points. It is usually denoted by d in math problems .

The rate is the speed at which an object or person travels. It is usually denoted by  r  in equations . Time is the measured or measurable period during which an action, process, or condition exists or continues. In distance, rate, and time problems, time is measured as the fraction in which a particular distance is traveled. Time is usually denoted by t in equations. 

Solving for Distance, Rate, or Time

When you are solving problems for distance, rate, and time, you will find it helpful to use diagrams or charts to organize the information and help you solve the problem. You will also apply the formula that solves distance, rate, and time, which is  distance = rate x tim e. It is abbreviated as:

There are many examples where you might use this formula in real life. For example, if you know the time and rate a person is traveling on a train, you can quickly calculate how far he traveled. And if you know the time and distance a passenger traveled on a plane, you could quickly figure the distance she traveled simply by reconfiguring the formula.

Distance, Rate, and Time Example

You'll usually encounter a distance, rate, and time question as a word problem in mathematics. Once you read the problem, simply plug the numbers into the formula.

For example, suppose a train leaves Deb's house and travels at 50 mph. Two hours later, another train leaves from Deb's house on the track beside or parallel to the first train but it travels at 100 mph. How far away from Deb's house will the faster train pass the other train?

To solve the problem, remember that d represents the distance in miles from Deb's house and t  represents the time that the slower train has been traveling. You may wish to draw a diagram to show what is happening. Organize the information you have in a chart format if you haven't solved these types of problems before. Remember the formula:

distance = rate x time

When identifying the parts of the word problem, distance is typically given in units of miles, meters, kilometers, or inches. Time is in units of seconds, minutes, hours, or years. Rate is distance per time, so its units could be mph, meters per second, or inches per year.

Now you can solve the system of equations:

50t = 100(t - 2) (Multiply both values inside the parentheses by 100.) 50t = 100t - 200 200 = 50t (Divide 200 by 50 to solve for t.) t = 4

Substitute t = 4 into train No. 1

d = 50t = 50(4) = 200

Now you can write your statement. "The faster train will pass the slower train 200 miles from Deb's house."

Sample Problems

Try solving similar problems. Remember to use the formula that supports what you're looking for—distance, rate, or time.

d = rt (multiply) r = d/t (divide) t = d/r (divide)

Practice Question 1

A train left Chicago and traveled toward Dallas. Five hours later another train left for Dallas traveling at 40 mph with a goal of catching up with the first train bound for Dallas. The second train finally caught up with the first train after traveling for three hours. How fast was the train that left first going?

Remember to use a diagram to arrange your information. Then write two equations to solve your problem. Start with the second train, since you know the time and rate it traveled:

Second train t x r = d 3 x 40 = 120 miles First train t x r = d 8 hours x r = 120 miles Divide each side by 8 hours to solve for r. 8 hours/8 hours x r = 120 miles/8 hours r = 15 mph

Practice Question 2

One train left the station and traveled toward its destination at 65 mph. Later, another train left the station traveling in the opposite direction of the first train at 75 mph. After the first train had traveled for 14 hours, it was 1,960 miles apart from the second train. How long did the second train travel? First, consider what you know:

First train r = 65 mph, t = 14 hours, d = 65 x 14 miles Second train r = 75 mph, t = x hours, d = 75x miles

Then use the d = rt formula as follows:

d (of train 1) + d (of train 2) = 1,960 miles 75x + 910 = 1,960 75x = 1,050 x = 14 hours (the time the second train traveled)

• What Is Velocity in Physics?
• Distance, Rate, and Time Worksheets
• Realistic Math Problems Help 6th-graders Solve Real-Life Questions
• 4th-Grade Math Word Problems
• Circumference of a Circle
• What Speed Actually Means in Physics
• Understanding the Distance Formula
• Help Kids Calculate the Area and Circumference of Circles
• How to Calculate Commissions Using Percents
• How to Derive the Formula for Combinations
• How to Determine the Geometry of a Circle
• Rate of Change Worksheet with Solutions
• Dimensional Analysis: Know Your Units
• Problem Solving in Mathematics
• Perimeter and Surface Area Formulas
• Mathematical Properties of Waves

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

Multiplication and division

Converting units of length (distance)

Rearranging the subject of a formula

Substitution into formulae

This topic is relevant for:

Speed Distance Time

Speed Distance Time Triangle

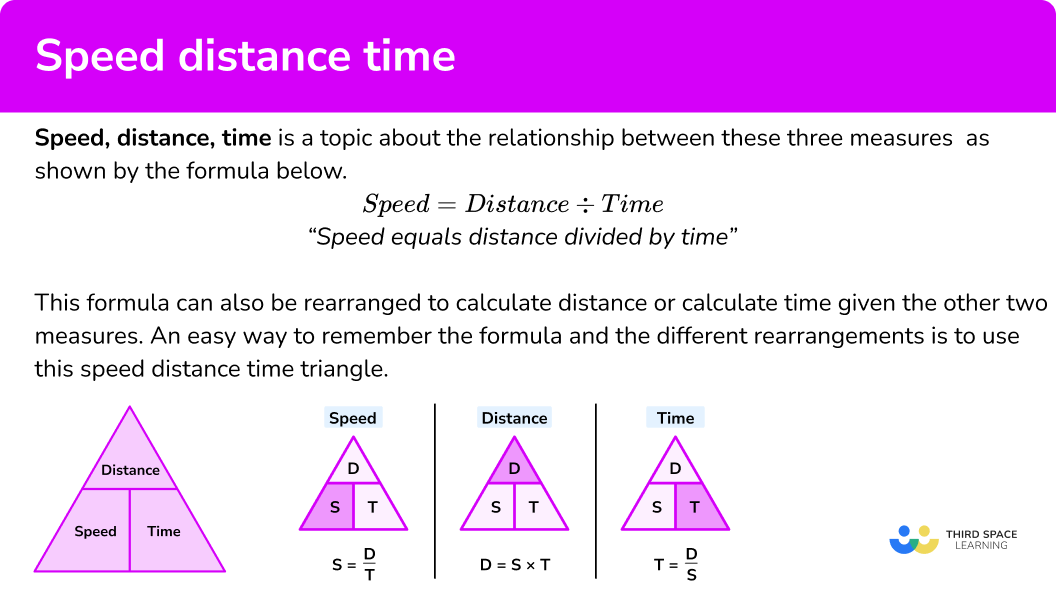
Here we will learn about the speed distance time triangle including how they relate to each other, how to calculate each one and how to solve problems involving them.

There are also speed distance time triangle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is speed distance time?

Speed distance time is the formula used to explain the relationship between speed, distance and time. That is speed = distance ÷ time . Or to put it another way distance divided by speed will give you the time. Provided you know two of the inputs you can work out the third.

For example if a car travels for 2 hours and covers 120 miles we can work out speed as 120 ÷ 2 = 60 miles per hour.

The units of the the distance and time tell you the units for the speed.

What is the speed distance time triangle?

The speed distance time triangle is a way to describe the relationship between speed, distance and time as shown by the formula below.

\textbf{Speed } \bf{=} \textbf{ distance } \bf{\div} \textbf{ time}

“Speed equals distance divided by time”

Let’s look at an example to calculate speed.

If a car travels 66km in 1.5 hours then we can use this formula to calculate the speed.

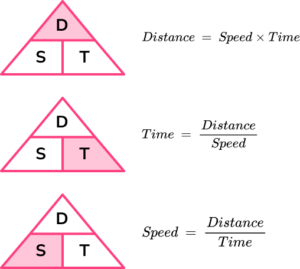
This formula can also be rearranged to calculate distance or calculate time given the other two measures. An easy way to remember the formula and the different rearrangements is to use this speed distance time triangle. 

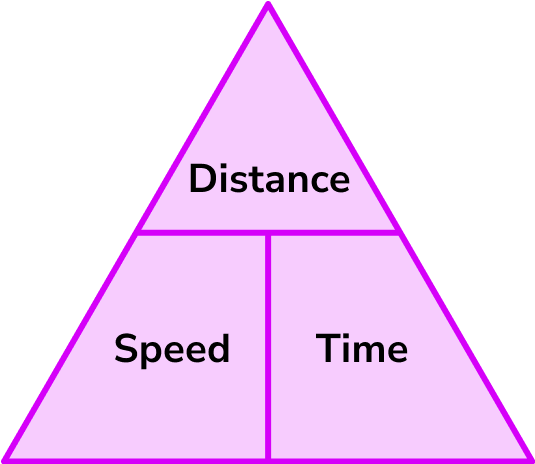
From this triangle we can work out how to calculate each measure: We can ‘cover up’ what we are trying to find and the formula triangle tells us what calculation to do.

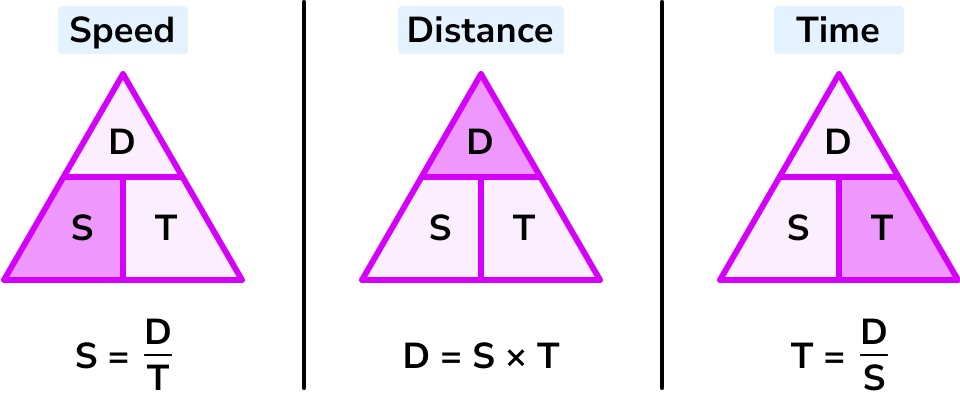
Let’s look at an example to calculate time.

How long does it take for a car to travel 34 miles at a speed of 68 miles per hour?

Let’s look at an example to calculate distance.

What distance does a bike cover if it travels at a speed of 7 metres per second for 50 seconds?

What is the speed distance time formula?

The speed distance time formula is just another way of referring to the speed distance time triangle or calculation you can use to determine speed, time or distance.

• speed = distance ÷ time
• time = distance ÷ speed
• distance = speed x time

Time problem

We can solve problems involving time by remembering the formula for speed , distance and time . 

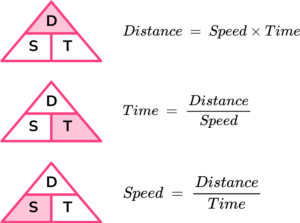
Calculate the time if a car travels at 15 miles at a speed of 36 mph.

Time = distance ÷ speed

Time = 15 ÷ 36 = 0.42 hours

0.42 ✕ 60 = 25.2 minutes

A train travels 42km between two stops at an average speed of 36 km/h. 

If the train departs at 4 pm, when does the train arrive?

Time = 42 ÷ 36 = 1.17 hours

1.17 ✕ 60= 70 minutes = 1 hour 10 minutes.

The average speed of a scooter is 18 km/h and the average speed of a cycle is 10 km/h. 

When both have travelled 99 km what is the difference in the time taken?

Time A = 99 ÷ 18 = 5.5 hours

Time B= 99 ÷ 10 = 9.9 hours

Difference in time = 9.9 – 5.5 = 4.4 hours

4.4 hours = 4 hours and 24 minutes

Units of speed, distance and time

• The speed of an object is the magnitude of its velocity. We measure speed most commonly in metres per second (m/s), miles per hour (mph) and kilometres per hour (km/hr).

The average speed of a small plane is 124mph.

The average walking speed of a person is 1.4m/s.

• We measure the distance an object has travelled most commonly in millimetres (mm), centimetres (cm), metres (m) and kilometres (km).

The distance from London to Birmingham is 162.54km.

• We measure time taken in milliseconds, seconds, minutes, hours, days, weeks, months and years. 

The time taken for the Earth to orbit the sun is 1 year or 365 days. We don’t measure this in smaller units like minutes of hours.

A short bus journey however, would be measured in minutes.

Speed, distance and time are proportional.

If we know two of the measurements we can find the other.

A car drives 150 miles in 3 hours.

Calculate the average speed, in mph, of the car.

Distance = 150 miles

Time = 3 hours

Speed = 150÷ 3= 50mph

Speed, distance, time and units of measure

It is very important to be aware of the units being used when calculating speed, distance and time.

• Examples of units of distance: mm, \ cm, \ m, \ km, \ miles
• Examples of units of time: seconds (sec), minutes, (mins) hours (hrs), days
• Examples of units of speed: metres per second (m/s), miles per hour (mph)

Note that speed is a compound measure and therefore involves two units; a combination of a distance in relation to a time.

When you use the speed distance time formula you must check that each measure  is in the appropriate unit before you carry out the calculation. Sometimes you will need to convert a measure into different units. Here are some useful conversions to remember.

Units of length

Units of time

1 minute = 60 seconds

1 hour = 60 minutes

1 day = 24 hours

Let’s look at an example.

What distance does a bike cover if it travels at a speed of 5 metres per second for 3 minutes?

Note here that the speed involves seconds, but the time given is in minutes. So before using the formula you must change 3 minutes into seconds.

3 minutes = 3\times 60 =180 seconds

Note also that sometimes you may need to convert an answer into different units at the end of a calculation.

Constant speed / average speed

For the GCSE course you will be asked to calculate either a constant speed or an average speed . Both of these can be calculated using the same formula as shown above.

However, this terminology is used because in real life speed varies throughout a journey. You should also be familiar with the terms acceleration (getting faster) and deceleration (getting slower).

Constant speed

A part of a journey where the speed stays the same.

Average speed

A journey might involve a variety of different constant speeds and some acceleration and deceleration. We can use the formula for speed to calculate the average speed over the course of the whole journey.

Average Speed Formula

Average speed is the total distance travelled by an object divided by the total time taken. To do this we can use the formula

Average speed =\frac{Total\, distance}{Total\, time}

If we are calculating an average speed in mph or km/h, we will need to ensure we have decimalised the time before we divide.

How to calculate speed distance time

In order to calculate speed, distance or time:

Write down the values of the measures you know with the units.

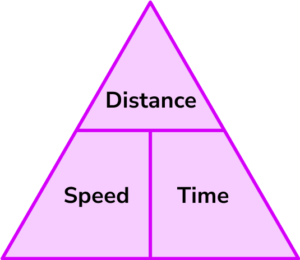
Check that the units are compatible with each other, converting them if necessary.

Substitute the values into the selected formula and carry out the resulting calculation.

Write your final answer with the required units.

Explain how to calculate speed distance time

Speed distance time triangle worksheet

Get your free speed distance time triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on   compound measures

Speed distance time  is part of our series of lessons to support revision on  compound measures . You may find it helpful to start with the main compound measures lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Compound measures
• Mass density volume
• Pressure force area
• Formula for speed
• Average speed formula

Speed distance time triangle examples

Example 1: calculating average speed.

Calculate the average speed of a car which travels 68 miles in 2 hours.

Speed: unknown

Distance: 68 miles

Time: 2 hours

2 Write down the formula you need to use from the speed, distance, time triangle.

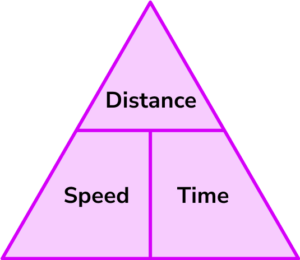
3 Check that the units are compatible with each other, converting them if necessary.

The distance is in miles and the time is in hours. These units are compatible to give the speed in miles per hour.

4 Substitute the values into the formula and carry out the resulting calculation.

5 Write your final answer with the required units.

Example 2: calculating time

A golden eagle can fly at a speed of 55 kilometres per hour. Calculate the time taken for a golden eagle to fly 66 \ km, giving your answer in hours.

Speed: 55 \ km/hour

Distance: 66 \ km

Time: unknown

Write down the formula  you need to use from the speed, distance, time  triangle.

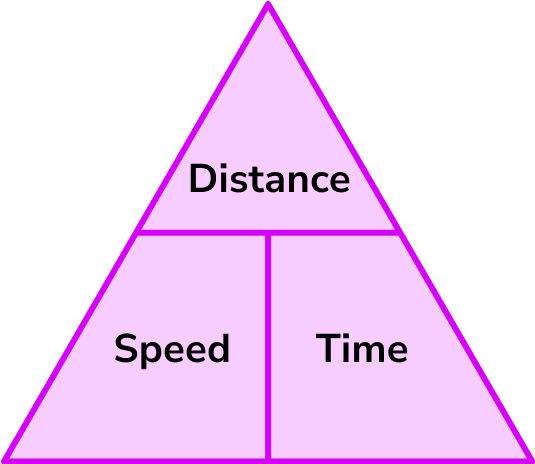
T=\frac{D}{S}

Time = distance \div speed

Speed is in km per hour and the distance is in km , so these are compatible to give an answer for time in hours.

Example 3: calculating distance

Calculate the distance covered by a train travelling at a constant speed of 112 miles per hour for 4 hours.

Speed: 112 \ mph

Distance: unknown

Time: 4 hours

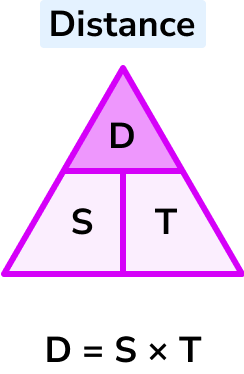
D= S \times T

Distance = speed \times time

Speed is in miles per hour. The time is in hours. These units are compatible to find the distance in miles.

Example 4: calculating speed with unit conversion

A car travels for 1 hour and 45 minutes, covering a distance of 63 miles. Calculate the average speed of the car giving your answer in miles per hour (mph) .

Distance: 63 miles

Time: 1 hour and 45 minutes

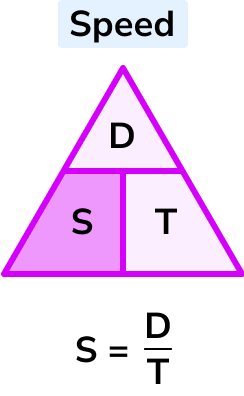
S = \frac{D}{T}

Speed = distance \div time

The distance is in miles . The time is in hours and minutes. To calculate the speed in miles per hour , the time needs to be converted into hours only.

1 hour 45 minutes = 1\frac{3}{4} hours = 1.75 hours

Example 5: calculating time with unit conversion

A small plane can travel at an average speed of 120 miles per hour. Calculate the time taken for this plane to fly 80 miles giving your answer in minutes.

Speed: 120 \ mph

Distance: 80 \ miles

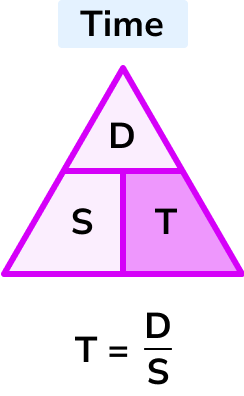
T = \frac{D}{S}

Speed is in miles per hour and the distance is in miles . These units are compatible to find the time in hours.

\frac{2}{3} hours in minutes

\frac{2}{3} \times 60 = 40

Example 6: calculating distance with unit conversion

A train travels at a constant speed of 96 miles per hour for 135 minutes. Calculate the distance covered giving your answer in miles.

Speed: 96 \ mph

Time: 135 minutes

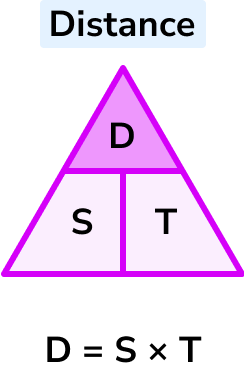
D = S \times T

The speed is in miles per hour , but the time is in minutes. To make these compatible the time needs changing into hours and then the calculation will give the distance in miles .

135 minutes

135 \div 60 = \frac{9}{4} = 2\frac{1}{4} = 2.25

Common misconceptions

• Incorrectly rearranging the formula Speed = distance \div time

Make sure you rearrange the formula correctly. One of the simplest ways of doing this is to use the formula triangle. In the triangle you cover up the measure you want to find out and then the triangle shows you what calculation to do with the other two measures.

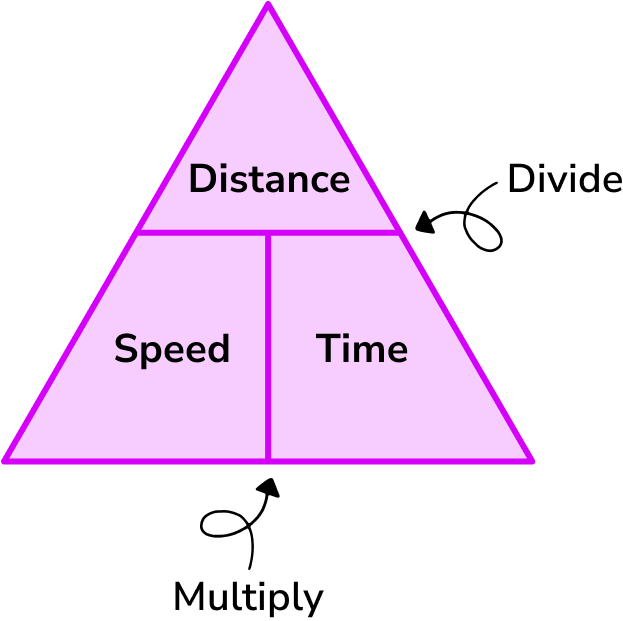
• Using incompatible units in a calculation

When using the speed distance time formula you must ensure that the units of the measures are compatible. For example, if a car travels at 80 \ km per hour for 30 minutes and you are asked to calculate the distance, a common error is to substitute the values straight into the formula and do the following calculation. Distance = speed \times time = 80 \times 30 = 2400 \ km The correct way is to notice that the speed uses hours but the time given is in minutes. Therefore you must change 30 minutes into 0.5 hours and substitute these compatible values into the formula and do the following calculation. Distance = speed \times time = 80 \times 0.5 = 40 \ km

Practice speed distance time triangle questions

1. A car drives 120 miles in 3 hours. Calculate its average speed.

2. A cyclist travels 100 miles at an average speed of 20 \ mph. Calculate how long the journey takes.

3. An eagle flies for 30 minutes at a speed of 66 \ km per hour. Calculate the total distance the bird has flown.

30 minutes = 0.5 hours

4. Calculate the average speed of a lorry travelling 54 miles in 90 minutes. Give your answer in miles per hour (mph).

Firstly convert 90 minutes to hours. 90 minutes = 1.5 hours

5. Calculate the time taken for a plane to fly 90 miles at an average speed of 120 \ mph. Give your answer in minutes.

180 minutes

Convert 0.75 hours to minutes

6. A helicopter flies 18 \ km in 20 minutes. Calculate its average speed in km/h .

Firstly convert 20 minutes to hours. 20 minutes is a third of an hour or \frac{1}{3} hours. \begin{aligned} &Speed = distance \div time \\\\ &Speed =18 \div \frac{1}{3} \\\\ &Speed = 54 \\\\ &54 \ km/h \end{aligned}

Speed distance time triangle GCSE questions

1. A commercial aircraft travels from its origin to its destination in a time of 2 hours and 15 minutes. The journey is 1462.5 \ km.

What is the average speed of the plane in km/hour?

2 hours 15 minutes = 2\frac{15}{60} = 2\frac{1}{4} = 2.25

2. John travelled 30 \ km in 90 minutes.

Nadine travelled 52.5 \ km in 2.5 hours.

Who had the greater average speed?

You must show your working.

90 minutes = 1.5 hours

John = 30 \div 1.5 = 20 \ km/h

Nadine = 52.5 \div 2.5 = 21 \ km/h

Nadine has the greater average speed.

3. The distance from Birmingham to Rugby is 40 miles.

Omar drives from Rugby to Birmingham at 60 \ mph.

Ayushi drives from Rugby to Birmingham at 50 \ mph.

How much longer was Ayushi’s journey compared to Omar’s journey? Give your answer in minutes.

For calculating time in hours for Omar or Ayushi.

For converting hours into minutes for Omar or Ayushi.

For correct final answer of 8 minutes.

Learning checklist

You have now learned how to:

• Use compound units such as speed
• Solve simple kinematic problem involving distance and speed
• Change freely between related standard units (e.g. time, length) and compound units (e.g. speed) in numerical contexts
• Work with compound units in a numerical context

The next lessons are

• Best buy maths
• Scale maths

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Distance, speed, time

In this lesson we will look at three physical quantities: distance , speed , and time .

We have already studied distance in the units of measurement lesson . Simply put, distance is the length from one point to another. (Example: the distance from home to school is 2 kilometers.)

When dealing with long distances, they will mostly be measured in meters and kilometers. Distance is denoted by the Latin letter S . You can also denote by another letter, but the letter S is generally accepted.

Speed is the distance traveled by a body in a unit of time. A unit of time is one hour, one minute, or one second.

Suppose that two students decided to compete and run from the yard to the playground. The distance from the yard to the playground is 100 meters. The first pupil runs in 25 seconds. The second one ran in 50 seconds. Who is the fastest student?

The one who ran the greater distance in 1 second is the fastest. He is said to have more speed. In this case, the speed of the students is the distance they run in 1 second.

To find the speed, you have to divide the distance by the time of movement.  Let's find the speed of the first schoolboy. To do this, divide 100 meters by the time of movement of the first schoolboy, that is, by 25 seconds:

100 m : 25 s = 4

If distance is given in meters and travel time in seconds, speed is measured in meters per second (m/s) . If distance is given in kilometers and travel time in hours, speed is measured in kilometers per hour (km/h) . 

We have distance in meters and time in seconds. So the speed is measured in meters per second (m/s).

100 m : 25 s = 4 (m/s)

So, the speed of the first student is 4 meters per second (m/s).

Now let's find the speed of the second pupil. To do this, divide the distance by the time of movement of the second student, i.e., by 50 seconds:

100 m : 50 s = 2 (m/s)

So the speed of the second student is 2 meters per second (m/s).

The speed of the first student is 4 (m/s) The speed of the second student is 2 (m/s)

4 (m/s) > 2 (m/s)

The speed of the first student is faster. So he got to the playground faster. Speed is denoted by the Latin letter - v .

Sometimes there is a situation where you want to know how long it takes the object to cover a particular distance (travel that distance).

For example, it is 1000 meters from the house to the sports club. We need to get there on a bicycle. Our speed will be 500 meters per minute (500 m/min). How long will it take us to get to the athletic section?

If we will travel 500 meters in one minute, how many such minutes (with five hundred meters each) will be in 1000 meters?

Obviously, we have to divide 1,000 meters by the distance we travel in one minute. That is, 500 meters. The result will be the time in which we will reach a sports club:

1000 : 500 = 2 (min)

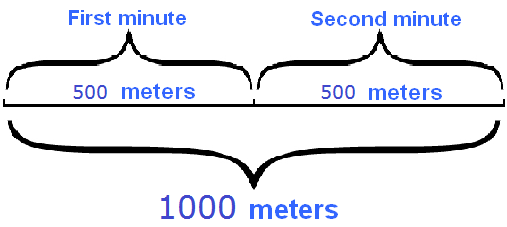
The time of movement is denoted by the small Latin letter - t .

The relationship of speed, time, distance

Speed is usually denoted by the small Latin letter v ,

time of movement by the small letter - t ,

the distance traveled by the small letter - s .

Speed, time and distance are related to each other.

If you know the speed and time of movement, you can find the distance. It is equal to speed multiplied by time:

For example, we left the house and went to the store. It took us 10 minutes to get to the store. Our speed was 50 meters per minute. If we know our speed and time, we can find the distance.

If we walked 50 meters in one minute, how many of these 50 meters will we walk in 10 minutes? Obviously, by multiplying 50 meters by 10, we will determine the distance from the house to the store:

v = 50 (m/min)

t = 10 minutes

s = v × t = 50 × 10 = 500 (meters to the store)

If time and distance are known, you can find the speed:

For example, the distance from home to the school is 900 meters. It took the student 10 minutes to reach the school. What was his speed?

The speed of a schoolboy is the distance he travels in one minute. If he traveled 900 meters in 10 minutes, what distance did he travel in one minute?

To answer this one, you have to divide the distance by the time of the schoolboy's movement:

s = 900 meters

v = s : t = 900 : 10 = 90 (m/min)

If you know the speed and distance, you can find the time:

For example, we have to walk 500 meters from our house to the sport club. Our speed will be 100 meters per minute (100 m/min). How long will it take us to reach it?

If we walk 100 meters in one minute, how many such minutes with 100 meters are in 500 meters?

To answer this question we need to divide 500 meters by the distance we will walk in one minute, that is, by 100. Then we will get the time in which we will reach the sports section:

s = 500 meters

v = 100 (m/minute)

t = s : v = 500 : 100 = 5 (minutes to the sports section)

Video lesson

• Direct and inverse proportions

Add comment

Name (required)

E-mail (required, but will not display)

Notify me of follow-up comments

• You are here:  
• Home >>
• 26. Distance, speed, time
• 2. Basic operations
• 3. Expressions
• 4. Substitutions in expressions
• 5. Place value for beginners
• 6. Multiplication
• 7. Division
• 8. Order of operations
• Basic Laws of Math
• 9. Basic Laws of Math
• 10. Divisors and multiples
• 11. GCD and LCM
• 12. Fractions
• 13. Actions with fractions
• 14. Mixed numbers
• 15. Comparing Fractions
• 16. Units of Measurement
• 17. Ways to use fractions
• 18. Decimals
• 19. Operations with decimals
• 20. Using decimals
• 21. Rounding numbers
• 22. Repeating Decimals
• 23. Unit conversion
• Ratios & Proportion
• 25. Proportion
• 27. Direct and inverse proportions
• 28. What are percentages?
• Additional topic & Number line
• 29. Negative numbers
• 30. Absolute value or modulus
• 31. What is a set?
• 32. Adding and subtracting integers
• 33. Multiplication and division of integers
• Rational numbers
• 34. Rational numbers
• 35. Comparing rational numbers
• 36. Adding and subtracting rational numbers
• 37. Multiplying and dividing rational numbers
• 38. More information about fractions
• 39. Algebraic expressions
• 40. Taking out a common factor
• 41. Expanding brackets
• 42. Simple math problems
• 43. Tasks on fractions
• 44. Percent worksheets for practice
• 45. Speed, distance, time tasks
• 46. Productivity problem
• 47. Statistics in Math
• 48. Basic theory of equation
• 49. Problem solving with equations
• 50. Proportions: exercises
• 51. Systems of linear equations
• 52. Introduction to Inequalities
• 53. Systems of linear inequalities with one variable
• 54. Set Operations | Union | Intersection
• 55. Power with a natural exponent
• 56. Power with integer exponent
• 57. Perimeter, area and volume
• 58. Monomials
• 59. Polynomials
• 60. Reduced multiplication formulas
• 61. Polynomial decomposition
• 62. Dividing polynomials
• 63. Identical transformations of polynomials
• 64. Square root
• 65. Algorithm for extracting the square root
• 66. Quadratic equation
• 67. A quadratic equation with an even second coefficient
• 68. Viette's Theorem
• 69. Factoring a trinomial using decomposition
• 70. More about modules
• 71. Absolute value equations
• 72. Solving equations with module by method of intervals
• 73. Inequalities with module
• 74. Solving inequalities with module by method intervals
• 75. Square root from both parts of an equation
• Functions and graphs
• 76. What is a function?
• 77. Linear function and its graph
• 78. Power function
• 79. Direct Proportion and its Graph
• 80. Function y=x² and its graph
• 81. Function y = √x its properties and graph
• 82. Function y=k*x² its properties and graph
• 83. Function y=k/x its properties and graph
• 84. Graphical solution of equations and inequalities
• coming soon... (new lessons every month)

Forgot password? New user? Sign up

Existing user? Log in

Speed, Distance, and Time

Already have an account? Log in here.

Recommended Course

Classical mechanics.

Hardcore training for the aspiring physicist.

A common set of physics problems ask students to determine either the speed, distance, or travel time of something given the other two variables. These problems are interesting since they describe very basic situations that occur regularly for many people. For example, a problem might say: "Find the distance a car has traveled in fifteen minutes if it travels at a constant speed of \(75 \text {km/hr}\)." Often in these problems, we work with an average velocity or speed, which simplifies the laws of motion used to calculate the desired quantity. Let's see how that works.

Application and Extensions

As long as the speed is constant or average, the relationship between speed , distance , and time is expressed in this equation

\[\mbox{Speed} = \frac{\mbox{Distance}}{\mbox{Time}},\]

which can also be rearranged as

\[\mbox{Time} = \frac{\mbox{Distance}}{\mbox{Speed}}\]

\[\mbox{Distance} = \mbox{Speed} \times \mbox{Time}.\]

Speed, distance, and time problems ask to solve for one of the three variables given certain information. In these problems, objects are moving at either constant speeds or average speeds.

Most problems will give values for two variables and ask for the third.

Bernie boards a train at 1:00 PM and gets off at 5:00 PM. During this trip, the train traveled 360 kilometers. What was the train's average speed in kilometers per hour? In this problem, the total time is 4 hours and the total distance is \(360\text{ km},\) which we can plug into the equation: \[\mbox{Speed} = \frac{\mbox{Distance}}{\mbox{Time}}= \frac{360~\mbox{km}}{4~\mbox{h}} = 90~\mbox{km/h}. \ _\square \]

When working with these problems, always pay attention to the units for speed, distance, and time. Converting units may be necessary to obtaining a correct answer.

A horse is trotting along at a constant speed of 8 miles per hour. How many miles will it travel in 45 minutes? The equation for calculating distance is \[\mbox{Distance} = \mbox{Speed} \times \mbox{Time},\] but we won't arrive at the correct answer if we just multiply 8 and 45 together, as the answer would be in units of \(\mbox{miles} \times \mbox{minute} / \mbox{hour}\). To fix this, we incorporate a unit conversion: \[\mbox{Distance} = \frac{8~\mbox{miles}}{~\mbox{hour}} \times 45~\mbox{minutes} \times \frac{1~\mbox{hour}}{60~\mbox{minutes}} = 6~\mbox{miles}. \ _\square \] Alternatively, we can convert the speed to units of miles per minute and calculate for distance: \[\mbox{Distance} = \frac{2}{15}~\frac{\mbox{miles}}{\mbox{minute}} \times 45~\mbox{minutes} = 6~\mbox{miles},\] or we can convert time to units of hours before calculating: \[\mbox{Distance} = 8~\frac{\mbox{miles}}{\mbox{hour}} \times \frac{3}{4}~\mbox{hours} = 6~\mbox{miles}.\] Any of these methods will give the correct units and answer. \(_\square\)

In more involved problems, it is convenient to use variables such as \(v\), \(d\), and \(t\) for speed, distance, and velocity, respectively.

Alice, Bob, Carly, and Dave are in a flying race!

Alice's plane is twice as fast as Bob's plane. When Alice finishes the race, the distance between her and Carly is \(D.\) When Bob finishes the race, the distance between him and Dave is \(D.\)

If Bob's plane is three times as fast as Carly's plane, then how many times faster is Alice's plane than Dave's plane?

Albert and Danny are running in a long-distance race. Albert runs at 6 miles per hour while Danny runs at 5 miles per hour. You may assume they run at a constant speed throughout the race. When Danny reaches the 25 mile mark, Albert is exactly 40 minutes away from finishing. What is the race's distance in miles? \[\] Let's begin by calculating how long it takes for Danny to run 25 miles: \[\mbox{Time} = \frac{\mbox{Distance}}{\mbox{Speed}}= \frac{25~\mbox{miles}}{5~\mbox{miles/hour}}= 5~\mbox{hours}.\] So, it will take Albert \(5~\mbox{hours} + 40~\mbox{minutes}\), or \(\frac{17}{3}~\mbox{hours}\), to finish the race. Now we can calculate the race's distance: \[\begin{align} \mbox{Distance} &= \mbox{Speed} \times \mbox{Time} \\ &= (6~\mbox{miles/hour}) \times \left(\frac{17}{3}~\mbox{hours}\right) \\ &= 34~\mbox{miles}.\ _\square \end{align}\]

A cheetah spots a gazelle \(300\text{ m}\) away and sprints towards it at \(100\text{ km/h}.\) At the same time, the gazelle runs away from the cheetah at \(80\text{ km/h}.\) How many seconds does it take for the cheetah to catch the gazelle? \[\] Let's set up equations representing the distance the cheetah travels and the distance the gazelle travels. If we set distance \(d\) equal to \(0\) as the cheetah's starting point, we have \[\begin{align} d_\text{cheetah} &= 100t \\ d_\text{gazelle} &= 0.3 + 80t. \end{align}\] Note that time \(t\) here is in units of hours, and \(300\text{ m}\) was converted to \(0.3\text{ km}.\) The cheetah catches the gazelle when \[\begin{align} d_\text{cheetah} &=d_\text{gazelle} \\ 100t &= 0.3 + 80t \\ 20t &= 0.3 \\ t &= 0.015~\mbox{hours}. \end{align}\] Converting that answer to seconds, we find that the cheetah catches the gazelle in \(54~\mbox{seconds}\). \(_\square\)

Two friends are crossing a hundred meter railroad bridge when they suddenly hear a train whistle. Desperate, each friend starts running, one towards the train and one away from the train. The one that ran towards the train gets to safety just before the train passes, and so does the one that ran in the same direction as the train.

If the train is five times faster than each friend, then what is the train-to-friends distance when the train whistled (in meters)?

Master concepts like these

Learn more in our Classical Mechanics course, built by experts for you.

Problem Loading...

Note Loading...

Set Loading...

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Algebra Topics  - Distance Word Problems

Algebra topics  -, distance word problems, algebra topics distance word problems.

Algebra Topics: Distance Word Problems

Lesson 10: distance word problems.

/en/algebra-topics/introduction-to-word-problems/content/

What are distance word problems?

Distance word problems are a common type of algebra word problems. They involve a scenario in which you need to figure out how fast , how far , or how long one or more objects have traveled. These are often called train problems because one of the most famous types of distance problems involves finding out when two trains heading toward each other cross paths.

In this lesson, you'll learn how to solve train problems and a few other common types of distance problems. But first, let's look at some basic principles that apply to any distance problem.

The basics of distance problems

There are three basic aspects to movement and travel: distance , rate , and time . To understand the difference among these, think about the last time you drove somewhere.

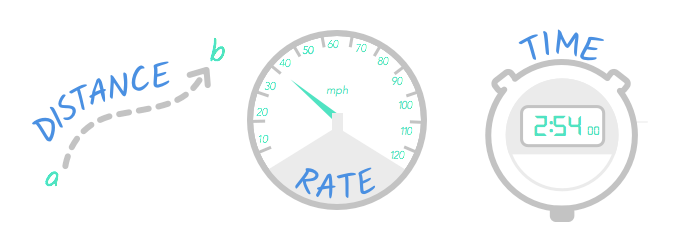
The distance is how far you traveled. The rate is how fast you traveled. The time is how long the trip took.

The relationship among these things can be described by this formula:

distance = rate x time d = rt

In other words, the distance you drove is equal to the rate at which you drove times the amount of time you drove. For an example of how this would work in real life, just imagine your last trip was like this:

• You drove 25 miles—that's the distance .
• You drove an average of 50 mph—that's the rate .
• The drive took you 30 minutes, or 0 .5 hours—that's the time .

According to the formula, if we multiply the rate and time , the product should be our distance.

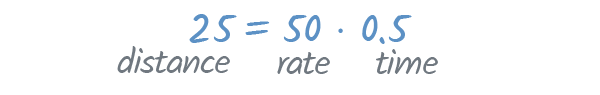
And it is! We drove 50 mph for 0.5 hours—and 50 ⋅ 0.5 equals 25 , which is our distance.

What if we drove 60 mph instead of 50? How far could we drive in 30 minutes? We could use the same formula to figure this out.

60 ⋅ 0.5 is 30, so our distance would be 30 miles.

Solving distance problems

When you solve any distance problem, you'll have to do what we just did—use the formula to find distance , rate , or time . Let's try another simple problem.

On his day off, Lee took a trip to the zoo. He drove an average speed of 65 mph, and it took him two-and-a-half hours to get from his house to the zoo. How far is the zoo from his house?

First, we should identify the information we know. Remember, we're looking for any information about distance, rate, or time. According to the problem:

• The rate is 65 mph.
• The time is two-and-a-half hours, or 2.5 hours.
• The distance is unknown—it's what we're trying to find.

You could picture Lee's trip with a diagram like this:

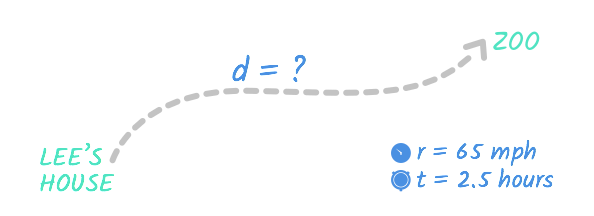
This diagram is a start to understanding this problem, but we still have to figure out what to do with the numbers for distance , rate , and time . To keep track of the information in the problem, we'll set up a table. (This might seem excessive now, but it's a good habit for even simple problems and can make solving complicated problems much easier.) Here's what our table looks like:

We can put this information into our formula: distance = rate ⋅ time .

We can use the distance = rate ⋅ time formula to find the distance Lee traveled.

The formula d = rt looks like this when we plug in the numbers from the problem. The unknown distance is represented with the variable d .

d = 65 ⋅ 2.5

To find d , all we have to do is multiply 65 and 2.5. 65 ⋅ 2.5 equals 162.5 .

We have an answer to our problem: d = 162.5. In other words, the distance Lee drove from his house to the zoo is 162.5 miles.

Be careful to use the same units of measurement for rate and time. It's possible to multiply 65 miles per hour by 2.5 hours because they use the same unit: an hour . However, what if the time had been written in a different unit, like in minutes ? In that case, you'd have to convert the time into hours so it would use the same unit as the rate.

Solving for rate and time

In the problem we just solved we calculated for distance , but you can use the d = rt formula to solve for rate and time too. For example, take a look at this problem:

After work, Janae walked in her neighborhood for a half hour. She walked a mile-and-a-half total. What was her average speed in miles per hour?

We can picture Janae's walk as something like this:

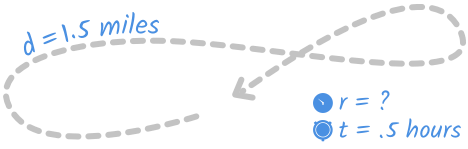
And we can set up the information from the problem we know like this:

The table is repeating the facts we already know from the problem. Janae walked one-and-a-half miles or 1.5 miles in a half hour, or 0.5 hours.

As always, we start with our formula. Next, we'll fill in the formula with the information from our table.

The rate is represented by r because we don't yet know how fast Janae was walking. Since we're solving for r , we'll have to get it alone on one side of the equation.

1.5 = r ⋅ 0.5

Our equation calls for r to be multiplied by 0.5, so we can get r alone on one side of the equation by dividing both sides by 0.5: 1.5 / 0.5 = 3 .

r = 3 , so 3 is the answer to our problem. Janae walked 3 miles per hour.

In the problems on this page, we solved for distance and rate of travel, but you can also use the travel equation to solve for time . You can even use it to solve certain problems where you're trying to figure out the distance, rate, or time of two or more moving objects. We'll look at problems like this on the next few pages.

Two-part and round-trip problems

Do you know how to solve this problem?

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph, then he drove on the interstate at an average of 70 mph. The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

This problem is a classic two-part trip problem because it's asking you to find information about one part of a two-part trip. This problem might seem complicated, but don't be intimidated!

You can solve it using the same tools we used to solve the simpler problems on the first page:

• The travel equation d = rt
• A table to keep track of important information

Let's start with the table . Take another look at the problem. This time, the information relating to distance , rate , and time has been underlined.

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph , then he drove on the interstate at an average of 70 mph . The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

If you tried to fill in the table the way we did on the last page, you might have noticed a problem: There's too much information. For instance, the problem contains two rates— 30 mph and 70 mph . To include all of this information, let's create a table with an extra row. The top row of numbers and variables will be labeled in town , and the bottom row will be labeled interstate .

We filled in the rates, but what about the distance and time ? If you look back at the problem, you'll see that these are the total figures, meaning they include both the time in town and on the interstate. So the total distance is 225 . This means this is true:

Interstate distance + in-town distance = Total distance

Together, the interstate distance and in-town distance are equal to the total distance. See?

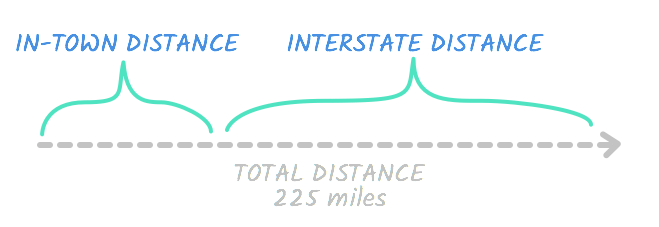
In any case, we're trying to find out how far Bill drove on the interstate , so let's represent this number with d . If the interstate distance is d , it means the in-town distance is a number that equals the total, 225 , when added to d . In other words, it's equal to 225 - d .

We can fill in our chart like this:

We can use the same technique to fill in the time column. The total time is 3.5 hours . If we say the time on the interstate is t , then the remaining time in town is equal to 3.5 - t . We can fill in the rest of our chart.

Now we can work on solving the problem. The main difference between the problems on the first page and this problem is that this problem involves two equations. Here's the one for in-town travel :

225 - d = 30 ⋅ (3.5 - t)

And here's the one for interstate travel :

If you tried to solve either of these on its own, you might have found it impossible: since each equation contains two unknown variables, they can't be solved on their own. Try for yourself. If you work either equation on its own, you won't be able to find a numerical value for d . In order to find the value of d , we'll also have to know the value of t .

We can find the value of t in both problems by combining them. Let's take another look at our travel equation for interstate travel.

While we don't know the numerical value of d , this equation does tell us that d is equal to 70 t .

Since 70 t and d are equal , we can replace d with 70 t . Substituting 70 t for d in our equation for interstate travel won't help us find the value of t —all it tells us is that 70 t is equal to itself, which we already knew.

But what about our other equation, the one for in-town travel?

When we replace the d in that equation with 70 t , the equation suddenly gets much easier to solve.

225 - 70t = 30 ⋅ (3.5 - t)

Our new equation might look more complicated, but it's actually something we can solve. This is because it only has one variable: t . Once we find t , we can use it to calculate the value of d —and find the answer to our problem.

To simplify this equation and find the value of t , we'll have to get the t alone on one side of the equals sign. We'll also have to simplify the right side as much as possible.

Let's start with the right side: 30 times (3.5 - t ) is 105 - 30 t .

225 - 70t = 105 - 30t

Next, let's cancel out the 225 next to 70 t . To do this, we'll subtract 225 from both sides. On the right side, it means subtracting 225 from 105 . 105 - 225 is -120 .

- 70t = -120 - 30t

Our next step is to group like terms—remember, our eventual goal is to have t on the left side of the equals sign and a number on the right . We'll cancel out the -30 t on the right side by adding 30 t to both sides. On the right side, we'll add it to -70 t . -70 t + 30 t is -40 t .

- 40t = -120

Finally, to get t on its own, we'll divide each side by its coefficient: -40. -120 / - 40 is 3 .

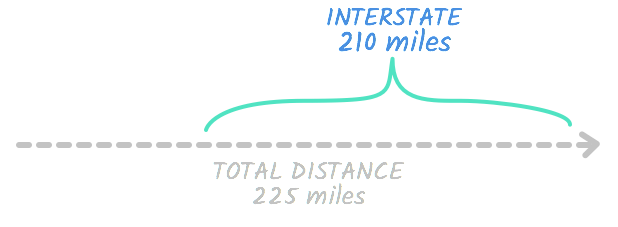
So t is equal to 3 . In other words, the time Bill traveled on the interstate is equal to 3 hours . Remember, we're ultimately trying to find the distanc e Bill traveled on the interstate. Let's look at the interstate row of our chart again and see if we have enough information to find out.

It looks like we do. Now that we're only missing one variable, we should be able to find its value pretty quickly.

To find the distance, we'll use the travel formula distance = rate ⋅ time .

We now know that Bill traveled on the interstate for 3 hours at 70 mph , so we can fill in this information.

d = 3 ⋅ 70

Finally, we finished simplifying the right side of the equation. 3 ⋅ 70 is 210 .

So d = 210 . We have the answer to our problem! The distance is 210 . In other words, Bill drove 210 miles on the interstate.

Solving a round-trip problem

It might have seemed like it took a long time to solve the first problem. The more practice you get with these problems, the quicker they'll go. Let's try a similar problem. This one is called a round-trip problem because it describes a round trip—a trip that includes a return journey. Even though the trip described in this problem is slightly different from the one in our first problem, you should be able to solve it the same way. Let's take a look:

Eva drove to work at an average speed of 36 mph. On the way home, she hit traffic and only drove an average of 27 mph. Her total time in the car was 1 hour and 45 minutes, or 1.75 hours. How far does Eva live from work?

If you're having trouble understanding this problem, you might want to visualize Eva's commute like this:

As always, let's start by filling in a table with the important information. We'll make a row with information about her trip to work and from work .

1.75 - t to describe the trip from work. (Remember, the total travel time is 1.75 hours , so the time to work and from work should equal 1.75 .)

From our table, we can write two equations:

• The trip to work can be represented as d = 36 t .
• The trip from work can be represented as d = 27 (1.75 - t ) .

In both equations, d represents the total distance. From the diagram, you can see that these two equations are equal to each other—after all, Eva drives the same distance to and from work .

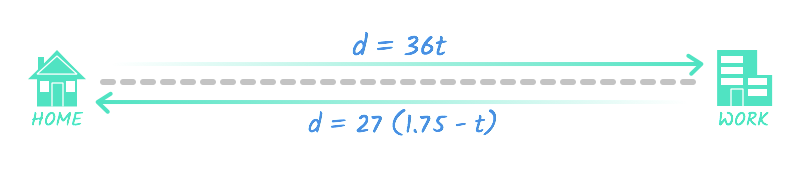
Just like with the last problem we solved, we can solve this one by combining the two equations.

We'll start with our equation for the trip from work .

d = 27 (1.75 - t)

Next, we'll substitute in the value of d from our to work equation, d = 36 t . Since the value of d is 36 t , we can replace any occurrence of d with 36 t .

36t = 27 (1.75 - t)

Now, let's simplify the right side. 27 ⋅(1.75 - t ) is 47.25 .

36t = 47.25 - 27t

Next, we'll cancel out -27 t by adding 27 t to both sides of the equation. 36 t + 27 t is 63 t .

63t = 47.25

Finally, we can get t on its own by dividing both sides by its coefficient: 63 . 47.25 / 63 is .75 .

t is equal to .75 . In other words, the time it took Eva to drive to work is .75 hours . Now that we know the value of t , we'll be able to can find the distance to Eva's work.

If you guessed that we were going to use the travel equation again, you were right. We now know the value of two out of the three variables, which means we know enough to solve our problem.

First, let's fill in the values we know. We'll work with the numbers for the trip to work . We already knew the rate : 36 . And we just learned the time : .75 .

d = 36 ⋅ .75

Now all we have to do is simplify the equation: 36 ⋅ .75 = 27 .

d is equal to 27 . In other words, the distance to Eva's work is 27 miles . Our problem is solved.

Intersecting distance problems

An intersecting distance problem is one where two things are moving toward each other. Here's a typical problem:

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading to Springfield at the same time a train leaves Springfield heading to Pawnee. One train is moving at a speed of 45 mph, and the other is moving 60 mph. How long will they travel before they meet?

This problem is asking you to calculate how long it will take these two trains moving toward each other to cross paths. This might seem confusing at first. Even though it's a real-world situation, it can be difficult to imagine distance and motion abstractly. This diagram might help you get a sense of what this situation looks like:

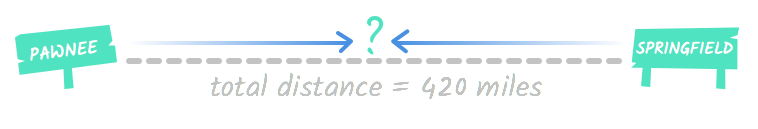
If you're still confused, don't worry! You can solve this problem the same way you solved the two-part problems on the last page. You'll just need a chart and the travel formula .

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading toward Springfield at the same time a train leaves Springfield heading toward Pawnee. One train is moving at a speed of 45 mph , and the other is moving 60 mph . How long will they travel before they meet?

Let's start by filling in our chart. Here's the problem again, this time with the important information underlined. We can start by filling in the most obvious information: rate . The problem gives us the speed of each train. We'll label them fast train and slow train . The fast train goes 60 mph . The slow train goes only 45 mph .

We can also put this information into a table:

We don't know the distance each train travels to meet the other yet—we just know the total distance. In order to meet, the trains will cover a combined distance equal to the total distance. As you can see in this diagram, this is true no matter how far each train travels.

This means that—just like last time—we'll represent the distance of one with d and the distance of the other with the total minus d. So the distance for the fast train will be d , and the distance for the slow train will be 420 - d .

Because we're looking for the time both trains travel before they meet, the time will be the same for both trains. We can represent it with t .

The table gives us two equations: d = 60 t and 420 - d = 45 t . Just like we did with the two-part problems, we can combine these two equations.

The equation for the fast train isn't solvable on its own, but it does tell us that d is equal to 60 t .

The other equation, which describes the slow train, can't be solved alone either. However, we can replace the d with its value from the first equation.

420 - d = 45t

Because we know that d is equal to 60 t , we can replace the d in this equation with 60 t . Now we have an equation we can solve.

420 - 60t = 45t

To solve this equation, we'll need to get t and its coefficients on one side of the equals sign and any other numbers on the other. We can start by canceling out the -60 t on the left by adding 60 t to both sides. 45 t + 60 t is 105 t .

Now we just need to get rid of the coefficient next to t . We can do this by dividing both sides by 105 . 420 / 105 is 4 .

t = 4 . In other words, the time it takes the trains to meet is 4 hours . Our problem is solved!

If you want to be sure of your answer, you can check it by using the distance equation with t equal to 4 . For our fast train, the equation would be d = 60 ⋅ 4 . 60 ⋅ 4 is 240 , so the distance our fast train traveled would be 240 miles. For our slow train, the equation would be d = 45 ⋅ 4 . 45 ⋅ 4 is 180 , so the distance traveled by the slow train is 180 miles . Remember how we said the distance the slow train and fast train travel should equal the total distance? 240 miles + 180 miles equals 420 miles , which is the total distance from our problem. Our answer is correct.

Practice problem 1

Here's another intersecting distance problem. It's similar to the one we just solved. See if you can solve it on your own. When you're finished, scroll down to see the answer and an explanation.

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove an average of 70 mph. How long did they drive before they met up?

Problem 1 answer

Here's practice problem 1:

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove 70 mph. How long did they drive before they met up?

Answer: 2 hours .

Let's solve this problem like we solved the others. First, try making the chart. It should look like this:

Here's how we filled in the chart:

• Distance: Together, Dani and Jon will have covered the total distance between them by the time they meet up. That's 270 . Jon's distance is represented by d , so Dani's distance is 270 - d .
• Rate: The problem tells us Dani and Jon's speeds. Dani drives 65 mph , and Jon drives 70 mph .
• Time: Because Jon and Dani drive the same amount of time before they meet up, both of their travel times are represented by t .

Now we have two equations. The equation for Jon's travel is d = 65 t . The equation for Dani's travel is 270 - d = 70 t . To solve this problem, we'll need to combine them.

The equation for Jon tells us that d is equal to 65 t . This means we can combine the two equations by replacing the d in Dani's equation with 65 t .

270 - 65t = 70t

Let's get t on one side of the equation and a number on the other. The first step to doing this is to get rid of -65 t on the left side. We'll cancel it out by adding 65 t to both sides: 70 t + 65 t is 135 t .

All that's left to do is to get rid of the 135 next to the t . We can do this by dividing both sides by 135 : 270 / 135 is 2 .

That's it. t is equal to 2 . We have the answer to our problem: Dani and Jon drove 2 hours before they met up.

Overtaking distance problems

The final type of distance problem we'll discuss in this lesson is a problem in which one moving object overtakes —or passes —another. Here's a typical overtaking problem:

The Hill family and the Platter family are going on a road trip. The Hills left 3 hours before the Platters, but the Platters drive an average of 15 mph faster. If it takes the Platter family 13 hours to catch up with the Hill family, how fast are the Hills driving?

You can picture the moment the Platter family left for the road trip a little like this:

The problem tells us that the Platter family will catch up with the Hill family in 13 hours and asks us to use this information to find the Hill family's rate . Like some of the other problems we've solved in this lesson, it might not seem like we have enough information to solve this problem—but we do. Let's start making our chart. The distance can be d for both the Hills and the Platters—when the Platters catch up with the Hills, both families will have driven the exact same distance.

Filling in the rate and time will require a little more thought. We don't know the rate for either family—remember, that's what we're trying to find out. However, we do know that the Platters drove 15 mph faster than the Hills. This means if the Hill family's rate is r , the Platter family's rate would be r + 15 .

Now all that's left is the time. We know it took the Platters 13 hours to catch up with the Hills. However, remember that the Hills left 3 hours earlier than the Platters—which means when the Platters caught up, they'd been driving 3 hours more than the Platters. 13 + 3 is 16 , so we know the Hills had been driving 16 hours by the time the Platters caught up with them.

Our chart gives us two equations. The Hill family's trip can be described by d = r ⋅ 16 . The equation for the Platter family's trip is d = ( r + 15) ⋅ 13 . Just like with our other problems, we can combine these equations by replacing a variable in one of them.

The Hill family equation already has the value of d equal to r ⋅ 16. So we'll replace the d in the Platter equation with r ⋅ 16 . This way, it will be an equation we can solve.

r ⋅ 16 = (r + 15) ⋅ 13

First, let's simplify the right side: r ⋅ 16 is 16 r .

16r = (r + 15) ⋅ 13

Next, we'll simplify the right side and multiply ( r + 15) by 13 .

16r = 13r + 195

We can get both r and their coefficients on the left side by subtracting 13 r from 16 r : 16 r - 13 r is 3 r .

Now all that's left to do is get rid of the 3 next to the r . To do this, we'll divide both sides by 3: 195 / 3 is 65 .

So there's our answer: r = 65. The Hill family drove an average of 65 mph .

You can solve any overtaking problem the same way we solved this one. Just remember to pay special attention when you're setting up your chart. Just like the Hill family did in this problem, the person or vehicle who started moving first will always have a greater travel time.

Practice problem 2

Try solving this problem. It's similar to the problem we just solved. When you're finished, scroll down to see the answer and an explanation.

A train moving 60 mph leaves the station at noon. An hour later, a train moving 80 mph leaves heading the same direction on a parallel track. What time does the second train catch up to the first?

Problem 2 answer

Here's practice problem 2:

Answer: 4 p.m.

To solve this problem, start by making a chart. Here's how it should look:

Here's an explanation of the chart:

• Distance: Both trains will have traveled the same distance by the time the fast train catches up with the slow one, so the distance for both is d .
• Rate: The problem tells us how fast each train was going. The fast train has a rate of 80 mph , and the slow train has a rate of 60 mph .
• Time: We'll use t to represent the fast train's travel time before it catches up. Because the slow train started an hour before the fast one, it will have been traveling one hour more by the time the fast train catches up. It's t + 1 .

Now we have two equations. The equation for the fast train is d = 80 t . The equation for the slow train is d = 60 ( t + 1) . To solve this problem, we'll need to combine the equations.

The equation for the fast train says d is equal to 80 t . This means we can combine the two equations by replacing the d in the slow train's equation with 80 t .

80t = 60 (t + 1)

First, let's simplify the right side of the equation: 60 ⋅ ( t + 1) is 60 t + 60 .

80t = 60t + 60

To solve the equation, we'll have to get t on one side of the equals sign and a number on the other. We can get rid of 60 t on the right side by subtracting 60 t from both sides: 80 t - 60 t is 20 t .

Finally, we can get rid of the 20 next to t by dividing both sides by 20 . 60 divided by 20 is 3 .

So t is equal to 3 . The fast train traveled for 3 hours . However, it's not the answer to our problem. Let's look at the original problem again. Pay attention to the last sentence, which is the question we're trying to answer.

Our problem doesn't ask how long either of the trains traveled. It asks what time the second train catches up with the first.

The problem tells us that the slow train left at noon and the fast one left an hour later. This means the fast train left at 1 p.m . From our equations, we know the fast train traveled 3 hours . 1 + 3 is 4 , so the fast train caught up with the slow one at 4 p.m . The answer to the problem is 4 p.m .

/en/algebra-topics/algebra-quiz/content/

Distance Word Problems

In these lessons, we will learn to solve word problems involving distance, rate (speed) and time.

Related Pages Rate Distance Time Word Problems Distance Problems Average Speed Problems

What Are Distance Word Problems Or Distance Rate Time Problems?

Distance problems are word problems that involve the distance an object will travel at a certain average rate for a given period of time .

The formula for distance problems is: distance = rate × time or d = r × t

Things to watch out for: Make sure that you change the units when necessary. For example, if the rate is given in miles per hour and the time is given in minutes then change the units appropriately.

It would be helpful to use a table to organize the information for distance problems. A table helps you to think about one number at a time instead being confused by the question.

The following diagrams give the steps to solve Distance-Rate-Time Problems. Scroll down the page for examples and solutions.

Distance Problems: Traveling At Different Rates

Example: A bus traveling at an average rate of 50 kilometers per hour made the trip to town in 6 hours. If it had traveled at 45 kilometers per hour, how many more minutes would it have taken to make the trip?

Solution: Step 1: Set up a rtd table.

Step 2: Fill in the table with information given in the question.

A bus traveling at an average rate of 50 kilometers per hour made the trip to town in 6 hours. If it had traveled at 45 kilometers per hour, how many more minutes would it have taken to make the trip?

Let t = time to make the trip in Case 2.

Step 3: Fill in the values for d using the formula d = rt

Step 4: Since the distances traveled in both cases are the same, we get the equation:

Step 5: Beware - the question asked for “how many more minutes would it have taken to make the trip”, so we need to deduct the original 6 hours taken.

Answer: The time taken would have been 40 minutes longer.

How to solve different types of distance, rate, time problems?

The following examples illustrate three types of problems involving distance, rate and time: opposite directions, same direction and roundtrip. Example 1: Lea left home and drove toward the ferry office at an average speed of 22 km.h. Trevon left at the same time and drove in the opposite direction with an average speed of 43 km/h. How long does Trevon need to drive before they are 65 km apart?

Example 2: Maria left home and traveled toward the capital at an average speed of 80 km/h. Some time later, Imani left traveling in the opposite direction with an average speed of 45 km/h. After Maria has traveled for six hours they were 705 km apart. Find the number of hours Imani traveled.

Example 3: A passenger train traveled to the repair yards and back. On the trip there, it traveled 68 mph and on the return trip it went 85 mph. How long did the trip there take if the return trip took four hours?

Example 4: A submarine traveled to St. Vincent and back. It took three hours less time to get there than it did to get back. The average speed on the trip there was 30 km/h. The average speed on the way back was 20 km/h. How many hours did the trip there take?

Example 5: Micaela left the hardware store and traveled toward her friend’s house at an average speed of 25 km/h. Nicole left some time later traveling in the same direction at the average speed of 30 km/h. After traveling for five hours Nicole caught up with Micaela. How long did Micaela travel before Nicole caught up?

Example 6: A passenger plane left New York and flew east. A jet left one hour later flying at 280 km/h in a effort to catch up to the passenger plane. After flying for seven hours the jet finally caught up. Find the passenger plane’s average speed.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Rate, Time Distance Problems With Solutions

The relationship between distance, rate (speed) and time

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Physics library

Course: physics library   >   unit 1.

• Intro to vectors and scalars
• Introduction to reference frames
• What is displacement?
• Calculating average velocity or speed

Solving for time

• Displacement from time and velocity example
• Instantaneous speed and velocity
• What is velocity?
• Position vs. time graphs
• What are position vs. time graphs?
• Average velocity and average speed from graphs
• Instantaneous velocity and instantaneous speed from graphs

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

"Distance" Word Problems

Explanation More Examples

What is a "distance" word problem?

"Distance" word problems, often also called "uniform rate" problems, involve something travelling at some fixed and steady ("uniform") pace ("rate", "velocity", or "speed"), or else you are told to regard to object as moving at some average speed.

Content Continues Below

MathHelp.com

Distance Word Problems

Whenever you read a problem that involves "how fast", "how far", or "for how long", you should think of the distance equation, d = rt , where d stands for distance, r stands for the (constant or average) rate of speed, and t stands for time.

Make sure that the units for time and distance agree with the units for the rate. For instance, if they give you a rate of feet per second, then your time must be in seconds and your distance must be in feet. Sometimes they try to trick you by using mis-matched units, and you have to catch this and convert to the correct units.

In case you're wondering, this type of exercise requires that the rate be fixed and steady (that is, unchanging) for the d = rt formula to work. The only way you can deal with a speed that might be changing over time is to take the average speed over the time or distance in question. Working directly with changing speeds will be something you'll encounter in calculus, as it requires calculus-based (or more advanced) methods.

What is the difference between a fixed speed and an average speed?

A fixed-speed exercise is one in which the car, say, is always going exactly sixty miles an hour; in three hours, the car, on cruise-control, will have gone 180 miles. An average-speed exercise is one in which the car, say, averaged forty miles an hour, but this average includes the different speeds related to stop lights, highways, and back roads; in three hours the car went 120 miles, though the car's speed was not constant. Most of the exercises you'll see will be fixed-speed exercises, but obviously they're not very "real world". It's a simplification they do in order to make the situation feasible using only algebraic methods.

What is an example of a "distance" word problem?

• A 555 -mile, 5 -hour plane trip was flown at two speeds. For the first part of the trip, the average speed was 105 mph. Then the tailwind picked up, and the remainder of the trip was flown at an average speed of 115 mph. For how long did the plane fly at each speed?

There is a method for setting up and solving these exercises that I first encountered well after I'd actually been doing them while taking a class as an undergraduate. But, as soon as I was introduced to the method, I switched over, because it is *so* way easier.

First I set up a grid, with the columns being labelled with the variables from the "distance" formula, and the rows being labelled with the "parts" involved:

In the first part, the plane covered some distance. I don't know how much, so I'll need a variable to stand for this unknown value. I'll use the variable they give me in the distance equation:

They gave me the speed, or rate, for this part, so I'll add this to my table:

The plane flew for some amount of time during this first part, but I don't know how long that was. So I need a variable to stand for this unknown value; I'll use the variable from the distance equation:

For the second part, the plane travelled the rest of the total distance. I don't know the exact distance that was flown during this second part, but I do know that it was "however much was left of the 555 miles, after the first d miles were flown in the first part. "How much was left after [some amount] was taken out" is expressed with subtraction: I take the amount that has been taken care of already, and subtract this from whatever was the total. Adding this to my table, I get:

They've given me the speed, or rate, for the second part, and I can use the same "How much is left?" construction for whatever was the time for this second part. So now my table looks like this:

For the "total" row, I add down (or take info from the exercise statement):

Advertisement

Why did I not add down in the "rate" column? Because I cannot add rates! In this exercise, adding the rates would have said that the average rate for the entire trip was 105 + 115 = 220 miles per hour. But obviously this makes no sense.

The genius of this table-based method of set-up is that I can now create equations from the rows and columns. In this exercise, there is more than one way to proceed. I'll work with the "distance" equation to create expressions for the distances covered in each part.

Multiplying across, the first row tells me that the distance covered in the first part of the flight was:

1st part distance: 105 t

Again multiplying across, the second row tells me that the distance covered in the second part of the flight was:

2nd part distance: 115(5 − t )

I can add these two partial-distance expressions, and set them equal to the known total distance:

105 t + 115(5 − t ) = 555

This is an equation in one variable, which I can solve:

105 t + 115(5 − t ) = 555 105 t + 575 − 115 t = 555 575 − 10 t = 555 20 = 10 t 2 = t

Looking back at my table, I see the I had defined t to be the time that the plane spent in the air on the first part of its journey. Looking back at the original exercise, I see that they want to know the times that the plane spent at each of the two speeds.

I now have the time for the first part of the flight; the time was two hours. The exercise said that the entire trip was five hours, so the second part must have taken three hours (found by subtracting the first-part time from the total time). They haven't asked for the partial distances, so I now have all the information I need; no further computations are necessary. My answer is:

first part: 2 hours second part: 3 hours

When I was setting up my equation, I mentioned that there was more than one way to proceed. What was the other way? I could have used the table to create an expression for each of the two partial times, added, set the result equal to the given total, and solved for the variable d . Since the distance equation is d  =  rt , then the expressions for the partial times would be created by solving the equation for t  = . My work would have looked like this:

first part: d /105

second part: (555 − d )/115

adding: d /105 + (555 − d )/115 = 5 23 d + 11,655 − 21 d = 12,075 2 d = 420 d = 210

Looking back at my table, I would have seen that this gives me the distance covered in the first half of the flight. Looking back at the exercise, I would have seeing that they are wanting times, not distances. So I would have back-solved for the time for the first part, and then done the subtraction to find the time for the second part. My work would have had more steps, but my answer would have been the same.

There are three things that I hope you take from the above example:

• Using a table or grid to keep track of what you're doing can be incredibly helpful.
• It is important to clearly define your variables, so you know (by the end) what you'd meant (back in the beginning), so you can apply your results correctly.
• You should always check the original exercise, so you can be sure that you're answering the question that they'd actually asked.

(My value for the distance, found above, is correct, but was not what they'd asked for.) But even more important to understand is this:

NEVER TRY TO ADD RATES! Think about it: If you drive 20 mph on one street, and 40 mph on another street, does that mean you averaged 60 mph? Of course not.

Can I even average the rates? If I drove at 20 mph for one hour, and then drove 60 mph for two hours, then I would have travelled 140 miles in three hours, or a little under 47 mph. But 47 is not the average of 20 and 60 .

As you can see, the actual math involved in solving this type of exercise is often quite simple. It's the set-up that's the hard part. So what follows are some more examples, but with just the set-up displayed. Try your hand at solving, and click on the links to get pop-ups from which to check your equations and solutions.

• An executive drove from home at an average speed of 30 mph to an airport where a helicopter was waiting. The executive boarded the helicopter and flew to the corporate offices at an average speed of 60 mph. The entire distance was 150 miles; the entire trip took three hours. Find the distance from the airport to the corporate offices.

I will start in the usual way, by setting up my table:

I have labelled my rows so it's clear how they relate to the exercise. Now I need to fill in the rows. As before, I don't know the distance or the time for the part where the executive was driving, so I'll use variables for these unknowns, along with the given rate.

For the flying portion of the trip, I'll use the "how much is left" construction, along with the given rate, to fill in my second row. I'll also fill in the totals.

The first row gives me the equation d  = 30 t . The second row is messier, giving me the equation:

150 − d = 60(3 − t )

There are various ways I can go from here; I think I'll solve this second equation for the variable d , and then set the results equal to each other.

150 − d = 60(3 − t ) 150 − 60(3 − t ) = d

Setting equal these two expressions for d , I get:

30 t = 150 − 60(3 − t )

Solve for t ; interpret the value; state the final answer.

• A car and a bus set out at 2 p.m. from the same point, headed in the same direction. The average speed of the car is 30 mph slower than twice the speed of the bus. In two hours, the car is 20 miles ahead of the bus. Find the rate of the car.

Both vehicles travelled for the same amount of time.

The car's values are expressed in terms of the bus' values, so I'll use variables for the bus' unknowns, and then define the car in terms of the bus' variables. This gives me:

(As it turns out, I won't need the "total" row this time.) The car's row gives me:

d + 20 = 2(2 r − 30)

This is not terribly helpful. The second row gives me:

I'll use the second equation to simplify the first equation by substituting " 2 r " from the second equation in for the " d " in the first equation. Then I'll solve the equation for the value of " r ". Finally, I'll need to interpret this value within the context of the exercise, and then I'll state the final answer.

(Remember that the expression for the car's speed, from the table, was 2 r  − 30 , so all you need to do is find the numerical value of this expression. Just evaluate; don't try to solve — again — for the value of r .)

URL: https://www.purplemath.com/modules/distance.htm

Page 1 Page 2

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Home / United States / Math Classes / Formulas / Distance Speed Time Formulas

Distance Speed Time Formulas

This article explores the formula describing the relationship between distance, speed and time. If the values of any two of the three quantities, among speed, distance or time are given, the formula can be used to find the third quantity. ...Read More Read Less

Formula for Speed, Distance and Time

Distance is the numerical measure of how far a point or an object is from another point or object. Time is the measure of the time taken for an entity to reach from one point to another. Lastly, the measure of how fast or slow an object or a point moves is known as speed.

Speed, distance and time are related to each other by the formula:

Speed = \(\frac{\text{Distance}}{\text{Time}}\)

So, speed can be defined as the distance traveled per unit time. It indicates the rate at which an object moves between two points. The formula connecting speed, distance and time can also be given as:

\(x=\frac{d}{t}\)

\(x\) = Speed

\(d\) = Distance traveled

\(t\) = Time taken

Distance is measured in units of length like meters, kilometers, miles and other units like feet or inches. Time is measured in seconds, minutes and hours. Speed is measured in distance per unit time, for example, meters per second (m/s), kilometers per hour (km/hour), or miles per hour.

The above formula can also be used to determine distance or time.

• Distance = Speed \(\times\) Time (or) \(d\ =\ x\ \times\ t\)
• Time = \(\frac{\text{Distance}}{\text{Speed}} = \frac{d}{x}\)

Therefore, distance is the product of speed and time, and time is distance per unit speed.

Rapid Recall

Solved Examples

Example 1: Laura was going to the mall from her house in her car at an average speed of 36 mph. She took 0.2 hours to reach the mall. Calculate the distance she traveled from her house to the mall?

Solution: Speed of the car, \(x\) = 36 mph

Time taken by the car to reach the mall, \(t\) = 0.2 hr

We need to find the distance covered by Laura.

The formula relating speed, distance and time is,

Distance traveled, \(d=x \times t\)

\(d=36 \times 0.2\)  Substitute 36 for \(x\) and 0.2 for \(t\)

   \(=7.2\)           Multiply

Therefore the distance traveled by Laura from her house to the mall is 7.2 miles.

Example 2: Ronald covered a distance of 280 miles in 4 hours on his motorbike. Calculate how fast the bike would have moved to cover this distance.

Distance covered, \(d\) = 280 miles,

Time taken, \(t\) = 4 hours

\(x=\frac{d}{t}\)     Formula for speed

\(x =\frac{280}{4}\)  Substitute 280 for d and 4 for \(t\)

\(x=70\)    Divide

Therefore, the bike would have moved at a speed of 70 miles per hour to cover a distance of 280 miles.

Example 3: In a cycle race, cyclist A is moving with a speed of 2 km/hr and cyclist B is moving at a speed of 3 km/hr. The cyclists need to cover a distance of 12 km to reach the destination. Which cyclist will reach the destination first?

Solution: To determine which cyclist reaches the destination, first, we need to compare the time taken by each cyclist to reach the destination.

Speed of cyclist A, \(x_a\) = 2 km/hr

Speed of cyclist B, \(x_b\) = 3 km/hr

Distance covered by both the cyclists, \(d\) = 12 km

We need to find the time taken by cyclist A and cyclist B.

\(t=\frac{d}{x}\)              Formula for time taken

\(t_a = \frac{12}{2}=6\)    Substitute 12 for \(d\) and 2 for \(x\) and solve

\(t_b = \frac{12}{3}=4\)    Substitute 12 for \(d\) and 3 for \(x\) and solve

So the time taken by cyclist A is 6 hours and the time taken by cyclist B is 4 hours.

Now since 6 hours is greater than 4 hours, that is, cyclist B takes less time to reach the destination.

Therefore cyclist B will reach the destination first.

What is the definition of speed?

The rate of change of the position of an object in any direction is called the speed of the object.

What is the definition of time?

The ratio of distance traveled or covered by an object to its unit speed is defined as time.

What is the definition of distance?

Distance is the numerical measure of how far a point or an object is from another point or object. Distance is calculated as the product of speed and time.

For a given speed if the distance is doubled then what will be the change in time taken?

For a given speed, if the distance is doubled then the time taken will also be doubled.

Check out our other courses

Grades 1 - 12

Level 1 - 10

SPEED DISTANCE TIME PROBLEMS WITH SOLUTIONS

Problem 1 :

A passenger train takes 3 hours less than a slow train for journey of 600 km. If the speed of the slow train is 10 km/hr less than that of the passenger train, find the speed of two trains.

Let x be the speed of the of the passenger train

Speed of the slow train is 10 km/hr less than that of the passenger train

So x-10 be the speed of the slow train

Distance has to be covered  =  600 km

Time  =  Distance/speed

Let T 1 be the time taken by passenger train

Let T 2 be the time taken by the slow train

The differences of time taken by both trains are 3 hours

T 1  =  600/x

T 2   =  600/(x-0)

T 2 –T 1   =  3 hours

(600/(x–10)) – (600/x)  =  3

600[(1/(x-10)-(1/x)]  =  3

x-(x-10)/(x 2 -10x)  =  1/200

(x-x+10)/(x 2 -10x)  =  1/200

2000  =  x 2 -10x

x 2 -10x-2000  =  0

x 2 –50x+40x-2000  =  0

x(x–50)+40(x–50)  =  0

(x+40) (x–50)  =  0

By solving, we get x  =  -40 and x  =  50

Therefore the speed of passenger train  =  50 km/hr

Speed of slow train  =  40 m/hr.

Problem 2 :

The distance between two stations A and B is 192 km. Traveling by a fast train takes 48 minutes less than another train. Calculate the speed of the fast train if the speeds of two trains differ by 20 km/hr

Distance between two stations A and B  =  192 km

Fast train takes 48 minutes less then the time taken by the slow train.

Let x be the speed taken by the fast train

Speeds of two trains differ by 20 km/hr

So speed of slow train is x – 20.

Let T 1 be the time taken by the fast train

T 1   =  192/x

T 2   =  192/(x–20)

48/60  =  4/5 hours

T 1 – T 2   =  4/5

[192/(x-20)-192/x]  =  4/5

192[(x–x+20)/x(x - 20)]  =  4/5

192(20)/x 2 –20 x  =  4/5

3840 (5)  =  4(x 2 –20 x)

19200  =  4x 2 – 80 x

4800  =  x 2 – 20 x

x 2 –20x–4800  =  0

x 2 –60x+40x-4800  =  0

(x–60) (x+40)  =  0

x  =  60 and x  =  -40

Speed of fast train is 60 km/hr.

Problem 3 :

A train covers a distance of 300 km at a certain average speed. If its speed was decreased by 10km/hr, the journey would take 1 hour longer. What is the average speed.

Let x be the average speed of the train

So x–10 be the decreased speed

Time  =  Distance/Speed

T 1  and T 2  be the time taken by the train to cover the distance with speed of x km/hr and (x-10) km/hr respectively.

T 1   =  300/x

T 2   =  300/(x–10)

T 1 – T 2   =  1

[300/x] - [300/(x-10)]  =  1

3000/(x 2 – 10x)  =  1

3000  =  x 2 – 10 x

x 2 – 10x  =  3000

x 2 –10x–3000  =  0

x 2 –60x+50x–3000  =  0

x (x – 60) + 50 (x – 60) = 0

(x + 50)(x – 60) = 0

By solving, we get

x  =  -50 and x  =  60

So speed of the 60 km/hr.

Problem 4 :

The time taken by a train to travel a distance of 250 km was reduced by 5/4 hours when average speed was increased by 10km/hr. Calculate the average speed.

Distance to be covered  =  250 km

Let x be the required average speed.

If the average speed was increased by 10 km/hr

x+10 be the increased speed

Let T 1 be the time taken to cover the distance in the average speed of x km/hr

Let T 2 be the time taken to cover the distance in the average speed of (x + 10) km/hr

T 1   =  250/x

T 2   =  250/(x+10)

T 1 – T 2   =  5/4

250/x – 250/(x + 10)  =  5/4

250 [(x+10–x)/x(x+10)]  =  5/4

2500/(x 2 + 10x)  =  5/4

2500 (4)  =  5(x 2 +10x)

10000  =  5x 2 +10 x

Now we are going to divide the whole equation by 5, so we get

x 2 +10x  =  2000

x 2 +10x–2000 = 0

  x 2 + 50x-40x-2000 = 0

x(x+50)–40(x+50) = 0

(x–40) (x+50) = 0

x  =  40 and x  =  -50

Therefore the required average speed = 40 km/hr

Increased speed  =  (40+10)

Problem 5 :

An express train makes run 240 km t a certain speed. Another train whose speed is 12 km/hr less takes an hour longer to make the same trip. Find the speed of the express train.

Let x be speed of express train

So x–12 be the speed of another train

Distance to be covered  =  240 km

Let T 1 be the time taken by the train to cover the distance 240 km at the speed of x km/hr

Let T 2 be the time taken by the train to cover the distance 240 km at the speed of (x + 12) km/hr

Time = Distance /speed

T 1   =  240/x

T 2   =  240/(x - 12)

T 2 - T 1 = 1 hour

[240/(x- 12)]  - [240/x]  =  1

240[(1/(x -12) - 1/x]  =  1

240[(x - x + 12)/x(x - 12)]  =  1

240[12/(x 2 - 12 x)]  =   1

2880  =  (x 2 -12 x)

x 2 -12x-2880  =  0

x 2 +60x-48x-2880  =  0

x(x+60)- 48 (x+60)  =  0

(x-48) (x+60) = 0

x = 48              x = -60

Speed of express train  =  48 km/hr

Speed of other train  =  (x - 12)

=  (48-12)

=  36 km/hr

Problem 6 :

A plane traveled a distance of 400 km at an average speed of x km/hr. On the return journey, the speed was increased by 40 km/hr. Write down an expression for the time taken for

(i) the onward journey and

(ii) the return journey. If the journey took 30 minutes less than  onward journey, write down an equation in x and its value.

Let “x” be average speed of plane

On the return journey, the speed was increased by 40 km/hr

So “x + 40” be the speed of plane

Distance to be covered = 400 km

Let T 1 be the time taken for onward journey in the speed of x km/hr

Let T 2 be the time taken for downward journey to cover the same distance 400 km at the speed of (x + 40) km/hr

T 1   =  400/x

T 2   =  400/(x+40)

T 1 - T 2   =  30 minutes

[400/x]-[400/(x + 40)]  =  30/60

400[(1/x) - 1/(x+40)]  =  1/2

400[40/(x 2 + 40 x)]  =  1/2

16000 (2)  =  (x 2 +40 x)

x 2 +40x-32000  =  0

x 2 +160x-100x-32000  =  0

(x - 100) (x + 160) = 0

 x = 100              x = -160

Speed of the plane  =  48 km/hr

Increased speed  =  (x+40)

=  (48+40)

=  88 km/hr

Apart from the stuff given in this section ,    if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

First Fundamental Theorem of Calculus - Part 1

Apr 17, 24 11:27 PM

Polar Form of a Complex Number

Apr 16, 24 09:28 AM

Conjugate of a Complex Number

Apr 15, 24 11:17 PM

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 6.8: Rate Word Problems: Speed, Distance and Time

Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance .

For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h)(4h) = 120 km.

The problems to be solved here will have a few more steps than described above. So to keep the information in the problem organized,  use a table. An example of the basic structure of the table is below:

The third column, distance, will always be filled in by multiplying the rate and time columns together. If given a total distance of both persons or trips,  put this information in the distance column. Now use this table to set up and solve the following examples.

Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?

The distance travelled by both is 30 km. Therefore, the equation to be solved is:

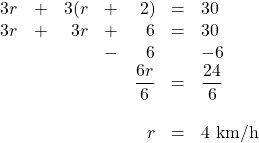
This means that Natasha walks at 4 km/h and Joey walks at 6 km/h.

Nick and Chloe left their campsite by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. After how much time did the campers turn around downstream?

The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:

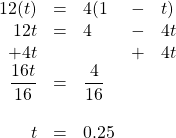
This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling back.

Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h later on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?

The distance travelled by both is the same. Therefore, the equation to be solved is:

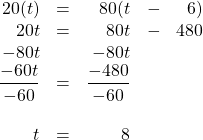
This means that Terry travels for 8 h and Sally only needs 2 h to catch up to him.

On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the car travel 40 km/h?

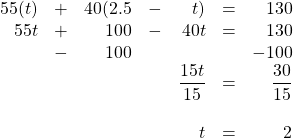
This means that the time spent travelling at 40 km/h was 0.5 h.

Distance, time and rate problems have a few variations that mix the unknowns between distance, rate and time. They generally involve solving a problem that uses the combined distance travelled to equal some distance or a problem in which the distances travelled by both parties is the same. These distance, rate and time problems will be revisited later on in this textbook where quadratic solutions are required to solve them.

For Questions 1 to 8, find the equations needed to solve the problems. Do not solve.

• A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long will it be before the automobiles meet?
• Two automobiles are 276 kilometres apart and start to travel toward each other at the same time. They travel at rates differing by 5 km/h. If they meet after 6 h, find the rate of each.
• Two trains starting at the same station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon will they be 195 kilometres apart?
• Two bike messengers, Jerry and Susan, ride in opposite directions. If Jerry rides at the rate of 20 km/h, at what rate must Susan ride if they are 150 kilometres apart in 5 hours?
• A passenger and a freight train start toward each other at the same time from two points 300 kilometres apart. If the rate of the passenger train exceeds the rate of the freight train by 15 km/h, and they meet after 4 hours, what must the rate of each be?
• Two automobiles started travelling in opposite directions at the same time from the same point. Their rates were 25 and 35 km/h, respectively. After how many hours were they 180 kilometres apart?
• A man having ten hours at his disposal made an excursion by bike, riding out at the rate of 10 km/h and returning on foot at the rate of 3 km/h. Find the distance he rode.
• A man walks at the rate of 4 km/h. How far can he walk into the country and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?

Solve Questions 9 to 22.

• A boy rides away from home in an automobile at the rate of 28 km/h and walks back at the rate of 4 km/h. The round trip requires 2 hours. How far does he ride?
• A motorboat leaves a harbour and travels at an average speed of 15 km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of 5 hours?
• A family drove to a resort at an average speed of 30 km/h and later returned over the same road at an average speed of 50 km/h. Find the distance to the resort if the total driving time was 8 hours.
• As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was 90 km/h, and the average speed returning was 120 km/h. Find the distance between the two airports if the total flying time was 7 hours.
• Sam starts travelling at 4 km/h from a campsite 2 hours ahead of Sue, who travels 6 km/h in the same direction. How many hours will it take for Sue to catch up to Sam?
• A man travels 5 km/h. After travelling for 6 hours, another man starts at the same place as the first man did, following at the rate of 8 km/h. When will the second man overtake the first?
• A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small island. Two hours later, a cabin cruiser leaves the same harbour and travels at an average speed of 16 km/h toward the same island. How many hours after the cabin cruiser leaves will it be alongside the motorboat?
• A long distance runner started on a course, running at an average speed of 6 km/h. One hour later, a second runner began the same course at an average speed of 8 km/h. How long after the second runner started will they overtake the first runner?
• Two men are travelling in opposite directions at the rate of 20 and 30 km/h at the same time and from the same place. In how many hours will they be 300 kilometres apart?
• Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres apart at the end of 4 hours, what is the rate of each?
• Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours, they are 72 kilometres apart. Find the rate of each cyclist.
• Two small planes start from the same point and fly in opposite directions. The first plane is flying 25 km/h slower than the second plane. In two hours, the planes are 430 kilometres apart. Find the rate of each plane.
• On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of 2.5 hours. For how long did the car travel at 40 km/h?
• Running at an average rate of 8 m/s, a sprinter ran to the end of a track and then jogged back to the starting point at an average of 3 m/s. The sprinter took 55 s to run to the end of the track and jog back. Find the length of the track.

Answers to odd questions

Pre-Calculus Copyright © 2022 by St. Clair College is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Talk to our experts

1800-120-456-456

• Speed Distance Time Word Problems with Solutions

Introduction

Speed, distance, and time are the three main pillars behind mathematics and physics. Whenever you are presented with a question related to any kind of transportation, you should immediately relate to these concepts. The train speed, the relation between the time taken by two cars at different speeds or even a simple question about a person walking from one place to another can be answered using simple formulas.

What is Speed?

When you think of speed, you must think of how fast? Speed is all about calculating the rate at which something can be accomplished.

A Device Used to Measure Speed Known as a ‘Speedometer’

What is Distance?

Distance in this concept refers to the distance travelled. It means how far? It can be measured in meters, for small distances and kilometres, for larger distances.

Distance is the Measurement From One Place to Another

What is Time?

Time is the answer to the question, how long? The best way to measure time is using the ‘world clock.’ In ancient times, time was measured with the help of the sun and the moon, and other celestial objects.

Time as Shown by a Clock

Relation Between Speed Distance and Time

There is a very simple mathematical relation between speed, distance and time.

$\text{speed=}\frac{\text{distance}}{\text{time}}$

$\text{time=}\frac{\text{distance}}{\text{speed}}$

$\text{distance=speed }\!\!\times\!\!\text{ time}$

These relations can be memorised using the triangle method. See the following image to understand the use of this method.

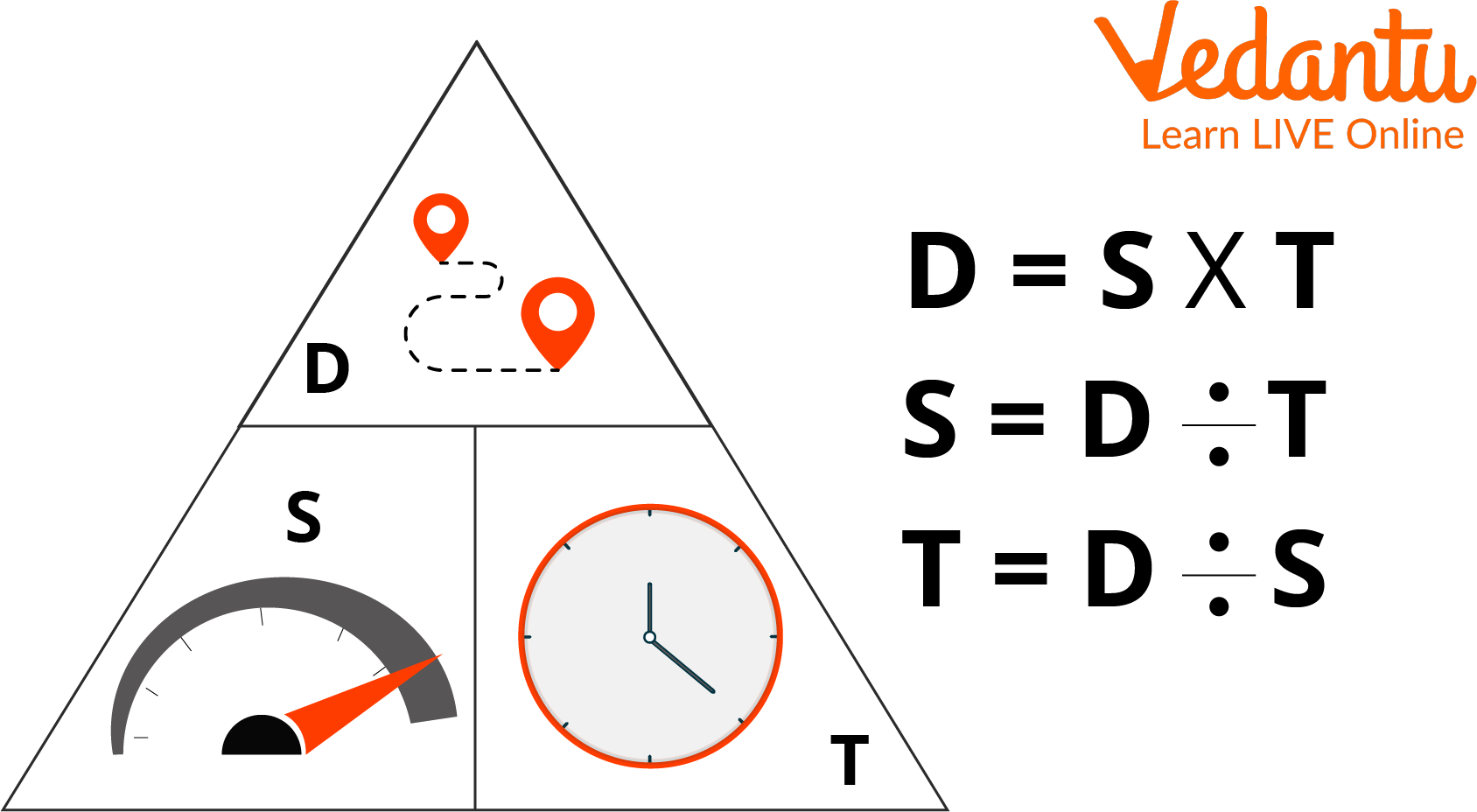
Explaining the Triangle Method

Speed Distance Time Word Problems With Solutions

Q1. A train is travelling at a speed of 160 km/hour. It takes 15 hours to cover the distance from city A to city B. Find the distance between the two cities.

Speed= 160 km/hr

Time= 15 hours

Using the formula, $\text{distance=speed }\!\!\times\!\!\text{ time}$

Distance= $160\times 15=2400km$

Answer: The distance between city A and city B is 2400km

Q2. A car travelling from city A to city C completes the journey in 3 hours, whereas a person travelling on a bike completes the journey in 5 hours. What is the speed of the man on the bike if the car is travelling at 45 kmph?

Find the distance using the information on the car

Speed= 45km/hour

Time= 3 hours

$\therefore \text{distance}=45\times 3=135km$

Using the distance, we can find the speed of the bike

Formula used, $\text{speed=}\frac{\text{distance}}{\text{time}}$

Time taken by bike is 5 hours

$\therefore \text{speed}=\frac{135}{5}=27$

Answer: The bike is moving at a speed of 27 kmph.

Q3. A person travels at a speed of 15 kmph from point A to point B, which are 25 km from each other. Another person is travelling from point C to point B, 44 km from each other. Both people start their journey at the same time; the second person arrives at the point 2 hours after the first. What is the speed at which the second person was travelling?

Speed of person 1 = 15km/hour

Distance travelled by person 1= 25 km/hour

Time taken by first-person = $\frac{\text{distance}}{\text{speed}}=\frac{25}{15}=\frac{5}{3}$hours

Note: While solving the questions, keep the answers in fractions until you reach the final answer to make calculations easier.

Time taken by second person =$\frac{5}{3}+2=\frac{11}{3}$hours

Distance travelled by second person= 44 km

$\therefore \text{speed}=\frac{\text{distance}}{\text{time}}=\frac{44}{\frac{11}{3}}=\frac{44\times 3}{11}=4\times 3=12$kmph

Answer: The second person was travelling at a speed of 12kmph.

Q4. Raju is travelling from one station to another 560km away in a train which is moving at a speed of 125kmph. Monu is travelling to the same destination at a speed of 80kmph. Monu starts his journey 3 hours after Raju, from 120 km closer to the destination. How long will Raju have to wait at the train station for Monu to arrive?

Distance travelled by Raju = 560km

Speed of Raju= 125km/hour

∴ Time taken by Raju to reach the station = $\frac{\text{distance}}{\text{speed}}=\frac{560}{125}=\frac{112}{25}$hours

Distance travelled by Monu = $560-120=440$km

The speed at which Monu travelled = 80kmph

Time taken by Monu to complete journey = $\frac{440}{80}=\frac{22}{4}=\frac{11}{2}$hours

Total time taken by Monu = $\frac{11}{2}+3=\frac{17}{2}$hours

Therefore, the time Raju had to wait = difference between the two times taken

$\therefore \frac{17}{2}-\frac{112}{25}=\frac{17\times 25}{50}-\frac{112\times 2}{50}=\frac{201}{50}=4.02$hours

Answer: Raju had to wait for 4.02 hours at the train station

Convert 4.02 hours to hours and minutes

$\therefore 0.02=\frac{2}{100}\times 60=1.2$minutes

$\therefore 0.2=\frac{2}{10}\times 60=12$seconds

Therefore, to be precise, Raju had to wait at the train station for 4 hours, 1 minute and 12 seconds.

FAQs on Speed Distance Time Word Problems with Solutions

1. Is there any other formula to relate the speed distance and time?

No, there is only one relation that one must remember to solve all speed distance time problems. The triangle method is the easiest and fastest way to remember these relations.

2. What are other speed measures, and how to convert them to km/hour?

The other speed measures include meters per second, denoted as m/sec or m/s and miles per hour, denoted as mph.

 To convert m/sec into km/hour, one must use the following formula—

$\frac{m}{s}\times \frac{5}{18}=\frac{km}{hr}$ ($\because $1 m/s = 3.6 km/h)

To convert mph into kmph one must use the following relation—

1 mile= approximately 1.609 km

1 km= 0.6214 miles

3. What is the device that records distance called?

The device that calculates the distance travelled is known as an odometer.

4. What other factors need to be considered when calculating real-life problems?

Simple formulas are not useful when solving speed distance time problems in real life since many other factors affect the outcome. One must consider air drag, frictional forces, repulsion, wear and tear and, most importantly, gravitational forces when solving these real-life problems. The formulas of relation, however, remain the same.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.8: Applications of Rational Functions

• Last updated
• Save as PDF
• Page ID 22235

In this section, we will investigate the use of rational functions in several applications.

Number Problems

We start by recalling the definition of the reciprocal of a number.

For any nonzero real number a, the reciprocal of a is the number 1/a. Note that the product of a number and its reciprocal is always equal to the number 1. That is, \[a \cdot \frac{1}{a}=1 \nonumber \]

For example, the reciprocal of the number 3 is 1/3. Note that we simply “invert” the number 3 to obtain its reciprocal 1/3. Further, note that the product of 3 and its reciprocal 1/3 is

\[3 \cdot \frac{1}{3}=1 \nonumber \]

As a second example, to find the reciprocal of −3/5, we could make the calculation

\[\frac{1}{-\frac{3}{5}}=1 \div\left(-\frac{3}{5}\right)=1 \cdot\left(-\frac{5}{3}\right)=-\frac{5}{3} \nonumber \]

but it’s probably faster to simply “invert” −3/5 to obtain its reciprocal −5/3. Again, note that the product of −3/5 and its reciprocal −5/3 is

\[\left(-\frac{3}{5}\right) \cdot\left(-\frac{5}{3}\right)=1 \nonumber \]

Let’s look at some applications that involve the reciprocals of numbers.

Example \(\PageIndex{1}\)

The sum of a number and its reciprocal is 29/10. Find the number(s).

Let x represent a nonzero number. The reciprocal of x is 1/x. Hence, the sum of x and its reciprocal is represented by the rational expression x + 1/x. Set this equal to 29/10.

\[x+\frac{1}{x}=\frac{29}{10} \nonumber \]

To clear fractions from this equation, multiply both sides by the common denominator 10x.

\[\begin{aligned} \color{blue}{10 x}\left(x+\frac{1}{x}\right) &=\left(\frac{29}{10}\right) \color{blue}{10 x}\\ 10 x^{2}+10 &=29 x \end{aligned} \nonumber \]

This equation is nonlinear (it has a power of x larger than 1), so make one side equal to zero by subtracting 29x from both sides of the equation.

\[10 x^{2}-29 x+10=0 \nonumber \]

Let’s try to use the ac-test to factor. Note that ac = (10)(10) = 100. The integer pair {−4, −25} has product 100 and sum −29. Break up the middle term of the quadratic trinomial using this pair, then factor by grouping.

\[\begin{aligned} 10 x^{2}-4 x-25 x+10 &=0 \\ 2 x(5 x-2)-5(5 x-2) &=0 \\(2 x-5)(5 x-2) &=0 \end{aligned} \nonumber \]

Using the zero product property, either

\[2 x-5=0 \quad \text { or } \quad 5 x-2=0 \nonumber \]

Each of these linear equations is easily solved.

\[x=\frac{5}{2} \quad \text { or } \quad x=\frac{2}{5} \nonumber \]

Hence, we have two solutions for x. However, they both lead to the same number-reciprocal pair. That is, if x = 5/2, then its reciprocal is 2/5. On the other hand, if x = 2/5, then its reciprocal is 5/2.

Let’s check our solution by taking the sum of the solution and its reciprocal. Note that

\[\frac{5}{2}+\frac{2}{5}=\frac{25}{10}+\frac{4}{10}=\frac{29}{10} \nonumber \]

as required by the problem statement.

Let’s look at another application of the reciprocal concept.

Example \(\PageIndex{2}\)

There are two numbers. The second number is 1 larger than twice the first number. The sum of the reciprocals of the two numbers is 7/10. Find the two numbers.

Let x represent the first number. If the second number is 1 larger than twice the first number, then the second number can be represented by the expression 2x + 1.

Thus, our two numbers are x and 2x+1. Their reciprocals, respectively, are 1/x and 1/(2x + 1). Therefore, the sum of their reciprocals can be represented by the rational expression 1/x + 1/(2x + 1). Set this equal to 7/10.

\[\frac{1}{x}+\frac{1}{2 x+1}=\frac{7}{10} \nonumber \]

Multiply both sides of this equation by the common denominator 10x(2x + 1).

\[\begin{aligned} \color{blue}{10 x(2 x+1)}\left[\frac{1}{x}+\frac{1}{2 x+1}\right] &=\left[\frac{7}{10}\right] \color{blue}{10 x(2 x+1)}\\ 10(2 x+1)+10 x &=7 x(2 x+1) \end{aligned} \nonumber \]

Expand and simplify each side of this result.

\[\begin{aligned} 20 x+10+10 x &=14 x^{2}+7 x \\ 30 x+10 &=14 x^{2}+7 x \end{aligned} \nonumber \]

Again, this equation is nonlinear. We will move everything to the right-hand side of this equation. Subtract 30x and 10 from both sides of the equation to obtain

\[\begin{array}{l}{0=14 x^{2}+7 x-30 x-10} \\ {0=14 x^{2}-23 x-10}\end{array} \nonumber \]

Note that the right-hand side of this equation is quadratic with ac = (14)(−10) = −140. The integer pair {5, −28} has product −140 and sum −23. Break up the middle term using this pair and factor by grouping.

\[\begin{array}{l}{0=14 x^{2}+5 x-28 x-10} \\ {0=x(14 x+5)-2(14 x+5)} \\ {0=(x-2)(14 x+5)}\end{array} \nonumber \]

\[x-2=0 \quad \text { or } \quad 14 x+5=0 \nonumber \]

These linear equations are easily solved for x, providing

\[x=2 \quad \text { or } \quad x=-\frac{5}{14} \nonumber \]

We still need to answer the question, which was to find two numbers such that the sum of their reciprocals is 7/10. Recall that the second number was 1 more than twice the first number and the fact that we let x represent the first number.

Consequently, if the first number is x = 2, then the second number is 2x + 1, or 2(2) + 1. That is, the second number is 5. Let’s check to see if the pair {2, 5} is a solution by computing the sum of the reciprocals of 2 and 5.

\[\frac{1}{2}+\frac{1}{5}=\frac{5}{10}+\frac{2}{10}=\frac{7}{10} \nonumber \]

Thus, the pair {2, 5} is a solution.

However, we found a second value for the first number, namely x = −5/14. If this is the first number, then the second number is

\[2\left(-\frac{5}{14}\right)+1=-\frac{5}{7}+\frac{7}{7}=\frac{2}{7} \nonumber \]

Thus, we have a second pair {−5/14, 2/7}, but what is the sum of the reciprocals of these two numbers? The reciprocals are −14/5 and 7/2, and their sum is

\[-\frac{14}{5}+\frac{7}{2}=-\frac{28}{10}+\frac{35}{10}=\frac{7}{10} \nonumber \]

as required by the problem statement. Hence, the pair {−14/5, 7/2} is also a solution.

Distance, Speed, and Time Problems

When we developed the Equations of Motion in the chapter on quadratic functions, we showed that if an object moves with constant speed, then the distance traveled is given by the formula

\[d=v t \nonumber \]

where d represents the distance traveled, v represents the speed, and t represents the time of travel.

For example, if a car travels down a highway at a constant speed of 50 miles per hour (50 mi/h) for 4 hours (4 h), then it will travel

\[\begin{aligned} d &=v t \\ d &=50 \frac{\mathrm{mi}}{\mathrm{h}} \times 4 \mathrm{h} \\ d &=200 \mathrm{mi} \end{aligned} \nonumber \]

Let’s put this relation to use in some applications.

Example \(\PageIndex{3}\)

A boat travels at a constant speed of 3 miles per hour in still water. In a river with unknown current, it takes the boat twice as long to travel 60 miles upstream (against the current) than it takes for the 60 mile return trip (with the current). What is the speed of the current in the river?

The speed of the boat in still water is 3 miles per hour. When the boat travels upstream, the current is against the direction the boat is traveling and works to reduce the actual speed of the boat. When the boat travels downstream, then the actual speed of the boat is its speed in still water increased by the speed of the current. If we let c represent the speed of the current in the river, then the boat’s speed upstream (against the current) is 3 − c, while the boat’s speed downstream (with the current) is 3 + c. Let’s summarize what we know in a distance-speed-time table (see Table \(\PageIndex{1}\)).

Here is a useful piece of advice regarding distance, speed, and time tables.

Distance, Speed, and Time Tables

Because distance, speed, and time are related by the equation d = vt, whenever you have two boxes in a row of the table completed, the third box in that row can be calculated by means of the formula d = vt.

Note that each row of Table \(\PageIndex{1}\) has two entries entered. The third entry in each row is time. Solve the equation d = vt for t to obtain

\[t=\frac{d}{v} \nonumber \]

The relation t = d/v can be used to compute the time entry in each row of Table \(\PageIndex{1}\).

For example, in the first row, d = 60 miles and v = 3 − c miles per hour. Therefore, the time of travel is

\[t=\frac{d}{v}=\frac{60}{3-c} \nonumber \]

Note how we’ve filled in this entry in Table \(\PageIndex{2}\). In similar fashion, the time to travel downstream is calculated with

\[t=\frac{d}{v}=\frac{60}{3+c} \nonumber \]

We’ve also added this entry to the time column in Table \(\PageIndex{2}\).

To set up an equation, we need to use the fact that the time to travel upstream is twice the time to travel downstream. This leads to the result

\[\frac{60}{3-c}=2\left(\frac{60}{3+c}\right) \nonumber \]

or equivalently,

\[\frac{60}{3-c}=\frac{120}{3+c} \nonumber \]

Multiply both sides by the common denominator, in this case, (3 − c)(3 + c).

\[\begin{aligned}\color{blue}{(3-c)(3+c)}\left[\frac{60}{3-c}\right] &=\left[\frac{120}{3+c}\right]\color{blue}{(3-c)(3+c)} \\ 60(3+c) &=120(3-c) \end{aligned} \nonumber \]

Expand each side of this equation.

\[180+60 c=360-120 c \nonumber \]

This equation is linear (no power of c other than 1). Hence, we want to isolate all terms containing c on one side of the equation. We add 120c to both sides of the equation, then subtract 180 from both sides of the equation.

\[60 c+120 c=360-180 \nonumber \]

From here, it is simple to solve for c.

\[\begin{aligned} 180 c &=180 \\ c &=1 \end{aligned} \nonumber \]

Hence, the speed of the current is 1 mile per hour.

It is important to check that the solution satisfies the constraints of the problem statement.

• If the speed of the boat in still water is 3 miles per hour and the speed of the current is 1 mile per hour, then the speed of the boat upstream (against the current) will be 2 miles per hour. It will take 30 hours to travel 60 miles at this rate.
• The speed of the boat as it goes downstream (with the current) will be 4 miles per hour. It will take 15 hours to travel 60 miles at this rate.

Note that the time to travel upstream (30 hours) is twice the time to travel downstream (15 hours), so our solution is correct.

Let’s look at another example.

Example \(\PageIndex{4}\)

A speedboat can travel 32 miles per hour in still water. It travels 150 miles upstream against the current then returns to the starting location. The total time of the trip is 10 hours. What is the speed of the current?

Let c represent the speed of the current. Going upstream, the boat struggles against the current, so its net speed is 32−c miles per hour. On the return trip, the boat benefits from the current, so its net speed on the return trip is 32 + c miles per hour. The trip each way is 150 miles. We’ve entered this data in Table \(\PageIndex{3}\).

Solving d = vt for the time t,

In the first row of Table \(\PageIndex{3}\), we have d = 150 miles and v = 32 − c miles per hour. Hence, the time it takes the boat to go upstream is given by

\[t=\frac{d}{v}=\frac{150}{32-c} \nonumber \]

Similarly, upon examining the data in the second row of Table \(\PageIndex{3}\), the time it takes the boat to return downstream to its starting location is

\[t=\frac{d}{v}=\frac{150}{32+c} \nonumber \]

These results are entered in Table \(\PageIndex{4}\).

Because the total time to go upstream and return is 10 hours, we can write

\[\frac{150}{32-c}+\frac{150}{32+c}=10 \nonumber \]

Multiply both sides by the common denominator (32 − c)(32 + c).

\[\begin{aligned}\color{blue}{(32-c)(32+c)}\left(\frac{150}{32-c}+\frac{150}{32+c}\right) &=10\color{blue}{(32-c)(32+c)} \\ 150(32+c)+150(32-c) &=10\left(1024-c^{2}\right) \end{aligned} \nonumber \]

We can make the numbers a bit smaller by noting that both sides of the last equation are divisible by 10.

\[15(32+c)+15(32-c)=1024-c^{2} \nonumber \]

Expand, simplify, make one side zero, then factor.

\[\begin{aligned} 480+15 c+480-15 c &=1024-c^{2} \\ 960 &=1024-c^{2} \\ 0 &=64-c^{2} \\ 0 &=(8+c)(8-c) \end{aligned} \nonumber \]

\[8+c=0 \quad \text { or } \quad 8-c=0 \nonumber \]

providing two solutions for the current,

\[c=-8 \quad \text { or } \quad c=8 \nonumber \]

Discarding the negative answer (speed is a positive quantity in this case), the speed of the current is 8 miles per hour.

Does our answer make sense?

• Because the speed of the current is 8 miles per hour, the boat travels 150 miles upstream at a net speed of 24 miles per hour. This will take 150/24 or 6.25 hours.
• The boat travels downstream 150 miles at a net speed of 40 miles per hour. This will take 150/40 or 3.75 hours.

Note that the total time to go upstream and return is 6.25 + 3.75, or 10 hours.

Let’s look at another class of problems.

Work Problems

A nice application of rational functions involves the amount of work a person (or team of persons) can do in a certain amount of time. We can handle these applications involving work in a manner similar to the method we used to solve distance, speed, and time problems. Here is the guiding principle.

The amount of work done is equal to the product of the rate at which work is being done and the amount of time required to do the work. That is,

\[\text { Work }=\text { Rate } \times \text { Time. } \nonumber \]

For example, suppose that Emilia can mow lawns at a rate of 3 lawns per hour. After 6 hours,

\[\text { Work }=3 \frac{\text { lawns }}{\mathrm{hr}} \times 6 \mathrm{hr}=18 \text { lawns. } \nonumber \]

A second important concept is the fact that rates add. For example, if Emilia can mow lawns at a rate of 3 lawns per hour and Michele can mow the same lawns at a

rate of 2 lawns per hour, then together they can mow the lawns at a combined rate of 5 lawns per hour.

Let’s look at an example.

Example \(\PageIndex{5}\)

Bill can finish a report in 2 hours. Maria can finish the same report in 4 hours. How long will it take them to finish the report if they work together?

A common misconception is that the times add in this case. That is, it takes Bill 2 hours to complete the report and it takes Maria 4 hours to complete the same report, so if Bill and Maria work together it will take 6 hours to complete the report. A little thought reveals that this result is nonsense. Clearly, if they work together, it will take them less time than it takes Bill to complete the report alone; that is, the combined time will surely be less than 2 hours.

However, as we saw above, the rates at which they are working will add. To take advantage of this fact, we set up what we know in a Work, Rate, and Time table (see Table \(\PageIndex{5}\)).

• It takes Bill 2 hours to complete 1 report. This is reflected in the entries in the first row of Table \(\PageIndex{5}\).

• It takes Maria 4 hours to complete 1 report. This is reflected in the entries in the second row of Table \(\PageIndex{5}\).

• Let t represent the time it takes them to complete 1 report if they work together. This is reflected in the entries in the last row of Table \(\PageIndex{5}\).

We have advice similar to that given for distance, speed, and time tables.

Work, Rate, and Time Tables

Because work, rate, and time are related by the equation \[\text { Work }=\text { Rate } \times \text { Time } \nonumber \] whenever you have two boxes in a row completed, the third box in that row can be calculated by means of the relation Work \(=\) Rate \(\times\) Time.

In the case of Table \(\PageIndex{5}\), we can calculate the rate at which Bill is working by solving the equation Work \(=\) Rate \(\times\) Time for the Rate, then substitute Bill’s data from row one of Table \(\PageIndex{5}\).

\[Rate \(=\frac{\text { Work }}{\text { Time }}=\frac{1 \text { report }}{2 \mathrm{h}}\) \nonumber \]

Thus, Bill is working at a rate of 1/2 report per hour. Note how we’ve entered this result in the first row of Table 6. Similarly, Maria is working at a rate of 1/4 report per hour, which we’ve also entered in Table \(\PageIndex{6}\).

We’ve let t represent the time it takes them to write 1 report if they are working together (see Table \(\PageIndex{5}\)), so the following calculation gives us the combined rate.

\[Rate \(=\frac{\text { Work }}{\text { Time }}=\frac{1 \text { report }}{t \mathrm{h}}\) \nonumber \]

That is, together they work at a rate of 1/t reports per hour. This result is also recorded in Table \(\PageIndex{6}\).

In our discussion above, we pointed out the fact that rates add. Thus, the equation we seek lies in the Rate column of Table \(\PageIndex{6}\). Bill is working at a rate of 1/2 report per hour and Maria is working at a rate of 1/4 report per hour. Therefore, their combined rate is 1/2 + 1/4 reports per hour. However, the last row of Table \(\PageIndex{6}\) indicates that the combined rate is also 1/t reports per hour. Thus,

\[\frac{1}{2}+\frac{1}{4}=\frac{1}{t} \nonumber \]

Multiply both sides of this equation by the common denominator 4t.

\[\begin{aligned}\color{blue}{(4 t)}\left[\frac{1}{2}+\frac{1}{4}\right] &=\left[\frac{1}{t}\right]\color{blue}{(4 t)} \\ 2 t+t &=4 \end{aligned} \nonumber \]

This equation is linear (no power of t other than 1) and is easily solved.

\[\begin{aligned} 3 t &=4 \\ t &=4 / 3 \end{aligned} \nonumber \]

Thus, it will take 4/3 of an hour to complete 1 report if Bill and Maria work together.

Again, it is very important that we check this result.

• We know that Bill does 1/2 reports per hour. In 4/3 of an hour, Bill will complete

\[\text { Work }=\frac{1}{2} \frac{\text { reports }}{\mathrm{h}} \times \frac{4}{3} \mathrm{h}=\frac{2}{3} \text { reports. } \nonumber \]

That is, Bill will complete 2/3 of a report.

• We know that Maria does 1/4 reports per hour. In 4/3 of an hour, Maria will complete

\[\text { Work }=\frac{1}{4} \frac{\text { reports }}{\mathrm{h}} \times \frac{4}{3} \mathrm{h}=\frac{1}{3} \mathrm{reports} \nonumber \]

That is, Maria will complete 1/3 of a report.

Clearly, working together, Bill and Maria will complete 2/3 + 1/3 reports, that is, one full report.

Example \(\PageIndex{6}\)

It takes Liya 7 more hours to paint a kitchen than it takes Hank to complete the same job. Together, they can complete the same job in 12 hours. How long does it take Hank to complete the job if he works alone?

Let H represent the time it take Hank to complete the job of painting the kitchen when he works alone. Because it takes Liya 7 more hours than it takes Hank, let H + 7 represent the time it takes Liya to paint the kitchen when she works alone. This leads to the entries in Table \(\PageIndex{7}\).

We can calculate the rate at which Hank is working alone by solving the equation Work \(=\) Rate \(\times\) Time for the Rate, then substituting Hank’s data from row one of Table \(\PageIndex{7}\).

\[\text { Rate }=\frac{\text { Work }}{\text { Time }}=\frac{1 \text { kitchen }}{H \text { hour }} \nonumber \]

Thus, Hank is working at a rate of 1/H kitchens per hour. Similarly, Liya is working at a rate of 1/(H + 7) kitchens per hour. Because it takes them 12 hours to complete the task when working together, their combined rate is 1/12 kitchens per hour. Each of these rates is entered in Table \(\PageIndex{8}\).

Because the rates add, we can write

\[\frac{1}{H}+\frac{1}{H+7}=\frac{1}{12} \nonumber \]

Multiply both sides of this equation by the common denominator 12H(H + 7).

\[\begin{aligned} \color{blue}{12 H(H+7)}\left(\frac{1}{H}+\frac{1}{H+7}\right) &=\left(\frac{1}{12}\right)\color{blue}{12 H(H+7)} \\ 12(H+7)+12 H &=H(H+7) \end{aligned} \nonumber \]

Expand and simplify.

\[\begin{aligned} 12 H+84+12 H &=H^{2}+7 H \\ 24 H+84 &=H^{2}+7 H \end{aligned} \nonumber \]

This last equation is nonlinear, so make one side zero by subtracting 24H and 84 from both sides of the equation.

\[\begin{array}{l}{0=H^{2}+7 H-24 H-84} \\ {0=H^{2}-17 H-84}\end{array} \nonumber \]

Note that ac = (1)(−84) = −84. The integer pair {4, −21} has product −84 and sums to −17. Hence,

\[0=(H+4)(H-21) \nonumber \]

\[H+4=0 \quad \text { or } \quad H-21=0 \nonumber \]

leading to the solutions

\[H=-4 \quad \text { or } \quad H=21 \nonumber \]

We eliminate the solution H = −4 from consideration (it doesn’t take Hank negative time to paint the kitchen), so we conclude that it takes Hank 21 hours to paint the kitchen.

Does our solution make sense?

• It takes Hank 21 hours to complete the kitchen, so he is finishing 1/21 of the kitchen per hour.
• It takes Liya 7 hours longer than Hank to complete the kitchen, namely 28 hours, so she is finishing 1/28 of the kitchen per hour.

Together, they are working at a combined rate of

\[\frac{1}{21}+\frac{1}{28}=\frac{4}{84}+\frac{3}{84}=\frac{7}{84}=\frac{1}{12} \nonumber \]

or 1/12 of a kitchen per hour. This agrees with the combined rate in Table \(\PageIndex{8}\).

Exercise \(\PageIndex{1}\)

The sum of the reciprocals of two consecutive odd integers is \(−\frac{16}{63}\). Find the two numbers.

−9, −7

Exercise \(\PageIndex{2}\)

The sum of the reciprocals of two consecutive odd integers is \(\frac{28}{195}\). Find the two numbers.

Exercise \(\PageIndex{3}\)

The sum of the reciprocals of two consecutive integers is \(−\frac{19}{90}\). Find the two numbers.

−10, −9

Exercise \(\PageIndex{4}\)

The sum of a number and its reciprocal is \(\frac{41}{20}\). Find the number(s).

Exercise \(\PageIndex{5}\)

The sum of the reciprocals of two consecutive even integers is \(\frac{5}{12}\). Find the two numbers.

Exercise \(\PageIndex{6}\)

The sum of the reciprocals of two consecutive integers is \(\frac{19}{90}\). Find the two numbers.

Exercise \(\PageIndex{7}\)

The sum of a number and twice its reciprocal is \(\frac{9}{2}\). Find the number(s).

\(\frac{1}{2}\), 4

Exercise \(\PageIndex{8}\)

The sum of a number and its reciprocal is \(\frac{5}{2}\). Find the number(s).

Exercise \(\PageIndex{9}\)

The sum of the reciprocals of two consecutive even integers is \(\frac{11}{60}\). Find the two numbers.

Exercise \(\PageIndex{10}\)

The sum of a number and twice its reciprocal is \(\frac{17}{6}\). Find the number(s).

Exercise \(\PageIndex{11}\)

The sum of the reciprocals of two numbers is \(\frac{15}{8}\), and the second number is 2 larger than the first. Find the two numbers.

{\(\frac{2}{3}\), \(\frac{8}{3}\)} and {\(−\frac{8}{5}\), \(\frac{2}{5}\)}

Exercise \(\PageIndex{12}\)

The sum of the reciprocals of two numbers is \(\frac{16}{15}\), and the second number is 1 larger than the first. Find the two numbers.

Exercise \(\PageIndex{13}\)

Moira can paddle her kayak at a speed of 2 mph in still water. She paddles 3 miles upstream against the current and then returns to the starting location. The total time of the trip is 9 hours. What is the speed (in mph) of the current? Round your answer to the nearest hundredth.

Exercise \(\PageIndex{14}\)

Boris is kayaking in a river with a 6 mph current. Suppose that he can kayak 4 miles upstream in the same amount of time as it takes him to kayak 9 miles downstream. Find the speed (mph) of Boris’s kayak in still water.

Exercise \(\PageIndex{15}\)

Jacob can paddle his kayak at a speed of 6 mph in still water. He paddles 5 miles upstream against the current and then returns to the starting location. The total time of the trip is 5 hours. What is the speed (in mph) of the current? Round your answer to the nearest hundredth.

Exercise \(\PageIndex{16}\)

Boris can paddle his kayak at a speed of 6 mph in still water. If he can paddle 5 miles upstream in the same amount of time as it takes his to paddle 9 miles downstream, what is the speed of the current?

Exercise \(\PageIndex{17}\)

Jacob is canoeing in a river with a 5 mph current. Suppose that he can canoe 4 miles upstream in the same amount of time as it takes him to canoe 8 miles downstream. Find the speed (mph) of Jacob’s canoe in still water.

Exercise \(\PageIndex{18}\)

The speed of a freight train is 16 mph slower than the speed of a passenger train. The passenger train travels 518 miles in the same time that the freight train travels 406 miles. Find the speed of the freight train.

Exercise \(\PageIndex{19}\)

The speed of a freight train is 20 mph slower than the speed of a passenger train. The passenger train travels 440 miles in the same time that the freight train travels 280 miles. Find the speed of the freight train.

Exercise \(\PageIndex{20}\)

Emily can paddle her canoe at a speed of 2 mph in still water. She paddles 5 miles upstream against the current and then returns to the starting location. The total time of the trip is 6 hours. What is the speed (in mph) of the current? Round your answer to the nearest hundredth.

Exercise \(\PageIndex{21}\)

Jacob is canoeing in a river with a 2 mph current. Suppose that he can ca- noe 2 miles upstream in the same amount of time as it takes him to canoe 5 miles downstream. Find the speed (mph) of Jacob’s canoe in still water.

\(\frac{14}{3}\) mph

Exercise \(\PageIndex{22}\)

Moira can paddle her kayak at a speed of 2 mph in still water. If she can paddle 4 miles upstream in the same amount of time as it takes her to paddle 8 miles downstream, what is the speed of the current?

Exercise \(\PageIndex{23}\)

Boris can paddle his kayak at a speed of 6 mph in still water. If he can paddle 5 miles upstream in the same amount of time as it takes his to paddle 10 miles downstream, what is the speed of the current?

Exercise \(\PageIndex{24}\)

The speed of a freight train is 19 mph slower than the speed of a passenger train. The passenger train travels 544 miles in the same time that the freight train travels 392 miles. Find the speed of the freight train.

Exercise \(\PageIndex{25}\)

It takes Jean 15 hours longer to complete an inventory report than it takes Sanjay. If they work together, it takes them 10 hours. How many hours would it take Sanjay if he worked alone?

Exercise \(\PageIndex{26}\)

Jean can paint a room in 5 hours. It takes Amelie 10 hours to paint the same room. How many hours will it take if they work together?

Exercise \(\PageIndex{27}\)

It takes Amelie 18 hours longer to complete an inventory report than it takes Jean. If they work together, it takes them 12 hours. How many hours would it take Jean if she worked alone?

Exercise \(\PageIndex{28}\)

Sanjay can paint a room in 5 hours. It takes Amelie 9 hours to paint the same room. How many hours will it take if they work together?

Exercise \(\PageIndex{29}\)

It takes Ricardo 12 hours longer to complete an inventory report than it takes Sanjay. If they work together, it takes them 8 hours. How many hours would it take Sanjay if he worked alone?

Exercise \(\PageIndex{30}\)

It takes Ricardo 8 hours longer to complete an inventory report than it takes Amelie. If they work together, it takes them 3 hours. How many hours would it take Amelie if she worked alone?

Exercise \(\PageIndex{31}\)

Jean can paint a room in 4 hours. It takes Sanjay 7 hours to paint the same room. How many hours will it take if they work together?

\(\frac{28}{11}\) mph

Exercise \(\PageIndex{32}\)

Amelie can paint a room in 5 hours. It takes Sanjay 9 hours to paint the same room. How many hours will it take if they work together?

Distance, Time and Speed Word Problems | GMAT GRE Maths

Before you get into distance, time and speed word problems, check out how you can add a little power to your resume by getting our mini-MBA certificate.  

Problems involving Time, Distance and Speed are solved based on one simple formula.

Distance = Speed * Time

Which implies →

Speed = Distance / Time   and

Time = Distance / Speed

Let us take a look at some simple examples of distance, time and speed problems.   Example 1. A boy walks at a speed of 4 kmph. How much time does he take to walk a distance of 20 km?

Time = Distance / speed = 20/4 = 5 hours.   Example 2. A cyclist covers a distance of 15 miles in 2 hours. Calculate his speed.

Speed = Distance/time = 15/2 = 7.5 miles per hour.   Example 3. A car takes 4 hours to cover a distance, if it travels at a speed of 40 mph. What should be its speed to cover the same distance in 1.5 hours?

Distance covered = 4*40 = 160 miles

Speed required to cover the same distance in 1.5 hours = 160/1.5 = 106.66 mph   Now, take a look at the following example:

Example 4. If a person walks at 4 mph, he covers a certain distance. If he walks at 9 mph, he covers 7.5 miles more. How much distance did he actually cover?

Now we can see that the direct application of our usual formula Distance = Speed * Time or its variations cannot be done in this case and we need to put in extra effort to calculate the given parameters.

Let us see how this question can be solved.

For these kinds of questions, a table like this might make it easier to solve.

  Let the distance covered by that person be ‘d’.

Walking at 4 mph and covering a distance ‘d’ is done in a time of ‘d/4’

IF he walks at 9 mph, he covers 7.5 miles more than the actual distance d, which is ‘d+7.5’.

He does this in a time of (d+7.5)/9.

Since the time is same in both the cases →

d/4 = (d+7.5)/9            →        9d = 4(d+7.5)   →        9d=4d+30        →        d = 6.

So, he covered a distance of 6 miles in 1.5 hours.   Example 5. A train is going at 1/3 of its usual speed and it takes an extra 30 minutes to reach its destination. Find its usual time to cover the same distance.

Here, we see that the distance is same.

Let us assume that its usual speed is ‘s’ and time is ‘t’, then

  s*t = (1/3)s*(t+30)      →        t = t/3 + 10      →        t = 15.

So the actual time taken to cover the distance is 15 minutes.

Note: Note the time is expressed in terms of ‘minutes’. When we express distance in terms of miles or kilometers, time is expressed in terms of hours and has to be converted into appropriate units of measurement.

Solved Questions on Trains

Example 1. X and Y are two stations which are 320 miles apart. A train starts at a certain time from X and travels towards Y at 70 mph. After 2 hours, another train starts from Y and travels towards X at 20 mph. At what time do they meet?

Let the time after which they meet be ‘t’ hours.

Then the time travelled by second train becomes ‘t-2’.

Distance covered by first train+Distance covered by second train = 320 miles

70t+20(t-2) = 320

Solving this gives t = 4.

So the two trains meet after 4 hours.   Example 2. A train leaves from a station and moves at a certain speed. After 2 hours, another train leaves from the same station and moves in the same direction at a speed of 60 mph. If it catches up with the first train in 4 hours, what is the speed of the first train?

Let the speed of the first train be ‘s’.

Distance covered by the first train in (2+4) hours = Distance covered by second train in 4 hours

Therefore, 6s = 60*4

Solving which gives s=40.

So the slower train is moving at the rate of 40 mph.  

Questions on Boats/Airplanes

For problems with boats and streams,

Speed of the boat upstream (against the current) = Speed of the boat in still water – speed of the stream

[As the stream obstructs the speed of the boat in still water, its speed has to be subtracted from the usual speed of the boat]

Speed of the boat downstream (along with the current) = Speed of the boat in still water + speed of the stream

[As the stream pushes the boat and makes it easier for the boat to reach the destination faster, speed of the stream has to be added]

Similarly, for airplanes travelling with/against the wind,

Speed of the plane with the wind = speed of the plane + speed of the wind

Speed of the plane against the wind = speed of the plane – speed of the wind

Let us look at some examples.

Example 1. A man travels at 3 mph in still water. If the current’s velocity is 1 mph, it takes 3 hours to row to a place and come back. How far is the place?

Let the distance be ‘d’ miles.

Time taken to cover the distance upstream + Time taken to cover the distance downstream = 3

Speed upstream = 3-1 = 2 mph

Speed downstream = 3+1 = 4 mph

So, our equation would be d/2 + d/4 = 3 → solving which, we get d = 4 miles.   Example 2. With the wind, an airplane covers a distance of 2400 kms in 4 hours and against the wind in 6 hours. What is the speed of the plane and that of the wind?

Let the speed of the plane be ‘a’ and that of the wind be ‘w’.

Our table looks like this:  

  4(a+w) = 2400 and 6(a-w) = 2400

Expressing one unknown variable in terms of the other makes it easier to solve, which means

a+w = 600 → w=600-a

Substituting the value of w in the second equation,

a-(600-a) = 400 → a = 500

The speed of the plane is 500 kmph and that of the wind is 100 kmph.  

More solved examples on Speed, Distance and Time

Example 1. A boy travelled by train which moved at the speed of 30 mph. He then boarded a bus which moved at the speed of 40 mph and reached his destination. The entire distance covered was 100 miles and the entire duration of the journey was 3 hours. Find the distance he travelled by bus.

Let the time taken by the train be ‘t’. Then that of bus is ‘3-t’.

The entire distance covered was 100 miles

So, 30t + 40(3-t) = 100

Solving which gives t=2.

Substituting the value of t in 40(3-t), we get the distance travelled by bus is 40 miles.

Alternatively, we can add the time and equate it to 3 hours, which directly gives the distance.

d/30 + (100-d)/40 = 3

Solving which gives d = 60, which is the distance travelled by train. 100-60 = 40 miles is the distance travelled by bus.   Example 2. A plane covered a distance of 630 miles in 6 hours. For the first part of the trip, the average speed was 100 mph and for the second part of the trip, the average speed was 110 mph. what is the time it flew at each speed?

Our table looks like this.

Assuming the distance covered in the 1 st part of journey to be ‘d’, the distance covered in the second half becomes ‘630-d’.

Assuming the time taken for the first part of the journey to be ‘t’, the time taken for the second half becomes ‘6-t’.

From the first equation, d=100t

The second equation is 630-d = 110(6-t).

Substituting the value of d from the first equation, we get

630-100t = 110(6-t)

Solving this gives t=3.

So the plane flew the first part of the journey in 3 hours and the second part in 3 hours.   Example 2. Two persons are walking towards each other on a walking path that is 20 miles long. One is walking at the rate of 3 mph and the other at 4 mph. After how much time will they meet each other?

  Assuming the distance travelled by the first person to be ‘d’, the distance travelled by the second person is ’20-d’.

The time is ‘t’ for both of them because when they meet, they would have walked for the same time.

Since time is same, we can equate as

d/3 = (20-d)/4

Solving this gives d=60/7 miles (8.5 miles approximately)

Then t = 20/7 hours

So the two persons meet after 2 6/7 hours.  

Practice Questions for you to solve

Problem 1: Click here

A boat covers a certain distance in 2 hours, while it comes back in 3 hours. If the speed of the stream is 4 kmph, what is the boat’s speed in still water?

A) 30 kmph B) 20 kmph C) 15 kmph D) 40 kmph

Answer 1: Click here

Explanation

Let the speed of the boat be ‘s’ kmph.

Then, 2(s+4) = 3(s-4) → s = 20

Problem 2: Click here

A cyclist travels for 3 hours, travelling for the first half of the journey at 12 mph and the second half at 15 mph. Find the total distance he covered.

A) 30 miles B) 35 miles C) 40 miles D) 180 miles

Answer 2: Click here

Since it is mentioned, that the first ‘half’ of the journey is covered in 12 mph and the second in 15, the equation looks like

(d/2)/12 + (d/2)/15 = 3

Solving this gives d = 40 miles

Mini-MBA | Start here | Success stories | Reality check | Knowledgebase | Scholarships | Services Serious about higher ed? Follow us:                

17 thoughts on “Distance, Time and Speed Word Problems | GMAT GRE Maths”

Meera walked to school at a speed of 3 miles per hour. Once she reached the school, she realized that she forgot to bring her books, so rushed back home at a speed of 6 miles per hour. She then walked back to school at a speed of 4 miles per hour. All the times, she walked in the same route. please explain above problem

When she walks faster the time she takes to reach her home and school is lower. There is nothing wrong with the statement. They never mentioned how long she took every time.

a man covers a distance on a toy train.if the train moved 4km/hr faster,it would take 30 min. less. if it moved 2km/hr slower, it would have taken 20 min. more .find the distance.

Let the speed be x. and time be y. A.T.Q, (x+4)(y-1/2)=d and (x-2)(y+1/3)=d. Equate these two and get the answer

Could you explain how ? you have two equations and there are 3 variables.

The 3rd equation is d=xy. Now, you have 3 equations with 3 unknowns. The variables x and y represent the usual speed and usual time to travel distance d.

Speed comes out to be 20 km/hr and the time taken is 3 hrs. The distance traveled is 60 km.

(s + 4) (t – 1/2)= st 1…new equotion = -1/2s + 4t = 2

(s – 2) (t + 1/3)= st 2…new equotion = 1/3s – 2t = 2/3

Multiply all by 6 1… -3s + 24t = 12 2… 2s – 12t = 4 Next, use elimination t= 3 Find s: -3s + 24t = 12 -3s + 24(3) = 12 -3s = -60 s= 20

st or distance = 3 x 20 = 60 km/h

It’s probably the average speed that we are looking for here. Ave. Speed= total distance/ total time. Since it’s harder to look for one variable since both are absent, you can use, 3d/ d( V2V3 + V1V3 + V1V2/ V1V2V3)

2 girls meenu and priya start at the same time to ride from madurai to manamadurai, 60 km away.meenu travels 4kmph slower than priya. priya reaches manamadurai and at turns back meeting meenu 12km from manamaduai. find meenu’s speed?

Hi, when the two girls meet, they have taken equal time to travel their respective distance. So, we just need to equate their time equations

Distance travelled by Meenu = 60 -12 = 48 Distance travelled by Priya = 60 + 12 = 72 Let ‘s’ be the speed of Meenu

Time taken by Meenu => t1 = 48/s Time taken by Priya => t2 = 72/(s+4)

t1=t2 Thus, 48/s = 72/(s+4) => 24s = 192 => s = 8Km/hr

A train can travel 50% faster than a car. Both start from point A at the same time and reach point B 75 KMS away from A at the same time. On the way, however the train lost about 12.5 minutes while stopping at the stations. The speed of the car is:

Let speed of the CAR BE x kmph.

Then, speed of the train = 3/2(x) .’. 75/x – 75/(3/2)x= 125/(10*60) — subtracting the times travelled by two them hence trains wastage time

therefore x= 120 kmph

A cyclist completes a distance of 60 km at the same speed throughout. She travels 10 km in one hour. She stops every 20 km for one hour to have a break. What are the two variables involved in this situation?

For the answer, not variables: 60km divided by 10km/h=6 hours 60 divided by 20= 3 hours 3 hours+6 hours= 9 hours Answer: 9 hours

Let the length of the train to prod past a point be the intrinsic distance (D) of the train and its speed be S. Its speed, S in passing the electric pole of negligible length is = D/12. The length of the platform added to the intrinsic length of the train. So, the total distance = D + 200. The time = 20 secs. The Speed, S = (D + 200)/20 At constant speed, D/12 = (D + 200)/20 Cross-multiplying, 20D = 12D + 200*12 20D – 12D = 200*12; 8D = 200*12 D = 200*12/8 = 300m. 4th Aug, 2018

Can anyone solve this? Nathan and Philip agree to meet up at the park at 5:00 pm. Nathan lives 300 m due north of the park, and Philip lives 500 m due west of the park. Philip leaves his house at 4:54 pm and walks towards the park at a pace of 1.5 m/s, but Nathan loses track of time and doesn’t leave until 4:59 pm. Trying to avoid being too late, he jogs towards the park at 2.5 m/s. At what rate is the distance between the two friends changing 30 seconds after Nathan has departed?

Leave a Comment Cancel reply

Speed Practice Questions

Click here for questions, click here for answers.

speed, distance, time

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024