random assignment problems on 2d manifolds

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

We're Hiring!
Help Center

Random assignment problems on 2d manifolds

2021, Journal of Statistical Physics

We consider the assignment problem between two sets of N random points on a smooth, two-dimensional manifold Ω of unit area. It is known that the average cost scales as E Ω (N) ∼ 1 2π ln N with a correction that is at most of order √ ln N ln ln N. In this paper, we show that, within the linearization approximation of the field-theoretical formulation of the problem, the first Ω-dependent correction is on the constant term, and can be exactly computed from the spectrum of the Laplace-Beltrami operator on Ω. We perform the explicit calculation of this constant for various families of surfaces, and compare our predictions with extensive numerics.

Related Papers

Journal of Statistical Physics

Matteo D'Achille

We consider the random Euclidean assignment problem on the line between two sets of N random points, independently generated with the same probability density function 𝜚. The cost of the matching is supposed to be dependent on a power 𝑝>1 of the Euclidean distance of the matched pairs. We discuss an integral expression for the average optimal cost for 𝑁≫1 that generalizes a previous result obtained for 𝑝=2. We also study the possible divergence of the given expression due to the vanishing of the probability density function. The provided regularization recipe allows us to recover the proper scaling law for the cost in the divergent cases, and possibly some of the involved coefficients. The possibility that the support of 𝜚 is a disconnected interval is also analysed. We exemplify the proposed procedure and we compare our predictions with the results of numerical simulations.

Electronic Journal of Probability

Luigi Ambrosio

Thèse de l'Université Paris-Saclay

Given 2𝑛 points, 𝑛 ``red'' and 𝑛 ``blue'', in a Euclidean space, solving the associated Euclidean Assignment Problem consists in finding the bijection between red and blue points that minimizes a functional of the point positions. In the stochastic version of this problem, the points are a Poisson Point Process, and some interest has developed over the years on the typical and average properties of the solution in the large 𝑛 limit. This PhD thesis investigates this problem in a number of cases (many exact results in 𝑑=1, the derivation of some fine properties in 𝑑=2, in part still conjectural, an investigation on self-similar fractals with intermediate dimensions,...). In particular, we present new contributions on the asymptotic behavior of the cost of the solution, motivated (among others) by the physics of Disordered Systems, and by results in Functional Analysis on the Monge--Kantorovich problem in the continuum.

Panos M Pardalos

The multidimensional assignment problem (MAP) is a NP-hard combinatorial optimization problem, occurring in many applications, such as data association. In this paper, we prove two conjectures made in Ref. 1 and based on data from computational experiments on MAPs. We show that the mean optimal objective function cost of random instances of the MAP goes to zero as the problem size increases, when assignment costs are independent exponentially or uniformly distributed random variables.

In a pioneering work , Mézard and Parisi proved that methods from the theory of disordered systems at low temperature can be used to solve very difﬁcult combinatorial optimisation problems, being possible to assign an energy to their conﬁgurations and proceed with the usual apparatus of statistical mechanics. Moreover, numerical simulations showed reach behaviors that, as well as being approachable by replica calculations, opened a lot of interesting questions. Among the variety of problems that one can study in this context this work focused on the linear sum assignment problem, which can be described for example as the assignment of n tasks to n workers in such a way that the total time of execution of the tasks is minimum, being known that worker i spends tij seconds to complete the task j. The work was developed in two stages: ﬁrst it was constructed and tested a C++ implementation of the Jonker-Volgenant algorithm that solves a general linear sum assignment problem; this code was used to study the Euclidean bipartite matching problem in D dimensions, where frustration is imposed by the geometry of the ambient space, and to see how this problem reaches its mean ﬁeld approximation in the D → ∞limit (the random assignment problem), where the assignment cost is completely aleatory.

Abstract The Multidimensional Assignment Problem (MAP) is a higher-dimensional version of the Linear Assignment Problem that arises in the areas of data association, target tracking, resource allocation, etc. This paper elucidates the question of asymptotical behavior of the expected optimal value of the large-scale MAP whose assignment costs are independent identically distributed random variables with a prescribed probability distribution.

Abstract The multidimensional assignment problem (MAP) is a combinatorial problem where elements of a variable number of sets must be matched, in order to find a minimum cost solution. The MAP has applications in a large number of areas, and is known to be NP-hard. We survey some of the recent work being done in the determination of the asymptotic value of optimal solutions to the MAP, when costs are drawn from a known distribution (eg, exponential, uniform, or normal).

Physical Review E

Matteo D'Achille , Gabriele Sicuro

We analytically derive, in the context of the replica formalism, the first finite size corrections to the average optimal cost in the random assignment problem for a quite generic distribution law for the costs. We show that, when moving from a power law distribution to gamma distribution, the leading correction changes both in sign and in its scaling properties. We also examine the behavior of the corrections when approaching a delta function distribution. By using a numerical solution of the saddle-point equations, we provide predictions which are very well confirmed by numerical simulations.

Probability Theory and Related Fields

We discuss the optimal matching solution for both the assignment problem and the matching problem in one dimension for a large class of convex cost functions. We consider the problem in a compact set with the topology both of the interval and of the circumference. Afterwards, we assume the points' positions to be random variables identically and independently distributed on the considered domain. We analytically obtain the average optimal cost in the asymptotic regime of very large number of points N and some correlation functions for a power-law type cost function in the form c(z) = z p , both in the p > 1 case and in the p < 0 case. The scaling of the optimal cost with the number of points is N p /2 for the assignment and N p for the matching when p > 1, whereas in both cases it is a constant when p < 0. Finally, our predictions are compared with the results of numerical simulations.

Subscribe to the PwC Newsletter

Join the community, edit social preview.

random assignment problems on 2d manifolds

Add a new code entry for this paper

Remove a code repository from this paper, mark the official implementation from paper authors, add a new evaluation result row, remove a task, add a method, remove a method, edit datasets, random assignment problems on ${2d}$ manifolds.

4 Aug 2020 · Dario Benedetto , Emanuele Caglioti , Sergio Caracciolo , Matteo D'Achille , Gabriele Sicuro , Andrea Sportiello · Edit social preview

We consider the assignment problem between two sets of $N$ random points on a smooth, two-dimensional manifold $\Omega$ of unit area. It is known that the average cost scales as $E_{\Omega}(N)\sim\frac{1}{2\pi}\ln N$ with a correction that is at most of order $\sqrt{\ln N\ln\ln N}$. In this paper, we show that, within the linearization approximation of the field-theoretical formulation of the problem, the first $\Omega$-dependent correction is on the constant term, and can be exactly computed from the spectrum of the Laplace--Beltrami operator on $\Omega$. We perform the explicit calculation of this constant for various families of surfaces, and compare our predictions with extensive numerics.

Code Edit Add Remove Mark official

The topology of probability distributions on manifolds

Published: 22 March 2014
Volume 161 , pages 651–686, ( 2015 )

Cite this article

Omer Bobrowski 1 &
Sayan Mukherjee 2

2046 Accesses

33 Citations

Explore all metrics

Let $\mathcal {P}$ be a set of $n$ random points in $\mathbb {R}^d$ , generated from a probability measure on a $m$ -dimensional manifold $\mathcal {M}\subset \mathbb {R}^d$ . In this paper we study the homology of $\mathcal {U}(\mathcal {P},r)$ —the union of $d$ -dimensional balls of radius $r$ around $\mathcal {P}$ , as $n\rightarrow \infty $ , and $r\rightarrow 0$ . In addition we study the critical points of $d_{\mathcal {P}}$ —the distance function from the set $\mathcal {P}$ . These two objects are known to be related via Morse theory. We present limit theorems for the Betti numbers of $\mathcal {U}(\mathcal {P},r)$ , as well as for number of critical points of index $k$ for $d_{\mathcal {P}}$ . Depending on how fast $r$ decays to zero as $n$ grows, these two objects exhibit different types of limiting behavior. In one particular case ( $n r^m \ge C \log n$ ), we show that the Betti numbers of $\mathcal {U}(\mathcal {P},r)$ perfectly recover the Betti numbers of the original manifold $\mathcal {M}$ , a result which is of significant interest in topological manifold learning.

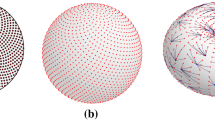
Random Assignment Problems on 2d Manifolds

On the Maximum $$f$$ -Divergence of Probability Distributions Given the Value of Their Coupling

The reach of subsets of manifolds

Avoid common mistakes on your manuscript.

1 Introduction

The incorporation of geometric and topological concepts for statistical inference is at the heart of spatial point process models, manifold learning, and topological data analysis. The motivating principle behind manifold learning is using low dimensional geometric summaries of the data for statistical inference [ 4 , 10 , 21 , 47 , 50 ]. In topological data analysis, topological summaries of data are used to infer or extract underlying structure in the data [ 19 , 25 , 39 , 49 , 52 ]. In the analysis of spatial point processes, limiting distributions of integral-geometric quantities such as area and boundary length [ 23 , 35 , 41 , 48 ], Euler characteristic of patterns of discs centered at random points [ 35 , 51 ], and the Palm mean (the mean number of pairs of points within a radius $r$ ) [ 23 , 41 , 48 , 51 ] have been used to characterize parameters of point processes, see [ 35 ] for a short review.

A basic research topic in both manifold learning and topological data analysis is understanding the distribution of geometric and topological quantities generated by a stochastic process. In this paper we consider the standard model in topological data analysis and manifold learning—the stochastic process is a random sample of points $\mathcal {P}$ drawn from a distribution supported on a compact $m$ -dimensional manifold $\mathcal {M}$ , embedded in $\mathbb {R}^d$ . In both geometric and topological data analysis, understanding the local neighborhood structure of the data is important. Thus, a central parameter in any analysis is the size $r$ (radius) of a local neighborhood and how this radius scales with the number of observations.

We study two different, yet related, objects. The first object is the union of the $r$ -balls around the random sample, denoted by $\mathcal {U}(\mathcal {P},r)$ . For this object, we wish to study its homology, and in particular its Betti numbers. Briefly, the Betti numbers are topological invariants measuring the number of components and holes of different dimensions. Equivalently, all the results in this paper can be phrased in terms of the Čech complex $\check{C}(\mathcal {P},r)$ . A simplicial complex is a collection of vertices, edges, triangles, and higher dimensional faces, and can be thought of as a generalization of a graph. The Čech complex $\check{C}(\mathcal {P},r)$ is a simplicial complex where each $k$ -dimensional face corresponds to an intersection of $k+1$ balls in $\mathcal {U}(\mathcal {P},r)$ (see Definition 2.4). By the famous ‘Nerve Lemma’ (cf. [ 15 ]), $\mathcal {U}(\mathcal {P},r)$ has the same homology as $\check{C}(\mathcal {P},r)$ . The second object of study is the distance function from the set $\mathcal {P}$ , denoted by $d_{\mathcal {P}}$ , and its critical points. The connection between these two objects is given by Morse theory, which will be reviewed later. In a nutshell, Morse theory describes how critical points of a given function either create or destroy homology elements (connected components and holes) of sublevel sets of that function.

We characterize the limit distribution of the number of critical points of $d_{\mathcal {P}}$ , as well as the Betti numbers of $\mathcal {U}(\mathcal {P},r)$ . Similarly to many phenomena in random geometric graphs as well as random geometric complexes in Euclidean spaces [ 29 , 30 , 32 , 45 ], the qualitative behavior of these distributions falls into three main categories based on how the radius $r$ scales with the number of samples $n$ . This behavior is determined by the term $nr^m$ , where $m$ is the intrinsic dimension of the manifold. This term can be thought of as the expected number of points in a ball of radius $r$ . We call the different categories—the sub-critical ( $nr^m\rightarrow 0$ ), critical ( $nr^m\rightarrow \lambda $ ) and super-critical ( $nr^m\rightarrow \infty $ ) regimes. The union $\mathcal {U}(\mathcal {P},r)$ exhibits very different limiting behavior in each of these three regimes. In the sub-critical regime, $\mathcal {U}(\mathcal {P},r)$ is very sparse and consists of many small particles, with very few holes. In the critical regime, $\mathcal {U}(\mathcal {P},r)$ has $O(n)$ components as well as holes of any dimension $k<m$ . From the manifold learning perspective, the most interesting regime would be the super-critical. One of the main results in this paper (see Theorem 4.9) states that if we properly choose the radius $r$ within the super-critical regime, the homology of the random space $\mathcal {U}(\mathcal {P},r)$ perfectly recovers the homology of the original manifold $\mathcal {M}$ . This result extends the work in [ 44 ] for a large family of distributions on $\mathcal {M}$ , requires much weaker assumptions on the geometry of the manifold, and is proved to happen almost surely.

The study of critical points for the distance function provides additional insights on the behavior of $\mathcal {U}(\mathcal {P},r)$ via Morse theory, we return to this later in the paper. While Betti numbers deal with ‘holes’ which are typically determined by global phenomena, the structure of critical points is mostly local in nature. Thus, we are able to derive precise results for critical points even in cases where we do not have precise analysis of Betti numbers. One of the most interesting consequence of the critical point analysis in this paper relates to the Euler characteristic of $\mathcal {U}(\mathcal {P},r)$ . One way to think about the Euler characteristic of a topological spaces $\mathcal {S}$ is as an integer “summary” of the Betti numbers given by $\chi (\mathcal {S}) = \sum _{k} (-1)^k \beta _k(\mathcal {S})$ . Morse theory enables us to compute $\chi (\mathcal {U}(\mathcal {P},r))$ using the critical points of the distance function $d_{\mathcal {P}}$ (see Sect. 4.2 ). This computation may provide important insights on the behavior of the Betti numbers in the critical regime. We note that the equivalent result for Euclidean spaces appeared in [ 13 ].

In topological data analysis there has been work on understanding properties of random abstract simplicial complexes generated from stochastic processes [ 1 , 2 , 5 , 13 , 28 – 31 , 45 , 46 ] and non-asymptotic bounds on the convergence or consistency of topological summaries as the number of points increase [ 11 , 17 , 18 , 20 , 22 , 43 , 44 ]. The central idea in these papers has been to study statistical properties of topological summaries of point cloud data. There has also been an effort to characterize the topology of a distribution (for example a noise model) [ 1 , 2 , 30 ]. Specifically, the results in our paper adapt the results in [ 13 , 29 , 30 ] from the setting of a distribution in Euclidean space to one supported on a manifold.

There is a natural connection of the results in this paper with results in point processes, specifically random set models such as the Poisson–Boolean model [ 36 ]. The stochastic process we study in this paper is an example of a random set model–stochastic models that place probability distributions on regions or geometric objects [ 33 , 40 ]. Classically, people have studied limiting distributions of quantities such as volume, surface area, integral of mean curvature and Euler characteristic generated from the random set model. Initial studies examined second order statistics, summaries of observations that measure position or interaction among points, such as the distribution function of nearest neighbors, the spherical contact distribution function, and a variety of other summaries such as Ripley’s K-function, the L-function and the pair correlation function, see [ 23 , 41 , 48 , 51 ]. It is known that there are limitations in only using second order statistics since one can state different point processes that have the same second order statistics [ 8 ]. In the spatial statistics literature our work is related to the use of morphological functions for point processes where a ball of radius $r$ is placed around each point sampled from the point process and the topology or morphology of the union of these balls is studied. Our results are also related to ideas in the statistics and statistical physics of random fields, see [ 3 , 7 , 14 , 53 , 54 ], a random process on a manifold can be thought of as an approximation of excursion sets of Gaussian random fields or energy landscapes.

The paper is structured as follows. In Sect. 2 we give a brief introduction to the topological objects we study in this paper. In Sect. 3 we state the probability model and define the relevant topological and geometric quantities of study. In Sect. 4 and 5 we state our main results and proofs, respectively.

2 Topological ingredients

In this paper we study two topological objects generated from a finite random point cloud $\mathcal {P}\subset \mathbb {R}^d$ (a set of points in $\mathbb {R}^d$ ).

Given the set $\mathcal {P}$ we define

where $B_\epsilon (p)$ is a $d$ -dimensional ball of radius $\epsilon $ centered at $p$ . Our interest in this paper is in characterizing the homology —in particular the Betti numbers of this space, i.e. the number of components, holes, and other types of voids in the space.

We define the distance function from $\mathcal {P}$ as

As a real valued function, $d_{\mathcal {P}}:\mathbb {R}^d\rightarrow \mathbb {R}$ might have critical points of different types (i.e. minimum, maximum and saddle points). We would like to study the amount and type of these points.

In this section we give a brief introduction to the topological concepts behind these two objects. Observe that the sublevel sets of the distance function are

Morse theory, discussed later in this section, describes the interplay between critical points of a function and the homology of its sublevel sets, and hence provides the link between our two objects of study.

2.1 Homology and betti numbers

Let $X$ be a topological space. The $k$ -th Betti number of $X$ , denoted by $\beta _k(X)$ is the rank of $H_k(X)$ —the $k$ -th homology group of $X$ . This definition assumes that the reader has a basic grounding in algebraic topology. Otherwise, the reader should be willing to accept a definition of $\beta _k(X)$ as the number of $k$ -dimensional ‘cycles’ or ‘holes’ in $X$ , where a $k$ -dimensional hole can be thought of as anything that can be continuously transformed into the boundary of a $(k+1)$ -dimensional shape. The zeroth Betti number, $\beta _0(X)$ , is merely the number of connected components in $X$ . For example, the $2$ -dimensional torus $T^2$ has a single connected component, two non-trivial $1$ -cycles, and a $2$ -dimensional void. Thus, we have that $\beta _0(T^2) = 1,\ \beta _1(T^2) = 2,$ and $\beta _2(T^2)=1$ . Formal definitions of homology groups and Betti numbers can be found in [ 27 , 42 ].

2.2 Critical points of the distance function

The classical definition of critical points using calculus is as follows. Let $f:\mathbb {R}^d\rightarrow \mathbb {R}$ be a $C^2$ function. A point $c\in \mathbb {R}$ is called a critical point of $f$ if $\nabla f (c) =0$ , and the real number $f(c)$ is called a critical value of $f$ . A critical point $c$ is called non-degenerate if the Hessian matrix $H_f(c)$ is non-singular. In that case, the Morse index of $f$ at $c$ , denoted by $\mu (c)$ is the number of negative eigenvalues of $H_f(c)$ . A $C^2$ function $f$ is a Morse function if all its critical points are non-degenerate, and its critical levels are distinct.

Note, the distance function $d_{\mathcal {P}}$ is not everywhere differentiable, therefore the definition above does not apply. However, following [ 26 ], one can still define a notion of non-degenerate critical points for the distance function, as well as their Morse index. Extending Morse theory to functions that are non-smooth has been developed for a variety of applications [ 9 , 16 , 26 , 34 ]. The class of functions studied in these papers have been the minima (or maxima) of a functional and called ‘min-type’ functions. In this section, we specialize those results to the case of the distance function.

We start with the local (and global) minima of $d_{\mathcal {P}}$ , the points of $\mathcal {P}$ where $d_{\mathcal {P}} = 0$ , and call these critical points with index $0$ . For higher indices, we have the following definition.

Definition 2.1

A point $c\in \mathbb {R}^d$ is a critical point of index $k$ of $d_{\mathcal {P}}$ , where $1 \le k \le d$ , if there exists a subset $\mathcal {Y}$ of $k+1$ points in $\mathcal {P}$ such that:

$\forall y\in \mathcal {Y}: d_{\mathcal {P}}(c) = \left\| c-y\right\| $ , and, $\forall p\in \mathcal {P}\backslash \mathcal {Y}$ we have $\left\| c-p\right\| > d_{\mathcal {P}}(p)$ .

The points in $\mathcal {Y}$ are in general position (i.e. the $k+1$ points of $\mathcal {Y}$ do not lie in a $(k-1)$ -dimensional affine space).

$c \in {{\mathrm{conv}}}^{\circ }(\mathcal {Y})$ , where ${{\mathrm{conv}}}^{\circ }(\mathcal {Y})$ is the interior of the convex hull of $\mathcal {Y}$ (an open $k$ -simplex in this case).

The first condition implies that $d_{\mathcal {P}} \equiv d_{\mathcal {Y}}$ in a small neighborhood of $c$ . The second condition implies that the points in $\mathcal {Y}$ lie on a unique $(k-1)$ -dimensional sphere. We shall use the following notation:

Note that $S(\mathcal {Y})$ is a $(k-1)$ -dimensional sphere, whereas $B(\mathcal {Y})$ is a $d$ -dimensional ball. Obviously, $S(\mathcal {Y}) \subset B(\mathcal {Y})$ , but unless $k=d,\,S$ is not the boundary of $B$ . Since the critical point $c$ in Definition 2.1 is equidistant from all the points in $\mathcal {Y}$ , we have that $c=C(\mathcal {Y})$ . Thus, we say that $c$ is the unique index $k$ critical point generated by the $k+1$ points in $\mathcal {Y}$ . The last statement can be rephrased as follows:

A subset $\mathcal {Y}\subset \mathcal {P}$ of $k+1$ points in general position generates an index $k$ critical point if, and only if, the following two conditions hold:

CP1 $\quad C(\mathcal {Y}) \in {{\mathrm{conv}}}^{\circ }(\mathcal {Y})$ ,

CP2 $\quad \mathcal {P}\cap {B(\mathcal {Y})}= \emptyset $ .

Furthermore, the critical point is $C(\mathcal {Y})$ and the critical value is $R(\mathcal {Y})$ .

Figure 1 depicts the generation of an index $2$ critical point in $\mathbb {R}^2$ by subsets of $3$ points. We shall also be interested in ‘local’ critical points, points where $d_{\mathcal {P}}(c)\le \epsilon $ . This adds a third condition,

CP3 $\quad R(\mathcal {Y}) \le \epsilon $ .

Generating a critical point of index $2$ in $\mathbb {R}^2$ , a maximum point. The small blue disks are the points of $\mathcal {P}$ . We examine three subsets of $\mathcal {P}$ : $\mathcal {Y}_1 = \left\{ y_1,y_2,y_3\right\} \!,\,\mathcal {Y}_2 = \left\{ y_4,y_5,y_6\right\} $ , and $\mathcal {Y}_3 = \left\{ y_7,y_8,y_9\right\} $ . $S(\mathcal {Y}_i)$ are the dashed circles , whose centers are $C(\mathcal {Y}_i) = c_i$ . The shaded balls are $B(\mathcal {Y}_i)$ , and the interior of the triangles are ${{\mathrm{conv}}}^{\circ }(\mathcal {Y}_i)$ . (1) We see that both $C(\mathcal {Y}_1) \in {{\mathrm{conv}}}^{\circ }(\mathcal {Y}_1)$ ( CP1 ) and $\mathcal {P}\cap B(\mathcal {Y}_1) = \emptyset $ ( CP2 ). Hence $c_1$ is a critical point of index $2$ . (2) $C(\mathcal {Y}_2) \not \in {{\mathrm{conv}}}^{\circ }(\mathcal {Y}_2)$ , which means that ( CP1 ) does not hold, and therefore $c_2$ is not a critical point (as can be observed from the flow arrows ). (3) $C(\mathcal {Y}_3) \in {{\mathrm{conv}}}^{\circ }(\mathcal {Y}_3)$ , so ( CP1 ) holds. However, we have $\mathcal {P}\cap B(\mathcal {Y}_3) = \left\{ p\right\} $ , so ( CP2 ) does not hold, and therefore $c_3$ is also not a critical point. Note that in a small neighborhood of $c_3$ we have $d_{\mathcal {P}} \equiv d_{\left\{ p\right\} }$ , completely ignoring the existence of $\mathcal {Y}_3$ (color figure online)

The following indicator functions, related to CP1–CP3, will appear often.

Definition 2.3

Using the notation above,

2.3 Morse theory

The study of homology is strongly connected to the study of critical points of real valued functions. The link between them is called Morse theory, and we shall describe it here briefly. For a deeper introduction, we refer the reader to [ 38 ].

Let $\mathcal {M}$ be a smooth manifold embedded in $\mathbb {R}^d$ , and let $f:\mathcal {M}\rightarrow \mathbb {R}$ be a Morse function (see Sect. 2.2 ).

The main idea of Morse theory is as follows. Suppose that $\mathcal {M}$ is a closed manifold (a compact manifold without a boundary), and let $f:\mathcal {M}\rightarrow \mathbb {R}$ be a Morse function. Denote

(sublevel sets of $f$ ). If there are no critical levels in $(a,b]$ , then $\mathcal {M}_a$ and $\mathcal {M}_b$ are homotopy equivalent , and in particular have the same homology. Next, suppose that $c$ is a critical point of $f$ with Morse index $k$ , and let $v=f(c)$ be the critical value at $c$ . Then the homology of $\mathcal {M}_{\rho }$ changes at $v$ in the following way. For a small enough $\epsilon $ we have that the homology of $\mathcal {M}_{v+\epsilon }$ is obtained from the homology of $\mathcal {M}_{v-\epsilon }$ by either adding a generator to $H_k$ (increasing $\beta _k$ by one) or terminating a generator of $H_{k-1}$ (decreasing $\beta _{k-1}$ by one). In other words, as we pass a critical level, either a new $k$ -dimensional hole is formed, or an existing $(k-1)$ -dimensional hole is terminated (filled up).

Note, that while classical Morse theory deals with Morse functions (and in particular, $C^2$ ) on compact manifolds, its extension for min-type functions presented in [ 26 ] enables us to apply these concepts to the distance function $d_{\mathcal {P}}$ as well.

2.4 Čech complexes and the nerve lemma

The Čech complex generated by a set of points $\mathcal {P}$ is a simplicial complex, made up of vertices, edges, triangles and higher dimensional faces. While its general definition is quite broad, and uses intersections of arbitrary nice sets, the following special case using intersection of Euclidean balls will be sufficient for our analysis.

Definition 2.4

(Čech complex) Let $\mathcal {P}= \left\{ x_1,x_2,\ldots \right\} $ be a collection of points in $\mathbb {R}^d$ , and let $\epsilon >0$ . The Čech complex $\check{C}(\mathcal {P}, \epsilon )$ is constructed as follows:

The $0$ -simplices (vertices) are the points in $\mathcal {P}$ .

An $n$ -simplex $[x_{i_0},\ldots ,x_{i_n}]$ is in $\check{C}(\mathcal {P},\epsilon )$ if $\bigcap _{k=0}^{n} {B_{\epsilon }(x_{i_k})} \ne \emptyset $ .

Figure 2 depicts a simple example of a Čech complex in $\mathbb {R}^2$ . An important result, known as the ‘Nerve Lemma’, links the Čech complex $\check{C}(\mathcal {P},\epsilon )$ and the neighborhood set $\mathcal {U}(\mathcal {P}, \epsilon )$ , and states that they are homotopy equivalent, and in particular they have the same homology groups (cf. [ 15 ]). Thus, for example, they have the same Betti numbers.

The Čech complex $\check{C}(\mathcal {P},\epsilon )$ , for $\mathcal {P}= \left\{ x_1,\ldots ,x_6\right\} \subset \mathbb {R}^2$ , and some $\epsilon $ . The complex contains 6 vertices, 7 edges, and a single 2-dimensional face

Our interest in the Čech complex is twofold. Firstly, the Čech complex is a high-dimensional analogue of a geometric graph. The study of random geometric graphs is well established (cf. [ 45 ]). However, the study of higher dimensional geometric complexes is at its early stages. Secondly, many of the proofs in this paper are combinatorial in nature. Hence, it is usually easier to examine the Čech complex $\check{C}(\mathcal {P}, \epsilon )$ , rather than the geometric structure $\mathcal {U}(\mathcal {P},\epsilon )$ .

3 Model specification and relevant definitions

In this section we specify the stochastic process on a manifold that generates the point sample and topological summaries we will characterize.

The point processes we examine in this paper live in $\mathbb {R}^d$ and are supported on a $m$ -dimensional manifold $\mathcal {M}\subset \mathbb {R}^d$ ( $m<d$ ). Throughout this paper we assume that $\mathcal {M}$ is closed (i.e. compact and without a boundary) and smooth.

Let $\mathcal {M}$ be such a manifold, and let $f:\mathcal {M}\rightarrow \mathbb {R}$ be a probability density function on $\mathcal {M}$ , which we assume to be bounded and measurable. If $X$ is a random variable in $\mathbb {R}^d$ with density $f$ , then for every $A\subset \mathbb {R}^d$

where $d x$ is the volume form on $\mathcal {M}$ .

We consider two models for generating point clouds on the manifold $\mathcal {M}$ :

Random sample: $n$ points are drawn $\mathcal {X}_n = \left\{ X_1, X_2, \ldots , X_n\right\} \mathop {\sim }\limits ^{iid} f$ ,

Poisson process: the points are drawn from a spatial Poisson process with intensity function $\lambda _n := n f$ . The spatial Poisson process has the following two properties:

For every region $A\subset \mathcal {M}$ , the number of points in the region $N_A := \left| {\mathcal {P}_n \cap A}\right| $ is distributed as a Poisson random variable

For every $A,B\subset \mathcal {M}$ such that $A\cap B = \emptyset $ , the random variables $N_A$ and $N_B$ are independent.

These two models behave very similarly. The main difference is that the number of points in $\mathcal {X}_n$ is exactly $n$ , while the number of points in $\mathcal {P}_n$ is distributed $\mathrm {Poisson}\left( {n}\right) $ . Since the Poisson process has computational advantages, we will present all the results and proofs in this paper in terms of $\mathcal {P}_n$ . However, the reader should keep in mind that the results also apply to samples generated by the first model ( $\mathcal {X}_n$ ), with some minor adjustments. For a full analysis of the critical points in the Euclidean case for both models, see [ 12 ].

The stochastic objects we study in this paper are the union $\mathcal {U}(\mathcal {P}_n, \epsilon )$ (defined in ( 2.1 )), and the distance function $d_{\mathcal {P}_n}$ (defined in ( 2.2 )). The random variables we examine are the following. Let $r_n$ be a sequence of positive numbers, and define

to be the $k$ -th Betti number of $\mathcal {U}(\mathcal {P}_n,r_n)$ , for $0\le k \le d-1$ . The values $\beta _{k,n}$ form a set of well defined integer random variables.

For $0\le k \le d$ , denote by $\mathcal {C}_{k,n}$ the set of critical points with index $k$ of the distance function $d_{\mathcal {P}_n}$ . Let $r_n$ be positive , and define the set of ‘local’ critical points as

and its size as

The values $N_{k,n}$ also form a set of integer valued random variables. From the discussion in Sect. 2.3 we know that there is a strong connection between the set of values $\left\{ \beta _{k,n}\right\} _{k=0}^{d-1}$ and $\left\{ N_{k,n}\right\} _{k=0}^{d}$ . We are interested in studying the limiting behavior of these two sets of random variables, as $n\rightarrow \infty $ , and $r_n\rightarrow 0$ .

In this section we present limit theorems for the random variables $\beta _{k,n}$ and $N_{k,n}$ , as $n\rightarrow \infty $ , and $r_n\rightarrow 0$ . Similarly to the results presented in [ 13 , 29 ], the limiting behavior splits into three main regimes. In [ 13 , 29 ] the term controlling the behavior is $nr_n^d$ , where $d$ is the ambient dimension. This value can be thought of as representing the expected number of points occupying a ball of radius $r_n$ . Generating samples from a $m$ -dimensional manifold (rather than the entire $d$ -dimensional space) changes the controlling term to be $nr_n^m$ . This new term can be thought of as the expected number of points occupying a geodesic ball of radius $r_n$ on the manifold. We name the different regimes the sub-critical ( $nr_n^m\rightarrow 0$ ), the critical ( $nr_n^m\rightarrow \lambda $ ), and the super-critical ( $nr_n^m\rightarrow \infty $ ). In this section we will present limit theorems for each of these regimes separately. First, however, we present a few statements common to all regimes.

The index $0$ critical points (minima) of $d_{\mathcal {P}_n}$ are merely the points in $\mathcal {P}_n$ . Therefore, $N_{0,n} = \left| {\mathcal {P}_n}\right| \sim \mathrm {Poisson}\left( {n}\right) $ , so our focus is on the higher indexes critical points.

Next, note that if the radius $r_n$ is small enough, one can show that $\mathcal {U}(\mathcal {P}_n,r_n)$ can be continuously transformed into a subset $\mathcal {M}'$ of $\mathcal {M}$ (by a ‘deformation retract’), and this implies that $\mathcal {U}(\mathcal {P}_n,r_n)$ has the same homology as $\mathcal {M}'$ . Since $\mathcal {M}$ is $m$ -dimensional, $\beta _k(\mathcal {M}) = 0$ for every $k>m$ , and the same goes for every subset of $\mathcal {M}$ . In addition, except for the coverage regime (see Sect. 4.3 ), $\mathcal {M}'$ is a union of strict subsets of the connected components of $\mathcal {M}$ , and thus must have $\beta _m(\mathcal {M}') = 0$ as well. Therefore, we have that $\beta _{k,n}= 0$ for every $k\ge m$ . By Morse theory, this also implies that $N_{k,n}=0$ for every $k>m$ . The results we present in the following sections therefore focus on $\beta _{0,n},\ldots ,\beta _{m-1,n}$ and $N_{1,n},\ldots ,N_{m,n}$ only.

4.1 The sub-critical range $(nr_n^m\rightarrow 0)$

In this regime, the radius $r_n$ goes to zero so fast, that the average number of points in a ball of radius $r_n$ goes to zero. Hence, it is very unlikely for points to connect, and $\mathcal {U}(\mathcal {P}_n,r_n)$ is very sparse. Consequently this phase is sometimes called the ‘dust’ phase. We shall see that in this case $\beta _{0,n}$ is dominating all the other Betti numbers, which appear in a descending order of magnitudes.

Theorem 4.1

(Limit mean and variance) If $nr_n^m\rightarrow 0$ , then

For $1\le k \le m-1$ ,

For $1 \le k \le m$ ,

The function $h^b_\epsilon $ is an indicator function on subsets $\mathcal {Y}$ of size $k+2$ , testing that a subset forms a non-trivial $k$ -cycle, i.e.

The function $h_\epsilon ^c$ is defined in ( 2.8 ).

Finally, we note that for $\mathbf {y}= (y_1,\ldots ,y_{k+1}) \in (\mathbb {R}^d)^{k+1},\,h_\epsilon ^b(0,\mathbf {y}) := h_\epsilon ^b(0,y_1,\ldots ,y_{k+1})$ , and for $\mathbf {y}= (y_1,\ldots ,y_{k}) \in (\mathbb {R}^d)^{k},\,h_\epsilon ^c(0,\mathbf {y}) := h_\epsilon ^c(0,y_1,\ldots ,y_{k})$ .

Note that these results are analogous to the limits in the Euclidean case, presented in [ 30 ] (for the Betti numbers) and [ 13 ] (for the critical points). In general, as is common for results of this nature, it is difficult to express the integral formulae above in a more transparent form. Some numerics as well as special cases evaluations are presented in [ 13 ].

Since $nr_n^m\rightarrow 0$ , the comparison between the different limits yields the following picture,

where by $a_n\approx b_n$ we mean that $a_n/b_n \rightarrow c\in (0,\infty )$ and by $a_n \gg b_n$ we mean that $a_n/b_n \rightarrow \infty $ . This diagram implies that in the sub-critical phase the dominating Betti number is $\beta _0$ . It is significantly less likely to observe any cycle, and it becomes less likely as the cycle dimension increases. In other words, $\mathcal {U}(\mathcal {P}_n,r_n)$ consists mostly of small disconnected particles, with relatively few holes.

Note that the limit of the term $n^{k+1} r_n^{mk}$ can be either zero, infinity, or anything in between. For each of these cases, the limiting distribution of either $\beta _{k-1,n}$ or $N_{k,n}$ is completely different. The results for the number of critical points are as follows.

Theorem 4.2

(Limit distribution) Let $nr_n^m\rightarrow 0$ , and $1 \le k \le m$ ,

If $\lim _{n\rightarrow \infty } n^{k+1}r_n^{k} = 0$ , then

If, in addition, $\sum _{n=1}^\infty n^{k+1} r_n^{mk}< \infty $ , then

If $\lim _{n\rightarrow \infty } n^{k+1}r_n^{mk} = \alpha \in (0,\infty )$ , then

If $\lim _{n\rightarrow \infty } n^{k+1}r_n^{mk} = \infty $ , then

For $\beta _{k,n}$ the theorem above needs two adjustments. Firstly, we need to replace the term $n^{k+1}r_n^{mk}$ with $n^{k+2}r_n^{m(k+1)}$ , and $\mu ^c_k$ with $\mu _k^b$ (similarly to Theorem 4.1). Secondly, the proof of the central limit theorem in part 3 is more delicate, and requires an additional assumption that $nr_n^m \le n^{-\epsilon }$ for some $\epsilon > 0$ .

4.2 The critical range ( $nr_n^m\rightarrow \lambda \in (0,\infty )$ )

In the dust phase, $\beta _{0,n}$ was $O(n)$ , while the other Betti numbers of $\mathcal {U}(\mathcal {P}_n, r_n)$ were of a much lower magnitude. In the critical regime, this behavior changes significantly, and we observe that all the Betti numbers (as well as counts of all critical points) are $O(n)$ . In other words, the behavior of $\mathcal {U}(\mathcal {P}_n, r_n)$ is much more complex, in the sense that it consists of many cycles of any dimension $1\le k \le m-1$ .

Unfortunately, in the critical regime, the combinatorics of cycle counting becomes highly complicated. However, we can still prove the following qualitative result, which shows that $\mathbb {E}\left\{ {\beta _{k,n}}\right\} = O(n)$ .

Theorem 4.3

If $nr_n^m\rightarrow \lambda \in (0,\infty )$ , then for $1\le k \le m-1$ ,

Fortunately, the situation with the critical points is much better. A critical point of index $k$ is always generated by subsets $\mathcal {Y}$ of exactly $k+1$ points. Therefore, nothing essentially changes in our methods when we turn to examine the limits of $N_{k,n}$ . We can prove the following limit theorems.

Theorem 4.4

If $nr_n^m\rightarrow \lambda \in (0,\infty )$ , then for $1 \le k \le m$ ,

$R,\ h_\epsilon ^c$ , are defined in ( 2.5 ), ( 2.8 ), respectively. The expression defining $\sigma ^2_k(\lambda )$ is rather complicated, and will be discussed in the proof.

The term $\omega _m$ stands for the volume of the unit ball in $\mathbb {R}^m$ . As mentioned above, in general it is difficult to present a more explicit formula for $\gamma _k(\lambda )$ . However, for $m\le 3$ and $f\equiv 1$ (the uniform distribution) it is possible to evaluate $\gamma _k(\lambda )$ (using tedious calculus arguments which we omit here). For $m=3$ these computations yield—

where $\frac{d}{d\lambda }\gamma _k(\lambda )$ can be thought of as the rate at which critical points appear. Figure 3 a, b are the graphs of these curves.

The graphs of the $\gamma _k$ functions for the case where $m=3$ , and $f\equiv 1$ . a The graphs for the limiting number of critical points $\gamma _k(\lambda )$ . b The graphs for the rate of appearance of critical points given by $\frac{d}{d\lambda }\gamma _k(\lambda )$ . c The limiting (normalized) Euler characteristic given by $1 - \gamma _1(\lambda ) + \gamma _2(\lambda ) - \gamma _3(\lambda )$

As mentioned earlier, in this regime we cannot get exact limits for the Betti numbers. However, we can use the limits of the critical points to compute the limit of another important topological invariant of $\mathcal {U}(\mathcal {P}_n,r_n)$ —its Euler characteristic. The Euler characteristic $\chi _n$ of $\mathcal {U}(\mathcal {P}_n, r_n)$ (or, equivalently, of $\check{C}(\mathcal {P}_n, r_n)$ ) has a number of equivalent definitions. One of the definitions, via Betti numbers, is

In other words, the Euler characteristic “summarizes” the information contained in Betti numbers to a single integer. Using Morse theory, we can also compute $\chi _n$ from the critical points of the distance function by

Thus, using Theorem 4.4 we have the following result.

Corollary 4.5

If $nr_n^m\rightarrow \lambda \in (0,\infty )$ , then

This limit provides us with partial, yet important, topological information about the complex $\mathcal {U}(\mathcal {P}_n,r_n)$ in the critical regime. While we are not able to derive the precise limits for each of the Betti numbers individually, we can provide the asymptotic result for their “summary”. In addition, numerical experiments (cf. [ 30 ]) seem to suggest that at different ranges of radii there is at most a single degree of homology which dominates the others. This implies that $\chi _n \approx (-1)^k\beta _{k,n} $ for the appropriate range. If this heuristic could be proved in the future, the result above could be used to approximate $\beta _{k,n}$ in the critical regime. In Fig. 3 c we present the curve of the limit Euler characteristic (normalized) for $m=3$ and $f\equiv 1$ . Finally, we note that while we presented the limit for the first moment of the Euler characteristic, using Theorem 4.4 one should be able to prove stronger limit results as well.

4.3 The super-critical range ( $nr_n^m\rightarrow \infty $ )

Once we move from the critical range into the super-critical, the complex $\mathcal {U}(\mathcal {P}_n,r_n)$ becomes more and more connected, and less porous. The “noisy” behavior (in the sense that there are many holes of any possible dimension) we observed in the critical regime vanishes. This, however does not happen immediately. The scale at which major changes occur is when $nr_n^m\propto \log n$ .

The main difference between this regime and the previous two, is that while the number of critical points is still $O(n)$ , the Betti numbers are of a much lower magnitude. In fact, for $r_n$ big enough, we observe that $\beta _{k,n}\sim \beta _k(\mathcal {M})$ , which implies that these values are $O(1)$ .

For the super-critical phase we have to assume that $f_{\min }:= \inf _{x\in \mathcal {M}} f(x) >0$ . This condition is required for the proofs, but is not a technical issue only. Having a point $x\in \mathcal {M}$ where $f(x)=0$ implies that in the vicinity of $x$ we expect to have relatively few points in $\mathcal {P}_n$ . Since the radius of the balls generating $\mathcal {U}(\mathcal {P}_n, r_n)$ goes to zero, this area might become highly porous or disconnected , and look more similar to other regimes. However, we postpone this study for future work.

We start by describing the limit behavior of the critical points, which is very similar to that of the critical regime.

Theorem 4.6

If $r_n\rightarrow 0$ , and $nr_n^m\rightarrow \infty $ , then for $1 \le k \le m$ ,

$R,\ h^c$ , are defined in ( 2.5 ), ( 2.7 ), respectively.

$\omega _m$ is the volume of the unit ball in $\mathbb {R}^m$ . The combinatorial analysis of the Betti numbers $\beta _{k,n}$ in the super-critical regime suffers from the same difficulties described in the critical regime. However, in the special case that $r_n$ is big enough so that $\mathcal {U}(\mathcal {P}_n,r_n)$ covers $\mathcal {M}$ , we can use a different set of methods to derive limit results for $\beta _{k,n}$ .

The Coverage Regime

In [ 45 ](Section 13.2), it is shown that for samples generated on a $m$ -dimensional torus, the complex $\mathcal {U}(\mathcal {P}_n, r_n)$ becomes connected when $nr_n^m \approx (\omega _m f_{\min }2^m)^{-1} \log n$ . This result could be easily extended to the general class of manifolds studied in this paper (although we will not pursue that here). While the complex is reaching a finite number of components ( $\beta _{0,n} \rightarrow \beta _0(\mathcal {M})$ ), it is still possible for it to have very large Betti numbers for $k\ge 1$ . In this paper we are interested in a threshold for which we have $\beta _{k,n}= \beta _k(\mathcal {M})$ for all $k$ (and not just $\beta _0$ ). We will show that this threshold is when $nr_n^m = (\omega _m f_{\min })^{-1}\log n$ , so that $r_n$ is twice than the radius required for connectivity.

To prove this result we need two ingredients. The first one is a coverage statement, presented in the following proposition.

Proposition 4.7

(Coverage) If $nr_n^m\ge C \log n$ , then:

If $C> (\omega _m f_{\min })^{-1}$ , then

If $C >2(\omega _m f_{\min })^{-1}$ , then almost surely there exists $M>0$ (possibly random), such that for every $n>M$ we have $\mathcal {M}\subset \mathcal {U}(\mathcal {P}_n, r_n)$ .

The second ingredient is a statement about the critical points of the distance function, unique to the coverage regime. Let $\hat{r}_n$ be any sequence of positive numbers such that (a) $\hat{r}_n \rightarrow 0$ , and (b) $\hat{r}_n > r_n$ for every $n$ . Define $\widehat{N}_{k,n}$ to be the number of critical points of $d_{\mathcal {P}_n}$ with critical value bounded by $\hat{r}_n$ . Obviously, $\widehat{N}_{k,n}\ge N_{k,n}$ , but we will prove that choosing $r_n$ properly, these two quantities are asymptotically equal.

Proposition 4.8

If $nr_n^m\ge C \log n$ , then:

If $C > (\omega _m f_{\min })^{-1}$ , then

If $C>2(\omega _m f_{\min })^{-1}$ , then almost surely there exists $M>0$ (possibly random), such that for $n>M$

In other words, if $r_n$ is chosen properly, then $\mathcal {U}(\mathcal {P}_n, r_n)$ contains all the ‘local’ (small valued) critical points of $d_{\mathcal {P}_n}$ .

Combining the fact that $\mathcal {M}$ is covered, the deformation retract argument in [ 44 ], and the fact that there are no local critical points outside $\mathcal {U}(\mathcal {P}_n, r_n)$ , using Morse theory, we have the desired statement about the Betti numbers.

Theorem 4.9

(Convergence of the Betti numbers) If $r_n \rightarrow 0$ , and $nr_n^m\ge C \log n$ , then:

If $C>2(\omega _m f_{\min })^{-1}$ , then almost surely there exists $M>0$ , such that for $n>M$

Note that $M$ (the exact point of convergence) is random.

A common problem in topological manifold learning is the following:

Given a set of random points $\mathcal {P}$ , sampled from an unknown manifold $\mathcal {M}$ , how can one infer the topological features of $\mathcal {M}$ ?

The last theorem provides a possible solution. Draw balls around $\mathcal {P}$ , with a radius $r$ satisfying the condition in Theorem 4.9. As the sample size grows it is guaranteed that the Betti numbers computed from the union of the balls will recover those of the original manifold $\mathcal {M}$ . This solution is in the spirit of the result in [ 44 ], where a bound on the recovery probability is given as a function of the sample size and the condition number of the manifold, for a uniform measure on $\mathcal {M}$ . The result in 4.9 applies for a larger class of probability measures on $\mathcal {M}$ , require much weaker assumptions on the geometry of the manifold (the result in [ 44 ] requires the knowledge of the condition number, or the reach, of the manifold), and convergence is shown to occur almost surely.

In this section we provide proofs for the statements in this paper. We note that the proofs of theorems 4.1–4.6 are similar to the proofs of the equivalent statements in [ 29 , 30 ] (for the Betti numbers), and in [ 13 ] (for the critical points). There are, however, significant differences when dealing with samples on a closed manifold. We provide detailed proofs for the limits of the first moments, demonstrating these differences, and refer the reader to [ 13 , 29 , 30 ] for the rest of the details.

5.1 Some notation and elementary considerations

In this section we list some common notation and note some simple facts that will be used in the proofs.

Henceforth, $k$ will be fixed, and whenever we use $\mathcal {Y},\mathcal {Y}'$ or $\mathcal {Y}_i$ we implicitly assume (unless stated otherwise) that either $\left| {\mathcal {Y}}\right| =\left| {\mathcal {Y}'}\right| = \left| {\mathcal {Y}_i}\right| = k+2$ for $k$ -cycles, or $\left| {\mathcal {Y}}\right| =\left| {\mathcal {Y}'}\right| = \left| {\mathcal {Y}_i}\right| = k+1$ for index $k$ critical points.

Usually, finite subsets of $\mathbb {R}^d$ will be denoted calligraphically ( $\mathcal {X},\mathcal {Y}$ ). However inside integrals we use boldfacing and lower case ( $\mathbf {x},\mathbf {y}$ ).

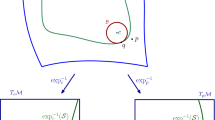
For every $x\in \mathcal {M}$ we denote by $T_x\mathcal {M}$ the tangent space of $\mathcal {M}$ at $x$ , and define $\exp _x:T_x\mathcal {M}\rightarrow \mathcal {M}$ to be the exponential map at $x$ . Briefly, this means that for every $v\in T_x\mathcal {M}$ , the point $\exp _x(v)$ is the point on the unique geodesic leaving $x$ in the direction of $v$ , after traveling a geodesic distance equal to $\left\| v\right\| $ .

For $x\in \mathbb {R}^d,\,\mathbf {x}\in \mathcal {M}^{k+1}$ and $\mathbf {y}\in (\mathbb {R}^m)^{k}$ , we use the shorthand

Throughout the proofs we will use the following notation. Let $x\in \mathcal {M}$ , and let $v\in T_x\mathcal {M}$ be a tangent vector. We define

By definition, it follows that

The following lemmas will be useful when we will be required to approximate geodesic distances and volumes by Euclidean ones.

Let $\delta > 0$ . If $\left\| \nabla _\epsilon (x,v)\right\| \le C$ for all $\epsilon >0$ , and for some $C>0$ . Then there exists a small enough $\tilde{\epsilon } > 0$ such that for every $\epsilon < \tilde{\epsilon }$

If $\left\| \nabla _\epsilon (x,v)\right\| \le C$ , then the $(C\epsilon )$ -tube around $\mathcal {M}$ , contains the line segment connecting $x$ and $\exp _x(\epsilon v)$ . Therefore, using Theorem 5 in [ 37 ] we have that

This implies that

for some $C'>0$ . Therefore, if $\epsilon $ is small enough we have that

which completes the proof. $\square $

Throughout the proofs we will repeatedly use two different occupancy probabilities, defined as follows,

where $B(\mathcal {Y})$ is defined in ( 2.6 ). The next lemma is a version of Lebesgue differentiation theorem, which we will be using.

For every $x\in \mathcal {M}$ and $\mathbf {y}\in (T_x(\mathcal {M}))^k$ , if $r_n\rightarrow 0 $ , then

where $V(\mathcal {Y}) = {{\mathrm{Vol}}}(\mathcal {U}(\mathcal {Y},1))$ .

where $\omega _m$ is the volume of a unit ball in $\mathbb {R}^m$ .

We start with the proof for $p_c$ . Set $B_n := B(x,\exp _x(r_n \mathbf {y}))\subset \mathbb {R}^d$ . Then

Next, use the change of variables $\xi \rightarrow \exp _x(r_n v)$ , for $v\in T_x\mathcal {M}\simeq \mathbb {R}^m$ . Then,

where $J_x(v) = \frac{\partial \exp _x}{\partial v}$ .

We would like to apply the Dominated Convergence Theorem (DCT) to this integral, to find its limit. First, assuming that the DCT condition holds, we find the limit.

By definition, $\exp _x(r_n v) \rightarrow x$ , and therefore,

Note that the function $H(v,\mathbf {y}) := 1\!\!1\left\{ v\in B(0,\mathbf {y}))\right\} $ is almost everywhere continuous in $\mathbb {R}^d\times (\mathbb {R}^d)^k$ , and also that

Since $\nabla {r_n}(x,v) \rightarrow v$ , and $\nabla {r_n}(x,\mathbf {y}) \rightarrow \mathbf {y}$ (when $n\rightarrow \infty $ ), we have that for almost every $v,\mathbf {y}$ ,

By definition,

Putting it all together, we have that

which is the limit we are seeking.

To conclude the proof we have to show that the DCT condition holds for the integrand in ( 5.3 ). For a fixed $\mathbf {y}$ , for every $v$ for which the integrand is nonzero, we have that $\exp _x(r_nv) \in B_n$ which implies that

Since $R(0,\nabla _{r_n}(x,\mathbf {y})) \rightarrow R(0,\mathbf {y})$ , we have that $n$ for large enough

Using Lemma 5.1 we then have that

for some $\delta >0$ . This means that the support of the integrand in ( 5.3 ) is bounded. Since $f$ is bounded, and $J_x$ is continuous, we deduce that the integrand is well bounded, and we can safely apply the DCT to it.

The proof for $p_b$ follows the same line of arguments, replacing $B_n$ with

To bound the integrand we use the fact that if $\exp _x(r_n v) \in U_n$ , then

and as $n\rightarrow \infty $ , we have ${{\mathrm{diam}}}(\mathcal {U}(0, \nabla _{r_n}(x,\mathbf {y}), 1))\rightarrow {{\mathrm{diam}}}(\mathcal {U}(0,\mathbf {y}),1)$ . $\square $

In [ 13 , 29 , 30 ] full proofs are presented for statements similar to those in this paper, only for sampling in Euclidean spaces rather than compact manifolds. The general method of proving statements on compact manifold is quite similar, but important adjustments are required. We are going to present those adjustments for proving the basic claims, and refer the reader to the proofs in [ 13 , 29 , 30 ] taking into consideration the necessary adjustments.

5.2 The sub-critical range ( $nr_n^m\rightarrow 0$ )

Proof of theorem 4.1.

We give a full proof for the limit expectations for both the Betti numbers and critical points, and then discuss the limit of the variances.

The expected number of critical points:

From the definition of $N_{k,n}$ (see ( 3.3 )), using the fact that index- $k$ critical points are generated by subsets of size $k+1$ (see Definition 2.1), we can compute $N_{k,n}$ by iterating over all possible subsets of $\mathcal {P}_n$ of size $k+1$ in the following way,

where $g_\epsilon $ is defined in ( 2.9 ). Using Palm theory (Theorem 6.1), we have that

where $\mathcal {Y}'$ is a set of $\mathrm {i.i.d.}$ random variables, with density $f$ , independent of $\mathcal {P}_n$ . Using the definition of $g_{r_n}$ , we have that

where $p_c$ is defined in ( 5.2 ). Thus,

To evaluate this integral, recall that $\mathbf {x}= (x_0, \ldots , x_k) \in \mathcal {M}^{k+1}$ and use the following change of variables

where $\mathbf {v}= (v_1,\ldots , v_k),\,\exp _x(\mathbf {v}) = (\exp _x(v_1),\ldots , \exp _x(v_k))$ , and $J_x(v) = \frac{\partial {\exp _x}}{\partial {v}}$ . From now on we will think of $v_i$ as vectors in $\mathbb {R}^m$ . Thus, the change of variables $v_i \rightarrow r_n y_i$ yields,

The integrand above admits the DCT conditions, and therefore we can take a point-wise limit. We compute the limit now, and postpone showing that the integrand is bounded to the end of the proof.

Taking the limit term by term, we have that:

$f$ is continuous almost everywhere in $\mathcal {M}$ , therefore

for almost every $x\in \mathcal {M}$ .

The discontinuities of the function $h_1^c:(\mathbb {R}^d)^{k+1} \rightarrow \left\{ 0,1\right\} $ are either subsets $\mathbf {x}$ for which $C(\mathbf {x})$ is on the boundary of ${{\mathrm{conv}}}(\mathbf {x})$ , or where $R(\mathbf {x}) = 1$ . This entire set has a Lebesgue measure zero in $(\mathbb {R}^d)^{k+1}$ . Therefore, we have

for almost every $x,\mathbf {y}$ .

Using Lemma 5.2, and the fact that $nr_n^m\rightarrow 0$ , we have that

Finally, $\lim _{n\rightarrow \infty }J_x(r_n y_i) = J_x(0) = 1$ .

Putting all the pieces together (rolling back to ( 5.4 ) and ( 5.5 )), we have that

Finally, to justify the use of the DCT, we need to find an integrable bound for the integrand in ( 5.5 ).

The main step would be to show that the integration over $(y_1,\ldots , y_k)$ is done over a bounded region in $(\mathbb {R}^m)^k$ . First, note that if $h_{r_n}^c(x,\exp _x(r_n\mathbf {y})) = h_1^c(0,\nabla _{r_n}(x,\mathbf {y})) = 1$ , then necessarily $R(0, \nabla _{r_n}(x,\mathbf {y})) < 1$ . This implies that $\left\| \nabla _{r_n}(x, y_i)\right\| < 2$ . Using Lemma 5.1, and the fact that $r_n\rightarrow 0$ , we can choose $n$ large enough so that $\left\| y_i\right\| < 3$ for every $i$ . In other words, we can assume that the integration $dy_i$ is over $B_3(0)\subset \mathbb {R}^m$ only.

Next, we will bound each of the terms in the integrand in ( 5.5 ).

The density function $f$ is bounded, therefore,

where $f_{\max }:= \sup _{x\in \mathcal {M}} f(x)$ .

The term $h_{r_n}^c(x,\exp _x(r_n\mathbf {y})) e^{-np_c(x,\exp _x(r_n\mathbf {y}))}$ is bounded from above by $1$ .

The function $J_x(v)$ is continuous in $x,v$ . Therefore, it is bounded in the compact subspace $\mathcal {M}\times B_3(0)$ , by some constant $C$ . Since we know that $y_i\in B_3(0)$ , then for $n$ large enough (such that $r_n<1$ we have that $J_x(r_n\mathbf {y}) \le C^k$ .

Putting it all together, we have that the integrand in ( 5.5 ) is bounded by $f(x)\times \mathrm {const}$ , and since we proved that the $y_i$ -s are bounded, we are done.

The expected Betti numbers:

As mentioned in Sect. 2.4 , most of the results for $\beta _{k,n}$ will be proved using the Čech complex $\check{C}(\mathcal {P}_n,r_n)$ rather than the union $\mathcal {U}(\mathcal {P}_n,r_n)$ . From the Nerve theorem, the Betti numbers of these spaces are equal.

The smallest simplicial complex forming a non-trivial $k$ -cycle is the boundary of a $(k+1)$ -simplex which consists of $k+2$ vertices. Recall that for $\mathcal {Y}\in (\mathbb {R}^d)^{k+2},\,h_\epsilon ^b(\mathcal {Y})$ is an indicator function testing whether $\check{C}(\mathcal {Y}, \epsilon )$ forms a non-trivial $k$ -cycle (see ( 4.1 )), and define

Then iterating over all possible subsets $\mathcal {Y}$ of size $k+2$ we have that

is the number of minimal isolated cycles in $\check{C}(\mathcal {P}_n,r_n)$ . Next, define $F_{k,n}$ to be the number of $k$ dimensional faces in $\check{C}(\mathcal {P}_n, r_n)$ that belong to a component with at least $k+3$ vertices. Then

This stems from three main facts:

Every cycle which is not accounted for by $S_{k,n}$ belongs to a components with at least $k+3$ vertices.

If $C_1, C_2,\ldots , C_m$ are the different connected components of a space $X$ , then

For every simplicial complex $C$ it is true that $\beta _k(C) \le F_k(C)$ , where $F_k$ is the number of $k$ -dimensional simplices.

For more details regarding the inequality in ( 5.7 ), see the proof of the analogous theorem in [ 30 ].

Next, we should find the limits of $S_{k,n}$ and $F_{k,n}$ . For $S_{k,n}$ , from ( 5.6 ) using Palm theory (Theorem 6.1) we have that

where $\mathcal {Y}'$ is a set of $k+2\,\mathrm {i.i.d.}$ random variables with density $f$ , independent of $\mathcal {P}_n$ . Using the definition of $g_{r_n}^b$ we have that

where $p_b$ is defined in ( 5.1 ). Following the same steps as in the proof for the number of critical points, leads to

Thus, to complete the proof we need to show that $(n^{k+2}r_n^{m(k+1)})^{-1} \mathbb {E}\left\{ {F_{k,n}}\right\} \rightarrow 0$ . To do that, we consider sets $\mathcal {Y}$ of $k+3$ vertices, and define

Using Palm Theory, we have that

Since $h_{r_n}^f$ requires that $\check{C}(\mathcal {Y},r_n)$ is connected, similar localizing arguments to the ones used previously in this proof show that

Thus, since $nr_n^m\rightarrow 0$ , we have that

which completes the proof.

For $\beta _{0,n}$ , using Morse theory we have that $N_{0,n}-N_{1,n} \le \beta _{0,n} \le N_{0,n}$ . Since $\mathbb {E}\left\{ {N_{0,n}}\right\} = n$ , and $n^{-1}\mathbb {E}\left\{ {N_{1,n}}\right\} \rightarrow 0$ , we have that $\lim _{n\rightarrow \infty }n^{-1}\mathbb {E}\left\{ {\beta _{0,n}}\right\} = 1$ .

The limit variance:

To prove the limit variance result, the computations are similar to the ones in [ 13 , 30 ]. The only adjustment required is to change the domain of integration to be $\mathcal {M}$ instead of $\mathbb {R}^d$ , the same way we did in proving the limit expectations. We refer the reader to ‘Appendix C’ for an outline of these proofs. $\square $

Proof of Theorem 4.2

We start with the case when $n^{k+1} r_n^{mk}\rightarrow 0$ . In this case, the $L^2$ convergence is a direct result of the fact that

Next, observe that

and since $(n^{k+1} r_n^{mk})^{-1}\mathbb {E}\left\{ {N_{k,n}}\right\} \rightarrow 0$ , there exists a constant $C$ such that

Thus, if $\sum _{n=1}^\infty n^{k+1} r_n^{mk}< \infty $ , we can use the Borel-Cantelli Lemma, to conclude that a.s. there exists $M>0$ such that for every $n>M$ we have $N_{k,n}= 0$ . This completes the proof for the first case.

For the other cases, we refer the reader to [ 13 , 30 ]. The proofs in these papers use Stein’s method (see Appendix B), and mostly rely on moments evaluation (up to the forth moment). We observed in the previous proof that moment computation in the manifold case is essentially the same as in the Euclidean case, and therefore all that is needed are a few minor adjustments. $\square $

5.3 The critical range ( $nr_n^m\rightarrow \lambda $ )

We prove the result for the number of critical points first.

Proof of Theorem 4.4

For the critical phase, we start the same way as in the proof of Theorem 4.6. All the steps and bounds are exactly the same, the only difference is in the limit of the exponential term inside the integral in ( 5.5 ). Using Lemma (5.2), and the fact that $nr_n^m\rightarrow \lambda $ we conclude that,

Thus, we have

and using the fact that $n^{k+1} r_n^{mk}\sim n\lambda ^k$ completes the proof.

For the proofs for the variance and the CLT we refer the reader to Appendix C and [ 13 ]. $\square $

Proof of Theorem 4.3

From the proof of Theorem 4.1 we know that

Similar methods to the ones we used above, can be used to show that

where $V(\mathcal {Y}) = {{\mathrm{Vol}}}(\mathcal {U}(\mathcal {Y},1))$ (see Lemma 5.2), and also that

Since $nr_n^m\rightarrow \lambda $ , we have that $n^{k+2}r_n^{m(k+1)}\sim n \lambda ^{k+1}$ . Thus we have shown that

for some positive constants $A,B$ , which completes the proof.

5.4 The super-critical range ( $nr_n^m\rightarrow \infty $ )

Proof of theorem 4.6.

For the super-critical regime, we repeat the steps we took in the other phases, with the main difference being that instead of using the change of variables $x_i \rightarrow \exp _x(r_ny_i)$ , we now use $x_i \rightarrow \exp _x(s_n y_i)$ where $s_n = n^{-1/m}$ . Thus, instead of the formula in ( 5.5 ) we now have

As we did before, we wish to apply the DCT to the integral in ( 5.8 ). We will compute the limit first, and show that the integrand is bounded at the end.

As before we have

The limit of the indicator function is now a bit different.

Now, since $R(0,\nabla _{s_n}(x,\mathbf {y})) \rightarrow R(0,\mathbf {y})$ and $r_n^{-1}s_n \rightarrow 0$ , we have that

Using Lemma 5.2 we have that

These computations yield,

Finally, for the inner integral, use the following change of variables— $y_i \rightarrow (f(x))^{-1/m} v_i$ , so that $d\mathbf {y}= f^{-k}(x)d\mathbf {v}$ . This yields,

Using the fact that $\int \nolimits _{\mathcal {M}}f(x)dx = 1$ completes the proof.

It remains to show that the DCT condition applies to the integral in ( 5.8 ). The main difficulty in this case stems from the fact that the variables $y_i$ are no longer bounded. Nevertheless, we can still bound the integrand, taking advantage of the exponential term.

As before, we have $f(x,\exp _x(s_n,\mathbf {y})) \le f(x) f_{\max }^k$ .

Being an indicator function, it is obvious that $h_{r_n}^c(x,\exp _x(s_n\mathbf {y})) \le 1$ .

To bound the exponential term from above, we will find a lower bound to $p_c(x,\exp _x(s_n\mathbf {y}))$ . Define a function $G:\mathcal {M}\times (\mathbb {R}^m)^k \times [0,1]\rightarrow \mathbb {R}$ as follows,

From Lemma 5.2 we know that $G$ is continuous in the compact subspace $\mathcal {M}\times (B_3(0))^k \times [0,1]$ , and thus uniformly continuous. Therefore, for every $\alpha > 0, x\in \mathcal {M},\mathbf {v}\in (B_3(0))^k$ , there exists $\tilde{\rho } > 0 $ such that for every $\rho < \tilde{\rho }$ we have

Now, consider $\mathbf {v}= \frac{s_n}{r_n} \mathbf {y}$ , then as we proved in the sub-critical phase, $\mathbf {v}\in (B_3(0))^k$ . Thus, for $n$ large enough (such that $r_n < \tilde{\rho }$ ), we have that for every $x,\mathbf {y}$

which implies that

Therefore, we have

Finally, note that $R(0,\mathbf {y}) \ge \left\| y_i\right\| /2$ for every $i$ . Thus,

Overall, we have that the integrand in ( 5.8 ) is bounded by

This function is integrable in $\mathcal {M}\times (\mathbb {R}^m)^k$ , and therefore we are done. For the proof of the limit variance and CLT, see Appendix C and [ 13 ]. $\square $

Proof of Proposition 4.7

Since $\mathcal {M}$ is $m$ -dimensional, it can be shown that there exists $D>0$ such that for every $\epsilon $ we can find a (deterministic) set of points $\mathcal {S}\subset \mathcal {M}$ such that (a) $\mathcal {M}\subset \mathcal {U}(\mathcal {S}, \epsilon )$ , i.e. $\mathcal {S}$ is $\epsilon $ -dense in $\mathcal {M}$ , and (b) $\left| {\mathcal {S}}\right| \le D \epsilon ^{-m}$ (cf. [ 24 ]).

If $\mathcal {M}$ is not covered by $\mathcal {U}(\mathcal {P}_n, r_n)$ , then there exists $x\in \mathcal {M}$ , such that $\left\| x-X\right\| > r_n$ for every $X\in \mathcal {P}_n$ . For $\alpha >0$ , let $\mathcal {S}_n$ be a $( \alpha r_n)$ -dense set in $\mathcal {M}$ , and let $s \in \mathcal {S}_n$ be the closest point to $x$ in $\mathcal {S}_n$ . Then,

Since $\left\| x-s\right\| \le \alpha r_n$ , then necessarily $\left\| s-X\right\| > (1-\alpha )r_n$ . Thus,

Similarly to Lemma 5.2 we can show that for every $x\in \mathcal {M}$

then $G:\mathcal {M}\times [0,1]\rightarrow \mathbb {R}$ is continuous on a compact space, and therefore uniformly continuous. Thus, for every $\beta >0$ there exists $\tilde{\rho } >0$ such that for all $\rho < \tilde{rho}$ we have $G(x,\rho ) \ge 1-\beta $ for every $x\in \mathcal {M}$ . In other words, for $n$ large enough, we have that

for every $x\in \mathcal {M}$ . Since $f(x) \ge f_{\min }> 0$ , we have that,

We can now prove the two parts of the proposition.

If we take $nr_n^m\ge C \log n$ with $C \ge \frac{1}{(1-\alpha )^m(1-\beta )f_{\min }\omega _m}$ , then we have

Since we can choose $\alpha ,\beta $ to be arbitrarily small, this statement holds for every $C >\frac{1}{f_{\min }\omega _m}$ .

Similarly, if we take $nr_n^m\ge C \log n$ with $C \ge \frac{2+\epsilon }{(1-\alpha )^m(1-\beta )f_{\min }\omega _m}$ , then we have

Therefore, we have that

and from the Borel-Cantelli Lemma, we conclude that a.s. there exists $M>0$ such that for every $n>M$ we have $\mathcal {M}\subset \mathcal {U}(\mathcal {P}_n,r_n)$ .

$\square $

To prove the result on $\widehat{N}_{k,n}$ , we first prove the following lemma.

For every $\epsilon > 0 $ , if $C> \frac{1+\epsilon }{f_{\min }\omega _m}$ , and $nr_n^m\ge C \log n$ , then there exists $D\ge 0$ , such that

Similarly to the computation of $N_{k,n}$ , we have that

Next, using Lemma 5.2 we have that

We can use similar uniform continuity arguments to the ones used in the proof of Theorem 4.4, to show that for a large enough $n$ we have that both

for any $\alpha >0$ . Now, if

then necessarily $R(x, \exp _x(s_n\mathbf {y})) \ge r_n$ , and from ( 5.10 ) we have that

Combining that with ( 5.11 ), for every $\beta \in (0,1)$ we have that

Thus, we have that

The integral on the RHS is bounded. Thus, for any $\epsilon > 0$ , if $C \ge \frac{1}{(1-\alpha )(1-\beta )}\frac{1+\epsilon }{f_{\min }\omega _m}$ , and $nr_n^m \ge C \log n$ , then

This is true for any $\alpha ,\beta >0$ . Therefore, the statement holds for any $C>\frac{1+\epsilon }{f_{\min }\omega _m}$ . $\square $

Proof of Proposition 4.8

For every $1\le k \le m$ ,

From Lemma 5.3 we have that if $nr_n^d\ge C\log n$ with $C>(f_{\min }\omega _m)^{-1}$ then

we have that

Next, if $C > 2(f_{\min }\omega _m)^{-1}$ , then there exists $\epsilon > 0$ such that $2C > \frac{2+\epsilon }{f_{\min }\omega _m}$ . Using Lemma 5.3 we have that for $1\le k \le d$ there exists $D_k>0$ such that

Using the Borel-Cantelli Lemma, we deduce that almost surely there exists $M_k>0$ (possibly random) such that for every $n>M_k$ we have

Taking $M = \max _{1\le k \le m} M_k$ , yields that for every $n>M$

Proof of Theorem 4.9

If $nr_n^m\ge C\log n$ , and $C>(\omega _m f_{\min })^{-1}$ , then from Proposition 4.7 we have that

The deformation retract argument in [ 44 ] (Proposition 3.1) states that if $\mathcal {M}\subset \mathcal {U}(\mathcal {P}_n, r_n)$ , then $\mathcal {U}(\mathcal {P}_n, 2r_n)$ deformation retracts to $\mathcal {M}$ , and in particular— $\beta _k(\mathcal {U}(\mathcal {P}_n, 2r_n)) = \beta _k(\mathcal {M})$ for all $k$ . Thus, we have that

Next,from Proposition 4.8 we have that

By Morse theory, if $N_{k,n}= \widehat{N}_{k,n}$ for every $k$ , then necessarily $\beta _k(\mathcal {U}(\mathcal {P}_n,r_n)) = \beta _k(\mathcal {U}(\mathcal {P}_n,\hat{r}_n))$ for every $0\le k \le m$ (no critical points between $r_n$ and $\hat{r}_n$ implies no changes in the homology). Choosing $\hat{r}_n = 2r_n$ , we have that

Combining ( 5.12 ) with ( 5.13 ) yields

which completes the proof of the first part. For the second part of the theorem , repeat the same arguments using the second part of Propositions 4.7 and 4.8. $\square $

Adler, R.J., Bobrowski, O., Borman, M.S., Subag, E., Weinberger, S.: Persistent homology for random fields and complexes. Inst. Math. Stat. Collect. 6 , 124–143 (2010)

MathSciNet Google Scholar

Adler, R.J., Bobrowski, O., Weinberger, S.: Crackle: The persistent homology of noise. ArXiv, preprint arXiv:1301.1466 (2013)

Adler, R.J., Taylor, J.E.: Random fields and geometry. Springer Monographs in Mathematics. Springer, New York (2007)

Google Scholar

Aswani, P.B.A., Tomlin, C.: Regression on manifolds: Estimation of the exterior derivative. Ann. Stat. 39 (1), 48–81 (2011)

Article MATH MathSciNet Google Scholar

Aronshtam, L., Linial, N., Luczak, T., Meshulam, R.: Vanishing of the top homology of a random complex. Arxiv, preprint arXiv:1010.1400 (2010)

Arratia, R., Goldstein, L., Gordon, L.: Two moments suffice for poisson approximations: the Chen-Stein method. Ann. Probab. 17 (1), 9–25 (1989)

Auffinger, A., Arous, G.B.: Complexity of random smooth functions of many variables. Ann. Probab. (2013)

Baddeley, A.J., Silverman, B.W.: A cautionary example on the use of second-order methods for analyzing point patterns. Biometrics 40 , 1089–1094 (1984)

Article MathSciNet Google Scholar

Baryshnikov, Y., Bubenik, P., Kahle, M.: Min-type morse theory for configuration spaces of hard spheres. Int. Math. Res. Notices, page rnt012 (2013)

Belkin, M., Niyogi, P.: Towards a theoretical foundation for laplacian-based manifold methods. In: Auer, P., Meir, R. (eds.) Learning Theory, Volume 3559 of Lecture Notes in Computer Science, pp. 486–500. Springer, Berlin (2005)

Bendich, P., Mukherjee, S., Wang, B.: Local homology transfer and stratification learning. ACM-SIAM Symposium on Discrete Algorithms (2012)

Bobrowski, O.: Algebraic topology of random fields and complexes. PhD Thesis (2012)

Bobrowski, O., Adler, R.J.: Distance functions, critical points, and topology for some random complexes. arXiv:1107.4775 , July (2011)

Bobrowski, O., Borman, M.S.: Euler integration of Gaussian random fields and persistent homology. J. Topol. Anal. 4 (01), 49–70 (2012)

Borsuk, K.: On the imbedding of systems of compacta in simplicial complexes. Fund. Math. 35 (217–234), 5 (1948)

Bryzgalova, L.N.: The maximum functions of a family of functions that depend on parameters. Funktsional. Anal. i Prilozhen 12 (1), 66–67 (1978)

Bubenik, P., Carlsson, G., Kim, P.T., Luo, Z.: Statistical topology via Morse theory, persistence and nonparametric estimation. 0908.3668, August 2009. Contemp. Math. 516 , 75–92 (2010)

Bubenik, P., Kim, P.T.: A statistical approach to persistent homology. Homol. Homot. Appl. 9 (2), 337–362 (2007)

Chamandy, N., Worsley, K.J., Taylor, J.E., Gosselin, F.: Tilted Euler characteristic densities for central limit random fields. with applications to “bubbles”. Ann. Stat. 36 (5), 2471–2507 (2008)

Chazal, F., Cohen-Steiner, D., Lieutier, A.: A sampling theory for compact sets in Euclidean space. Discrete Comput. Geom. 41 , 461–479 (2009)

Chen, D., Müller, H.-G.: Nonlinear manifold representations for functional data. Ann. Stat. 40 (1), 1–29 (2012)

Article Google Scholar

Chung, M.K., Bubenik, P., Kim, P.T.: Persistence diagrams of cortical surface data. In: Information processing in medical imaging, pp 386–397 (2009)

Diggle, P.J.: Statistical Analysis of Spatial Point Patterns. Academic Press, Waltham (2003)

MATH Google Scholar

Flatto, L., Newman, D.J.: Random coverings. Acta. Mathematica 138 (1), 241–264 (1977)

Genovese, I.V.C.R.: Marco Perone-Pacifico and Larry Wasserman. On the path density of a gradient field. Ann. Stat. 37 (6A), 3236–3271 (2009)

Gershkovich, V., Rubinstein, H.: Morse theory for min-type functions. Asian J. Math. 1 (4), 696–715 (1997)

MATH MathSciNet Google Scholar

Hatcher, A.: Algebraic Topology. Cambridge University Press, Cambridge (2002)

Kahle, M.: Topology of random clique complexes. Discrete Math. 309 (6), 1658–1671 (2009)

Kahle, M.: Random geometric complexes. Discrete Comput. Geom. Int. J. Math. Comput. Sci. 45 (3), 553–573 (2011)

Kahle, M., Meckes, E., et al.: Limit the theorems for Betti numbers of random simplicial complexes. Homol. Homot. Appl. 15 (1), 343–374 (2013)

Linial, N., Meshulam, R.: Homological connectivity of random 2-complexes. Combinatorica 26 (4), 475–487 (2006)

Lunagómez, S., Mukherjee, S., Wolpert, Robert L.: Geometric representations of hypergraphs for prior specification and posterior sampling (2009). http://arxiv.org/abs/0912.3648

Matheron, G.: Random sets and integral geometry. Wiley, New York-London-Sydney (1975) With a foreword by Geoffrey S. Watson, Wiley Series in Probability and Mathematical Statistics

Matov, V.I.: Topological classication of the germs of functions of the maximum and minimax of families of functions in general position. Uspekhi Mat. Nauk 37 (4(226)), 167–168 (1982)

Mecke, K.R., Stoyan, D.: Morphological characterization of point patterns. Biometric. J. 47 (5), 473–488 (2005)

Meester, R., Roy, R.: Continuum percolation. Cambridge University Press, Cambridge (1996)

Book MATH Google Scholar

Mémoli, F., Sapiro, G.: Distance functions and geodesics on submanifolds of $\mathbb{R}^d$ and point clouds. SIAM J. Appl. Math. 65 (4), 1227–1260 (2005)

Milnor, J.W.: Morse theory. Based on lecture notes by M. Spivak and R. Wells. Ann. Math. Stud. No. 51. Princeton University Press, Princeton (1963)

Mischaikow, K., Wanner, T.: Probabilistic validation of homology computations for nodal domains. Ann. Appl. Probab. 17 (3), 980–1018 (2007)

Molchanov, I.: Theory of Random Sets. Springer, Berlin (2005)

Moller, J., Waagepetersen, R.: Statistical Inference for Spatial Point Processes. Chapman & Hall, London (2003)

Book Google Scholar

Munkres, J.R.: Elements of Algebraic Topology, vol. 2. Addison-Wesley, Reading (1984)

Niyogi, P., Smale, S., Weinberger, S.: A topological view of unsupervised learning from noisy data. SIAM J. Comput. 40 (3), 646 (2011)

Partha, N., Smale, S., Weinberger, S.: Finding the homology of submanifolds with high confidence from random samples. Discrete Comput. Geom. Int. J. Math. Comput. Sci. 39 (1–3), 419–441 (2008)

Penrose, M.D.: Random Geometric Graphs, volume 5 of Oxford Studies in Probability. Oxford University Press, Oxford (2003)

Penrose, M.D., Yukich, J.E.: Limit theory for point processes in manifolds. 1104.0914, April (2011)

Qiang, W., Mukherjee, S., Zhou, D.-X.: Learning gradients on manifolds. Bernoulli 16 (1), 181–207 (2010)

Ripley, B.D.: The second-order analysis of stationary point processes. Ann. Appl. Probab. 13 (2), 255–266 (1976)

Robert, E.S., Adler, J.: Rotation and scale space random fields and the gaussian kinematic formula. Ann. Stat. 40 (6), 2910–2942 (2012)

Article MATH Google Scholar

Rohe, S.C.K., Yu, B.: Spectral clustering and the high-dimensional stochastic blockmodel. Ann. Stat. 39 (4), 1878–1915 (2011)

Stoyan, D., Kendall, W.S., Mecke, J.: Stochastic geometry and its applications. Wiley Series in Probability and Mathematical Statistics: applied Probability and Statistics. Wiley, Chichester (1987). With a foreword by D. G. Kendall

Taylor, J.E., Worsley, K.J.: Random fields of multivariate test statistics, with applications to shape analysis. Ann. Stat. 36 (1), 1–27 (2008)

Worsley, K.J.: Boundary corrections for the expected euler characteristic of excursion sets of random fields, with an application to astrophysics. Adv. Appl. Probab. 943–959 (1995)

Worsley, K.J.: Estimating the number of peaks in a random field using the Hadwiger characteristic of excursion sets, with applications to medical images. Ann. Stat. 23 (2), 640–669 April (1995). Mathematical Reviews number (MathSciNet): MR1332586; Zentralblatt MATH identifier; 0898.62120

Download references

Acknowledgments

The authors would like to thank: Robert Adler, Shmuel Weinberger, John Harer, Paul Bendich, Guillermo Sapiro, Matthew Kahle, Matthew Strom Borman, and Alan Gelfand for many useful discussions. We would also like to thank the anonymous referee.

Author information

Authors and affiliations.

Department of Mathematics, Duke University, Durham, NC , 27708, USA

Omer Bobrowski

Departments of Statistical Science, Computer Science, and Mathematics, Institute for Genome Sciences and Policy, Duke University, Durham, NC , 27708, USA

Sayan Mukherjee

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Omer Bobrowski .

Additional information

OB was supported by DARPA: N66001-11-1-4002Sub#8. SM is pleased to acknowledge the support of NIH (Systems Biology): 5P50-GM081883, AFOSR: FA9550-10-1-0436, NSF CCF-1049290, and NSF DMS-1209155.

Appendix A: Palm theory for poisson processes

This appendix contains a collection of definitions and theorems which are used in the proofs of this paper. Most of the results are cited from [ 45 ], although they may not necessarily have originated there. However, for notational reasons we refer the reader to [ 45 ], while other resources include [ 6 , 51 ]. The following theorem is very useful when computing expectations related to Poisson processes.

Theorem 6.1

(Palm theory for Poisson processes, [ 45 ] Theorem 1.6) Let $f$ be a probability density on $\mathbb {R}^d$ , and let $\mathcal {P}_n$ be a Poisson process on $\mathbb {R}^d$ with intensity $\lambda _n = n f$ . Let $h(\mathcal {Y},\mathcal {X})$ be a measurable function defined for all finite subsets $\mathcal {Y}\subset \mathcal {X}\subset \mathbb {R}^d$ with $\left| {\mathcal {Y}}\right| = k$ . Then

where $\mathcal {Y}'$ is a set of $k\,iid$ points in $\mathbb {R}^d$ with density $f$ , independent of $\mathcal {P}_n$ .

We shall also need the following corollary, which treats second moments:

Corollary 6.2

With the notation above, assuming $\left| {\mathcal {Y}_1}\right| = \left| {\mathcal {Y}_2}\right| = k$ ,

where $\mathcal {Y}'_{12} = \mathcal {Y}'_1 \cup \mathcal {Y}'_2$ is a set of $2k-j\,iid$ points in $\mathbb {R}^d$ with density $f(x)$ , independent of $\mathcal {P}_n$ , and $\left| {\mathcal {Y}_1'\cap \mathcal {Y}_2'}\right| = j$ .

Appendix B: Stein’s method

In this paper we omitted the proofs for the limit distributions in Theorems 4.2, 4.4, and 4.6, referring the reader to [ 13 ], where these results were proved for point processes in a Euclidean space. These proof mainly rely on moment computations similar to the ones presented in this paper, but technically more complicated. In this section we wish to introduce the main theorems used in these proofs.

The theorems below are two instances of Stein’s method , used to prove limit distribution for sums of weakly dependent variables. To adapt these method to the statements in this paper, one can think of the random variables $\xi _i$ as some version of the Bernoulli variables $g_{r_n}^b(\mathcal {Y},\mathcal {P}_n), g_{r_n}^c(\mathcal {Y},\mathcal {P}_n)$ used in this paper.

Definition 7.1

Let $(I,E)$ be a graph. For $i,j\in I$ we denote $i \sim j$ if $(i,j) \in E$ . Let $\left\{ \xi _i\right\} _{i\in I}$ be a set of random variables. We say that $(I,\sim )$ is a dependency graph for $\left\{ \xi _i\right\} $ if for every $I_1\cap I_2 = \emptyset $ , with no edges between $I_1$ and $I_2$ , the set of variables $\left\{ \xi _i\right\} _{i\in I_1}$ is independent of $\left\{ \xi _i\right\} _{i\in I_2}$ . We also define the neighborhood of $i$ as $\mathcal {N}_i := \left\{ i\right\} \cup \left\{ j \in I \, j\sim i\right\} $ .

Theorem 7.2

(Stein-Chen Method for Bernoulli Variables, Theorem 2.1 in [ 45 ]) Let $\left\{ \xi _i\right\} _{i\in I}$ be a set of Bernoulli random variables, with dependency graph $(I,\sim )$ . Let

Theorem 7.3

(CLT for sums of weakly dependent variables, Theorem 2.4 in [ 45 ]) Let $(\xi _i)_{i\in I}$ be a finite collection of random variables, with $\mathbb {E}\left\{ {\xi _i}\right\} = 0$ . Let $(I,\sim )$ be the dependency graph of $(\xi _i)_{i\in I}$ , and assume that its maximal degree is $D-1$ . Set $W:=\sum _{i\in I} \xi _i$ , and suppose that $\mathbb {E}\left\{ {W^2}\right\} =1$ . Then for all $w\in \mathbb {R}$ ,

where $F_W$ is the distribution function of $W$ and $\Phi $ that of a standard Gaussian.

Appendix C: Second moment computations

In this section we briefly review the steps required to evaluate the second moment of either $\beta _{k,n}$ or $N_{k,n}$ in order to compute the limit variance in Theorems 4.2, 4.4, and 4.6. Similar computations are required to evaluate higher moments, which are needed in order to apply Stein’s method for the limit distributions. The proofs follow the same steps as the proofs in both [ 29 ] and [ 13 ]. These proofs are long and technically complicated, and since repeating them again for the manifold case should add no insight, we refer the reader to these papers for the complete proofs.

We present the statements in terms of $N_{k,n}$ , but the same line of arguments can be applied to $S_{k,n}$ as well (defined in 5.6 ).

The variance of $N_{k,n}$ is

The first term on the right hand side can be written as

and we know the limit of the expectation of this term in each of the regimes.

Next, for $0\le j<k+1$ , using Corollary 6.2 we have

where $\mathcal {Y}'_{12} = \mathcal {Y}'_1 \cup \mathcal {Y}'_2$ is a set of $(2k-j)\,iid$ points in $\mathbb {R}^d$ with density $f(x)$ , independent of $\mathcal {P}_n,\,\left| {\mathcal {Y}_1'}\right| = \left| {\mathcal {Y}_2'}\right| = k$ , and $\left| {\mathcal {Y}_1'\cap \mathcal {Y}_2'}\right| = j$ . For $j>0$ , the functional inside the expectation is nonzero for subsets $\mathcal {Y}_{1,2} '$ contained in a ball of radius $4r_n$ . Thus, a change of variables similar to the ones used in the proof of Theorems 4.2, 4.4 and 4.6, can be used to show that this expectation on the right hand side of ( 5.17 ) is $O(r_n^{m(2k+1-j)})$ . If $j=0$ the sets are disjoint, and given $\mathcal {Y}_1'$ and $\mathcal {Y}_2'$ we have two options: If $B(\mathcal {Y}_1') \cap B(\mathcal {Y}_2') \ne \emptyset $ , then a similar bound to the on above applies. Otherwise, the two balls are disjoint, and therefore the processes $B(\mathcal {Y}_1') \cap \mathcal {P}_n$ and $B(\mathcal {Y}_1') \cap \mathcal {P}_n$ are independent. In this case it can be show that the expected value cancels with $\mathbb {E}\{{N_{k,n}^2}\}$ in ( 5.14 ).

In the subcritical regime, the dominated term in ( 5.15 ) would be $\mathbb {E}\left\{ {I_{k+1}}\right\} $ , and from ( 5.16 ) we have that $\mathrm {Var}\left( {N_k}\right) \approx \mathbb {E}\left\{ {N_k}\right\} $ . In the other regimes, all the terms in ( 5.15 ) are $O(n)$ , and thus the limit variance is $O(n)$ as well.

Rights and permissions

Reprints and permissions

About this article

Bobrowski, O., Mukherjee, S. The topology of probability distributions on manifolds. Probab. Theory Relat. Fields 161 , 651–686 (2015). https://doi.org/10.1007/s00440-014-0556-x

Download citation

Received : 05 July 2013

Revised : 26 February 2014

Published : 22 March 2014

Issue Date : April 2015

DOI : https://doi.org/10.1007/s00440-014-0556-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Random complexes
Point process
Random Betti numbers
Stochastic topology

Mathematics Subject Classification (2000)

Primary 60D05
Secondary 55U10
Find a journal
Publish with us
Track your research

Organization chart
Prizes and Awards
Activity Reports
Information for visitors
Employments & Internships
Financial Services
Human Resources Department
Communication
Experimental Science Library
Design office
Electronics
Clean room, materials
Infrastructures, shops
Electricity
Cleaning and maintenance service

ASTROPHYSICS, COSMOLOGY AND GRAVITATION

Presentation
Astrophysics
Cosmology and Gravitation
Multiscale physics of living systems
Theoretical neuroscience and biophysics
Microfluidics, emulsion and biology
Molecular membrane mechanisms
Active Cell Matter
Statistical physics and inference for biology

FLUIDS AND INTERFACES

Non-linear physics
Folding, Sliding, Stretching Lab
Micromegas : nano-fluidics

FUNDAMENTAL INTERACTIONS

Fields, Gravity and Strings

QUANTUM MATERIALS AND DEVICES

Nano-optics
Mesoscopic physics
QUAD : Quantum physics and devices
Condensed matter theory
Hybrid Quantum Circuits

STATISTICAL PHYSICS

Physics of fluctuations, correlations and information
Disordered systems and applications
Classical and quantum many-body systems

Thematics schools and conferences
Doctoral schools
Predoctoral trainings at ENS
Defended theses

DISSEMINATION

News archive
Science mediation
Partnerships and valorization
Communication / logos

Select Page

Publications

Statistical physics.

Browse Course Material

Course info.

Prof. Scott Sheffield

Departments

Mathematics

As Taught In

Mathematical Analysis
Probability and Statistics
Topology and Geometry

Learning Resource Types

Universal random structures in 2d, course description.

Multi-colored circles of various sizes all inside of a larger circle.

You are leaving MIT OpenCourseWare

Random Assignment Problems on 2d Manifolds

INFN - Istituto Nazionale di Fisica Nucleare (Italy) 300039
PSL - Université Paris Sciences et Lettres (60 rue Mazarine 75006 Paris - France) 564132
CdF (institution) - Collège de France (France) 300026
INSERM - Institut National de la Santé et de la Recherche Médicale : U1050 (101, rue de Tolbiac, 75013 Paris - France) 303623
CNRS - Centre National de la Recherche Scientifique : UMR7241 (France) 441569
UVSQ - Université de Versailles Saint-Quentin-en-Yvelines (55 avenue de Paris - 78035 Versailles cedex - France) 81173
Université Paris-Saclay (Bâtiment Bréguet, 3 Rue Joliot Curie 2e ét, 91190 Gif-sur-Yvette - France) 419361
CNRS - Centre National de la Recherche Scientifique : UMR8628 (France) 441569
SU - Sorbonne Université (21 rue de l’École de médecine - 75006 Paris - France) 413221
CNRS - Centre National de la Recherche Scientifique : UMR8023 (France) 441569
UPCité - Université Paris Cité (85 boulevard Saint-Germain 75006 Paris - France) 557826
Function : Author
PersonId : 742681
IdHAL : matteodachille
ORCID : 0000-0002-8750-1275
IdRef : 252465164

Andrea Sportiello : Connect in order to contact the contributor

https://hal.science/hal-02944904

Submitted on : Monday, September 21, 2020-6:15:06 PM

Last modification on : Saturday, April 27, 2024-3:12:31 AM

Long-term archiving on: Saturday, December 5, 2020-2:45:41 AM

Dates and versions

Identifiers.

HAL Id : hal-02944904 , version 1
ARXIV : 2008.01462
DOI : 10.1007/s10955-021-02768-4

Collections

IMAGES

(PDF) Random assignment problems on 2d manifolds
Figure 1 from Adsorption-Freezing Transition for Random Heteropolymers
(PDF) Riemannian metrics on 2D-manifolds related to the Euler-Poinsot
differential geometry
(PDF) Random assignment problems on 2d manifolds
6 Problems on Differentiable Manifolds I

VIDEO

ANSYS MECHANICAL TUTORIAL_4: Transmission simulation of gear and rack
Assignment 8 Problem 2
random sampling & assignment
RANDOM ASSIGNMENT
How to Solve 2D Kinematics Problems
International Zoom Inverse Problems Seminar, February 8, 2024, Boya Liu (NC State)

COMMENTS

Random Assignment Problems on 2d Manifolds
The Euclidean assignment problem is a transportation problem between a set of N "red" points and a set of N "blue" points. Both sets are supposed to be on a given n-dimensional Riemannian manifold $\Omega $.A transportation map is a bijective map , that is, a pairing among the red and blue points.A transportation cost $w_{xy}$ is given for each pair , and the cost of the map T is ...
PDF Random Assignment Problems on 2 Manifolds
RANDOM ASSIGNMENT PROBLEMS ON 2d MANIFOLDS D. BENEDETTO, E. CAGLIOTI, S. CARACCIOLO, M. D'ACHILLE, G. SICURO, AND A. SPORTIELLO Abstract. We consider the assignment problem between two sets of N random points on a smooth, two-dimensional manifold Ω of unit area. It is known that the average cost scales as E Ω(N) ∼1 √ 2π
PDF Random Assignment Problems on 2d Manifolds
Random Assignment Problems on 2d Manifolds Page 3 of 40 34 Let us put this result in context, by summarising (part of) the state of the art for this problem. In contrast with the transportation problem for continuous measures, in this case the candidate optimal transportation maps are just the N! permutations, that is, the possible
[2008.01462] Random assignment problems on ${2d}$ manifolds
Title: Random assignment problems on ${2d}$ manifolds Authors: Dario Benedetto , Emanuele Caglioti , Sergio Caracciolo , Matteo D'Achille , Gabriele Sicuro , Andrea Sportiello Download PDF
(PDF) Random Assignment Problems on 2d Manifolds
Random Assignment Problems on 2 d Manifolds Page 11 of 40 34 with 2-dimensional electrostatics, namely with the classical problem of the ﬁeld self-energy for a distribution of point charges.
Random Assignment Problems on 2d Manifolds
Random Assignment Problems on 2d Manifolds @article{Benedetto2020RandomAP, title={Random Assignment Problems on 2d Manifolds}, author={Dario Benedetto and Emanuele Caglioti and Sergio Caracciolo and Matteo D'Achille and Gabriele Sicuro and Andrea Sportiello}, journal={Journal of Statistical Physics}, year={2020}, volume={183}, url={https ...
PDF Random Assignment Problems on 2d Manifolds
Random Assignment Problems on 2 d Manifolds ... Weconsider the assignment problembetween two sets of N random points on a smooth,two-dimensional manifold of unit area. It is known that the average ...
Random Assignment Problems on 2d Manifolds
We consider the assignment problem between two sets of N random points on a smooth, two-dimensional manifold Ω of unit area. It is known that the average cost scales as E[Ω (N)] ∼ 1/2π ln N with a correction that is at most of order √ ln N ln ln N. In this paper, we show that, within the linearization approximation of the field-theoretical formulation of the problem, the first Ω ...
Random assignment problems on 2d manifolds
PDF | We consider the assignment problem between two sets of $N$ random points on a smooth, two-dimensional manifold $\\Omega$ of unit area. It is known... | Find ...
Random assignment problems on 2d manifolds
RANDOM ASSIGNMENT PROBLEMS ON 2d MANIFOLDS D. BENEDETTO, E. CAGLIOTI, S. CARACCIOLO, M. D'ACHILLE, G. SICURO, AND A. SPORTIELLO Abstract. We consider the assignment problem between two sets of N random points on a smooth, two-dimensional manifold Ω of unit area. It is known that the 1 average cost scales as EΩ (N ) ∼ 2π ln N with a ...
Random assignment problems on ${2d}$ manifolds
task dataset model metric name metric value global rank remove
PDF Assignment Problems
been an increasing amount of literature on PDE methods for studying this 2d problem [2,23,27]. Further consequences of the CLPS ansatz have been investigated in the case Ω a 2d manifold [5]. See [17] for further details. In this paper, we prove a theorem to compare E[HΩ1,Ω2 opt] and E[H Ω3,Ω4 opt] by using stochastic order of c(B (Ω1) 1,R ...
Random Assignment Problems on 2d Manifolds
toggle menu. close close menu. Search. Research products. Publications; Research data
The topology of probability distributions on manifolds
Random Assignment Problems on 2d Manifolds Article Open access 12 May 2021. Topology at a Scale in Metric Spaces ... a random process on a manifold can be thought of as an approximation of excursion sets of Gaussian random fields or energy landscapes. ... A common problem in topological manifold learning is the following:
Open Problems
Suggested research problems for a final project on universal random structures in 2D. Browse Course Material Syllabus Readings Lecture Notes Assignments Course Info Instructor ... assignment Problem Sets. notes Lecture Notes. assignment Written Assignments. Download Course.
RANDOM ASSIGNMENT PROBLEMS ON d
RANDOM ASSIGNMENT PROBLEMS ON 2d MANIFOLDS D. BENEDETTO, E. CAGLIOTI, S. CARACCIOLO, M. D'ACHILLE, G. SICURO, AND A. SPORTIELLO Abstract. We consider the assignment problem between two sets of Nrandom points on a smooth, two-dimensional manifold Ω of unit area. It is known that the average cost scales as E Ω(N) ∼ 1
Emanuele Caglioti
Random Assignment Problems on 2d Manifolds: JOURNAL OF STATISTICAL PHYSICS: 2021: Comparison between the Cauchy problem and the scattering problem for the Landau damping in the Vlasov-HMF equation: ASYMPTOTIC ANALYSIS: 2021: MEAN-FIELD LIMIT FOR PARTICLE SYSTEMS WITH TOPOLOGICAL INTERACTIONS: MATHEMATICS AND MECHANICS OF COMPLEX SYSTEMS: 2021
Publications
35 Random Assignment Problems on 2d Manifolds Dario Benedetto, Emanuele Caglioti, Sergio Caracciolo, Matteo d'Achille, Gabriele Sicuro, Andrea Sportiello Journal of Statistical Physics. DOI PDF HAL. 36 Low-frequency vibrational spectrum of mean-field disordered systems
On the optimal map in the $ 2 $-dimensional random matching problem
Erhan Bayraktar. Gaoyue Guo. ... The optimal matching problem is one of the classical random optimization problems which has received constant attention in the probability and mathematical physics ...
Universal Random Structures in 2D
assignment Written Assignments. This graduate-level course introduces students to some fundamental 2D random objects, explains how they are related to each other, and explores some open problems in the field.
Random Assignment Problems on 2d Manifolds
We consider the assignment problem between two sets of N random points on a smooth, two-dimensional manifold Ω of unit area. It is known that the average cost scales as E[Ω (N)] ∼ 1/2π ln N with a correction that is at most of order √ ln N ln ln N. ... Matteo d'Achille, Gabriele Sicuro, et al.. Random Assignment Problems on 2d Manifolds ...
Statistical Properties of the Euclidean Random Assignment Problem
Given 2n points, n ``red'' and n ``blue'', in a Euclidean space,solving the associated Euclidean Assignment Problem consists infinding the bijection between red and blue points that minimizes ...
On the concave one-dimensional random assignment problem and Young
The aim of this paper is to prove that the variance of the multi-level MC estimated reach probability under fixed assignment splitting is smaller or equal than under random assignment splitting ...

Random assignment problems on 2d manifolds

Related Papers

RELATED TOPICS

Subscribe to the PwC Newsletter

Add a new code entry for this paper

Code Edit Add Remove Mark official

The topology of probability distributions on manifolds

Cite this article

Similar content being viewed by others

Random Assignment Problems on 2d Manifolds

On the Maximum $$f$$ -Divergence of Probability Distributions Given the Value of Their Coupling

The reach of subsets of manifolds

1 Introduction

2 Topological ingredients

2.1 Homology and betti numbers

2.2 Critical points of the distance function

Definition 2.1

Definition 2.3

2.3 Morse theory

2.4 Čech complexes and the nerve lemma

Definition 2.4

3 Model specification and relevant definitions

4.1 The sub-critical range \((nr_n^m\rightarrow 0)\)

Theorem 4.1

Theorem 4.2

4.2 The critical range ( \(nr_n^m\rightarrow \lambda \in (0,\infty )\) )

Theorem 4.3

Theorem 4.4

Corollary 4.5

4.3 The super-critical range ( \(nr_n^m\rightarrow \infty \) )

Theorem 4.6

Proposition 4.7

Proposition 4.8

Theorem 4.9

5.1 Some notation and elementary considerations

5.2 The sub-critical range ( \(nr_n^m\rightarrow 0\) )

Proof of Theorem 4.2

5.3 The critical range ( \(nr_n^m\rightarrow \lambda \) )

Proof of Theorem 4.4

Proof of Theorem 4.3

5.4 The super-critical range ( \(nr_n^m\rightarrow \infty \) )

Proof of Proposition 4.7

Proof of Proposition 4.8

Proof of Theorem 4.9

Acknowledgments

Author information

Corresponding author

Additional information

Appendix A: Palm theory for poisson processes

Theorem 6.1

Corollary 6.2

Appendix B: Stein’s method

Definition 7.1

Theorem 7.2

Theorem 7.3

Appendix C: Second moment computations

Rights and permissions

About this article

Share this article

Mathematics Subject Classification (2000)

ASTROPHYSICS, COSMOLOGY AND GRAVITATION

FLUIDS AND INTERFACES

FUNDAMENTAL INTERACTIONS

QUANTUM MATERIALS AND DEVICES

STATISTICAL PHYSICS

DISSEMINATION

Publications

Browse Course Material

Departments

As Taught In

Learning Resource Types

You are leaving MIT OpenCourseWare

Random Assignment Problems on 2d Manifolds

Dates and versions

Collections

IMAGES

VIDEO

COMMENTS