math problem solving absolute value

Forgot password? New user? Sign up

Existing user? Log in

Absolute Value Equations

Already have an account? Log in here.

• Pranshu Gaba
• Alan Enrique Ontiveros Salazar
• Kai Hsien Boo
• Agnishom Chattopadhyay
• Aditya Virani
• Prince Loomba
• Keshav Ramesh

Absolute value equations are equations involving expressions with the absolute value functions . This wiki intends to demonstrate and discuss problem solving techniques that let us solve such equations.

A very basic example would be as follows:

Find all values of \(x\) satisfying \(|x-2| + |x-4| = 4.\)

Usually, the basic approach is to analyze the behavior of the function before and after the point where they reach 0. For example, for \(|x-a|\) one could analyze the cases where \(x > a\) or \(x < a\), or even \(x = a\) if required. However, these problems are often simplified with a more sophisticated approach like being able to eliminate some of the cases, or graphing the functions. In this wiki, we intend to discuss this techniques along with strategies on when to use which.

Methodology

Technique - squaring both sides, technique - casework, technique - sketching graph, problem solving - miscellaneous.

Introduction to absolute value equations

Methodology to solve absolute value equations: the techniques used to solve absolute value equations and when to use which one

Take an example to describe the following methodology:

1) Understanding absolute value--positive, negative case (or graph approach) 2) Determining possible solutions 3) Verifying solutions

Explain - How do we use this technique to solve absolute value equations?

Remember to verify the possible solutions - why and how?

2-3 examples in increasing order of difficulty - explaining how we squared both sides to solve more difficult problems

Followed by 1-2 TIY problems - relevant to be solved by case work technique

Suppose we have an equation of the form \(\lvert a \rvert = \lvert b \rvert\). Since both sides are positive, we can square them without adding extraneous solutions: \[a^2=b^2.\] Then solve it as an ordinary equation: \[\begin{align} a^2-b^2&=0 \\ (a+b)(a-b)&=0. \end{align}\] So we see that \(a=-b\) or \(a=b\).

Solve the equation \(\lvert 3x+4 \rvert = \lvert 2x-7 \rvert\) for real \(x\). We square both sides to obtain \[(3x+4)^2=(2x-7)^2.\] Here we don't need to expand both sides; just apply the difference of two squares to find the factors: \[\begin{align} (3x+4+2x-7)(3x+4-2x+7)&=0 \\ (5x-3)(x+11)&=0. \end{align} \] The solutions are \(\left\{\frac{3}{5}, -11\right\}. \ _ \square\)

Because absolute value can be defined as piecewise functions, depending on where the value of \(x \) is with respect to the number line, you have to work with a different "piece" of the piecewise function.

General steps:

Using the definition of absolute value as a piecewise function, "undo" the absolute value sign(s) and write cases. For example, we know that the expression in the absolute value sign can either be positive or negative.

Solve each case for \( x\).

Verify the solutions.

Find all real values of \(x\) such that \( | 3x – 4 | – 2 = 3.\) We first isolate the absolute value onto one side: \[\begin{align} | 3x – 4 | – 2 & = 3\\ | 3x – 4 | &= 5. \end{align}\] Now, we "undo" the absolute value signs and split the equation into its two cases, the positive case and the negative case: \[\begin{array}{rlcccrl} (3x – 4) &= 5 &&\text{ or } && –(3x – 4) &= 5\\ 3x – 4 &= 5 &&\text{ or } && –3x + 4 &= 5\\ 3x &= 9 &&\text{ or } && –3x &= 1\\ x &= 3 &&\text{ or } && x &= –\frac{1}{3}. \ _\square \end{array}\]

Find all real values of \(x \) such that \( |x+1| + |2x+3| = 5 \). There are four possible cases, but one will be eliminated due to impossibility: Case 1. If \(x+1 \) and \( 2x+3 \) are both positive, then \[\begin{align} x+1 + 2x+3 &= 5 \\ 3x + 4 &= 5 \\ 3x &= 1 \\ x &= \dfrac{1}{3}. \end{align} \] Case 2. If \( x+1 \) is negative and \( 2x + 3 \) is positive, then \[\begin{align} - x - 1 + 2x + 3 &= 5 \\ x + 2 &= 5 \\ x &= 3. \end{align} \] However, when \( x = 3 \), \( x+1 \) and \( 2x+3 \) are both positive, so this is not a valid solution to the equation. Case 3. If \( x+1 \) and \( 2x+3 \) are both negative, then \[\begin{align} -x - 1 - 2x - 3 &= 5 \\ -3x - 4 &= 5 \\ -3x &= 9 \\ x &= -3. \end{align} \] Case 4. If \( x +1 \) is positive and \( 2x + 3 \) is negative, it is an impossible case. Graph the two lines if you are not convinced. Therefore, the solution set is \(\left \{ -3, \frac{1}{3} \right \}.\ _\square\)

Find all real values of \(x\) such that \[|x+2|+|2x+6|+|3x-3|=12.\] In this problem we are dealing with 3 terms of absolute values. Their turning points (the values of \(x\) such that they change sign) of the three terms are \(x=-2, x=-3, x=1,\) respectively. Hence, we need to check the cases \(-\infty < x \leq -3\), \(-3<x\leq -2\), \(-2 < x \leq 1\), \(1<x<\infty\). Case 1. \(\, -\infty < x \leq -3\) In this case, the three terms will always be negative. Hence, \[\begin{aligned} -(x+2)-(2x+6)-(3x-3)&=12 \\ x &= -\frac{17}{6}. \end{aligned}\] However, \(x=-\frac{17}{6} >-3\) is not within the domain \(-\infty < x \leq -3\). Thus this solution is not valid. Case 2. \(\, -3<x\leq -2\) In this case, the three terms will be negative, positive, and negative, respectively. Hence, \[\begin{aligned} -(x+2)+(2x+6)-(3x-3)&=12 \\ x &= -\frac{5}{2}. \end{aligned}\] \(x=-\frac{5}{2}\) lies between \(-3\) and \(-2\). Thus \(\boxed{x=-\frac{5}{2}}\) is one of the solutions. Case 3. \(\, -2 < x \leq 1\) In this case, the three terms will be positive, positive, and negative, respectively. However, \[\begin{aligned} (x+2)+(2x+6)-(3x-3)=11 \neq 12. \end{aligned}\] Thus there is no solution within this domain. Case 4. \(\, 1<x<\infty\) In this case, the three terms are always positive. Hence, \[\begin{aligned} (x+2)+(2x+6)+(3x-3)&=12 \\ x &= \frac{7}{6}, \end{aligned}\] which lies between \(1\) and \(\infty\). Thus \(\boxed{x=\frac{7}{6}}\) is another solution. In conclusion, \(x=-\frac{5}{2}\) and \(x=\frac{7}{6}\) are the solutions for the given equation. \(_\square\)

Find all real values of \( x \) such that \( |x||x+1| = 2 \). Case 1. \(\, x, x+1 \) both positive \[\begin{align} x(x+1)-2 &= 0 \\ x^2 +x - 2 &= 0 \\ x &= 1, x = -2. \end{align} \] Reject \( x = -2 \) because it does not make both \(x \) and \( x +1 \) positive. Case 2. \(\, x\) negative, \( x + 1 \) positive \[\begin{align} -x(x+1)-2 &= 0 \\ -x^2 - x - 2 &= 0 \\ x^2 + x + 2 &= 0 \\ x &= \dfrac{-1 \pm \sqrt{1 - 4 \cdot 1 \cdot 2 }}{2}. \end{align} \] We only asked for real solutions, so at this point we ignore this case because we're going to get imaginary results. Case 3. \(\, x\) positive, \( x +1 \) negative This is an impossible case (graph the lines and you'll see why), so we can ignore it. Case 4. \(\, x, x+1 \) both negative Because they're both negative, the negatives end up "canceling" and become positive, which was what we had in Case 1. However, the restriction is different from Case 1 (here, both \( x \) and \( x +1 \) have to be negative, not positive ), so instead of rejecting \( x = -2 \), we reject \( x = 1 \) from this case. Basically, in this specific case 4, \( x = 1 \) is not a possible solution, but it does not mean it's not a possible solution for Case 1 because we're simply going piece by piece in this piecewise function--in the end we will take the union of all possible solutions. Thus, the solutions are \( \left \{ -2, 1 \right \} \). \(_\square\)

Sometimes absolute value equations have a ridiculous number of cases and it would take too long to go through every single case. Therefore, we can instead graph the absolute value equations using the definition of absolute value as a piecewise function. To get each piece, you must figure out the domain of each piece. This method is highly beneficial when the question writer asks for the number of solutions instead of the actual solutions. Let's work through some examples to see how this is done.

Find all real solutions to \( |3x-4| = 5 \). To graph this, there are two possible cases: when \( 3x - 4\) is positive, and when \( 3x-4 \) is negative. When is \( 3x-4 \) positive? \[\begin{align} 3x - 4 &> 0 \\ 3x &> 4 \\ x &> \dfrac{4}{3}. \end{align} \] (Also, when \( x < \frac{4}{3} \), \( 3x- 4 \) will be negative.) We know that there will be a "turning point" at \( x = \frac{4}{3} \) for the graph of \( y = |3x-4| \). Finally, using the definition of absolute value, we know that when \( x > \frac{4}{3} \), \( y = 3x - 4 \), and when \( x \leqslant \frac{4}{3} \), \( y = -3x + 4 \). We now just need to graph \( y = 5 \) and look for the intersections. You can see that the solutions are \(\left \{ -\frac{1}{3} , 3 \right \}.\ _\square\). Another benefit of this graphing technique is that you do not need to verify any of the solutions--since we are only graphing the pieces that are actually mathematically possible, we get all the solutions we are looking for, no less and no more. If you could not discern the solutions from the picture, you can simply solve the equation for each case.

Find all real solutions to \( |x+1| + |2x+3| = 5 \). The possible cases are that \(\hspace{0.5cm}\) 1. \( \, x+1, 2x+3 \) are both positive; \(\hspace{0.5cm}\) 2. \( \, x+1 \) is negative and \( 2x+3 \) is positive; \(\hspace{0.5cm}\) 3. \( \, x+1 , 2x + 3 \) are both negative. We need to figure out the domains for which each of these holds. Case 1 holds when \( x > -1 \). Case 2 holds when \( -\frac{3}{2} < x< -1 \). Case 3 holds when \( x < -\frac{3}{2} \). Now, let's write our piecewise function. When \( x > -1 \), we have \( y = x+1 + 2x + 3 = 3x + 4 \). When \( -\dfrac{3}{2} < x< -1 \), we have\( y = -x -1 + 2x + 3 = x + 2 \). When \( x < - \dfrac{3}{2} \), we have \( y = -x - 1 -2x - 3 = -3x -4 \). As you can see in the graph, the solutions for the given equation are \(\left \{ -3, \frac{1}{3} \right \}.\ _\square\) .

Find all real solutions to \( |x||x+1| = 2 \). To graph this, we again only look at the possible cases and when they would occur: \(\hspace{0.5cm}\) 1. \(\, x, x+1 \) both positive \(\hspace{0.5cm}\) 2. \(\, x \) negative, \( x+1 \) positive \(\hspace{0.5cm}\) 3. \(\, x, x+1 \) both negative. Case 1 is true when \( x>0 \). Case 2 is true when \( -1 < x < 0 \). Case 3 is true when \( x<-1 \). When \( x>0 \) and when \( x< -1 \), we have \( y = x(x+1) = x^2 + x \). When \( -1 < x < 0 \), we have \( y = -x(x+1) = -x^2 - x \). It is evident that the solutions are \(\{-2, 1\}.\ _\square\)

Any other technique (fact, definition) you can use to solve the problems? Otherwise move on to the followings.

3-4 examples solved by using a mix of more than one of above techniques

Add guiding text in between. Guiding text means phrasing the section in a way that it keeps on telling the reader what's going on in this section.

3-4 TIY problems - using multiple techniques to solve

What is the sum of all real numbers \(x\) satisfying \[ x^2-\sqrt{x^2} = \lvert x-1 \rvert +5?\] Observe that \(\sqrt{x^2}=\lvert x \rvert.\) Then the given equation becomes \[ x^2-\lvert x \rvert= \lvert x-1 \rvert +5.\] If \(x<0,\) then we rewrite the equation to obtain \[\begin{align} x^2-(-x)&=-(x-1)+5\\ x^2+2x-6&=0\\ x&=-1\pm \sqrt{7}\\ x&=-1-\sqrt{7}. \qquad (\text{since } x<0) \end{align}\] If \(0\le x<1,\) then we rewrite the equation to obtain \[\begin{align} x^2-x&=-(x-1)+5\\ x^2&=6\\ x&=\pm \sqrt{6}, \end{align}\] which do not satisfy the assumption \(0\leq x<1.\) Thus there are no solutions in this interval. If \(x\ge 1,\) then we rewrite the equation to obtain \[\begin{align} x^2-x&=x-1+5\\ x^2-2x-4&=0\\ x&=1\pm \sqrt{5}\\ x&=1+\sqrt{5}. \qquad (\text{since } x\ge 1) \end{align}\] Therefore, the above three cases give two solutions \(x=-1-\sqrt{7}\) and \(x=1+\sqrt{5},\) the sum of which is \(\sqrt{5}-\sqrt{7}.\) \(_\square\)

[IMO 1959/2] Solve the equation \(\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}=A\) for real \(x\) (where the square roots are only defined for non-negative values), when \(A=\sqrt{2}\); \(A=1\); \(A=2\). Here we don't see any absolute value involved with the equation. Before doing anything, note that our first restriction for \(x\) is \(x \geq \frac{1}{2}\) and for \(A\) is \(A>0\). Intuitively, we could square both sides to get rid of some square roots: \[\begin{align} x+\sqrt{2x-1}+x-\sqrt{2x-1}+2\sqrt{x^2-(2x-1)}&=A^2 \\ 2x+2\sqrt{(x-1)^2}&=A^2. \end{align}\] Great! We find a perfect square inside the square root, so an absolute value will appear: \[2x+2|x-1|=A^2.\] Now we are going to find the possible cases for \(A\): When \(x-1 > 0\), we have \[\begin{align} 2x+2(x-1)&=A^2 \\ x&=\dfrac{A^2+2}{4}. \end{align}\] Then, by our assumption of \(x-1 > 0\), we get that this solution only works when \(A^2 > 2\). When \(x-1 \leq 0\), something interesting happens: \[\begin{align} 2x-2(x-1)&=A^2 \\ 2&=A^2. \end{align}\] So, when \(A^2=2 (\text{or }A=\sqrt{2})\), the equation becomes independent of \(x\), implying that any value of the interval \(x \in \left[\frac{1}{2},1\right]\) will be a solution for the first point. When \(A=1\), there are no solutions by our restriction of \(A^2 \geq 2\). Finally, when \(A=2\) we have \[x=\dfrac{2^2+2}{4}=\frac{3}{2}.\ _\square\] What happens if we allow the square roots to admit negative values?

Sometimes, in minimization problems, it often helps us to see that the value of an expression inside the absolute value is at least 0.

No problem found with slug "absolute-warm-up"

Problem Loading...

Note Loading...

Set Loading...

Absolute Value in Algebra

Absolute value means ....

... how far a number is from zero:

"6" is 6 away from zero, and "−6" is also 6 away from zero.

So the absolute value of 6 is 6 , and the absolute value of −6 is also 6

Absolute Value Symbol

To show we want the absolute value we put "|" marks either side (called "bars"), like these examples:

More Formal

More formally we have:

Which says the absolute value of x equals:

• x when x is greater than zero
• 0 when x equals 0
• −x when x is less than zero (this "flips" the number back to positive)

So when a number is positive or zero we leave it alone, when it is negative we change it to positive using −x.

Example: what is |−17| ?

Well, it is less than zero, so we need to calculate "−x":

− ( −17 ) = + 17

(Because two minuses make a plus )

Useful Properties

Here are some properties of absolute values that can be useful:

That makes sense ... |a| can never be less than zero.

Squaring a makes it positive or zero (for a as a Real Number). Then taking the square root will "undo" the squaring, but leave it positive or zero.

Means these are the same:

• the absolute value of (a times b), and
• (the absolute value of a) times (the absolute value of b)

Which can also be useful when solving

Which is often the key to solving most absolute value questions.

Example: Solve |x+2| = 5

Using "|u| = a is the same as u = ±a ":

Which has two solutions:

Graphically

Let us graph that example:

It is easier to graph when we have an "=0" equation, so subtract 5 from both sides:

|x+2| − 5 = 0

Now let's plot y=|x+2|−5 and find where it equals zero.

Here is the plot of y=|x+2|−5 , but just for fun let's make the graph by shifting it around :

And the two solutions (circled) are −7 and +3 .

Absolute Value Inequalities

Mixing Absolute Values and Inequalites needs a little care!

There are 4 inequalities:

Less Than, Less Than or Equal To

With " < " and " ≤ " we get one interval centered on zero:

Example: Solve |x| < 3

This means the distance from x to zero must be less than 3:

Everything in between (but not including) −3 and 3

It can be rewritten as:

−3 < x < 3

As an interval it can be written as:

The same thing works for "Less Than or Equal To":

Example: Solve |x| ≤ 3

Everything in between and including -3 and 3

How about a bigger example?

Example: Solve |3x-6| ≤ 12

Rewrite it as:

−12  ≤  3x−6  ≤  12

−6  ≤  3x  ≤  18

Lastly, multiply by (1/3). Because we are multiplying by a positive number, the inequalities will not change:

−2  ≤  x  ≤  6

Greater Than, Greater Than or Equal To

This is different ... we get two separate intervals :

Example: Solve |x| > 3

It looks like this:

less than -3 or from 3 onwards

It can be rewritten as

x < −3   or   x > 3

(−∞, −3) U (3, +∞)

Note: U means "Union" of the two intervals.

Careful! Do not write it as

Because x cannot be less than -3 and greater than 3 at the same time

It is really:

x is less than −3 or greater than 3

The same thing works for "Greater Than or Equal To":

Example: Solve |x| ≥ 3

Can be rewritten as

x ≤ −3   or   x ≥ 3

(−∞, −3] U [3, +∞)

Absolute Value Equation Calculator

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Example (Click to try)

About absolute value equations.

• Get the absolve value expression by itself.
• Set up two equations and solve them separately.

Absolute Value Equation Video Lesson

• Khan Academy Video: Absolute Value Equations

Need more problem types? Try MathPapa Algebra Calculator

Clear Absolute Value Equation Calculator »

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Solving Simpler Absolute-Value Equations

Simpler Harder Special Case

When we take the absolute value of a number, we always end up with a positive number (or zero). Whether the input was positive or negative (or zero), the output is always positive (or zero). For instance, | 3 | = 3 , and | −3 | = 3 also.

This property — that both the positive and the negative become positive — makes solving absolute-value equations a little tricky. But once you learn the "trick", they're not so bad. Let's start with something simple:

Content Continues Below

MathHelp.com

Solving Absolute Value Equations

Solve | x | = 3

I've pretty much already solved this, in my discussion above:

| −3 | = 3

So then x must be equal to 3 or equal to −3 .

But how am I supposed to solve this if I don't already know the answer? I will use the positive / negative property of the absolute value to split the equation into two cases, and I will use the fact that the "minus" sign in the negative case indicates "the opposite sign", not "a negative number".

For example, if I have x = −6 , then " − x " indicates "the opposite of x " or, in this case, −(−6) = +6 , a positive number. The "minus" sign in " − x " just indicates that I am changing the sign on x . It does not indicate a negative number. This distinction is crucial!

Whatever the value of x might be, taking the absolute value of x makes it positive. Since x might originally have been positive and might originally have been negative, I must acknowledge this fact when I remove the absolute-value bars. I do this by splitting the equation into two cases. For this exercise, these cases are as follows:

a. If the value of x was non-negative (that is, if it was positive or zero) to start with, then I can bring that value out of the absolute-value bars without changing its sign, giving me the equation x = 3 .

b. If the value of x was negative to start with, then I can bring that value out of the absolute-value bars by changing the sign on x , giving me the equation − x = 3 , which solves as x = −3 .

Then my solution is

x = ±3

We can, by the way, verify the above solution graphically. When we attempt to solve the absolute-value equation | x  | = 3 , we are, in effect, setting two line equations equal to each other and finding where they cross. For instance:

In the above, I've plotted the graph of y 1  = |  x  | (being the blue line that looks like a "V") and y 2  = 3 (being the green horizontal line). These two graphs cross at x  = −3 and at x  = +3 (being the two red dots).

If you're wanting to check your answers on a test (before you hand it in), it can be helpful to plug each side of the original absolute-value equation into your calculator as their own functions; then ask the calculator for the intersection points.

Of course, any solution can also be verified by plugging it back into the original exercise, and confirming that the left-hand side (LHS) of the equation simplifies to the same value as does the right-hand side (RHS) of the equation. For the equation above, here's my check:

x = −3

LHS: | x | = | −3 |

LHS: | x | = | +3 |

If you're ever in doubt about your solution to an equation, try graphing or else try plugging your solution back into the original question. Checking your work is always okay!

The step in the above, where the absolute-value equation was restated in two forms, one with a "plus" and one with a "minus", gives us a handy way to simplify things: When we have isolated the absolute value and go to take off the bars, we can split the equation into two cases; we will signify these cases by placing a "minus" on the opposite side of the equation (for one case) and a "plus" on the opposite side (for the other). Here's how this works:

Solve | x + 2 | = 7 , and check your solution(s).

Advertisement

The absolute value is isolated on the left-hand side of the equation, so it's already set up for me to split the equation into two cases. To clear the absolute-value bars, I must split the equation into its two possible two cases, one each for if the contents of the absolute-value bars (that is, if the "argument" of the absolute value) is negative and if it's non-negative (that is, if it's positive or zero). To do this, I create two new equations, where the only difference between then is the sign on the right-hand side. First, I'll do the "minus" case:

x + 2 = −7

x = −9

Now I'll do the non-negative case, where I can just drop the bars and solve:

Now I need to check my solutions. I'll do this by plugging them back into the original equation, since the grader can't see me checking plots on my graphing calculator.

x = −9:

LHS: |(−9) + 2|

= |−7| = 7 = RHS

LHS: |(5) + 2|

= |7| = 7 = RHS

Both solutions check, so my answer is:

x = −9, 5

Solve | 2 x − 3 | − 4 = 3

First, I'll isolate the absolute-value part of the equation; that is, I'll get the absolute-value expression by itself on one side of the "equals" sign, with everything else on the other side:

| 2 x − 3 | − 4 = 3

| 2 x − 3 | = 7

Now I'll clear the absolute-value bars by splitting the equation into its two cases, one for each sign on the argument. First I'll do the negative case:

2 x − 3 = −7

2 x = −4

x = −2

And then I'll do the non-negative case:

2 x − 3 = 7

The exercise doesn't tell me to check, so I won't. (But, if I'd wanted to, I could have plugged "abs(2X−3)−4" and "3" into my calculator (as Y1 and Y2, respectively), and seen that the intersection points were at my x -values.) My answer is:

x = −2, 5

URL: https://www.purplemath.com/modules/solveabs.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

• Math Articles
• Absolute value

Absolute value equations and inequalities

2.8  Absolute value equations and inequalities

  In this section we describe methods of solving equations and inequalities involving absolute value. Recall from Chapter 1 that the absolute value of a number a , written |a| , gives the distance from a to 0 on a number line. By this definition, the absolute value equation |x| = 3 can be solved by finding all real numbers at a distance of 3 units from 0 . As shown in Figure 2.15, there are two numbers satisfying this condition, 3 and -3 , so that the solution set of the equation |x| = 3 is the set {3,-3} .

   FIGURE 2.15

   ABSOLUTE VALUE EQUATIONS If a and b represent two real numbers, then the absolute value of their difference, |a-b| or |b-a| , represents the distance between the points on the number line whose coordinates are a and b. (Verify this for 3 and -3 in Figure 2.15.) This concept is used in simple equations involving absolute value.

USING THE DISTANCE DEFINITION TO SOLVE AN ABSOLUTE VALUE EQUATION

  Solve  |p-4|=5 .

  The expression |p-4| represents the distance between p and 4 . The equation |p-4|=5  can be solved by finding all real numbers that are 5 units from 4 . As shown in Figure 2.16, these numbers are  -1 and 9 . The solution set is {-1,9} .

   FIGURE 2.16

   The definition of absolute value leads to the following properties of absolute value that can be used to solve absolute value equations algebraically.

SOLVING  ABSOLUTE VALUE EQUATIONS

   Solve each equation

  (a)  |5-3m|=12

  Use property (1) above, with a=5-3m , to write

   5-3m=12   or   5-3m=-12 .

  Solve each equation

   5-3m=12

   -3m=7

   m=-7/3

  or

   5-3m=-12

   -3m=-17

   m=17/3

  The solution set is  {-7/3,17/3} .

  (b)  |4m-3|=|m+6|

  By property (2) above, this equation will be true if

   4m-3=m+6   or   4m-3=-(m+6) .

  Solve each equation.

   4m-3=m+6

   3m=9

   m=3

   4m-3=-(m+6)

   4m-3=-m-6

   5m=-3

   m=-3/5

  The solution set of  |4m-3|=|m+6| is thus  {3,-3/5} .

   ABSOLUTE VALUE INEQUALITIES The method used to solve absolute value equations can be extended to solve inequalities with absolute value.

USING THE DISTANCE DEFINITION FOR ABSOLUTE VALUE INEQUALITIES

  (a) Solve  |x|<5 .

   FIGURE 2.17

   (b) Solve  |x|>5 .

  In a manner similar to pan (a), we see that the solution of |x|>5 consists of all real numbers whose distance from 0 is greater than 5 . This includes those numbers greater than 5 or those less than -5 : x<-5 or  x>5 .

   FIGURE 2.18

  In interval notation, the solution is written (-∞,-5) {union} (5,∞) . The solution set is shown in Figure 2.18. 

  The following properties of absolute value, which can be obtained from the definition of absolute value, are used to solve absolute value inequalities.

SOLVING AN ABSOLUTE VALUE INEQUALITIES

  For any positive number b

  1.  |a|<b if and only if  -b<a<b ;

  2.  |a|>b if and only if  a<-b or  a>b .

SOLVING AN ABSOLUTE VALUE INEQUALITY

  Solve  |x-2|<5 .

  This inequality is satisfied by all real numbers whose distance from 2 is less than 5 . As shown in Figure 2.19, the solution set is the interval (-3, 7) . Property (1) above can be used to solve the inequality as follows. Let a=x-2 and b=5 , so that |x-2|<5 if and only if

   -5<x-2<5 .

  Adding 2 to each part of this three-pan inequality produces

   -3<x<7 ,

  giving the interval solution  (-3,7) .

   FIGURE 2.19

  Solve  |x-8|>=1 .

  All numbers whose distance from 8 is greater than or equal to 1 are solutions. To find the solution using property (2) above, let a = x - 8 and b = 1 so that |x-8|>=1  if and only if

   x-8<=-1   or   x-8>=1

   x<=7   or   x>=9 .

  The solution set, (-∞,7) {union} (9,∞) , is shown in Figure 2.20

   FIGURE 2.20

  The properties given above for solving absolute value inequalities require that the absolute value expression be alone on one side of the inequality. Example 6 shows how to meet this requirement when this is not the case at first.

SOLVING AN ABSOLUTE VALUE INEQUALITY REQUIRING A TRANSFORMATION

  Solve  |2-7m|-1>4 .

  In order to use the properties of absolute value given above, first add l to both sides; this gives 

   |2-7m|>5 .

  Now use property (2) above. By this property,  |2-7m|>5 if and only if

   2-7m<-5   or   2-7m>5 .

  Solve each of these inequalities separately to get the solution set  (-∞,-3/7) {union} (1,∞) .

  If an absolute value equation or inequality is written with 0 or a negative number on one side. such as |2-5x|>=-4 , we do not solve by applying the methods of the earlier examples. Use the fact that the absolute value of any expression must be a nonnegative number to solve the equation or inequality.

SOLVING SPECIAL CASES OF ABSOLUTE VALUE EQUATIONS AND INEQUALITIES

  Use the fact that absolute value is always inequality. ways nonnegative to solve each equation or inequality.

  (a)  |2-5x|>=-4

  Since the absolute value of a number is always nonnegalive, |2-5x|>=-4 is always true. The solution set includes all real numbers, written (-∞,∞) .

  (b)  |4x-7|<-3

  The absolute value of any number will never be less than -3 (or less than any negative number). For this reason, the solution set of this inequality is {empty} .

  (c)  |5x+15|=0

  The absolute value of a number will be zero only if that number is 0 . There fore, this equation is equivalent to 5x+15=0 , which has solution set {-3} .

Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.

   We end this section with an example showing how certain statements involving distance can be described using absolute value inequalities.

USING ABSOLUTE VALUE INEQUALITIES TO DESCRIBE DISTANCES

  Write each statement using an absolute value inequality.

  (a)  k is not less than  5 units from  8 .

  Since the distance from k to 8 , written |k-8| or |8-k| . is not less than 5 the distance is greater than or equal to 5 . Write this as

   |k-8|>=5 .

  (b)  n is within  0.001 of  6 .

  This statement indicates that  n may be  0.001 more than  6 or  0.001 less than  6 . That is the distance of  n from  6 is no more than  0.001 , Written

   |n-6|<=0.001 .

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.7e: Exercises - Absolute Value

• Last updated
• Save as PDF
• Page ID 45456

A: Absolute Value Equations (I)

Exercise \(\PageIndex{A}\)

\( \bigstar \) Solve the following absolute value equations.

B: Absolute Value Linear Inequalities (I)

Exercise \(\PageIndex{B}\): Absolute Value Linear Inequalities I

\( \bigstar \)  Solve. State the solution in interval notation and graph the solution set on the number line.

51. \(( - 5,5 )\);

53. \([ - 4 , - 2 ]\);

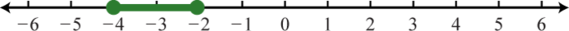
55. \(\emptyset\);

57. \([ - 1,4 ]\);

59. \(\left\{ \frac { 3 } { 5 } \right\}\);

61. \([ - 1,5 ]\);

63. \(( - \infty , - 5 ] \cup [ 5 , \infty )\);

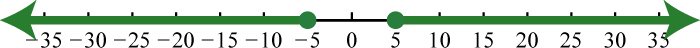
65. \(( - \infty , - 10 ) \cup ( 6 , \infty )\);

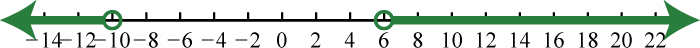
67. \(\mathbb { R }\);

69. \(( - \infty , - 2 ] \cup [ 7 , \infty )\);

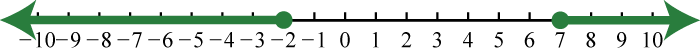
71. \(\left( - \infty , - \frac { 3 } { 2 } \right) \cup ( 3 , \infty )\);

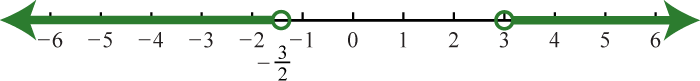
73. \(( - \infty , - 2 ) \cup ( 5 , \infty )\);

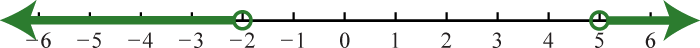
C: Absolute Value Linear Inequalities (II)

Exercise \(\PageIndex{C}\): Absolute Value Linear Inequalities II

81. \(( - \infty , - 2 ) \cup ( 3 , \infty )\);

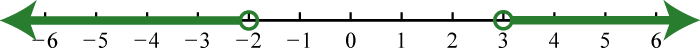
83. \(( 1,7 )\);

85. \(( - \infty , 3 ) \cup ( 5 , \infty )\);

87. \(( - \infty , - 8 ) \cup ( 3 , \infty )\);

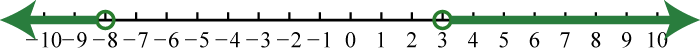
89. \(( - \infty , - 19 ] \cup [ - 6 , \infty )\);

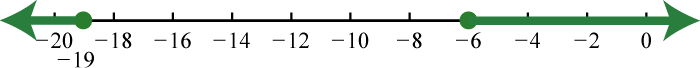
91. \(\mathbb { R }\);

93. \(\left[ \frac { 2 } { 3 } , 2 \right]\);

95. \(( - 12 , - 2 )\);

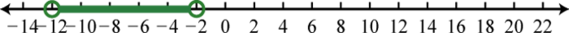
97. \(( - \infty , 0 ) \cup ( 6 , \infty )\);

99.  \(\left( 0 , \frac { 1 } { 2 } \right)\);

101. \(\frac { 1 } { 2 }\);

103. \(\left( - \frac { 1 } { 2 } , \frac { 3 } { 2 } \right)\);

105. \([ 0,3 ]\);

107. \(( - \infty , 3 ) \cup ( 9 , \infty )\);

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Integers and Absolute Value Problems? (+FREE Worksheet!)

Two vertical lines around a number or expression are used to indicate the absolute value of that number or expression. Here, you can learn how to find the absolute value of a number and how to solve math problems containing absolute values and integers.

The absolute value of the real number \(a\) Is written in the form of \(| a |\) and is a positive number. Two vertical lines around a number or expression are used to indicate the absolute value of that number or expression. The output value of the absolute value is always greater than or equal to zero. Absolute value is used to indicate the distance of a number from zero on the line of real numbers.

Related Topics

• How to Add and Subtract Integers
• How to Multiply and Divide Integers
• How to Use Order of Operations
• How to Order Integers and Numbers

The Absolute Best Books to Ace Pre-Algebra to Algebra II

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Step-by-step guide to solving integers and absolute value problems.

• The absolute value of a positive number is equal to the same positive number.
• The absolute value of zero is equal to zero.
• The absolute value of a negative number is the positive value of that number.
• Note: To find the absolute value of a number, just find its distance from \(0\) on a number line! For example, the distance of \(12\) and \(- \ 12\) from zero on number line is \(12\)!

Integers and Absolute Value – Example 1:

Solve. \(|8 \ – \ 2| \ × \ \frac{ |- \ 4 \ × \ 6|}{3}=\)

First solve \(|8 \ – \ 2|, →|8 \ – \ 2|=|6|\), the absolute value of \(6\) is \(6\), \(|6|=6\) \(6 \ × \ \frac{ |- \ 4 \ × \ 6|}{3}=\) Now solve \(|- \ 4 \ × \ 6|, → |- \ 4 \ × \ 6|=|- \ 24|\), the absolute value of \(- \ 24\) is \(24\), \(|- \ 24|=24\) Then: \(6 \ × \ \frac{ 24}{3}= 6 \ × \ 8=48 \)

Integers and Absolute Value – Example 2:

Solve. \(\frac{ |- \ 12|}{3} \ × \ |9 \ – \ 4|=\)

First find \(|- \ 12| , →\) the absolute value of \(- \ 12\) is \(12\), then: \(|- \ 12|=12\) \(\frac{12}{3} \ × \ |9 \ – \ 4|= \) Next, solve \(|9 \ – \ 4|, → |9 \ – \ 4|=| \ 5|\), the absolute value of \( \ 5\) is \(5\), \(| \ 5|=5\) Then: \(\frac{12}{3} \ × \ 5=4 \ × \ 5=20\)

Integers and Absolute Value – Example 3:

Solve. \(\frac{ |-18|}{9}×|5-8|=\)

First find \(|-18| , →\) the absolute value of \(-18\) is \(18\), then: \(|-18|=18\) \( \frac{18}{9}×|5-8|=\) Next, solve \(|5-8|, → |5-8|=|-3|\), the absolute value of \(-3\) is \(3\), \(|-3|=3\) Then: \(\frac{18}{9}×3=2×3=6\)

The Best Book to Help You Ace Pre-Algebra

Pre-Algebra for Beginners The Ultimate Step by Step Guide to Preparing for the Pre-Algebra Test

Integers and absolute value – example 4:.

Solve. \(|10-5|×\frac{ |-2×6|}{3}=\)

First solve \(|10-5|, →|10-5|=|5|\), the absolute value of \(5\) is \(5, |5|=5\) \( 5×\frac{ |-2×6|}{3}= \) Now solve \(|-2×6|, → |-2×6|=|-12|\), the absolute value of \(-12\) is \(12, |-12|=12\) Then: \(5×\frac{ 12}{3}= 5×4=20\)

Exercises for Solving Integers and Absolute Value Problems

• \(\color{blue}{|-43| – |12| + 10}\)
• \(\color{blue}{76 + |-15-45| – |3|}\)
• \(\color{blue}{30 + |-62| – 46}\)
• \(\color{blue}{|32| – |-78| + 90}\)
• \(\color{blue}{|-35+4| + 6 – 4}\)
• \(\color{blue}{|-4| + |-11|}\)

Download Integers and Absolute Value Worksheet

• \(\color{blue}{41}\)
• \(\color{blue}{133}\)
• \(\color{blue}{46}\)
• \(\color{blue}{44}\)
• \(\color{blue}{33}\)
• \(\color{blue}{15}\)

The Greatest Books for Students to Ace the Algebra

Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests

Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.

by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• Riemann Sums Made Easy: Step-by-Step Tutorial
• 10 Most Common 5th Grade STAAR Math Questions
• FTCE General Knowledge Math Formulas
• How to Find Slope? (+FREE Worksheet!)
• The Best ALEKS Math Worksheets: FREE & Printable
• How to Sketch Trigonometric Graphs?
• Top Calculators for the ACT Math Test 2023: Quick Review
• 6th Grade NDSA Math Worksheets: FREE & Printable
• How to Write a Quadratic Function from Its Vertex and Another Point
• A Comprehensive Collection of Free ParaPro Math Practice Tests

What people say about "How to Solve Integers and Absolute Value Problems? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra

Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra i for beginners the ultimate step by step guide to acing algebra i, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra tutor everything you need to help achieve an excellent score.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \left|3x+1\right|=4
• \left|a-6\right|=\left|6-a\right|
• 1.5\left|3p\right|=4.5
• 4\left|2x-8\right|=9
• \left|3x+4\right|=-3
• 5-\left|2(x+3)\right|=0

absolute-equation-calculator

• High School Math Solutions – Absolute Value Equation Calculator Solving absolute value equations is somewhat tricky; it requires understanding of the absolute value property....

Please add a message.

Message received. Thanks for the feedback.