hypothesis test for a population mean calculator

Teach yourself statistics

Hypothesis Test for a Mean

This lesson explains how to conduct a hypothesis test of a mean, when the following conditions are met:

• The sampling method is simple random sampling .
• The sampling distribution is normal or nearly normal.

Generally, the sampling distribution will be approximately normally distributed if any of the following conditions apply.

• The population distribution is normal.
• The population distribution is symmetric , unimodal , without outliers , and the sample size is 15 or less.
• The population distribution is moderately skewed , unimodal, without outliers, and the sample size is between 16 and 40.
• The sample size is greater than 40, without outliers.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

The table below shows three sets of hypotheses. Each makes a statement about how the population mean μ is related to a specified value M . (In the table, the symbol ≠ means " not equal to ".)

The first set of hypotheses (Set 1) is an example of a two-tailed test , since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests , since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the one-sample t-test to determine whether the hypothesized mean differs significantly from the observed sample mean.

Analyze Sample Data

Using sample data, conduct a one-sample t-test. This involves finding the standard error, degrees of freedom, test statistic, and the P-value associated with the test statistic.

SE = s * sqrt{ ( 1/n ) * [ ( N - n ) / ( N - 1 ) ] }

SE = s / sqrt( n )

• Degrees of freedom. The degrees of freedom (DF) is equal to the sample size (n) minus one. Thus, DF = n - 1.

t = ( x - μ) / SE

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the t statistic, given the degrees of freedom computed above. (See sample problems at the end of this lesson for examples of how this is done.)

Sample Size Calculator

As you probably noticed, the process of hypothesis testing can be complex. When you need to test a hypothesis about a mean score, consider using the Sample Size Calculator. The calculator is fairly easy to use, and it is free. You can find the Sample Size Calculator in Stat Trek's main menu under the Stat Tools tab. Or you can tap the button below.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

In this section, two sample problems illustrate how to conduct a hypothesis test of a mean score. The first problem involves a two-tailed test; the second problem, a one-tailed test.

Problem 1: Two-Tailed Test

An inventor has developed a new, energy-efficient lawn mower engine. He claims that the engine will run continuously for 5 hours (300 minutes) on a single gallon of regular gasoline. From his stock of 2000 engines, the inventor selects a simple random sample of 50 engines for testing. The engines run for an average of 295 minutes, with a standard deviation of 20 minutes. Test the null hypothesis that the mean run time is 300 minutes against the alternative hypothesis that the mean run time is not 300 minutes. Use a 0.05 level of significance. (Assume that run times for the population of engines are normally distributed.)

Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

Null hypothesis: μ = 300

Alternative hypothesis: μ ≠ 300

• Formulate an analysis plan . For this analysis, the significance level is 0.05. The test method is a one-sample t-test .

SE = s / sqrt(n) = 20 / sqrt(50) = 20/7.07 = 2.83

DF = n - 1 = 50 - 1 = 49

t = ( x - μ) / SE = (295 - 300)/2.83 = -1.77

where s is the standard deviation of the sample, x is the sample mean, μ is the hypothesized population mean, and n is the sample size.

Since we have a two-tailed test , the P-value is the probability that the t statistic having 49 degrees of freedom is less than -1.77 or greater than 1.77. We use the t Distribution Calculator to find P(t < -1.77) is about 0.04.

• If you enter 1.77 as the sample mean in the t Distribution Calculator, you will find the that the P(t < 1.77) is about 0.04. Therefore, P(t >  1.77) is 1 minus 0.96 or 0.04. Thus, the P-value = 0.04 + 0.04 = 0.08.
• Interpret results . Since the P-value (0.08) is greater than the significance level (0.05), we cannot reject the null hypothesis.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the population was normally distributed, and the sample size was small relative to the population size (less than 5%).

Problem 2: One-Tailed Test

Bon Air Elementary School has 1000 students. The principal of the school thinks that the average IQ of students at Bon Air is at least 110. To prove her point, she administers an IQ test to 20 randomly selected students. Among the sampled students, the average IQ is 108 with a standard deviation of 10. Based on these results, should the principal accept or reject her original hypothesis? Assume a significance level of 0.01. (Assume that test scores in the population of engines are normally distributed.)

Null hypothesis: μ >= 110

Alternative hypothesis: μ < 110

• Formulate an analysis plan . For this analysis, the significance level is 0.01. The test method is a one-sample t-test .

SE = s / sqrt(n) = 10 / sqrt(20) = 10/4.472 = 2.236

DF = n - 1 = 20 - 1 = 19

t = ( x - μ) / SE = (108 - 110)/2.236 = -0.894

Here is the logic of the analysis: Given the alternative hypothesis (μ < 110), we want to know whether the observed sample mean is small enough to cause us to reject the null hypothesis.

The observed sample mean produced a t statistic test statistic of -0.894. We use the t Distribution Calculator to find P(t < -0.894) is about 0.19.

• This means we would expect to find a sample mean of 108 or smaller in 19 percent of our samples, if the true population IQ were 110. Thus the P-value in this analysis is 0.19.
• Interpret results . Since the P-value (0.19) is greater than the significance level (0.01), we cannot reject the null hypothesis.

Hypothesis Testing Calculator for Population Mean English Español

A free online hypothesis testing calculator for population mean to find the Hypothesis for the given population mean. Enter the sample mean, population mean, sample standard deviation, population size and the significance level to know the T score test value, P value and result of hypothesis.

• 1-800-234-2933
• [email protected]

Hypothesis testing for the mean Calculator

State the null and alternative hypothesis:

Calculate our test statistic z:, determine rejection region:, you have 2 free calculationss remaining, what is the answer, how does the hypothesis testing for the mean calculator work, what 1 formula is used for the hypothesis testing for the mean calculator, what 7 concepts are covered in the hypothesis testing for the mean calculator.

• alternative hypothesis
• hypothesis testing for the mean
• null hypothesis
• test statistic

An Automated Online Math Tutor serving 8.1 million parents and students in 235 countries and territories.

Our Services

• All Courses
• Our Experts

Top Categories

• Development
• Photography
• Refer a Friend
• Festival Offer
• Limited Membership
• Scholarship

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.6: Hypothesis Test of a Single Population Mean with Examples

• Last updated
• Save as PDF
• Page ID 130297

Steps for performing Hypothesis Test of a Single Population Mean

Step 1: State your hypotheses about the population mean. Step 2: Summarize the data. State a significance level. State and check conditions required for the procedure

• Find or identify the sample size, n, the sample mean, \(\bar{x}\) and the sample standard deviation, s .

The sampling distribution for the one-mean test statistic is, approximately, T- distribution if the following conditions are met

• Sample is random with independent observations .
• Sample is large. The population must be Normal or the sample size must be at least 30.

Step 3: Perform the procedure based on the assumption that \(H_{0}\) is true

• Find the Estimated Standard Error: \(SE=\frac{s}{\sqrt{n}}\).
• Compute the observed value of the test statistic: \(T_{obs}=\frac{\bar{x}-\mu_{0}}{SE}\).
• Check the type of the test (right-, left-, or two-tailed)
• Find the p-value in order to measure your level of surprise.

Step 4: Make a decision about \(H_{0}\) and \(H_{a}\)

• Do you reject or not reject your null hypothesis?

Step 5: Make a conclusion

• What does this mean in the context of the data?

The following examples illustrate a left-, right-, and two-tailed test.

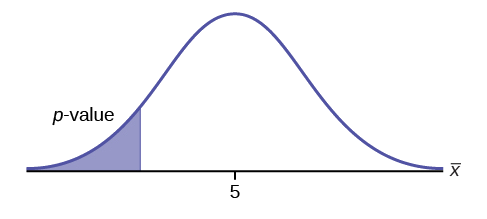
Example \(\pageindex{1}\).

\(H_{0}: \mu = 5, H_{a}: \mu < 5\)

Test of a single population mean. \(H_{a}\) tells you the test is left-tailed. The picture of the \(p\)-value is as follows:

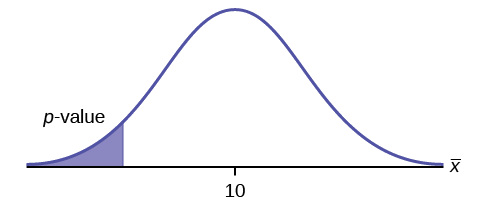
Exercise \(\PageIndex{1}\)

\(H_{0}: \mu = 10, H_{a}: \mu < 10\)

Assume the \(p\)-value is 0.0935. What type of test is this? Draw the picture of the \(p\)-value.

left-tailed test

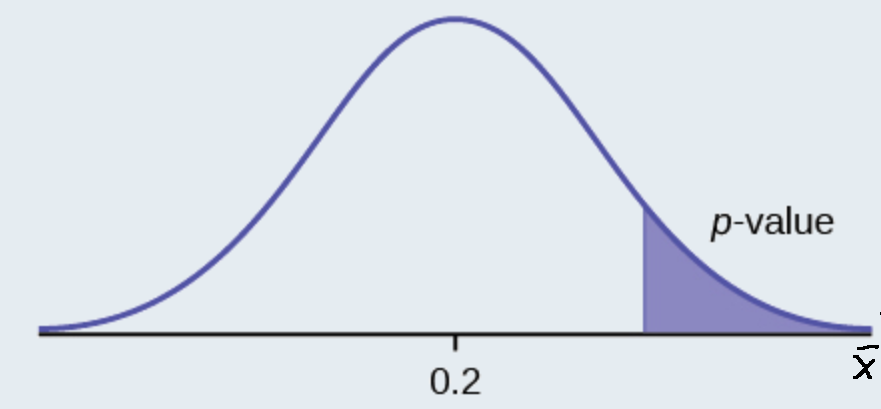
Example \(\PageIndex{2}\)

\(H_{0}: \mu \leq 0.2, H_{a}: \mu > 0.2\)

This is a test of a single population proportion. \(H_{a}\) tells you the test is right-tailed . The picture of the p -value is as follows:

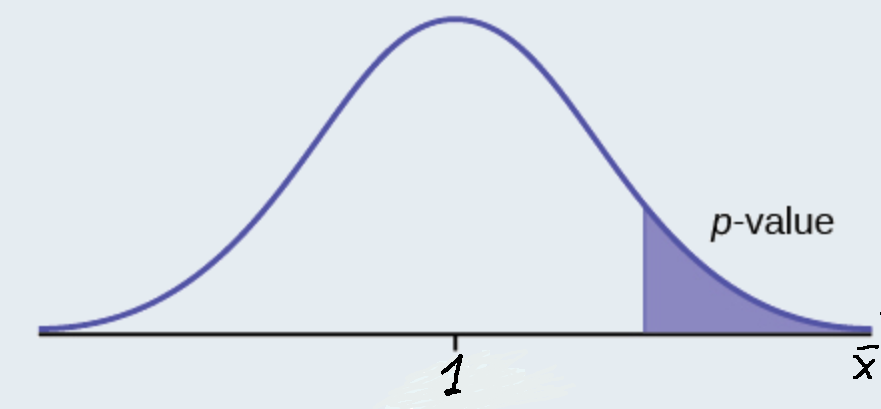
Exercise \(\PageIndex{2}\)

\(H_{0}: \mu \leq 1, H_{a}: \mu > 1\)

Assume the \(p\)-value is 0.1243. What type of test is this? Draw the picture of the \(p\)-value.

right-tailed test

Example \(\PageIndex{3}\)

\(H_{0}: \mu = 50, H_{a}: \mu \neq 50\)

This is a test of a single population mean. \(H_{a}\) tells you the test is two-tailed . The picture of the \(p\)-value is as follows.

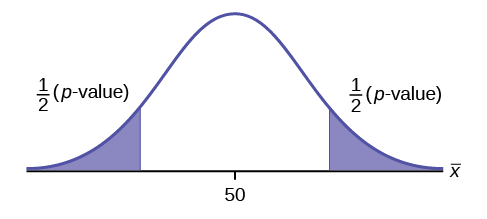
Exercise \(\PageIndex{3}\)

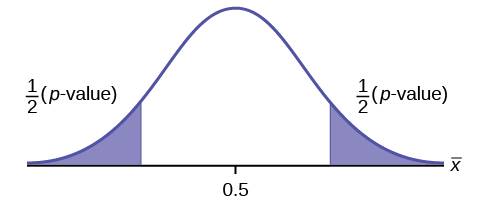
\(H_{0}: \mu = 0.5, H_{a}: \mu \neq 0.5\)

Assume the p -value is 0.2564. What type of test is this? Draw the picture of the \(p\)-value.

two-tailed test

Full Hypothesis Test Examples

Example \(\pageindex{4}\).

Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores 65 65 70 67 66 63 63 68 72 71. He performs a hypothesis test using a 5% level of significance. The data are assumed to be from a normal distribution.

Set up the hypothesis test:

A 5% level of significance means that \(\alpha = 0.05\). This is a test of a single population mean .

\(H_{0}: \mu = 65  H_{a}: \mu > 65\)

Since the instructor thinks the average score is higher, use a "\(>\)". The "\(>\)" means the test is right-tailed.

Determine the distribution needed:

Random variable: \(\bar{X} =\) average score on the first statistics test.

Distribution for the test: If you read the problem carefully, you will notice that there is no population standard deviation given . You are only given \(n = 10\) sample data values. Notice also that the data come from a normal distribution. This means that the distribution for the test is a student's \(t\).

Use \(t_{df}\). Therefore, the distribution for the test is \(t_{9}\) where \(n = 10\) and \(df = 10 - 1 = 9\).

The sample mean and sample standard deviation are calculated as 67 and 3.1972 from the data.

Calculate the \(p\)-value using the Student's \(t\)-distribution:

\[t_{obs} = \dfrac{\bar{x}-\mu_{\bar{x}}}{\left(\dfrac{s}{\sqrt{n}}\right)}=\dfrac{67-65}{\left(\dfrac{3.1972}{\sqrt{10}}\right)}\]

Use the T-table or Excel's t_dist() function to find p-value:

\(p\text{-value} = P(\bar{x} > 67) =P(T >1.9782 )= 1-0.9604=0.0396\)

Interpretation of the p -value: If the null hypothesis is true, then there is a 0.0396 probability (3.96%) that the sample mean is 65 or more.

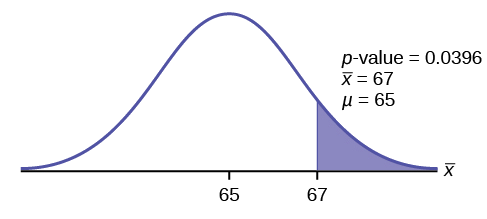
Compare \(\alpha\) and the \(p-\text{value}\):

Since \(α = 0.05\) and \(p\text{-value} = 0.0396\). \(\alpha > p\text{-value}\).

Make a decision: Since \(\alpha > p\text{-value}\), reject \(H_{0}\).

This means you reject \(\mu = 65\). In other words, you believe the average test score is more than 65.

Conclusion: At a 5% level of significance, the sample data show sufficient evidence that the mean (average) test score is more than 65, just as the math instructor thinks.

The \(p\text{-value}\) can easily be calculated.

Put the data into a list. Press STAT and arrow over to TESTS . Press 2:T-Test . Arrow over to Data and press ENTER . Arrow down and enter 65 for \(\mu_{0}\), the name of the list where you put the data, and 1 for Freq: . Arrow down to \(\mu\): and arrow over to \(> \mu_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator not only calculates the \(p\text{-value}\) (p = 0.0396) but it also calculates the test statistic ( t -score) for the sample mean, the sample mean, and the sample standard deviation. \(\mu > 65\) is the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(t = 1.9781\) (test statistic) and \(p = 0.0396\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

Exercise \(\PageIndex{4}\)

It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, find the p -value, state your conclusion, and identify the Type I and Type II errors.

• \(H_{0}: \mu = 5\)
• \(H_{a}: \mu < 5\)
• \(p = 0.0082\)

Because \(p < \alpha\), we reject the null hypothesis. There is sufficient evidence to suggest that the stock price of the company grows at a rate less than $5 a week.

• Type I Error: To conclude that the stock price is growing slower than $5 a week when, in fact, the stock price is growing at $5 a week (reject the null hypothesis when the null hypothesis is true).
• Type II Error: To conclude that the stock price is growing at a rate of $5 a week when, in fact, the stock price is growing slower than $5 a week (do not reject the null hypothesis when the null hypothesis is false).

Example \(\PageIndex{5}\)

The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.

1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95

Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05. Assume the population is normal.

Let’s follow a four-step process to answer this statistical question.

• \(H_{0}: \mu \leq 1\)
• \(H_{a}: \mu > 1\)
• Plan : We are testing a sample mean without a known population standard deviation. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
• Do the calculations : \(p\text{-value} ( = 0.036)\)

4. State the Conclusions : Since the \(p\text{-value} (= 0.036)\) is less than our alpha value, we will reject the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Determine the random variable.
• Determine the distribution for the test.
• Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A t -score is an example of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

Z-test for One Population Mean

Instructions: This calculator conducts a Z-test for one population mean (\(\mu\)), with known population standard deviation (\(\sigma\)). Please select the null and alternative hypotheses, type the hypothesized mean, the significance level, the sample mean, the population standard deviation, and the sample size, and the results of the z-test will be displayed for you:

How to Conduct a Z-Test for One Population Mean?

More about the z-test for one mean so you can better interpret the results obtained by this solver: A z-test for one mean is a hypothesis test that attempts to make a claim about the population mean (\(\mu\)).

The test has two non-overlapping hypotheses, the null and the alternative hypothesis. The null hypothesis is a statement about the population mean, under the assumption of no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis. The main properties of a one sample z-test for one population mean are:

• Depending on our knowledge about the "no effect" situation, the z-test can be two-tailed, left-tailed or right-tailed
• The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true
• The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true
• In a hypothesis tests there are two types of errors. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis

Uses of this z-test calculator

What can you do with this z-test statistic calculator for hypothesis testing? The formula for a z-statistic is

The null hypothesis is rejected when the z-statistic lies on the rejection region, which is determined by the significance level (\(\alpha\)) and the type of tail (two-tailed, left-tailed or right-tailed).

What if the population standard deviation is not known?

It frequently happens that you don't actually know the population standard deviation, in which case you need to use a t-test for one mean calculator instead, which adjusts for that by using the sample standard deviation, by using a slightly different distribution (the t-distribution)

How to calculate p-value in the context of a z-test?

The answer depends on whether you are using a two-tailed, a left-tailed or a right-tailed test. Say you have the calculated z-statistic, \(Z_{obs}\).

• For a two-tailed test, the p-value is computed as: \(p = \Pr( Z > |Z_{obs}|) \)
• For a left-tailed test, the p-value is computed as: \(p = \Pr( Z < Z_{obs}) \)
• For a right-tailed test, the p-value is computed as: \(p = \Pr( Z > Z_{obs}) \)

where \(Z\) has a standard normal distribution.

Other types of Z-calculators

In case that you need to compare two population means, when you know the corresponding population standard deviations, you need to use this z-test for two means with known population standard deviations instead.

Outlier Detection

Don't forget to detect outliers before running a z-test for one mean. It is important that outliers are detected and removed before conducting the test, but the results of the test statistics may be slanted.

Example: Application of the Z-test calculator

Question : Assume that you want to test whether or not the population mean is 12.3. You collect a representative random sample of size n = 16, and you find that the sample mean is 11.3. Also, you know that the population is 2.3. Do the sample data provide enough evidence to reject the claim that the population mean is 12.3? Use a two-tailed test, with a significance level of 0.01.

The following information has been provided:

(1) Null and Alternative Hypotheses

The following null and alternative hypotheses need to be tested:

This corresponds to a two-tailed test, for which a z-test for one mean, with known population standard deviation will be used.

(2) Rejection Region

Based on the information provided, the significance level is \(\alpha = 0.01\), and the critical value for a two-tailed test is \(z_c = 2.58\).

The rejection region for this two-tailed test is \(R = \{z: |z| > 2.576\}\)

(3) Test Statistics

The z-statistic is computed as follows:

(4) Decision about the null hypothesis

Since it is observed that \(|z| = 1.739 \le z_c = 2.576\), it is then concluded that the null hypothesis is not rejected.

Using the P-value approach: The p-value is \(p = 0.082\), and since \(p = 0.082 \ge 0.01\), it is concluded that the null hypothesis is not rejected.

(5) Conclusion

It is concluded that the null hypothesis Ho is not rejected. Therefore, there is not enough evidence to claim that the population mean \(\mu\) is different than 12.3, at the \(\alpha = 0.01\) significance level.

Confidence Interval

The 99% confidence interval is \(9.819 < \mu < 12.781\).

Related Calculators

log in to your account

Reset password.

Module 10: Inference for Means

Hypothesis test for a population mean (1 of 5), learning outcomes.

• Recognize when to use a hypothesis test or a confidence interval to draw a conclusion about a population mean.
• Under appropriate conditions, conduct a hypothesis test about a population mean. State a conclusion in context.

Introduction

In Inference for Means , our focus is on inference when the variable is quantitative, so the parameters and statistics are means. In “Estimating a Population Mean,” we learned how to use a sample mean to calculate a confidence interval. The confidence interval estimates a population mean. In “Hypothesis Test for a Population Mean,” we learn to use a sample mean to test a hypothesis about a population mean.

We did hypothesis tests in earlier modules. In Inference for One Proportion , each claim involved a single population proportion. In Inference for Two Proportions , the claim was a statement about a treatment effect or a difference in population proportions. In “Hypothesis Test for a Population Mean,” the claims are statements about a population mean. But we will see that the steps and the logic of the hypothesis test are the same. Before we get into the details, let’s practice identifying research questions and studies that involve a population mean.

Cell Phone Data

Cell phones and cell phone plans can be very expensive, so consumers must think carefully when choosing a cell phone and service. This decision is as much about choosing the right cellular company as it is about choosing the right phone. Many people use the data/Internet capabilities of a phone as much as, if not more than, they use voice capability. The data service of a cell company is therefore an important factor in this decision. In the following example, a student named Melanie from Los Angeles applies what she learned in her statistics class to help her make a decision about buying a data plan for her smartphone.

Melanie read an advertisement from the Cell Phone Giants (CPG, for short, and yes, we’re using a fictitious company name) that she thinks is too good to be true. The CPG ad states that customers in Los Angeles get average data download speeds of 4 Mbps. With this speed, the ad claims, it takes, on average, only 12 seconds to download a typical 3-minute song from iTunes.

Only 12 seconds on average to download a 3-minute song from iTunes! Melanie has her doubts about this claim, so she gathers data to test it. She asks a friend who uses the CPG plan to download a song, and it takes 13 seconds to download a 3-minute song using the CPG network. Melanie decides to gather more evidence. She uses her friend’s phone and times the download of the same 3-minute song from various locations in Los Angeles. She gets a mean download time of 13.5 seconds for her sample of downloads.

What can Melanie conclude? Her sample has a mean download time that is greater than 12 seconds. Isn’t this evidence that the CPG claim is wrong? Why is a hypothesis test necessary? Isn’t the conclusion clear?

Let’s review the reason Melanie needs to do a hypothesis test before she can reach a conclusion.

Why should Melanie do a hypothesis test?

Melanie’s data (with a mean of 13.5 seconds) suggest that the average download time overall is greater than the 12 seconds claimed by the manufacturer. But wait. We know that samples will vary. If the CPG claim is correct, we don’t expect all samples to have a mean download time exactly equal to 12 seconds. There will be variability in the sample means. But if the overall average download time is 12 seconds, how much variability in sample means do we expect to see? We need to determine if the difference Melanie observed can be explained by chance.

We have to judge Melanie’s data against random samples that come from a population with a mean of 12. For this reason, we must do a simulation or use a mathematical model to examine the sampling distribution of sample means. Based on the sampling distribution, we ask, Is it likely that the samples will have mean download times that are greater than 13.5 seconds if the overall mean is 12 seconds? This probability (the P-value) determines whether Melanie’s data provides convincing evidence against the CPG claim.

Now let’s do the hypothesis test.

Step 1: Determine the hypotheses.

As always, hypotheses come from the research question. The null hypothesis is a hypothesis that the population mean equals a specific value. The alternative hypothesis reflects our claim. The alternative hypothesis says the population mean is “greater than” or “less than” or “not equal to” the value we assume is true in the null hypothesis.

Melanie’s hypotheses:

• H 0 : It takes 12 seconds on average to download Melanie’s song from iTunes with the CPG network in Los Angeles.
• H a : It takes more than 12 seconds on average to download Melanie’s song from iTunes using the CPG network in Los Angeles.

We can write the hypotheses in terms of µ. When we do so, we should always define µ. Here μ = the average number of seconds it takes to download Melanie’s song on the CPG network in Los Angeles.

• H 0 : μ = 12
• H a : μ > 12

Step 2: Collect the data.

To conduct a hypothesis test, Melanie knows she has to use a t-model of the sampling distribution. She thinks ahead to the conditions required, which helps her collect a useful sample.

Recall the conditions for use of a t-model.

• There is no reason to think the download times are normally distributed (they might be, but this isn’t something Melanie could know for sure). So the sample has to be large (more than 30).
• The sample has to be random. Melanie decides to use one phone but randomly selects days, times, and locations in Los Angeles.

Melanie collects a random sample of 45 downloads by using her friend’s phone to download her song from iTunes according to the randomly selected days, times, and locations.

Melanie’s sample of size 45 downloads has an average download time of 13.5 seconds. The standard deviation for the sample is 3.2 seconds. Now Melanie needs to determine how unlikely this data is if CPG’s claim is actually true.

Step 3: Assess the evidence.

Assuming the average download time for Melanie’s song is really 12 seconds, what is the probability that 45 random downloads of this song will have a mean of 13.5 seconds or more?

This is a question about sampling variability. Melanie must determine the standard error. She knows the standard error of random sample means is [latex]\sigma \text{}/\sqrt{n}[/latex]. Since she has no way of knowing the population standard deviation, σ, Melanie uses the sample standard deviation, s = 3.2, as an approximation. Therefore, Melanie approximates the standard error of all sample means ( n = 45) to be

[latex]s\text{}/\sqrt{n}\text{}=\text{}3.2\text{}/\sqrt{45}\text{}=\text{}0.48[/latex]

Now she can assess how far away her sample is from the claimed mean in terms of standard errors. That is, she can compute the t-score of her sample mean.

[latex]T\text{}=\text{}\frac{\mathrm{statistic}-\mathrm{parameter}}{\mathrm{standard}\text{}\mathrm{error}}\text{}=\text{}\frac{\stackrel{¯}{x}-μ}{s\text{}/\sqrt{n}}\text{}=\text{}\frac{13.5-12}{0.48}\text{}=\text{}3.14[/latex]

The sample mean for Melanie’s random sample is approximately 3.14 standard errors above the overall mean of 12. We know from previous experience that a sample mean this far above µ is very unlikely. With a t-score this large, the P-value is very small. We use a simulation of the t-model for 44 degrees of freedom to verify this.

We want the probability that the sample mean is greater than 13.5. This corresponds to the probability that T is greater than 3.14. The P-value is 0.0015.

Step 4: State a conclusion.

Here the logic is the same as for other hypothesis tests. We use the P-value to make a decision. The P-value helps us determine if the difference we see between the data and the hypothesized value of µ is statistically significant or due to chance. One of two outcomes can occur:

• One possibility is that results similar to the actual sample are extremely unlikely. This means the data does not fit with results from random samples selected from the population described by the null hypothesis. In this case, it is unlikely that the data came from this population. The probability as measured by the P-value is small, so we view this as strong evidence against the null hypothesis. We reject the null hypothesis in favor of the alternative hypothesis.
• The other possibility is that results similar to the actual sample are fairly likely (not unusual). This means the data fits with typical results from random samples selected from the population described by the null hypothesis. The probability as measured by the P-value is large. In this case, we do not have evidence against the null hypothesis, so we cannot reject it in favor of the alternative hypothesis.

Melanie’s data is very unlikely if µ = 12. The probability is essentially zero (P-value = 0.0015). This means we will rarely see sample means greater than 13.5 if µ = 12. So we reject the null and accept the alternative hypothesis. In other words, this sample provides strong evidence that CPG has overstated the speed of its data download capability.

The following activities give you an opportunity to practice parts of the hypothesis testing process for a population mean. Later you will have the opportunity to practice the hypothesis test from start to finish.

For the following scenarios, give the null and alternative hypotheses and state in words what µ represents in your hypotheses. A good definition of µ describes both the variable and the population.

In the previous example, Melanie did not state a significance level for her test. If she had, the logic is the same as we used for hypothesis tests in Modules 8 and 9. To come to a conclusion about H 0 , we compare the P-value to the significance level α.

• If P ≤ α, we reject H 0 . We conclude there is significant evidence in favor of H a .
• If P > α, we fail to reject H 0 . We conclude the sample does not provide significant evidence in favor of H a .

Use this simulation when needed to answer questions below.

Contribute!

Improve this page Learn More

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Two Population Calculator

Related: hypothesis testing calculator, confidence interval, hypothesis testing.

When computing confidence intervals for two population means, we are interested in the difference between the population means ($ \mu_1 - \mu_2 $). A confidence interval is made up of two parts, the point estimate and the margin of error. The point estimate of the difference between two population means is simply the difference between two sample means ($ \bar{x}_1 - \bar{x}_2 $). The standard error of $ \bar{x}_1 - \bar{x}_2 $, which is used in computing the margin of error, is given by the formula below.

The formula for the margin of error depends on whether the population standard deviations ($\sigma_1$ and $\sigma_2$) are known or unknown. If the population standard deviations are known, then they are used in the formula. If they are unknown, then the sample standard deviations ($s_1$ and $s_2$)are used in their place. To change from $\sigma$ known to $\sigma$ unknown, click on $\boxed{σ}$ and select $\boxed{s}$ in the Two Population Calculator.

While the formulas for the margin of error in the two population case are similar to those in the one population case, the formula for the degrees of freedom is quite a bit more complicated. Although this formula does seem intimidating at first sight, there is a shortcut to get the answer faster. Notice that the terms $\frac{s_1^2}{n_1}$ and $\frac{s_2^2}{n_2}$ each repeat twice. The terms are actually computed previously when finding the margin of error so they don't need to be calculated again.

If the two population variances are assumed to be equal, an alternative formula for computing the degrees of freedom is used. It's simply df = n1 + n2 - 2. This is a simple extension of the formula for the one population case. In the one population case the degrees of freedom is given by df = n - 1. If we add up the degrees of freedom for the two samples we would get df = (n1 - 1) + (n2 - 1) = n1 + n2 - 2. This formula gives a pretty good approximation of the more complicated formula above.

Just like in hypothesis tests about a single population mean, there are lower-tail, upper-tail and two tailed tests. However, the null and alternative are slightly different. First of all, instead of having mu on the left side of the equality, we have $\mu_1 - \mu_2$. On the right side of the equality, we don't have $\mu_0$, the hypothesized value of the population mean. Instead we have $D_0$, the hypothesized difference between the population means. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

Again, hypothesis testing for a single population mean is very similar to hypothesis testing for two population means. For a single population mean, the test statistics is the difference between mu and mu0 dividied by the standard error. For two population means, the test statistic is the difference between $\bar{x}_1 - \bar{x}_2$ and $D_0$ divided by the standard error. The procedure after computing the test statistic is identical to the one population case. That is, you proceed with the p-value approach or critical value approach in the same exact way.

The calculator above computes confidence intervals and hypothesis tests for the difference between two population means. The simpler version of this is confidence intervals and hypothesis tests for a single population mean. For confidence intervals about a single population mean, visit the Confidence Interval Calculator . For hypothesis tests about a single population mean, visit the Hypothesis Testing Calculator .

Critical Value Calculator

How to use critical value calculator, what is a critical value, critical value definition, how to calculate critical values, z critical values, t critical values, chi-square critical values (χ²), f critical values, behind the scenes of the critical value calculator.

Welcome to the critical value calculator! Here you can quickly determine the critical value(s) for two-tailed tests, as well as for one-tailed tests. It works for most common distributions in statistical testing: the standard normal distribution N(0,1) (that is when you have a Z-score), t-Student, chi-square, and F-distribution .

What is a critical value? And what is the critical value formula? Scroll down – we provide you with the critical value definition and explain how to calculate critical values in order to use them to construct rejection regions (also known as critical regions).

The critical value calculator is your go-to tool for swiftly determining critical values in statistical tests, be it one-tailed or two-tailed. To effectively use the calculator, follow these steps:

In the first field, input the distribution of your test statistic under the null hypothesis: is it a standard normal N (0,1), t-Student, chi-squared, or Snedecor's F? If you are not sure, check the sections below devoted to those distributions, and try to localize the test you need to perform.

In the field What type of test? choose the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

If needed, specify the degrees of freedom of the test statistic's distribution. If you need more clarification, check the description of the test you are performing. You can learn more about the meaning of this quantity in statistics from the degrees of freedom calculator .

Set the significance level, α \alpha α . By default, we pre-set it to the most common value, 0.05, but you can adjust it to your needs.

The critical value calculator will display your critical value(s) and the rejection region(s).

Click the advanced mode if you need to increase the precision with which the critical values are computed.

For example, let's envision a scenario where you are conducting a one-tailed hypothesis test using a t-Student distribution with 15 degrees of freedom. You have opted for a right-tailed test and set a significance level (α) of 0.05. The results indicate that the critical value is 1.7531, and the critical region is (1.7531, ∞). This implies that if your test statistic exceeds 1.7531, you will reject the null hypothesis at the 0.05 significance level.

👩‍🏫 Want to learn more about critical values? Keep reading!

In hypothesis testing, critical values are one of the two approaches which allow you to decide whether to retain or reject the null hypothesis. The other approach is to calculate the p-value (for example, using the p-value calculator ).

The critical value approach consists of checking if the value of the test statistic generated by your sample belongs to the so-called rejection region , or critical region , which is the region where the test statistic is highly improbable to lie . A critical value is a cut-off value (or two cut-off values in the case of a two-tailed test) that constitutes the boundary of the rejection region(s). In other words, critical values divide the scale of your test statistic into the rejection region and the non-rejection region.

Once you have found the rejection region, check if the value of the test statistic generated by your sample belongs to it :

• If so, it means that you can reject the null hypothesis and accept the alternative hypothesis; and
• If not, then there is not enough evidence to reject H 0 .

But how to calculate critical values? First of all, you need to set a significance level , α \alpha α , which quantifies the probability of rejecting the null hypothesis when it is actually correct. The choice of α is arbitrary; in practice, we most often use a value of 0.05 or 0.01. Critical values also depend on the alternative hypothesis you choose for your test , elucidated in the next section .

To determine critical values, you need to know the distribution of your test statistic under the assumption that the null hypothesis holds. Critical values are then points with the property that the probability of your test statistic assuming values at least as extreme at those critical values is equal to the significance level α . Wow, quite a definition, isn't it? Don't worry, we'll explain what it all means.

First, let us point out it is the alternative hypothesis that determines what "extreme" means. In particular, if the test is one-sided, then there will be just one critical value; if it is two-sided, then there will be two of them: one to the left and the other to the right of the median value of the distribution.

Critical values can be conveniently depicted as the points with the property that the area under the density curve of the test statistic from those points to the tails is equal to α \alpha α :

Left-tailed test: the area under the density curve from the critical value to the left is equal to α \alpha α ;

Right-tailed test: the area under the density curve from the critical value to the right is equal to α \alpha α ; and

Two-tailed test: the area under the density curve from the left critical value to the left is equal to α / 2 \alpha/2 α /2 , and the area under the curve from the right critical value to the right is equal to α / 2 \alpha/2 α /2 as well; thus, total area equals α \alpha α .

As you can see, finding the critical values for a two-tailed test with significance α \alpha α boils down to finding both one-tailed critical values with a significance level of α / 2 \alpha/2 α /2 .

The formulae for the critical values involve the quantile function , Q Q Q , which is the inverse of the cumulative distribution function ( c d f \mathrm{cdf} cdf ) for the test statistic distribution (calculated under the assumption that H 0 holds!): Q = c d f − 1 Q = \mathrm{cdf}^{-1} Q = cdf − 1 .

Once we have agreed upon the value of α \alpha α , the critical value formulae are the following:

• Left-tailed test :
• Right-tailed test :
• Two-tailed test :

In the case of a distribution symmetric about 0 , the critical values for the two-tailed test are symmetric as well:

Unfortunately, the probability distributions that are the most widespread in hypothesis testing have somewhat complicated c d f \mathrm{cdf} cdf formulae. To find critical values by hand, you would need to use specialized software or statistical tables. In these cases, the best option is, of course, our critical value calculator! 😁

Use the Z (standard normal) option if your test statistic follows (at least approximately) the standard normal distribution N(0,1) .

In the formulae below, u u u denotes the quantile function of the standard normal distribution N(0,1):

Left-tailed Z critical value: u ( α ) u(\alpha) u ( α )

Right-tailed Z critical value: u ( 1 − α ) u(1-\alpha) u ( 1 − α )

Two-tailed Z critical value: ± u ( 1 − α / 2 ) \pm u(1- \alpha/2) ± u ( 1 − α /2 )

Check out Z-test calculator to learn more about the most common Z-test used on the population mean. There are also Z-tests for the difference between two population means, in particular, one between two proportions.

Use the t-Student option if your test statistic follows the t-Student distribution . This distribution is similar to N(0,1) , but its tails are fatter – the exact shape depends on the number of degrees of freedom . If this number is large (>30), which generically happens for large samples, then the t-Student distribution is practically indistinguishable from N(0,1). Check our t-statistic calculator to compute the related test statistic.

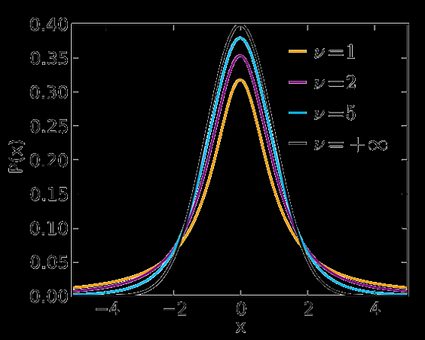
In the formulae below, Q t , d Q_{\text{t}, d} Q t , d ​ is the quantile function of the t-Student distribution with d d d degrees of freedom:

Left-tailed t critical value: Q t , d ( α ) Q_{\text{t}, d}(\alpha) Q t , d ​ ( α )

Right-tailed t critical value: Q t , d ( 1 − α ) Q_{\text{t}, d}(1 - \alpha) Q t , d ​ ( 1 − α )

Two-tailed t critical values: ± Q t , d ( 1 − α / 2 ) \pm Q_{\text{t}, d}(1 - \alpha/2) ± Q t , d ​ ( 1 − α /2 )

Visit the t-test calculator to learn more about various t-tests: the one for a population mean with an unknown population standard deviation , those for the difference between the means of two populations (with either equal or unequal population standard deviations), as well as about the t-test for paired samples .

Use the χ² (chi-square) option when performing a test in which the test statistic follows the χ²-distribution .

You need to determine the number of degrees of freedom of the χ²-distribution of your test statistic – below, we list them for the most commonly used χ²-tests.

Here we give the formulae for chi square critical values; Q χ 2 , d Q_{\chi^2, d} Q χ 2 , d ​ is the quantile function of the χ²-distribution with d d d degrees of freedom:

Left-tailed χ² critical value: Q χ 2 , d ( α ) Q_{\chi^2, d}(\alpha) Q χ 2 , d ​ ( α )

Right-tailed χ² critical value: Q χ 2 , d ( 1 − α ) Q_{\chi^2, d}(1 - \alpha) Q χ 2 , d ​ ( 1 − α )

Two-tailed χ² critical values: Q χ 2 , d ( α / 2 ) Q_{\chi^2, d}(\alpha/2) Q χ 2 , d ​ ( α /2 ) and Q χ 2 , d ( 1 − α / 2 ) Q_{\chi^2, d}(1 - \alpha/2) Q χ 2 , d ​ ( 1 − α /2 )

Several different tests lead to a χ²-score:

Goodness-of-fit test : does the empirical distribution agree with the expected distribution?

This test is right-tailed . Its test statistic follows the χ²-distribution with k − 1 k - 1 k − 1 degrees of freedom, where k k k is the number of classes into which the sample is divided.

Independence test : is there a statistically significant relationship between two variables?

This test is also right-tailed , and its test statistic is computed from the contingency table. There are ( r − 1 ) ( c − 1 ) (r - 1)(c - 1) ( r − 1 ) ( c − 1 ) degrees of freedom, where r r r is the number of rows, and c c c is the number of columns in the contingency table.

Test for the variance of normally distributed data : does this variance have some pre-determined value?

This test can be one- or two-tailed! Its test statistic has the χ²-distribution with n − 1 n - 1 n − 1 degrees of freedom, where n n n is the sample size.

Finally, choose F (Fisher-Snedecor) if your test statistic follows the F-distribution . This distribution has a pair of degrees of freedom .

Let us see how those degrees of freedom arise. Assume that you have two independent random variables, X X X and Y Y Y , that follow χ²-distributions with d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ degrees of freedom, respectively. If you now consider the ratio ( X d 1 ) : ( Y d 2 ) (\frac{X}{d_1}):(\frac{Y}{d_2}) ( d 1 ​ X ​ ) : ( d 2 ​ Y ​ ) , it turns out it follows the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom. That's the reason why we call d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ the numerator and denominator degrees of freedom , respectively.

In the formulae below, Q F , d 1 , d 2 Q_{\text{F}, d_1, d_2} Q F , d 1 ​ , d 2 ​ ​ stands for the quantile function of the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom:

Left-tailed F critical value: Q F , d 1 , d 2 ( α ) Q_{\text{F}, d_1, d_2}(\alpha) Q F , d 1 ​ , d 2 ​ ​ ( α )

Right-tailed F critical value: Q F , d 1 , d 2 ( 1 − α ) Q_{\text{F}, d_1, d_2}(1 - \alpha) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α )

Two-tailed F critical values: Q F , d 1 , d 2 ( α / 2 ) Q_{\text{F}, d_1, d_2}(\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( α /2 ) and Q F , d 1 , d 2 ( 1 − α / 2 ) Q_{\text{F}, d_1, d_2}(1 -\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α /2 )

Here we list the most important tests that produce F-scores: each of them is right-tailed .

ANOVA : tests the equality of means in three or more groups that come from normally distributed populations with equal variances. There are ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where k k k is the number of groups, and n n n is the total sample size (across every group).

Overall significance in regression analysis . The test statistic has ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where n n n is the sample size, and k k k is the number of variables (including the intercept).

Compare two nested regression models . The test statistic follows the F-distribution with ( k 2 − k 1 , n − k 2 ) (k_2 - k_1, n - k_2) ( k 2 ​ − k 1 ​ , n − k 2 ​ ) degrees of freedom, where k 1 k_1 k 1 ​ and k 2 k_2 k 2 ​ are the number of variables in the smaller and bigger models, respectively, and n n n is the sample size.

The equality of variances in two normally distributed populations . There are ( n − 1 , m − 1 ) (n - 1, m - 1) ( n − 1 , m − 1 ) degrees of freedom, where n n n and m m m are the respective sample sizes.

I'm Anna, the mastermind behind the critical value calculator and a PhD in mathematics from Jagiellonian University .

The idea for creating the tool originated from my experiences in teaching and research. Recognizing the need for a tool that simplifies the critical value determination process across various statistical distributions, I built a user-friendly calculator accessible to both students and professionals. After publishing the tool, I soon found myself using the calculator in my research and as a teaching aid.

Trust in this calculator is paramount to me. Each tool undergoes a rigorous review process , with peer-reviewed insights from experts and meticulous proofreading by native speakers. This commitment to accuracy and reliability ensures that users can be confident in the content. Please check the Editorial Policies page for more details on our standards.

What is a Z critical value?

A Z critical value is the value that defines the critical region in hypothesis testing when the test statistic follows the standard normal distribution . If the value of the test statistic falls into the critical region, you should reject the null hypothesis and accept the alternative hypothesis.

How do I calculate Z critical value?

To find a Z critical value for a given confidence level α :

Check if you perform a one- or two-tailed test .

For a one-tailed test:

Left -tailed: critical value is the α -th quantile of the standard normal distribution N(0,1).

Right -tailed: critical value is the (1-α) -th quantile.

Two-tailed test: critical value equals ±(1-α/2) -th quantile of N(0,1).

No quantile tables ? Use CDF tables! (The quantile function is the inverse of the CDF.)

Verify your answer with an online critical value calculator.

Is a t critical value the same as Z critical value?

In theory, no . In practice, very often, yes . The t-Student distribution is similar to the standard normal distribution, but it is not the same . However, if the number of degrees of freedom (which is, roughly speaking, the size of your sample) is large enough (>30), then the two distributions are practically indistinguishable , and so the t critical value has practically the same value as the Z critical value.

What is the Z critical value for 95% confidence?

The Z critical value for a 95% confidence interval is:

• 1.96 for a two-tailed test;
• 1.64 for a right-tailed test; and
• -1.64 for a left-tailed test.

AND Probability

Combination, ideal egg boiling.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (294)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (104)
• Statistics (182)
• Other (182)
• Discover Omni (40)

Test Statistic Calculator

$$ \frac{\overline{x} - μ_0}{\frac{σ}{\sqrt{n}}} $$

$$ \frac{\overline{x} - \overline{y}}{\sqrt{\frac{σ^2_x}{n_1} + \frac{σ^2_y}{n_2}}} $$

$$ \frac{\stackrel{\text{^}}{p} - \ p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} $$

$$ \frac{\stackrel{\text{^}}{p_1} - \stackrel{\text{^}}{p_2}}{\sqrt{\stackrel{\text{^}}{p}(1-\stackrel{\text{^}}{p})(\frac{1}{n_1} + \frac{1}{n_2})}} $$

Table of Content

In order to calculate the test statistics for one population mean, compare two means, a single population proportion, and two population proportions the test statistic calculator is used. It has the ability to summarize your data into a single number. 

What Is Test Statistics?

“The measurement that evaluates the strength of evidence by refuting the hypothesis is known as test statistics”.  

It helps to determine the population hypothesis and helps us to summarize the data. Therefore it is also known as the significance hypothesis. 

Test Statistics Formula:

The test statistic formula calculator is used to evaluate the strength of evidence from the sample. However, the formula varies with the size of the population and the sample, and with these, you can evaluate how far your observed data is from the null hypothesis. 

One Population Mean:

For one population mean the test statistics formula is as follows:

$$ \frac{\overline{x} - μ_0}{\frac{σ}{\sqrt{n}}} $$

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

Comparing Two Means: 

The formula to evaluate the independent samples are given below:

$$ \frac{\overline{x} - \overline{y}}{\sqrt{\frac{σ^2_x}{n_1} + \frac{σ^2_y}{n_2}}} $$

• x and y are the means 
• σx are the standard deviation of the x values
• σy are the standard deviation of the y values
• n1 is the sample size of the x 
• n2 is the sample size of the y

Single Population Portion: 

• P is the sample proportion
• P0  is the claimed proportion
• n is the sample size

Two Population Portions: 

• P1 and  P2 are the populations
• n1 and n2 are the sample sizes

How to Calculate Test Statistic?

In this type of statistics, the quantitative measures assess the strength of evidence against the hypothesis. So look at the below example which indicates how the value of test statistic calculator summarizes your data into a single number. 

Suppose a cricket series was held against Pakistan and Sri Lanka in Colombo in which Baber Azam makes an average score of about 78 in five matches. As you know the average batting for a player is 40. In this case, the deviation in scoring is 4, what are the performance stats of Baber Azam?

Given Data:

• Deviation = 4

$$ \text{Test Statistic}=\frac{78 – 40}{\frac{4}{\sqrt{5}}} $$

$$ \text{Test Statistic}=\frac{38}{\frac{4}{2.236}} $$

$$ \text{Test Statistic}=\frac{26}{1.79} $$

$$ \text{Test Statistic}= 14.53 $$

Suppose there is a 3% and it means that the performance for 5 matches is considerably better than average. 

Working of Sample Test Statistic Calculator:

The test value calculator transforms the data analysis by simplifying the hypothesis testing. Attach to the guide below to utilize the test statistics calculator.

• Choose the point that you want to calculate 
• Put the values according to the chosen value 
• Tap on “Calculate”

Our standardized test statistic calculator will give you the following results. 

• Test statistics for sample and population mean 
• Complete calculation in the steps given 

Test Statistics Table:

One tail table:, two tail table:, what indicates the negative test statistics.

A negative test statistics value indicates that it occurs on the left side of the mean. All left values are negative and all right values are positive. A negative test is just like a standard normal that has a zero mean. 

What are the applications of test statistics related to data sets?

• Product quality with the sample measurement 
• Market research to analyze the survey data 
• Strategies of investment and impact of market trends also analyzed 
• Determination of significant change and physiological experiments 

What does a 0 test value mean?

If the test statistics value is equal to zero it means that sample results are equal to the null hypothesis.  

References:

From the source Wikipedia: Test statistic , Example.

From the source Khan Academy: Significance tests (hypothesis testing), 

Alan Walker

Studies mathematics sciences, and Technology. Tech geek and a content writer. Wikipedia addict who wants to know everything. Loves traveling, nature, reading. Math and Technology have done their part, and now it's the time for us to get benefits.

Submit Your Review

Related converters.

Follow Us on Social Media

Difference in Means Hypothesis Test Calculator

Use the calculator below to analyze the results of a difference in sample means hypothesis test. Enter your sample means, sample standard deviations, sample sizes, hypothesized difference in means, test type, and significance level to calculate your results.

You will find a description of how to conduct a two sample t-test below the calculator.

Define the Two Sample t-test

The difference between the sample means under the null distribution, conducting a hypothesis test for the difference in means.

When two populations are related, you can compare them by analyzing the difference between their means.

A hypothesis test for the difference in samples means can help you make inferences about the relationships between two population means.

Testing for a Difference in Means

For the results of a hypothesis test to be valid, you should follow these steps:

Check Your Conditions

State your hypothesis, determine your analysis plan, analyze your sample, interpret your results.

To use the testing procedure described below, you should check the following conditions:

• Independence of Samples - Your samples should be collected independently of one another.
• Simple Random Sampling - You should collect your samples with simple random sampling. This type of sampling requires that every occurrence of a value in a population has an equal chance of being selected when taking a sample.
• Normality of Sample Distributions - The sampling distributions for both samples should follow the Normal or a nearly Normal distribution. A sampling distribution will be nearly Normal when the samples are collected independently and when the population distribution is nearly Normal. Generally, the larger the sample size, the more normally distributed the sampling distribution. Additionally, outlier data points can make a distribution less Normal, so if your data contains many outliers, exercise caution when verifying this condition.

You must state a null hypothesis and an alternative hypothesis to conduct an hypothesis test of the difference in means.

The null hypothesis is a skeptical claim that you would like to test.

The alternative hypothesis represents the alternative claim to the null hypothesis.

Your null hypothesis and alternative hypothesis should be stated in one of three mutually exclusive ways listed in the table below.

D is the hypothesized difference between the populations' means that you would like to test.

Before conducting a hypothesis test, you must determine a reasonable significance level, α, or the probability of rejecting the null hypothesis assuming it is true. The lower your significance level, the more confident you can be of the conclusion of your hypothesis test. Common significance levels are 10%, 5%, and 1%.

To evaluate your hypothesis test at the significance level that you set, consider if you are conducting a one or two tail test:

• Two-tail tests divide the rejection region, or critical region, evenly above and below the null distribution, i.e. to the tails of the null sampling distribution. For example, in a two-tail test with a 5% significance level, your rejection region would be the upper and lower 2.5% of the null distribution. An alternative hypothesis of μ 1 - μ 2 ≠ D requires a two tail test.
• One-tail tests place the rejection region entirely on one side of the distribution i.e. to the right or left tail of the null distribution. For example, in a one-tail test evaluating if the actual difference in means, D, is above the null distribution with a 5% significance level, your rejection region would be the upper 5% of the null distribution. μ 1 - μ 2 > D and μ 1 - μ 2 < D alternative hypotheses require one-tail tests.

The graphical results section of the calculator above shades rejection regions blue.

After checking your conditions, stating your hypothesis, determining your significance level, and collecting your sample, you are ready to analyze your hypothesis.

Sample means follow the Normal distribution with the following parameters:

• The Difference in the Population Means, D - The true difference in the population means is unknown, but we use the hypothesized difference in the means, D, from the null hypothesis in the calculations.
• The Standard Error, SE - The standard error of the difference in the sample means can be computed as follows:      SE = (s 1 2 /n 1 + s 2 2 /n 2 ) (1/2) with s 1 being the standard deviation of sample one, n 1 being the sample size of sample one, s 2 being the standard deviation of sample one, and n 2 being the sample size of sample two. The standard error defines how differences in sample means are expected to vary around the null difference in means sampling distribution given the sample sizes and under the assumption that the null hypothesis is true.
• The Degrees of Freedom, DF - The degrees of freedom calculation can be estimated as the smaller of n 1 - 1 or n 2 - 1. For more accurate results, use the following formula for the degrees of freedom (DF):      DF = (s 1 2 /n 1 + s 2 2 /n 2 ) 2 / ((s 1 2 /n 1 ) 2 / (n 1 - 1) + (s 2 2 /n 2 ) 2 / (n 2 - 1))

In a difference in means hypothesis test, we calculate the probability that we would observe the difference in sample means (x̄ 1 - x̄ 2 ), assuming the null hypothesis is true, also known as the p-value . If the p-value is less than the significance level, then we can reject the null hypothesis.

You can determine a precise p-value using the calculator above, but we can find an estimate of the p-value manually by calculating the t-score, or t-statistic, as follows: t = (x̄ 1 - x̄ 2 - D) / SE

The t-score is a test statistic that tells you how far our observation is from the null hypothesis's difference in means under the null distribution. Using any t-score table, you can look up the probability of observing the results under the null distribution. You will need to look up the t-score for the type of test you are conducting, i.e. one or two tail. A hypothesis test for the difference in means is sometimes known as a two sample mean t-test because of the use of a t-score in analyzing results.

The conclusion of a hypothesis test for the difference in means is always either:

• Reject the null hypothesis
• Do not reject the null hypothesis

If you reject the null hypothesis, you cannot say that your sample difference in means is the true difference between the means. If you do not reject the null hypothesis, you cannot say that the hypothesized difference in means is true.

A hypothesis test is simply a way to look at evidence and conclude if it provides sufficient evidence to reject the null hypothesis.

Example: Hypothesis Test for the Difference in Two Means

Let’s say you are a manager at a company that designs batteries for smartphones. One of your engineers believes that she has developed a battery that will last more than two hours longer than your standard battery.

Before you can consider if you should replace your standard battery with the new one, you need to test the engineer’s claim. So, you decided to run a difference in means hypothesis test to see if her claim that the new battery will last two hours longer than the standard one is reasonable.

You direct your team to run a study. They will take a sample of 100 of the new batteries and compare their performance to 1,000 of the old standard batteries.

• Check the conditions - Your test consists of independent samples . Your team collects your samples using simple random sampling , and you have reason to believe that all your batteries' performances are always close to normally distributed . So, the conditions are met to conduct a two sample t-test.
• State Your Hypothesis - Your null hypothesis is that the charge of the new battery lasts at most two hours longer than your standard battery (i.e. μ 1 - μ 2 ≤ 2). Your alternative hypothesis is that the new battery lasts more than two hours longer than the standard battery (i.e. μ 1 - μ 2 > 2).
• Determine Your Analysis Plan - You believe that a 1% significance level is reasonable. As your test is a one-tail test, you will evaluate if the difference in mean charge between the samples would occur at the upper 1% of the null distribution.
• Analyze Your Sample - After collecting your samples (which you do after steps 1-3), you find the new battery sample had a mean charge of 10.4 hours, x̄ 1 , with a 0.8 hour standard deviation, s 1 . Your standard battery sample had a mean charge of 8.2 hours, x̄ 2 , with a standard deviation of 0.2 hours, s 2 . Using the calculator above, you find that a difference in sample means of 2.2 hours [2 = 10.4 – 8.2] would results in a t-score of 2.49 under the null distribution, which translates to a p-value of 0.72%.
• Interpret Your Results - Since your p-value of 0.72% is less than the significance level of 1%, you have sufficient evidence to reject the null hypothesis.

In this example, you found that you can reject your null hypothesis that the new battery design does not result in more than 2 hours of extra battery life. The test does not guarantee that your engineer’s new battery lasts two hours longer than your standard battery, but it does give you strong reason to believe her claim.