the assignment problem is always

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

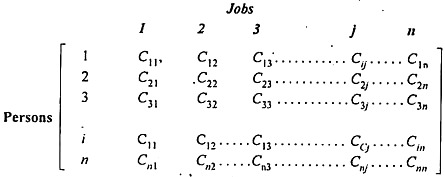
www.springer.com The European Mathematical Society

StatProb Collection
Recent changes
Current events
Random page
Project talk
Request account
What links here
Related changes
Special pages
Printable version
Permanent link
Page information
View source

Assignment problem

The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :

maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $

$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$

(origins or supply),

$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$

(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.

If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).

In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.

The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.

In turn, the transportation problem is a special case of the network optimization problem.

A totally different assignment problem is the pole assignment problem in control theory.

This page was last edited on 5 April 2020, at 18:48.
Privacy policy
About Encyclopedia of Mathematics
Disclaimers
Impressum-Legal

International Symposium on Combinatorial Optimization

ISCO 2022: Combinatorial Optimization pp 172–186 Cite as

Nash Balanced Assignment Problem

Minh Hieu Nguyen 11 ,
Mourad Baiou 11 &
Viet Hung Nguyen 11
Conference paper
First Online: 21 November 2022

325 Accesses

2 Citations

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13526))

In this paper, we consider a variant of the classic Assignment Problem (AP), called the Balanced Assignment Problem (BAP) [ 2 ]. The BAP seeks to find an assignment solution which has the smallest value of max-min distance : the difference between the maximum assignment cost and the minimum one. However, by minimizing only the max-min distance, the total cost of the BAP solution is neglected and it may lead to an inefficient solution in terms of total cost. Hence, we propose a fair way based on Nash equilibrium [ 1 , 3 , 4 ] to inject the total cost into the objective function of the BAP for finding assignment solutions having a better trade-off between the two objectives: the first aims at minimizing the total cost and the second aims at minimizing the max-min distance. For this purpose, we introduce the concept of Nash Fairness (NF) solutions based on the definition of proportional-fair scheduling adapted in the context of the AP: a transfer of utilities between the total cost and the max-min distance is considered to be fair if the percentage increase in the total cost is smaller than the percentage decrease in the max-min distance and vice versa.

We first show the existence of a NF solution for the AP which is exactly the optimal solution minimizing the product of the total cost and the max-min distance. However, finding such a solution may be difficult as it requires to minimize a concave function. The main result of this paper is to show that finding all NF solutions can be done in polynomial time. For that, we propose a Newton-based iterative algorithm converging to NF solutions in polynomial time. It consists in optimizing a sequence of linear combinations of the two objective based on Weighted Sum Method [ 5 ]. Computational results on various instances of the AP are presented and commented.

Combinatorial optimization
Balanced assignment problem
Proportional fairness
Proportional-fair scheduling
Weighted sum method

This is a preview of subscription content, log in via an institution .

Buying options

Available as PDF
Read on any device
Instant download
Own it forever
Available as EPUB and PDF
Compact, lightweight edition
Dispatched in 3 to 5 business days
Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Bertsimas, D., Farias, V.F., Trichakis, N.: The price of fairness. Oper. Res. January–February 59 (1), 17–31 (2011)

MathSciNet MATH Google Scholar

Martello, S., Pulleyblank, W.R., Toth, P., De Werra, D.: Balanced optimization problems. Oper. Res. Lett. 3 (5), 275–278 (1984)

Article MathSciNet MATH Google Scholar

Kelly, F.P., Maullo, A.K., Tan, D.K.H.: Rate control for communication networks: shadow prices, proportional fairness and stability. J. Oper. Res. Soc. 49 (3), 237–252 (1997). https://doi.org/10.1057/palgrave.jors.2600523

Article Google Scholar

Ogryczak, W., Luss, H., Pioro, M., Nace, D., Tomaszewski, A.: Fair optimization and networks: a survey. J. Appl. Math. 2014 , 1–26 (2014)

Marler, R.T., Arora, J.S.: The weighted sum method for multi-objective optimization: new insights. Struct. Multi. Optim. 41 (6), 853–862 (2010)

Heller, I., Tompkins, C.B.: An extension of a theorem of Dantzig’s. Ann. Math. Stud. (38), 247–254 (1956)

Google Scholar

Kuhn, H.W.: The Hungarian method for assignment problem. Naval Res. Logist. Q. 2 (1–2), 83–97 (1955)

Martello, S.: Most and least uniform spanning trees. Discrete Appl. Math. 15 (2), 181–197 (1986)

Beasley, J.E.: Linear programming on Clay supercomputer. J. Oper. Res. Soc. 41 , 133–139 (1990)

Nguyen, M.H, Baiou, M., Nguyen, V.H., Vo, T.Q.T.: Nash fairness solutions for balanced TSP. In: International Network Optimization Conference (INOC2022) (2022)

Download references

Author information

Authors and affiliations.

INP Clermont Auvergne, Univ Clermont Auvergne, Mines Saint-Etienne, CNRS, UMR 6158 LIMOS, 1 Rue de la Chebarde, Aubiere Cedex, France

Minh Hieu Nguyen, Mourad Baiou & Viet Hung Nguyen

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Viet Hung Nguyen .

Editor information

Editors and affiliations.

ESSEC Business School of Paris, Cergy Pontoise Cedex, France

Ivana Ljubić

IBM TJ Watson Research Center, Yorktown Heights, NY, USA

Francisco Barahona

Georgia Institute of Technology, Atlanta, GA, USA

Santanu S. Dey

Université Paris-Dauphine, Paris, France

A. Ridha Mahjoub

Proposition 1 . There may be more than one NF solution for the AP.

Let us illustrate this by an instance of the AP having the following cost matrix

By verifying all feasible assignment solutions in this instance, we obtain easily three assignment solutions $(1-1, 2-2, 3-3), (1-2, 2-3, 3-1)$ , $(1-3, 2-2, 3-1)$ and $(1-3, 2-1, 3-2)$ corresponding to 4 NF solutions (280, 36), (320, 32), (340, 30) and (364, 28). Note that $i-j$ where $1 \le i,j \le 3$ represents the assignment between worker i and job j in the solution of this instance. $\square $

We recall below the proofs of some recent results that we have published in [ 10 ]. They are needed to prove the new results presented in this paper.

Theorem 2 [ 10 ] . $(P^{*},Q^{*}) = {{\,\mathrm{arg\,min}\,}}_{(P,Q) \in \mathcal {S}} PQ$ is a NF solution.

Obviously, there always exists a solution $(P^{*},Q^{*}) \in \mathcal {S}$ such that

Now $\forall (P',Q') \in \mathcal {S}$ we have $P'Q' \ge P^{*}Q^{*}$ . Then

The first inequality holds by the Cauchy-Schwarz inequality.

Hence, $(P^{*},Q^{*})$ is a NF solution. $\square $

Theorem 3 [ 10 ] . $(P^{*},Q^{*}) \in \mathcal {S}$ is a NF solution if and only if $(P^{*},Q^{*})$ is an optimal solution of $\mathcal {P(\alpha ^{*})}$ where $\alpha ^{*} = \frac{Q^{*}}{P^{*}}$ .

Firstly, let $(P^{*},Q^{*})$ be a NF solution and $\alpha ^{*} = \frac{Q^{*}}{P^{*}}$ . We will show that $(P^{*},Q^{*})$ is an optimal solution of $\mathcal {P(\alpha ^{*})}$ .

Since $(P^{*},Q^{*})$ is a NF solution, we have

Since $\alpha ^{*} = \frac{Q^{*}}{P^{*}}$ , we have $\alpha ^{*}P^{*}+Q^{*} = 2Q^{*}$ .

Dividing two sides of ( 6 ) by $P^{*} > 0$ we obtain

So we deduce from ( 7 )

Hence, $(P^{*},Q^{*})$ is an optimal solution of $\mathcal {P}(\alpha ^{*})$ .

Now suppose $\alpha ^{*} = \frac{Q^{*}}{P^{*}}$ and $(P^{*},Q^{*})$ is an optimal solution of $\mathcal {P}(\alpha ^{*})$ , we show that $(P^{*},Q^{*})$ is a NF solution.

If $(P^{*},Q^{*})$ is not a NF solution, there exists a solution $(P',Q') \in \mathcal {S}$ such that

We have then

which contradicts the optimality of $(P^{*},Q^{*})$ . $\square $

Lemma 3 [ 10 ] . Let $\alpha , \alpha ' \in \mathbb {R}_+$ and $(P_{\alpha }, Q_{\alpha })$ , $(P_{\alpha '}, Q_{\alpha '})$ be the optimal solutions of $\mathcal {P(\alpha )}$ and $\mathcal {P(\alpha ')}$ respectively, if $\alpha \le \alpha '$ then $P_{\alpha } \ge P_{\alpha '}$ and $Q_{\alpha } \le Q_{\alpha '}$ .

The optimality of $(P_{\alpha }, Q_{\alpha })$ and $(P_{\alpha '}, Q_{\alpha '})$ gives

By adding both sides of ( 8a ) and ( 8b ), we obtain $(\alpha - \alpha ') (P_{\alpha } - P_{\alpha '}) \le 0$ . Since $\alpha \le \alpha '$ , it follows that $P_{\alpha } \ge P_{\alpha '}$ .

On the other hand, inequality ( 8a ) implies $Q_{\alpha '} - Q_{\alpha } \ge \alpha (P_{\alpha } - P_{\alpha '}) \ge 0$ that leads to $Q_{\alpha } \le Q_{\alpha '}$ . $\square $

Lemma 4 [ 10 ] . During the execution of Procedure Find ( $\alpha _{0})$ in Algorithm 1 , $\alpha _{i} \in [0,1], \, \forall i \ge 1$ . Moreover, if $T_{0} \ge 0$ then the sequence $\{\alpha _i\}$ is non-increasing and $T_{i} \ge 0, \, \forall i \ge 0$ . Otherwise, if $T_{0} \le 0$ then the sequence $\{\alpha _i\}$ is non-decreasing and $T_{i} \le 0, \, \forall i \ge 0$ .

Since $P \ge Q \ge 0, \, \forall (P, Q) \in \mathcal {S}$ , it follows that $\alpha _{i+1} = \frac{Q_i}{P_i} \in [0,1], \, \forall i \ge 0$ .

We first consider $T_{0} \ge 0$ . We proof $\alpha _i \ge \alpha _{i+1}, \, \forall i \ge 0$ by induction on i . For $i = 0$ , we have $T_{0} = \alpha _{0} P_{0} - Q_{0} = P_{0}(\alpha _{0}-\alpha _{1}) \ge 0$ , it follows that $\alpha _{0} \ge \alpha _{1}$ . Suppose that our hypothesis is true until $i = k \ge 0$ , we will prove that it is also true with $i = k+1$ .

Indeed, we have

The inductive hypothesis gives $\alpha _k \ge \alpha _{k+1}$ that implies $P_{k+1} \ge P_k > 0$ and $Q_{k} \ge Q_{k+1} \ge 0$ according to Lemma 3 . It leads to $Q_{k}P_{k+1} - P_{k}Q_{k+1} \ge 0$ and then $\alpha _{k+1} - \alpha _{k+2} \ge 0$ .

Hence, we have $\alpha _{i} \ge \alpha _{i+1}, \, \forall i \ge 0$ .

Consequently, $T_{i} = \alpha _{i}P_{i} - Q_{i} = P_{i}(\alpha _{i}-\alpha _{i+1}) \ge 0, \, \forall i \ge 0$ .

Similarly, if $T_{0} \le 0$ we obtain that the sequence $\{\alpha _i\}$ is non-decreasing and $T_{i} \le 0, \, \forall i \ge 0$ . That concludes the proof. $\square $

Lemma 5 [ 10 ] . From each $\alpha _{0} \in [0,1]$ , Procedure Find $(\alpha _{0})$ converges to a coefficient $\alpha _{k} \in \mathcal {C}_{0}$ satisfying $\alpha _{k}$ is the unique element $\in \mathcal {C}_{0}$ between $\alpha _{0}$ and $\alpha _{k}$ .

As a consequence of Lemma 4 , Procedure $\textit{Find}(\alpha _{0})$ converges to a coefficient $\alpha _{k} \in [0,1], \forall \alpha _{0} \in [0,1]$ .

By the stopping criteria of Procedure Find $(\alpha _{0})$ , when $T_{k} = \alpha _{k} P_{k} - Q_{k} = 0$ we obtain $\alpha _{k} \in C_{0}$ and $(P_{k},Q_{k})$ is a NF solution. (Theorem 3 )

If $T_{0} = 0$ then obviously $\alpha _{k} = \alpha _{0}$ . We consider $T_{0} > 0$ and the sequence $\{\alpha _i\}$ is now non-negative, non-increasing. We will show that $[\alpha _{k},\alpha _{0}] \cap \mathcal {C}_{0} = \alpha _{k}$ .

Suppose that we have $\alpha \in (\alpha _{k},\alpha _{0}]$ and $\alpha \in \mathcal {C}_{0}$ corresponding to a NF solution ( P , Q ). Then there exists $1 \le i \le k$ such that $\alpha \in (\alpha _{i}, \alpha _{i-1}]$ . Since $\alpha \le \alpha _{i-1}$ , $P \ge P_{i-1}$ and $Q \le Q_{i-1}$ due to Lemma 3 . Thus, we get

By the definitions of $\alpha $ and $\alpha _{i}$ , inequality ( 9 ) is equivalent to $\alpha \le \alpha _{i}$ which leads to a contradiction.

By repeating the same argument for $T_{0} < 0$ , we also have a contradiction. $\square $

Rights and permissions

Reprints and permissions

Copyright information

About this paper

Cite this paper.

Nguyen, M.H., Baiou, M., Nguyen, V.H. (2022). Nash Balanced Assignment Problem. In: Ljubić, I., Barahona, F., Dey, S.S., Mahjoub, A.R. (eds) Combinatorial Optimization. ISCO 2022. Lecture Notes in Computer Science, vol 13526. Springer, Cham. https://doi.org/10.1007/978-3-031-18530-4_13

Download citation

DOI : https://doi.org/10.1007/978-3-031-18530-4_13

Published : 21 November 2022

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-18529-8

Online ISBN : 978-3-031-18530-4

eBook Packages : Computer Science Computer Science (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Publish with us

Policies and ethics

Find a journal
Track your research

Quantitative Techniques: Theory and Problems by P. C. Tulsian, Vishal Pandey

Get full access to Quantitative Techniques: Theory and Problems and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

WHAT IS ASSIGNMENT PROBLEM

Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons.

The assignment problem in the general form can be stated as follows:

“Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to assign each facility to one and only one job in such a way that the measure of effectiveness is optimised (Maximised or Minimised).”

Several problems of management has a structure identical with the assignment problem.

Example I A manager has four persons (i.e. facilities) available for four separate jobs (i.e. jobs) and the cost of assigning (i.e. effectiveness) each job to each ...

Get Quantitative Techniques: Theory and Problems now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Linear Programming using Pyomo
Networking and Professional Development for Machine Learning Careers in the USA
Predicting Employee Churn in Python
Airflow Operators
MLOps Tutorial

Solving Assignment Problem using Linear Programming in Python

Learn how to use Python PuLP to solve Assignment problems using Linear Programming.

In earlier articles, we have seen various applications of Linear programming such as transportation, transshipment problem, Cargo Loading problem, and shift-scheduling problem. Now In this tutorial, we will focus on another model that comes under the class of linear programming model known as the Assignment problem. Its objective function is similar to transportation problems. Here we minimize the objective function time or cost of manufacturing the products by allocating one job to one machine.

If we want to solve the maximization problem assignment problem then we subtract all the elements of the matrix from the highest element in the matrix or multiply the entire matrix by –1 and continue with the procedure. For solving the assignment problem, we use the Assignment technique or Hungarian method, or Flood’s technique.

The transportation problem is a special case of the linear programming model and the assignment problem is a special case of transportation problem, therefore it is also a special case of the linear programming problem.

In this tutorial, we are going to cover the following topics:

Assignment Problem

A problem that requires pairing two sets of items given a set of paired costs or profit in such a way that the total cost of the pairings is minimized or maximized. The assignment problem is a special case of linear programming.

For example, an operation manager needs to assign four jobs to four machines. The project manager needs to assign four projects to four staff members. Similarly, the marketing manager needs to assign the 4 salespersons to 4 territories. The manager’s goal is to minimize the total time or cost.

Problem Formulation

A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. The manager has stated his goal is to develop a set of job assignments that will minimize the total cost of getting all 4 jobs.

Initialize LP Model

In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.

Define Decision Variable

In this step, we will define the decision variables. In our problem, we have two variable lists: workers and jobs. Let’s create them using LpVariable.dicts() class. LpVariable.dicts() used with Python’s list comprehension. LpVariable.dicts() will take the following four values:

First, prefix name of what this variable represents.
Second is the list of all the variables.
Third is the lower bound on this variable.
Fourth variable is the upper bound.
Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are LpContinuous or LpInteger .

Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.

Define Objective Function

In this step, we will define the minimum objective function by adding it to the LpProblem object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.

Define the Constraints

Here, we are adding two types of constraints: Each job can be assigned to only one employee constraint and Each employee can be assigned to only one job. We have added the 2 constraints defined in the problem by adding them to the LpProblem object.

Solve Model

In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.

From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.

In this article, we have learned about Assignment problems, Problem Formulation, and implementation using the python PuLp library. We have solved the Assignment problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. You can also run other case studies on Cargo Loading problems , Staff scheduling problems . In upcoming articles, we will write more on different optimization problems such as transshipment problem, balanced diet problem. You can revise the basics of mathematical concepts in this article and learn about Linear Programming in this article .

Solving Blending Problem in Python using Gurobi
Transshipment Problem in Python Using PuLP

Pandas DataFrame

Grid Search in scikit-learn

Text Analytics for Beginner using Python TextBlob

Quadratic assignment problem

Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)

1 Introduction
2.1 Koopmans-Beckman Mathematical Formulation
2.2.1 Parameters
2.3.1 Optimization Problem
2.4 Computational Complexity
2.5 Algorithmic Discussions
2.6 Branch and Bound Procedures
2.7 Linearizations
3.1 QAP with 3 Facilities
4.1 Inter-plant Transportation Problem
4.2 The Backboard Wiring Problem
4.3 Hospital Layout
4.4 Exam Scheduling System
5 Conclusion
6 References

Introduction

The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.

Theory, Methodology, and/or Algorithmic Discussions

Koopmans-beckman mathematical formulation.

Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.

Quadratic Assignment Problem Formulation

$F=(F_{ij})$

Inner Product

$A,B$

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

$F_{i,j}(X_{\phi }DX_{\phi }^{T})_{i,j}$

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.

Optimization Problem

With all of this information, the QAP can be summarized as:

$\min _{X\in P}\langle F,XDX^{T}\rangle$

Computational Complexity

QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]

Algorithmic Discussions

While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:

Dynamic Program
Cutting Plane

Branch and Bound Procedures

The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.

The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.

A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.

Linearizations

The first attempts to solve the QAP eliminated the quadratic term in the objective function of

$min\sum _{i=1}^{n}\sum _{j=1}^{n}c{_{\phi (i)\phi (j)}}+\sum _{i=1}^{n}b{_{\phi (i)}}$

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.

Numerical Example

Qap with 3 facilities.

$D={\begin{bmatrix}0&5&6\\5&0&3.6\\6&3.6&0\end{bmatrix}}$

Applications

Inter-plant transportation problem.

The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.

The Backboard Wiring Problem

As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]

When defining the problem Steinberg states that we have a set of n elements

$E=\left\{E_{1},E_{2},...,E_{n}\right\}$

as well as a set of r points

$P_{1},P_{2},...,P_{r}$

In his paper he derives the below formula:

$min\sum _{1\leq i\leq j\leq n}^{}C_{ij}(d_{s(i)s(j))})$

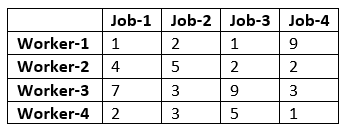
In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.

The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.

Hospital Layout

Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.

Elshafei identified the following QAP to determine where clinics should be placed:

$min\sum _{i,j}\sum _{k,q}f_{ik}d_{jq}y_{ij}y_{kq}$

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.

Exam Scheduling System

The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

$n!$

↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.

Solving an Assignment Problem

This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.

In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .

The costs of assigning workers to tasks are shown in the following table.

The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.

MIP solution

The following sections describe how to solve the problem using the MPSolver wrapper .

Import the libraries

The following code imports the required libraries.

Create the data

The following code creates the data for the problem.

The costs array corresponds to the table of costs for assigning workers to tasks, shown above.

Declare the MIP solver

The following code declares the MIP solver.

Create the variables

The following code creates binary integer variables for the problem.

Create the constraints

Create the objective function.

The following code creates the objective function for the problem.

The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.

Invoke the solver

The following code invokes the solver.

Print the solution

The following code prints the solution to the problem.

Here is the output of the program.

Complete programs

Here are the complete programs for the MIP solution.

CP SAT solution

The following sections describe how to solve the problem using the CP-SAT solver.

Declare the model

The following code declares the CP-SAT model.

The following code sets up the data for the problem.

The following code creates the constraints for the problem.

Here are the complete programs for the CP-SAT solution.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

Operations Research

31. Using ______________ method, we can never have an unbounded solution

Dual simplex

32. The customers of high priority are given service over the low priority customers is ______________.

Pre emptive

33. A queuing system is said to be a ______________ when its operating characteristic are independent upon time

pure birth model
pure death model
transient state
steady state

34. An activity which does not consume neither any resource nor time is known as ______________.

predecessor activity
successor activity
dummy activity

35. The difference between total and free float is ______________.

independent
interference

36. The number of time estimates involved in Program Evaluation Review Technique problem is ______________.

37. The assignment problem is always a ______________matrix.

38. The slack variables indicate ______________.

excess resource available.
shortage of resource
nil resource
idle resource

39. If the net evaluation corresponding to any non -basic variable is zero, it is an indication of the existence of an ______________.

initial basic feasible solution
optimum basic feasible solution
optimum solution.
alternate optimum solution.

40. Mathematical model of linear programming problem is important because ______________.

it helps in converting the verbal description and numerical data into mathematical expression
decision makers prefer to work with formal models
it captures the relevant relationship among decision factors
it enables the use of algebraic technique

Search MBA MCQ.com

MCQ Problems / Explanations