problem solving using systems of equations

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.4: Solve Applications with Systems of Equations

• Last updated
• Save as PDF
• Page ID 15154

Learning Objectives

By the end of this section, you will be able to:

• Translate to a system of equations
• Solve direct translation applications
• Solve geometry applications
• Solve uniform motion applications

Before you get started, take this readiness quiz.

• The sum of twice a number and nine is 31. Find the number. If you missed this problem, review Example 3.1.10 .
• Twins Jon and Ron together earned $96,000 last year. Ron earned $8,000 more than three times what Jon earned. How much did each of the twins earn? If you missed this problem, review Example 3.1.31 .
• Alessio rides his bike \(3\frac{1}{2}\) hours at a rate of 10 miles per hour. How far did he ride? If you missed this problem, review Example 2.6.1 .

Previously in this chapter we solved several applications with systems of linear equations. In this section, we’ll look at some specific types of applications that relate two quantities. We’ll translate the words into linear equations, decide which is the most convenient method to use, and then solve them.

We will use our Problem Solving Strategy for Systems of Linear Equations.

USE A PROBLEM SOLVING STRATEGY FOR SYSTEMS OF LINEAR EQUATIONS.

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose variables to represent those quantities.
• Translate into a system of equations.
• Solve the system of equations using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

Translate to a System of Equations

Many of the problems we solved in earlier applications related two quantities. Here are two of the examples from the chapter on Math Models .

The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.

A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?

In that chapter we translated each situation into one equation using only one variable. Sometimes it was a bit of a challenge figuring out how to name the two quantities, wasn’t it?

Let’s see how we can translate these two problems into a system of equations with two variables. We’ll focus on Steps 1 through 4 of our Problem Solving Strategy.

Example \(\PageIndex{1}\): How to Translate to a System of Equations

Translate to a system of equations:

Try It \(\PageIndex{2}\)

The sum of two numbers is negative twenty-three. One number is 7 less than the other. Find the numbers.

\(\left\{\begin{array}{l}{m+n=-23} \\ {m=n-7}\end{array}\right.\)

Try It \(\PageIndex{3}\)

The sum of two numbers is negative eighteen. One number is 40 more than the other. Find the numbers.

\(\left\{\begin{array}{l}{m+n=-18} \\ {m=n+40}\end{array}\right.\)

We’ll do another example where we stop after we write the system of equations.

Example \(\PageIndex{4}\)

\(\begin{array}{ll}{\text {We are looking for the amount that }} & {\text {Let } h=\text { the amount the husband earns. }} \\ {\text {the husband and wife each earn. }} & { w=\text { the amount the wife earns }} \\ {\text{Translate.}} & {\text{A married couple together earns \$110,000.} }\\ {} & {w+h=110000} \\ & \text{The wife earns \$16,000 less than twice what} \\ & \text{husband earns.} \\ & w=2h−16,000 \\ \text{The system of equations is:} & \left\{\begin{array}{l}{w+h=110,000} \\ {w=2 h-16,000}\end{array}\right.\end{array}\)

Try It \(\PageIndex{5}\)

A couple has a total household income of $84,000. The husband earns $18,000 less than twice what the wife earns. How much does the wife earn?

\(\left\{\begin{array}{l}{w+h=84,000} \\ {h=2 w-18,000}\end{array}\right.\)

Try It \(\PageIndex{6}\)

A senior employee makes $5 less than twice what a new employee makes per hour. Together they make $43 per hour. How much does each employee make per hour?

\(\left\{\begin{array}{l}{s=2 n-5} \\ {s+n=43}\end{array}\right.\)

Solve Direct Translation Applications

We set up, but did not solve, the systems of equations in Example \(\PageIndex{1}\) and Example \(\PageIndex{4}\) Now we’ll translate a situation to a system of equations and then solve it.

Example \(\PageIndex{7}\)

Translate to a system of equations and then solve:

Devon is 26 years older than his son Cooper. The sum of their ages is 50. Find their ages.

Try It \(\PageIndex{8}\)

Ali is 12 years older than his youngest sister, Jameela. The sum of their ages is 40. Find their ages.

Ali is 26 and Jameela is 14.

Try It \(\PageIndex{9}\)

Jake’s dad is 6 more than 3 times Jake’s age. The sum of their ages is 42. Find their ages.

Jake is 9 and his dad is 33.

Example \(\PageIndex{10}\)

When Jenna spent 10 minutes on the elliptical trainer and then did circuit training for 20 minutes, her fitness app says she burned 278 calories. When she spent 20 minutes on the elliptical trainer and 30 minutes circuit training she burned 473 calories. How many calories does she burn for each minute on the elliptical trainer? How many calories does she burn for each minute of circuit training?

Try It \(\PageIndex{11}\)

Mark went to the gym and did 40 minutes of Bikram hot yoga and 10 minutes of jumping jacks. He burned 510 calories. The next time he went to the gym, he did 30 minutes of Bikram hot yoga and 20 minutes of jumping jacks burning 470 calories. How many calories were burned for each minute of yoga? How many calories were burned for each minute of jumping jacks?

Mark burned 11 calories for each minute of yoga and 7 calories for each minute of jumping jacks.

Try It \(\PageIndex{12}\)

Erin spent 30 minutes on the rowing machine and 20 minutes lifting weights at the gym and burned 430 calories. During her next visit to the gym she spent 50 minutes on the rowing machine and 10 minutes lifting weights and burned 600 calories. How many calories did she burn for each minutes on the rowing machine? How many calories did she burn for each minute of weight lifting?

Erin burned 11 calories for each minute on the rowing machine and 5 calories for each minute of weight lifting.

Solve Geometry Applications

When we learned about Math Models , we solved geometry applications using properties of triangles and rectangles. Now we’ll add to our list some properties of angles.

The measures of two complementary angles add to 90 degrees. The measures of two supplementary angles add to 180 degrees.

COMPLEMENTARY AND SUPPLEMENTARY ANGLES

Two angles are complementary if the sum of the measures of their angles is 90 degrees.

Two angles are supplementary if the sum of the measures of their angles is 180 degrees.

If two angles are complementary, we say that one angle is the complement of the other.

If two angles are supplementary, we say that one angle is the supplement of the other.

Example \(\PageIndex{13}\)

The difference of two complementary angles is 26 degrees. Find the measures of the angles.

Try It \(\PageIndex{14}\)

The difference of two complementary angles is 20 degrees. Find the measures of the angles.

The angle measures are 55 degrees and 35 degrees.

Try It \(\PageIndex{15}\)

The difference of two complementary angles is 80 degrees. Find the measures of the angles.

The angle measures are 5 degrees and 85 degrees.

Example \(\PageIndex{16}\)

Two angles are supplementary. The measure of the larger angle is twelve degrees less than five times the measure of the smaller angle. Find the measures of both angles.

Try It \(\PageIndex{17}\)

Two angles are supplementary. The measure of the larger angle is 12 degrees more than three times the smaller angle. Find the measures of the angles.

The angle measures are 42 degrees and 138 degrees.

Try It \(\PageIndex{18}\)

Two angles are supplementary. The measure of the larger angle is 18 less than twice the measure of the smaller angle. Find the measures of the angles.

The angle measures are 66 degrees and 114 degrees.

Example \(\PageIndex{19}\)

Randall has 125 feet of fencing to enclose the rectangular part of his backyard adjacent to his house. He will only need to fence around three sides, because the fourth side will be the wall of the house. He wants the length of the fenced yard (parallel to the house wall) to be 5 feet more than four times as long as the width. Find the length and the width.

Try It \(\PageIndex{20}\)

Mario wants to put a rectangular fence around the pool in his backyard. Since one side is adjacent to the house, he will only need to fence three sides. There are two long sides and the one shorter side is parallel to the house. He needs 155 feet of fencing to enclose the pool. The length of the long side is 10 feet less than twice the width. Find the length and width of the pool area to be enclosed.

The length is 60 feet and the width is 35 feet.

Try It \(\PageIndex{21}\)

Alexis wants to build a rectangular dog run in her yard adjacent to her neighbor’s fence. She will use 136 feet of fencing to completely enclose the rectangular dog run. The length of the dog run along the neighbor’s fence will be 16 feet less than twice the width. Find the length and width of the dog run.

The length is 60 feet and the width is 38 feet.

Solve Uniform Motion Applications

We used a table to organize the information in uniform motion problems when we introduced them earlier. We’ll continue using the table here. The basic equation was D = rt where D is the distance traveled, r is the rate, and t is the time.

Our first example of a uniform motion application will be for a situation similar to some we have already seen, but now we can use two variables and two equations.

Example \(\PageIndex{22}\)

Joni left St. Louis on the interstate, driving west towards Denver at a speed of 65 miles per hour. Half an hour later, Kelly left St. Louis on the same route as Joni, driving 78 miles per hour. How long will it take Kelly to catch up to Joni?

A diagram is useful in helping us visualize the situation.

Try It \(\PageIndex{23}\)

Translate to a system of equations and then solve: Mitchell left Detroit on the interstate driving south towards Orlando at a speed of 60 miles per hour. Clark left Detroit 1 hour later traveling at a speed of 75 miles per hour, following the same route as Mitchell. How long will it take Clark to catch Mitchell?

It will take Clark 4 hours to catch Mitchell.

Try It \(\PageIndex{24}\)

Translate to a system of equations and then solve: Charlie left his mother’s house traveling at an average speed of 36 miles per hour. His sister Sally left 15 minutes (1/4 hour) later traveling the same route at an average speed of 42 miles per hour. How long before Sally catches up to Charlie?

It will take Sally \(1\frac{1}{2}\) hours to catch up to Charlie.

Many real-world applications of uniform motion arise because of the effects of currents—of water or air—on the actual speed of a vehicle. Cross-country airplane flights in the United States generally take longer going west than going east because of the prevailing wind currents.

Let’s take a look at a boat traveling on a river. Depending on which way the boat is going, the current of the water is either slowing it down or speeding it up.

Figure \(\PageIndex{1}\) and Figure \(\PageIndex{2}\) show how a river current affects the speed at which a boat is actually traveling. We’ll call the speed of the boat in still water b and the speed of the river current c .

In Figure \(\PageIndex{1}\) the boat is going downstream, in the same direction as the river current. The current helps push the boat, so the boat’s actual speed is faster than its speed in still water. The actual speed at which the boat is moving is b + c .

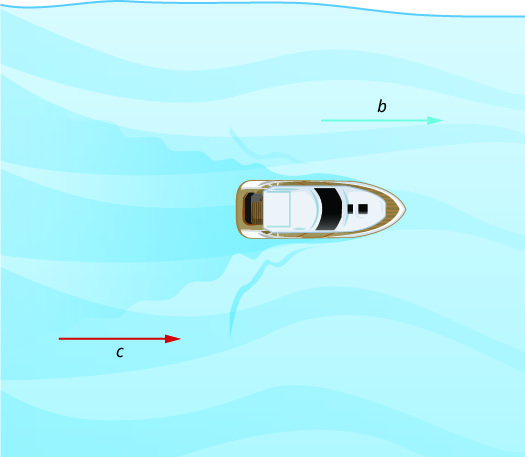
In Figure \(\PageIndex{2}\) the boat is going upstream, opposite to the river current. The current is going against the boat, so the boat’s actual speed is slower than its speed in still water. The actual speed of the boat is b−c.

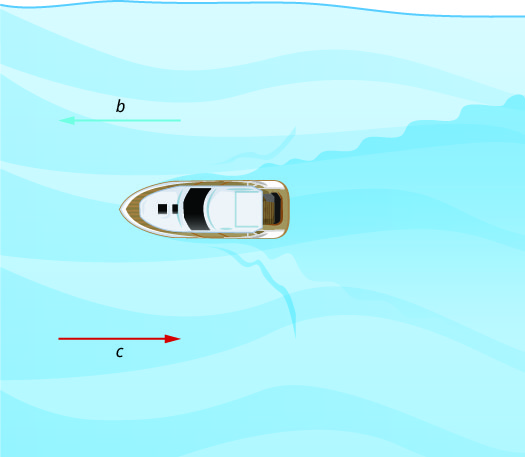
We’ll put some numbers to this situation in Example \(\PageIndex{25}\).

Example \(\PageIndex{25}\)

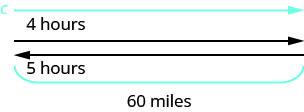
A river cruise ship sailed 60 miles downstream for 4 hours and then took 5 hours sailing upstream to return to the dock. Find the speed of the ship in still water and the speed of the river current.

Read the problem.

This is a uniform motion problem and a picture will help us visualize the situation.

Try It \(\PageIndex{26}\)

Translate to a system of equations and then solve: A Mississippi river boat cruise sailed 120 miles upstream for 12 hours and then took 10 hours to return to the dock. Find the speed of the river boat in still water and the speed of the river current.

The rate of the boat is 11 mph and the rate of the current is 1 mph.

Try It \(\PageIndex{27}\)

Translate to a system of equations and then solve: Jason paddled his canoe 24 miles upstream for 4 hours. It took him 3 hours to paddle back. Find the speed of the canoe in still water and the speed of the river current.

The speed of the canoe is 7 mph and the speed of the current is 1 mph.

Wind currents affect airplane speeds in the same way as water currents affect boat speeds. We’ll see this in Example \(\PageIndex{28}\). A wind current in the same direction as the plane is flying is called a tailwind . A wind current blowing against the direction of the plane is called a headwind .

Example \(\PageIndex{28}\)

A private jet can fly 1095 miles in three hours with a tailwind but only 987 miles in three hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

This is a uniform motion problem and a picture will help us visualize.

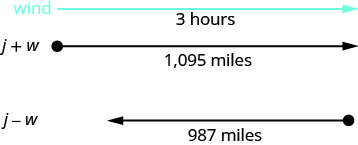
Try It \(\PageIndex{29}\)

Translate to a system of equations and then solve: A small jet can fly 1,325 miles in 5 hours with a tailwind but only 1025 miles in 5 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

The speed of the jet is 235 mph and the speed of the wind is 30 mph.

Try It \(\PageIndex{30}\)

Translate to a system of equations and then solve: A commercial jet can fly 1728 miles in 4 hours with a tailwind but only 1536 miles in 4 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

The speed of the jet is 408 mph and the speed of the wind is 24 mph.

• Pre-Algebra Topics
• Algebra Topics
• Algebra Calculator
• Algebra Cheat Sheet
• Algebra Practice Test
• Algebra Readiness Test
• Algebra Formulas
• Want to Build Your Own Website?

Sign In / Register

Solving Systems of Equations Real World Problems

Wow! You have learned many different strategies for solving systems of equations! First we started with Graphing Systems of Equations . Then we moved onto solving systems using the Substitution Method . In our last lesson we used the Linear Combinations or Addition Method to solve systems of equations.

Now we are ready to apply these strategies to solve real world problems! Are you ready? First let's look at some guidelines for solving real world problems and then we'll look at a few examples.

Steps For Solving Real World Problems

• Highlight the important information in the problem that will help write two equations.
• Define your variables
• Write two equations
• Use one of the methods for solving systems of equations to solve.
• Check your answers by substituting your ordered pair into the original equations.
• Answer the questions in the real world problems. Always write your answer in complete sentences!

Ok... let's look at a few examples. Follow along with me. (Having a calculator will make it easier for you to follow along.)

Example 1: Systems Word Problems

You are running a concession stand at a basketball game. You are selling hot dogs and sodas. Each hot dog costs $1.50 and each soda costs $0.50. At the end of the night you made a total of $78.50. You sold a total of 87 hot dogs and sodas combined. You must report the number of hot dogs sold and the number of sodas sold. How many hot dogs were sold and how many sodas were sold?

1.  Let's start by identifying the important information:

• hot dogs cost $1.50
• Sodas cost $0.50
• Made a total of $78.50
• Sold 87 hot dogs and sodas combined

2.  Define your variables.

• Ask yourself, "What am I trying to solve for? What don't I know?

In this problem, I don't know how many hot dogs or sodas were sold. So this is what each variable will stand for. (Usually the question at the end will give you this information).

Let x = the number of hot dogs sold

Let y = the number of sodas sold

3. Write two equations.

One equation will be related to the price and one equation will be related to the quantity (or number) of hot dogs and sodas sold.

1.50x + 0.50y = 78.50    (Equation related to cost)

 x + y = 87   (Equation related to the number sold)

4.  Solve! 

We can choose any method that we like to solve the system of equations. I am going to choose the substitution method since I can easily solve the 2nd equation for y.

5. Think about what this solution means.

x is the number of hot dogs and x = 35. That means that 35 hot dogs were sold.

y is the number of sodas and y = 52. That means that 52 sodas were sold.

6.  Write your answer in a complete sentence.

35 hot dogs were sold and 52 sodas were sold.

7.  Check your work by substituting.

1.50x + 0.50y = 78.50

1.50(35) + 0.50(52) = 78.50

52.50 + 26 = 78.50

35 + 52 = 87

Since both equations check properly, we know that our answers are correct!

That wasn't too bad, was it? The hardest part is writing the equations. From there you already know the strategies for solving. Think carefully about what's happening in the problem when trying to write the two equations.

Example 2: Another Word Problem

You and a friend go to Tacos Galore for lunch. You order three soft tacos and three burritos and your total bill is $11.25. Your friend's bill is $10.00 for four soft tacos and two burritos. How much do soft tacos cost? How much do burritos cost?

• 3 soft tacos + 3 burritos cost $11.25
• 4 soft tacos + 2 burritos cost $10.00

In this problem, I don't know the price of the soft tacos or the price of the burritos.

Let x = the price of 1 soft taco

Let y = the price of 1 burrito

One equation will be related your lunch and one equation will be related to your friend's lunch.

3x + 3y = 11.25  (Equation representing your lunch)

4x + 2y = 10   (Equation representing your friend's lunch)

We can choose any method that we like to solve the system of equations. I am going to choose the combinations method.

5. Think about what the solution means in context of the problem.

x = the price of 1 soft taco and x = 1.25.

That means that 1 soft tacos costs $1.25.

y = the price of 1 burrito and y = 2.5.

That means that 1 burrito costs $2.50.

Yes, I know that word problems can be intimidating, but this is the whole reason why we are learning these skills. You must be able to apply your knowledge!

If you have difficulty with real world problems, you can find more examples and practice problems in the Algebra Class E-course.

Take a look at the questions that other students have submitted:

Problem about the WNBA

Systems problem about ages

Problem about milk consumption in the U.S.

Vans and Buses? How many rode in each?

Telephone Plans problem

Systems problem about hats and scarves

Apples and guavas please!

How much did Alice spend on shoes?

All about stamps

Going to the movies

Small pitchers and large pitchers - how much will they hold?

Chickens and dogs in the farm yard

• System of Equations
• Systems Word Problems

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.

ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!

Affiliate Products...

On this site, I recommend only one product that I use and love and that is Mathway   If you make a purchase on this site, I may receive a small commission at no cost to you. 

Privacy Policy

Let Us Know How we are doing!

  send us a message to give us more detail!

Would you prefer to share this page with others by linking to it?

• Click on the HTML link code below.
• Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.

Math Made Easy

Systems of Linear Equations and Word Problems

Note that we saw how to solve linear inequalities here in the Coordinate System and Graphing Lines section . Note also that we solve Algebra Word Problems without Systems here , and we solve systems using matrices in the Matrices and Solving Systems with Matrices  section here.

Introduction to Systems

“Systems of equations” just means that we are dealing with more than one equation and variable. So far, we’ve basically just played around with the equation for a line, which is $ y=mx+b$. Let’s say we have the following situation:

Now, you can always do “guess and check” to see what would work, but you might as well use algebra! It’s much better to learn the algebra way, because even though this problem is fairly simple to solve, the algebra way will let you solve any algebra problem – even the really complicated ones.

The first trick in problems like this is to figure out what we want to know. This will help us decide what variables (unknowns) to use. What we want to know is how many pairs of jeans we want to buy (let’s say “$ j$”) and how many dresses we want to buy (let’s say “$ d$”). Always write down what your variables will be:

Let $ j=$ the number of jeans you will buy Let $ d=$ the number of dresses you’ll buy

Like we did before, let’s translate word-for-word from math to English:

Now we have the 2 equations as shown below. Notice that the $ j$ variable is just like the $ x$ variable and the $ d$ variable is just like the $ y$. It’s easier to put in $ j$   and $ d$ so we can remember what they stand for when we get the answers.

This is what we call a system, since we have to solve for more than one variable – we have to solve for 2 here. The cool thing is to solve for 2   variables , you typically need 2   equations , to solve for 3   variables , you need 3   equations , and so on. That’s easy to remember, right?

We need to get an answer that works in both equations ; this is what we’re doing when we’re solving; this is called solving simultaneous systems , or solving system simultaneously . There are several ways to solve systems; we’ll talk about graphing first.

Solving Systems by Graphing

Remember that when you graph a line, you see all the different coordinates (or $ x/y$ combinations) that make the equation work. In systems, you have to make both equations work, so the intersection of the two lines shows the point that fits both equations (assuming the lines do in fact intersect; we’ll talk about that later).  The points of intersections satisfy both equations simultaneously. 

Put these equations into the $ y=mx+b$ ($ d=mj+b$) format, by solving for the $ d$ (which is like the $ y$):

$ \displaystyle j+d=6;\text{ }\,\text{ }\text{solve for }d:\text{ }d=-j+6\text{ }$

$ \displaystyle 25j+50d=200;\text{ }\,\,\text{solve for }d:\text{ }d=\frac{{200-25j}}{{50}}=-\frac{1}{2}j+4$

Now graph both lines:

Note that with non-linear equations, there will most likely be more than one intersection; an example of how to get more than one solution via the Graphing Calculator can be found in the  Exponents and Radicals in Algebra section. Also, t here are some examples of systems of inequality  here in the Coordinate System and Graphing Lines section .

Solving Systems with Substitution

Substitution is the favorite way to solve for many students! It involves exactly what it says: substituting one variable in another equation so that you only have one variable in that equation. Here is the same problem:

You’re going to the mall with your friends and you have $200 to spend from your recent birthday money. You discover a store that has all jeans for $25 and all dresses for $50 .  You really, really want to take home 6 items of clothing because you “need” that many new things. How many pairs of jeans and how many dresses you can buy so you use the whole $200 (tax not included)?

Below are our two equations, and let’s solve for “$ d$” in terms of “$ j$” in the first equation. Then, let’s substitute what we got for “$ d$” into the next equation. Even though it doesn’t matter which equation you start with, remember to always pick the “easiest” equation first (one that we can easily solve for a variable) to get a variable by itself.

We could buy 4 pairs of jeans and 2 dresses . Note that we could have also solved for “$ j$” first; it really doesn’t matter. You’ll want to pick the variable that’s most easily solved for. Let’s try another substitution problem that’s a little bit different:

Solving Systems with Linear Combination or Elimination

Probably the most useful way to solve systems is using linear combination, or linear elimination. The reason it’s most useful is that usually in real life we don’t have one variable in terms of another (in other words, a “$ y=$” situation).

The main purpose of the linear combination method is to add or subtract the equations so that one variable is eliminated. We can add, subtract, or multiply both sides of equations by the same numbers – let’s use real numbers as shown below. We are using the Additive Property of Equality , Subtraction Property of Equality , Multiplicative Property of Equality , and/or Division Property of Equality that we saw here in the Types of Numbers and Algebraic Properties section :

If we have a set of 2 equations with 2 unknowns, for example, we can manipulate them by adding, multiplying or subtracting (we usually prefer adding) so that we get one equation with one variable. Let’s use our previous problem:

We could buy 4 pairs of jeans and 2 dresses .

Here’s another example:

Types of equations

In the example above, we found one unique solution to the set of equations. Sometimes, however, for a set of equations, there are no solutions (when lines are parallel) or an infinite number of solutions or infinitely many solutions (when the two lines are actually the same line, and one is just a “multiple” of the other).

When there is at least one solution , the equations are consistent equations , since they have a solution. When there is only one solution, the system is called independent , since they cross at only one point. When equations have infinite solutions, they are the same equation, are consistent , and are called dependent or coincident (think of one just sitting on top of the other).

When equations have no solutions , they are called inconsistent equations , since we can never get a solution . 

Here are graphs of inconsistent and dependent equations that were created on a graphing calculator:

Systems with Three Equations

Let’s get a little more complicated with systems; in real life, we rarely just have two unknowns to solve for.

Let’s say at the same store, they also had pairs of shoes for $20 and we managed to get $60 more to spend! Now we have a new problem. To spend the even $260 , how many pairs of jeans, dresses, and pairs of shoes should we get if want, for example, exactly 10 total items (Remember that jeans cost $25 each and dresses cost $50 each).

Let’s let $ j=$ the number of pair of jeans, $ d=$ the number of dresses, and $ s=$ the number of pairs of shoes we should buy. So far, we’ll have the following equations:

$ \displaystyle \begin{array}{c}j+d+s=10\text{ }\\25j+\text{ }50d+\,20s=260\end{array}$

We’ll need another equation, since for three variables, we need three equations (otherwise, we theoretically might have infinite ways to solve the problem). In this type of problem, you would also need something like this: We want twice as many pairs of jeans as pairs of shoes . Now, since we have the same number of equations as variables , we can potentially get one solution for the system of equations. Here are the three equations:

We’ll learn later how to put these in our calculator to easily solve using matrices (see the  Matrices and Solving Systems with Matrices section). For now, we can use two equations at a time to eliminate a variable (using substitution and/or elimination), and keep doing this until we’ve solved for all variables. These can get really difficult to solve, but remember that in “real life”, there are computers to do all this work!

Remember again, that if we ever get to a point where we end up with something like this, it means there are an infinite number of solutions : $ 4=4$  (variables are gone and a number equals another number and they are the same). And if we up with something like this, it means there are no solutions : $ 5=2$ (variables are gone and two numbers are left and they don’t equal each other).

Let’s solve our system:      $ \displaystyle \begin{array}{c}j+d+s=10\text{ }\\25j+\text{ }50d+20s=260\\j=2s\end{array}$ :

We could buy 6 pairs of jeans, 1 dress, and 3 pairs of shoes .

Here’s one more example of a three-variable system of equations, where we’ll only use linear elimination:

$ \displaystyle \begin{align}5x-6y-\,7z\,&=\,7\\6x-4y+10z&=\,-34\\2x+4y-\,3z\,&=\,29\end{align}$

I know – this is really difficult stuff! But if you do it step-by-step and keep using the equations you need with the right variables, you can do it. Think of it like a puzzle – you may not know exactly where you’re going, but do what you can in baby steps, and you’ll get there (sort of like life sometimes, right?!). And we’ll learn much easier ways to do these types of problems.

Algebra Word Problems with Systems

Let’s do more word problems; you’ll notice that many of these are the same type that we did earlier in the Algebra Word Problems  section , but now we can use more than one variable. This will actually make the problems easier! Again, when doing these word problems:

• If you’re wondering what the variables (or unknowns) should be when working on a word problem, look at what the problem is asking. These are usually (but not always) what your variables are!
• If you’re not sure how to set up the equations, use regular numbers (simple ones!) and see what you’re doing. Then put the variables back in!

Here are some problems:

Investment Word Problem

We also could have set up this problem with a table:

Mixture Word Problems

Here’s a mixture word problem . With mixture problems, remember if the problem calls for a pure solution or concentrate , use 100% (if the percentage is that solution) or 0% (if the percentage is another solution).

Let’s do the math (use substitution )!

$ \displaystyle \begin{array}{c}x\,\,+\,\,y=10\\.01x+.035y=10(.02)\end{array}$          $ \displaystyle \begin{array}{c}\,y=10-x\\.01x+.035(10-x)=.2\\.01x\,+\,.35\,\,-\,.035x=.2\\\,-.025x=-.15;\,\,\,\,\,x=6\\\,y=10-6=4\end{array}$

We would need 6 liters of the 1% milk, and 4 liters of the 3.5% milk.

Here’s another mixture problem:

$ \displaystyle \begin{array}{c}x+y=50\\8x+4y=50\left( {6.4} \right)\end{array}$                   $ \displaystyle \begin{array}{c}y=50-x\\8x+4\left( {50-x} \right)=320\\8x+200-4x=320\\4x=120\,;\,\,\,\,x=30\\y=50-30=20\\8x+4y=50(6.4)\end{array}$

We would need 30 pounds of the $8 coffee bean, and 20 pounds of the $4 coffee bean. See how similar this problem is to the one where we use percentages?

Distance Word Problem:

Here’s a distance word problem using systems ; distance problems have to do with an object’s speed, time, and distance. Note that, as well as the distance word problem here in the Algebra Word Problems section , there’s an example of a Parametric Distance Problem here in the Parametric Equations section .

Which Plumber Problem

Many word problems you’ll have to solve have to do with an initial charge or setup charge, and a charge or rate per time period. In these cases, the initial charge will be the $ \boldsymbol {y}$ -intercept , and the  rate will be the slope . Here is an example:

Geometry Word Problem:

Many times, we’ll have a geometry problem as an algebra word problem; these might involve perimeter, area, or sometimes angle measurements (so don’t forget these things!). Let’s do one involving angle measurements.

See – these are getting easier! Here’s one that’s a little tricky though:

Work Problem : 

Let’s do a “ work problem ” that is typically seen when studying Rational Equations (fraction with variables in them) and can be found here in the Rational Functions, E quations and Inequalities  section .

Note that there’s also a simpler version of this problem here in the Direct, Inverse, Joint and Combined Variation section .

Three Variable Word Problem:

Let’s do one more with three equations and three unknowns:

The “Candy” Problem

Sometimes we get lucky and can solve a system of equations where we have more unknowns (variables) then equations. (Actually, I think it’s not so much luck, but having good problem writers!) Here’s one like that:

There are more Systems Word Problems in the  Matrices and Solving Systems with Matrices section , Linear Programming section , and Right Triangle Trigonometry section .

Understand these problems, and practice, practice, practice!

For Practice : Use the Mathway  widget below to try a  Systems of Equations  problem. Click on Submit (the blue arrow to the right of the problem) and click on Solve by Substitution or Solve by Addition/Elimination  to see the answer .

You can also type in your own problem, or click on the three dots in the upper right hand corner and click on “Examples” to drill down by topic.

If you click on Tap to view steps , or Click Here , you can register at Mathway for a free trial , and then upgrade to a paid subscription at any time (to get any type of math problem solved!).

On to Algebraic Functions, including Domain and Range   – you’re ready! 

4.4 Solve Systems of Equations with Three Variables

Learning objectives.

By the end of this section, you will be able to:

• Determine whether an ordered triple is a solution of a system of three linear equations with three variables
• Solve a system of linear equations with three variables
• Solve applications using systems of linear equations with three variables

Be Prepared 4.10

Before you get started, take this readiness quiz.

Evaluate 5 x − 2 y + 3 z 5 x − 2 y + 3 z when x = −2 , x = −2 , y = −4 , y = −4 , and z = 3 . z = 3 . If you missed this problem, review Example 1.21 .

Be Prepared 4.11

Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. { − 2 x + y = −11 x + 3 y = 9 . { − 2 x + y = −11 x + 3 y = 9 . If you missed this problem, review Example 2.6 .

Be Prepared 4.12

Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. { 7 x + 8 y = 4 3 x − 5 y = 27 . { 7 x + 8 y = 4 3 x − 5 y = 27 . If you missed this problem, review Example 2.8 .

Determine Whether an Ordered Triple is a Solution of a System of Three Linear Equations with Three Variables

In this section, we will extend our work of solving a system of linear equations. So far we have worked with systems of equations with two equations and two variables. Now we will work with systems of three equations with three variables. But first let's review what we already know about solving equations and systems involving up to two variables.

We learned earlier that the graph of a linear equation , a x + b y = c , a x + b y = c , is a line. Each point on the line, an ordered pair ( x , y ) , ( x , y ) , is a solution to the equation. For a system of two equations with two variables, we graph two lines. Then we can see that all the points that are solutions to each equation form a line. And, by finding what the lines have in common, we’ll find the solution to the system.

Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions

We know when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.

Similarly, for a linear equation with three variables a x + b y + c z = d , a x + b y + c z = d , every solution to the equation is an ordered triple, ( x , y , z ) ( x , y , z ) , that makes the equation true.

Linear Equation in Three Variables

A linear equation with three variables, where a, b, c, and d are real numbers and a, b , and c are not all 0, is of the form

Every solution to the equation is an ordered triple, ( x , y , z ) ( x , y , z ) that makes the equation true.

All the points that are solutions to one equation form a plane in three-dimensional space. And, by finding what the planes have in common, we’ll find the solution to the system.

When we solve a system of three linear equations represented by a graph of three planes in space, there are three possible cases.

To solve a system of three linear equations, we want to find the values of the variables that are solutions to all three equations. In other words, we are looking for the ordered triple ( x , y , z ) ( x , y , z ) that makes all three equations true. These are called the solutions of the system of three linear equations with three variables .

Solutions of a System of Linear Equations with Three Variables

Solutions of a system of equations are the values of the variables that make all the equations true. A solution is represented by an ordered triple ( x , y , z ) . ( x , y , z ) .

To determine if an ordered triple is a solution to a system of three equations, we substitute the values of the variables into each equation. If the ordered triple makes all three equations true, it is a solution to the system.

Example 4.31

Determine whether the ordered triple is a solution to the system: { x − y + z = 2 2 x − y − z = −6 2 x + 2 y + z = −3 . { x − y + z = 2 2 x − y − z = −6 2 x + 2 y + z = −3 .

ⓐ ( −2 , −1 , 3 ) ( −2 , −1 , 3 ) ⓑ ( −4 , −3 , 4 ) ( −4 , −3 , 4 )

Try It 4.61

Determine whether the ordered triple is a solution to the system: { 3 x + y + z = 2 x + 2 y + z = −3 3 x + y + 2 z = 4 . { 3 x + y + z = 2 x + 2 y + z = −3 3 x + y + 2 z = 4 .

ⓐ ( 1 , −3 , 2 ) ( 1 , −3 , 2 ) ⓑ ( 4 , −1 , −5 ) ( 4 , −1 , −5 )

Try It 4.62

Determine whether the ordered triple is a solution to the system: { x − 3 y + z = −5 − 3 x − y − z = 1 2 x − 2 y + 3 z = 1 . { x − 3 y + z = −5 − 3 x − y − z = 1 2 x − 2 y + 3 z = 1 .

ⓐ ( 2 , −2 , 3 ) ( 2 , −2 , 3 ) ⓑ ( −2 , 2 , 3 ) ( −2 , 2 , 3 )

Solve a System of Linear Equations with Three Variables

To solve a system of linear equations with three variables, we basically use the same techniques we used with systems that had two variables. We start with two pairs of equations and in each pair we eliminate the same variable. This will then give us a system of equations with only two variables and then we know how to solve that system!

Next, we use the values of the two variables we just found to go back to the original equation and find the third variable. We write our answer as an ordered triple and then check our results.

Example 4.32

How to solve a system of equations with three variables by elimination.

Solve the system by elimination: { x − 2 y + z = 3 2 x + y + z = 4 3 x + 4 y + 3 z = −1 . { x − 2 y + z = 3 2 x + y + z = 4 3 x + 4 y + 3 z = −1 .

Try It 4.63

Solve the system by elimination: { 3 x + y − z = 2 2 x − 3 y − 2 z = 1 4 x − y − 3 z = 0 . { 3 x + y − z = 2 2 x − 3 y − 2 z = 1 4 x − y − 3 z = 0 .

Try It 4.64

Solve the system by elimination: { 4 x + y + z = −1 − 2 x − 2 y + z = 2 2 x + 3 y − z = 1 . { 4 x + y + z = −1 − 2 x − 2 y + z = 2 2 x + 3 y − z = 1 .

The steps are summarized here.

Solve a system of linear equations with three variables.

• If any coefficients are fractions, clear them.
• Decide which variable you will eliminate.
• Work with a pair of equations to eliminate the chosen variable.
• Multiply one or both equations so that the coefficients of that variable are opposites.
• Add the equations resulting from Step 2 to eliminate one variable
• Step 3. Repeat Step 2 using two other equations and eliminate the same variable as in Step 2.
• Step 4. The two new equations form a system of two equations with two variables. Solve this system.
• Step 5. Use the values of the two variables found in Step 4 to find the third variable.
• Step 6. Write the solution as an ordered triple.
• Step 7. Check that the ordered triple is a solution to all three original equations.

Example 4.33

Solve: { 3 x − 4 z = 0 3 y + 2 z = −3 2 x + 3 y = −5 . { 3 x − 4 z = 0 3 y + 2 z = −3 2 x + 3 y = −5 .

We can eliminate z z from equations (1) and (2) by multiplying equation (2) by 2 and then adding the resulting equations.

Notice that equations (3) and (4) both have the variables x x and y y . We will solve this new system for x x and y y .

To solve for y , we substitute x = −4 x = −4 into equation (3).

We now have x = −4 x = −4 and y = 1 . y = 1 . We need to solve for z . We can substitute x = −4 x = −4 into equation (1) to find z .

We write the solution as an ordered triple. ( −4 , 1 , −3 ) ( −4 , 1 , −3 )

We check that the solution makes all three equations true.

3 x − 4 z = 0 ( 1 ) 3 ( −4 ) − 4 ( −3 ) = ? 0 0 = 0 ✓ 3 y + 2 z = −3 ( 2 ) 3 ( 1 ) + 2 ( −3 ) = ? − 3 −3 = −3 ✓ 2 x + 3 y = −5 ( 3 ) 2 ( −4 ) + 3 ( 1 ) = ? − 5 −5 = −5 ✓ The solution is ( −4 , 1 , −3 ) . 3 x − 4 z = 0 ( 1 ) 3 ( −4 ) − 4 ( −3 ) = ? 0 0 = 0 ✓ 3 y + 2 z = −3 ( 2 ) 3 ( 1 ) + 2 ( −3 ) = ? − 3 −3 = −3 ✓ 2 x + 3 y = −5 ( 3 ) 2 ( −4 ) + 3 ( 1 ) = ? − 5 −5 = −5 ✓ The solution is ( −4 , 1 , −3 ) .

Try It 4.65

Solve: { 3 x − 4 z = −1 2 y + 3 z = 2 2 x + 3 y = 6 . { 3 x − 4 z = −1 2 y + 3 z = 2 2 x + 3 y = 6 .

Try It 4.66

Solve: { 4 x − 3 z = −5 3 y + 2 z = 7 3 x + 4 y = 6 . { 4 x − 3 z = −5 3 y + 2 z = 7 3 x + 4 y = 6 .

When we solve a system and end up with no variables and a false statement, we know there are no solutions and that the system is inconsistent. The next example shows a system of equations that is inconsistent.

Example 4.34

Solve the system of equations: { x + 2 y − 3 z = −1 x − 3 y + z = 1 2 x − y − 2 z = 2 . { x + 2 y − 3 z = −1 x − 3 y + z = 1 2 x − y − 2 z = 2 .

Use equation (1) and (2) to eliminate z .

Use (2) and (3) to eliminate z z again.

Use (4) and (5) to eliminate a variable.

There is no solution.

We are left with a false statement and this tells us the system is inconsistent and has no solution.

Try It 4.67

Solve the system of equations: { x + 2 y + 6 z = 5 − x + y − 2 z = 3 x − 4 y − 2 z = 1 . { x + 2 y + 6 z = 5 − x + y − 2 z = 3 x − 4 y − 2 z = 1 .

Try It 4.68

Solve the system of equations: { 2 x − 2 y + 3 z = 6 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 . { 2 x − 2 y + 3 z = 6 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 .

When we solve a system and end up with no variables but a true statement, we know there are infinitely many solutions. The system is consistent with dependent equations. Our solution will show how two of the variables depend on the third.

Example 4.35

Solve the system of equations: { x + 2 y − z = 1 2 x + 7 y + 4 z = 11 x + 3 y + z = 4 . { x + 2 y − z = 1 2 x + 7 y + 4 z = 11 x + 3 y + z = 4 .

Use equation (1) and (3) to eliminate x .

Use equation (1) and (2) to eliminate x again.

Use equation (4) and (5) to eliminate y y .

The true statement 0 = 0 0 = 0 tells us that this is a dependent system that has infinitely many solutions. The solutions are of the form ( x , y , z ) ( x , y , z ) where x = 5 z − 5 ; y = −2 z + 3 x = 5 z − 5 ; y = −2 z + 3 and z is any real number.

Try It 4.69

Solve the system by equations: { x + y − z = 0 2 x + 4 y − 2 z = 6 3 x + 6 y − 3 z = 9 . { x + y − z = 0 2 x + 4 y − 2 z = 6 3 x + 6 y − 3 z = 9 .

Try It 4.70

Solve the system by equations: { x − y − z = 1 − x + 2 y − 3 z = −4 3 x − 2 y − 7 z = 0 . { x − y − z = 1 − x + 2 y − 3 z = −4 3 x − 2 y − 7 z = 0 .

Solve Applications using Systems of Linear Equations with Three Variables

Applications that are modeled by a systems of equations can be solved using the same techniques we used to solve the systems. Many of the application are just extensions to three variables of the types we have solved earlier.

Example 4.36

The community college theater department sold three kinds of tickets to its latest play production. The adult tickets sold for $15, the student tickets for $10 and the child tickets for $8. The theater department was thrilled to have sold 250 tickets and brought in $2,825 in one night. The number of student tickets sold is twice the number of adult tickets sold. How many of each type did the department sell?

Try It 4.71

The community college fine arts department sold three kinds of tickets to its latest dance presentation. The adult tickets sold for $20, the student tickets for $12 and the child tickets for $10.The fine arts department was thrilled to have sold 350 tickets and brought in $4,650 in one night. The number of child tickets sold is the same as the number of adult tickets sold. How many of each type did the department sell?

Try It 4.72

The community college soccer team sold three kinds of tickets to its latest game. The adult tickets sold for $10, the student tickets for $8 and the child tickets for $5. The soccer team was thrilled to have sold 600 tickets and brought in $4,900 for one game. The number of adult tickets is twice the number of child tickets. How many of each type did the soccer team sell?

Access this online resource for additional instruction and practice with solving a linear system in three variables with no or infinite solutions.

• Solving a Linear System in Three Variables with No or Infinite Solutions
• 3 Variable Application

Section 4.4 Exercises

Practice makes perfect.

In the following exercises, determine whether the ordered triple is a solution to the system.

{ 2 x − 6 y + z = 3 3 x − 4 y − 3 z = 2 2 x + 3 y − 2 z = 3 { 2 x − 6 y + z = 3 3 x − 4 y − 3 z = 2 2 x + 3 y − 2 z = 3

ⓐ ( 3 , 1 , 3 ) ( 3 , 1 , 3 ) ⓑ ( 4 , 3 , 7 ) ( 4 , 3 , 7 )

{ − 3 x + y + z = −4 − x + 2 y − 2 z = 1 2 x − y − z = −1 { − 3 x + y + z = −4 − x + 2 y − 2 z = 1 2 x − y − z = −1

ⓐ ( −5 , −7 , 4 ) ( −5 , −7 , 4 ) ⓑ ( 5 , 7 , 4 ) ( 5 , 7 , 4 )

{ y − 10 z = −8 2 x − y = 2 x − 5 z = 3 { y − 10 z = −8 2 x − y = 2 x − 5 z = 3

ⓐ ( 7 , 12 , 2 ) ( 7 , 12 , 2 ) ⓑ ( 2 , 2 , 1 ) ( 2 , 2 , 1 )

{ x + 3 y − z = 15 y = 2 3 x − 2 x − 3 y + z = −2 { x + 3 y − z = 15 y = 2 3 x − 2 x − 3 y + z = −2

ⓐ ( −6 , 5 , 1 2 ) ( −6 , 5 , 1 2 ) ⓑ ( 5 , 4 3 , −3 ) ( 5 , 4 3 , −3 )

In the following exercises, solve the system of equations.

{ 5 x + 2 y + z = 5 − 3 x − y + 2 z = 6 2 x + 3 y − 3 z = 5 { 5 x + 2 y + z = 5 − 3 x − y + 2 z = 6 2 x + 3 y − 3 z = 5

{ 6 x − 5 y + 2 z = 3 2 x + y − 4 z = 5 3 x − 3 y + z = −1 { 6 x − 5 y + 2 z = 3 2 x + y − 4 z = 5 3 x − 3 y + z = −1

{ 2 x − 5 y + 3 z = 8 3 x − y + 4 z = 7 x + 3 y + 2 z = −3 { 2 x − 5 y + 3 z = 8 3 x − y + 4 z = 7 x + 3 y + 2 z = −3

{ 5 x − 3 y + 2 z = −5 2 x − y − z = 4 3 x − 2 y + 2 z = −7 { 5 x − 3 y + 2 z = −5 2 x − y − z = 4 3 x − 2 y + 2 z = −7

{ 3 x − 5 y + 4 z = 5 5 x + 2 y + z = 0 2 x + 3 y − 2 z = 3 { 3 x − 5 y + 4 z = 5 5 x + 2 y + z = 0 2 x + 3 y − 2 z = 3

{ 4 x − 3 y + z = 7 2 x − 5 y − 4 z = 3 3 x − 2 y − 2 z = −7 { 4 x − 3 y + z = 7 2 x − 5 y − 4 z = 3 3 x − 2 y − 2 z = −7

{ 3 x + 8 y + 2 z = −5 2 x + 5 y − 3 z = 0 x + 2 y − 2 z = −1 { 3 x + 8 y + 2 z = −5 2 x + 5 y − 3 z = 0 x + 2 y − 2 z = −1

{ 11 x + 9 y + 2 z = −9 7 x + 5 y + 3 z = −7 4 x + 3 y + z = −3 { 11 x + 9 y + 2 z = −9 7 x + 5 y + 3 z = −7 4 x + 3 y + z = −3

{ 1 3 x − y − z = 1 x + 5 2 y + z = −2 2 x + 2 y + 1 2 z = −4 { 1 3 x − y − z = 1 x + 5 2 y + z = −2 2 x + 2 y + 1 2 z = −4

{ x + 1 2 y + 1 2 z = 0 1 5 x − 1 5 y + z = 0 1 3 x − 1 3 y + 2 z = −1 { x + 1 2 y + 1 2 z = 0 1 5 x − 1 5 y + z = 0 1 3 x − 1 3 y + 2 z = −1

{ x + 1 3 y − 2 z = −1 1 3 x + y + 1 2 z = 0 1 2 x + 1 3 y − 1 2 z = −1 { x + 1 3 y − 2 z = −1 1 3 x + y + 1 2 z = 0 1 2 x + 1 3 y − 1 2 z = −1

{ 1 3 x − y + 1 2 z = 4 2 3 x + 5 2 y − 4 z = 0 x − 1 2 y + 3 2 z = 2 { 1 3 x − y + 1 2 z = 4 2 3 x + 5 2 y − 4 z = 0 x − 1 2 y + 3 2 z = 2

{ x + 2 z = 0 4 y + 3 z = −2 2 x − 5 y = 3 { x + 2 z = 0 4 y + 3 z = −2 2 x − 5 y = 3

{ 2 x + 5 y = 4 3 y − z = 3 4 x + 3 z = −3 { 2 x + 5 y = 4 3 y − z = 3 4 x + 3 z = −3

{ 2 y + 3 z = −1 5 x + 3 y = −6 7 x + z = 1 { 2 y + 3 z = −1 5 x + 3 y = −6 7 x + z = 1

{ 3 x − z = −3 5 y + 2 z = −6 4 x + 3 y = −8 { 3 x − z = −3 5 y + 2 z = −6 4 x + 3 y = −8

{ 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 2 x − 2 y + 3 z = 6 { 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 2 x − 2 y + 3 z = 6

{ x − 2 y + 2 z = 1 − 2 x + y − z = 2 x − y + z = 5 { x − 2 y + 2 z = 1 − 2 x + y − z = 2 x − y + z = 5

{ 2 x + 3 y + z = 12 x + y + z = 9 3 x + 4 y + 2 z = 20 { 2 x + 3 y + z = 12 x + y + z = 9 3 x + 4 y + 2 z = 20

{ x + 4 y + z = −8 4 x − y + 3 z = 9 2 x + 7 y + z = 0 { x + 4 y + z = −8 4 x − y + 3 z = 9 2 x + 7 y + z = 0

{ x + 2 y + z = 4 x + y − 2 z = 3 − 2 x − 3 y + z = −7 { x + 2 y + z = 4 x + y − 2 z = 3 − 2 x − 3 y + z = −7

{ x + y − 2 z = 3 − 2 x − 3 y + z = −7 x + 2 y + z = 4 { x + y − 2 z = 3 − 2 x − 3 y + z = −7 x + 2 y + z = 4

{ x + y − 3 z = −1 y − z = 0 − x + 2 y = 1 { x + y − 3 z = −1 y − z = 0 − x + 2 y = 1

{ x − 2 y + 3 z = 1 x + y − 3 z = 7 3 x − 4 y + 5 z = 7 { x − 2 y + 3 z = 1 x + y − 3 z = 7 3 x − 4 y + 5 z = 7

In the following exercises, solve the given problem.

The sum of the measures of the angles of a triangle is 180. The sum of the measures of the second and third angles is twice the measure of the first angle. The third angle is twelve more than the second. Find the measures of the three angles.

The sum of the measures of the angles of a triangle is 180. The sum of the measures of the second and third angles is three times the measure of the first angle. The third angle is fifteen more than the second. Find the measures of the three angles.

After watching a major musical production at the theater, the patrons can purchase souvenirs. If a family purchases 4 t-shirts, the video, and 1 stuffed animal, their total is $135.

A couple buys 2 t-shirts, the video, and 3 stuffed animals for their nieces and spends $115. Another couple buys 2 t-shirts, the video, and 1 stuffed animal and their total is $85. What is the cost of each item?

The church youth group is selling snacks to raise money to attend their convention. Amy sold 2 pounds of candy, 3 boxes of cookies and 1 can of popcorn for a total sales of $65. Brian sold 4 pounds of candy, 6 boxes of cookies and 3 cans of popcorn for a total sales of $140. Paulina sold 8 pounds of candy, 8 boxes of cookies and 5 cans of popcorn for a total sales of $250. What is the cost of each item?

Writing Exercises

In your own words explain the steps to solve a system of linear equations with three variables by elimination.

How can you tell when a system of three linear equations with three variables has no solution? Infinitely many solutions?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/4-4-solve-systems-of-equations-with-three-variables

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Systems of Linear Equations

A linear equation is not always in the form y = 3.5 − 0.5x ,

It can also be like y = 0.5(7 − x)

Or like y + 0.5x = 3.5

Or like y + 0.5x − 3.5 = 0 and more.

(Note: those are all the same linear equation!)

A System of Linear Equations is when we have two or more linear equations working together.

Example: Here are two linear equations:

Together they are a system of linear equations.

Can you discover the values of x and y yourself? (Just have a go, play with them a bit.)

Let's try to build and solve a real world example:

Example: You versus Horse

It's a race!

You can run 0.2 km every minute.

The Horse can run 0.5 km every minute. But it takes 6 minutes to saddle the horse.

How far can you get before the horse catches you?

We can make two equations ( d =distance in km, t =time in minutes)

• You run at 0.2km every minute, so d = 0.2t
• The horse runs at 0.5 km per minute, but we take 6 off its time: d = 0.5(t−6)

So we have a system of equations (that are linear ):

• d = 0.5(t−6)

We can solve it on a graph:

Do you see how the horse starts at 6 minutes, but then runs faster?

It seems you get caught after 10 minutes ... you only got 2 km away.

Run faster next time.

So now you know what a System of Linear Equations is.

Let us continue to find out more about them ....

There can be many ways to solve linear equations!

Let us see another example:

Example: Solve these two equations:

• −3x + y = 2

The two equations are shown on this graph:

Our task is to find where the two lines cross.

Well, we can see where they cross, so it is already solved graphically.

But now let's solve it using Algebra!

Hmmm ... how to solve this? There can be many ways! In this case both equations have "y" so let's try subtracting the whole second equation from the first:

Now let us simplify it:

So now we know the lines cross at x=1 .

And we can find the matching value of y using either of the two original equations (because we know they have the same value at x=1). Let's use the first one (you can try the second one yourself):

And the solution is:

x = 1 and y = 5

And the graph shows us we are right!

Linear Equations

Only simple variables are allowed in linear equations. No x 2 , y 3 , √x, etc :

Common Variables

Equations that "work together" share one or more variables:

A System of Equations has two or more equations in one or more variables

Many Variables

So a System of Equations could have many equations and many variables.

Example: 3 equations in 3 variables

There can be any combination:

• 2 equations in 3 variables,
• 6 equations in 4 variables,
• 9,000 equations in 567 variables,

When the number of equations is the same as the number of variables there is likely to be a solution. Not guaranteed, but likely.

In fact there are only three possible cases:

• No solution
• One solution
• Infinitely many solutions

When there is no solution the equations are called "inconsistent" .

One or infinitely many solutions are called "consistent"

Here is a diagram for 2 equations in 2 variables :

Independent

"Independent" means that each equation gives new information. Otherwise they are "Dependent" .

Also called "Linear Independence" and "Linear Dependence"

• 2x + 2y = 6

Those equations are "Dependent" , because they are really the same equation , just multiplied by 2.

So the second equation gave no new information .

Where the Equations are True

The trick is to find where all equations are true at the same time .

True? What does that mean?

The "you" line is true all along its length (but nowhere else).

Anywhere on that line d is equal to 0.2t

• at t=5 and d=1, the equation is true (Is d = 0.2t? Yes, as 1 = 0.2×5 is true)
• at t=5 and d=3, the equation is not true (Is d = 0.2t? No, as 3 = 0.2×5 is not true )

Likewise the "horse" line is also true all along its length (but nowhere else).

But only at the point where they cross (at t=10, d=2) are they both true .

So they have to be true simultaneously ...

... that is why some people call them "Simultaneous Linear Equations"

Solve Using Algebra

It is common to use Algebra to solve them.

Here is the "Horse" example solved using Algebra:

The system of equations is:

In this case it seems easiest to set them equal to each other:

d = 0.2t = 0.5(t−6)

Now we know when you get caught!

And our solution is:

t = 10 minutes and d = 2 km

Algebra vs Graphs

Why use Algebra when graphs are so easy? Because:

More than 2 variables can't be solved by a simple graph.

So Algebra comes to the rescue with two popular methods:

Solving By Substitution

Solving by elimination.

We will see each one, with examples in 2 variables, and in 3 variables. Here goes ...

These are the steps:

• Write one of the equations so it is in the style "variable = ..."
• Replace (i.e. substitute) that variable in the other equation(s).
• Solve the other equation(s)
• (Repeat as necessary)

Here is an example with 2 equations in 2 variables :

• 3x + 2y = 19

We can start with any equation and any variable .

Let's use the second equation and the variable "y" (it looks the simplest equation).

Write one of the equations so it is in the style "variable = ...":

We can subtract x from both sides of x + y = 8 to get y = 8 − x . Now our equations look like this:

Now replace "y" with "8 − x" in the other equation:

• 3x + 2 (8 − x) = 19

Solve using the usual algebra methods:

Expand 2(8−x) :

• 3x + 16 − 2x = 19

Then 3x−2x = x :

• x + 16 = 19

And lastly 19−16=3

Now we know what x is, we can put it in the y = 8 − x equation:

• y = 8 − 3 = 5

And the answer is:

x = 3 y = 5

Note: because there is a solution the equations are "consistent"

Check: why don't you check to see if x = 3 and y = 5 works in both equations?

Solving By Substitution: 3 equations in 3 variables

OK! Let's move to a longer example: 3 equations in 3 variables .

This is not hard to do... it just takes a long time !

• 2x + y + 3z = 15

We should line up the variables neatly, or we may lose track of what we are doing:

We can start with any equation and any variable. Let's use the first equation and the variable "x".

Now replace "x" with "6 − z" in the other equations:

(Luckily there is only one other equation with x in it)

2(6−z) + y + 3z = 15 simplifies to y + z = 3 :

Good. We have made some progress, but not there yet.

Now repeat the process , but just for the last 2 equations.

Let's choose the last equation and the variable z:

Now replace "z" with "3 − y" in the other equation:

−3y + (3−y) = 7 simplifies to −4y = 4 , or in other words y = −1

Almost Done!

Knowing that y = −1 we can calculate that z = 3−y = 4 :

And knowing that z = 4 we can calculate that x = 6−z = 2 :

x = 2 y = −1 z = 4

Check: please check this yourself.

We can use this method for 4 or more equations and variables... just do the same steps again and again until it is solved.

Conclusion: Substitution works nicely, but does take a long time to do.

Elimination can be faster ... but needs to be kept neat.

"Eliminate" means to remove : this method works by removing variables until there is just one left.

The idea is that we can safely :

• multiply an equation by a constant (except zero),
• add (or subtract) an equation on to another equation

Like in these two examples:

CAN we safely add equations to each other?

Yes, because we are "keeping the balance".

Imagine two really simple equations:

x − 5 = 3 5 = 5

We can add the "5 = 5" to "x − 5 = 3":

x − 5 + 5 = 3 + 5 x = 8

Try that yourself but use 5 = 3+2 as the 2nd equation

It works just fine, because both sides are equal (that is what the = is for)

We can also swap equations around, so the 1st could become the 2nd, etc, if that helps.

OK, time for a full example. Let's use the 2 equations in 2 variables example from before:

Very important to keep things neat:

Now ... our aim is to eliminate a variable from an equation.

First we see there is a "2y" and a "y", so let's work on that.

Multiply the second equation by 2:

Subtract the second equation from the first equation:

Yay! Now we know what x is!

Next we see the 2nd equation has "2x", so let's halve it, and then subtract "x":

Multiply the second equation by ½ (i.e. divide by 2):

Subtract the first equation from the second equation:

x = 3 and y = 5

And here is the graph:

The blue line is where 3x + 2y = 19 is true

The red line is where x + y = 8 is true

At x=3, y=5 (where the lines cross) they are both true. That is the answer.

Here is another example:

• 6x − 3y = 3

Lay it out neatly:

Multiply the first equation by 3:

0 − 0 = 9 ???

What is going on here?

Quite simply, there is no solution.

And lastly:

• 6x − 3y = 12

Well, that is actually TRUE! Zero does equal zero ...

... that is because they are really the same equation ...

... so there are an Infinite Number of Solutions

And so now we have seen an example of each of the three possible cases:

Solving By Elimination: 3 equations in 3 variables

Before we start on the next example, let's look at an improved way to do things.

Follow this method and we are less likely to make a mistake.

First of all, eliminate the variables in order :

• Eliminate x s first (from equation 2 and 3, in order)
• then eliminate y (from equation 3)

Start with:

Eliminate in this order:

We then have this "triangle shape":

Now start at the bottom and work back up (called "Back-Substitution") (put in z to find y , then z and y to find x ):

And we are solved:

ALSO, it is easier to do some of the calculations in our head, or on scratch paper, instead of always working within the set of equations:

• x + y + z = 6
• 2y + 5z = −4
• 2x + 5y − z = 27

Written neatly:

First, eliminate x from 2nd and 3rd equation.

There is no x in the 2nd equation ... move on to the 3rd equation:

Subtract 2 times the 1st equation from the 3rd equation (just do this in your head or on scratch paper):

And we get:

Next, eliminate y from 3rd equation.

We could subtract 1½ times the 2nd equation from the 3rd equation (because 1½ times 2 is 3) ...

... but we can avoid fractions if we:

• multiply the 3rd equation by 2 and
• multiply the 2nd equation by 3

and then do the subtraction ... like this:

And we end up with:

We now have that "triangle shape"!

Now go back up again "back-substituting":

We know z , so 2y+5z=−4 becomes 2y−10=−4 , then 2y=6 , so y=3 :

Then x+y+z=6 becomes x+3−2=6 , so x=6−3+2=5

x = 5 y = 3 z = −2

Please check this for yourself, it is good practice.

General Advice

Once you get used to the Elimination Method it becomes easier than Substitution, because you just follow the steps and the answers appear.

But sometimes Substitution can give a quicker result.

• Substitution is often easier for small cases (like 2 equations, or sometimes 3 equations)
• Elimination is easier for larger cases

And it always pays to look over the equations first, to see if there is an easy shortcut ... so experience helps ... so get experience!

Module 3: Systems of Equations and Inequalities

Applications of systems, learning outcomes, write a system of linear equations representing a mixture problem, solve the system and interpret the results.

• Write a system of linear equations representing a number problem
• Determine and apply an appropriate method for solving the system
• Specify what the variables in a cost/ revenue system of linear equations represent
• Write a system of inequalites that represents the profit region
• Interpret the solutions to a system of cost/ revenue equations and inequalities

One application of systems of equations are mixture problems. Mixture problems are ones where two different solutions are mixed together resulting in a new final solution.  A solution is a mixture of two or more different substances like water and salt or vinegar and oil.  Most biochemical reactions occur in liquid solutions, making them important for doctors, nurses, and researchers to understand.  There are many other disciplines that use solutions as well.

The concentration or strength of a liquid solution is often described  as a percentage.  This number comes from the ratio of how much mass is in a specific volume of liquid.  For example if you have 50 grams of salt in a 100mL of water you have a 50% salt solution based on the following ratio:

[latex]\frac{50\text{ grams }}{100\text{ mL }}=0.50\frac{\text{ grams }}{\text{ mL }}=50\text{ % }[/latex]

Solutions used for most purposes typically come in pre-made concentrations from manufacturers, so if you need a custom concentration, you would need to mix two different strengths.  In this section, we will practice writing equations that represent the outcome from mixing two different concentrations of solutions.

We will use the following table to help us solve mixture problems:

To demonstrate why the table is helpful in solving for unknown amounts or concentrations of a solution, consider two solutions that are mixed together, one is 120mL of a 9% solution, and the other is 75mL of a 23% solution. If we mix both of these solutions together we will have a new volume and a new mass of solute and with those we can find a new concentration.

First, find the total mass of solids for each solution by multiplying the volume by the concentration.

Next we add the new volumes and new masses.

Now we have used mathematical operations to describe the result of mixing two different solutions. We know the new volume, concentration and mass of solute in the new solution.  In the following examples, you will see that we can use the table to find an unknown final volume or concentration. These problems can have either one or two variables. We will start with one variable problems, then move to two variable problems.

A chemist has 70 mL of a 50% methane solution. How much of an 80% solution must she add so the final solution is 60% methane?

Let’s use the problem solving process outlined in Module 1 to help us work through a solution to the problem.

Read and Understand:  We are looking for a new amount – in this case a volume –  based on the words “how much”.  We know two starting  concentrations and the final concentration, as well as one volume.

Define and Translate:  Solution 1 is the 70 mL of 50% methane and solution 2 is the unknown amount with 80% methane.  We can call our unknown amount x.

Write and Solve:   Set up the mixture table. Remember that concentrations are written as decimals before we can perform mathematical operations on them.

Multiply amount by concentration to get total, be sure to distribute on the last row: [latex]\left(70 + x\right)0.6[/latex]Add the entries in the amount column to get final amount. The concentration for this amount is 0.6 because we want the final solution to be 60% methane.

Add the total mass for solution 1 and solution 2 to get the total mass for the 60% solution. This is our equation for finding the unknown volume.

[latex]35+0.8x=42+0.6x[/latex]

[latex]\begin{array}{c}35+0.8x=42+0.6x\\\underline{-0.6x}\,\,\,\,\,\,\,\underline{-0.6x}\\35+0.2x=42\\\end{array}[/latex]

Subtract 35 from both sides

[latex]\begin{array}{c}35+0.2x=42\\\underline{-35}\,\,\,\,\,\,\,\underline{-35}\\0.2x=7\end{array}[/latex]

Divide both sides by 0.2

[latex]\begin{array}{c}0.2x=7\\\frac{0.2x}{0.2}=\frac{7}{0.2}\end{array}[/latex] x=35

35mL must be added to the original 70 mL to gain a solution with a concentration of 60%

The above problem illustrates how we can use the mixture table to define an equation to solve for an unknown volume. In the next example we will start with two known concentrations and use a system of equations to find two starting volumes necessary to achieve a specified final concentration.

A farmer has two types of milk, one that is 24% butterfat and another which is 18% butterfat. How much of each should he use to end up with 42 gallons of 20% butterfat?

Read and Understand:  We are asked to find two starting volumes of milk whose concentrations of butterfat are both known. We also know the final volume is 42 gallons. There are two unknowns in this problem.

Define and Translate:  We will call the unknown volume of the  24% solution x, and the unknown volume of the 18% solution y.

Write and Solve:  Fill in the table with the information we know.

Find the total mass by multiplying the amount of each solution by the concentration. The total mass of the final solution comes from

When you sum the amount column you get one equation: x+ y = 42 When you sum the total column you get a second equation: 0.24x + 0.18y = 8.4

Use elimination to find a value for x, and y.

Multiply the first equation by -0.18

-0.18(x+y) = (42)(-0.18)

-0.18x – -0.18y = -7.56

Now our system of equations looks like this:

0.24x + 0.18y = 8.4

Adding the two equations together to eliminate the y terms gives this equation:

0.06x = 8.4

Divide by 0.06 on each side:

Now substitute the value for x into one of the equations in order to solve for y.

(14) + y = 42

This can be interpreted as 14 gallons of 24% butterfat milk added to 28 gallons of 18% butterfat milk will give 42 gallons of 20% butterfat milk.

In the following video you will be given an example of how to solve a mixture problem without using a table, and interpret the results.

Write a system of linear equations representing a value problem

Systems of equations are a very useful tool for modeling real-life situations and answering questions about them. If you can translate the application into two linear equations with two variables, then you have a system of equations that you can solve to find the solution. You can use any method to solve the system of equations.

One application of system of equations are known as value problems. Value problems are ones where each variable has a value attached to it. For example, the marketing team for an event venue wants to know how to focus their advertising based on who is attending specific events—children, or adults?  They know the cost of a ticket to a basketball game is $25.00 for children and $50.00 for adults. Additionally, on a certain day, attendance at the game is 2,000 and the total gate revenue is $70,000.  How can the marketing team use this information to find out whether to spend more money on advertising directed toward children or adults?

We will use a table to help us set up and solve this value problem. The basic structure of the table is shown below:

The first column in the table is used for the number of things we have. Quite often, this will be our variables. The second column is used for the value each item has. The third column is used for the total value which we calculate by multiplying the number by the value.

Find the total number of child and adult tickets sold given that the cost of a ticket to a basketball game is $25.00 for children and $50.00 for adults. Additionally, on a certain day, attendance at the game is 2,000 and the total gate revenue is $70,000.

Read and Understand: We want to find the number of child and adult tickets, we know the total number of tickets sold, the total revenue and the cost of a child and adult ticket.

Define and Translate:  Let c = the number of children and a = the number of adults in attendance.  Revenue comes from number of tickets sold multiplied by the price of the ticket.  We will get revenue for adults by multiplying $50.00 times a.  $25.00 times c will give the revenue from the number of child tickets sold.

Write and Solve:  We can use a table as we did in the mixture problems section to organize the information we have.  Although a table is not necessary, it can help you get started.  For this problem, we labeled columns as amount, value, and total revenue because that is the information we are given.

The total number of people is [latex]2,000[/latex].

The total revenue is $70,000. We can use this and the revenue from child and adult tickets to write an equation for the revenue.[latex]25c+50a=70,000[/latex]

The number of people at the game that day is the total number of child tickets sold plus the total number of adult tickets, [latex]c+a=2,000[/latex]

We now have a system of linear equations in two variables.[latex]\begin{array}{r}c+a=2,000\,\,\,\\ 25c+50a=70,000\end{array}[/latex].

We can use any method of solving systems of equations to solve this system for a and c.  Substitution looks easiest because we can  solve the first equation for either [latex]c[/latex] or [latex]a[/latex]. We will solve for [latex]a[/latex].

[latex]\begin{array}{c}c+a=2,000\\ a=2,000-c\end{array}[/latex]

Substitute the expression [latex]2,000-c[/latex] in the second equation for [latex]a[/latex] and solve for [latex]c[/latex].

[latex]\begin{array}{r} 25c+50\left(2,000-c\right)=70,000\,\,\,\, \\ 25c+100,000 - 50c=70,000\,\,\,\, \\ -25c=-30,000 \\ c=1,200\,\,\,\,\,\,\, \end{array}[/latex]

Substitute [latex]c=1,200[/latex] into the first equation to solve for [latex]a[/latex].

[latex]\begin{array}{r}1,200+a=2,000 \\ a=800\,\,\,\,\,\, \end{array}[/latex]

We find that [latex]1,200[/latex] children and [latex]800[/latex] adults bought tickets to the game that day. The marketing group may want to focus their advertising toward attracting young people.

This example showed you how to find two unknown values given information that connected the two unknowns. With two equations, you are able to find a solution for two unknowns.  If you were to have three unknowns, you would need three equations to find them, and so on.

In the following video, you are given an example of how to use a system of equations to find the number of children and adults admitted to an amusement park based on entrance fees and total revenue. This example shows how to write equations and solve the system without a table.

In the next example, we will find the number of coins in a change jar given the total amount of money in the jar and the fact that the coins are either quarters or dimes.

In a change jar there are 11 coins that have a value of S1.85. The coins are either quarters or dimes. How many of each kind of coin is in the jar?

Read and Understand:  We want to find the number of quarters and the number of dimes in the jar.  We know that dimes are $0.10 and quarters are $0.25, and the total number of coins is 11.

Define and Translate:  We will call the number of quarters q and the number of dimes d. The part of the total $1.85 that comes from quarters will be determined by how many quarters and the fact that each one is worth $0.25, so $0.25q represents the amount of $1.85 that is quarters.  The same idea can be used for dimes, so $0.10d represents the amount of $1.85 that is dimes.

Write and Solve: We can label a new table with the information we are given.

We can write our two equations, remember that we need two to solve for two unknowns.

 [latex]\begin{array}{r}q+d=11\,\,\,\\0.25q+0.10d=1.85\end{array}[/latex]

Substitution looks like the easiest path to a solution, solve for q.

[latex]\begin{array}{c}q+d=11\\ q=11-d\end{array}[/latex]

Substitute this into the other equation, and solve for d.

[latex]\begin{array}{r}0.25\left(11-d\right)+0.10d=1.85\,\,\,\, \\2.75-0.25d+0.10d=1.85\,\,\,\,\\ 2.75-0.15d=1.85\\-0.15d=-0.9\\\,\,\,\,\,\,\, d=6\end{array}[/latex]

Substitute [latex]d=6[/latex] into the first equation to solve for [latex]q[/latex].

[latex]\begin{array}{r}q+6=11 \\q=5\,\,\,\,\,\, \end{array}[/latex]

We have 6 dimes and 5 quarters.

In the following video, you will see an example similar to the previous one, except that the equations are written and solved without the use of a table.

Cost and Revenue Problems

A skateboard manufacturer introduces a new line of boards. The manufacturer tracks its costs, which is the amount it spends to produce the boards, and its revenue, which is the amount it earns through sales of its boards. How can the company determine if it is making a profit with its new line? How many skateboards must be produced and sold before a profit is possible?

Using what we have learned about systems of equations, we can answer these questions. The skateboard manufacturer’s revenue equation is the equation used to calculate the amount of money that comes into the business. It can be represented as [latex]y=xp[/latex], where [latex]x=[/latex] quantity and [latex]p=[/latex] price. The revenue equation is shown in orange in the graph below.

The cost equation is the equation used to calculate the costs of doing business. It includes fixed costs, such as rent and salaries, and variable costs, such as utilities. The cost equation is shown in blue in the graph below. The [latex]x[/latex] -axis represents quantity in hundreds of units. The y -axis represents both cost and revenue in hundreds of dollars. We won’t learn how to write a cost equation in this example, they will be given to you. If you take any business or economics courses, you will learn more about how to write a cost equation.

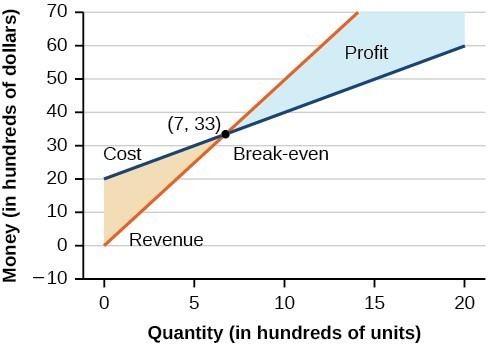
The point at which the two lines intersect is called the break-even point, we learned that this is the solution to the system of linear equations that in this case comprise the cost and revenue equations.

Read the axes of the graph carefully, note that quantity is in hundreds, and money is in thousands. The solution to the graphed system is (7, 33). This means that if 700 units are produced, the cost to make them is $3,300 and the revenue is also $3,300. In other words, the company breaks even if they produce and sell 700 units. They neither make money nor lose money.

The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The shaded region to the left represents quantities for which the company suffers a loss.

A business wants to manufacture bike frames. Before they start production, they need to make sure they can make a profit with the materials and labor force they have. Their accountant has given them a cost equation of [latex]y=0.85x+35,000[/latex] and a revenue equation of [latex]y=1.55x[/latex]:

• Interpret x and y for the cost equation
• Interpret x and y for the revenue equation

Cost: [latex]y=0.85x+35,000[/latex]

Revenue:[latex]y=1.55x[/latex]

The cost equation represents money leaving the company, namely how much it costs to produce a given number of bike frames. If we use the skateboard example as a model, x would represent the number of frames produced (instead of skateboards) and y would represent the amount of money it would cost to produce them (the same as the skateboard problem).

The revenue equation represents money coming into the company, so in this context x still represents the number of bike frames manufactured, and y now represents the amount of money made from selling them.  Let’s organize this information in a table:

Given the same cost and revenue equations from the previous example, find the break-even point for the bike manufacturer.  Interpret the solution with words.

Revenue: [latex]y=1.55x[/latex]

Read and Understand:  We want the break even point for this system that represents cost and revenue.  This means we want to find where the two lines cross, and we have learned a few different methods for doing this because this is the solution to the system of equations!  Substitution looks like the easiest method since the revenue equation is already solved for y, [latex]y=1.55x[/latex].

Define and Translate:  Write the system of equations.

[latex]\begin{array}{l}\\ y=0.85x+35,000\hfill \\ y=1.55x\hfill \end{array}\\[/latex]

Write and Solve:  The equations are already written for us, so we just need to solve the system using substitution.

Substitute the expression [latex]0.85x+35,000[/latex] from the first equation into the second equation and solve for [latex]x[/latex]. [latex]\begin{array}{r}0.85x+35,000=1.55x\\ 35,000=0.7x\,\,\,\\ 50,000=x\,\,\,\,\,\,\,\,\,\,\end{array}\\[/latex] Then, we substitute [latex]x=50,000[/latex] into either the cost equation or the revenue equation. [latex]1.55\left(50,000\right)=77,500\\[/latex] The break-even point is [latex]\left(50,000,77,500\right)[/latex].

Check and Interpret:

The solution to this system is[latex]\left(50,000,77,500\right)[/latex], but what does that mean? Think of a point as  [latex]\left(x,y)[/latex], where in this case x is the quantity of bikes manufactured and y is an amount of money. For our system y represents two different things and x represents one thing.  Refer to tehe table we made in the first example, shown below:

Let’s interpret the solution with respect to the Cost equation first. x = 50,000 and y = 77,500.  Using our table, we can translate this as “the cost for producing 50,000 bike frames is $75,500”.

In the same way, the Revenue equation can be interpreted as “the amount of money the company makes from selling 50,000 bike frames is $77,500”.

In the next example, you will see how the information you learned about systems of linear inequalities can be applied to answering questions about cost and revenue.  Below is a graph of the Cost/ Revenue system in the previous system:

Note how the blue shaded region between the Cost and Revenue equations is labeled Profit. This is the “sweet spot” that the company wants to achieve where they produce enough bike frames at a minimal enough cost to make money. They don’t want more money going out than coming in!

The following example shows how to write the system of linear equations as a system of linear inequalities whose solution set is the profit region for the system.

Define the profit region for the bike manufacturing business using inequalities, given the system of linear equations:

Read and Understand: We know that graphically,  solutions to linear inequalities are entire regions, and we learned how to graph systems of linear inequalities earlier in this module. Based on the graph below and the equations that define cost and revenue, we can use inequalities to define the region for which the bike manufacturer will make a profit.

Let’s start with the revenue equation.  We know that the break even point is at (50,000, 77,500) and the profit region is the blue area.  If we choose a point in the region and test it like we did for finding solution regions to inequalities, we will know which kind of inequality sign to use.

Let’s test the point [latex]\left(65,00,100,000\right)[/latex] in both equations to determine which inequality sign to use.

[latex]\begin{array}{l}y=0.85x+{35,000}\\{100,000}\text{ ? }0.85\left(65,000\right)+35,000\\100,000\text{ ? }90,250\end{array}[/latex]

We need to use > because 100,000 is greater than 90,250

The cost inequality that will ensure the company makes profit – not just break even – is [latex]y>0.85x+35,000[/latex]

Now test the point in the revenue equation:

[latex]\begin{array}{l}y=1.55x\\100,000\text{ ? }1.55\left(65,000\right)\\100,000\text{ ? }100,750\end{array}[/latex]

We need to use < because 100,000 is less than 100,750

The revenue inequality that will ensure the company makes profit – not just break even – is [latex]y<1.55x[/latex]

The systems of inequalities that defines the profit region for the bike manufacturer:

[latex]\begin{array}{l}y>0.85x+35,000\\y<1.55x\end{array}[/latex]

The cost to produce 50,000 units is $77,500, and the revenue from the sales of 50,000 units is also $77,500. To make a profit, the business must produce and sell more than 50,000 units. The system of linear inequalities that represents the number of units that the company must produce in order to earn a profit is:

In the following video you will see an example of how to find the break even point for a small sno-cone business.

In this section, we saw two examples of writing a system of two linear equations to find two unknowns that were related to each other.  In the first, the equations were related by the sum of the number of tickets bought and the sum of the total revenue brought in by the tickets sold.  In the second problem, the relationships were similar.  The two variables were related by the sum of the number of coins, and the total value of the coins.

We have seen that systems of linear equations and inequalities can help to define market behaviors that are very helpful to businesses.  The intersection of cost and revenue equations gives the break even point, and also helps define the region for which a company will make a profit.

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• System of Equations App: Break-Even Point. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/qey3FmE8saQ . License : CC BY: Attribution
• Ex: System of Equations Application - Mixture Problem. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/4s5MCqphpKo . License : CC BY: Attribution
• Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. Located at : http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/ . License : CC BY: Attribution
• College Algebra. Authored by : Jay Abrams, et al.. Provided by : OpenStax. Located at : https://openstaxcollege.org/textbooks/college-algebra. . License : CC BY: Attribution
• Beginning and Intermediate Algebra Textbook. Authored by : Tyler Wallace. Located at : http://www.wallace.ccfaculty.org/book/book.html . License : CC BY: Attribution
• College Algebra. Authored by : Abramson, Jay. Provided by : OpenStax. Located at : https://openstaxcollege.org/textbooks/college-algebra . License : CC BY: Attribution

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 6

• Age word problem: Imran
• Age word problem: Ben & William
• Age word problem: Arman & Diya
• Age word problems
• System of equations word problem: walk & ride

Systems of equations word problems

• System of equations word problem: no solution
• System of equations word problem: infinite solutions
• Systems of equations word problems (with zero and infinite solutions)
• Systems of equations with elimination: TV & DVD
• Systems of equations with elimination: apples and oranges
• Systems of equations with substitution: coins
• Systems of equations with elimination: coffee and croissants
• Systems of equations: FAQ
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x+y+z=25,\:5x+3y+2z=0,\:y-z=6
• x+2y=2x-5,\:x-y=3
• 5x+3y=7,\:3x-5y=-23
• x^2+y=5,\:x^2+y^2=7
• xy+x-4y=11,\:xy-x-4y=4
• 3-x^2=y,\:x+1=y
• xy=10,\:2x+y=1
• How do you solve a system of equations by substitution?
• To solve a system of equations by substitution, solve one of the equations for one of the variables, and substitute this expression into the other equation. Then, solve the resulting equation for the remaining variable and substitute this value back into the original equation to find the value of the other variable.
• How do you solve a system of equations by graphing?
• To solve a system of equations by graphing, graph both equations on the same set of axes and find the points at which the graphs intersect. Those points are the solutions.
• How do you solve a system of equations by elimination?
• To solve a system of equations by elimination, write the system of equations in standard form: ax + by = c, and multiply one or both of the equations by a constant so that the coefficients of one of the variables are opposite. Then, add or subtract the two equations to eliminate one of the variables. Solve the resulting equation for the remaining variable.
• What are the solving methods of a system of equations?
• There are several methods for solving a system of equations, including substitution, elimination, and graphing.
• What is a system of linear equations?
• A system of linear equations is a system of equations in which all the equations are linear and in the form ax + by = c, where a, b, and c are constants and x and y are variables.

system-of-equations-calculator

• High School Math Solutions – Systems of Equations Calculator, Nonlinear In a previous post, we learned about how to solve a system of linear equations. In this post, we will learn how...

Please add a message.

Message received. Thanks for the feedback.

Online Systems of Equations Solver

Solve equations and systems of equations with wolfram|alpha, a powerful tool for finding solutions to systems of equations and constraints.

Wolfram|Alpha is capable of solving a wide variety of systems of equations. It can solve systems of linear equations or systems involving nonlinear equations, and it can search specifically for integer solutions or solutions over another domain. Additionally, it can solve systems involving inequalities and more general constraints.

Learn more about:

• Systems of equations

Tips for entering queries

Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about solving systems of equations.

• solve y = 2x, y = x + 10
• solve system of equations {y = 2x, y = x + 10, 2x = 5y}
• y = x^2 - 2, y = 2 - x^2
• solve 4x - 3y + z = -10, 2x + y + 3z = 0, -x + 2y - 5z = 17
• solve system {x + 2y - z = 4, 2x + y + z = -2, z + 2y + z = 2}
• solve 4 = x^2 + y^2, 4 = (x - 2)^2 + (y - 2)^2
• x^2 + y^2 = 4, y = x
• View more examples

Access instant learning tools

Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator

• Step-by-step solutions
• Wolfram Problem Generator

What are systems of equations?

A system of equations is a set of one or more equations involving a number of variables..

The solutions to systems of equations are the variable mappings such that all component equations are satisfied—in other words, the locations at which all of these equations intersect. To solve a system is to find all such common solutions or points of intersection.

Systems of linear equations are a common and applicable subset of systems of equations. In the case of two variables, these systems can be thought of as lines drawn in two-dimensional space. If all lines converge to a common point, the system is said to be consistent and has a solution at this point of intersection. The system is said to be inconsistent otherwise, having no solutions. Systems of linear equations involving more than two variables work similarly, having either one solution, no solutions or infinite solutions (the latter in the case that all component equations are equivalent).

More general systems involving nonlinear functions are possible as well. These possess more complicated solution sets involving one, zero, infinite or any number of solutions, but work similarly to linear systems in that their solutions are the points satisfying all equations involved. Going further, more general systems of constraints are possible, such as ones that involve inequalities or have requirements that certain variables be integers.

Solving systems of equations is a very general and important idea, and one that is fundamental in many areas of mathematics, engineering and science.

Solving Systems of Equations Using Algebra Calculator

Example problem, how to solve the system of equations in algebra calculator.

• The first equation x+y=7
• Then a comma ,
• Then the second equation x+2y=11

Clickable Demo

More Examples

• Solve y=x+3, y=2x+1: y=x+3, y=2x+1
• Solve 2x+3y=5, x+y=4: 2x+3y=5, x+y=4

Related Articles

• Algebra Calculator Tutorial

A New Hybrid Algorithm for Multivariate Polynomial System Solving

• Original Research
• Published: 27 March 2024
• Volume 5 , article number  341 , ( 2024 )

Cite this article

• Debasish Roy   ORCID: orcid.org/0000-0002-1244-5950 1  

Explore all metrics

The method of solving a polynomial system of equations plays a crucial role in various domains of cryptography. For instance, multivariate cryptography using public keys relies on the computational difficulty of solving a multivariate polynomial problem over a finite field. Aram Harrow, Avinatan Hassidam, and Seth Loyd proposed a quantum algorithm (HHL) to solve the Equation Ax = b , where A is a Hermitian matrix. Compared to the fastest classical approach, which has an \(O(N \sqrt{\kappa })\) run time, the HHL algorithm has a poly \((\text {Log}N, \kappa )\) runtime that offers exponential speed-up. To solve a set of multivariate polynomial equations, we turned to the HHL method for assistance. In particular, our proposed algorithm will be a building block for future quantum XL algorithms. Here, we have proposed a new hybrid quantum XL algorithm and used it to solve a standard problem to demonstrate its efficacy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

An Efficient $$F_4$$ -style Based Algorithm to Solve MQ Problems

Extended Algorithm for Solving Underdefined Multivariate Quadratic Equations

Improving Thomae-Wolf Algorithm for Solving Underdetermined Multivariate Quadratic Polynomial Problem

Data availability.

The data that support the findings of this study are available from the corresponding author, [Debasish], upon reasonable request.

Adams WW, Loustaunau P. An introduction to Gröbner bases, vol. 3. American Mathematical Society; 2022.

Ambainis A. Variable time amplitude amplification and a faster quantum algorithm for solving systems of linear equations. 2010. arXiv:1010.4458 .

Bard GV, Courtois NT, Jefferson C. Efficient methods for conversion and solution of sparse systems of low-degree multivariate polynomials over gf (2) via sat-solvers. Cryptology ePrint Archive. 2007.

Bard G. Algebraic cryptanalysis. Springer, New York; 2009. https://doi.org/10.1007/978-0-387-88757-9 .

Bouillaguet C, Chen HC, Cheng CM, Chou T, Niederhagen R, Shamir A, Yang BY. Fast exhaustive search for polynomial systems in. In: International workshop on cryptographic hardware and embedded systems. Springer. 2010. pp. 203–18.

Buchberger B, Winkler F. Gröbner bases and applications, vol. 251. Cambridge: Cambridge University Press; 1998.

Book   Google Scholar  

Chen YA, Gao XS. Quantum algorithms for boolean equation solving and quantum algebraic attack on cryptosystems. 2018.

Childs AM, Kothari R. Limitations on the simulation of non-sparse Hamiltonians. 2009. arXiv:0908.4398 .

Childs AM, Kothari R, Somma RD. Quantum algorithm for systems of linear equations with exponentially improved dependence on precision. SIAM J Comput. 2017;46(6):1920–50.

Article   MathSciNet   Google Scholar  

Courtois N. The security of cryptographic primitives based on multivariate algebraic problems: Mq, Minrank, Ip, Hfe. Paris: Paris 6 University; 2001.

Courtois N, Klimov A, Patarin J, Shamir A. Efficient algorithms for solving overdefined systems of multivariate polynomial equations. In: Preneel B, editor. Advances in cryptology—EUROCRYPT 2000. Berlin: Springer; 2000. pp. 392–407.

Courtois NT, Patarin J. About the xl algorithm over gf (2). In: Topics in cryptology-CT-RSA 2003: the cryptographers’ track at the RSA conference 2003 San Francisco, CA, USA, April 13–17, 2003 Proceedings. Springer; 2003. pp. 141–57.

Diem C. The xl-algorithm and a conjecture from commutative algebra. In: Advances in cryptology-ASIACRYPT 2004: 10th international conference on the theory and application of cryptology and information security, Jeju Island, Korea, December 5–9, 2004. Proceedings 10. Springer; 2004. pp. 323–37.

Ding J, Gheorghiu V, Gilyén A, Hallgren S, Li J. Limitations of the Macaulay matrix approach for using the hhl algorithm to solve multivariate polynomial systems. Quantum. 2023;7:1069. https://doi.org/10.22331/q-2023-07-26-1069 .

Article   Google Scholar  

Grover LK. A fast quantum mechanical algorithm for database search. 1996.

Harrow AW, Hassidim A, Lloyd S. Quantum algorithm for linear systems of equations. Phys Rev Lett. 2009;103(15): 150502.

Lee Y, Joo J, Lee S. Hybrid quantum linear equation algorithm and its experimental test on ibm quantum experience. Sci Rep. 2019;9(1):4778.

Livingston WP, Blok MS, Flurin E, Dressel J, Jordan AN, Siddiqi I. Experimental demonstration of continuous quantum error correction. Nat Commun. 2022;13(1):2307.

Moh T. On the method of “xl’’ and its inefficiency to ttm. IACR Cryptol ePrint Arch. 2001;2001:47.

Google Scholar  

Preskill J. Quantum computing in the nisq era and beyond. Quantum. 2018;2:79.

Shor PW. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J Comput. 1997;26(5):1484–509. https://doi.org/10.1137/s0097539795293172 .

Xiao L. Applicability of xsl attacks to block ciphers. Electron Lett. 2003;39(25):1.

Zhang M, Dong L, Zeng Y, Cao N. Circuit implementation of the globally optimized hhl algorithm and experiments on qiskit. Researchsquare. 2022. https://doi.org/10.21203/rs.3.rs-1505699/v1 .

Download references

Author information

Authors and affiliations.

IIT, Kharagpur, India

Debasish Roy

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Debasish Roy .

Ethics declarations

Conflict of interest.

The author Debasish Roy declares that he has no conflict of interest.

Ethical approval

This article does not contain any studies with animals performed by the author. This article does not contain any studies with human participants or animals performed by the author.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This article is part of the topical collection “Security and Privacy 2020” guest edited by Pantelimon Stanica, Odelu Vanga and Sumit Kumar Debnath.

Appendix: Experimental Results

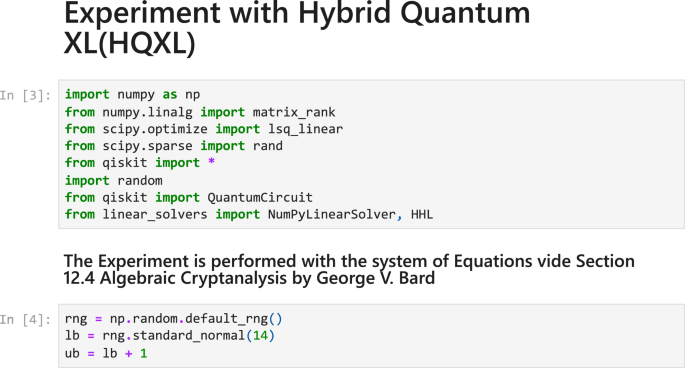
Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Roy, D. A New Hybrid Algorithm for Multivariate Polynomial System Solving. SN COMPUT. SCI. 5 , 341 (2024). https://doi.org/10.1007/s42979-024-02645-3

Download citation

Received : 19 December 2023

Accepted : 20 January 2024

Published : 27 March 2024

DOI : https://doi.org/10.1007/s42979-024-02645-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Quantum algorithms
• Quantum computation
• HHL algorithm
• XL algorithm

Advertisement

• Find a journal
• Publish with us
• Track your research

ORIGINAL RESEARCH article

Numerical modeling of mixed convective nanofluid flow with fractal stochastic heat and mass transfer using finite differences provisionally accepted.

• 1 Air University, Pakistan
• 2 Prince Sultan University, Saudi Arabia

The final, formatted version of the article will be published soon.

This study presents the first comprehensive numerical simulation of heat and mass transfer in fractal-like mixed convective nanofluid flows. The flow of non-Newtonian nanofluids over flat and oscillating sheets is modelled mathematically, and a finite difference scheme is used to solve this model. The two-stage scheme can tackle fractal and fractal stochastic mathematical models of partial differential equations. The consistency in the mean square is proved, and Fourier series stability analysis is adopted to find stability conditions for fractal stochastic partial differential equation. The scheme is applied to solve the unsteady Casson nanofluid flow over the flat and oscillatory sheet, which affects thermal radiation, heat source, and chemical reaction. The existence of the solution is also provided for the Navier-Stokes equation of the considered flow model using fractal time derivative. The graph illustrates that the proposed fractal technique achieves faster convergence than the Crank-Nicolson approach. Applications in energy systems, materials science, and environmental engineering are just a few of the domains that could benefit from a better understanding of mixed convective nanofluid flows with fractal features, and that is what this research study hopes to accomplish. Scientists and engineers may better develop efficient and environmentally friendly systems by simulating and analyzing these complicated processes with the suggested finite difference technique.

Keywords: Fractal Stochastic Scheme, Consistency in Mean Square Sense, heat and mass transfer, Existence of solution, stability

Received: 19 Jan 2024; Accepted: 02 Apr 2024.

Copyright: © 2024 Arif, Abodayeh and Nawaz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

* Correspondence: Dr. Muhammad Shoaib Arif, Air University, Islamabad, Pakistan

People also looked at