problem solving with algebraic fractions

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Algebraic Fractions

Here we will learn about algebraic fractions , including operations with fractions, and solving linear and quadratic equations written in the form of algebraic fractions.

There are also algebraic fractions worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are algebraic fractions?

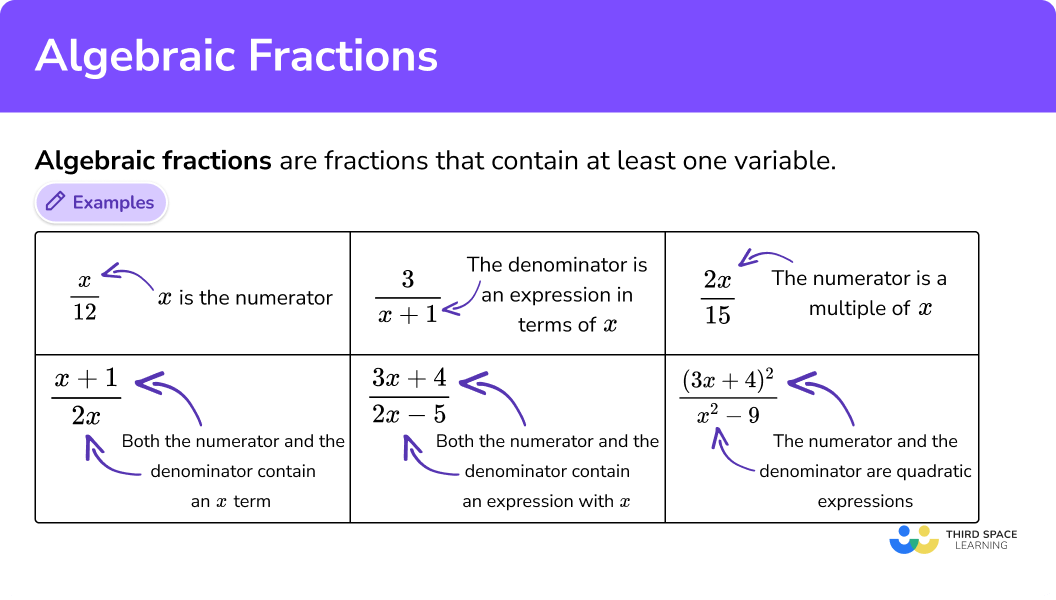
Algebraic fractions are fractions that contain at least one variable.

The following algebraic expressions are examples of algebraic fractions:

x is the numerator:       \quad \quad \quad \frac{x}{12}   Both the numerator and the denominator contain an x term:       \quad \quad \quad \frac{x+1}{2x}

   An expression in    terms of x is the    denominator:       \quad \quad \frac{3}{x+1}\      Both the numerator    and the    denominator    contain an    expression with x :       \quad \quad \frac{3x+4}{2x-5}

   The numerator is a multiple of x :           \quad\quad \quad \quad \frac{2x}{15}      The numerator and the denominator are    quadratic expressions:             \quad\quad \quad \quad \frac{(x+3)^{2}}{x^{2}-9}

The main aim of this lesson is to understand how to solve equations that include algebraic fractions.

All the examples above are expressions whereas the examples below are equations as we can find specific values for x for each example to solve the equation.

One step equation:     \quad \quad \frac{x}{12}=4   A separate constant term:   \quad \frac{x+1}{2x}+4=x

   A quadratic    equation:       \quad\frac{3}{x+1}=x+5      A linear equation:         \quad \frac{3x+4}{2x-5}=6

   A second fraction:         \quad \frac{2x}{15}=\frac{5x}{2}      Double brackets, difference of two    squares and simultaneous equations:       \quad \frac{(x+3)^{2}}{x^{2}-9}=2x-1

It is important to be able to simplify algebraic fractions into their simplest form. If you need to practice this or need a quick refresher, see the lesson on simplifying algebraic fractions for further information.

Step-by-step guide: Simplifying algebraic fractions

How to solve equations including algebraic fractions

We need to be able to solve equations including algebraic fractions. 

Let’s look at a simple example when \frac{8}{x}=2 .

Here, the denominator of the fraction contains the variable, so we first need to get the variable out of the denominator.

Rearranging the equation by multiplying both sides by x and then dividing by 2 , we get the value of x=4 .

We can substitute this into the original equation to prove that the answer is correct.

Here, \frac{8}{4}=2 so we have the correct answer.

We shall now consider more complicated cases when equations involve algebraic fractions.

In order to solve equations including algebraic fractions.

Convert each fraction so they all have a common denominator.

• Multiply the equation throughout by the common denominator.
• Solve the equation (linear or quadratic).

Explain how to solve equations including algebraic fractions

Algebraic fractions worksheet

Get your free algebraic fractions worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Algebraic fractions examples

Example 1: equation with one fraction.

Solve the equation

Here, we only have one fraction and so we do not need to convert any other term into a fraction.

2 Multiply the equation throughout by the common denominator .

Multiplying the equation throughout by 3 (the denominator of the fractional term), we get

Make sure that you multiply every term in the equation by 3 .

3 Solve the equation (linear or quadratic) .

You can check your solution by substituting the value for x into the original equation and evaluating it.

Example 2: Equation with two fractions

Here, we have the two fractions with the denominators of 2 and 5 . The lowest common multiple of 2 and 5 is 10 and so we can convert the two fractions so that they have the same denominator.

Remember to use brackets to ensure that you multiply the entire numerator by 5 .

Remember to use brackets to ensure that you multiply the entire numerator by 2 .

We now have the equation

Multiply the equation throughout by the common denominator .

Multiplying the equation throughout by 10 (the denominator of the fractional terms), we get

Solve the equation (linear or quadratic) .

Example 3: Equation with x in the denominator

Here, we have one fraction so we do not need to find a common denominator.

Multiplying the equation throughout by x + 1 (the denominator of the fractional terms), we get

Example 4: Equation with three fractions

Here, we need to find the lowest common multiple of x, 2x, and 3x . As x is the highest common factor, x \times 1 \times 2 \times 3 is the lowest common multiple, which is equal to 6x. .

So by multiplying the numerator and denominator of each fraction by a constant, we can convert each fraction to have the common denominator of 6x: .

We now have an equation which we can immediately simplify.

Multiplying the equation throughout by 6x (the denominator of the fractional terms), we get

Example 5: Denominators are expressions in terms of x

Here, we need to find a common denominator for (x + 2) and (x − 4) .

The easiest way to do this is to multiply the two expressions together.

Top tip: do not expand the brackets too soon as you may be able to simplify the fraction before solving the equation.

By multiplying each fraction by the denominator of the other fraction, we get

Multiplying the equation throughout by (x+2)(x-4) (the denominator of the fractional term), we get

Example 6: Equation including a quadratic

Here, we have a single fraction and so we do not need to find a common denominator.

Multiplying the equation throughout by x (the denominator of the fractional terms), we get

Here, we have two possible solutions for x so we can check both:

Common misconceptions

• Multiplying the numerator by the denominator

Let us look at example 2 . When multiplying throughout by 10 to remove the denominator from each fraction, the numerator has also been multiplied by 10 . This means that the fractions have been multiplied by 100 , instead of 10 , leaving the next line of work to be incorrect.

• Ignoring the denominators

When given an equation including an algebraic fraction, if the denominators are ignored the question will be answered incorrectly.

• Not multiplying all terms by the denominator

When rearranging an equation, the denominator is moved to the other side of the equals sign, instead of each term being multiplied by it. You must remember to multiply throughout by any value, not just the opposite side of the equals sign.

• Simplifying fractions incorrectly (1)

When adding two fractions, the denominator must be the same. A common misconception for adding two fractions is to add the numerators and the denominators together because this method is emphasised when looking at multiplying fractions.

• Simplifying fractions incorrectly (2)

Seeing the same term on the numerator and denominator allow the misconception that they can both be cancelled. 

Practice algebraic fractions questions

1. Solve the equation

2. Solve the equation

3. Solve the equation

4. Solve the equation

5. Solve the equation

6. Solve the equation

Algebraic fractions GCSE questions

1. Arron earns £40 per hour. One day, he receives a bonus of £5 . He shares this day’s earnings equally with his brother and sister. If he gives away £190 , how many hours did Arron work that day?

2. Use the quadratic formula to solve the equation

2x(x+2)+5x(x+3)=4(x+3)(x+2) or equivalent

x=3 or x=-\frac{8}{3}

3. Two shapes given below have the same area. Calculate the value for x .

Area of Triangle = \frac{2(x+8)}{2}=x+8

Area of Square = \left(\frac{3}{\sqrt{x}}\right)^{2}=\frac{9}{x}

x=1 or x=-9

Conclusion: x=1 only

Learning checklist

You have now learned how to:

• use algebraic methods to solve linear equations in 1 variable (including all forms that require rearrangement)
• simplify and manipulate algebraic fractions

The next lessons are

• Expanding brackets
• Factorising
• Solving equations

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Fractions in Algebra

We can add, subtract, multiply and divide fractions in algebra in the same way we do in simple arithmetic.

Adding Fractions

To add fractions there is a simple rule:

(See why this works on the Common Denominator page).

x 2 + y 5 = (x)(5) + (2)(y) (2)(5)

x + 4 3 + x − 3 4 = (x+4)(4) + (3)(x−3) (3)(4)

= 4x+16 + 3x−9 12

Subtracting Fractions

Subtracting fractions is very similar, except that the + is now −

x + 2 x  −  x x − 2  =  (x+2)(x−2) − (x)(x) x(x−2)  

=  (x 2 − 2 2 ) − x 2 x 2 − 2x

=  −4 x 2 − 2x

Multiplying Fractions

Multiplying fractions is the easiest one of all: multiply the tops together, and the bottoms together:

3x x−2  ×  x 3  =  (3x)(x) 3(x−2)  

=  3x 2 3(x−2)  

=  x 2 x−2

Dividing Fractions

To divide fractions first "flip" the fraction we want to divide by, then use the same method as for multiplying:

3y 2 x+1  ÷  y 2  =  3y 2 x+1  ×  2 y  

= (3y 2 )(2) (x+1)(y)

= 6y 2 (x+1)(y)  

=  6y x+1

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 2

• Why we do the same thing to both sides: Variable on both sides
• Intro to equations with variables on both sides
• Equations with variables on both sides: 20-7x=6x-6
• Equations with variables on both sides

Equation with variables on both sides: fractions

• Equations with variables on both sides: decimals & fractions
• Equation with the variable in the denominator

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Algebraic Fractions: Worksheets with Answers

Whether you want a homework, some cover work, or a lovely bit of extra practise, this is the place for you. And best of all they all (well, most!) come with answers.

Mathster keyboard_arrow_up Back to Top

Mathster is a fantastic resource for creating online and paper-based assessments and homeworks. They have kindly allowed me to create 3 editable versions of each worksheet, complete with answers.

Corbett Maths keyboard_arrow_up Back to Top

Corbett Maths offers outstanding, original exam style questions on any topic, as well as videos, past papers and 5-a-day. It really is one of the very best websites around.

Algebra: Fraction Problems

Related Topics: More Algebra Word Problems

In these lessons, we will learn how to solve fraction word problems that deal with fractions and algebra. Remember to read the question carefully to determine the numerator and denominator of the fraction.

We will also learn how to solve word problems that involve comparing fractions, adding mixed numbers, subtracting mixed numbers, multiplying fractions and dividing fractions.

Fraction Word Problems using Algebra

Example: 2/3 of a number is 14. What is the number?

Answer: The number is 21.

Example: The numerator of a fraction is 3 less than the denominator. When both the numerator and denominator are increased by 4, the fraction is increased by fraction.

Solution: Let the numerator be x, then the denominator is x + 3, and the fraction is \(\frac{x}{{x + 3}}\) When the numerator and denominator are increased by 4, the fraction is \(\frac{{x + 4}}{{x + 7}}\) \(\frac{{x + 4}}{{x + 7}} - \frac{x}{{x + 3}} = \frac{{12}}{{77}}\) 77(x + 4)(x + 3) – 77x(x+7) = 12(x + 7)(x + 3) 77x 2 + 539x + 924 – 77x 2 – 539x = 12x 2 + 120x + 252 12x 2 + 120x – 672 = 0 x 2 + 10x – 56 = 0 (x – 4)(x + 14) = 0 x = 4 (negative answer not applicable in this case)

How to solve Fraction Word Problems using Algebra? Examples: (1) The denominator of a fraction is 5 more than the numerator. If 1 is subtracted from the numerator, the resulting fraction is 1/3. Find the original fraction. (2) If 3 is subtracted from the numerator of a fraction, the value of the resulting fraction is 1/2. If 13 is added to the denominator of the original fraction, the value of the new fraction is 1/3. Find the original fraction. (3) A fraction has a value of 3/4. When 14 is added to the numerator, the resulting fraction has a value equal to the reciprocal of the original fraction, Find the original fraction.

Algebra Word Problems with Fractional Equations Solving a fraction equation that appears in a word problem Example: One third of a number is 6 more than one fourth of the number. Find the number.

Fraction and Decimal Word Problems How to solve algebra word problems with fractions and decimals? Examples: (1) If 1/2 of the cards had been sold and there were 172 cards left, how many cards were printed? (2) Only 1/3 of the university students wanted to become teachers. If 3,360 did not wan to become teachers, how many university were there? (3) Rodney guessed the total was 34.71, but this was 8.9 times the total. What was the total?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Pre-Algebra Topics
• Algebra Topics
• Algebra Calculator
• Algebra Cheat Sheet
• Algebra Practice Test
• Algebra Readiness Test
• Algebra Formulas
• Want to Build Your Own Website?

Sign In / Register

Solving Equations with Fractions

I know fractions are difficult, but with these easy step-by step instructions you'll be solving equations with fractions in no time.

Do you start to get nervous when you see fractions? Do you have to stop and review all the rules for adding, subtracting, multiplying and dividing fractions?

If so, you are just like almost every other math student out there! But... I am going to make your life so much easier when it comes to solving equations with fractions!

Our first step when solving these equations is to get rid of the fractions because they are not easy to work with!

Let see what happens with a typical two-step equation with the distributive property.

In this problem, we would typically distribute the 3/4 throughout the parenthesis and then solve. Let's see what happens:

Yuck! That just made this problem worse! Now we have two fractions to contend with and that means subtracting fractions and multiplying fractions.

So... let's stop here and say,

We DO NOT want to do this! DO NOT distribute fractions.

We are going to learn how to get rid of the fractions and make this much more simple!

So... what do we do? We are going to get rid of just the denominator in the fraction, so we will be left with the numerator, or just an integer!

I know, easier said than done! It's really not hard, but before I get into it, I want to go over one algebra definition.

We need to discuss the word term.

In Algebra, each term within an equation is separated by a plus (+) sign, minus (-) sign or an equals sign (=). Variable or quantities that are multiplied or divided are considered the same term.

That last example is the most important to remember. If a quantity is in parentheses, it it considered one term!

Let's look at a few examples of how to solve these crazy looking problems!

Example 1 - Equations with Fractions

Take a look at this example on video if you are feeling overwhelmed.

Hopefully you were able to follow that example. I know it's tough, but if you can get rid of the fraction, it will make these problems so much easier. Keep going, you'll get the hang of it!

In the next example, you will see two fractions.  Since they have the same denominator, we will multiply by the denominator and get rid of both fractions.

Example 2 - Equations with Fractions with the Same Denominator

Did you notice how multiplying by 2 (the denominator of both fractions) allowed us to get rid of the fractions?  This is the best way to deal with equations that contain fractions.

In the next example, you will see what happens when you have 2 fractions that have different denominators. 

We still want to get rid of the fractions all in one step. Therefore, we need to multiply all terms by the least common multiple.  Remember how to find the LCM?  If not, check out the LCM lesson here .

Example 3 - Equations with Two Fractions with Different Denominators

Yes, the equations are getting harder, but if you take it step-by-step, you will arrive at the correct solution. Keep at it - I know you'll get it!

• Solving Equations
• Equations with Fractions

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.

ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!

Affiliate Products...

On this site, I recommend only one product that I use and love and that is Mathway   If you make a purchase on this site, I may receive a small commission at no cost to you. 

Privacy Policy

Let Us Know How we are doing!

  send us a message to give us more detail!

Would you prefer to share this page with others by linking to it?

• Click on the HTML link code below.
• Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.26: Solving Fractional Equations

• Last updated
• Save as PDF
• Page ID 48329

A fractional equation is an equation involving fractions which has the unknown in the denominator of one or more of its terms.

Example 24.1

The following are examples of fractional equations:

a) \(\frac{3}{x}=\frac{9}{20}\)

b) \(\frac{x-2}{x+2}=\frac{3}{5}\)

c) \(\frac{3}{x-3}=\frac{4}{x-5}\)

d) \(\frac{3}{4}-\frac{1}{8 x}=0\)

e) \(\frac{x}{6}-\frac{2}{3 x}=\frac{2}{3}\)

The Cross-Product property can be used to solve fractional equations.

Cross-Product Property

If \(\frac{A}{B}=\frac{C}{D}\) then \(A \cdot D=B \cdot C\).

Using this property we can transform fractional equations into non-fractional ones. We must take care when applying this property and use it only when there is a single fraction on each side of the equation. So, fractional equations can be divided into two categories.

I. Single Fractions on Each Side of the Equation

Equations a), b) and c) in Example 24.1 fall into this category. We solve these equations here.

a) Solve \(\frac{3}{x}=\frac{9}{20}\)

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot 20=9 \cdot x \\ \text{Linear Equation} & 60=9 x \\ \text{Divide by 9 both sides} & \frac{60}{9}=x \end{array}\nonumber\]

The solution is \(x=\frac{60}{9}=\frac{20}{3}\).

\[\begin{array}{ll} \text{Cross-Product} & 5 \cdot(x-2)=3 \cdot(x+2) \\ \text{Remove parentheses} & 5 x-10=3 x+6 \\ \text{Linear Equation: isolate the variable} & 5 x-3 x=10+6 \\ & 2 x=16 \\ \text{Divide by 2 both sides} & \frac{2 x}{2}=\frac{16}{2}\end{array}\nonumber\]

the solution is \(x=8\).

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot(x-5)=4 \cdot(x-3) \\ \text{Remove parentheses} & 3 x-15=4 x-12 \\ \text{Linear Equation: isolate the variable} & 3 x-4 x=15-12 \\ & -x=3 \\ \text{Divide by 2 both sides} & \frac{-x}{-1}=\frac{3}{-1}\end{array}\nonumber\]

The solution is \(x=-3\)

Note: If you have a fractional equation and one of the terms is not a fraction, you can always account for that by putting 1 in the denominator. For example:

\[\frac{3}{x}=15\nonumber\]

We re-write the equation so that all terms are fractions.

\[\frac{3}{x}=\frac{15}{1}\nonumber\]

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot 1=15 \cdot x \\ \text{Linear Equation: isolate the variable} & 3=15 x \\ \text{Divide by 15 both sides} & \frac{3}{15}=\frac{15 x}{15} \end{array}\nonumber\]

The solution is \(x=\frac{3}{15}=\frac{3 \cdot 1}{3 \cdot 5}=\frac{1}{5}\).

II. Multiple Fractions on Either Side of the Equation

Equations d) and e) in Example 24.1 fall into this category. We solve these equations here.

We use the technique for combining rational expressions we learned in Chapter 23 to reduce our problem to a problem with a single fraction on each side of the equation.

d) Solve \(\frac{3}{4}-\frac{1}{8 x}=0\)

First we realize that there are two fractions on the LHS of the equation and thus we cannot use the Cross-Product property immediately. To combine the LHS into a single fraction we do the following:

\[\begin{array}{ll} \text{Find the LCM of the denominators} & 8 x \\ \text{Rewrite each fraction using the LCM} & \frac{3 \cdot 2 x}{8 x}-\frac{1}{8 x}=0 \\ \text{Combine into one fraction} & \frac{6 x-1}{8 x}=0 \\ \text{Re-write the equation so that all terms are fractions} & \frac{6 x-1}{8 x}=\frac{0}{1} \\ \text{Cross-Product} & (6 x-1) \cdot 1=8 x \cdot 0 \\ \text{Remove parentheses} & 6 x-1=0 \\\text{Linear Equation: isolate the variable} & 6 x=1 \\ \text{Divide by 6 both sides} & \frac{6 x}{6}=\frac{1}{6} \end{array}\nonumber\]

The solution is \(x=\frac{1}{6}\).

e) Solve \(\frac{x}{6}+\frac{2}{3 x}=\frac{2}{3}\)

\[\begin{array}{ll} \text{Find the LCM of the denominators of LHS} & 6x \\ \text{Rewrite each fraction on LHS using their LCM} & \frac{x \cdot x}{6 x}+\frac{2 \cdot 2}{6 x}=\frac{2}{3} \\ \frac{x^{2}+4}{6 x}=\frac{2}{3} \text{Combine into one fraction} & \left(x^{2}+4\right) \cdot 3=6 x \cdot 2 \\ \text{Cross-Product} & 3 x^{2}+12=12 x \\ \text{Remove parentheses} & 3 x^{2}-12 x+12=0 \\ \text{Quadratic Equation: Standard form} & 3 x^{2}-12 x+12=0 \\\text{Quadratic Equation: Factor} & 3 \cdot x^{2}-3 \cdot 4 x+3 \cdot 4=0 \\ & 3\left(x^{2}-4 x+4\right)=0 \\ & 3(x-2)(x-2)=0 \\ \text{Divide by 3 both sides} & \frac{3(x-2)(x-2)}{3}=\frac{0}{3} \\ & (x-2)(x-2)=0 \\ \text{Quadratic Equation: Zero-Product Property} & (x-2)=0 \text { or }(x-2)=0 \end{array}\nonumber\]

Since both factors are the same, then \(x-2=0\) gives \(x=2\). The solution is \(x=2\)

Note: There is another method to solve equations that have multiple fractions on either side. It uses the LCM of all denominators in the equation. We demonstrate it here to solve the following equation: \(\frac{3}{2}-\frac{9}{2 x}=\frac{3}{5}\)

\[\begin{array} \text{Find the LCM of all denominators in the equation} & 10x \\ \text{Multiply every fraction (both LHS and RHS) by the LCM} & 10 x \cdot \frac{3}{2}-10 x \cdot \frac{9}{2 x}=10 x \cdot \frac{3}{5} \\ & \frac{10 x \cdot 3}{2}-\frac{10 x \cdot 9}{2 x}=\frac{10 x \cdot 3}{5} \\ \text{Simplify every fraction} & \frac{5 x \cdot 3}{1}-\frac{5 \cdot 9}{1}=\frac{2 x \cdot 3}{1} \\ \text{See how all denominatiors are now 1, thus can be disregarded} & 5 x \cdot 3-5 \cdot 9=2 x \cdot 3 \\ \text{Solve like you would any other equation} & 15 x-45=6 x \\ \text{Linear equation: islolate the variable} & 15 x-6 x=45 \\ & 9 x=45 \\ & x=\frac{45}{9} \\ & x=5 \end{array} \nonumber\]

The solution is \(x=5\)

Exit Problem

Solve: \(\frac{2}{x}+\frac{1}{3}=\frac{1}{2}\)

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

SAT Math : Algebraic Fractions

Study concepts, example questions & explanations for sat math, all sat math resources, example questions, example question #1 : how to simplify a fraction.

Example Question #1 : Algebraic Fractions

Another way to represent this question is:

The one carries to the ten's column.

One way to simplify this complex fraction is to find the least common multiple of all the denominators, i.e. the least common denominator (LCD). If we find this, then we can multiply every fraction by the LCD and thereby be left with only whole numbers. This will make more sense in a little bit.

The denominators we are dealing with are 2, 3, 4, 5, and 6. We want to find the smallest multiple that these numbers have in common. First, it will help us to notice that 6 is a multiple of both 2 and 3. Thus, if we find the least common multiple of 4, 5, and 6, it will automatically be a multiple of both 2 and 3. Let's list out the first several multiples of 4, 5, and 6.

4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60

5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60

6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60

The smallest multiple that 4, 5, and 6 have in common is 60. Thus, the least common multiple of 4, 5, and 6 is 60. This also means that the least common multiple of 2, 3, 4, 5, and 6 is 60. Therefore, the LCD of all the fractions is 60.

Let's think of the expression we want to simplify as one big fraction. The numerator contains the fractions 1/4, 1/3, and –1/5. The denominator of the fraction is 1/2, –1/6 and 1. Remember that if we have a fraction, we can multiply the numerator and denominator by the same number without changing the value of the fraction. In other words, x / y = ( xz )/( yz ). This will help us because we can multiply the numerator (which consists of 1/4, 1/3, and –1/5) by 60, and then mutiply the denominator (which consists of 1/2, –1/6, and 1) by 60, thereby ridding us of fractions in the numerator and denominator. This process is shown below:

This means that a / b = 23/80. We are told that a and b are both positive and that their greatest common factor is 1. In other words, a / b must be the simplified form of 23/80. When a fraction is in simplest form, the greatest common factor of the numerator and denominator equals one. Since 23/80 is simplified, a = 23, and b = 80. The sum of a and b is thus 23 + 80 = 103.

The answer is 103.

Change to a mixed number 

To convert from a fraction to a mixed number we must find out how many times the denominator goes into the numerator using division and the remainder becomes the new fraction. 

To average, we have to add the values and divide by two. To do this we need to find a common denomenator of 6. We then add and divide by 2, yielding 4.5/6. This reduces to 3/4.

Normal 0 false false false EN-US X-NONE X-NONE MicrosoftInternetExplorer4

None of the answers are correct

This problem is solved the same way ½ + 1/3 is solved.  For example,  ½ + 1/3 = 3/6 + 2/6 = 5/6.  Find a common denominator then convert each fraction into an equivalent fraction using that common denominator.  The final step is to add the two new fractions and simplify.

Set up the conversions as fractions and solve:

Example Question #11 : How To Simplify A Fraction

Can't be simplified

To simplify exponents which are being divided, subtract the exponents on the bottom from exponents on the top.  Remember that only exponents with the same bases can be simplified

Example Question #5 : Algebraic Fractions

x 2  –  y 2 can be also expressed as ( x + y )( x –  y ).

Therefore, the fraction now can be re-written as ( x + y )( x  –  y )/( x + y ).

This simplifies to ( x –  y ).

Example Question #6 : Algebraic Fractions

Now multiply both the numerator and denominator by the conjugate of the denominator:

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Two-step without parentheses
• Two-step with parentheses
• Three/four steps without parentheses
• Three/four steps with parentheses
• Multi-step without parentheses
• Multi-step with parentheses
• Prime Factorization
• Negative Factors
• Positive Factors
• Odd Factors
• Even Factors
• Biggest Factor
• Equivalent Fractions
• Add, Subtract
• Add, Subtract Like Denominators
• Add, Subtract Unlike Denominators
• Multiply with Whole Number
• Divide with Whole Number
• Mixed Numbers
• Complex Fractions
• Improper Fractions
• Long Addition
• Long Subtraction
• Long Multiplication
• Long Division
• Add/Subtract
• Multiplication
• Decimal to Fraction
• Fraction to Decimal
• Square Root
• Ratios & Proportions

Number Line

• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

• reduce\:fraction\:\frac{4}{8}
• \frac{1}{2}+\frac{1}{4}+\frac{3}{4}
• \frac{1}{2}\cdot\frac{8}{7}
• \frac{-\frac{1}{5}}{\frac{7}{4}}
• descending\:order\:\frac{1}{2},\:\frac{3}{6},\:\frac{7}{2}
• decimal\:to\:fraction\:0.35
• What is a mixed number?
• A mixed number is a combination of a whole number and a fraction.
• How can I compare two fractions?
• To compare two fractions, first find a common denominator, then compare the numerators.Alternatively, compare the fractions by converting them to decimals.
• How do you add or subtract fractions with different denominators?
• To add or subtract fractions with different denominators, convert the fractions to have a common denominator. Then you can add or subtract the numerators of the fractions, leaving the denominator unchanged.

fractions-calculator

• Practice, practice, practice Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing...

Please add a message.

Message received. Thanks for the feedback.

Problems on Algebraic Fractions

Here we will learn how to simplify the problems on algebraic fractions to its lowest term.

1.  Reduce the algebraic fractions to their lowest terms:  \(\frac{x^{2}  -  y^{2}}{x^{3}  -  x^{2}y}\)

\(\frac{x^{2}  -  y^{2}}{x^{3}  -  x^{2}y}\)

Factorizing the numerator and denominator separately and cancelling the common factors we get,

=  \(\frac{(x  +  y) (x  -  y)}{x^{2} (x  -  y)} \)

=  \(\frac{x  +  y}{x^{2}}\)

2. Reduce to lowest terms \(\frac{x^{2}  +  x  -  6}{x^{2}  -  4}\)

\(\frac{x^{2}  +  x  -  6}{x^{2} -  4}\)

Step 1: Factorize the numerator x\(^{2}\) + x – 6

                                         = x\(^{2}\) + 3x – 2x – 6

                                         = x(x + 3) – 2(x + 3)

                                         = (x + 3) (x – 2)

Step 2: Factorize the denominator: x\(^{2}\) – 4

                                             = x\(^{2}\) – 2\(^{2}\)

                                             = (x + 2) (x – 2)

Step 3: From steps 1 and 2: \(\frac{x^{2}  +  x  -  6}{x^{2}  -  4}\)

                                     = \(\frac{x^{2}  +  x  -  6}{x^{2}  -  2^{2}}\)

                                     = \(\frac{(x  +  3) (x  -  2)}{(x  +  2) (x  -  2)}\)

                                     = \(\frac{(x  +  3)}{(x  +  2)}\)

3. Simplify the algebraic fractions \(\frac{36x^{2}  -  4}{9x^{2}  +  6x  +  1}\)

\(\frac{36x^{2}  -  4}{9x^{2}  +  6x  +  1}\)

Step 1: Factorize the numerator: 36x\(^{2}\) – 4

                                           = 4(9x\(^{2}\) – 1)

                                           = 4[(3x)\(^{2}\) – (1)\(^{2}\)]

                                           = 4(3x + 1) (3x – 1)

Step 2: Factorize the denominator: 9x\(^{2}\) + 6x + 1

                                             = 9x\(^{2}\) + 3x + 3x + 1

                                             = 3x(3x + 1) + 1(3x + 1)

                                             = (3x + 1) (3x + 1)

Step 3: Simplification of the given expression after factorizing the numerator and the denominator:

= \(\frac{4(3x  +  1)(3x  -  1)}{(3x  +  1)(3x  +  1)}\)

= \(\frac{4(3x  -  1)}{(3x  +  1)}\)

4.  Reduce and simplify:  \(\frac{8x^{3}y^{2}z}{2xy^{3}} of \left ( \frac{5x^{5}y^{2}z^{2}}{25xy^{3}z} \div \frac{7xy^{2}}{35x^{2}yz^{3}}\right )\)

\(\frac{8x^{3}y^{2}z}{2xy^{3}} of \left ( \frac{5x^{5}y^{2}z^{2}}{25xy^{3}z} \div \frac{7xy^{2}}{35x^{2}yz^{3}}\right )\)

=  \(\frac{8x^{3}y^{2}z}{2xy^{3}} of \frac{5x^{5}y^{2}z^{2}}{25xy^{3}z} \times \frac{35x^{2}yz^{3}}{7xy^{2}}\)

=  \(\frac{4x^{3}y^{2}z}{xy^{3}} \left ( \frac{x^{5}y^{2}z^{2}}{xy^{3}z} \times \frac{x^{2}yz^{3}}{xy^{2}} \right )\)

= 4x\(^{10 - 3}\) ∙ y\(^{-3}\) ∙ z\(^{5}\)

=  \(\frac{4x^{7}\cdot z^{5}}{y^{3}}\)

5.  Simplify:  \(\frac{2x^{2}  -  3x  -  2}{x^{2}  +  x  -  2} \div \frac{2x^{2}  +  3x  +  1}{3x^{2}  +  3x  -  6}\)

\(\frac{2x^{2}  -  3x  -  2}{x^{2}  +  x   -   2} \div \frac{2x^{2}  +  3x  +  1}{3x^{2}  +  3x  -  6}\)

Step 1: First factorize each of the polynomials separately:

2x\(^{2}\) – 3x – 2 = 2x\(^{2}\) – 4x + x – 2

                 = 2x(x – 2) + 1 (x – 2)

                 = (x – 2) (2x + 1)

x\(^{2}\) + x – 2 = x\(^{2}\) + 2x - x – 2

              = x(x + 2) - 1 (x + 2)

              = (x + 2) (x - 1)

2x\(^{2}\) + 3x + 1 = 2x\(^{2}\) + 2x + x + 1

                 = 2x(x + 1) + 1 (x + 1)

                 = (x + 1) (2x + 1)

3x\(^{2}\) + 3x – 6 = 3[x\(^{2}\) + x – 2]

                 = 3[x\(^{2}\) + 2x - x – 2]

                 = 3[x(x + 2) – 1(x + 2)]                   

                 = 3[(x + 2) (x - 1)]

                 = 3(x + 2) (x - 1)

Step 2: Simplify the given expressions by substituting with their factors

\(\frac{2x^{2}  -  3x  -  2}{x^{2}  +  x  -  2} \div \frac{2x^{2}  +  3x  +  1}{3x^{2}  +  3x  -  6}\)

=  \(\frac{2x^{2}  -  3x  -  2}{x^{2}  +  x  -  2} \times \frac{3x^{2}  +  3x  -  6}{2x^{2}  +  3x  +  1}\)

=  \(\frac{(x  -  2) (2x  +  1)}{(x  +  2) (x  -  1)}\times\frac{3(x  +  2) (x  -  1)}{(x  +  1) (2x  +  1)}\)

=  \(\frac{3(x  -  2)}{(x  +  1)}\)

8th Grade Math Practice From Problems on Algebraic Fractions to HOME PAGE

New! Comments

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Multiplication of a Number by a 3-Digit Number |3-Digit Multiplication

Mar 28, 24 06:33 PM

Multiply a Number by a 2-Digit Number | Multiplying 2-Digit by 2-Digit

Mar 27, 24 05:21 PM

Multiplication by 1-digit Number | Multiplying 1-Digit by 4-Digit

Mar 26, 24 04:14 PM

Multiplying 3-Digit Number by 1-Digit Number | Three-Digit Multiplicat

Mar 25, 24 05:36 PM

Multiplying 2-Digit Number by 1-Digit Number | Multiply Two-Digit Numb

Mar 25, 24 04:18 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Solving Equations with Algebraic Fractions

Hello! Today we are going to take a look at how to solve equations that have algebraic fractions . But first, let’s review what algebraic fractions are. An algebraic fraction is any fraction that contains an algebraic expression. In other words, it’s a fraction that has a variable in it anywhere. For example,

\(\frac{5}{x}\), \(\frac{2x-9}{7}\), and \(\frac{3x}{2}\)

are all algebraic fractions.

So, now that we know what they are, let’s jump into a problem where we have to solve these. So we’re going to take a look at:

\(\frac{x}{8}=7\)

This is a nice and simple one. We know that in order to solve an equation, we need to isolate our variable. Here we can see that our variable, \(x\), is being divided by 8. So, to undo this division, we simply need to multiply both sides by 8.

\(8\cdot \frac{x}{8}=7\cdot 8\)

When we do that, our division is canceled out and we’re left with \(x\) on the left side, and \(7\times 8=56\), so:

Not too hard, right? Let’s try one that’s a little bit more complicated.

\(\frac{3x}{4}-\frac{2x}{12}=7\)

To solve this, I’m first going to simplify my fractions on the left side. To do this, I’ll need to convert \(\frac{3x}{4}\) to a fraction with a denominator of 12. I can do this by multiplying both the numerator and denominator by 3.

\(\frac{3x\cdot 3}{4\cdot 3}=\frac{9x}{12}\)

So that gives me the fraction, \(\frac{9x}{12}\). And then the rest of our equation is going to stay the same, so:

\(\frac{9x}{12}-\frac{2x}{12}=7\)

Since our denominators are the same, we can now subtract our numerators, so \(9x-2x=7x\).

\(\frac{7x}{12}=7\)

Another way we can write this is:

\(\frac{7}{12}\cdot x=7\)

So if we look at it this way, the way that we can get rid of this \(\frac{7}{12}\) over here is by multiplying by the reciprocal. So the reciprocal of \(\frac{7}{12}\), is \(\frac{12}{7}\), so we’ll multiply by that on both sides.

\(\frac{12}{7}\cdot \frac{7}{12}\cdot x=7\cdot \frac{12}{7}\)

When we do that, it cancels our fractions out over here, and we’re left with \(x\), which is what we want. And then if we do that over here, we can simplify first by doing \(7\div 7\), which gives us 1, and then do \(1\times 12\), which is 12.

So \(x=12\), which is our answer.

Let’s take a look at another problem.

\(\frac{4x}{5}=\frac{3x}{10}+9\)

This one we’re going to solve a little bit differently. For this problem, I’m going to solve for \(x\) by eliminating the fractions in our first step. To do this, we simply multiply the entire equation by the least common multiple of the denominators, of the fractions in the problem.

In this case, our denominators are 5 and 10, and the least common multiple of 5 and 10 is 10. So multiply the entire equation by 10.

\(10(\frac{4x}{5}=\frac{3x}{10}+9)\)

So that means we’re going to multiply each part of our equation by 10. So, \(10\cdot \frac{4x}{5}\). We can do \(10\div 5\) first, because remember it doesn’t matter if you multiply or divide first, multiplication and division can happen simultaneously. So for this, I’m going to divide \(10\div 5\) and get 2, and then multiply by \(4x\) to get \(8x\). If I multiply 10 by \(\frac{3x}{10}\), our 10s will cancel out and we’ll be left with \(3x\). And \(10\cdot 9=90\).

\(8x=3x+90\)

Now we can solve it like a normal algebra problem . So I’m going to subtract \(3x\) from both sides.

\(8x-3x=3x-3x+90\)

That gives us:

And then we divide both sides by 5.

\(\frac{5x}{5}=\frac{90}{5}\)

Either of these methods will help you get the right answer when solving equations with algebraic fractions, so feel free to use whichever one you feel most comfortable with.

Before we go, I want to show you one more problem you might come across.

\(\frac{x+17}{5}=21\)

So we have an expression in the numerator instead of just a variable, and maybe a number being multiplied by it, so it’s a little bit different than the ones we’ve looked at before. So, to solve problems like these, we first get rid of the fraction by multiplying by the denominator on both sides of the equation. So we’re going to multiply by 5 on both sides.

\(5\cdot \frac{x+17}{5}=21\cdot 5\)

That cancels out our denominator, so we no longer have a fraction, and we’re just left with the expression in the numerator: \(x+17\). And \(21\cdot 5=105\).

\(x+17=105\)

So now we’re going to solve it like normal. We’ll subtract 17 from both sides,

\(x+17-17=105-17\)   \(x=88\)

And that’s it! I hope this video helped you better understand how to solve equations with algebraic fractions. Thanks for watching, and happy studying!

Solving Equations with Algebraic Fractions Practice Questions

  Solve the equation: \(\frac{2x}{3}-\frac{4x}{9}=6\).

We can combine the fractions on the left side by converting \(\frac{2x}{3}\) to a fraction with a denominator of 9. To do so, multiply the first fraction by \(\frac{3}{3}\).

\(\frac{3}{3}\cdot\frac{2x}{3}-\frac{4x}{9}=6\)   \(\frac{6x}{9}-\frac{4x}{9}=6\)   \(\frac{2x}{9}=6\)

Now, multiply both sides by 9.

\(9\cdot\frac{2x}{9}=6\cdot9\)   \(2x=54\)

Finally, divide both sides by 2.

\(\frac{2x}{2}=\frac{54}{2}\)   \(x=27\)

  Solve the equation: \(\frac{5x}{6}=\frac{11x}{15}+2\).

We can multiply both sides of the equation by the least common multiple of the denominators. The least common multiple of 6 and 15 is 30, so multiply the entire equation by 30

\(30\left(\frac{5}{6}x=\frac{11}{15}x+2\right)\)   \(\frac{30\cdot5}{6}x=\frac{30\cdot11}{15}x+30\cdot2\)   \(25x=22x+60\)

To get the variable terms on the left side, subtract 22x from both sides of the equation.

\(25x-22x=22x+60-22x\)   \(3x=60\)

Now, divide both sides by 3.

\(\frac{3x}{3}=\frac{60}{3}\)   \(x=20\)

Solve the equation: \(2x+79=5\).

We can get rid of the fraction by multiplying by the denominator on both sides of the equation. That is, multiply both sides of the equation by 9.

\(9\cdot \frac{2x+7}{9}=5\cdot9\)   \(2x+7=45\)

Now, subtract 7 from both sides.

\(2x+7-7=45-7\)   \(2x=38\)

Then, divide both sides by 2.

\(\frac{2x}{2}=\frac{38}{2}\)   \(x=19\)

  The quotient of thirteen less than a number and 7 equals twice the number. What is the number?

Let x be the number you are trying to find. Since quotient means to divide, we can write the quotient of thirteen less than a number and 7 as \(\frac{x-13}{7}\). Twice the number can be written as \(2x\). Set these two expressions equal to each other to get the equation:

\(\frac{x-13}{7}=2x\)

To solve for x, first, get rid of the fraction by multiplying by the denominator on both sides of the equation. That is, multiply both sides of the equation by 7.

\(7\cdot\frac{x-13}{7}=2x\cdot7\)   \(x-13=14x\)

To get the variable terms on the left side, subtract \(14x\) from both sides of the equation.

\(x-13-14x=14x-14x\)   \(-13x-13=0\)

Now, add the constant of 13 to both sides.

\(-13x-13+13=0+13\)   \(-13x=13\)

Then, divide both sides by –13.

\(\frac{-13x}{-13}=\frac{13}{-13}\)   \(x=-1\)

So, the number is –1.

  You and a friend play on the same soccer team. Both of you decide to save money to buy a soccer goal to practice shooting. One-third of the money, in dollars, you and your friend have saved is $30 less than twice of what you have saved. If your friend has saved $25, how much money have you saved?

Let x be the amount of money you have saved. Since your friend has saved $25, we can write one-third of the money you and your friend have saved as \(\frac{x+25}{3}\). Thirty dollars less than twice of what you have saved can be written as \(2x-30\). Setting these two expressions equal to each other gives us the equation:

\(\frac{x+25}{3}=2x-30\)

To solve for x, first, get rid of the fraction by multiplying by the denominator on both sides of the equation. That is, multiply both sides of the equation by 3.

\(3\cdot\frac{x+25}{3}=3(2x-30)\)   \(x+25=6x-90\)

To get the variable terms on the left side, subtract \(6x\) from both sides of the equation.

\(x+25-6x=6x-90-6x\)   \(-5x+25=-90\)

Now, subtract 25 from both sides.

\(-5x+25-25=-90-25\)   \(-5x=-115\)

Then, divide both sides by –5.

\(\frac{-5x}{-5}=\frac{115}{-5}\)   \(x=23\)

So, you have saved $23.

Return to Algebra I Videos

by Mometrix Test Preparation | This Page Last Updated: December 26, 2023

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

Algebraic Fractions

You have encountered fractions many times since early in the study of mathematics. They occur in formulas and in many day-to-day practical problems. However, the fractions of arithmetic are made up strictly of numbers. We will now study operations on fractions whose components are algebraic expressions.

SOLVING EQUATIONS INVOLVING SIGNED NUMBERS

• Factor the numerator and denominator of a fraction.
• Simplify algebraic fractions.
• An algebraic fraction is the indicated ratio of two algebraic expressions.

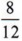
A fraction is in simplified (or reduced) form if the numerator and denominator contain no common factor (other than 1).

To obtain the simplified form of a fraction apply the following rule.

To simplify a fraction factor the numerator and denominator completely and then divide both numerator and denominator by all common factors.

Next divide by the common factors, giving

Now divide by the common factor (x + 2) in both numerator and denominator to get

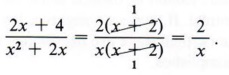
Notice that even though we were able to factor the numerator and denominator, we still cannot divide since no factors are common to both. The given fraction is already in simplified form.

The fact that a given fraction might require any of the methods of factoring you have studied emphasizes again the importance of being proficient in factoring.

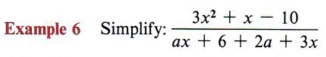
Solution Here you may use "trial and error" for the numerator and "grouping" for the denominator.

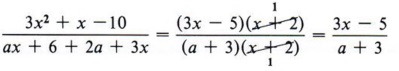
Solution This type of problem requires special attention because it is a common cause for error. At first glance the factors might be mistakenly considered as common, or the fraction might be mistakenly considered as already simplified. Note that the factors cannot be divided since the signs keep them from being identical. If, however, negative 1 is factored from one of the factors, then there are like factors and division can be accomplished.

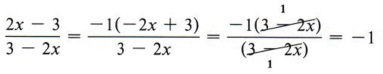
MULTIPLICATION OF ALGEBRAIC FRACTIONS

• Factor numerators and denominators of all fractions being multiplied.
• Identify and divide by all common factors.
• Write the product in simplest form.

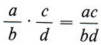
However, remember that all fractional answers must be in simplified form. We could follow the above definition and then simplify the answer as in the previous section. But with algebraic fractions this can lead to very difficult expressions. The following rule allows us to simplify as we multiply, so the answer will then be in simplified form.

When multiplying algebraic fractions , factor all numerators and denominators completely, then divide by all factors common to a numerator and denominator before multiplying.

The product of the remaining factors of the numerator will be the numerator of the answer and the product of the remaining factors of the denominator will be the denominator of the answer.

DIVISION OF ALGEBRAIC FRACTIONS

• Change a division problem to a related multiplication problem.
• Divide algebraic fractions.

Division of fractions is defined in terms of multiplication.

To divide multiply by the inverse of the divisor.

To divide one algebraic expression by another invert the divisor and change the operation to multiplication.

After the problem is changed from a division problem to a multiplication problem, it is completed as in the previous section.

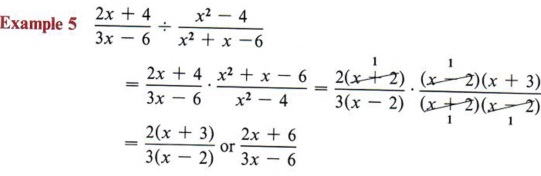
FINDING THE LEAST COMMON DENOMINATOR

• Factor a denominator of a fraction completely.
• Find the least common denominator of two or more fractions.

The rule for addition and subtraction of fractions requires that the fractions to be combined must have the same denominator. As preparation for performing these operations we will now investigate the method of finding the least common denominator for any group of fractions.

A common denominator lot two or more fractions is an expression that contains all factors of the denominator of each fraction. A least common denominator contains the minimum number of factors to be a common denominator.

Solution This problem would require a considerable amount of guesswork, or testing possibilities, if we had no general method.

Let's consider the definition. From it we know that a common denominator for these numbers must contain all factors of each. In other words, we are looking for the smallest number divisible by 12, 14, 15, and 18. First completely factor each number.

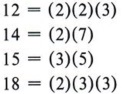
The number we are looking for must contain (2)(2)(3) in order to be divisible by 12. It must contain (2)(7) in order to be divisible by 14, and so on. Proceed as follows: Write the factors of the first number, 12. (2)(2)(3) Now look at the factors of the next number, 14, and see that we need (2)(7). But since we already have a 2, we only need the factor (7). This gives (2)(2)(3)(7). This number is now divisible by 12 and by 14. The factors of the next number, 15, are (3) and (5). Since we already have a 3, we need only the factor 5, giving (2)(2)(3)(7)(5). This number is now divisible by 12, 14, and 15. The factors of the next number, 18, are (2)(3)(3). We already have 2 and one 3. Hence, we need another 3. (2)(2)(3)(7)(5)(3) = 1,260 This number, 1,260, is a common denominator of 12, 14, 15, and 18 because it contains all factors of each and is therefore divisible by each. It is the least common denominator because it contains only those factors necessary to make it divisible by 12, 14, 15, and 18.

The preceding discussion gives rise to a rule for obtaining a least common denominator for any number of fractions, whether they be numbers or algebraic expressions.

To find the least common denominator for two or more fractions: 1. Factor each denominator completely. 2. Write the denominator of the first fraction in factored form as the proposed common denominator. 3. By inspection determine which factors of the second denominator are not already in the proposed common denominator and include them. 4. Repeat step three for each fraction.

By inspection of the second denominator we need the additional factor (x - 2). The least common denominator is (3x - 4)(2x + l)(x - 2).

Solution First denominator: 3(x + 2) Second denominator: 2(2)(3) Third denominator: 2(x + 3)(x + 2) Proposed common denominator: 3(x + 2) By inspection of the second denominator we see we need to include the factors (2) and (2). We now have 2(2)(3)(x + 2). By inspection of the third denominator we see we need the factor (x + 3). The least common denominator is 2(2)(3)(x + 2)(x + 3) or 12(x + 2)(x + 3).

EQUIVALENT FRACTIONS

• Understand the fundamental principle of fractions.
• Change a fraction to an equivalent fraction.

In further preparation for adding and subtracting fractions, we must be able to change a given fraction to one with a new denominator without changing the value of the original fraction.

• To change a fraction to an equivalent fraction multiply numerator and denominator by the same nonzero expression.

Solution Since the new denominator is in factored form, by inspection we see that the original denominator (2x + 3) has been multiplied by the factor (x - 4). Therefore, the original numerator (x + 1) must also be multiplied by the factor (x - 4), giving

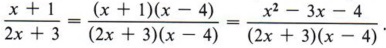
Solution Since the original denominator (x - 3) has been multiplied by (2) and (x + 1), the original numerator (2x + 1) must also be multiplied by (2) and (x + 1).

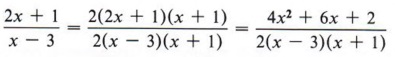
ADDITION OF ALGEBRAIC FRACTIONS

• Add fractions having the same denominator.
• Apply the rule for adding fractions.

We are now prepared to add algebraic fractions by using the techniques discussed in the preceding two sections. You should recall the following rule from arithmetic.

The sum of two or more fractions which have the same denominator is the sum of the numerators over their common denominator.

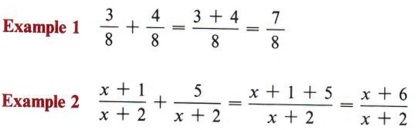
Take note that this rule only allows the sum of fractions that have the same denominator. In other words, two or more fractions can only be added if they have a common denominator. The rule for adding any two or more fractions will require the skills developed in the last two sections in addition to knowledge of combining like terms.

To add two or more fractions follow these steps: Step 1 Find the least common denominator (LCD) for all fractions involved using the method developed in section 9-4. Step 2 Change each fraction to an equivalent fraction having the least common denominator (section 9-5). Step 3 Find the sum of the numerators and place this sum over the least common denominator. Step 4 Simplify (or reduce) the fraction obtained in step 3.

This answer is in reduced form.

We can use fewer written steps if we note that "common denominator" means all the fractions have the same denominator, and if all have the same denominator, then it is necessary to write the denominator only once. To illustrate this we will re-work the preceding example.

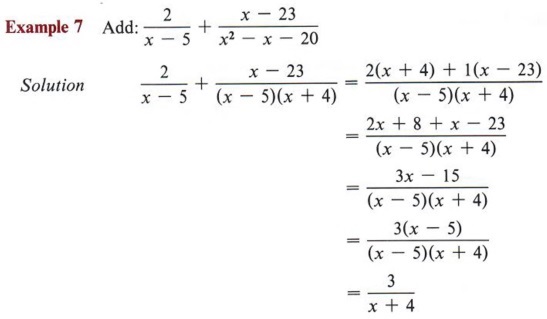
SUBTRACTION OF ALGEBRAIC FRACTIONS

• Subtract fractions having the same denominator.
• Apply the rule for subtracting fractions with unlike denominators.

Subtraction is defined in terms of addition, so the method of subtracting algebraic fractions will be the same as adding algebraic fractions discussed in the preceding section. You will soon see why we have presented them separately.

The difference of any two fractions having the same denominator is the difference of their numerators over their common denominator.

Notice that this rule is the same as the rule for adding two fractions with the same denominator.

The steps for subtracting fractions are, therefore, the same as for adding fractions.

To subtract fractions: Step 1 Find the least common denominator of the two fractions. Step 2 Change each fraction to an equivalent fraction having the least common denominator. Step 3 Find the difference of the numerators and place this result over the least common denominator. Step 4 Simplify (or reduce) the fraction obtained in step 3.

The obvious question is, "If these two operations are the same, why study them separately?" The answer is that the subtraction gives rise to a very common error that the student must be prepared to avoid.

The error referred to is often made by not recognizing that the minus sign affects the entire numerator of the second fraction and NOT just the first term.

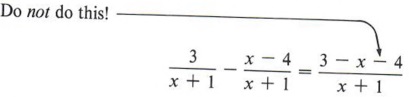
The arrow points out the error most commonly made in subtraction of fractions. The best way to avoid this is to always use parentheses

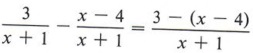
and you are not so likely to fail to change the sign properly.

COMPLEX FRACTIONS

• Recognize a complex fraction.
• Simplify a complex fraction.

Fractions are defined as the indicated quotient of two expressions. In this section we will present a method for simplifying fractions in which the numerator or denominator or both are themselves composed of fractions. Such fractions are called complex fractions .

Thus if the numerator and denominator of a complex fraction are composed of single fractions, it can be simplified by dividing the numerator by the denominator.

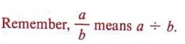
A generally more efficient method of simplifying a complex fraction involves using the fundamental principle of fractions. We multiply both numerator and denominator by the common denominator of all individual fractions in the complex fraction.

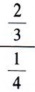
EQUATIONS HAVING ALGEBRAIC FRACTIONS

• Apply the method of solving fractional equations.
• Determine when a fractional equation does not have a solution.

In chapter 2 we encountered equations that have fractions. However, those fractions all had numerical denominators. Now we will discuss equations that have fractions involving variables in the denominators.

The method of solving these equations will follow the same pattern as in chapter 2, but there are some additional cautions that you must be prepared to take.

To refresh your memory the steps for solving such equations are repeated here. First: Eliminate fractions by multiplying each term of the equation by the least common denominator of all fractions in the equation. Second: Simplify by combining like terms on each side of the equation. Third: Add or subtract the necessary quantities to get the unknown quantity on one side and the numbers of arithmetic on the other. Fourth: Divide by the coefficient of the unknown quantity. Fifth: Check your answer.

The main difference in solving equations with arithmetic fractions and those with algebraic fractions comes in checking. The checking process will not just be to find a possible error, but will also be to determine if the equation has an answer.

This last possibility arises because with algebraic fractions we multiply by an unknown quantity. This unknown quantity could actually be zero, which would make all the work invalid.

Since division by zero is not possible, we must conclude that x = 1 is not a solution. And since we made no error in the computations we must conclude that this equation has no solution. The correct answer is "no solution."

Thus, x = -5 is a solution.

Therefore, 11 is the amount by which the numerator was increased.

• A fraction is in simplified form if the numerator and denominator have no common factor other than 1.
• A common denominator for two or more fractions is an expression that contains all factors of the denominators of each fraction.
• A least common denominator contains the minimum number of factors to be a common denominator.

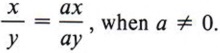
• Complex fractions are those in which the numerator or denominator (or both) contains a fraction.
• To simplify or reduce fractions to lowest terms factor the numerator and denominator and divide by all like factors.
• To multiply fractions factor all numerators and denominators and divide by all like factors before multiplying.
• To divide by a fraction invert the divisor and then multiply.
• To find a least common denominator (LCD) first factor all denominators, then find a denominator that contains all factors of each denominator but does not contain any unnecessary factors.
• Find the least common denominator.
• Change each fraction to an equivalent fraction having the LCD as its denominator.
• Add the numerators and place over the LCD.
• Simplify or reduce the answer.
• To subtract fractions proceed as in addition but combine the numerators by subtracting.
• Complex fractions may be simplified by multiplying numerator and denominator of the complex fraction by the LCD of all fractions in the expression.
• To solve equations having fractions first eliminate all fractions by multiplying the entire equation by the LCD of the fractions involved. The resulting equation is then solved, and the solution must be checked in the original equation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

• calculators
• Algebraic Fractions

Algebraic Fractions Calculator

Get detailed solutions to your math problems with our algebraic fractions step-by-step calculator . practice your math skills and learn step by step with our math solver. check out all of our online calculators here .,  example,  solved problems,  difficult problems.

Solved example of algebraic fractions

Divide $x^2$ by $x^2+1$

Resulting polynomial

 Final Answer

Struggling with math.

Access detailed step by step solutions to thousands of problems, growing every day!

 Popular problems

Equations involving Fractions Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Game Central

Similar Problems from Web Search