Is mathematical reasoning important to study?
Table of Contents
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. |

January 18, 2021
Reading Time: 9 minutes
Introduction
The purpose of mathematics is not just to earn grades. Students who wish to aim high in life need to figure out their purpose. Broadly speaking, Mathematics is implemented in every sphere of life. Nowadays, organizations require measurable input and output for performance assessment, and career outcomes are not based on qualitative or verbal feedback.
Students need to gear up and prepare for a future that will depend solely on mathematics. The evolution of newer technologies like data science will bring a renewed emphasis on Mathematics.

Mathematical reasoning, on the other hand, helps individuals build mathematical critical thinking and logical reasoning. A lack of mathematical reasoning skills may reflect not just in mathematics performance but also in Physics, Chemistry, or Economics.
In the subsequent sections, we will try to understand What is Mathematical reasoning and what are the basic terms used in mathematical reasoning. We will also have a look at different types of mathematical reasoning and go through mathematical reasoning questions and answers.
Later in the article, we will look at a few Frequently Asked Questions with solutions to solidify the idea behind learning mathematical reasoning.
- The importance of developing mathematical thinking in children
- Logical Reasoning: Topics, Examples, Syllabus, Questions
- Slow Learners
Here is a downloadable PDF. After downloading, you will be able to read 'Mathematical Reasoning’ offline at your convenience and as many times as you want. Click on the download button to explore them.
| 📥 |
|
What is Mathematical Reasoning?
Mathematical reasoning is a critical skill that enables students to analyze a given hypothesis without any reference to a particular context or meaning. In layman's words, when a scientific inquiry or statement is examined, the reasoning is not based on an individual's opinion. Derivations and proofs require a factual and scientific basis.
Mathematical critical thinking and logical reasoning are important skills that are required to solve maths reasoning questions.
When we learn literature, we follow certain rules of grammar. Likewise, there are certain rules and parts of a scientific hypothesis. It is important to note that most books and texts written on mathematical reasoning follow scientific grammar or relevant terminologies and notations.
What are the basic terms used in Mathematical Reasoning?
In this section, the basic terminologies associated with Mathematical reasoning are discussed.
Any sentence in mathematics which follows the following rules is a statement.
A sentence needs to be either true or false but not both to be considered a mathematically accepted statement.
Any sentence which is either imperative or interrogative or exclamatory cannot be considered a mathematically validated statement.
A Sentence containing one or many variables is termed an open statement. An open statement can become a statement if the variables present in the sentence are replaced by definite values
Example: The distance from the center of a circle to any point on the circumference of the circle is equal.
Conjunction and Disjunction
Whenever statements are joined to make a new statement and all the conditions need to be fulfilled, it is a Conjunction. ‘And’, ‘with’ are commonly used to join such statements.
Whenever statements are joined to make a new statement and only one of the conditions needs to be fulfilled, it is a Disjunction. ‘Or’, ‘But’ are commonly used to join such statements.
The conjunction is true only if the original statements are found to be true. The conjunction is false if the original statement or statements are found to be false.
The conjunction is true if only one statement is found to be true. The conjunction is false if none of the original statements are found to be true.
Example: Square is a polygon and a parallelogram can also be a square.
These are a few mathematical terminologies that will help you comprehend and apply mathematical reasoning. These terms will also help you solve and understand reasoning questions.
What are the types of mathematical reasoning?
Inductive reasoning.
Inductive reasoning is based on observations and not any hypothesis. If any phenomena are observed for n number of times, it can be generalized. This generalization is based on observation and therefore it may be false. Inductive reasoning is a logical guess which can be backed up by using valid reasons.

This type of reasoning is not used in geometry, for instance, one may observe a few right triangles and conclude all triangles to be right triangles. Therefore, other mathematical tools are used to prove geometrical results. An example of inductive reasoning will help elucidate the concept.
Example of Inductive Reasoning:
Statement: I picked a ball from the bag and it happens to be a red ball. I picked a second red ball. A third ball from the bag is also red. Therefore, all the balls in the bag are red.
Reasoning : All the balls picked up from the bag are red. Therefore, we can say all the balls are red. This is an example of inductive reasoning where existing data is analyzed to come to a general conclusion.
Deductive Reasoning
Deductive reasoning is based on the exact opposite principles of induction. Unlike Inductive reasoning, Deductive reasoning is not based on simple generalizations. A Hypothesis is required or a statement that has to be true under specified conditions for deductive reasoning to be valid. In the case of Inductive reasoning, the conclusion may be false but Deductive reasoning is true in all cases.
Therefore, Deductive reading is used for geometrical and mathematical proofs. The following example will simplify the concepts discussed in this section.
Example of Deductive Reasoning:
Statement: The sum of angles in a triangle is always equal to 180° and ABC is a Triangle.
Reasoning: Here in the given statement we are considering two hypotheses, where the sum of angles in a triangle is said to be 180° and ABC is a triangle. Based on the given hypotheses we deduce that the sum of angles of ABC is 180°.
Abductive Reasoning
Abductive reasoning is a modified version of Inductive Reasoning and takes a more practical approach. In the case of inductive reasoning, the data or observation is complete but in real situations, most of the data is not available at the time of making a decision.

So based on the data and its availability, the conclusion may vary and reasoning may change.
Example of Abductive Reasoning:
Statement: The heights of four students studying in a class were found to be 160cm, 162cm, 163 cm, 167 cm respectively. The measuring scale available had the least count of 1cm.
Reasoning : As per the data and hypotheses available at the time of observation, the average height comes out to be 163cm. But once a new measuring scale was installed the least count was found to be 0.1 cm and the recorded height of students changed. This also impacted the Average height which came to be 63.8 cm.
As discussed in this section, reasoning techniques are categorized in three major sections. An understanding of Inductive, Abductive and Deductive reasoning will help you solve any reasoning question. It is important to identify the reasoning technique which has to be used to solve a question from examination point of view.
What are the types of reasoning statements?
Reasoning statements in mathematics are broadly classified into three types:
Simple Statements
Compound Statements
If-Then Statements
We will look into each type of reasoning statement along with their examples.
If the truth value of a statement or proposition does not directly depend on another statement, it is a simple statement. In other words, a simple statement should not be composed of simpler statements.
Therefore a simple statement can never be broken down into simpler statements. It is easiest to work with simple statements and direct reasoning approach can be implemented. A few examples have been provided to clear the concept of simple statements.
Example 1: Square is a parallelogram.
Reasoning: There are no modifiers in the given statement. Therefore we can say that the given statement is simple.
Compound Statement
In simple words, the combination of simple statements is a compound statement. Therefore, such statements are made of either two or more simple statements joined together by connectives like 'and', 'or'.
A variety of connectives can be used instead of the two connectives as mentioned. These statements are crucial for Deduction reasoning in Mathematics. Have a look at the detailed example below for a better understanding:
Example 1: We have taken two simple statements that can be joined together by the use of a connector.
Statement 1: Parallel lines do not intersect.
Statement 2: Transversal lines make equal alternate angles with parallel lines
Compound Statement: Parallel lines do not intersect and Transversal lines make equal alternate angles with parallel lines.
Example 2: In this example, a compound statement is being dissected into its simple statement components.
Compound Statement: Triangle has three sides and the square has four sides.
The Simple Statements for this statement is:
Statement 1: Triangle has three sides.
Statement 2: The square has four sides.
If-then Statement
Conditional statements where a hypothesis is followed by a conclusion are known as the If-then statement. If the hypothesis is true and the conclusion is false then the conditional statement is false. Likewise, if the hypothesis is false the whole statement is false.
Example 1: If 40% population is female then 60% population is male.
Reasoning: Here the 40% female is the hypothesis and if that condition is met then the conclusion is satisfying.
Sample Mathematical Reasoning Questions With Answers
Now that we have an understanding of Mathematical Reasoning and the various terminologies and reasoning associated, we will go through two sample questions with an explanation to understand maths and reasoning in depth.
Q1. Look at this series: 12, 10, 13, 11, 14, 12, … What number should come next?
A. 15 B. 16 C. 13 D. 10
Answer: Option D.
Explanation: First, 2 is subtracted, then 3 is added therefore when 3 is added to 12 it becomes 15. This is an example of an alternating number of subtraction series.
Q2. SQUARE:PERIMETER::CIRCLE :?
A.RADIUS B. CHORD C. SECTOR D. CIRCUMFERENCE
Answer: D.CIRCUMFERENCE.
Explanation: The boundary of a square is given by its perimeter just as the boundary of a circle is given by circumference.
Most kids study mathematics for the sake of grades. That will improve grades temporarily but cause great damage in the longer run. Kids need to ask questions to understand how a particular concept is being used. If children do not understand the concepts in their initial days, they will struggle at a later stage.
Practice Proofs
Proofs will help Children Ideate their own set of techniques to understand complex problems. Students need to focus on Geometry Proofs, results, and maths reasoning questions.
Cuemath Activities
Some kids do need additional support and tools. Sometimes kids underperform in mathematics due to stress and fear of bad grades. Such kids are unable to ask questions in class and eventually start lagging. Cuemath provides a customized learning journey for such kids.
The most basic concepts are cleared and corrected. Individual attention by professional Mathematics Teachers helps them cope better. Once a child gains confidence, mathematics is a cakewalk.
Begin teaching mathematical reasoning at an early age to avoid struggling with it at a later stage. Children need to understand the principles of mathematics rather than mugging up proofs and theorems.
This will help them solve higher-order problems and develop mathematical aptitude. Over time you will find your child solving complex problems on their own without much intervention or assistance.
About Cuemath
Cuemath, a student-friendly mathematics and coding platform, conducts regular Online Classes for academics and skill-development, and their Mental Math App, on both iOS and Android , is a one-stop solution for kids to develop multiple skills. Understand the Cuemath fee structure and sign up for a free trial.
Frequently asked questions (FAQs)
What is a fallacy in mathematical reasoning.
Fallacy refers to errors in hypotheses caused due to logical inaccuracy.
Why is mathematical reasoning important?
Students have the potential to solve higher-order thinking questions which are frequently asked in competitive examinations. But a lack of mathematical reasoning skills may render their potential. Encouragement is needed to develop a student's natural inclination to strive for purpose and meaning.
The reasoning is the most fundamental and essential tool of mathematics. It helps one understand and justify mathematical theorems. A good grip in reasoning will help students apply the concepts they learn in the classroom.
What are the two types of fallacy?
The two types of fallacies are as follows:
Formal fallacy: When the relationship between premises and conclusion is not valid or when premises are unsound, Formal fallacies are created.
Informal Fallacy: Misuse of language and evidence is classified as an Informal fallacy.

Mathematical Reasoning & Problem Solving
In this lesson, we’ll discuss mathematical reasoning and methods of problem solving with an eye toward helping your students make the best use of their reasoning skills when it comes to tackling complex problems.
Previously Covered:
- Over the course of the previous lesson, we reviewed some basics about chance and probability, as well as some basics about sampling, surveys, etc. We also covered some ideas about data sets, how they’re represented, and how to interpret the results.
Approaches to Problem Solving
When solving a mathematical problem, it is very common for a student to feel overwhelmed by the information or lack a clear idea about how to get started.
To help the students with their problem-solving “problem,” let’s look at some examples of mathematical problems and some general methods for solving problems:
Identify the following four-digit number when presented with the following information:
- One of the four digits is a 1.
- The digit in the hundreds place is three times the digit in the thousands place.
- The digit in the ones place is four times the digit in the ten’s place.
- The sum of all four digits is 13.
- The digit 2 is in the thousands place.
Help your students identify and prioritize the information presented.
In this particular example, we want to look for concrete information. Clue #1 tells us that one digit is a 1, but we’re not sure of its location, so we see if we can find a clue with more concrete information.
We can see that clue #5 gives us that kind of information and is the only clue that does, so we start from there.
Because this clue tells us that the thousands place digit is 2, we search for clues relevant to this clue. Clue #2 tells us that the digit in the hundreds place is three times that of the thousands place digit, so it is 6.
So now we need to find the tens and ones place digits, and see that clue #3 tells us that the digit in the ones place is four times the digit in the tens place. But we remember that clue #1 tells us that there’s a one somewhere, and since one is not four times any digit, we see that the one must be in the tens place, which leads us to the conclusion that the digit in the ones place is four. So then we conclude that our number is:
If you were following closely, you would notice that clue #4 was never used. It is a nice way to check our answer, since the digits of 2614 do indeed add up to be thirteen, but we did not need this clue to solve the problem.
Recall that the clues’ relevance were identified and prioritized as follows:
- clue #3 and clue #1
By identifying and prioritizing information, we were able to make the information given in the problem seem less overwhelming. We ordered the clues by relevance, with the most relevant clue providing us with a starting point to solve the problem. This method also utilized the more general method of breaking a problem into smaller and simpler parts to make it easier to solve.
Now let’s look at another mathematical problem and another general problem-solving method to help us solve it:
Two trees with heights of 20 m and 30 m respectively have ropes running from the top of each tree to the bottom of the other tree. The trees are 40 meters apart. We’ll assume that the ropes are pulled tight enough that we can ignore any bending or drooping. How high above the ground do the ropes intersect?
Let’s solve this problem by representing it in a visual way , in this case, a diagram:
You can see that we have a much simpler problem on our hands after drawing the diagram. A, B, C, D, E, and F are vertices of the triangles in the diagram. Now also notice that:
b = the base of triangle EFA
h = the height of triangle EFA and the height above the ground at which the ropes intersect
If we had not drawn this diagram, it would have been very hard to solve this problem, since we need the triangles and their properties to solve for h. Also, this diagram allows us to see that triangle BCA is similar to triangle EFC, and triangle DCA is similar to triangle EFA. Solving for h shows that the ropes intersect twelve meters above the ground.
Students frequently complain that mathematics is too difficult for them, because it is too abstract and unapproachable. Explaining mathematical reasoning and problem solving by using a variety of methods , such as words, numbers, symbols, charts, graphs, tables, diagrams, and concrete models can help students understand the problem better by making it more concrete and approachable.
Let’s try another one.
Given a pickle jar filled with marbles, about how many marbles does the jar contain?
Problems like this one require the student to make and use estimations . In this case, an estimation is all that is required, although, in more complex problems, estimates may help the student arrive at the final answer.
How would a student do this? A good estimation can be found by counting how many marbles are on the base of the jar and multiplying that by the number of marbles that make up the height of the marbles in the jar.
Now to make sure that we understand when and how to use these methods, let’s solve a problem on our own:
How many more faces does a cube have than a square pyramid?
Reveal Answer
The answer is B. To see how many more faces a cube has than a square pyramid, it is best to draw a diagram of a square pyramid and a cube:
From the diagrams above, we can see that the square pyramid has five faces and the cube has six. Therefore, the cube has one more face, so the answer is B.
Before we start having the same problem our model student in the beginning did—that is, being overwhelmed with too much information—let’s have a quick review of all the problem-solving methods we’ve discussed so far:
- Sort and prioritize relevant and irrelevant information.
- Represent a problem in different ways, such as words, symbols, concrete models, and diagrams.
- Generate and use estimations to find solutions to mathematical problems.
Mathematical Mistakes
Along with learning methods and tools for solving mathematical problems, it is important to recognize and avoid ways to make mathematical errors. This section will review some common errors.
Circular Arguments
These involve drawing a conclusion from a premise that is itself dependent on the conclusion. In other words, you are not actually proving anything. Circular reasoning often looks like deductive reasoning, but a quick examination will reveal that it’s far from it. Consider the following argument:
- Premise: Only an untrustworthy man would become an insurance salesman; the fact that insurance salesmen cannot be trusted is proof of this.
- Conclusion: Therefore, insurance salesmen cannot be trusted.
While this may be a simplistic example, you can see that there’s no logical procession in a circular argument.
Assuming the Truth of the Converse
Simply put: The fact that A implies B doesn’t not necessarily mean that B implies A. For example, “All dogs are mammals; therefore, all mammals are dogs.”
Assuming the Truth of the Inverse
Watch out for this one. You cannot automatically assume the inverse of a given statement is true. Consider the following true statement:
If you grew up in Minnesota , you’ve seen snow.
Now, notice that the inverse of this statement is not necessarily true:
If you didn’t grow up in Minnesota , you’ve never seen snow.
Faulty Generalizations
This mistake (also known as inductive fallacy) can take many forms, the most common being assuming a general rule based on a specific instance: (“Bridge is a hard game; therefore, all card games are difficult.”) Be aware of more subtle forms of faulty generalizations.
Faulty Analogies
It’s a mistake to assume that because two things are alike in one respect that they are necessarily alike in other ways too. Consider the faulty analogy below:
People who absolutely have to have a cup of coffee in the morning to get going are as bad as alcoholics who can’t cope without drinking.
False (or tenuous) analogies are often used in persuasive arguments.
Now that we’ve gone over some common mathematical mistakes, let’s look at some correct and effective ways to use mathematical reasoning.
Let’s look at basic logic, its operations, some fundamental laws, and the rules of logic that help us prove statements and deduce the truth. First off, there are two different styles of proofs: direct and indirect .
Whether it’s a direct or indirect proof, the engine that drives the proof is the if-then structure of a logical statement. In formal logic, you’ll see the format using the letters p and q, representing statements, as in:
If p, then q
An arrow is used to indicate that q is derived from p, like this:
This would be the general form of many types of logical statements that would be similar to: “if Joe has 5 cents, then Joe has a nickel or Joe has 5 pennies “. Basically, a proof is a flow of implications starting with the statement p and ending with the statement q. The stepping stones we use to link these statements in a logical proof on the way are called axioms or postulates , which are accepted logical tools.
A direct proof will attempt to lay out the shortest number of steps between p and q.
The goal of an indirect proof is exactly the same—it wants to show that q follows from p; however, it goes about it in a different manner. An indirect proof also goes by the names “proof by contradiction” or reductio ad absurdum . This type of proof assumes that the opposite of what you want to prove is true, and then shows that this is untenable or absurd, so, in fact, your original statement must be true.
Let’s see how this works using the isosceles triangle below. The indirect proof assumption is in bold.
Given: Triangle ABC is isosceles with B marking the vertex
Prove: Angles A and C are congruent.
Now, let’s work through this, matching our statements with our reasons.
- Triangle ABC is isosceles . . . . . . . . . . . . Given
- Angle A is the vertex . . . . . . . . . . . . . . . . Given
- Angles A and C are not congruent . . Indirect proof assumption
- Line AB is equal to line BC . . . . . . . . . . . Legs of an isosceles triangle are congruent
- Angles A and C are congruent . . . . . . . . The angles opposite congruent sides of a triangle are congruent
- Contradiction . . . . . . . . . . . . . . . . . . . . . . Angles can’t be congruent and incongruent
- Angles A and C are indeed congruent . . . The indirect proof assumption (step 3) is wrong
- Therefore, if angles A and C are not incongruent, they are congruent.
“Always, Sometimes, and Never”
Some math problems work on the mechanics that statements are “always”, “sometimes” and “never” true.
Example: x < x 2 for all real numbers x
We may be tempted to say that this statement is “always” true, because by choosing different values of x, like -2 and 3, we see that:
Example: For all primes x ≥ 3, x is odd.
This statement is “always” true. The only prime that is not odd is two. If we had a prime x ≥ 3 that is not odd, it would be divisible by two, which would make x not prime.
- Know and be able to identify common mathematical errors, such as circular arguments, assuming the truth of the converse, assuming the truth of the inverse, making faulty generalizations, and faulty use of analogical reasoning.
- Be familiar with direct proofs and indirect proofs (proof by contradiction).
- Be able to work with problems to identify “always,” “sometimes,” and “never” statements.
Reasoning Skills
Developing opportunities and ensuring progression in the development of reasoning skills
Achieving the aims of the new National Curriculum:
Developing opportunities and ensuring progression in the development of reasoning skills.
The aims of the National Curriculum are to develop fluency and the ability to reason mathematically and solve problems. Reasoning is not only important in its own right but impacts on the other two aims. Reasoning about what is already known in order to work out what is unknown will improve fluency; for example if I know what 12 × 12 is, I can apply reasoning to work out 12 × 13. The ability to reason also supports the application of mathematics and an ability to solve problems set in unfamiliar contexts.
Research by Nunes (2009) identified the ability to reason mathematically as the most important factor in a pupil’s success in mathematics. It is therefore crucial that opportunities to develop mathematical reasoning skills are integrated fully into the curriculum. Such skills support deep and sustainable learning and enable pupils to make connections in mathematics.
This resource is designed to highlight opportunities and strategies that develop aspects of reasoning throughout the National Curriculum programmes of study. The intention is to offer suggestions of how to enable pupils to become more proficient at reasoning throughout all of their mathematics learning rather than just at the end of a particular unit or topic.
We take the Progression Map for each of the National Curriculum topics, and augment it with a variety of reasoning activities (shaded sections) underneath the relevant programme of study statements for each year group. The overall aim is to support progression in reasoning skills. The activities also offer the opportunity for children to demonstrate depth of understanding, and you might choose to use them for assessment purposes as well as regular classroom activities.
Place Value Reasoning
Addition and subtraction reasoning, multiplication and division reasoning, fractions reasoning, ratio and proportion reasoning, measurement reasoning, geometry - properties of shapes reasoning, geometry - position direction and movement reasoning, statistics reasoning, algebra reasoning.
The strategies embedded in the activities are easily adaptable and can be integrated into your classroom routines. They have been gathered from a range of sources including real lessons, past questions, children’s work and other classroom practice.
Strategies include:
- Spot the mistake / Which is correct?
- True or false?
- What comes next?
- Do, then explain
- Make up an example / Write more statements / Create a question / Another and another
- Possible answers / Other possibilities
- What do you notice?
- Continue the pattern
- Missing numbers / Missing symbols / Missing information/Connected calculations
- Working backwards / Use the inverse / Undoing / Unpicking
- Hard and easy questions
- What else do you know? / Use a fact
- Fact families
- Convince me / Prove it / Generalising / Explain thinking
- Make an estimate / Size of an answer
- Always, sometimes, never
- Making links / Application
- Can you find?
- What’s the same, what’s different?
- Odd one out
- Complete the pattern / Continue the pattern
- Another and another
- Testing conditions
- The answer is…
- Visualising
These strategies are a very powerful way of developing pupils’ reasoning skills and can be used flexibly. Many are transferable to different areas of mathematics and can be differentiated through the choice of different numbers and examples.
Nunes, T. (2009) Development of maths capabilities and confidence in primary school, Research Report DCSF-RR118 (PDF)
Is there anything wrong with this page?
Subscribe to our newsletter
- Mathematics proficiencies
Introduction
The Australian Curriculum: Mathematics aims to be relevant and applicable to the 21st century. The inclusion of the proficiencies of understanding, fluency, problem-solving and reasoning in the curriculum is to ensure that student learning and student independence are at the centre of the curriculum. The curriculum focuses on developing increasingly sophisticated and refined mathematical understanding, fluency, reasoning, and problem-solving skills. These proficiencies enable students to respond to familiar and unfamiliar situations by employing mathematical strategies to make informed decisions and solve problems efficiently.
The proficiency strands describe the actions in which students can engage when learning and using the content of the Australian Curriculum: Mathematics.
Understanding
Students build a robust knowledge of adaptable and transferable mathematical concepts. They make connections between related concepts and progressively apply the familiar to develop new ideas. They develop an understanding of the relationship between the ‘why’ and the ‘how’ of mathematics. Students build understanding when they connect related ideas, when they represent concepts in different ways, when they identify commonalities and differences between aspects of content, when they describe their thinking mathematically and when they interpret mathematical information
Students develop skills in choosing appropriate procedures; carrying out procedures flexibly, accurately, efficiently and appropriately; and recalling factual knowledge and concepts readily. Students are fluent when they calculate answers efficiently, when they recognise robust ways of answering questions, when they choose appropriate methods and approximations, when they recall definitions and regularly use facts, and when they can manipulate expressions and equations to find solutions.
Problem-Solving
Students develop the ability to make choices, interpret, formulate, model and investigate problem situations, and communicate solutions effectively. Students formulate and solve problems when they use mathematics to represent unfamiliar or meaningful situations, when they design investigations and plan their approaches, when they apply their existing strategies to seek solutions, and when they verify that their answers are reasonable.
Students develop an increasingly sophisticated capacity for logical thought and actions, such as analysing, proving, evaluating, explaining, inferring, justifying and generalising. Students are reasoning mathematically when they explain their thinking, when they deduce and justify strategies used and conclusions reached, when they adapt the known to the unknown, when they transfer learning from one context to another, when they prove that something is true or false, and when they compare and contrast related ideas and explain their choices.
Useful Links
- Australian Curriculum: Mathematics F–10
- Review by Kaye Stacey of 'Adding it up: helping children learn mathematics' report
- Peter Sullivan presentation: Designing learning experiences to exemplify the proficiencies
- Peter Sullivan presentation: Create your own lessons
- Peter Sullivan paper: Using the proficiencies to enrich mathematics teaching and assessment
Explore Mathematics proficiencies portfolios and illustrations
- International
- Education Jobs
- Schools directory
- Resources Education Jobs Schools directory News Search

Reasoning and Problem Solving Questions Collection - KS1 and KS2
Subject: Mathematics
Age range: 5-7
Resource type: Worksheet/Activity
Last updated
10 March 2023
- Share through email
- Share through twitter
- Share through linkedin
- Share through facebook
- Share through pinterest

These booklets each contain over 40 reasoning and problem solving questions suitable for KS1, KS2 and KS3 classes. These are the questions that we have been putting out each day in March 2016 on Twitter in the run up to SATS.
The answers are provided with some simple notes at the back of the booklet and for some problems supplementary questions and variation has been provided.
As always we welcome any feedback on the work we are doing and the materials that we are releasing. Thank you for taking an interest in our work. The White Rose Maths Hub Team
Creative Commons "Sharealike"
Your rating is required to reflect your happiness.
It's good to leave some feedback.
Something went wrong, please try again later.
TES Resource Team
We are pleased to let you know that your resource Reasoning and Problem Solving Questions Collection - KS1 and KS2, has been hand-picked by the Tes resources content team to be featured in https://www.tes.com/teaching-resources/blog/fluency-reasoning-and-problem-solving-primary-maths in April 2024 on https://www.tes.com/teaching-resources/blog. Congratulations on your resource being chosen and thank you for your ongoing contributions to the Tes Resources marketplace.
Empty reply does not make any sense for the end user
graceamfo18
A very good and engaging way to teach mastery of maths. Thank you for sharing
thank you for sharing, this is really good
Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.
Not quite what you were looking for? Search by keyword to find the right resource:
Cookie Consent
We use cookies to help provide a better website experience for you, and help us to understand how people use our website. Our partners will also collect data and use cookies for ad personalisation and measurement.
Clicking "Accept" will allow us and our partners to use cookies, learn more in our cookie policy or to change your cookie preferences, click "Manage".
To find out more about cookies and the types of cookies we are setting please visit our cookie policy .
If you'd prefer that certain types of cookie are not saved on your browser when visiting our website, use the toggles below to adjust those preferences and click "Save choices".
Strictly Necessary
These cookies are necessary for the website to function and without them you would not be able to reliably use the website. For example, logging into your account or completing forms.
Analytics Cookies
A series of cookies that collect anonymised data on how users interact with our website. This anonymous data helps us improve the website with a focus on its users, for example, ensuring the most popular content is easier to access.
View associated providers +
Marketing Cookies
These cookies track your online activity to help advertisers deliver more relevant and personalised advertising or to limit how many times you see an ad. These cookies can share that information with other organisations or advertisers.
Intelliġenza Artifiċjali
- Claude 3.5 Sonnet: Redefining the Frontiers of AI Problem-Solving

Tabella tal-kontenut

Creative problem-solving, traditionally seen as a hallmark of human intelligence, is undergoing a profound transformation. Generative AI, once believed to be just a statistical tool for word patterns, has now become a new battlefield in this arena. Anthropic, once an underdog in this arena, is now starting to dominate the technology giants, including OpenAI, Google, and Meta. This development was made as Anthropic introduces Claude 3.5 Sonnet , an upgraded model in its lineup of multimodal generative AI systems. The model has demonstrated exceptional problem-solving abilities, outshining competitors such as ChatGPT-4o , Gemini 1.5 , u fjamma 3 in areas like graduate-level reasoning, undergraduate-level knowledge proficiency, and coding skills. Anthropic divides its models into tliet segmenti : small ( Claude Haiku ), medium (Claude Sonnet), and large ( Claude Opus ). An upgraded version of medium-sized Claude Sonnet has been recently launched, with plans to release the additional variants, Claude Haiku and Claude Opus, later this year. It's crucial for Claude users to note that Claude 3.5 Sonnet not only exceeds its large predecessor Claude 3 Opus in capabilities but also in speed. Beyond the excitement surrounding its karatteristiċi , this article takes a practical look at Claude 3.5 Sonnet as a foundational tool for AI problem solving. It's essential for developers to understand the specific strengths of this model to assess its suitability for their projects. We delve into Sonnet's performance across various benchmark tasks to gauge where it excels compared to others in the field. Based on these benchmark performances, we have formulated various use cases of the model.
How Claude 3.5 Sonnet Redefines Problem Solving Through Benchmark Triumphs and Its Use Cases
In this section, we explore the benchmarks where Claude 3.5 Sonnet stands out, demonstrating its impressive capabilities. We also look at how these strengths can be applied in real-world scenarios, showcasing the model's potential in various use cases.
- Undergraduate-level Knowledge : The benchmark Massive Multitask Language Understanding (MMLU) assesses how well a generative AI models demonstrate knowledge and understanding comparable to undergraduate-level academic standards. For instance, in an MMLU scenario, an AI might be asked to explain the fundamental principles of machine learning algorithms like decision trees and neural networks. Succeeding in MMLU indicates Sonnet's capability to grasp and convey foundational concepts effectively. This problem solving capability is crucial for applications in education, content creation, and basic problem-solving tasks in various fields.
- Computer Coding: il UmanEval benchmark assesses how well AI models understand and generate computer code, mimicking human-level proficiency in programming tasks. For instance, in this test, an AI might be tasked with writing a Python function to calculate Fibonacci numbers or sorting algorithms like quicksort. Excelling in HumanEval demonstrates Sonnet's ability to handle complex programming challenges, making it proficient in automated software development, debugging, and enhancing coding productivity across various applications and industries.
- Reasoning Over Text : The benchmark Discrete Reasoning Over Paragraphs (DROP) evaluates how well AI models can comprehend and reason with textual information. For example, in a DROP test, an AI might be asked to extract specific details from a scientific article about gene editing techniques and then answer questions about the implications of those techniques for medical research. Excelling in DROP demonstrates Sonnet's ability to understand nuanced text, make logical connections, and provide precise answers—a critical capability for applications in information retrieval, automated question answering, and content summarization.
- Graduate-level reasoning : The benchmark Graduate-Level Google-Proof Q&A (GPQA) evaluates how well AI models handle complex, higher-level questions similar to those posed in graduate-level academic contexts. For example, a GPQA question might ask an AI to discuss the implications of quantum computing advancements on cybersecurity—a task requiring deep understanding and analytical reasoning. Excelling in GPQA showcases Sonnet's ability to tackle advanced cognitive challenges, crucial for applications from cutting-edge research to solving intricate real-world problems effectively.
- Multilingual Math Problem Solving: Multilingual Grade School Math (MGSM) benchmark evaluates how well AI models perform mathematical tasks across different languages. For example, in an MGSM test, an AI might need to solve a complex algebraic equation presented in English, French, and Mandarin. Excelling in MGSM demonstrates Sonnet’s proficiency not only in mathematics but also in understanding and processing numerical concepts across multiple languages. This makes Sonnet an ideal candidate for developing AI systems capable of providing multilingual mathematical assistance.
- Mixed Problem Solving: il BIG-bench-hard benchmark assesses the overall performance of AI models across a diverse range of challenging tasks, combining various benchmarks into one comprehensive evaluation. For example, in this test, an AI might be evaluated on tasks like understanding complex medical texts, solving mathematical problems, and generating creative writing—all within a single evaluation framework. Excelling in this benchmark showcases Sonnet's versatility and capability to handle diverse, real-world challenges across different domains and cognitive levels.
- Math Problem Solving : Il- MATH benchmark evaluates how well AI models can solve mathematical problems across various levels of complexity. For example, in a MATH benchmark test, an AI might be asked to solve equations involving calculus or linear algebra, or to demonstrate understanding of geometric principles by calculating areas or volumes. Excelling in MATH demonstrates Sonnet's ability to handle mathematical reasoning and problem-solving tasks, which are essential for applications in fields such as engineering, finance, and scientific research.
- High Level Math Reasoning : The benchmark Graduate School Math (GSM8k) evaluates how well AI models can tackle advanced mathematical problems typically encountered in graduate-level studies. For instance, in a GSM8k test, an AI might be tasked with solving complex differential equations, proving mathematical theorems, or conducting advanced statistical analyses. Excelling in GSM8k demonstrates Claude’s proficiency in handling high-level mathematical reasoning and problem-solving tasks, essential for applications in fields such as theoretical physics, economics, and advanced engineering.
- Visual Reasoning: Beyond text, Claude 3.5 Sonnet also showcases an exceptional visual reasoning ability, demonstrating adeptness in interpreting charts, graphs, and intricate visual data. Claude not only analyzes pixels but also uncovers insights that evade human perception. This ability is vital in many fields such as medical imaging, autonomous vehicles, and environmental monitoring.
- Text Transcription: Claude 3.5 Sonnet excels at transcribing text from imperfect images, whether they're blurry photos, handwritten notes, or faded manuscripts. This ability has the potential for transforming access to legal documents, historical archives, and archaeological findings, bridging the gap between visual artifacts and textual knowledge with remarkable precision.
- Soluzzjoni Kreattiva ta' Problemi: Anthropic introduces Artifacts —a dynamic workspace for creative problem solving. From generating website designs to games, you could create these Artifacts seamlessly in an interactive collaborative environment. By collaborating, refining, and editing in real-time, Claude 3.5 Sonnet produce a unique and innovative environment for harnessing AI to enhance creativity and productivity.
Il Bottom Line
Claude 3.5 Sonnet is redefining the frontiers of AI problem-solving with its advanced capabilities in reasoning, knowledge proficiency, and coding. Anthropic's latest model not only surpasses its predecessor in speed and performance but also outshines leading competitors in key benchmarks. For developers and AI enthusiasts, understanding Sonnet's specific strengths and potential use cases is crucial for leveraging its full potential. Whether it's for educational purposes, software development, complex text analysis, or creative problem-solving, Claude 3.5 Sonnet offers a versatile and powerful tool that stands out in the evolving landscape of generative AI.

HeatWave GenAI ta' Oracle: Il-Futur ta' Databases li jaħdmu bl-AI

Dr Tehseen Zia huwa Professur Assoċjat Tenured fl-Università COMSATS ta’ Islamabad, li għandu PhD fl-AI mill-Università tat-Teknoloġija ta’ Vjenna, l-Awstrija. Jispeċjalizza fl-Intelliġenza Artifiċjali, it-Tagħlim tal-Magni, ix-Xjenza tad-Data u l-Viżjoni tal-Kompjuter, huwa għamel kontributi sinifikanti b'pubblikazzjonijiet f'ġurnali xjentifiċi ta' fama. Dr Tehseen mexxa wkoll diversi proġetti industrijali bħala l-Investigatur Prinċipali u serva bħala Konsulent AI.
Inti tista 'tixtieq

10 Affarijiet Biex Tkun Taf Dwar Claude 3.5 Sonnet

Il-Moħħ AI Żvelat: Kif Antropiku qed Demistifika l-Ħidmiet Interjuri tal-LLMs

Amazon Tinvesti Biljuni f'Antropiku hekk kif Claude 3 Tegħleb lil GPT-4

Il-Battalja tal-Mudelli tal-Lingwa Sors Miftuħ vs Magħluq: Analiżi Teknika

ChatGPT Jilħaq It-Tqabbil tiegħu: Iż-Żieda tal-Mudell tal-Lingwa Antropika Claude

L-Espansjoni Strateġika ta' Google fl-AI: Mħatra ta' $2 biljuni fuq Anthropic

Karigi riċenti
- Il-Futur tal-Manifattura: Kif Tewmin Diġitali, 3D AI, Awtomazzjoni tar-Robotika, u Tech Reality Immersive Qed jimmodernizzaw l-Industriji
- L-Impatt tal-Ibdel il-Logħba tal-AI fuq il-Proprjetà Immobbli Korporattiva
- Mill-Inġinerija fil-Prompt għal Tagħlim ta' Ftit Tir: It-Tisħiħ tar-Reazzjonijiet tal-Mudell tal-AI
- Id-definizzjoni mill-ġdid tas-CFO: In-navigazzjoni tar-Rivoluzzjoni tal-AI fil-Finanzi

- Advanced Search
Towards Better Quantity Representations for Solving Math Word Problems
New citation alert added.
This alert has been successfully added and will be sent to:
You will be notified whenever a record that you have chosen has been cited.
To manage your alert preferences, click on the button below.
New Citation Alert!
Please log in to your account
Information & Contributors
Bibliometrics & citations, index terms.
Computing methodologies
Artificial intelligence
Natural language processing
Recommendations
Number-enhanced representation with hierarchical recursive tree decoding for math word problem solving.
Automatic solving math word problems (MWPs) is a number-intensive application in natural language processing (NLP). However, these existing methods are far from achieving acceptable levels of numeracy learning. As a result, the performance of ...
- We propose a number-enhanced representation framework to model numbers and relations.
- We devise a new tree-structured decoder to address early-stage information loss.
- We outperform the state-of-the-art baselines on four benchmark ...
Reduced models for solving particle beams and plasma physics problems
In recent years, modelling and solving numerically problems which couple charged particle to electro-magnetic fields has given rise to challenging mathematical and scientific computing developments. In the industry, a variety of examples can be thought ...
Data Augmentation with In-Context Learning and Comparative Evaluation in Math Word Problem Solving
Math Word Problem (MWP) solving presents a challenging task in Natural Language Processing (NLP). This study aims to provide MWP solvers with a more diverse training set, ultimately improving their ability to solve various math problems. We ...
Information
Published in.

Association for Computing Machinery
New York, NY, United States
Publication History
Check for updates, author tags.
- Math word problem solving
- quantity representation
- attention mechanism
- auxiliary task
- Research-article
Funding Sources
- National Key R&D Program of China
- National Natural Science Foundation of China
- Youth Innovation Promotion Association CAS
Contributors
Other metrics, bibliometrics, article metrics.
- 0 Total Citations
- 64 Total Downloads
- Downloads (Last 12 months) 64
- Downloads (Last 6 weeks) 64
View Options
Login options.
Check if you have access through your login credentials or your institution to get full access on this article.
Full Access
View options.
View or Download as a PDF file.
View online with eReader .
View this article in Full Text.
Share this Publication link
Copying failed.
Share on social media
Affiliations, export citations.
- Please download or close your previous search result export first before starting a new bulk export. Preview is not available. By clicking download, a status dialog will open to start the export process. The process may take a few minutes but once it finishes a file will be downloadable from your browser. You may continue to browse the DL while the export process is in progress. Download
- Download citation
- Copy citation
We are preparing your search results for download ...
We will inform you here when the file is ready.
Your file of search results citations is now ready.
Your search export query has expired. Please try again.
Full-Length SAT Suite Practice Tests
Find full-length practice tests on Bluebook™ as well as downloadable paper (nonadaptive) practice tests to help you prepare for the SAT, PSAT/NMSQT, PSAT 10, and PSAT 8/9.
MathOdyssey: Benchmarking Mathematical Problem-Solving Skills in Large Language Models Using Odyssey Math Data
- Wan, Xiangpeng
Large language models (LLMs) have significantly advanced natural language understanding and demonstrated strong problem-solving abilities. Despite these successes, most LLMs still struggle with solving mathematical problems due to the intricate reasoning required. This paper investigates the mathematical problem-solving capabilities of LLMs using the newly developed "MathOdyssey" dataset. The dataset includes diverse mathematical problems at high school and university levels, created by experts from notable institutions to rigorously test LLMs in advanced problem-solving scenarios and cover a wider range of subject areas. By providing the MathOdyssey dataset as a resource to the AI community, we aim to contribute to the understanding and improvement of AI capabilities in complex mathematical problem-solving. We conduct benchmarking on open-source models, such as Llama-3 and DBRX-Instruct, and closed-source models from the GPT series and Gemini models. Our results indicate that while LLMs perform well on routine and moderately difficult tasks, they face significant challenges with Olympiad-level problems and complex university-level questions. Our analysis shows a narrowing performance gap between open-source and closed-source models, yet substantial challenges remain, particularly with the most demanding problems. This study highlights the ongoing need for research to enhance the mathematical reasoning of LLMs. The dataset, results, and code are publicly available.
- Computer Science - Computation and Language;
- Computer Science - Artificial Intelligence
Help | Advanced Search
Mathematics > Numerical Analysis
Title: a sherman--morrison--woodbury approach to solving least squares problems with low-rank updates.
Abstract: We present a simple formula to update the pseudoinverse of a full-rank rectangular matrix that undergoes a low-rank modification, and demonstrate its utility for solving least squares problems. The resulting algorithm can be dramatically faster than solving the modified least squares problem from scratch, just like the speedup enabled by Sherman--Morrison--Woodbury for solving linear systems with low-rank modifications.
| Comments: | 6 pages |
| Subjects: | Numerical Analysis (math.NA) |
| classes: | 65F20 |
| Cite as: | [math.NA] |
| (or [math.NA] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite |
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Or search by topic
Number and algebra
- The Number System and Place Value
- Calculations and Numerical Methods
- Fractions, Decimals, Percentages, Ratio and Proportion
- Properties of Numbers
- Patterns, Sequences and Structure
- Algebraic expressions, equations and formulae
- Coordinates, Functions and Graphs
Geometry and measure
- Angles, Polygons, and Geometrical Proof
- 3D Geometry, Shape and Space
- Measuring and calculating with units
- Transformations and constructions
- Pythagoras and Trigonometry
- Vectors and Matrices
Probability and statistics
- Handling, Processing and Representing Data
- Probability
Working mathematically
- Thinking mathematically
- Mathematical mindsets
- Cross-curricular contexts
- Physical and digital manipulatives
For younger learners
- Early Years Foundation Stage
Advanced mathematics
- Decision Mathematics and Combinatorics
- Advanced Probability and Statistics
Published 2018
The Problem-solving Classroom
- Visualising
- Working backwards
- Reasoning logically
- Conjecturing
- Working systematically
- Looking for patterns
- Trial and improvement.
- stage of the lesson
- level of thinking
- mathematical skill.
- The length of student response increases (300-700%)
- More responses are supported by logical argument.
- An increased number of speculative responses.
- The number of questions asked by students increases.
- Student - student exchanges increase (volleyball).
- Failures to respond decrease.
- 'Disciplinary moves' decrease.
- The variety of students participating increases. As does the number of unsolicited, but appropriate contributions.
- Student confidence increases.
- conceptual understanding
- procedural fluency
- strategic competence
- adaptive reasoning
- productive disposition

Mastery-Aligned Maths Tutoring
“The best thing has been the increase in confidence and tutors being there to deal with any misunderstandings straight away."
FREE daily maths challenges
A new KS2 maths challenge every day. Perfect as lesson starters - no prep required!

Developing Maths Reasoning in KS2: The Mathematical Skills Required And How To Teach Them
Developing maths reasoning skills at and before KS2 is crucial to succeeding in the new curriculum and its maths mastery approach to learning.
Moreover, as the results of the KS2 SATs , with their focus on maths reasoning questions have shown us, pupils need strong applied reasoning with their maths facts to be able to succeed.
My approach to primary school mathematics teaching and learning is that it should be about exploring, reasoning and challenging thinking rather than learning rote/abstract rules for calculations and facts.
Though I recognise that fluency in maths and memorising key number facts is essential in Key Stage 1 and Key Stage 2 mathematics, to acquire the basics, these skills ought to be used and applied in real life contexts.
The questions from the KS2 SATs Papers 2019 seem to align with my belief. To succeed in the national curriculum tests, it is clear that children require deep knowledge of facts and mathematical concepts. Moreover, they need to be able to use and apply these facts to a range of contexts, and different types of word problems , including the more complex multi-step and two-step word problems
What is reasoning in maths?
Let’s start with the definition of maths reasoning. Reasoning in maths is the process of applying logical and critical thinking to a mathematical problem in order to work out the correct strategy to use (and as importantly, not to use) in reaching a solution.
Reasoning is sometimes seen as the glue that bonds pupils’ mathematical skills together; it’s also seen as bridging the gap between fluency and problem solving, allowing pupils to use their fluency to accurately carry out problem solving.
In my opinion it is only when we teach children to reason and give them the freedom to look for different strategies when faced with an unfamiliar context that we are really teaching mathematics in primary school.
Why focus teaching and learning on reasoning?
Logical reasoning requires metacognition (thinking about thinking) . It influences behaviour and attitudes through greater engagement, requesting appropriate help (self-regulation) and seeking conceptual understanding.
Reasoning promotes these traits because it requires children to use their mathematical vocabulary . In short, reasoning requires a lot of active talk.
It is worth mentioning that with reasoning, active listening is equally important and if done right can also ensure increased learning autonomy for pupils.

The Ultimate Guide to Problem Solving Techniques
9 ready-to-go problem solving techniques with accompanying tasks to get KS2 reasoning independently
The theory behind mathematical reasoning at KS1 & KS2
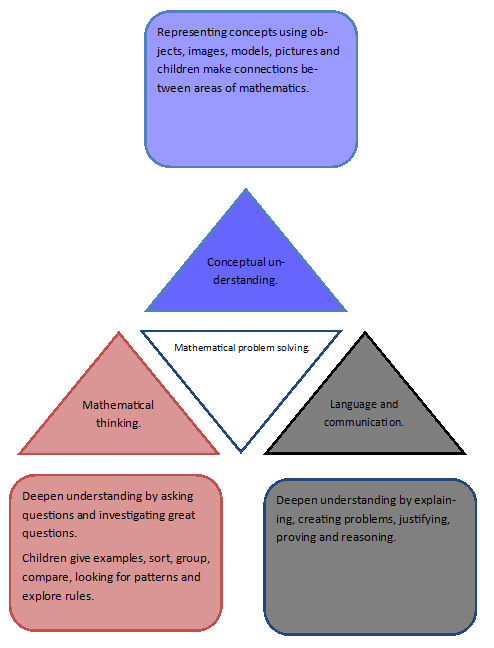
The infographic (below) from Helen Drury cleverly details what should underpin mathematics teaching and learning. It’s a good starting point when you’re thinking about your mathematics curriculum in the context of fluency reasoning and problem solving .
I’ve also been very influenced by the Five Principles of Extraordinary Math Teaching by Dan Finkel
These are as follows, and are a great starting point to developing maths reasoning at KS2
1. Start mathematics lessons with a question 2. Students need to wonder and struggle 3. You are not the answer key 4. Say yes to your students original ideas (but not yes to methodical answers) 5. Play!
See also this free guide to KS2 maths problem solving and reasoning techniques .
How to make reasoning central to Maths lessons in KS2
Pose lesson objectives as a question to ks1 & ks2 children.
A ‘light bulb’ idea from my own teaching and learning was to redesign learning objectives, fashioning them into a question for learning. Instead of ‘to identify multiples of a number’, for example, I’ll use ‘why is a square number a square number?’.
Phrasing LOs as a question instantly engages and enthuses children, they wonder what the answer is. It also ensures that they show their reasoning in a model or image when they answer.
In this instance – interestingly – children knew the process to calculate square numbers but could not articulate or mathematically reason why it worked until after the session.
It seems denying children answers allows them time to think, struggle and learn.
Ban the word ‘yes’ in Maths lessons
One of the simplest strategies I have found to make reasoning inseparable from mathematical learning is to ban the word ‘yes’ from the classroom.
Instead, asking children to reason their thoughts and explain why they think they are right can allow for greater learning gains and depth of understanding. Admittedly, this is still a work in progress and easier said than done.
To facilitate this, I always tell my children that I am not the answer key.
Using my example of square numbers, I allowed children time to struggle and wrestle with my question without providing an answer or giving hints. Instead, I questioned to unpick understanding at the beginning of the lesson and brought together mathematical ideas during a whole class discussion.
After a short discussion on how children might show or visualize a square number we began to show a model using arrays, like below:
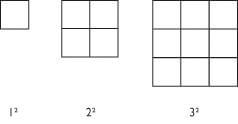
The children working at greater depth were encouraged to consider cubed numbers and show how they might be represented using multi-link cubes without any input from me. This made sure links were made between mathematical knowledge, mathematical vocabulary, and learning.
Use ‘sometimes, always, never’ classroom activities
A ‘sometimes, always, never’ activity is another great way to foster reasoning and problem-solving skills. Take the image below:

Here, children are first required to sort the statement into always, sometimes or never being true. The next day, they are moved on to the lesson with the title phrased as a question. So Not ‘to identify patterns’, but ‘how does this pattern work?’ with a pattern already presented on the board.
The children, instantly engaged, begin conjecturing, making predictions and thinking about the next patterns in the sequence (this lesson was actually inspired by an Nrich activity) .
5 tips for developing mathematical reasoning in the KS2 classroom
While small changes will not provide the framework you need to properly embed reasoning in the classroom when implemented alongside ideas such as those mentioned above. These tips can help instil greater depth in maths in your class for all ability levels.
1. Start lessons with a question.
2. Start lessons with a provocative mathematical statement and challenge your class to provide the mathematical proof: “ N will always = N” or “Multiples of 9 always have the digital sum of 9”.
3. Present answers to SATs question as a puzzle to generate discussion. When framed like this, children like to ‘come up’ with what the question could be:
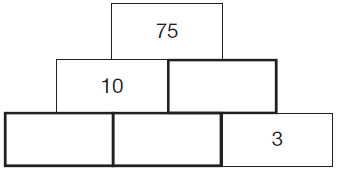
or
4. Grouping children in threes is the magic number when working through problems. Child one talks through the problem. Child two writes down everybody’s reasoning. Child three actively listens and watches.
5. Include reasoning prompting posters around the classroom. The image below, for example, can be useful to children who are starting to formulate thoughts, predictions and assertions.
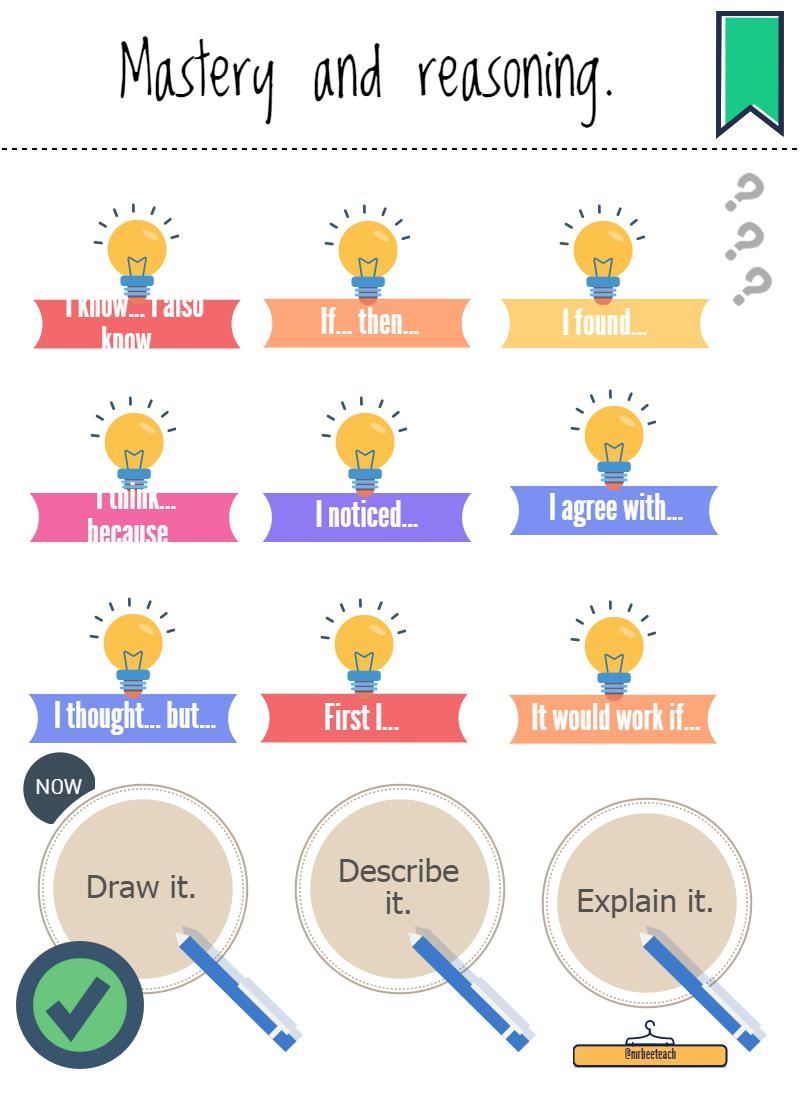
As the most recent KS2 Maths SATs tests proved, your pupils will need an in-depth understanding of facts and concepts to truly succeed. Plus, they will need to be able to use and apply that knowledge to a range of contexts. As such, it’s clear that we need to provide them with a strong foundation of reasoning skills to give them their very best shot at the assessments they must face.
- Maths Mastery Toolkit : A Practical Guide To Mastery Teaching And Learning
- Get to Grips with Maths Problem Solving KS2
- 21 Maths Challenges To Really Stretch Your More Able Pupils
- Maths Reasoning and Problem Solving CPD Powerpoint
- 20 Maths Strategies KS2 That Guarantee Progress
- Why You Should Be Incorporating Stem Sentences Into Your Primary Maths Teaching
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn how the programmes are aligned to maths mastery teaching or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
Related articles

Maths Problem Solving: Engaging Your Students And Strengthening Their Mathematical Skills

Free Year 7 Maths Test With Answers And Mark Scheme: Mixed Topic Questions

What Is A Number Square? Explained For Primary School Teachers, Parents & Pupils
What Is Numicon? Explained For Primary School Teachers, Parents And Pupils
FREE Guide to Maths Mastery
All you need to know to successfully implement a mastery approach to mathematics in your primary school, at whatever stage of your journey.
Ideal for running staff meetings on mastery or sense checking your own approach to mastery.
Privacy Overview

IMAGES
VIDEO
COMMENTS
Fluency, reasoning and problem solving are central strands of mathematical competency, as recognized by the National Council of Teachers of Mathematics (NCTM) and the National Research Council's report 'Adding It Up'. They are key components to the Standards of Mathematical Practice, standards that are interwoven into every mathematics ...
Now that we have an understanding of Mathematical Reasoning and the various terminologies and reasoning associated, we will go through two sample questions with an explanation to understand maths and reasoning in depth. Q1. Look at this series: 12, 10, 13, 11, 14, 12, ….
These are as follows, and are a great starting point to developing math reasoning at the elementary school level. 1. Start math lessons with a question. 2. Students need to wonder and struggle. 3. You are not the answer key. 4. Say yes to your students original ideas (but not yes to methodical answers)
Mathematical Reasoning is the foundation of problem-solving and critical thinking in mathematics. It involves the ability to analyze, deduce, and draw conclusions from mathematical concepts, principles, and relationships. In this guide, we will explore the key aspects of mathematical reasoning, provide examples to illustrate its application ...
Developing Excellence in Problem Solving with Young Learners. Age 5 to 11. Becoming confident and competent as a problem solver is a complex process that requires a range of skills and experience. In this article, Jennie suggests that we can support this process in three principal ways. Using NRICH Tasks to Develop Key Problem-solving Skills.
This is an essential element of mastering mathematics. As well as being part of the problem-solving process, we suggest that being able to prove is also the highest step on the reasoning journey (see our Reasoning Feature and particularly our article Reasoning: the Journey from Novice to Expert), following
Firstly, we have to use reasoning to recognise that information is missing. Secondly, we use reasoning to figure out what it is that we need to know. Thirdly, we use reasoning to draw on our existing knowledge and to work out that information. 6. When selecting a problem-solving skill.
Students frequently complain that mathematics is too difficult for them, because it is too abstract and unapproachable. Explaining mathematical reasoning and problem solving by using a variety of methods, such as words, numbers, symbols, charts, graphs, tables, diagrams, and concrete models can help students understand the problem better by ...
translate problems in mathematical or non-mathematical contexts into a process or a series of mathematical processes. make and use connections between different parts of mathematics. interpret results in the context of the given problem. evaluate methods used and results obtained. evaluate solutions to identify how they may have been affected ...
The ability to reason also supports the application of mathematics and an ability to solve problems set in unfamiliar contexts. Research by Nunes (2009) identified the ability to reason mathematically as the most important factor in a pupil's success in mathematics. It is therefore crucial that opportunities to develop mathematical reasoning ...
Mathematics provides a systematic and logical framework for problem-solving and critical thinking. The study of math helps to develop analytical skills, logical reasoning, and problem-solving abilities that can be applied to many areas of life.By using critical thinking skills to solve math problems, we can develop a deeper understanding of concepts, enhance our problem-solving skills, and ...
Brief. Problem solving plays an important role in mathematics and should have a prominent role in the mathematics education of K-12 students. However, knowing how to incorporate problem solving meaningfully into the mathematics curriculum is not necessarily obvious to mathematics teachers. (The term "problem solving" refers to mathematical ...
The Australian Curriculum: Mathematics aims to be relevant and applicable to the 21st century. The inclusion of the proficiencies of understanding, fluency, problem-solving and reasoning in the curriculum is to ensure that student learning and student independence are at the centre of the curriculum. The curriculum focuses on developing ...
This booklet contains over 40 reasoning and problem solving questions suitable for KS2 and KS3 classes. These are the questions that we have been putting out each day in March 2016 on Twitter in the run up to SATS. The answers are provided with some simple notes at the ... The White Rose Maths Hub Team . KS2
Fluency reasoning and problem solving have been central to the new maths national curriculum for primary schools introduced in 2014. Here we look at how these three approaches or elements of maths can be interwoven in a child's maths education through KS1 and KS2.
Develop fluency, reasoning and problem solving in Maths with the mastery approach. The skills of fluency, reasoning and problem solving are well-known to all primary Maths teachers, and in mastery teaching they play an essential role. To help you develop your mastery approach, we have hand-picked this selection of Maths resources, with ...
Here are five strategies to help students check their solutions. 1. Use the Inverse Operation. For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7.
pptx, 2.35 MB. pdf, 3.51 MB. These booklets each contain over 40 reasoning and problem solving questions suitable for KS1, KS2 and KS3 classes. These are the questions that we have been putting out each day in March 2016 on Twitter in the run up to SATS. The answers are provided with some simple notes at the back of the booklet and for some ...
Please check back soon, or follow our social media accounts for updates. Our maths problems of the day provide four problems across KS1, KS2 and Lower KS3 for pupils to solve. View our Maths resources from White Rose Maths.
Pattern spotting. Working backwards. Reasoning logically. Visualising. Conjecturing. The first two in this list are perhaps particularly helpful. As learners progress towards a solution, they may take the mathematics further (stage 3) and two more problem-solving skills become important: Generalising. Proving.
High Level Math Reasoning: The benchmark Graduate School Math (GSM8k) evaluates how well AI models can tackle advanced mathematical problems typically encountered in graduate-level studies. For instance, in a GSM8k test, an AI might be tasked with solving complex differential equations, proving mathematical theorems, or conducting advanced ...
the mathematical reasoning and problem-solving capabilities of large language models (LLMs). Algebra problems constitute 21.19% from Olympiad-level Competition and 17.83% from High School Mathematics, making them the most represented areas in the dataset.
Solving a math word problem requires selecting quantities in it and performing appropriate arithmetic operations to obtain the answer. For deep learning-based methods, it is vital to obtain good quantity representations, i.e., to selectively and emphatically aggregate information in the context of quantities.
Find full-length practice tests on Bluebook™ as well as downloadable paper (nonadaptive) practice tests to help you prepare for the SAT, PSAT/NMSQT, PSAT 10, and PSAT 8/9.
Large language models (LLMs) have significantly advanced natural language understanding and demonstrated strong problem-solving abilities. Despite these successes, most LLMs still struggle with solving mathematical problems due to the intricate reasoning required. This paper investigates the mathematical problem-solving capabilities of LLMs using the newly developed "MathOdyssey" dataset. The ...
Large language models (LLMs) have demonstrated impressive reasoning capabilities, particularly in textual mathematical problem-solving. However, existing open-source image instruction fine-tuning datasets, containing limited question-answer pairs per image, do not fully exploit visual information to enhance the multimodal mathematical reasoning capabilities of Multimodal LLMs (MLLMs). To ...
We present a simple formula to update the pseudoinverse of a full-rank rectangular matrix that undergoes a low-rank modification, and demonstrate its utility for solving least squares problems. The resulting algorithm can be dramatically faster than solving the modified least squares problem from scratch, just like the speedup enabled by Sherman--Morrison--Woodbury for solving linear systems ...
The Problem-solving Classroom. This article forms part of our Problem-solving Classroom Feature, exploring how to create a space in which mathematical problem solving can flourish. At NRICH, we believe that there are four main aspects to consider: • Highlighting key problem-solving skills. • Examining the teacher's role.
Enhance web development skills by mastering inductive reasoning for better problem-solving and logical analysis in coding challenges.
These tips can help instil greater depth in maths in your class for all ability levels. 1. Start lessons with a question. 2. Start lessons with a provocative mathematical statement and challenge your class to provide the mathematical proof: " N will always = N" or "Multiples of 9 always have the digital sum of 9". 3.