a visual representation of the real numbers

Examples for

Number Lines

A number line is an ordered visual representation of real numbers. Compare the size of numbers using number lines with Wolfram|Alpha. Solutions to inequalities or systems of inequalities typically involve unions of open or closed intervals that are easily visualized on a number line.

Represent numerical values and solutions to inequalities on a number line.

Plot a real number on a number line:

Visualize a set of real numbers on a number line:, show multiple sets on a number line:, create a dot plot of univariate data:, related examples.

• Real Intervals

Unlocking the Power of Real Numbers: A Comprehensive Chart Guide

Dive into the world of real numbers and explore the different types, properties, and charts that help visualize and understand these mathematical concepts.

Create an image featuring JavaScript code snippets and interview-related icons or graphics. Use a color scheme of yellows and blues. Include the title '7 Essential JavaScript Interview Questions for Freshers'.

Math Real Numbers Chart: A Comprehensive Guide

Introduction.

Real numbers are a fundamental concept in mathematics, and understanding them is crucial for success in various mathematical disciplines, including algebra, geometry, trigonometry, and calculus. A real numbers chart is a visual representation of the real number line, which helps to illustrate the relationships between different types of real numbers. In this blog post, we will delve into the world of real numbers, explore the different types of real numbers, and provide a comprehensive real numbers chart to help you better understand this essential mathematical concept.

What are Real Numbers?

Real numbers are a set of numbers that include all rational and irrational numbers. They can be expressed as a decimal expansion, and they have no terminating or repeating pattern. Real numbers can be positive, negative, or zero, and they can be represented on the number line.

Types of Real Numbers

Real numbers can be classified into several categories, including:

Rational Numbers

Rational numbers are real numbers that can be expressed as the ratio of two integers, i.e., p/q, where p and q are integers, and q is non-zero. Examples of rational numbers include:

• Integers: ..., -3, -2, -1, 0, 1, 2, 3, ...
• Fractions: 1/2, 3/4, 2/3, 5/6, ...

Irrational Numbers

Irrational numbers are real numbers that cannot be expressed as the ratio of two integers. They have an infinite number of digits that never repeat in a predictable pattern. Examples of irrational numbers include:

• Pi (π): 3.1415926535897932384626433832795...
• Euler's Number (e): 2.7182818284590452353602874713527...
• Square Root of 2: 1.4142135623730950488016887242097...

Algebraic Numbers

Algebraic numbers are real numbers that are the root of a polynomial equation with rational coefficients. Examples of algebraic numbers include:

• Cube Root of 2: 1.2599210498948731647672106072782...

Transcendental Numbers

Transcendental numbers are real numbers that are not the root of any polynomial equation with rational coefficients. Examples of transcendental numbers include:

Real Numbers Chart

Here is a comprehensive real numbers chart that illustrates the relationships between different types of real numbers:

In conclusion, real numbers are a fundamental concept in mathematics, and understanding the different types of real numbers is crucial for success in various mathematical disciplines. The real numbers chart provided in this blog post is a valuable resource for visualizing the relationships between different types of real numbers. By understanding the properties and characteristics of real numbers, you can develop a deeper appreciation for the beauty and complexity of mathematics.

What is the difference between rational and irrational numbers?

Rational numbers are real numbers that can be expressed as the ratio of two integers, while irrational numbers are real numbers that cannot be expressed as the ratio of two integers.

What is the difference between algebraic and transcendental numbers?

Algebraic numbers are real numbers that are the root of a polynomial equation with rational coefficients, while transcendental numbers are real numbers that are not the root of any polynomial equation with rational coefficients.

How can I remember the different types of real numbers?

A simple way to remember the different types of real numbers is to use the following mnemonic device: "RIATA" - Rational, Irrational, Algebraic, Transcendental, and Always (real numbers).

I hope this comprehensive guide to real numbers has been informative and helpful. If you have any questions or need further clarification on any of the concepts discussed in this blog post, please don't hesitate to ask.

Reset password New user? Sign up

Existing user? Log in

Representation on the Real Line

Already have an account? Log in here.

One way to visually represent the real numbers \(\mathbb{R}\) is by a real number line , a horizontal line such that each point on the line corresponds to a real number and each real number corresponds to a point on the line.

Representing Real Numbers

Since the number line represents all real numbers and since zero is a real number, there is a point on the line that represents zero (called the origin). Then the points on the line to the right of the origin represent positive numbers while the points on the line to the left of the origin represent negative numbers.

In the following visualization of the real number line, the integers are marked as evenly spaced points on the line, but the real number line also represents all real numbers in between the integers and extending to infinity in both directions.

In the problems below, we will assume that the evenly spaced tick marks correspond to integers, and one unit corresponds to the distance between consecutive integers.

On the number line pictured below, what is the real value represented by point \(a\)? Solution: Since the evenly spaced tick marks correspond to consecutive integers, we can label the tick marks around point \(a\) as follows: This shows point \(a\) represents the real value \(4\).

There are many useful properties of the real number line. Consider two real numbers \(a\) and \(b\) represented by points on the real number line such that the point \(a\) lies to the left of the point \(b\) on the line. Then the real numbers \(a\) and \(b\) satisfy

• \(a \leq b\)
• the distance between \(a\) and \(b\) is \( \lvert a - b \lvert = \lvert b - a \lvert \), or the length of the line segment with endpoints \(a\) and \(b\)

In other words, the points on the real number line respects the ordering of the real numbers. The real number line is useful in helping with visualizing addition, subtraction, and intervals of real numbers.

On the number line pictured below, which of the following is a possible value for the point \(a\)? A) 3.52 B) 1.89 C) 2.73 D) 4.65 Solution: Since the evenly spaced tick marks correspond to consecutive integers, we can label the tick marks around point \(a\) as follows: This shows that the real number \(a\) lies in between integers \(2\) and \(3\), and the only real number in the answers satisfying this property is 2.73, so the answer is (C)

What is the inequality represented by the red portion of the real number line? Solution: We first label the tick marks using the reference point corresponding to real number -1: Then the red portion of the real number line corresponds to all real numbers less than or equal to \(-3\), and the inequality is \(x \leq -3\).

Note that if the point \(a\) is the same as the point \(b\) on the number line, then

• the distance between \(a\) and \(b\) is \( \lvert a - b \lvert = 0\)

What is the length of the red line segment on the real number line? Solution: We first label the tick marks around the origin: The the length of the red line segment is \( \lvert 3 - (-2) \rvert = \lvert 3 + 2 \rvert = 5\). This can also be obtained by counting the number of units between the two points.

Mark the points on the real number line with distance \(5\) from the origin. Solution: The two points on the real number line with distance \(5\) from the origin are \(-5\) and \(5,\) which can be marked as follows:

Problem Loading...

Note Loading...

Set Loading...

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.1: Axioms of the Real Numbers

• Last updated
• Save as PDF
• Page ID 95441

• Northern Arizona University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

In this chapter we will take a deep dive into structure of the real numbers by building up the multitude of properties you are familiar with by starting with a collection of fundamental axioms. Recall that an axiom is a statement that is assumed to be true without proof. These are the basic building blocks from which all theorems are proved. It is worth pointing out that one can carefully construct the real numbers from the natural numbers. However, that will not be the approach we take. Instead, we will simply list the axioms that the real numbers satisfy

Our axioms for the real numbers fall into three categories:

• Field Axioms: These axioms provide the essential properties of arithmetic involving addition and subtraction.
• Order Axioms: These axioms provide the necessary properties of inequalities.
• Completeness Axiom: This axiom ensures that the familiar number line that we use to model the real numbers does not have any holes in it.

We begin with the Field Axioms.

Axioms 5.1. There exist operations \(+\) (addition) and \(\cdot\) (multiplication) on \(\mathbb{R}\) satisfying:

• (Associativity for Addition) For all \(a, b, c\in \mathbb{R}\) we have \((a+b)+c = a+(b+c)\) ;
• (Commutativity for Addition) For all \(a,b\in \mathbb{R}\) , we have \(a+b=b+a\) ;
• (Additive Identity) There exists \(0\in\mathbb{R}\) such that for all \(a\in\mathbb{R}\) , \(0+a=a\) ;
• (Additive Inverses) For all \(a\in\mathbb{R}\) there exists \(-a\in\mathbb{R}\) such that \(a+(-a)=0\) ;
• (Associativity for Multiplication) For all \(a, b, c\in \mathbb{R}\) we have \((ab)c = a(bc)\) ;
• (Commutativity for Multiplication) For all \(a,b\in \mathbb{R}\) , we have \(ab=ba\) ;
• (Multiplicative Identity) There exists \(1\in\mathbb{R}\) such that \(1\neq 0\) and for all \(a\in\mathbb{R}\) , \(1a=a\) ;
• (Multiplicative Inverses) For all \(a\in\mathbb{R}\setminus\{0\}\) there exists \(a^{-1}\in\mathbb{R}\) such that \(aa^{-1}=1\) .
• (Distributive Property) For all \(a,b,c\in \mathbb{R}\) , \(a(b+c)=ab+ac\) ;

In the language of abstract algebra, Axioms F1–F4 and F5–F8 make each of \(\mathbb{R}\) and \(\mathbb{R}\setminus\{0\}\) an abelian group under addition and multiplication, respectively. Axiom F9 provides a way for the operations of addition and multiplication to interact. Collectively, Axioms F1–F9 make the real numbers a field . It follows from the axioms that the elements \(0\) and \(1\) of \(\mathbb{R}\) are the unique additive and multiplicative identities in \(\mathbb{R}\) . To prove the following theorem, suppose \(0\) and \(0'\) are both additive identities in \(\mathbb{R}\) and then show that \(0=0'\) . This shows that there can only be one additive identity.

Theorem 5.2. The additive identity of \(\mathbb{R}\) is unique.

To prove the next theorem, mimic the approach you used to prove Theorem 5.2.

Theorem 5.3. The multiplicative identity of \(\mathbb{R}\) is unique.

For every \(a\in\mathbb{R}\) , the elements \(-a\) and \(a^{-1}\) (as long as \(a\neq 0\) ) are also the unique additive and multiplicative inverses , respectively.

Theorem 5.4. Every real number has a unique additive inverse.

Theorem 5.5. Every nonzero real number has a unique multiplicative inverse.

Since we are taking a formal axiomatic approach to the real numbers, we should make it clear how the natural numbers are embedded in \(\mathbb{R}\) .

Definition 5.6. We define the natural numbers , denoted by \(\mathbb{N}\) , to be the smallest subset of \(\mathbb{R}\) satisfying:

• \(1\in\mathbb{N}\) , and
• for all \(n\in\mathbb{N}\) , we have \(n+1\in\mathbb{N}\) .

Notice the similarity between the definition of the natural numbers presented above and the Axiom of Induction given in Section 4.1. Of course, we use the standard numeral system to represent the natural numbers, so that \(\mathbb{N}= \{1,2,3,4,5,6,7,8,9,10\ldots\}\) .

Given the natural numbers, Axiom F3/Theorem 5.2 and Axiom F4/Theorem 5.4 together with the operation of addition allow us to define the integers , denoted by \(\mathbb{Z}\) , in the obvious way. That is, the integers consist of the natural numbers together with the additive identity and all of the additive inverses of the natural numbers.

We now introduce some common notation that you are likely familiar with. Take a moment to think about why the following is a definition as opposed to an axiom or theorem.

Definition 5.7. For every \(a,b\in\mathbb{R}\) and \(n\in\mathbb{Z}\) , we define the following:

• \(a-b:= a+(-b)\)
• \(\displaystyle\frac{a}{b}:= ab^{-1}\) (for \(b\neq 0\) )
• \(\displaystyle a^n:= \begin{cases} \overbrace{aa\cdots a}^n, &\text{if }n\in \mathbb{N}\\ 1, & \text{if }n=0\text{ and }a\neq 0\\ \displaystyle\frac{1}{a^{-n}}, & \text{if }-n\in \mathbb{N}\text{ and }a\neq 0 \end{cases}\)

The set of rational numbers , denoted by \(\mathbb{Q}\) , is defined to be the collection of all real numbers having the form given in Part (b) of Definition 5.7 The irrational numbers are defined to be \(\mathbb{R}\setminus\mathbb{Q}\) .

Using the Field Axioms, we can prove each of the statements in the following theorem.

Theorem 5.8. For all \(a,b,c\in\mathbb{R}\) , we have the following:

• \(a=b\) if and only if \(a+c=b+c\) ;
• \(-a=(-1)a\) ;
• \((-1)^2 = 1\) ;
• \(-(-a)=a\) ;
• If \(a\neq 0\) , then \((a^{-1})^{-1}=a\) ;
• If \(a\neq 0\) and \(ab = ac\) , then \(b = c\) .
• If \(ab=0\) , then either \(a=0\) or \(b=0\) .

Carefully prove the next theorem by explicitly citing where you are utilizing the Field Axioms and Theorem 5.8.

Theorem 5.9. For all \(a,b\in\mathbb{R}\) , we have \((a+b)(a-b)=a^2-b^2\) .

We now introduce the Order Axioms of the real numbers.

Axioms 5.10. For \(a,b,c\in \mathbb{R}\) , there is a relation \(<\) on \(\mathbb{R}\) satisfying:

• (Trichotomy Law) If \(a\neq b\) , then either \(a<b\) or \(b<a\) but not both;
• (Transitivity) If \(a<b\) and \(b<c\) , then \(a<c\) ;
• If \(a<b\) , then \(a+c<b+c\) ;
• If \(a<b\) and \(0<c\) , then \(ac<bc\) ;

Given Axioms 1–4, we say that the real numbers are a linearly ordered field . We call numbers greater than zero positive and those greater than or equal to zero nonnegative . There are similar definitions for negative and nonpositive .

Notice that the Order Axioms are phrased in terms of “ \(<\) ". We would also like to be able to utilize “ \(>\) ", “ \(\leq\) ", and “ \(\geq\) ".

Definition 5.11. For \(a,b\in\mathbb{R}\) , we define:

• \(a>b\) if \(b<a\) ;
• \(a\leq b\) if \(a<b\) or \(a=b\) ;
• \(a\geq b\) if \(b\leq a\) .

Notice that we took the existence of the inequalities “ \(<\) ", “ \(>\) ", “ \(\leq\) ", and “ \(\geq\) " on the real numbers for granted when we defined intervals of real numbers in Definition 3.4.

Using the Order Axioms, we can prove many familiar facts.

Theorem 5.12. For all \(a,b\in\mathbb{R}\) , if \(a,b>0\) , then \(a+b>0\) ; and if \(a,b<0\) , then \(a+b<0\) .

The next result extends Axiom 3.

Theorem 5.13. For all \(a,b,c,d\in\mathbb{R}\) , if \(a<b\) and \(c<d\) , then \(a+c<b+d\) .

Theorem 5.14. For all \(a\in\mathbb{R}\) , \(a>0\) if and only if \(-a<0\) .

Theorem 5.15. If \(a\) , \(b\) , \(c\) , and \(d\) are positive real numbers such that \(a<b\) and \(c<d\) , then \(ac<bd\) .

Theorem 5.16. For all \(a,b\in\mathbb{R}\) , we have the following:

• \(ab>0\) if and only if either \(a,b>0\) or \(a,b<0\) ;
• \(ab<0\) if and only if \(a<0<b\) or \(b<0<a\) .

Theorem 5.17. For all positive real numbers \(a\) and \(b\) , \(a< b\) if and only if \(a^2< b^2\) .

Consider using three cases when approaching the proof of the following theorem.

Theorem 5.18. For all \(a\in\mathbb{R}\) , we have \(a^2\geq 0\) .

It might come as a surprise that the following result requires proof.

Theorem 5.19. We have \(0<1\) .

The previous theorem together with Theorem 5.14 implies that \(-1<0\) as you expect. It also follows from Axiom O3 that for all \(n\in\mathbb{Z}\) , we have \(n<n+1\) . We assume that there are no integers between \(n\) and \(n+1\) .

Theorem 5.20. For all \(a\in\mathbb{R}\) , if \(a>0\) , then \(a^{-1}>0\) , and if \(a<0\) , then \(a^{-1}<0\) .

Theorem 5.21. For all \(a,b\in \mathbb{R}\) , if \(a<b\) , then \(-b<-a\) .

The last few results allow us to take for granted our usual understanding of which real numbers are positive and which are negative. The next theorem yields a result that extends Theorem 5.21.

Theorem 5.22. For all \(a,b,c\in \mathbb{R}\) , if \(a<b\) and \(c<0\) , then \(bc<ac\) .

There is a special function that we can now introduce.

Definition 5.23. Given \(a\in\mathbb{R}\) , we define the absolute value of \(a\) , denoted \(|a|\) , via \[|a|:= \begin{cases} a, & \text{if }a\geq 0\\ -a, & \text{if }a<0. \end{cases}\]

Theorem 5.24. For all \(a\in\mathbb{R}\) , \(|a|\geq 0\) with equality only if \(a=0\) .

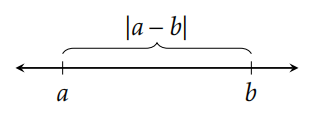
We can interpret \(|a|\) as the distance between \(a\) and 0 as depicted in Figure 5.1.

Theorem 5.25. For all \(a,b\in\mathbb{R}\) , we have \(|a-b|=|b-a|\) .

Given two points \(a\) and \(b\) , \(|a-b|\) , and hence \(|b-a|\) by the previous theorem, is the distance between \(a\) and \(b\) as shown in Figure 5.2.

Theorem 5.26. For all \(a,b\in\mathbb{R}\) , \(|ab|=|a||b|\) .

In the next theorem, writing \(\pm a\leq b\) is an abbreviation for \(a\leq b\) and \(-a\leq b\) .

Theorem 5.27. For all \(a,b\in\mathbb{R}\) , if \(\pm a\leq b\) , then \(|a|\leq b\) .

Theorem 5.28. For all \(a\in\mathbb{R}\) , \(|a|^2=a^2\) .

Theorem 5.29. For all \(a\in\mathbb{R}\) , \(\pm a\leq |a|\) .

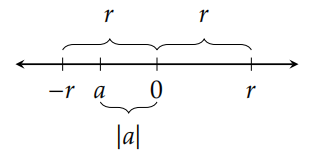
Theorem 5.30. For all \(a,r\in\mathbb{R}\) with \(r\) nonnegative, \(|a|\leq r\) if and only if \(-r\leq a\leq r\) .

The letter \(r\) was used in the previous theorem because it is the first letter of the word “radius". If \(r\) is positive, we can think of the interval \((-r,r)\) as the interior of a one-dimensional circle with radius \(r\) centered at 0. Figure 5.3 provides a visual interpretation of Theorem 5.30.

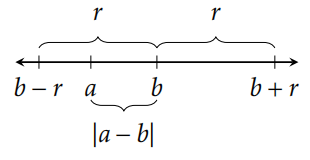
Corollary 5.31. For all \(a,b,r\in\mathbb{R}\) with \(r\) nonnegative, \(|a-b|\leq r\) if and only if \(b-r\leq a\leq b+r\) .

Since \(|a-b|\) represents the distance between \(a\) and \(b\) , we can interpret \(|a-b|\leq r\) as saying that the distance between \(a\) and \(b\) is less than or equal to \(r\) . In other words, \(a\) is within \(r\) units of \(b\) . See Figure 5.4.

Consider using Theorems 5.29 and 5.30 when attacking the next result, which is known as the Triangle Inequality . This result can be extremely useful in some contexts.

Theorem 5.32. For all \(a,b\in\mathbb{R}\) , \(|a+b|\leq |a|+|b|\) .

Figure 5.5 depicts two of the cases for the Triangle Inequality.

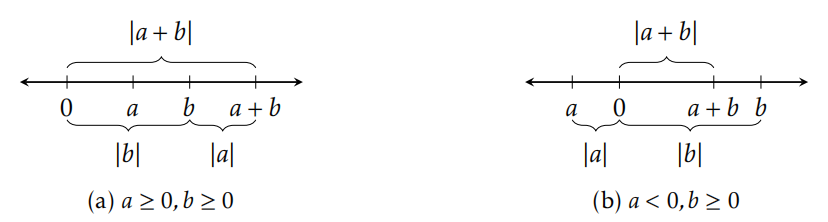
Problem 5.33. Under what conditions do we have equality for the Triangle Inequality?

Where did the Triangle Inequality get its name? Why “Triangle"? For any triangle (including degenerate triangles), the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. That is, if \(x\) , \(y\) , and \(z\) are the lengths of the sides of the triangle, then \(z\leq x+y\) , where we have equality only in the degenerate case of a triangle with no area. In linear algebra, the Triangle Inequality is a theorem about lengths of vectors. If \(\mathbf{a}\) and \(\mathbf{b}\) are vectors in \(\mathbb{R}^n\) , then the Triangle Inequality states that \(\lVert \mathbf{a}+\mathbf{b}\rVert \leq \lVert\mathbf{a}\rVert +\lVert\mathbf{b}\rVert\) . Note that \(\lVert \mathbf{a}\rVert\) denotes the length of vector \(\mathbf{a}\) . See Figure 5.6. The version of the Triangle Inequality that we presented in Theorem 5.32 is precisely the one-dimensional version of the Triangle Inequality in terms of vectors.

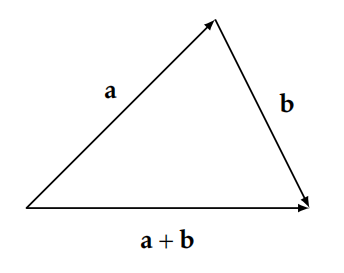
The next theorem is sometimes called the Reverse Triangle Inequality .

Theroem 5.34. For all \(a,b\in\mathbb{R}\) , \(|a-b|\geq \left||a|-|b| \right|\) .

Before we introduce the Completeness Axiom, we need some additional terminology.

Definition 5.35. Let \(A\subseteq \mathbb{R}\) . A point \(b\) is called an upper bound of \(A\) if for all \(a\in A\) , \(a\leq b\) . The set \(A\) is said to be bounded above if it has an upper bound.

Problem 5.36. The notion of a lower bound and the property of a set being bounded below are defined similarly. Try defining them.

Problem 5.37. Find all upper bounds and all lower bounds for each of the following sets when they exist.

• \(\{5,11,17,42,103\}\)
• \(\mathbb{N}\)
• \(\mathbb{Z}\)
• \((0,1]\cap \mathbb{Q}\)
• \((0,\infty)\)
• \(\{\frac{1}{n}\mid n\in\mathbb{N}\}\)
• \(\{\frac{1}{n}\mid n\in\mathbb{N}\}\cup\{0\}\)
• \(\emptyset\)

Definition 5.38. A set \(A\subseteq \mathbb{R}\) is bounded if \(A\) is bounded above and below.

Notice that a set \(A\subseteq\mathbb{R}\) is bounded if and only if it is a subset of some bounded closed interval.

Definition 5.39. Let \(A\subseteq \mathbb{R}\) . A point \(p\) is a supremum (or least upper bound ) of \(A\) if \(p\) is an upper bound of \(A\) and \(p\leq b\) for every upper bound \(b\) of \(A\) . Analogously, a point \(p\) is an infimum (or greatest lower bound ) of \(A\) if \(p\) is a lower bound of \(A\) and \(p\geq b\) for every lower bound \(b\) of \(A\) .

Our next result tells us that a supremum of a set and an infimum of a set are unique when they exist.

Theorem 5.40. If \(A\subseteq \mathbb{R}\) such that a supremum (respectively, infimum) of \(A\) exists, then the supremum (respectively, infimum) of \(A\) is unique.

In light of the previous theorem, if the supremum of \(A\) exists, it is denoted by \(\sup(A)\) . Similarly, if the infimum of \(A\) exists, it is denoted by \(\inf(A)\) .

Problem 5.41. Find the supremum and the infimum of each of the sets in Problem 5.37 when they exist.

It is important to recognize that the supremum or infimum of a set may or may not be contained in the set. In particular, we have the following theorem concerning suprema and maximums. The analogous result holds for infima and minimums.

Theorem 5.42. Let \(A\subseteq \mathbb{R}\) . Then \(A\) has a maximum if and only if \(A\) has a supremum and \(\sup(A)\in A\) , in which case the \(\max(A)=\sup(A)\) .

Intuitively, a point is the supremum of a set \(A\) if and only if no point smaller than the supremum can be an upper bound of \(A\) . The next result makes this more precise.

Theorem 5.43. Let \(A\subseteq \mathbb{R}\) such that \(A\) is bounded above and let \(b\) be an upper bound of \(A\) . Then \(b\) is the supremum of \(A\) if and only if for every \(\varepsilon >0\) , there exists \(a\in A\) such that \(b-\varepsilon <a\) .

Problem 5.44. State and prove the analogous result to Theorem 5.43 involving infimum.

The following axiom states that every nonempty subset of the real numbers that has an upper bound has a least upper bound.

Axioms 5.45. If \(A\) is a nonempty subset of \(\mathbb{R}\) that is bounded above, then \(\sup(A)\) exists.

Given the Completeness Axiom, we say that the real numbers satisfy the least upper bound property . It is worth mentioning that we do not need the Completeness Axiom to conclude that every nonempty subset of the integers that is bounded above has a supremum, as this follows from Theorem 4.40 (a generalized version of the Well-Ordering Principle).

Certainly, the real numbers also satisfy the analogous result involving infimum.

Theorem 5.46. If \(A\) is a nonempty subset of \(\mathbb{R}\) that is bounded below, then \(\inf(A)\) exists.

Our next result, called the Archimedean Property , tells us that for every real number, we can always find a natural number that is larger. To prove this theorem, consider a proof by contradiction and then utilize the Completeness Axiom and Theorem 5.43.

Theorem 5.47. For every \(x\in\mathbb{R}\) , there exists \(n\in\mathbb{N}\) such that \(x<n\) .

More generally, we can “squeeze" every real number between a pair of integers. The next result is sometimes referred to at the Generalized Archimedean Property .

Theorem 5.48. For every \(x\in\mathbb{R}\) , there exists \(k,n\in\mathbb{Z}\) such that \(k<x<n\) .

Theorem 5.49. For any positive real number \(x\) , there exists \(N\in \mathbb{N}\) such that \(0<\frac{1}{N}<x\) .

The next theorem strengthens the Generalized Archimedean Property and says that every real number is either an integer or lies between a pair of consecutive integers. To prove this theorem, let \(x\in\mathbb{R}\) and define \(L=\{k\in\mathbb{Z}\mid k\leq x\}\) . Use the Generalized Archimedean Property to conclude that \(L\) is nonempty and then utilize Theorem 4.40.

Theorem 5.50. For every \(x\in\mathbb{R}\) , there exists \(n\in \mathbb{Z}\) such that \(n\leq x<n+1\) .

To prove the next theorem, let \(a<b\) , utilize Theorem 5.49 on \(b-a\) to obtain \(N\in\mathbb{N}\) such that \(\frac{1}{N}<b-a\) , and then apply Theorem 5.50 to \(Na\) to conclude that there exists \(n\in\mathbb{N}\) such that \(n\leq Na<n+1\) . Lastly, argue that \(\frac{n+1}{N}\) is the rational number you seek.

Theorem 5.51. If \((a,b)\) is an open interval, then there exists a rational number \(p\) such that \(p\in(a,b)\) .

Recall that the real numbers consist of rational and irrational numbers. Two examples of an irrational number that you are likely familiar with are \(\pi\) and \(\sqrt{2}\) . In Section 6.2, we will prove that \(\sqrt{2}\) is irrational, but for now we will take this fact for granted. It turns out that \(\sqrt{2}\approx 1.41421356237\in (1,2)\) . This provides an example of an irrational number occurring between a pair of distinct rational numbers. The following theorem is a good challenge to generalize this.

Theorem 5.52. If \((a,b)\) is an open interval, then there exists an irrational number \(p\) such that \(p\in(a,b)\) .

Repeated applications of the previous two theorems implies that every open interval contains infinitely many rational numbers and infinitely many irrational numbers. In light of these two theorems, we say that both the rationals and irrationals are dense in the real numbers.

Module 1: Algebra Essentials

Real numbers, learning outcomes.

• Classify a real number.
• Perform calculations using order of operations.
• Use the properties of real numbers.
• Evaluate and simplify algebraic expressions.

Because of the evolution of the number system, we can now perform complex calculations using several categories of real numbers. In this section we will explore sets of numbers, perform calculations with different kinds of numbers, and begin to learn about the use of numbers in algebraic expressions.

Classify a Real Number

The numbers we use for counting, or enumerating items, are the natural numbers : 1, 2, 3, 4, 5, and so on. We describe them in set notation as {1, 2, 3, …} where the ellipsis (…) indicates that the numbers continue to infinity. The natural numbers are, of course, also called the counting numbers . Any time we enumerate the members of a team, count the coins in a collection, or tally the trees in a grove, we are using the set of natural numbers. The set of whole numbers is the set of natural numbers plus zero: {0, 1, 2, 3,…}.

The set of integers adds the opposites of the natural numbers to the set of whole numbers: {…,-3, -2, -1, 0, 1, 2, 3,…}. It is useful to note that the set of integers is made up of three distinct subsets: negative integers, zero, and positive integers. In this sense, the positive integers are just the natural numbers. Another way to think about it is that the natural numbers are a subset of the integers.

The set of rational numbers is written as [latex]\left\{\frac{m}{n}|m\text{ and }{n}\text{ are integers and }{n}\ne{ 0 }\right\}[/latex]. Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never 0. We can also see that every natural number, whole number, and integer is a rational number with a denominator of 1.

Because they are fractions, any rational number can also be expressed in decimal form. Any rational number can be represented as either:

• a terminating decimal: [latex]\frac{15}{8}=1.875[/latex], or
• a repeating decimal: [latex]\frac{4}{11}=0.36363636\dots =0.\overline{36}[/latex]

We use a line drawn over the repeating block of numbers instead of writing the group multiple times.

Example: Writing Integers as Rational Numbers

Write each of the following as a rational number.

Write a fraction with the integer in the numerator and 1 in the denominator.

• [latex]7=\dfrac{7}{1}[/latex]
• [latex]0=\dfrac{0}{1}[/latex]
• [latex]-8=-\dfrac{8}{1}[/latex]
• [latex]\dfrac{11}{1}[/latex]
• [latex]\dfrac{3}{1}[/latex]
• [latex]-\dfrac{4}{1}[/latex]

Example: Identifying Rational Numbers

Write each of the following rational numbers as either a terminating or repeating decimal.

• [latex]-\dfrac{5}{7}[/latex]
• [latex]\dfrac{15}{5}[/latex]
• [latex]\dfrac{13}{25}[/latex]

Write each fraction as a decimal by dividing the numerator by the denominator.

• [latex]-\dfrac{5}{7}=-0.\overline{714285}[/latex], a repeating decimal
• [latex]\dfrac{15}{5}=3[/latex] (or 3.0), a terminating decimal
• [latex]\dfrac{13}{25}=0.52[/latex], a terminating decimal

Irrational Numbers

At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not 2 or even [latex]\frac{3}{2}[/latex], but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than 3, but still not a rational number. Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers . Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. So we write this as shown.

Example: Differentiating Rational and Irrational Numbers

Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.

• [latex]\sqrt{25}[/latex]
• [latex]\dfrac{33}{9}[/latex]
• [latex]\sqrt{11}[/latex]
• [latex]\dfrac{17}{34}[/latex]
• [latex]0.3033033303333\dots[/latex]
• [latex]\sqrt{25}:[/latex] This can be simplified as [latex]\sqrt{25}=5[/latex]. Therefore, [latex]\sqrt{25}[/latex] is rational.
• [latex]\sqrt{11}:[/latex] This cannot be simplified any further. Therefore, [latex]\sqrt{11}[/latex] is an irrational number.
• 0.3033033303333… is not a terminating decimal. Also note that there is no repeating pattern because the group of 3s increases each time. Therefore it is neither a terminating nor a repeating decimal and, hence, not a rational number. It is an irrational number.

Given any number n , we know that n is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers . As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative.

The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as 0, with negative numbers to the left of 0 and positive numbers to the right of 0. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of 0. Any real number corresponds to a unique position on the number line. The converse is also true: each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line .

The real number line

Example: Classifying Real Numbers

Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?

• [latex]-\dfrac{10}{3}[/latex]
• [latex]\sqrt{5}[/latex]
• [latex]-\sqrt{289}[/latex]
• [latex]-6\pi[/latex]
• [latex]0.616161\dots[/latex]
• [latex] 0.13 [/latex]
• [latex]-\dfrac{10}{3}[/latex] is negative and rational. It lies to the left of 0 on the number line.
• [latex]\sqrt{5}[/latex] is positive and irrational. It lies to the right of 0.
• [latex]-\sqrt{289}=-\sqrt{{17}^{2}}=-17[/latex] is negative and rational. It lies to the left of 0.
• [latex]-6\pi [/latex] is negative and irrational. It lies to the left of 0.
• [latex]0.616161\dots [/latex] is a repeating decimal so it is rational and positive. It lies to the right of 0.
• [latex] 0.13 [/latex] is a finite decimal and may be written as 13/100.  So it is rational and positive.
• [latex]\sqrt{73}[/latex]
• [latex]-11.411411411\dots [/latex]
• [latex]\dfrac{47}{19}[/latex]
• [latex]-\dfrac{\sqrt{5}}{2}[/latex]
• [latex]6.210735[/latex]
• positive, irrational; right
• negative, rational; left
• positive, rational; right
• negative, irrational; left

Sets of Numbers as Subsets

Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram.

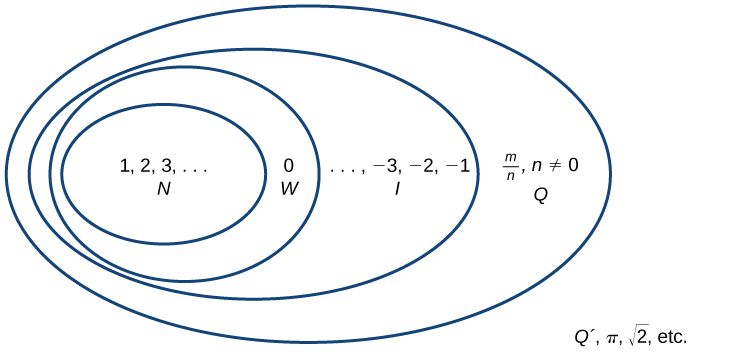
Sets of numbers.   N : the set of natural numbers   W : the set of whole numbers   I : the set of integers   Q : the set of rational numbers   Q´ : the set of irrational numbers

A General Note: Sets of Numbers

The set of natural numbers includes the numbers used for counting: [latex]\{1,2,3,\dots\}[/latex].

The set of whole numbers is the set of natural numbers plus zero: [latex]\{0,1,2,3,\dots\}[/latex].

The set of integers adds the negative natural numbers to the set of whole numbers: [latex]\{\dots,-3,-2,-1,0,1,2,3,\dots\}[/latex].

The set of rational numbers includes fractions written as [latex]\{\frac{m}{n}|m\text{ and }n\text{ are integers and }n\ne 0\}[/latex].

The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: [latex]\{h|h\text{ is not a rational number}\}[/latex].

Example: Differentiating the Sets of Numbers

Classify each number as being a natural number, whole number, integer, rational number, and/or irrational number.

• [latex]\sqrt{36}[/latex]
• [latex]\dfrac{8}{3}[/latex]
• [latex]-6[/latex]
• [latex]3.2121121112\dots [/latex]

Classify each number as being a natural number ( N ), whole number ( W ), integer ( I ), rational number ( Q ), and/or irrational number ( Q’ ).

• [latex]-\dfrac{35}{7}[/latex]
• [latex]0[/latex]
• [latex]\sqrt{169}[/latex]
• [latex]\sqrt{24}[/latex]
• [latex]4.763763763\dots [/latex]

Properties of Real Numbers

When we multiply a number by itself, we square it or raise it to a power of 2. For example, [latex]{4}^{2}=4\cdot 4=16[/latex]. We can raise any number to any power. In general, the exponential notation [latex]{a}^{n}[/latex] means that the number or variable [latex]a[/latex] is used as a factor [latex]n[/latex] times.

In this notation, [latex]{a}^{n}[/latex] is read as the n th power of [latex]a[/latex], where [latex]a[/latex] is called the base and [latex]n[/latex] is called the exponent . A term in exponential notation may be part of a mathematical expression, which is a combination of numbers and operations. For example, [latex]24+6\cdot \frac{2}{3}-{4}^{2}[/latex] is a mathematical expression.

To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations . This is a sequence of rules for evaluating such expressions.

Recall that in mathematics we use parentheses ( ), brackets [ ], and braces { } to group numbers and expressions so that anything appearing within the symbols is treated as a unit. Additionally, fraction bars, radicals, and absolute value bars are treated as grouping symbols. When evaluating a mathematical expression, begin by simplifying expressions within grouping symbols.

The next step is to address any exponents or radicals. Afterward, perform multiplication and division from left to right and finally addition and subtraction from left to right.

Let’s take a look at the expression provided.

There are no grouping symbols, so we move on to exponents or radicals. The number 4 is raised to a power of 2, so simplify [latex]{4}^{2}[/latex] as 16.

Next, perform multiplication or division, left to right.

Lastly, perform addition or subtraction, left to right.

Therefore, [latex]24+6\cdot \dfrac{2}{3}-{4}^{2}=12[/latex].

For some complicated expressions, several passes through the order of operations will be needed. For instance, there may be a radical expression inside parentheses that must be simplified before the parentheses are evaluated. Following the order of operations ensures that anyone simplifying the same mathematical expression will get the same result.

A General Note: Order of Operations

Operations in mathematical expressions must be evaluated in a systematic order, which can be simplified using the acronym PEMDAS :

P (arentheses)

E (xponents)

M (ultiplication) and D (ivision)

A (ddition) and S (ubtraction)

How To: Given a mathematical expression, simplify it using the order of operations.

• Simplify any expressions within grouping symbols.
• Simplify any expressions containing exponents or radicals.
• Perform any multiplication and division in order, from left to right.
• Perform any addition and subtraction in order, from left to right.

Example: Using the Order of Operations

Use the order of operations to evaluate each of the following expressions.

• [latex]{\left(3\cdot 2\right)}^{2}-4\left(6+2\right)[/latex]
• [latex]\dfrac{{5}^{2}-4}{7}-\sqrt{11 - 2}[/latex]
• [latex]6-|5 - 8|+3\left(4 - 1\right)[/latex]
• [latex]\dfrac{14 - 3\cdot 2}{2\cdot 5-{3}^{2}}[/latex]
• [latex]7\left(5\cdot 3\right)-2\left[\left(6 - 3\right)-{4}^{2}\right]+1[/latex]

[latex]\begin{align}\left(3\cdot 2\right)^{2} & =\left(6\right)^{2}-4\left(8\right) && \text{Simplify parentheses} \\ & =36-4\left(8\right) && \text{Simplify exponent} \\ & =36-32 && \text{Simplify multiplication} \\ & =4 && \text{Simplify subtraction}\end{align}[/latex]

[latex]\begin{align}\frac{5^{2}-4}{7}-\sqrt{11-2} & =\frac{5^{2}-4}{7}-\sqrt{9} && \text{Simplify grouping systems (radical)} \\ & =\frac{5^{2}-4}{7}-3 && \text{Simplify radical} \\ & =\frac{25-4}{7}-3 && \text{Simplify exponent} \\ & =\frac{21}{7}-3 && \text{Simplify subtraction in numerator} \\ & =3-3 && \text{Simplify division} \\ & =0 && \text{Simplify subtraction}\end{align}[/latex]

Note that in the first step, the radical is treated as a grouping symbol, like parentheses. Also, in the third step, the fraction bar is considered a grouping symbol so the numerator is considered to be grouped.

[latex]\begin{align}6-|5-8|+3\left(4-1\right) & =6-|-3|+3\left(3\right) && \text{Simplify inside grouping system} \\ & =6-3+3\left(3\right) && \text{Simplify absolute value} \\ & =6-3+9 && \text{Simplify multiplication} \\ & =3+9 && \text{Simplify subtraction} \\ & =12 && \text{Simplify addition}\end{align}[/latex]

[latex]\begin{align}\frac{14-3\cdot2}{2\cdot5-3^{2}} & =\frac{14-3\cdot2}{2\cdot5-9} && \text{Simplify exponent} \\ & =\frac{14-6}{10-9} && \text{Simplify products} \\ & =\frac{8}{1} && \text{Simplify quotient} \\ & =8 && \text{Simplify quotient}\end{align}[/latex] In this example, the fraction bar separates the numerator and denominator, which we simplify separately until the last step.

[latex]\begin{align}7\left(5\cdot3\right)-2[\left(6-3\right)-4^{2}]+1 & =7\left(15\right)-2[\left(3\right)-4^{2}]+1 && \text{Simplify inside parentheses} \\ & 7\left(15\right)-2\left(3-16\right)+1 && \text{Simplify exponent} \\ & =7\left(15\right)-2\left(-13\right)+1 && \text{Subtract} \\ & =105+26+1 && \text{Multiply} \\ & =132 && \text{Add}\end{align}[/latex]

Watch the following video for more examples of using the order of operations to simplify an expression.

Using Properties of Real Numbers

For some activities we perform, the order of certain operations does not matter, but the order of other operations does. For example, it does not make a difference if we put on the right shoe before the left or vice-versa. However, it does matter whether we put on shoes or socks first. The same thing is true for operations in mathematics.

Commutative Properties

The commutative property of addition states that numbers may be added in any order without affecting the sum.

We can better see this relationship when using real numbers.

Similarly, the commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.

Again, consider an example with real numbers.

It is important to note that neither subtraction nor division is commutative. For example, [latex]17 - 5[/latex] is not the same as [latex]5 - 17[/latex]. Similarly, [latex]20\div 5\ne 5\div 20[/latex].

Associative Properties

The associative property of multiplication tells us that it does not matter how we group numbers when multiplying. We can move the grouping symbols to make the calculation easier, and the product remains the same.

Consider this example.

The associative property of addition tells us that numbers may be grouped differently without affecting the sum.

This property can be especially helpful when dealing with negative integers. Consider this example.

Are subtraction and division associative? Review these examples.

As we can see, neither subtraction nor division is associative.

Distributive Property

The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.

This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.

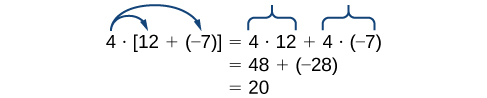
Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.

To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.

Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.

A special case of the distributive property occurs when a sum of terms is subtracted.

For example, consider the difference [latex]12-\left(5+3\right)[/latex]. We can rewrite the difference of the two terms 12 and [latex]\left(5+3\right)[/latex] by turning the subtraction expression into addition of the opposite. So instead of subtracting [latex]\left(5+3\right)[/latex], we add the opposite.

Now, distribute [latex]-1[/latex] and simplify the result.

This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.

Identity Properties

The identity property of addition states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.

The identity property of multiplication states that there is a unique number, called the multiplicative identity (1) that, when multiplied by a number, results in the original number.

For example, we have [latex]\left(-6\right)+0=-6[/latex] and [latex]23\cdot 1=23[/latex]. There are no exceptions for these properties; they work for every real number, including 0 and 1.

Inverse Properties

The inverse property of addition states that, for every real number a , there is a unique number, called the additive inverse (or opposite), denoted− a , that, when added to the original number, results in the additive identity, 0.

For example, if [latex]a=-8[/latex], the additive inverse is 8, since [latex]\left(-8\right)+8=0[/latex].

The inverse property of multiplication holds for all real numbers except 0 because the reciprocal of 0 is not defined. The property states that, for every real number a , there is a unique number, called the multiplicative inverse (or reciprocal), denoted [latex]\frac{1}{a}[/latex], that, when multiplied by the original number, results in the multiplicative identity, 1.

For example, if [latex]a=-\frac{2}{3}[/latex], the reciprocal, denoted [latex]\frac{1}{a}[/latex], is [latex]-\frac{3}{2}[/latex] because

A General Note: Properties of Real Numbers

The following properties hold for real numbers a , b , and c .

Example: Using Properties of Real Numbers

Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.

• [latex]3\cdot 6+3\cdot 4[/latex]
• [latex]\left(5+8\right)+\left(-8\right)[/latex]
• [latex]6-\left(15+9\right)[/latex]
• [latex]\dfrac{4}{7}\cdot \left(\frac{2}{3}\cdot \dfrac{7}{4}\right)[/latex]
• [latex]100\cdot \left[0.75+\left(-2.38\right)\right][/latex]

[latex]\begin{align}3\cdot6+3\cdot4 &=3\cdot\left(6+4\right) && \text{Distributive property} \\ &=3\cdot10 && \text{Simplify} \\ & =30 && \text{Simplify}\end{align}[/latex]

[latex]\begin{align}\left(5+8\right)+\left(-8\right) &=5+\left[8+\left(-8\right)\right] &&\text{Associative property of addition} \\ &=5+0 && \text{Inverse property of addition} \\ &=5 &&\text{Identity property of addition}\end{align}[/latex]

[latex]\begin{align}6-\left(15+9\right) & =6+(-15-9) && \text{Distributive property} \\ & =6+\left(-24\right) && \text{Simplify} \\ & =-18 && \text{Simplify}\end{align}[/latex]

[latex]\begin{align}\frac{4}{7}\cdot\left(\frac{2}{3}\cdot\frac{7}{4}\right) & =\frac{4}{7} \cdot\left(\frac{7}{4}\cdot\frac{2}{3}\right) && \text{Commutative property of multiplication} \\ & =\left(\frac{4}{7}\cdot\frac{7}{4}\right)\cdot\frac{2}{3} && \text{Associative property of multiplication} \\ & =1\cdot\frac{2}{3} && \text{Inverse property of multiplication} \\ & =\frac{2}{3} && \text{Identity property of multiplication}\end{align}[/latex]

[latex]\begin{align}100\cdot[0.75+\left(-2.38\right)] & =100\cdot0.75+100\cdot\left(-2.38\right) && \text{Distributive property} \\ & =75+\left(-238\right) && \text{Simplify} \\ & =-163 && \text{Simplify}\end{align}[/latex]

• [latex]\left(-\dfrac{23}{5}\right)\cdot \left[11\cdot \left(-\dfrac{5}{23}\right)\right][/latex]
• [latex]5\cdot \left(6.2+0.4\right)[/latex]
• [latex]18-\left(7 - 15\right)[/latex]
• [latex]\dfrac{17}{18}+\cdot \left[\dfrac{4}{9}+\left(-\dfrac{17}{18}\right)\right][/latex]
• [latex]6\cdot \left(-3\right)+6\cdot 3[/latex]
• 11, commutative property of multiplication, associative property of multiplication, inverse property of multiplication, identity property of multiplication;
• 33, distributive property;
• 26, distributive property;
• [latex]\dfrac{4}{9}[/latex], commutative property of addition, associative property of addition, inverse property of addition, identity property of addition;
• 0, distributive property, inverse property of addition, identity property of addition

Evaluate and Simplify Algebraic Expressions

So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as [latex]x+5,\frac{4}{3}\pi {r}^{3}[/latex], or [latex]\sqrt{2{m}^{3}{n}^{2}}[/latex]. In the expression [latex]x+5, 5[/latex] is called a constant because it does not vary and x is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.

We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.

In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.

Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.

Example: Describing Algebraic Expressions

List the constants and variables for each algebraic expression.

• [latex]\frac{4}{3}\pi {r}^{3}[/latex]
• [latex]\sqrt{2{m}^{3}{n}^{2}}[/latex]

Example: Evaluating an Algebraic Expression at Different Values

Evaluate the expression [latex]2x - 7[/latex] for each value for x.

• [latex]x=0[/latex]
• [latex]x=1[/latex]
• [latex]x=\dfrac{1}{2}[/latex]
• [latex]x=-4[/latex]
• Substitute 0 for [latex]x[/latex]. [latex]\begin{align}2x-7 & = 2\left(0\right)-7 \\ & =0-7 \\ & =-7\end{align}[/latex]
• Substitute 1 for [latex]x[/latex]. [latex]\begin{align}2x-7 & = 2\left(1\right)-7 \\ & =2-7 \\ & =-5\end{align}[/latex]
• Substitute [latex]\dfrac{1}{2}[/latex] for [latex]x[/latex]. [latex]\begin{align}2x-7 & = 2\left(\frac{1}{2}\right)-7 \\ & =1-7 \\ & =-6\end{align}[/latex]
• Substitute [latex]-4[/latex] for [latex]x[/latex]. [latex]\begin{align}2x-7 & = 2\left(-4\right)-7 \\ & =-8-7 \\ & =-15\end{align}[/latex]

Example: Evaluating Algebraic Expressions

Evaluate each expression for the given values.

• [latex]x+5[/latex] for [latex]x=-5[/latex]
• [latex]\frac{t}{2t - 1}[/latex] for [latex]t=10[/latex]
• [latex]\dfrac{4}{3}\pi {r}^{3}[/latex] for [latex]r=5[/latex]
• [latex]a+ab+b[/latex] for [latex]a=11,b=-8[/latex]
• [latex]\sqrt{2{m}^{3}{n}^{2}}[/latex] for [latex]m=2,n=3[/latex]
• Substitute [latex]-5[/latex] for [latex]x[/latex]. [latex]\begin{align}x+5 &=\left(-5\right)+5 \\ &=0\end{align}[/latex]
• Substitute 10 for [latex]t[/latex]. [latex]\begin{align}\frac{t}{2t-1} & =\frac{\left(10\right)}{2\left(10\right)-1} \\ & =\frac{10}{20-1} \\ & =\frac{10}{19}\end{align}[/latex]
• Substitute 5 for [latex]r[/latex]. [latex]\begin{align}\frac{4}{3}\pi r^{3} & =\frac{4}{3}\pi\left(5\right)^{3} \\ & =\frac{4}{3}\pi\left(125\right) \\ & =\frac{500}{3}\pi\end{align}[/latex]
• Substitute 11 for [latex]a[/latex] and –8 for [latex]b[/latex]. [latex]\begin{align}a+ab+b & =\left(11\right)+\left(11\right)\left(-8\right)+\left(-8\right) \\ & =11-8-8 \\ & =-85\end{align}[/latex]
• Substitute 2 for [latex]m[/latex] and 3 for [latex]n[/latex]. [latex]\begin{align}\sqrt{2m^{3}n^{2}} & =\sqrt{2\left(2\right)^{3}\left(3\right)^{2}} \\ & =\sqrt{2\left(8\right)\left(9\right)} \\ & =\sqrt{144} \\ & =12\end{align}[/latex]

In the following video we present more examples of how to evaluate an expression for a given value.

An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation [latex]2x+1=7[/latex] has the unique solution [latex]x=3[/latex] because when we substitute 3 for [latex]x[/latex] in the equation, we obtain the true statement [latex]2\left(3\right)+1=7[/latex].

A formula is an equation expressing a relationship between constant and variable quantities. Very often the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area [latex]A[/latex] of a circle in terms of the radius [latex]r[/latex] of the circle: [latex]A=\pi {r}^{2}[/latex]. For any value of [latex]r[/latex], the area [latex]A[/latex] can be found by evaluating the expression [latex]\pi {r}^{2}[/latex].

Example: Using a Formula

A right circular cylinder with radius [latex]r[/latex] and height [latex]h[/latex] has the surface area [latex]S[/latex] (in square units) given by the formula [latex]S=2\pi r\left(r+h\right)[/latex]. Find the surface area of a cylinder with radius 6 in. and height 9 in. Leave the answer in terms of [latex]\pi[/latex].

Right circular cylinder

Evaluate the expression [latex]2\pi r\left(r+h\right)[/latex] for [latex]r=6[/latex] and [latex]h=9[/latex].

The surface area is [latex]180\pi [/latex] square inches.

A photograph with length L and width W is placed in a mat of width 8 centimeters (cm). The area of the mat (in square centimeters, or cm 2 ) is found to be [latex]A=\left(L+16\right)\left(W+16\right)-L\cdot W[/latex]. Find the area of a mat for a photograph with length 32 cm and width 24 cm.

Simplify Algebraic Expressions

Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.

Example: Simplifying Algebraic Expressions

Simplify each algebraic expression.

• [latex]3x - 2y+x - 3y - 7[/latex]
• [latex]2r - 5\left(3-r\right)+4[/latex]
• [latex]\left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)[/latex]
• [latex]2mn - 5m+3mn+n[/latex]
• [latex]\begin{align}3x-2y+x-3y-7 & =3x+x-2y-3y-7 && \text{Commutative property of addition} \\ & =4x-5y-7 && \text{Simplify} \\ \text{ }\end{align}[/latex]
• [latex]\begin{align}2r-5\left(3-r\right)+4 & =2r-15+5r+4 && \text{Distributive property}\\&=2r+5r-15+4 && \text{Commutative property of addition} \\ & =7r-11 && \text{Simplify} \\ \text{ }\end{align}[/latex]
• [latex]\begin{align} 4t-\frac{5}{4}s -\left(\frac{2}{3}t+2s\right) &=4t-\frac{5}{4}s-\frac{2}{3}t-2s &&\text{Distributive property}\\&=4t-\frac{2}{3}t-\frac{5}{4}s-2s && \text{Commutative property of addition}\\&=\frac{12}{3}t-\frac{2}{3}t-\frac{5}{4}s-\frac{8}{4}s && \text{Common Denominators}\\ & =\frac{10}{3}t-\frac{13}{4}s && \text{Simplify} \\ \text{ }\end{align}[/latex]
• [latex]\begin{align}mn-5m+3mn+n & =2mn+3mn-5m+n && \text{Commutative property of addition} \\ & =5mn-5m+n && \text{Simplify}\end{align}[/latex]

Example: Simplifying a Formula

A rectangle with length [latex]L[/latex] and width [latex]W[/latex] has a perimeter [latex]P[/latex] given by [latex]P=L+W+L+W[/latex]. Simplify this expression.

If the amount [latex]P[/latex] is deposited into an account paying simple interest [latex]r[/latex] for time [latex]t[/latex], the total value of the deposit [latex]A[/latex] is given by [latex]A=P+Prt[/latex]. Simplify the expression. (This formula will be explored in more detail later in the course.)

[latex]A=P\left(1+rt\right)[/latex]

Key Concepts

• Rational numbers may be written as fractions or terminating or repeating decimals.
• Determine whether a number is rational or irrational by writing it as a decimal.
• The rational numbers and irrational numbers make up the set of real numbers. A number can be classified as natural, whole, integer, rational, or irrational.
• The order of operations is used to evaluate expressions.
• The real numbers under the operations of addition and multiplication obey basic rules, known as the properties of real numbers. These are the commutative properties, the associative properties, the distributive property, the identity properties, and the inverse properties.
• Algebraic expressions are composed of constants and variables that are combined using addition, subtraction, multiplication, and division. They take on a numerical value when evaluated by replacing variables with constants.
• Formulas are equations in which one quantity is represented in terms of other quantities. They may be simplified or evaluated as any mathematical expression.

algebraic expression  constants and variables combined using addition, subtraction, multiplication, and division

associative property of addition  the sum of three numbers may be grouped differently without affecting the result; in symbols, [latex]a+\left(b+c\right)=\left(a+b\right)+c[/latex]

associative property of multiplication  the product of three numbers may be grouped differently without affecting the result; in symbols, [latex]a\cdot \left(b\cdot c\right)=\left(a\cdot b\right)\cdot c[/latex]

base  in exponential notation, the expression that is being multiplied

commutative property of addition  two numbers may be added in either order without affecting the result; in symbols, [latex]a+b=b+a[/latex]

commutative property of multiplication  two numbers may be multiplied in any order without affecting the result; in symbols, [latex]a\cdot b=b\cdot a[/latex]

constant  a quantity that does not change value

distributive property  the product of a factor times a sum is the sum of the factor times each term in the sum; in symbols, [latex]a\cdot \left(b+c\right)=a\cdot b+a\cdot c[/latex]

equation  a mathematical statement indicating that two expressions are equal

exponent  in exponential notation, the raised number or variable that indicates how many times the base is being multiplied

exponential notation  a shorthand method of writing products of the same factor

formula  an equation expressing a relationship between constant and variable quantities

identity property of addition  there is a unique number, called the additive identity, 0, which, when added to a number, results in the original number; in symbols, [latex]a+0=a[/latex]

identity property of multiplication  there is a unique number, called the multiplicative identity, 1, which, when multiplied by a number, results in the original number; in symbols, [latex]a\cdot 1=a[/latex]

integers  the set consisting of the natural numbers, their opposites, and 0: [latex]\{\dots ,-3,-2,-1,0,1,2,3,\dots \}[/latex]

inverse property of addition  for every real number [latex]a[/latex], there is a unique number, called the additive inverse (or opposite), denoted [latex]-a[/latex], which, when added to the original number, results in the additive identity, 0; in symbols, [latex]a+\left(-a\right)=0[/latex]

inverse property of multiplication  for every non-zero real number [latex]a[/latex], there is a unique number, called the multiplicative inverse (or reciprocal), denoted [latex]\dfrac{1}{a}[/latex], which, when multiplied by the original number, results in the multiplicative identity, 1; in symbols, [latex]a\cdot \dfrac{1}{a}=1[/latex]

irrational numbers  the set of all numbers that are not rational; they cannot be written as either a terminating or repeating decimal; they cannot be expressed as a fraction of two integers

natural numbers  the set of counting numbers: [latex]\{1,2,3,\dots \}[/latex]

order of operations  a set of rules governing how mathematical expressions are to be evaluated, assigning priorities to operations

rational numbers  the set of all numbers of the form [latex]\dfrac{m}{n}[/latex], where [latex]m[/latex] and [latex]n[/latex] are integers and [latex]n\ne 0[/latex]. Any rational number may be written as a fraction or a terminating or repeating decimal.

real number line  a horizontal line used to represent the real numbers. An arbitrary fixed point is chosen to represent 0; positive numbers lie to the right of 0 and negative numbers to the left.

real numbers  the sets of rational numbers and irrational numbers taken together

variable  a quantity that may change value

whole numbers  the set consisting of 0 plus the natural numbers: [latex]\{0,1,2,3,\dots \}[/latex]

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Question ID 92383, 109700, 110263, 109667. Authored by : Alyson Day. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 13740. Authored by : David Lippman. License : CC BY: Attribution . License Terms : IMathAS Community License, CC-BY + GPL
• Question ID 13741, 259. Authored by : James Sousa. License : CC BY: Attribution . License Terms : IMathAS Community License CC- BY + GPL
• Identifying Sets of Real Numbers. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/htP2goe31MM . License : CC BY: Attribution
• Simplifying Expressions With Square Roots. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/9suc63qB96o . License : CC BY: Attribution
• Question ID 993379. Authored by : Desiree Davis. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 92360, 92361, 92388. Authored by : Michael Jenck. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Evaluating Algebraic Expressions. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/MkRdwV4n91g . License : CC BY: Attribution
• Question ID 50617. Authored by : Brenda Gardner. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 483. Authored by : Jeff Eldridge. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 1976, 1980. Authored by : Lawrence Morales. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 3616. Authored by : Shawn Triplett. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• College Algebra. Authored by : OpenStax College Algebra. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution

Using Visual Representations in Mathematics

On this page:, drawing on technology tools, in the classroom, online resources for visual representations, introduction.

All students can benefit from using visual representations, although struggling students may require additional, focused support and practice. Visual representations are a powerful way for students to access abstract mathematical ideas.  To be college and career ready, students need to be able to draw a situation, graph lists of data, or place numbers on a number line. Developing this strategy early during the elementary grades gives students tools for engaging with—and ways of thinking about—increasingly abstract concepts. Over time, they will work toward developing Common Core Standards for Mathematical Practice:

• CCSS.Math.Practice.MP2 (opens in a new window) Reason abstractly and quantitatively.
• CCSS.Math.Practice.MP4 (opens in a new window) Model with mathematics.
• CCSS.Math.Practice.MP5 (opens in a new window) Use appropriate tools strategically.

WAYS TO SUPPORT STUDENTS

Helping students choose the “right” visual representation often depends on content and context. In some contexts, there are multiple ways to represent the same idea. Show your students a variety of examples in order to demonstrate when (and why) they should choose each one (see UDL Checkpoint 2.5: Illustrate through multiple media (opens in a new window) ). Consider how you could use the following strategies to support your students:

• Check for understanding to determine a starting point. For example, you could ask the following questions: Why do you think that? How do you know that is correct? How does that picture represent the problem? Can you explain your answer? Is there another way you could do that?
• Ask students about features of the visual representation (including labels and scales, when appropriate).
• As students create visual representations, ask questions to ensure that they understand all the features of the representations. Prompt students to focus on the information the visual representations provide.
• When possible, include alternative visual representations and discuss the similarities and differences between them.
• Vary the shapes and orientations of representations so that students focus only on the important features as they learn about the objects and situations represented.
• Show your students a specific representation—a graph or a table—that is missing an important feature. Ask them to identify the missing feature.

New technologies are constantly expanding our ability to visualize data and explain mathematical concepts. For teachers looking to incorporate technology into the classroom, using virtual manipulatives (instead of physical ones) can be a good start. Students can begin with simple graphical representations of mathematical concepts and then work toward more complex modules that require them to create the data or work within a system of rules, like a game. Infographics (opens in a new window) —visualizations that are designed to communicate complex information effectively—have become increasingly popular. They can be used to “tell a story” with numbers, such as international democracy rankings (opens in a new window) or climate change impacts (opens in a new window) . Learning to create infographics gives students additional tools to communicate data and other quantitative information.

3D printing is a technology that, until recently, has been too expensive to make use of in a classroom. However, thanks to falling prices, they have now started to appear in high schools and it may not be long before elementary schools and middle schools also embrace this technology. 3D printing allows you to create solid, three-dimensional models from a digital design. You can explore what others have created (opens in a new window) to get a sense of what is possible. Imagine having students design and create their own mathematical models and manipulatives!

For more ideas on using technology to create visual representations, visit the Tech Matters blog (opens in a new window) or PowerUp’s Pinterest page (opens in a new window) . You can also check out the “ Virtual Manipulatives (opens in a new window) ” video, which supports students’ use of visual representations.

Geometry lends itself naturally to teaching with visual representations, as can be seen in Ms. Richardson’s Grade 6 class. So far, students have learned how to classify different quadrilaterals and triangles, and they are beginning to decompose polygons. They have also started using software (e.g., GeoGebra (opens in a new window) ) that can support their understanding by emphasizing the connections between mathematical language and visualization.

Ms. Richardson’s lesson objective is to have students decompose polygons into triangles, rectangles, and trapezoids. She will address two s Common Core State in this lesson:

• CCSS Math 6.G.1 (opens in a new window) Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems.
• CCSS Math MP4 (opens in a new window) Model with mathematics.

Ms. Richardson has students work on these standards within the context of a real-world example—a painting by the artist Sol LeWitt.

Sol LeWitt. Wall Drawing #1113. On a wall, a triangle within a rectangle, each with broken bands of color, 2003. Hirshhorn Museum and Sculpture Garden, Smithsonian Institution.

Students will build on their existing technology skills and create a model of this work, decomposing polygons and creating their own virtual LeWitt in the process. Ms. Richardson’s lesson plan is organized into three sections: a warm-up exercise to review concepts, the main learning task, and a closing discussion and assessment.

Lesson plan

This article draws from the PowerUp WHAT WORKS (opens in a new window) website, particularly the Visual Representations Instructional Strategy Guide (opens in a new window) . PowerUp is a free, teacher-friendly website that requires no log-in or registration. The Instructional Strategy Guide on visual representations includes a brief overview with an accompanying slide show; a list of the relevant mathematics Common Core State Standards; evidence-based teaching strategies to differentiate instruction using technology; short videos; and links to resources that will help you use technology to support mathematics instruction. If you want to dig deeper into the research foundation behind best practices in the use of virtual manipulatives, take a look at our Tech Research Brief (opens in a new window) on the topic. If you are responsible for professional development, the PD Support Materials (opens in a new window) provide helpful ideas and materials for using the resources. Want more information? See PowerUp WHAT WORKS (opens in a new window) .

Liked it? Share it!

Visit our sister websites:, reading rockets launching young readers (opens in a new window), start with a book read. explore. learn (opens in a new window), colorín colorado helping ells succeed (opens in a new window), adlit all about adolescent literacy (opens in a new window), reading universe all about teaching reading and writing (opens in a new window).

Number Line

A number line is a visual representation of numbers on a straight line. This line is used to compare numbers that are placed at equal intervals on an infinite line that extends on both sides, horizontally or vertically. As we move towards the right side of a horizontal number line, the numbers increase; as we move towards the left, the numbers decrease.

What is a Number Line?

A visual representation of numbers on a straight line drawn either horizontally or vertically is known as a number line . Writing down numbers on a number line makes it easy for us to compare them and to perform basic arithmetic operations on them. Zero (0) is considered to be the origin of a number line. The numbers to the left of 0 are negative numbers and the numbers to the right of 0 are all positive numbers. So, we can say that on a number line, as we move towards the right, the value of numbers increases. This means that the numbers present on the right are larger than the numbers on the left. For example, 3 comes to the right of 1, so 3 > 1. Observe the horizontal number line given below. 

How to Draw a Number Line?

In order to draw a number line or to plot a number on it, we use the following steps.

• Step 1: Draw a horizontal line with arrows on both ends. (You can also draw a vertical number line)
• Step 2: Choose a scale depending on the given number. For example, if you have to plot 5, then you can choose a scale of 1. If you have to plot 50, you can choose a scale of either 5, 10, or 25. (Determining an appropriate scale depends on the factors of the given number)
• Step 3: Mark the points at equal intervals. So, if you have chosen 1 as the scale, then mark 0, 1, 2, 3, 4, and so on.
• Step 4: Locate the given number. Highlight that point with a circle.

Negative and Positive Number Line

As we discussed above, a number line has positive and negative numbers. The section of the number line to the left side of zero forms a negative number line. While, the section on the right side of zero contains all positive numbers, and it forms a positive number line. It can be extended to infinity from both ends (right and left). The parts of a number line and some of its properties are given below.

Parts of a Number Line

Observe the parts of a number line given below to relate to the following features of a number line.

• The numbers on the right side are greater than the numbers on their left.
• The numbers on the left side are smaller than the numbers on their right.
• 0 is the point of origin or the middle point of the number line.
• Numbers are always placed at equal intervals in a number line.

Number Line with Decimals

We can represent various types of numbers on a number line, such as whole numbers , fractions, decimals, integers , rational numbers, and even irrational numbers. Now, let us learn how to draw a number line with decimals . For example, let us represent 2.4 on a number line using the steps given below:

• Step 1: Identify the whole number part of the given decimal. Here, in 2.4, the whole number part is 2.
• Step 2: Now, draw a number line and mark two points on it with a suitable gap in between. Since 2.4 lies between 2 and 3, mark 2 and 3 on the number line as shown below.
• Step 3: Observe the digit after the decimal, that is, the digit in the tenths place digit of the given number. In 2.4, the tenths place digit is 4. Make 10 equal intervals between 2 and 3 and mark 2.4 on the fourth bar to the right of 2.

This is how we draw a number line with decimals.

Inequalities on a Number Line

Inequality is a mathematical statement used for the comparison of quantities. We can graph inequalities on a number line by marking the part that the inequality represents.

Graphing Inequalities on a Number Line

Let us learn how to graph inequalities on a number line. Observe the figure given below that represents the following inequalities on a number line: x ≥ 5, x > 5, x ≤ 5, and x < 5.

Example 1: Represent x ≥ 5 on a number line.

Solution: In order to represent x ≥ 5 on a number line, we can follow the steps given below:

• Step 1: Draw a number line of a suitable length, mark 0, and draw equal intervals to the right and left, as shown in the figure given below.
• Step 2: In the given inequality x ≥ 5, the value of x can be 5 or greater than 5. So, we need to move to the right of 5.
• Step 3: Mark a black filled circle on 5 and shade the line from 5 towards the right side until the arrow as shown in the following figure.
• Step 5: This mark will represent the required inequality on the number line.

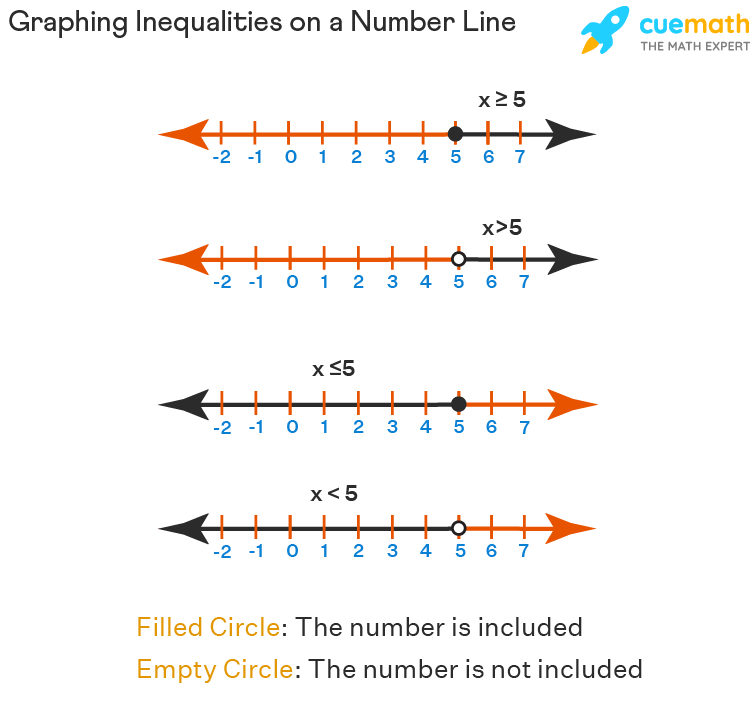
Note: It is to be noted that if the inequality says that the number is included, then we mark a filled circle on the particular number, whereas, if the inequality says that the number is not included then we mark an empty circle on the number. In the above case, it says that x is greater than or equal to 5, so we will mark a filled circle on 5.

Example 2: Represent x > 5 on a number line.

Solution: In order to represent x > 5 on a number line, we will follow the steps given below:

• Step 1: Draw a number line, mark 0, and draw equal intervals to the right and left, as shown in the figure given above.
• Step 2: In the given inequality x > 5, the value of x is greater than 5. So, we need to move to the right of 5.
• Step 3: Mark a black empty circle on 5 and shade the line from 5 towards the right side until the arrow as shown in the figure. The circle at point 5 will be left empty because a blank circle shows that 5 is not included. This means that x is greater than 5 and not equal to 5.

Example 3: Represent x ≤ 5 on a number line.

Solution: In order to represent x ≤ 5 on a number line, we will follow the steps given below:

• Step 2: In the given inequality x ≤ 5, the value of x is less than or equal to 5. So, we need to move to the left of 5.
• Step 3: Mark a black filled circle on 5 and shade the line from 5 towards the left side until the arrow as shown in the figure. The circle at point 5 will be filled because a filled circle shows that 5 is also included. This means that x is less than 5 or equal to 5.

Example 4: Represent x < 5 on a number line.

Solution: In order to represent x < 5 on a number line, we will follow the steps given below.

• Step 2: In the given inequality x < 5, the value of x is less than 5. So, we need to move to the left of 5.
• Step 3: Mark a black empty circle on 5 and shade the line from 5 towards the left side until the arrow as shown in the figure. The circle at point 5 will be left empty because a blank circle shows that 5 is not included. This means that x is less than 5 and not equal to 5.

Tips and Tricks on Number line

• We can represent various numbers on the number line, according to our requirements. For example, they can be only positive numbers, or integers between -4 and 3, or even fractions between -2 and 2.
• Number lines can help us in real-life situations. For example, they read the altitude (height) which is shown on a GPS device's screen, and can tell you how high or low you are below sea level!

☛ Related Topics

• Number Line Addition Worksheets
• Number Line Multiplication Worksheets
• Multiplication on Number Line
• Representation of Real Numbers on Number Line
• Decimals on Number Line

Number Line Examples

Example 1: A flower is hidden behind an integer which is at a position 7 less than the spot where the butterfly is placed. Can you find the integer?

From the above number line, it is clear that the butterfly is placed at 4. Now, 7 steps less than 4 means that 7 steps to the left of number 4 will take the butterfly to the flower. This can also be understood as: + 4 − 7 = −3.

This brings us to -3.

Thus, the flower is hidden behind -3.

∴ The integer is -3.

Example 2: Show the following addition on a number line.

To perform addition on a number line we first look for the numbers from where we have to start. Here, the starting number is 300 and we need to add 500 to it. The addition of 300 + 500 is shown in the following number line:

Example 3: Represent y ≥ 2 on a number line.

y ≥ 2 means that the value of a variable y is 2 or greater than 2. This can be easily represented on the number line as:

The black region on the line represents y ≥ 2.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Number Line

go to slide go to slide

FAQs on Number Line

What is a number line in math.

A number line is a visual representation of numbers on a straight line . This line is used to compare numbers that are placed at equal intervals on an infinite line that extends on both sides, horizontally or vertically.

What is a Number Line Model?

A number line model is a representation of numbers plotted on an infinite line that extends at both ends.

What all Operations can be Performed Using Number Line?

The four basic arithmetic operations of addition, subtraction, multiplication , and division can be easily performed using a number line. For addition and multiplication, we move towards the right side and for subtraction , we move towards the left side of the number line.

What all Numbers can be Represented on a Number Line?

We can represent real numbers on the number line. It includes the set of whole numbers, integers, fractions , decimals, rational and irrational numbers .

How to Perform Addition Using Number Line?

When we perform addition on a number line , we count by moving one interval at a time towards the right side. For example, if we need to solve 4 + 5, we start by marking the number 4 on the number line. Since we are adding 4 and 5, we will move 5 steps to the right. This brings us to 9. Hence, 4 + 5 = 9.

How to Graph an Inequality on a Number Line?

We can easily graph inequalities on a number line. For this, we just need to circle the value and shade the appropriate region on the number line. For example, let us represent x > 7 on the number line using the following steps:

• Step 1: Draw a number line and locate point 7 on it with respect to the origin.
• Step 2: Then, mark an empty circle at point 7 and shade the region to the right of 7 on the number line because we need to represent the part that is greater than 7.
• Step 3: This will represent that x can be any value greater than 7.
• Step 4: Make sure that you mark a blank circle at point 7. A blank (empty) circle shows that the given number is not included.
• Step 5: In case we need to show x ≥ 7, we will mark a filled circle on 7. A filled circle shows that 7 is also included, that is, the value of x is equal to and greater than 7.

(For more details, read the section 'Inequalities on a Number Line' on this page.)

How to Represent Fractions on a Number Line?

In order to represent fractions on a number line , we find two whole numbers between which the fraction lies. Then, we make equal intervals between those two whole numbers and appropriately mark the given fraction.

How to Represent Rational Numbers on Number Line?

In order to represent rational numbers on the number line, we locate two integers between which the number is lying. Then we mark the point by making equal intervals between those two points. If the rational number is in the form of an integer, then we can simply locate the point with respect to the origin and mark it.

What is an Open Number Line?

An open number line is an empty number line in which the numbers are not marked. It is used to create a visual model according to our requirement and convenience so that we can perform different arithmetic operations like addition and subtraction on a number line .

What is a Double Number Line?

Double number lines consist of 2 number lines that have corresponding pairs of values marked on them. Double number lines are commonly used to compare 2 quantities or ratios which represent a relationship. For example, the scale on a map is a double number line that shows the distance given in centimeters and the corresponding distance in kilometers.

Why are Number Lines Important?

Number lines are important because they make us visualize the position and order of all real numbers including positive numbers and negative numbers. They also help in understanding the basics of addition and subtraction.

Initial Thoughts

Perspectives & resources, what is high-quality mathematics instruction and why is it important.

• Page 1: The Importance of High-Quality Mathematics Instruction
• Page 2: A Standards-Based Mathematics Curriculum
• Page 3: Evidence-Based Mathematics Practices

What evidence-based mathematics practices can teachers employ?

• Page 4: Explicit, Systematic Instruction

Page 5: Visual Representations

• Page 6: Schema Instruction
• Page 7: Metacognitive Strategies
• Page 8: Effective Classroom Practices
• Page 9: References & Additional Resources
• Page 10: Credits

Research Shows

• Students who use accurate visual representations are six times more likely to correctly solve mathematics problems than are students who do not use them. However, students who use inaccurate visual representations are less likely to correctly solve mathematics problems than those who do not use visual representations at all. (Boonen, van Wesel, Jolles, & van der Schoot, 2014)
• Students with a learning disability (LD) often do not create accurate visual representations or use them strategically to solve problems. Teaching students to systematically use a visual representation to solve word problems has led to substantial improvements in math achievement for students with learning disabilities. (van Garderen, Scheuermann, & Jackson, 2012; van Garderen, Scheuermann, & Poch, 2014)
• Students who use visual representations to solve word problems are more likely to solve the problems accurately. This was equally true for students who had LD, were low-achieving, or were average-achieving. (Krawec, 2014)

Visual representations are flexible; they can be used across grade levels and types of math problems. They can be used by teachers to teach mathematics facts and by students to learn mathematics content. Visual representations can take a number of forms. Click on the links below to view some of the visual representations most commonly used by teachers and students.

How does this practice align?

High-leverage practice (hlp).

• HLP15 : Provide scaffolded supports

CCSSM: Standards for Mathematical Practice

• MP1 : Make sense of problems and persevere in solving them.

Number Lines

Definition : A straight line that shows the order of and the relation between numbers.

Common Uses : addition, subtraction, counting

Strip Diagrams

Definition : A bar divided into rectangles that accurately represent quantities noted in the problem.

Common Uses : addition, fractions, proportions, ratios

Definition : Simple drawings of concrete or real items (e.g., marbles, trucks).

Common Uses : counting, addition, subtraction, multiplication, division

Graphs/Charts

Definition : Drawings that depict information using lines, shapes, and colors.

Common Uses : comparing numbers, statistics, ratios, algebra

Graphic Organizers

Definition : Visual that assists students in remembering and organizing information, as well as depicting the relationships between ideas (e.g., word webs, tables, Venn diagrams).

Common Uses : algebra, geometry

Before they can solve problems, however, students must first know what type of visual representation to create and use for a given mathematics problem. Some students—specifically, high-achieving students, gifted students—do this automatically, whereas others need to be explicitly taught how. This is especially the case for students who struggle with mathematics and those with mathematics learning disabilities. Without explicit, systematic instruction on how to create and use visual representations, these students often create visual representations that are disorganized or contain incorrect or partial information. Consider the examples below.

Elementary Example

Mrs. Aldridge ask her first-grade students to add 2 + 4 by drawing dots.

Notice that Talia gets the correct answer. However, because Colby draws his dots in haphazard fashion, he fails to count all of them and consequently arrives at the wrong solution.

High School Example

Mr. Huang asks his students to solve the following word problem:

The flagpole needs to be replaced. The school would like to replace it with the same size pole. When Juan stands 11 feet from the base of the pole, the angle of elevation from Juan’s feet to the top of the pole is 70 degrees. How tall is the pole?

Compare the drawings below created by Brody and Zoe to represent this problem. Notice that Brody drew an accurate representation and applied the correct strategy. In contrast, Zoe drew a picture with partially correct information. The 11 is in the correct place, but the 70° is not. As a result of her inaccurate representation, Zoe is unable to move forward and solve the problem. However, given an accurate representation developed by someone else, Zoe is more likely to solve the problem correctly.

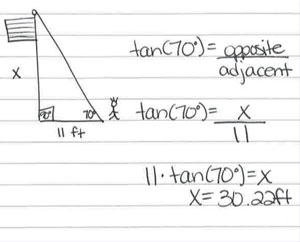
Manipulatives

Some students will not be able to grasp mathematics skills and concepts using only the types of visual representations noted in the table above. Very young children and students who struggle with mathematics often require different types of visual representations known as manipulatives. These concrete, hands-on materials and objects—for example, an abacus or coins—help students to represent the mathematical idea they are trying to learn or the problem they are attempting to solve. Manipulatives can help students develop a conceptual understanding of mathematical topics. (For the purpose of this module, the term concrete objects refers to manipulatives and the term visual representations refers to schematic diagrams.)

It is important that the teacher make explicit the connection between the concrete object and the abstract concept being taught. The goal is for the student to eventually understand the concepts and procedures without the use of manipulatives. For secondary students who struggle with mathematics, teachers should show the abstract along with the concrete or visual representation and explicitly make the connection between them.

A move from concrete objects or visual representations to using abstract equations can be difficult for some students. One strategy teachers can use to help students systematically transition among concrete objects, visual representations, and abstract equations is the Concrete-Representational-Abstract (CRA) framework.

If you would like to learn more about this framework, click here.

Concrete-Representational-Abstract Framework

• Concrete —Students interact and manipulate three-dimensional objects, for example algebra tiles or other algebra manipulatives with representations of variables and units.
• Representational — Students use two-dimensional drawings to represent problems. These pictures may be presented to them by the teacher, or through the curriculum used in the class, or students may draw their own representation of the problem.
• Abstract — Students solve problems with numbers, symbols, and words without any concrete or representational assistance.

CRA is effective across all age levels and can assist students in learning concepts, procedures, and applications. When implementing each component, teachers should use explicit, systematic instruction and continually monitor student work to assess their understanding, asking them questions about their thinking and providing clarification as needed. Concrete and representational activities must reflect the actual process of solving the problem so that students are able to generalize the process to solve an abstract equation. The illustration below highlights each of these components.

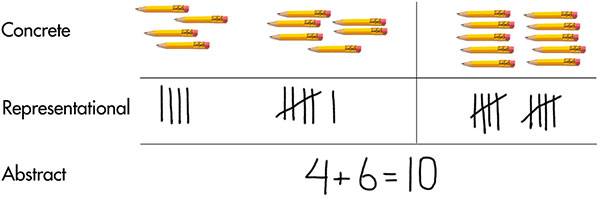
For Your Information

One promising practice for moving secondary students with mathematics difficulties or disabilities from the use of manipulatives and visual representations to the abstract equation quickly is the CRA-I strategy . In this modified version of CRA, the teacher simultaneously presents the content using concrete objects, visual representations of the concrete objects, and the abstract equation. Studies have shown that this framework is effective for teaching algebra to this population of students (Strickland & Maccini, 2012; Strickland & Maccini, 2013; Strickland, 2017).

Kim Paulsen discusses the benefits of manipulatives and a number of things to keep in mind when using them (time: 2:35).

Kim Paulsen, EdD Associate Professor, Special Education Vanderbilt University

View Transcript

Transcript: Kim Paulsen, EdD

Manipulatives are a great way of helping kids understand conceptually. The use of manipulatives really helps students see that conceptually, and it clicks a little more with them. Some of the things, though, that we need to remember when we’re using manipulatives is that it is important to give students a little bit of free time when you’re using a new manipulative so that they can just explore with them. We need to have specific rules for how to use manipulatives, that they aren’t toys, that they really are learning materials, and how students pick them up, how they put them away, the right time to use them, and making sure that they’re not distracters while we’re actually doing the presentation part of the lesson. One of the important things is that we don’t want students to memorize the algorithm or the procedures while they’re using the manipulatives. It really is just to help them understand conceptually. That doesn’t mean that kids are automatically going to understand conceptually or be able to make that bridge between using the concrete manipulatives into them being able to solve the problems. For some kids, it is difficult to use the manipulatives. That’s not how they learn, and so we don’t want to force kids to have to use manipulatives if it’s not something that is helpful for them. So we have to remember that manipulatives are one way to think about teaching math.

I think part of the reason that some teachers don’t use them is because it takes a lot of time, it takes a lot of organization, and they also feel that students get too reliant on using manipulatives. One way to think about using manipulatives is that you do it a couple of lessons when you’re teaching a new concept, and then take those away so that students are able to do just the computation part of it. It is true we can’t walk around life with manipulatives in our hands. And I think one of the other reasons that a lot of schools or teachers don’t use manipulatives is because they’re very expensive. And so it’s very helpful if all of the teachers in the school can pool resources and have a manipulative room where teachers can go check out manipulatives so that it’s not so expensive. Teachers have to know how to use them, and that takes a lot of practice.

Responsive Web Design

• About Math4Texas
• Getting Started
• Kindergarten
• First Grade
• Second Grade
• Third Grade
• Fourth Grade
• Fifth Grade
• Sixth Grade
• Seventh Grade

Eighth Grade

• Video Library
• Media Material

Page Navigation

• Big Ideas & Topics
• Bivariate Sets of Data
• Using Trend Lines with Bivariate Sets of Data
• Scatterplots with Linear, Non-linear, & No Associations
• Determining the Mean Absolute Deviation
• Generating Random Samples of Populations
• Ratios of Corresponding Sides
• Attributes of Shapes & Dilations on a Coordinate Plane
• Effect of Positive Rational Scale Factor
• Describing the Volume Formula of a Cylinder
• Relationship Between the Volume of a Cylinder & a Cone
• Using Models & Diagrams to Explain the Pythagorean Theorem
• Volume of Cylinders, Cones, & Spheres
• Lateral & Total Surface Area Involving Rectangular Prisms, Triangular Prisms, & Cylinders
• Using the Pythagorean Theorem
• Determining Distance using the Pythagorean Theorem
• Angle Sum & Exterior Angles of Triangles
• Properties of Orientation & Congruence on a Coordinate Plane
• Differentiate between Transformations
• Effects of Translations, Reflections, & Rotations on a Coordinate Plane
• Modeling Linear & Area Measurements
• Using Right Triangles to Develop Understanding of Slope
• Graphing Proportional Relationships
• Using Data to Determine the Slope & y-Intercept
• Representing Linear Proportional Situations
• Representing Linear Non-Proportional Situations
• Solving Problems Involving Direct Variation
• Distinguishing Between Proportional & Non-Proportional Situations
• Identifying Functions
• Identifying Examples of Proportional & Non-Proportional Functions
• Using y = mx + b to Model Linear Relationships
• Writing One-Variable Equations & Inequalities
• Writing Real-World Problems Given an Equation or Inequality
• Modeling & Solving One-Variable Equations
• Identifying & Verifying the Values of x & y
• Relationships Between Sets of Numbers
• Approximating the Value of Irrational Numbers
• Standard Decimal Notation & Scientific Notation
• Ordering a Set of Real Numbers
• Comparing Interest Rates & Loan Length
• Calculating the Cost of Repaying a Loan
• Investing Regularly
• Calculate & Compare Simple & Compound Interest Earnings
• Advantages & Disadvantages of Various Payment Methods
• Analyzing Financial Responsible Decisions
• Estimating Costs of a College Education

• Draw a Venn diagram which correctly represents the relationship between Set W, Set R and Set I, then place the numbers 5, -3, 0.3 ̅ ½, 0, π, √5 and -3/4. W = {} Whole numbers Z = {} Integers numbers Q = {} Rational numbers I = {} Irrational numbers R = {} Real numbers   Hint Possible Solution

Digital Tools

• Click on the following links for interactive games.   Classifying Numbers   Rational & Irrational Numbers   Primary Krypto
• Click on the following links for more information.
• Supporting Standard 8.2 Number and operations. The student applies mathematical process standards  to represent and use real numbers real numbers  in a variety of forms. The student is expected to: (A) extend previous knowledge of sets and subsets using a visual representation to describe relationships between sets of  real numbers

Education Service Center Region 11, 1451 South Cherry Lane, White Settlement, TX 76108 [email protected]   817-740-7550 fax:   Accessibility

Education Service Center Region 11, 1451 South Cherry Lane, White Settlement, TX 76108 [email protected]

  817-740-7550

Accessibility

• Questions or Feedback? |
• Web Community Manager Privacy Policy (Updated) |

• Business Essentials
• Leadership & Management
• Credential of Leadership, Impact, and Management in Business (CLIMB)
• Entrepreneurship & Innovation
• Digital Transformation
• Finance & Accounting
• Business in Society
• For Organizations
• Support Portal
• Media Coverage
• Founding Donors
• Leadership Team

• Harvard Business School →
• HBS Online →
• Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

• Career Development
• Communication
• Decision-Making
• Earning Your MBA
• Negotiation
• News & Events
• Productivity
• Staff Spotlight
• Student Profiles
• Work-Life Balance
• AI Essentials for Business
• Alternative Investments
• Business Analytics
• Business Strategy
• Business and Climate Change
• Design Thinking and Innovation
• Digital Marketing Strategy
• Disruptive Strategy
• Economics for Managers
• Entrepreneurship Essentials
• Financial Accounting
• Global Business
• Launching Tech Ventures
• Leadership Principles
• Leadership, Ethics, and Corporate Accountability
• Leading Change and Organizational Renewal
• Leading with Finance
• Management Essentials
• Negotiation Mastery
• Organizational Leadership
• Power and Influence for Positive Impact
• Strategy Execution
• Sustainable Business Strategy
• Sustainable Investing
• Winning with Digital Platforms

17 Data Visualization Techniques All Professionals Should Know

• 17 Sep 2019

There’s a growing demand for business analytics and data expertise in the workforce. But you don’t need to be a professional analyst to benefit from data-related skills.

Becoming skilled at common data visualization techniques can help you reap the rewards of data-driven decision-making , including increased confidence and potential cost savings. Learning how to effectively visualize data could be the first step toward using data analytics and data science to your advantage to add value to your organization.

Several data visualization techniques can help you become more effective in your role. Here are 17 essential data visualization techniques all professionals should know, as well as tips to help you effectively present your data.

Access your free e-book today.

What Is Data Visualization?

Data visualization is the process of creating graphical representations of information. This process helps the presenter communicate data in a way that’s easy for the viewer to interpret and draw conclusions.

There are many different techniques and tools you can leverage to visualize data, so you want to know which ones to use and when. Here are some of the most important data visualization techniques all professionals should know.

Data Visualization Techniques

The type of data visualization technique you leverage will vary based on the type of data you’re working with, in addition to the story you’re telling with your data .

Here are some important data visualization techniques to know:

• Gantt Chart
• Box and Whisker Plot
• Waterfall Chart
• Scatter Plot
• Pictogram Chart
• Highlight Table
• Bullet Graph
• Choropleth Map
• Network Diagram
• Correlation Matrices

1. Pie Chart

Pie charts are one of the most common and basic data visualization techniques, used across a wide range of applications. Pie charts are ideal for illustrating proportions, or part-to-whole comparisons.

Because pie charts are relatively simple and easy to read, they’re best suited for audiences who might be unfamiliar with the information or are only interested in the key takeaways. For viewers who require a more thorough explanation of the data, pie charts fall short in their ability to display complex information.

2. Bar Chart

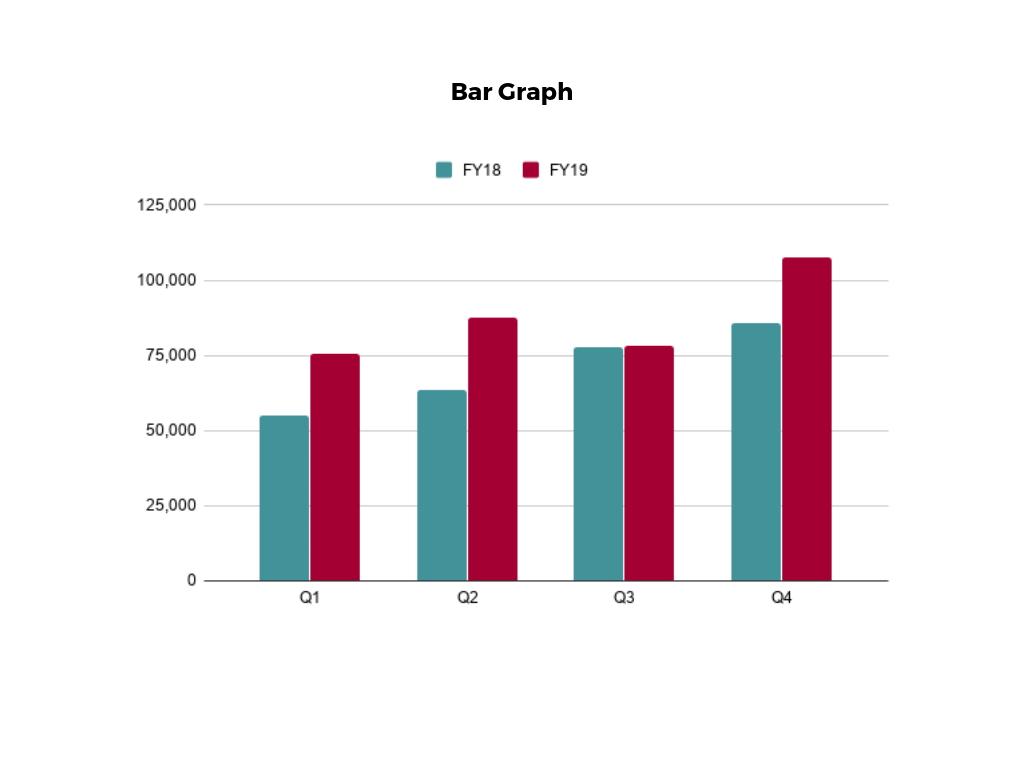
The classic bar chart , or bar graph, is another common and easy-to-use method of data visualization. In this type of visualization, one axis of the chart shows the categories being compared, and the other, a measured value. The length of the bar indicates how each group measures according to the value.

One drawback is that labeling and clarity can become problematic when there are too many categories included. Like pie charts, they can also be too simple for more complex data sets.

3. Histogram

Unlike bar charts, histograms illustrate the distribution of data over a continuous interval or defined period. These visualizations are helpful in identifying where values are concentrated, as well as where there are gaps or unusual values.

Histograms are especially useful for showing the frequency of a particular occurrence. For instance, if you’d like to show how many clicks your website received each day over the last week, you can use a histogram. From this visualization, you can quickly determine which days your website saw the greatest and fewest number of clicks.

4. Gantt Chart

Gantt charts are particularly common in project management, as they’re useful in illustrating a project timeline or progression of tasks. In this type of chart, tasks to be performed are listed on the vertical axis and time intervals on the horizontal axis. Horizontal bars in the body of the chart represent the duration of each activity.

Utilizing Gantt charts to display timelines can be incredibly helpful, and enable team members to keep track of every aspect of a project. Even if you’re not a project management professional, familiarizing yourself with Gantt charts can help you stay organized.

5. Heat Map

A heat map is a type of visualization used to show differences in data through variations in color. These charts use color to communicate values in a way that makes it easy for the viewer to quickly identify trends. Having a clear legend is necessary in order for a user to successfully read and interpret a heatmap.

There are many possible applications of heat maps. For example, if you want to analyze which time of day a retail store makes the most sales, you can use a heat map that shows the day of the week on the vertical axis and time of day on the horizontal axis. Then, by shading in the matrix with colors that correspond to the number of sales at each time of day, you can identify trends in the data that allow you to determine the exact times your store experiences the most sales.

6. A Box and Whisker Plot

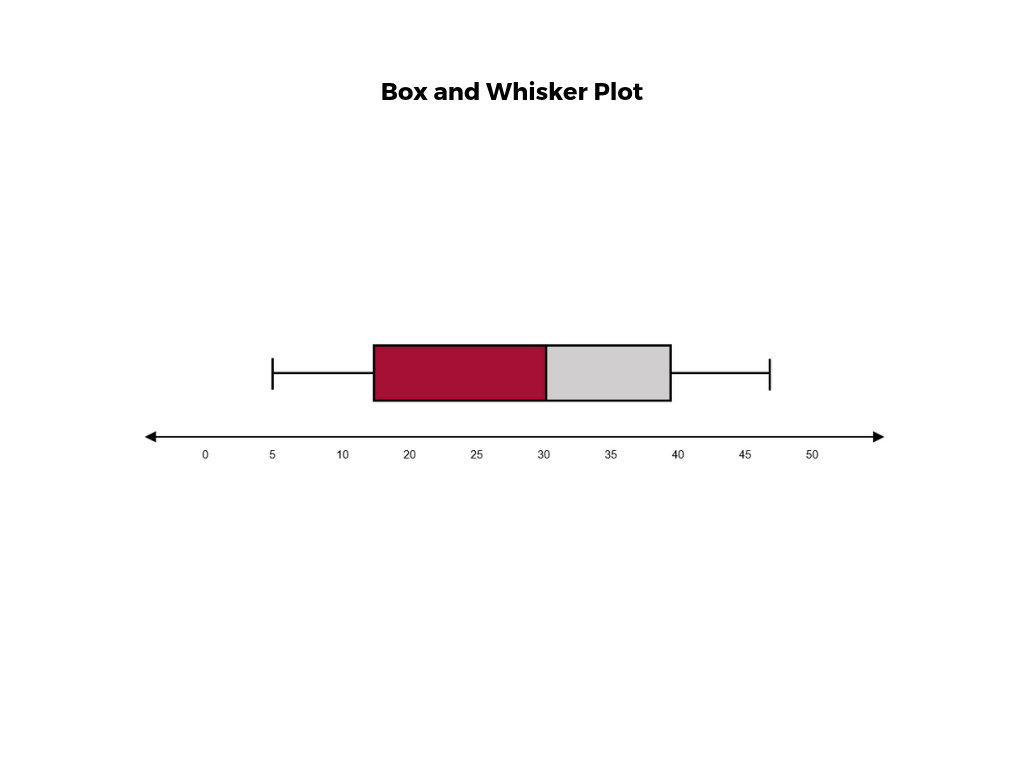
A box and whisker plot , or box plot, provides a visual summary of data through its quartiles. First, a box is drawn from the first quartile to the third of the data set. A line within the box represents the median. “Whiskers,” or lines, are then drawn extending from the box to the minimum (lower extreme) and maximum (upper extreme). Outliers are represented by individual points that are in-line with the whiskers.

This type of chart is helpful in quickly identifying whether or not the data is symmetrical or skewed, as well as providing a visual summary of the data set that can be easily interpreted.

7. Waterfall Chart

A waterfall chart is a visual representation that illustrates how a value changes as it’s influenced by different factors, such as time. The main goal of this chart is to show the viewer how a value has grown or declined over a defined period. For example, waterfall charts are popular for showing spending or earnings over time.

8. Area Chart

An area chart , or area graph, is a variation on a basic line graph in which the area underneath the line is shaded to represent the total value of each data point. When several data series must be compared on the same graph, stacked area charts are used.

This method of data visualization is useful for showing changes in one or more quantities over time, as well as showing how each quantity combines to make up the whole. Stacked area charts are effective in showing part-to-whole comparisons.

9. Scatter Plot

Another technique commonly used to display data is a scatter plot . A scatter plot displays data for two variables as represented by points plotted against the horizontal and vertical axis. This type of data visualization is useful in illustrating the relationships that exist between variables and can be used to identify trends or correlations in data.

Scatter plots are most effective for fairly large data sets, since it’s often easier to identify trends when there are more data points present. Additionally, the closer the data points are grouped together, the stronger the correlation or trend tends to be.

10. Pictogram Chart

Pictogram charts , or pictograph charts, are particularly useful for presenting simple data in a more visual and engaging way. These charts use icons to visualize data, with each icon representing a different value or category. For example, data about time might be represented by icons of clocks or watches. Each icon can correspond to either a single unit or a set number of units (for example, each icon represents 100 units).

In addition to making the data more engaging, pictogram charts are helpful in situations where language or cultural differences might be a barrier to the audience’s understanding of the data.

11. Timeline

Timelines are the most effective way to visualize a sequence of events in chronological order. They’re typically linear, with key events outlined along the axis. Timelines are used to communicate time-related information and display historical data.

Timelines allow you to highlight the most important events that occurred, or need to occur in the future, and make it easy for the viewer to identify any patterns appearing within the selected time period. While timelines are often relatively simple linear visualizations, they can be made more visually appealing by adding images, colors, fonts, and decorative shapes.

12. Highlight Table

A highlight table is a more engaging alternative to traditional tables. By highlighting cells in the table with color, you can make it easier for viewers to quickly spot trends and patterns in the data. These visualizations are useful for comparing categorical data.

Depending on the data visualization tool you’re using, you may be able to add conditional formatting rules to the table that automatically color cells that meet specified conditions. For instance, when using a highlight table to visualize a company’s sales data, you may color cells red if the sales data is below the goal, or green if sales were above the goal. Unlike a heat map, the colors in a highlight table are discrete and represent a single meaning or value.

13. Bullet Graph

A bullet graph is a variation of a bar graph that can act as an alternative to dashboard gauges to represent performance data. The main use for a bullet graph is to inform the viewer of how a business is performing in comparison to benchmarks that are in place for key business metrics.

In a bullet graph, the darker horizontal bar in the middle of the chart represents the actual value, while the vertical line represents a comparative value, or target. If the horizontal bar passes the vertical line, the target for that metric has been surpassed. Additionally, the segmented colored sections behind the horizontal bar represent range scores, such as “poor,” “fair,” or “good.”

14. Choropleth Maps

A choropleth map uses color, shading, and other patterns to visualize numerical values across geographic regions. These visualizations use a progression of color (or shading) on a spectrum to distinguish high values from low.

Choropleth maps allow viewers to see how a variable changes from one region to the next. A potential downside to this type of visualization is that the exact numerical values aren’t easily accessible because the colors represent a range of values. Some data visualization tools, however, allow you to add interactivity to your map so the exact values are accessible.

15. Word Cloud

A word cloud , or tag cloud, is a visual representation of text data in which the size of the word is proportional to its frequency. The more often a specific word appears in a dataset, the larger it appears in the visualization. In addition to size, words often appear bolder or follow a specific color scheme depending on their frequency.

Word clouds are often used on websites and blogs to identify significant keywords and compare differences in textual data between two sources. They are also useful when analyzing qualitative datasets, such as the specific words consumers used to describe a product.

16. Network Diagram

Network diagrams are a type of data visualization that represent relationships between qualitative data points. These visualizations are composed of nodes and links, also called edges. Nodes are singular data points that are connected to other nodes through edges, which show the relationship between multiple nodes.

There are many use cases for network diagrams, including depicting social networks, highlighting the relationships between employees at an organization, or visualizing product sales across geographic regions.

17. Correlation Matrix

A correlation matrix is a table that shows correlation coefficients between variables. Each cell represents the relationship between two variables, and a color scale is used to communicate whether the variables are correlated and to what extent.

Correlation matrices are useful to summarize and find patterns in large data sets. In business, a correlation matrix might be used to analyze how different data points about a specific product might be related, such as price, advertising spend, launch date, etc.

Other Data Visualization Options

While the examples listed above are some of the most commonly used techniques, there are many other ways you can visualize data to become a more effective communicator. Some other data visualization options include:

• Bubble clouds
• Circle views
• Dendrograms
• Dot distribution maps
• Open-high-low-close charts
• Polar areas
• Radial trees
• Ring Charts
• Sankey diagram
• Span charts
• Streamgraphs
• Wedge stack graphs
• Violin plots

Tips For Creating Effective Visualizations

Creating effective data visualizations requires more than just knowing how to choose the best technique for your needs. There are several considerations you should take into account to maximize your effectiveness when it comes to presenting data.

Related : What to Keep in Mind When Creating Data Visualizations in Excel

One of the most important steps is to evaluate your audience. For example, if you’re presenting financial data to a team that works in an unrelated department, you’ll want to choose a fairly simple illustration. On the other hand, if you’re presenting financial data to a team of finance experts, it’s likely you can safely include more complex information.

Another helpful tip is to avoid unnecessary distractions. Although visual elements like animation can be a great way to add interest, they can also distract from the key points the illustration is trying to convey and hinder the viewer’s ability to quickly understand the information.

Finally, be mindful of the colors you utilize, as well as your overall design. While it’s important that your graphs or charts are visually appealing, there are more practical reasons you might choose one color palette over another. For instance, using low contrast colors can make it difficult for your audience to discern differences between data points. Using colors that are too bold, however, can make the illustration overwhelming or distracting for the viewer.

Related : Bad Data Visualization: 5 Examples of Misleading Data

Visuals to Interpret and Share Information

No matter your role or title within an organization, data visualization is a skill that’s important for all professionals. Being able to effectively present complex data through easy-to-understand visual representations is invaluable when it comes to communicating information with members both inside and outside your business.

There’s no shortage in how data visualization can be applied in the real world. Data is playing an increasingly important role in the marketplace today, and data literacy is the first step in understanding how analytics can be used in business.

Are you interested in improving your analytical skills? Learn more about Business Analytics , our eight-week online course that can help you use data to generate insights and tackle business decisions.

This post was updated on January 20, 2022. It was originally published on September 17, 2019.

About the Author

• Math Article

Real Numbers

Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. At the same time, the imaginary numbers are the un-real numbers, which cannot be expressed in the number line and are commonly used to represent a complex number . Some of the examples of real numbers are 23, -12, 6.99, 5/2, π, and so on. In this article, we are going to discuss the definition of real numbers, the properties of real numbers and the examples of real numbers with complete explanations.

Table of contents:

• Set of real numbers
• Commutative
• Associative
• Distributive

Solved Examples

Practice questions, real numbers definition.

Real numbers can be defined as the union of both rational and irrational numbers. They can be both positive or negative and are denoted by the symbol “R”. All the natural numbers, decimals and fractions come under this category. See the figure, given below, which shows the classification of real numerals.

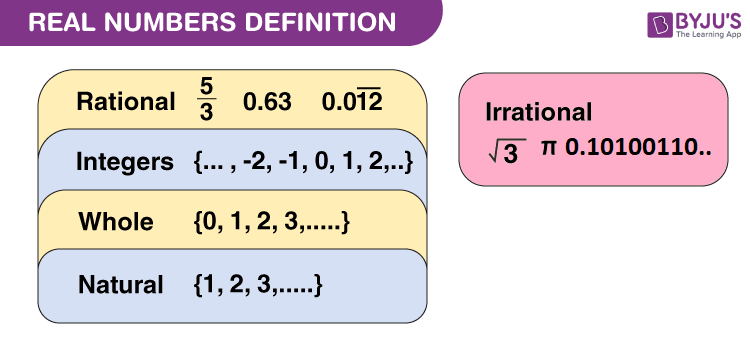
Set of Real Numbers

The set of real numbers consists of different categories, such as natural and whole numbers, integers, rational and irrational numbers. In the table given below, all the real numbers formulas (i.e.) the representation of the classification of real numbers are defined with examples.

Real Numbers Chart

The chart for the set of real numerals including all the types are given below:

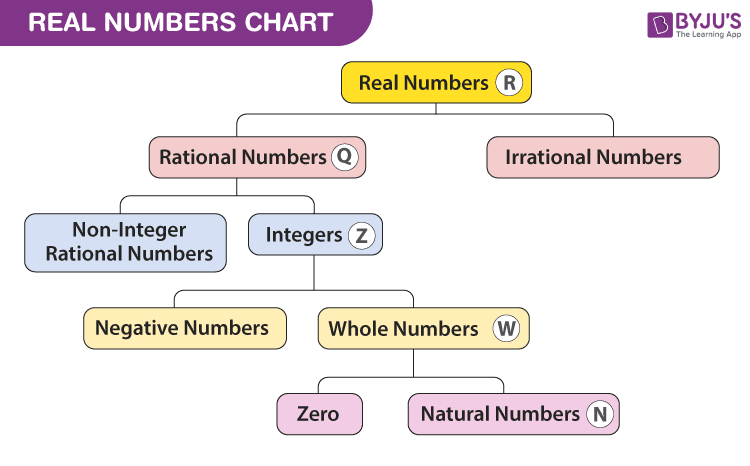
Properties of Real Numbers

The following are the four main properties of real numbers:

• Commutative property
• Associative property
• Distributive property
• Identity property

Consider “m, n and r” are three real numbers. Then the above properties can be described using m, n, and r as shown below:

Commutative Property

If m and n are the numbers, then the general form will be m + n = n + m for addition and m.n = n.m for multiplication.

• Addition: m + n = n + m. For example, 5 + 3 = 3 + 5, 2 + 4 = 4 + 2.
• Multiplication: m × n = n × m. For example, 5 × 3 = 3 × 5, 2 × 4 = 4 × 2.

Associative Property

If m, n and r are the numbers. The general form will be m + (n + r) = (m + n) + r for addition(mn) r = m (nr) for multiplication.

• Addition: The general form will be m + (n + r) = (m + n) + r. An example of additive associative property is 10 + (3 + 2) = (10 + 3) + 2.
• Multiplication: (mn) r = m (nr). An example of a multiplicative associative property is (2 × 3) 4 = 2 (3 × 4).

Distributive Property

For three numbers m, n, and r, which are real in nature, the distributive property is represented as:

m (n + r) = mn + mr and (m + n) r = mr + nr.

• Example of distributive property is: 5(2 + 3) = 5 × 2 + 5 × 3. Here, both sides will yield 25.

Identity Property

There are additive and multiplicative identities.

• For addition: m + 0 = m. (0 is the additive identity)
• For multiplication:  m × 1 = 1 × m = m. (1 is the multiplicative identity)

Video Lesson on Numbers

Find five rational numbers between 1/2 and 3/5.

We shall make the denominator same for both the given rational number

(1 × 5)/(2 × 5) = 5/10  and (3 × 2)/(5 × 2) = 6/10

Now, multiply both the numerator and denominator of both the rational number by 6, we have

(5 × 6)/(10 × 6) = 30/60  and (6 × 6)/(10 × 6) = 36/60

Five rational numbers between 1/2 = 30/60 and 3/5 = 36/60 are

31/60, 32/60, 33/60, 34/60, 35/60.  

Write the decimal equivalent of the following:

(i) 1/4  (ii) 5/8 (iii) 3/2

(i) 1/4 = (1 × 25)/(4 × 25) = 25/100 = 0.25

(ii) 5/8 = (5 × 125)/(8 × 125) = 625/1000 = 0.625

(iii) 3/2 = (3 × 5)/(2 × 5) = 15/10 = 1.5

What should be multiplied to 1.25 to get the answer 1?

Solution: 1.25 = 125/100 

Now if we multiply this by 100/125, we get

125/100 × 100/125 = 1

• Which is the smallest composite number?
• Prove that any positive odd integer is of the form 6x + 1, 6x + 3, or 6x + 5.
• Evaluate 2 + 3 × 6 – 5.
• What is the product of a non-zero rational number and an irrational number?

Can every positive integer be represented as 4x + 2 (where x is an integer)?

Real Numbers Class 9 and 10

In real numbers Class 9, the common concepts introduced include representing real numbers on a number line, operations on real numbers, properties of real numbers, and the law of exponents for real numbers. In Class 10, some advanced concepts related to real numbers are included. Apart from what are real numbers, students will also learn about the real numbers formulas and concepts such as Euclid’s Division Lemma, Euclid’s Division Algorithm and the fundamental theorem of arithmetic in class 10.

Frequently Asked Questions on Real Numbers

What are natural and real numbers.

Natural numbers are all positive integers starting from 1 to infinity. All natural numbers are integers but not all the integers are natural numbers. These are the set of all counting numbers such as 1, 2, 3, 4, 5, 6, 7, 8, 9, …….∞.

Real numbers are numbers that include both rational and irrational numbers. Rational numbers such as integers (-2, 0, 1), fractions(1/2, 2.5) and irrational numbers such as √3, π(22/7), etc., are all real numbers.

Is Zero a Real or an Imaginary Number?

Zero is considered to be both a real and an imaginary number. As we know, imaginary numbers are the square root of non-positive real numbers. And since 0 is also a non-positive number, therefore it fulfils the criteria of the imaginary number. Whereas 0 is also a rational number, which is defined in a number line and hence a real number.

Are there Real Numbers that are not Rational or Irrational?

No, there are no real numbers that are neither rational nor irrational. The definition of real numbers itself states that it is a combination of both rational and irrational numbers.

Is the real number a subset of a complex number?

Yes, because a complex number is the combination of a real and imaginary number. So, if the complex number is a set then the real and imaginary numbers are the subsets of it.

What are the properties of real numbers?

Is √3 a real number.

Yes, √3 is a real number. We know that a real number is a combination of both rational and irrational numbers. Since √3 is an irrational number, we can also say that √3 is a real number.

Is 3i a real number?

No, 3i is not a real number, as it has an imaginary part in it.

What are the different subsets of real numbers?

The subsets of real numbers include rational numbers, irrational numbers, natural numbers, and whole numbers.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

According to a new mathematical definition, whole numbers are divided into two sets, one of which is the merger of the sequence of prime numbers and numbers zero and one. Three other definitions, deduced from this first, subdivide the set of whole numbers into four classes of numbers with own and unique arithmetic properties. The geometric distribution of these different types of whole numbers, in various closed matrices, is organized into exact value ratios to 3/2 or 1/1.

can u use any real number of ur choice in mathematics

Where is the chat box?

please send explanation of this.

Sir,I want to know more about mathematics.

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• A Visual, Intuitive Guide to Imaginary Numbers

Imaginary numbers always confused me. Like understanding e , most explanations fell into one of two categories:

• It’s a mathematical abstraction, and the equations work out. Deal with it.
• It’s used in advanced physics, trust us. Just wait until college.

Gee, what a great way to encourage math in kids! Today we’ll assault this topic with our favorite tools:

• Focusing on relationships , not mechanical formulas.
• Seeing complex numbers as an upgrade to our number system , just like zero, decimals and negatives were.
• Using visual diagrams , not just text, to understand the idea.

And our secret weapon: learning by analogy. We’ll approach imaginary numbers by observing its ancestor, the negatives. Here’s your guidebook:

It doesn’t make sense yet, but hang in there. By the end we’ll hunt down i and put it in a headlock, instead of the reverse.

Video Walkthrough:

Really Understanding Negative Numbers

Negative numbers aren’t easy. Imagine you’re a European mathematician in the 1700s. You have 3 and 4, and know you can write 4 – 3 = 1. Simple.

But what about 3-4? What, exactly, does that mean? How can you take 4 cows from 3? How could you have less than nothing?

Negatives were considered absurd, something that “darkened the very whole doctrines of the equations” ( Francis Maseres, 1759 ). Yet today, it’d be absurd to think negatives aren’t logical or useful. Try asking your teacher whether negatives corrupt the very foundations of math.

What happened? We invented a theoretical number that had useful properties . Negatives aren’t something we can touch or hold, but they describe certain relationships well (like debt). It was a useful fiction.

Rather than saying “I owe you 30” and reading words to see if I’m up or down, I can write “-30” and know it means I’m in the hole. If I earn money and pay my debts (-30 + 100 = 70), I can record the transaction easily. I have +70 afterwards, which means I’m in the clear.

The positive and negative signs automatically keep track of the direction — you don’t need a sentence to describe the impact of each transaction. Math became easier, more elegant. It didn’t matter if negatives were “tangible” — they had useful properties, and we used them until they became everyday items. Today you’d call someone obscene names if they didn’t “get” negatives.

But let’s not be smug about the struggle: negative numbers were a huge mental shift. Even Euler, the genius who discovered e and much more, didn’t understand negatives as we do today. They were considered “meaningless” results (he later made up for this in style).

It’s a testament to our mental potential that today’s children are expected to understand ideas that once confounded ancient mathematicians.

Enter Imaginary Numbers

Imaginary numbers have a similar story. We can solve equations like this all day long:

The answers are 3 and -3. But suppose some wiseguy puts in a teensy, tiny minus sign:

Uh oh. This question makes most people cringe the first time they see it. You want the square root of a number less than zero? That’s absurd! (Historically, there were real questions to answer, but I like to imagine a wiseguy.)

It seems crazy, just like negatives, zero, and irrationals (non-repeating numbers) must have seemed crazy at first. There’s no “real” meaning to this question, right?

Wrong. So-called “imaginary numbers” are as normal as every other number (or just as fake): they’re a tool to describe the world. In the same spirit of assuming -1, .3, and 0 “exist”, let’s assume some number i exists where:

That is, you multiply i by itself to get -1. What happens now?

Well, first we get a headache. But playing the “Let’s pretend i exists” game actually makes math easier and more elegant. New relationships emerge that we can describe with ease.

You may not believe in i , just like those fuddy old mathematicians didn’t believe in -1. New, brain-twisting concepts are hard and they don’t make sense immediately, even for Euler. But as the negatives showed us, strange concepts can still be useful.

I dislike the term “imaginary number” — it was considered an insult, a slur, designed to hurt i ‘s feelings. The number i is just as normal as other numbers, but the name “imaginary” stuck so we’ll use it.

Visual Understanding of Negative and Complex Numbers

As we saw last time , the equation $x^2 = 9$ really means:

What transformation x, when applied twice, turns 1 to 9?

The two answers are “x = 3” and “x = -3”: That is, you can “scale by” 3 or “scale by 3 and flip” (flipping or taking the opposite is one interpretation of multiplying by a negative).

Now let’s think about $x^2 = -1$, which is really

What transformation x, when applied twice, turns 1 into -1? Hrm.

• We can’t multiply by a positive twice, because the result stays positive
• We can’t multiply by a negative twice, because the result will flip back to positive on the second multiplication

But what about… a rotation ! It sounds crazy, but if we imagine x being a “rotation of 90 degrees”, then applying x twice will be a 180 degree rotation, or a flip from 1 to -1!

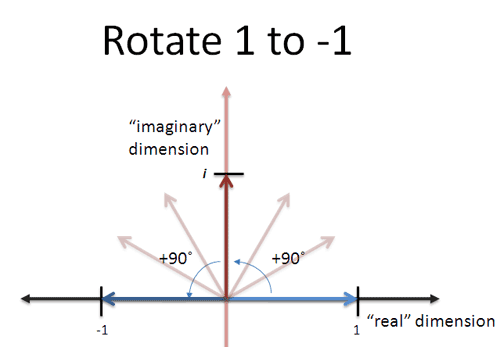
Yowza! And if we think about it more, we could rotate twice in the other direction (clockwise) to turn 1 into -1. This is “negative” rotation or a multiplication by -i:

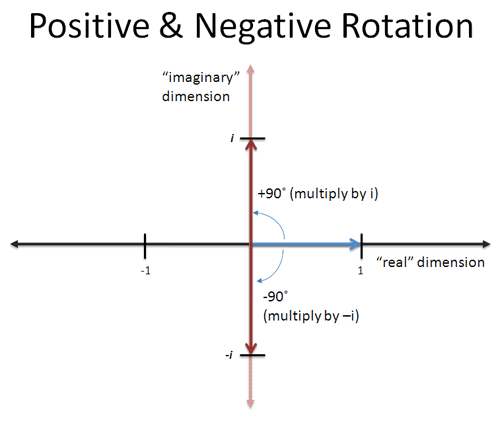
If we multiply by -i twice, the first multiplication would turn 1 into -i, and the second turns -i into -1. So there’s really two square roots of -1: i and -i .

This is pretty cool. We have some sort of answer, but what does it mean?

• i is a “new imaginary dimension” to measure a number
• i (or -i ) is what numbers “become” when rotated
• Multiplying i is a rotation by 90 degrees counter-clockwise
• Multiplying by -i is a rotation of 90 degrees clockwise
• Two rotations in either direction is -1: it brings us back into the “regular” dimensions of positive and negative numbers.

Numbers are 2-dimensional. Yes, it’s mind bending, just like decimals or long division would be mind-bending to an ancient Roman. ( What do you mean there’s a number between 1 and 2? ). It’s a strange, new way to think about math.

We asked “How do we turn 1 into -1 in two steps?” and found an answer: rotate it 90 degrees. It’s a strange, new way to think about math. But it’s useful. (By the way, this geometric interpretation of complex numbers didn’t arrive until decades after i was discovered).

Also, keep in mind that having counter-clockwise be positive is a human convention — it easily could have been the other way.

Finding Patterns

Let’s dive into the details a bit. When multiplying negative numbers (like -1), you get a pattern:

• 1, -1, 1, -1, 1, -1, 1, -1

Since -1 doesn’t change the size of a number, just the sign, you flip back and forth. For some number “x”, you’d get:

• x, -x, x, -x, x, -x…

This idea is useful. The number “x” can represent a good or bad hair week. Suppose weeks alternate between good and bad; this is a good week; what will it be like in 47 weeks?

So -x means a bad hair week. Notice how negative numbers “keep track of the sign”: we can throw $(-1)^{47}$ into a calculator without having to count (” Week 1 is good, week 2 is bad… week 3 is good… “). Things that flip back and forth can be modeled well with negative numbers.

Ok. Now what happens if we keep multiplying by $i$?

Very funny. Let’s reduce this a bit:

• $1 = 1$ (No questions here)
• $i = i$ (Can’t do much)
• $i^2 = -1$ (That’s what i is all about)
• $i^3 = (i \cdot i) \cdot i = -1 \cdot i = -i$ (Ah, 3 rotations counter-clockwise = 1 rotation clockwise. Neat.)
• $i^4 = (i \cdot i) \cdot (i \cdot i) = -1 \cdot -1 = 1$ (4 rotations bring us “full circle”)
• $i^5 = i^4 \cdot i = 1 \cdot i = i$ (Here we go again…)

Represented visually:

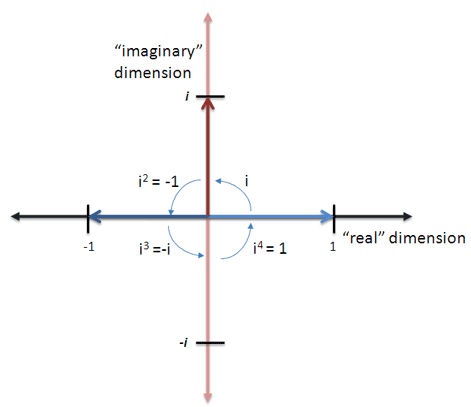
We cycle every 4th rotation. This makes sense, right? Any kid can tell you that 4 left turns is the same as no turns at all. Now rather than focusing on imaginary numbers ($i$, $i^2$), look at the general pattern:

• X, Y, -X, -Y, X, Y, -X, -Y…

Like negative numbers modeling flipping, imaginary numbers can model anything that rotates between two dimensions “X” and “Y”. Or anything with a cyclic, circular relationship — have anything in mind?

‘Cos it’d be a sin if you didn’t. There’ll de Moivre be more in future articles. [Editor’s note: Kalid is in electroshock therapy to treat his pun addiction.]

Understanding Complex Numbers

There’s another detail to cover: can a number be both “real” and “imaginary”?

You bet. Who says we have to rotate the entire 90 degrees? If we keep 1 foot in the “real” dimension and another in the imaginary one, it looks like this:

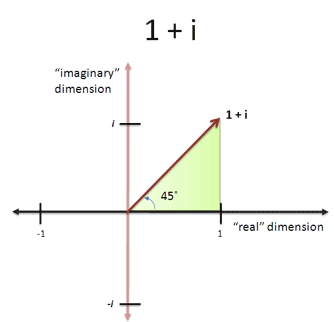
We’re at a 45 degree angle, with equal parts in the real and imaginary (1 + i). It’s like a hotdog with both mustard and ketchup — who says you need to choose?

In fact, we can pick any combination of real and imaginary numbers and make a triangle. The angle becomes the “angle of rotation”. A complex number is the fancy name for numbers with both real and imaginary parts. They’re written a + bi, where

• a is the real part
• b is the imaginary part

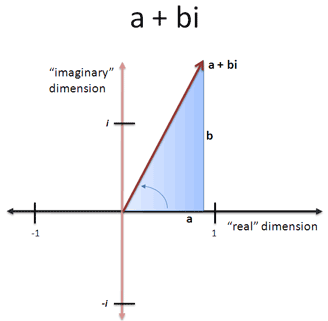
Not too bad. But there’s one last question: how “big” is a complex number? We can’t measure the real part or imaginary parts in isolation, because that would miss the big picture.

Let’s step back. The size of a negative number is not whether you can count it — it’s the distance from zero. In the case of negatives this is:

Which is another way to find the absolute value. But for complex numbers, how do we measure two components at 90 degree angles?

It’s a bird… it’s a plane… it’s Pythagoras!

Geez, his theorem shows up everywhere , even in numbers invented 2000 years after his time. Yes, we are making a triangle of sorts, and the hypotenuse is the distance from zero:

Neat. While measuring the size isn’t as easy as “dropping the negative sign”, complex numbers do have their uses. Let’s take a look.

A Real Example: Rotations

We’re not going to wait until college physics to use imaginary numbers. Let’s try them out today. There’s much more to say about complex multiplication, but keep this in mind:

• Multiplying by a complex number rotates by its angle

Let’s take a look. Suppose I’m on a boat, with a heading of 3 units East for every 4 units North. I want to change my heading 45 degrees counter-clockwise. What’s the new heading?

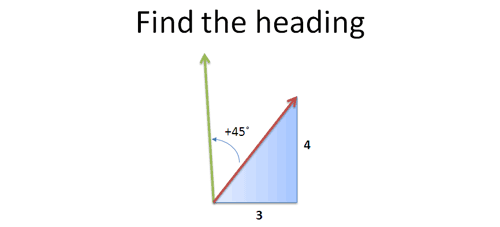
Some hotshot will say “ That’s simple! Just take the sine, cosine, gobbledegook by the tangent… fluxsom the foobar… and… “. Crack . Sorry, did I break your calculator? Care to answer that question again?

Let’s try a simpler approach: we’re on a heading of 3 + 4i (whatever that angle is; we don’t really care), and want to rotate by 45 degrees. Well, 45 degrees is 1 + i (perfect diagonal), so we can multiply by that amount!

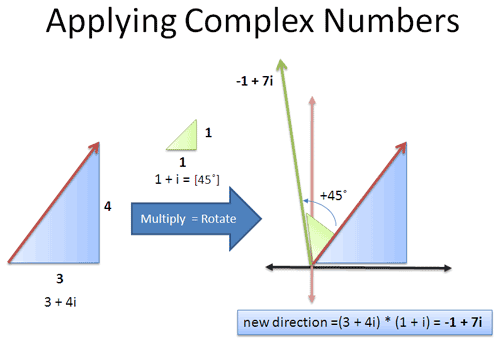
Here’s the idea:

• Original heading: 3 units East, 4 units North = 3 + 4i
• Rotate counter-clockwise by 45 degrees = multiply by 1 + i. ( Here's why multiplication, not addition, performs the rotation.)

If we multiply them together we get:

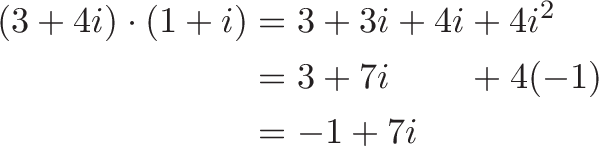
So our new orientation is 1 unit West (-1 East), and 7 units North, which you could draw out and follow.

But yowza! We found that out in 10 seconds, without touching sine or cosine. There were no vectors, matrices, or keeping track what quadrant we are in. It was just arithmetic with a touch of algebra to cross-multiply. Imaginary numbers have the rotation rules baked in: it just works.

Even better, the result is useful. We have a heading (-1, 7) instead of an angle (atan(7/-1) = 98.13, keeping in mind we’re in quadrant 2). How, exactly, were you planning on drawing and following that angle? With the protractor you keep around?

No, you’d convert it into cosine and sine (-.14 and .99), find a reasonable ratio between them (about 1 to 7), and sketch out the triangle. Complex numbers beat you to it, instantly, accurately, and without a calculator.

If you’re like me, you’ll find this use mind-blowing. And if you don’t, well, I’m afraid math doesn’t toot your horn. Sorry.

Trigonometry is great, but complex numbers can make ugly calculations simple (like calculating cosine(a+b) ). This is just a preview; later articles will give you the full meal.

Aside: Some people think “Hey, it’s not useful to have North/East headings instead of a degree angle to follow!”

Really? Ok, look at your right hand. What’s the angle from the bottom of your pinky to the top of your index finger? Good luck figuring that out on your own.

With a heading, you can at least say “Oh, it’s X inches across and Y inches up” and have some chance of working with that bearing.

Complex Numbers Aren’t

That was a whirlwind tour of my basic insights. Take a look at the first chart — it should make sense now.

There’s so much more to these beautiful, zany numbers, but my brain is tired. My goals were simple:

• Convince you that complex numbers were considered “crazy” but can be useful (just like negative numbers were)
• Show how complex numbers can make certain problems easier, like rotations

If I seem hot and bothered about this topic, there’s a reason. Imaginary numbers have been a bee in my bonnet for years — the lack of an intuitive insight frustrated me.

Now that I’ve finally had insights, I’m bursting to share them. But it frustrates me that you’re reading this on the blog of a wild-eyed lunatic, and not in a classroom. We suffocate our questions and “chug through” — because we don’t search for and share clean, intuitive insights. Egad.

But better to light a candle than curse the darkness: here’s my thoughts, and one of you will shine a spotlight. Thinking we’ve “figured out” a topic like numbers is what keeps us in Roman Numeral land.

There’s much more complex numbers: check out the details of complex arithmetic . Happy math.

Epilogue: But they’re still strange!

I know, they’re still strange to me too. I try to put myself in the mind of the first person to discover zero.

Zero is such a weird idea, having “something” represent “nothing”, and it eluded the Romans. Complex numbers are similar — it’s a new way of thinking. But both zero and complex numbers make math much easier. If we never adopted strange, new number systems, we’d still be counting on our fingers.

I repeat this analogy because it’s so easy to start thinking that complex numbers aren’t “normal”. Let’s keep our mind open: in the future they’ll chuckle that complex numbers were once distrusted, even until the 2000’s.

Carl Gauss, the famous mathematician, wrote :

"Hätte man +1, -1, √-1 nicht positiv, negative, imaginäre (oder gar ummögliche) Einheit, sondern etwa directe, inverse, laterale Einheit gennant, so hätte von einer solchen Dunklelheit kaum die Rede sein können." "If +1, -1, √-1 had not been called a positive, negative, imaginary (or even impossible) unit, but rather a direct, inverse, lateral unit, then there could hardly have been any talk of such obscurity."

If you want more nitty-gritty, check out wikipedia , the Dr. Math discussion , or another argument on why imaginary numbers exist .

Other Posts In This Series

• Intuitive Arithmetic With Complex Numbers
• Understanding Why Complex Multiplication Works
• Intuitive Guide to Angles, Degrees and Radians
• Intuitive Understanding Of Euler's Formula
• An Interactive Guide To The Fourier Transform
• Intuitive Guide to Convolution
• Intuitive Understanding of Sine Waves
• An Intuitive Guide to Linear Algebra
• A Programmer's Intuition for Matrix Multiplication
• Imaginary Multiplication vs. Imaginary Exponents
• Intuitive Guide to Hyperbolic Functions

Topic Reference

Imaginary number.

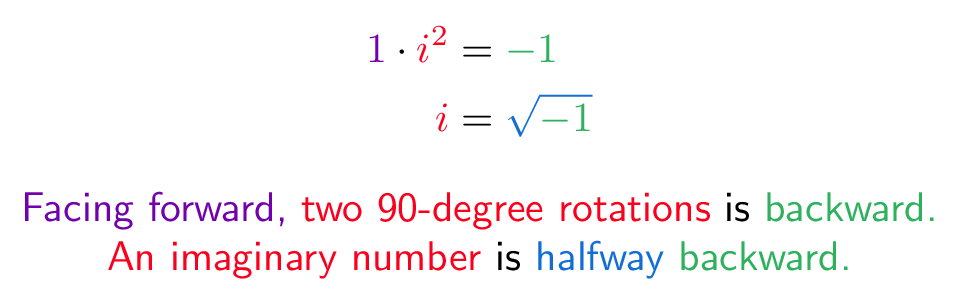
Join 450k Monthly Readers

• Reviews / Why join our community?
• For companies
• Frequently asked questions

Visual Representation

What is visual representation.

Visual Representation refers to the principles by which markings on a surface are made and interpreted. Designers use representations like typography and illustrations to communicate information, emotions and concepts. Color, imagery, typography and layout are crucial in this communication.

Alan Blackwell, cognition scientist and professor, gives a brief introduction to visual representation:

• Transcript loading…

We can see visual representation throughout human history, from cave drawings to data visualization :

Art uses visual representation to express emotions and abstract ideas.

Financial forecasting graphs condense data and research into a more straightforward format.

Icons on user interfaces (UI) represent different actions users can take.

The color of a notification indicates its nature and meaning.

Van Gogh's "The Starry Night" uses visuals to evoke deep emotions, representing an abstract, dreamy night sky. It exemplifies how art can communicate complex feelings and ideas.

© Public domain

Importance of Visual Representation in Design

Designers use visual representation for internal and external use throughout the design process . For example:

Storyboards are illustrations that outline users’ actions and where they perform them.

Sitemaps are diagrams that show the hierarchy and navigation structure of a website.

Wireframes are sketches that bring together elements of a user interface's structure.

Usability reports use graphs and charts to communicate data gathered from usability testing.

User interfaces visually represent information contained in applications and computerized devices.

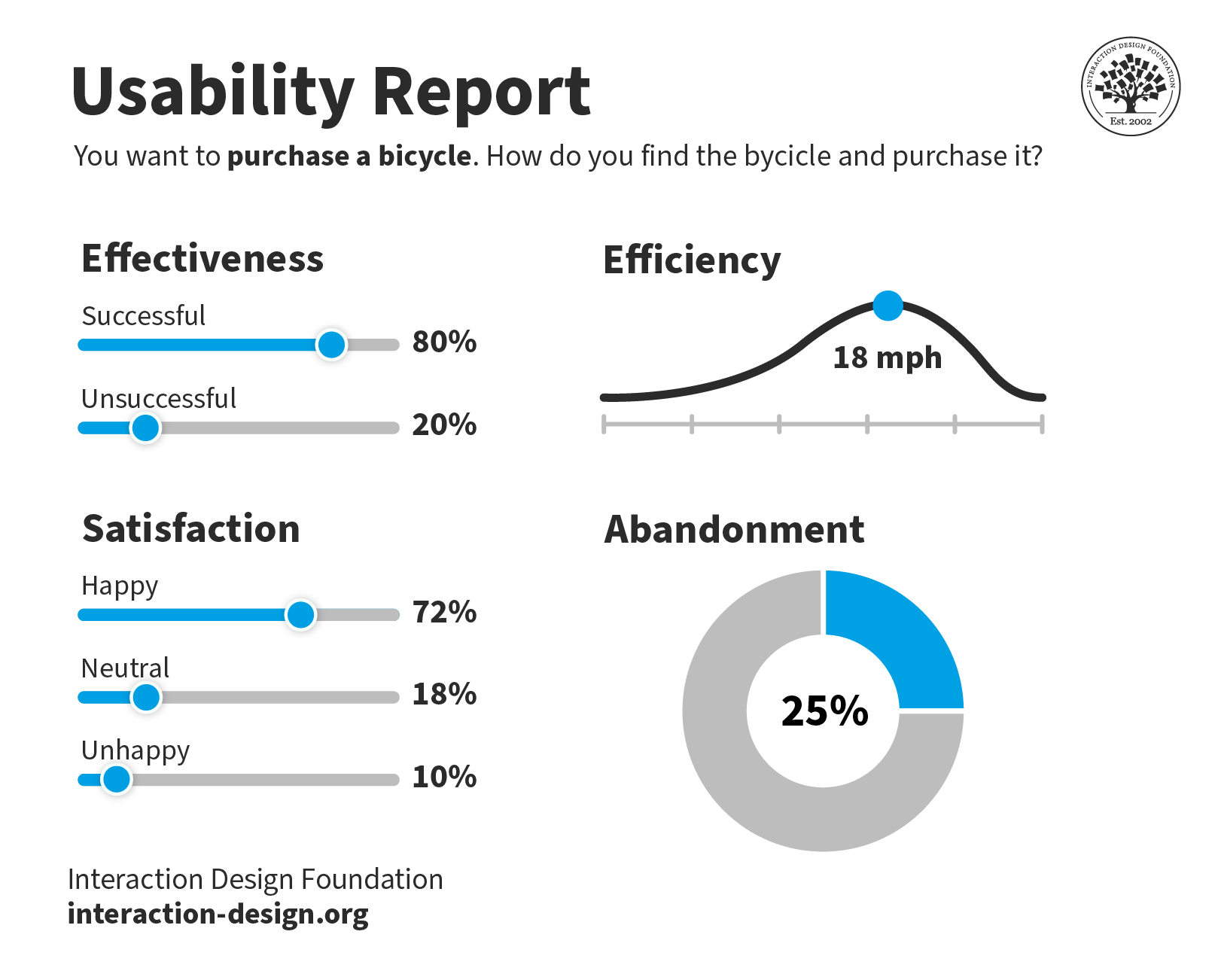
This usability report is straightforward to understand. Yet, the data behind the visualizations could come from thousands of answered surveys.

© Interaction Design Foundation, CC BY-SA 4.0

Visual representation simplifies complex ideas and data and makes them easy to understand. Without these visual aids, designers would struggle to communicate their ideas, findings and products . For example, it would be easier to create a mockup of an e-commerce website interface than to describe it with words.

Visual representation simplifies the communication of designs. Without mockups, it would be difficult for developers to reproduce designs using words alone.

Types of Visual Representation

Below are some of the most common forms of visual representation designers use.

Text and Typography

Text represents language and ideas through written characters and symbols. Readers visually perceive and interpret these characters. Typography turns text into a visual form, influencing its perception and interpretation.

We have developed the conventions of typography over centuries , for example, in documents, newspapers and magazines. These conventions include:

Text arranged on a grid brings clarity and structure. Gridded text makes complex information easier to navigate and understand. Tables, columns and other formats help organize content logically and enhance readability.

Contrasting text sizes create a visual hierarchy and draw attention to critical areas. For example, headings use larger text while body copy uses smaller text. This contrast helps readers distinguish between primary and secondary information.

Adequate spacing and paragraphing improve the readability and appearance of the text. These conventions prevent the content from appearing cluttered. Spacing and paragraphing make it easier for the eye to follow and for the brain to process the information.

Balanced image-to-text ratios create engaging layouts. Images break the monotony of text, provide visual relief and illustrate or emphasize points made in the text. A well-planned ratio ensures neither text nor images overwhelm each other. Effective ratios make designs more effective and appealing.

Designers use these conventions because people are familiar with them and better understand text presented in this manner.

This table of funerals from the plague in London in 1665 uses typographic conventions still used today. For example, the author arranged the information in a table and used contrasting text styling to highlight information in the header.

Illustrations and Drawings

Designers use illustrations and drawings independently or alongside text. An example of illustration used to communicate information is the assembly instructions created by furniture retailer IKEA. If IKEA used text instead of illustrations in their instructions, people would find it harder to assemble the furniture.

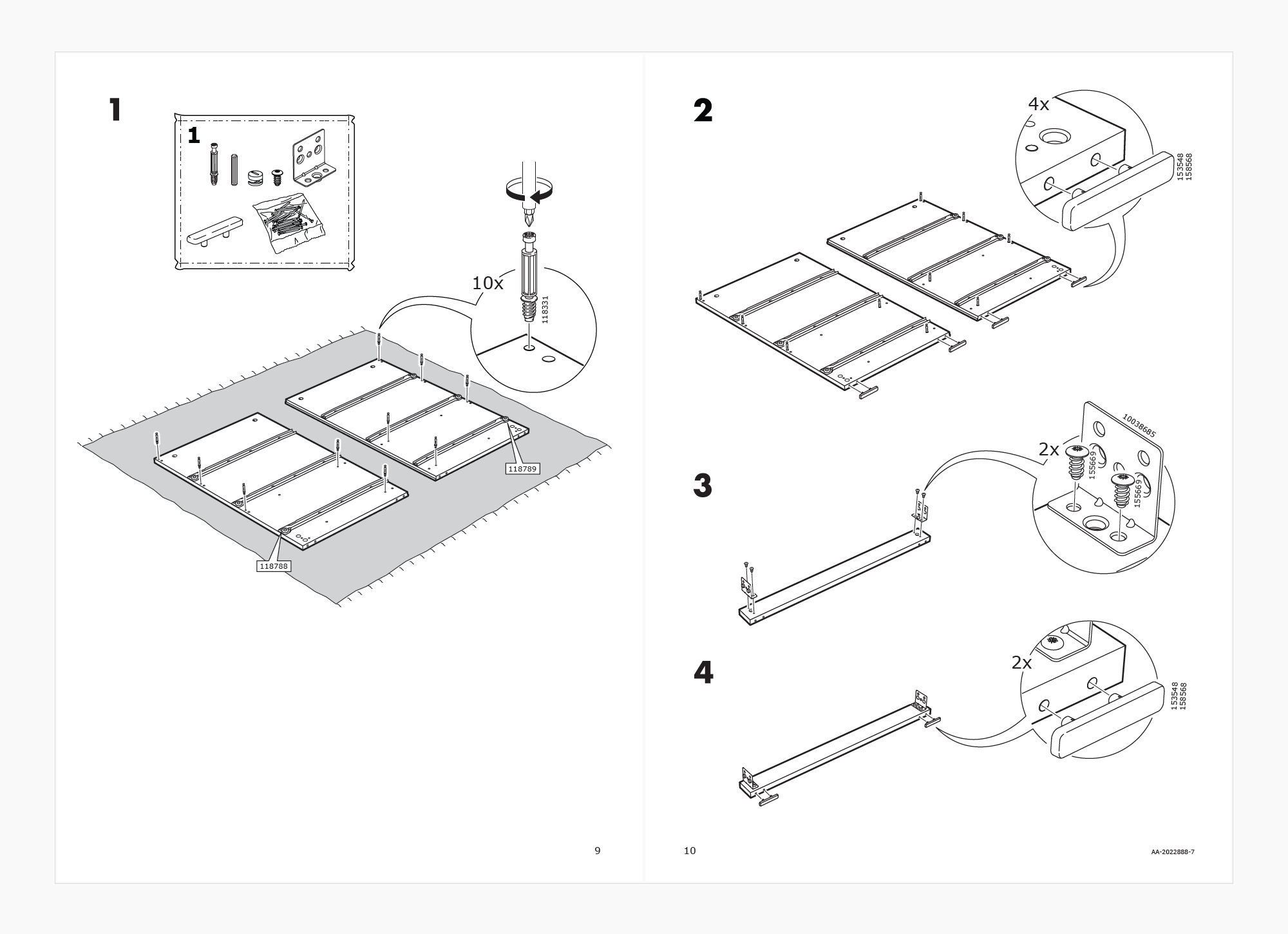
IKEA assembly instructions use illustrations to inform customers how to build their furniture. The only text used is numeric to denote step and part numbers. IKEA communicates this information visually to: 1. Enable simple communication, 2. Ensure their instructions are easy to follow, regardless of the customer’s language.

© IKEA, Fair use

Illustrations and drawings can often convey the core message of a visual representation more effectively than a photograph. They focus on the core message , while a photograph might distract a viewer with additional details (such as who this person is, where they are from, etc.)

For example, in IKEA’s case, photographing a person building a piece of furniture might be complicated. Further, photographs may not be easy to understand in a black-and-white print, leading to higher printing costs. To be useful, the pictures would also need to be larger and would occupy more space on a printed manual, further adding to the costs.

But imagine a girl winking—this is something we can easily photograph. 

Ivan Sutherland, creator of the first graphical user interface, used his computer program Sketchpad to draw a winking girl. While not realistic, Sutherland's representation effectively portrays a winking girl. The drawing's abstract, generic elements contrast with the distinct winking eye. The graphical conventions of lines and shapes represent the eyes and mouth. The simplicity of the drawing does not draw attention away from the winking.

A photo might distract from the focused message compared to Sutherland's representation. In the photo, the other aspects of the image (i.e., the particular person) distract the viewer from this message.

© Ivan Sutherland, CC BY-SA 3.0 and Amina Filkins, Pexels License

Information and Data Visualization

Designers and other stakeholders use data and information visualization across many industries.

Data visualization uses charts and graphs to show raw data in a graphic form. Information visualization goes further, including more context and complex data sets. Information visualization often uses interactive elements to share a deeper understanding.

For example, most computerized devices have a battery level indicator. This is a type of data visualization. IV takes this further by allowing you to click on the battery indicator for further insights. These insights may include the apps that use the most battery and the last time you charged your device.

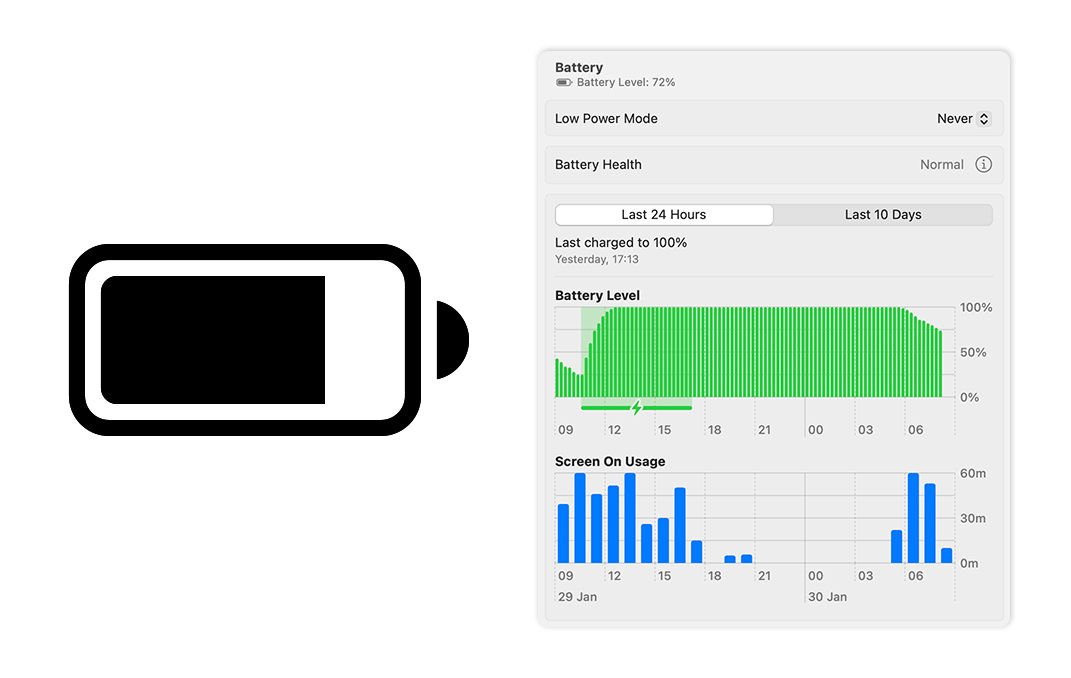
macOS displays a battery icon in the menu bar that visualizes your device’s battery level. This is an example of data visualization. Meanwhile, macOS’s settings tell you battery level over time, screen-on-usage and when you last charged your device. These insights are actionable; users may notice their battery drains at a specific time. This is an example of information visualization.

© Low Battery by Jemis Mali, CC BY-NC-ND 4.0, and Apple, Fair use

Information visualization is not exclusive to numeric data. It encompasses representations like diagrams and maps. For example, Google Maps collates various types of data and information into one interface:

Data Representation: Google Maps transforms complex geographical data into an easily understandable and navigable visual map.

Interactivity: Users can interactively customize views that show traffic, satellite imagery and more in real-time.

Layered Information: Google Maps layers multiple data types (e.g., traffic, weather) over geographical maps for comprehensive visualization.

User-Centered Design : The interface is intuitive and user-friendly, with symbols and colors for straightforward data interpretation.

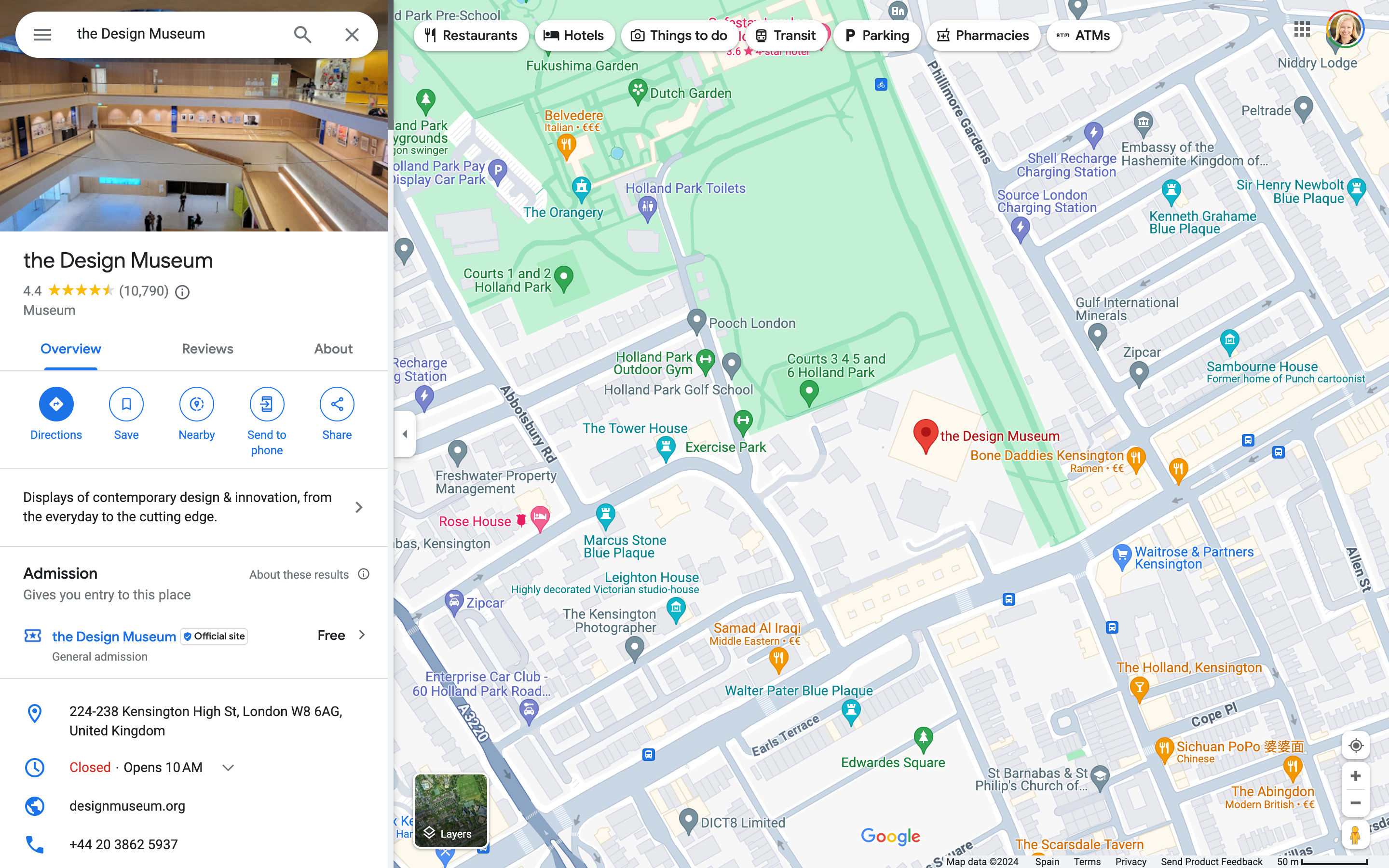
The volume of data contained in one screenshot of Google Maps is massive. However, this information is presented clearly to the user. Google Maps highlights different terrains with colors and local places and businesses with icons and colors. The panel on the left lists the selected location’s profile, which includes an image, rating and contact information.

© Google, Fair use

Symbolic Correspondence

Symbolic correspondence uses universally recognized symbols and signs to convey specific meanings . This method employs widely recognized visual cues for immediate understanding. Symbolic correspondence removes the need for textual explanation.

For instance, a magnifying glass icon in UI design signifies the search function. Similarly, in environmental design, symbols for restrooms, parking and amenities guide visitors effectively.

The Interaction Design Foundation (IxDF) website uses the universal magnifying glass symbol to signify the search function. Similarly, the play icon draws attention to a link to watch a video.

How Designers Create Visual Representations

Visual language.

Designers use elements like color , shape and texture to create a communicative visual experience. Designers use these 8 principles:

Size – Larger elements tend to capture users' attention readily.

Color – Users are typically drawn to bright colors over muted shades.

Contrast – Colors with stark contrasts catch the eye more effectively.

Alignment – Unaligned elements are more noticeable than those aligned ones.

Repetition – Similar styles repeated imply a relationship in content.

Proximity – Elements placed near each other appear to be connected.

Whitespace – Elements surrounded by ample space attract the eye.

Texture and Style – Users often notice richer textures before flat designs.

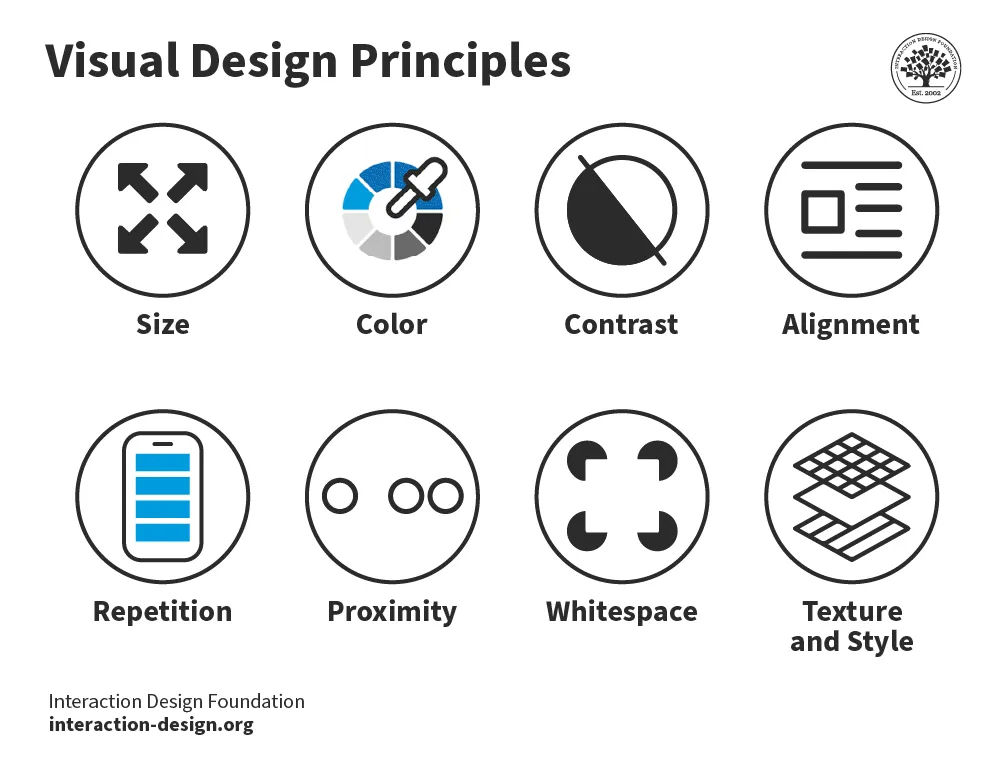
The 8 visual design principles.

In web design , visual hierarchy uses color and repetition to direct the user's attention. Color choice is crucial as it creates contrast between different elements. Repetition helps to organize the design—it uses recurring elements to establish consistency and familiarity.

In this video, Alan Dix, Professor and Expert in Human-Computer Interaction, explains how visual alignment affects how we read and absorb information:

Correspondence Techniques

Designers use correspondence techniques to align visual elements with their conceptual meanings. These techniques include color coding, spatial arrangement and specific imagery. In information visualization, different colors can represent various data sets. This correspondence aids users in quickly identifying trends and relationships .

Color coding enables the stakeholder to see the relationship and trend between the two pie charts easily.

In user interface design, correspondence techniques link elements with meaning. An example is color-coding notifications to state their nature. For instance, red for warnings and green for confirmation. These techniques are informative and intuitive and enhance the user experience.

The IxDF website uses blue for call-to-actions (CTAs) and red for warnings. These colors inform the user of the nature of the action of buttons and other interactive elements.

Perception and Interpretation

If visual language is how designers create representations, then visual perception and interpretation are how users receive those representations. Consider a painting—the viewer’s eyes take in colors, shapes and lines, and the brain perceives these visual elements as a painting.

In this video, Alan Dix explains how the interplay of sensation, perception and culture is crucial to understanding visual experiences in design:

Copyright holder: Michael Murphy _ Appearance time: 07:19 - 07:37 _ Link: https://www.youtube.com/watch?v=C67JuZnBBDc

Visual perception principles are essential for creating compelling, engaging visual representations. For example, Gestalt principles explain how we perceive visual information. These rules describe how we group similar items, spot patterns and simplify complex images. Designers apply Gestalt principles to arrange content on websites and other interfaces. This application creates visually appealing and easily understood designs.

In this video, design expert and teacher Mia Cinelli discusses the significance of Gestalt principles in visual design . She introduces fundamental principles, like figure/ground relationships, similarity and proximity.

Interpretation

Everyone's experiences, culture and physical abilities dictate how they interpret visual representations. For this reason, designers carefully consider how users interpret their visual representations. They employ user research and testing to ensure their designs are attractive and functional.

Leonardo da Vinci's "Mona Lisa", is one of the most famous paintings in the world. The piece is renowned for its subject's enigmatic expression. Some interpret her smile as content and serene, while others see it as sad or mischievous. Not everyone interprets this visual representation in the same way.

Color is an excellent example of how one person, compared to another, may interpret a visual element. Take the color red:

In Chinese culture, red symbolizes luck, while in some parts of Africa, it can mean death or illness.

A personal experience may mean a user has a negative or positive connotation with red.

People with protanopia and deuteranopia color blindness cannot distinguish between red and green.

In this video, Joann and Arielle Eckstut, leading color consultants and authors, explain how many factors influence how we perceive and interpret color:

Learn More about Visual Representation

Read Alan Blackwell’s chapter on visual representation from The Encyclopedia of Human-Computer Interaction.

Learn about the F-Shaped Pattern For Reading Web Content from Jakob Nielsen.

Read Smashing Magazine’s article, Visual Design Language: The Building Blocks Of Design .

Take the IxDF’s course, Perception and Memory in HCI and UX .

Questions related to Visual Representation

Some highly cited research on visual representation and related topics includes:

Roland, P. E., & Gulyás, B. (1994). Visual imagery and visual representation. Trends in Neurosciences, 17(7), 281-287. Roland and Gulyás' study explores how the brain creates visual imagination. They look at whether imagining things like objects and scenes uses the same parts of the brain as seeing them does. Their research shows the brain uses certain areas specifically for imagination. These areas are different from the areas used for seeing. This research is essential for understanding how our brain works with vision.

Lurie, N. H., & Mason, C. H. (2007). Visual Representation: Implications for Decision Making. Journal of Marketing, 71(1), 160-177.

This article looks at how visualization tools help in understanding complicated marketing data. It discusses how these tools affect decision-making in marketing. The article gives a detailed method to assess the impact of visuals on the study and combination of vast quantities of marketing data. It explores the benefits and possible biases visuals can bring to marketing choices. These factors make the article an essential resource for researchers and marketing experts. The article suggests using visual tools and detailed analysis together for the best results.

Lohse, G. L., Biolsi, K., Walker, N., & Rueter, H. H. (1994, December). A classification of visual representations. Communications of the ACM, 37(12), 36+.

This publication looks at how visuals help communicate and make information easier to understand. It divides these visuals into six types: graphs, tables, maps, diagrams, networks and icons. The article also looks at different ways these visuals share information effectively.

​​If you’d like to cite content from the IxDF website , click the ‘cite this article’ button near the top of your screen.

Some recommended books on visual representation and related topics include:

Chaplin, E. (1994). Sociology and Visual Representation (1st ed.) . Routledge.

Chaplin's book describes how visual art analysis has changed from ancient times to today. It shows how photography, post-modernism and feminism have changed how we see art. The book combines words and images in its analysis and looks into real-life social sciences studies.

Mitchell, W. J. T. (1994). Picture Theory. The University of Chicago Press.

Mitchell's book explores the important role and meaning of pictures in the late twentieth century. It discusses the change from focusing on language to focusing on images in cultural studies. The book deeply examines the interaction between images and text in different cultural forms like literature, art and media. This detailed study of how we see and read visual representations has become an essential reference for scholars and professionals.

Koffka, K. (1935). Principles of Gestalt Psychology. Harcourt, Brace & World.

"Principles of Gestalt Psychology" by Koffka, released in 1935, is a critical book in its field. It's known as a foundational work in Gestalt psychology, laying out the basic ideas of the theory and how they apply to how we see and think. Koffka's thorough study of Gestalt psychology's principles has profoundly influenced how we understand human perception. This book has been a significant reference in later research and writings.

A visual representation, like an infographic or chart, uses visual elements to show information or data. These types of visuals make complicated information easier to understand and more user-friendly.

Designers harness visual representations in design and communication. Infographics and charts, for instance, distill data for easier audience comprehension and retention.

For an introduction to designing basic information visualizations, take our course, Information Visualization .

Text is a crucial design and communication element, transforming language visually. Designers use font style, size, color and layout to convey emotions and messages effectively.

Designers utilize text for both literal communication and aesthetic enhancement. Their typography choices significantly impact design aesthetics, user experience and readability.

Designers should always consider text's visual impact in their designs. This consideration includes font choice, placement, color and interaction with other design elements.

In this video, design expert and teacher Mia Cinelli teaches how Gestalt principles apply to typography:

Designers use visual elements in projects to convey information, ideas, and messages. Designers use images, colors, shapes and typography for impactful designs.

In UI/UX design, visual representation is vital. Icons, buttons and colors provide contrast for intuitive, user-friendly website and app interfaces.

Graphic design leverages visual representation to create attention-grabbing marketing materials. Careful color, imagery and layout choices create an emotional connection.

Product design relies on visual representation for prototyping and idea presentation. Designers and stakeholders use visual representations to envision functional, aesthetically pleasing products.

Our brains process visuals 60,000 times faster than text. This fact highlights the crucial role of visual representation in design.

Our course, Visual Design: The Ultimate Guide , teaches you how to use visual design elements and principles in your work effectively.

Visual representation, crucial in UX, facilitates interaction, comprehension and emotion. It combines elements like images and typography for better interfaces.

Effective visuals guide users, highlight features and improve navigation. Icons and color schemes communicate functions and set interaction tones.

UX design research shows visual elements significantly impact emotions. 90% of brain-transmitted information is visual.

To create functional, accessible visuals, designers use color contrast and consistent iconography. These elements improve readability and inclusivity.

An excellent example of visual representation in UX is Apple's iOS interface. iOS combines a clean, minimalist design with intuitive navigation. As a result, the operating system is both visually appealing and user-friendly.

Michal Malewicz, Creative Director and CEO at Hype4, explains why visual skills are important in design:

Learn more about UI design from Michal in our Master Class, Beyond Interfaces: The UI Design Skills You Need to Know .

The fundamental principles of effective visual representation are:

Clarity : Designers convey messages clearly, avoiding clutter.

Simplicity : Embrace simple designs for ease and recall.

Emphasis : Designers highlight key elements distinctively.

Balance : Balance ensures design stability and structure.

Alignment : Designers enhance coherence through alignment.

Contrast : Use contrast for dynamic, distinct designs.

Repetition : Repeating elements unify and guide designs.

Designers practice these principles in their projects. They also analyze successful designs and seek feedback to improve their skills.

Read our topic description of Gestalt principles to learn more about creating effective visual designs. The Gestalt principles explain how humans group elements, recognize patterns and simplify object perception.

Color theory is vital in design, helping designers craft visually appealing and compelling works. Designers understand color interactions, psychological impacts and symbolism. These elements help designers enhance communication and guide attention.

Designers use complementary , analogous and triadic colors for contrast, harmony and balance. Understanding color temperature also plays a crucial role in design perception.

Color symbolism is crucial, as different colors can represent specific emotions and messages. For instance, blue can symbolize trust and calmness, while red can indicate energy and urgency.

Cultural variations significantly influence color perception and symbolism. Designers consider these differences to ensure their designs resonate with diverse audiences.

For actionable insights, designers should:

Experiment with color schemes for effective messaging. 

Assess colors' psychological impact on the audience. 

Use color contrast to highlight critical elements. 

Ensure color choices are accessible to all.

In this video, Joann and Arielle Eckstut, leading color consultants and authors, give their six tips for choosing color:

Learn more about color from Joann and Arielle in our Master Class, How To Use Color Theory To Enhance Your Designs .

Typography and font choice are crucial in design, impacting readability and mood. Designers utilize them for effective communication and expression.

Designers' perception of information varies with font type. Serif fonts can imply formality, while sans-serifs can give a more modern look.

Typography choices by designers influence readability and user experience. Well-spaced, distinct fonts enhance readability, whereas decorative fonts may hinder it.

Designers use typography to evoke emotions and set a design's tone. Choices in font size, style and color affect the emotional impact and message clarity.

Designers use typography to direct attention, create hierarchy and establish rhythm. These benefits help with brand recognition and consistency across mediums.

Read our article to learn how web fonts are critical to the online user experience .

Designers create a balance between simplicity and complexity in their work. They focus on the main messages and highlight important parts. Designers use the principles of visual hierarchy, like size, color and spacing. They also use empty space to make their designs clear and understandable.

The Gestalt law of Prägnanz suggests people naturally simplify complex images. This principle aids in making even intricate information accessible and engaging.

Through iteration and feedback, designers refine visuals. They remove extraneous elements and highlight vital information. Testing with the target audience ensures the design resonates and is comprehensible.

Michal Malewicz explains how to master hierarchy in UI design using the Gestalt rule of proximity:

Answer a Short Quiz to Earn a Gift

Why do designers use visual representation?

• To guarantee only a specific audience can understand the information
• To replace the need for any form of written communication
• To simplify complex information and make it understandable

Which type of visual representation helps to compare data?

• Article images
• Line charts
• Text paragraphs

What is the main purpose of visual hierarchy in design?

• To decorate the design with more colors
• To guide the viewer’s attention to the most important elements first
• To provide complex text for high-level readers

How does color impact visual representation?

• It has no impact on the design at all.
• It helps to distinguish different elements and set the mood.
• It makes the design less engaging for a serious mood.

Why is consistency important in visual representation?

• It limits creativity, but allows variation in design.
• It makes sure the visual elements are cohesive and easy to understand.
• It makes the design unpredictable yet interesting.

Better luck next time!

Do you want to improve your UX / UI Design skills? Join us now

Congratulations! You did amazing

You earned your gift with a perfect score! Let us send it to you.

Check Your Inbox

We’ve emailed your gift to [email protected] .

Literature on Visual Representation

Here’s the entire UX literature on Visual Representation by the Interaction Design Foundation, collated in one place:

Learn more about Visual Representation

Take a deep dive into Visual Representation with our course Perception and Memory in HCI and UX .

How does all of this fit with interaction design and user experience? The simple answer is that most of our understanding of human experience comes from our own experiences and just being ourselves. That might extend to people like us, but it gives us no real grasp of the whole range of human experience and abilities. By considering more closely how humans perceive and interact with our world, we can gain real insights into what designs will work for a broader audience: those younger or older than us, more or less capable, more or less skilled and so on.

“You can design for all the people some of the time, and some of the people all the time, but you cannot design for all the people all the time.“ – William Hudson (with apologies to Abraham Lincoln)

While “design for all of the people all of the time” is an impossible goal, understanding how the human machine operates is essential to getting ever closer. And of course, building solutions for people with a wide range of abilities, including those with accessibility issues, involves knowing how and why some human faculties fail. As our course tutor, Professor Alan Dix, points out, this is not only a moral duty but, in most countries, also a legal obligation.

Portfolio Project

In the “ Build Your Portfolio: Perception and Memory Project ”, you’ll find a series of practical exercises that will give you first-hand experience in applying what we’ll cover. If you want to complete these optional exercises, you’ll create a series of case studies for your portfolio which you can show your future employer or freelance customers.

This in-depth, video-based course is created with the amazing Alan Dix , the co-author of the internationally best-selling textbook  Human-Computer Interaction and a superstar in the field of Human-Computer Interaction . Alan is currently a professor and Director of the Computational Foundry at Swansea University.

Gain an Industry-Recognized UX Course Certificate

Use your industry-recognized Course Certificate on your resume , CV , LinkedIn profile or your website.

All open-source articles on Visual Representation

Data visualization for human perception.

The Key Elements & Principles of Visual Design

• 1.1k shares

Guidelines for Good Visual Information Representations

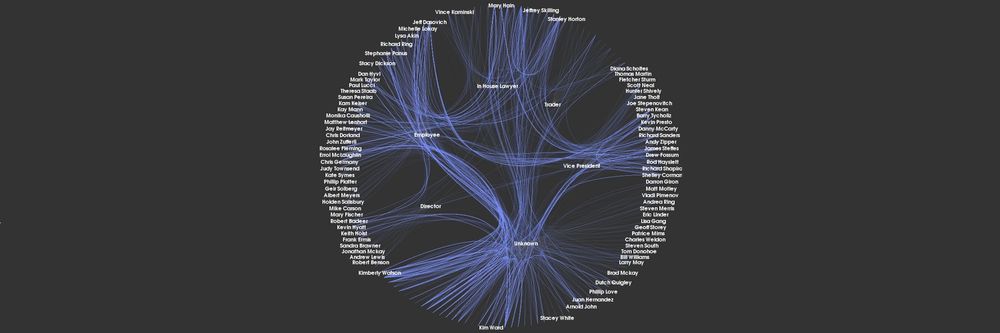
• 4 years ago

Philosophy of Interaction

Information visualization – an introduction to multivariate analysis.

• 8 years ago

Aesthetic Computing

How to represent linear data visually for information visualization.

• 5 years ago

Open Access—Link to us!

We believe in Open Access and the  democratization of knowledge . Unfortunately, world-class educational materials such as this page are normally hidden behind paywalls or in expensive textbooks.

If you want this to change , cite this page , link to us, or join us to help us democratize design knowledge !

Privacy Settings

Our digital services use necessary tracking technologies, including third-party cookies, for security, functionality, and to uphold user rights. Optional cookies offer enhanced features, and analytics.

Experience the full potential of our site that remembers your preferences and supports secure sign-in.

Governs the storage of data necessary for maintaining website security, user authentication, and fraud prevention mechanisms.

Enhanced Functionality

Saves your settings and preferences, like your location, for a more personalized experience.

Referral Program

We use cookies to enable our referral program, giving you and your friends discounts.

Error Reporting

We share user ID with Bugsnag and NewRelic to help us track errors and fix issues.

Optimize your experience by allowing us to monitor site usage. You’ll enjoy a smoother, more personalized journey without compromising your privacy.

Analytics Storage

Collects anonymous data on how you navigate and interact, helping us make informed improvements.

Differentiates real visitors from automated bots, ensuring accurate usage data and improving your website experience.

Lets us tailor your digital ads to match your interests, making them more relevant and useful to you.

Advertising Storage

Stores information for better-targeted advertising, enhancing your online ad experience.

Personalization Storage

Permits storing data to personalize content and ads across Google services based on user behavior, enhancing overall user experience.

Advertising Personalization

Allows for content and ad personalization across Google services based on user behavior. This consent enhances user experiences.

Enables personalizing ads based on user data and interactions, allowing for more relevant advertising experiences across Google services.

Receive more relevant advertisements by sharing your interests and behavior with our trusted advertising partners.

Enables better ad targeting and measurement on Meta platforms, making ads you see more relevant.

Allows for improved ad effectiveness and measurement through Meta’s Conversions API, ensuring privacy-compliant data sharing.

LinkedIn Insights

Tracks conversions, retargeting, and web analytics for LinkedIn ad campaigns, enhancing ad relevance and performance.

LinkedIn CAPI

Enhances LinkedIn advertising through server-side event tracking, offering more accurate measurement and personalization.

Google Ads Tag

Tracks ad performance and user engagement, helping deliver ads that are most useful to you.

Share Knowledge, Get Respect!

or copy link

Cite according to academic standards

Simply copy and paste the text below into your bibliographic reference list, onto your blog, or anywhere else. You can also just hyperlink to this page.

New to UX Design? We’re Giving You a Free ebook!

Download our free ebook The Basics of User Experience Design to learn about core concepts of UX design.

In 9 chapters, we’ll cover: conducting user interviews, design thinking, interaction design, mobile UX design, usability, UX research, and many more!

• Summer Math Camps Information
• Camp Applications for Students
• Teacher Recommendation Form
• Dorm Information and Form Information
• Make a Payment
• Camp-in-a-Box
• Mathworks Fellows Application
• Employment Response Form
• Teacher Professional Development Information
• Teacher Professional Development Application
• Professional Development Payment Portal
• MMC Information
• Registration - Mathworks Math Contest
• Previous MMC Tests
• PMWC Team Photos
• Photos From Past Trips
• Previous PMWC Tests
• Mathworks Guiding Principles
• Learn more about Math Explorations
• Math Explorations samples
• Order Math Explorations
• Additional resources for teachers
• Additional resources for students
• Donate to Mathworks
• Employment Opportunities
• COPPA Privacy Statement
• Alumni Stories
• Executive Summary (Annual Report)
• Organizational Chart
• Publications
• Other Summer Math Camps
• News and Archives
• Why Is Mathworks Newsworthy?
• Research, Publications, and Presentations
• Current Students
• Faculty & Staff
• Family & Visitors

Number and Operations - Represent and use Real Numbers

Want to learn more about how to do these type of questions?

Check out Math Explorations , a series of middle school math textbooks aligned to the TEKS!

Click here to navigate back to all 8th grade math flashcards.

(2)  Number and operations. The student applies mathematical process standards to represent and use real numbers in a variety of forms. The student is expected to:

(A)  extend previous knowledge of sets and subsets using a visual representation to describe relationships between sets of real numbers;

(B)  approximate the value of an irrational number, including π and square roots of numbers less than 225, and locate that rational number approximation on a number line;

(C)  convert between standard decimal notation and scientific notation; and

(D)  order a set of real numbers arising from mathematical and real-world contexts.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.2: Graphical Representation and Euler Relationship

• Last updated
• Save as PDF
• Page ID 106807

• Marcia Levitus
• Arizonia State University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Complex numbers can be represented graphically as a point in a coordinate plane. In cartesian coordinates, the \(x\)-axis is used for the real part of the number, and the \(y\)-axis is used for the imaginary component. For example, the complex number \(x+iy\) is represented as a point in Figure \(\PageIndex{1}\).

Complex numbers can be also represented in polar form. We know that, given a point \((x,y)\) in the plane, \(\cos\phi=x/r\) and \(\sin\phi=y/r\). Therefore, the complex number \(x+iy\) can be also represented as \(r\cos\phi+i r\sin\phi\).

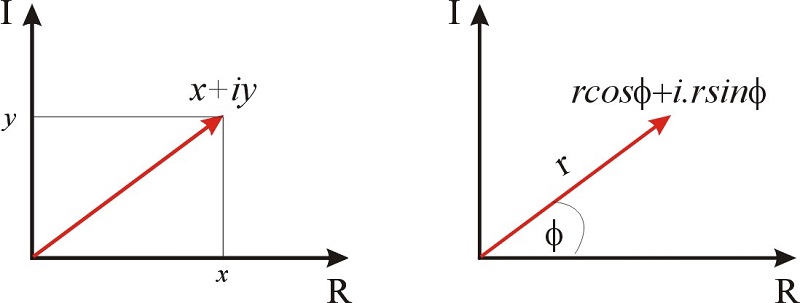
We can also represent complex numbers in terms of complex exponentials. This will sound weird for now, but we will see how common and useful this is in physical chemistry as we cover other topics this semester. The Euler relationship relates the trigonometric functions to a complex exponential:

\[\label{eq1} e^{\pm i\phi}=\cos\phi\pm i\sin\phi\]

We will prove this relationship using Taylor series later.

In summary, the complex number \(\displaystyle{\color{Maroon} x+iy}\) can be expressed in polar coordinates as \(\displaystyle{\color{Maroon}r\cos\phi+i r\sin\phi}\), and as a complex exponential as \(\displaystyle{\color{Maroon}r e^{i\phi}}\). The relationships between \(x,y\) and \(r,\phi\) are given by the familiar trigonometric relationships: \(x=r\cos\phi\) and \(y=r\sin\phi\). Notice that

\[r^2=x^2+y^2 \nonumber\]

\[\sin^2\phi+\cos^2\phi=1 \nonumber\]

as we know from Pythagoras’ theorem.

Example \(\PageIndex{1}\)

Express \(z= 1+i\) in the form \(r e^{i\phi}\)

\(x = 1\) and \(y=1\).

We know that

\(x=r\cos\phi\) and \(y=r\sin\phi\)

Dividing \(y/x\), we get \(y/x=\tan\phi\). In this problem \(y=x\), and therefore \(\pi/4\).

To obtain \(r\) we use \(r^2=x^2+y^2\). In this case:

\[x^2+y^2=2 \to r=\sqrt{2} \nonumber\]

Therefore, \(\displaystyle{\color{Maroon}z = \sqrt{2} e^{\frac{\pi}{4} i}}\)

From Equation \ref{eq1} we can see how the trigonometric functions can be expressed as complex exponentials:

\[ \begin{split} \cos\phi=\frac{e^{i \phi}+e^{-i \phi}}{2}\\ \sin\phi=\frac{e^{i \phi}-e^{-i \phi}}{2i} \end{split}\]

Again, this may look strange at this point, but it turns out that exponentials are much easier to manipulate than trigonometric functions (think about multiplying or dividing exponentials vs. trigonometric functions), so it is common that physical chemists write equations in terms of complex exponentials instead of cosines and sines.

In Equation \(2.1.1\) we saw that \((x+iy)(x-iy)=x^2+y^2\). Now we know that this equals \(r^2\), where \(r\) is the modulus or absolute value of the vector represented in red in Figure \(\PageIndex{1}\). Therefore, the modulus of a complex number, denoted as \(|z|\), can be calculated as:

\[\label{modulus} |z|^2= z z^* \to |z|=\sqrt{z z^*}\]

Example \(\PageIndex{2}\)

Obtain the modulus of the complex number \(z= 1+i\) (see Example \(\PageIndex{1}\))

\[|z|=\sqrt{z z^*}=\sqrt{(1+i)(1-i)}=\displaystyle{\color{Maroon}\sqrt{2}} \nonumber\]

external links

• Expressing a complex number in polar form I: http://www.youtube.com/watch?v=6z6fzPXUbSQs
• Expressing a complex number in polar form II: http://www.youtube.com/watch?v=tAIxdEVuTZ8
• Expressing a complex number in polar form III: http://www.youtube.com/watch?v=XIYDO_weAVA

• Personal Finance
• Today's Paper
• Partner Content
• Entertainment
• Social Viral
• Pro Kabaddi League

Sebi tweaks framework for price band formulation in derivatives segment

The regulator has enhanced the number of trades, unique client codes, and trading members for 'flexing' of price bands. flexing is changing the price band towards the direction of the trade.

Listen to This Article

Nandish shah of hdfc securities recommends bull spread on bank nifty, moth to a flame: why are retail traders inexorably drawn to derivatives, foreign exchange derivatives market in a fix before new rbi rules, samsung launches galaxy fit 3 fitness wearable in india at rs 4999: details, stock exchanges eye index derivatives with new stock additions in limbo, sebi action on fantasy games operating on real-time stock market data, aditya birla group's market capitalisation crosses $100 billion milestone, vodafone idea shares jump 7.5% on global broking firm ubs upgrade, sebi launches audio-visual representation of public issues' disclosures, adani ports to be included in sensex from june 24, wipro to be excluded.

Don't miss the most important news and views of the day. Get them on our Telegram channel

First Published: May 24 2024 | 9:32 PM IST

Explore News

• Suzlon Energy Share Price Adani Enterprises Share Price Adani Power Share Price IRFC Share Price Tata Motors Share Price Tata Steel Share Price Yes Bank Share Price Infosys Share Price SBI Share Price Tata Power Share Price
• Latest News Company News Market News India News Politics News Cricket News Personal Finance Technology News World News Industry News Education News Opinion Shows Economy News Lifestyle News Health News
• Today's Paper About Us T&C Privacy Policy Cookie Policy Disclaimer Investor Communication GST registration number List Compliance Contact Us Advertise with Us Sitemap Subscribe Careers BS Apps
• Budget 2024 Lok Sabha Election 2024 IPL 2024 Pro Kabaddi League IPL Points Table 2024 ICC T20 World Cup 2024 ICC T20 World Cup 2024 Schedule